Cross Entropy Method Based Hybridization of Dynamic Group Optimization Algorithm
Abstract
:1. Introduction
- The proposed algorithm aims at using CE to enhance the population diversity at local exploitation in DGO.
- It is interesting to set a new local optima avoiding mechanism to help DGO to strengthen the escape ability from premature convergence.
- To the best of our knowledge, the hybridization between these two methods has not been done before. It is an interesting approach to hybridize both methods in order to achieve better optimization performance.
2. Background
2.1. Cross Entropy Method
- Generate random samples from Gaussian distribution with mean mu and standard deviation s.
- Select a specific number of best samples from the whole samples.
- Update mu and s based on the best samples with better fitness.
| Algorithm 1: pseudo code of CE method |
| Initialize: mean mu, standard deviation s, size of population pop, the number of best samples np, terminal condition tmax |
| While t < tmax do |
| Generate sample vectors X as: |
| , where randn() produces a Gaussian distribution random number. |
| Evaluate xi |
| Select the np best samples from pop |
| Update the parameters mu, s |
| t = t + 1 |
| End |
2.2. Dynamic Group Optimization Algorithm (DGO)
3. Cross Entropy Dynamic Group Optimization (CEDGO)
| Algorithm 2: pseudo code of CEDGO method |
| Initialize: group numbers np, mean mu, standard deviation s, size of population pop, the number of best samples np, terminal condition tmax |
| Select group heads according to the fitness |
| While t < tmax do |
| Head moves by using levy flight (6). |
| Members moves by using CE operator (3). |
| Update the mu and s according the fitness. |
| Calculate the TtL |
| Group variation |
| Evaluate all population |
| Select new group heads |
| t = t + 1 |
| End |
3.1. Cross Entorpy Operator
3.2. Time-to-Live Mechnism (TtL)
- Rule (a)
- Each individual will only be graced a certain length of times to live when the animal shows inability to obtain any better food.
- Rule (b)
- The individual will die when the animal still yields no better food after the length of times to live are used up.
- Rule (c)
- The individual’s health condition stays the same as long as it finds better food.
- Rule (d)
- New individual is produced by obtaining three randomly selected heads’ information.
3.3. Complexity Analysis
4. Experimental Results
4.1. Effect of CEDGO
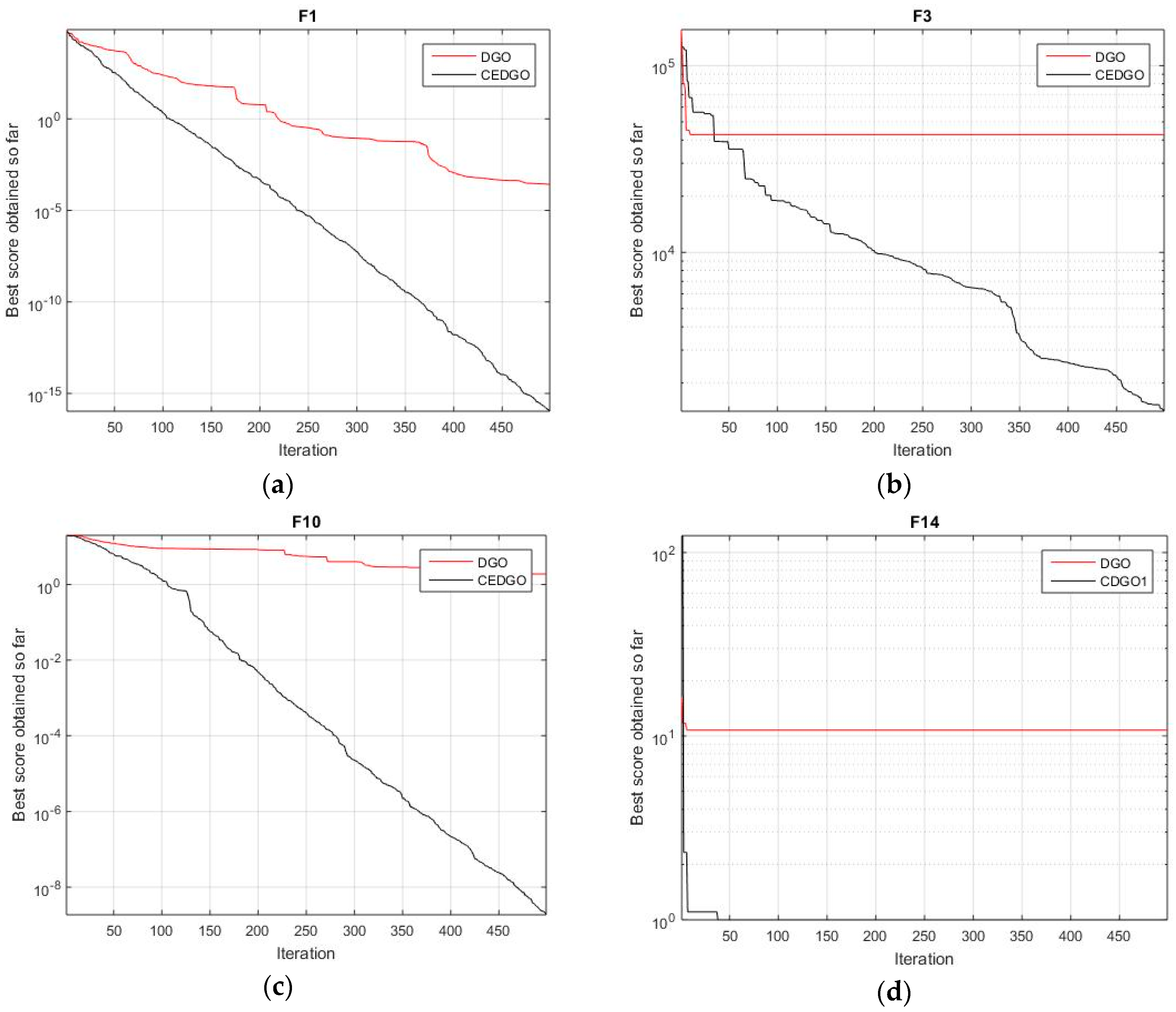
4.1.1. Unimodal Functions
4.1.2. Multimodal Functions
4.2. Comparison with the Latest Variant PSO Algorithms
4.3. Comparison with the Other Well-Known Evolutionary Algrotihms (EAs)
4.4. Scalability Study
4.5. Parameters Tuning Study
4.6. Comparision with DE Algrotihms
4.7. Algorithm Analysis and Disscusion
5. Conclusions
- Because the CE operator is employed into intragroup action, the capability of local search is enhanced.
- Because the original two mutation operators are removed, the diversity is increased.
- The TtL mechanism is set, the computation resource is saved compared to classical DGO.
- Due to the TtL, the capability of jumping out of local optimum is increased.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 760–766. [Google Scholar]
- Tang, R.; Fong, S.; Yang, X.-S.; Deb, S. Wolf search algorithm with ephemeral memory. In Proceedings of the 2012 IEEE Seventh International Conference on Digital Information Management (ICDIM), Macau, China, 22–24 August 2012; pp. 165–172. [Google Scholar]
- Tang, R.; Fong, S.; Deb, S.; Wong, R. Dynamic group search algorithm for solving an engineering problem. Oper. Res. 2017. [Google Scholar] [CrossRef]
- Tang, R.; Simon, F.; Suash, D.; Wong, R. Dynamic Group Search Algorithm. In Proceedings of the International Symposium on Computational and Business Intelligence, Olten, Switzerland, 5–7 September 2016. [Google Scholar] [CrossRef]
- Kwiecień, J.; Pasieka, M. Cockroach Swarm Optimization Algorithm for Travel Planning. Entropy 2017, 19, 213. [Google Scholar] [CrossRef]
- Hu, W.; Liang, H.; Peng, C.; Du, B.; Hu, Q. A hybrid chaos-particle swarm optimization algorithm for the vehicle routing problem with time window. Entropy 2013, 15, 1247–1270. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ji, G.; Yang, J.; Wu, J.; Wei, L. Fruit classification by wavelet-entropy and feedforward neural network trained by fitness-scaled chaotic ABC and biogeography-based optimization. Entropy 2015, 17, 5711–5728. [Google Scholar] [CrossRef]
- Xiao, Y.; Kang, N.; Hong, Y.; Zhang, G. Misalignment Fault Diagnosis of DFWT Based on IEMD Energy Entropy and PSO-SVM. Entropy 2017, 19, 6. [Google Scholar] [CrossRef]
- Song, Q.; Fong, S.; Tang, R. Self-Adaptive Wolf Search Algorithm. In Proceedings of the 2016 IEEE 5th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Kumamoto, Japan, 10–14 July 2016; pp. 576–582. [Google Scholar]
- Rubinstein, R. The cross-entropy method for combinatorial and continuous optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Kroese, D.P.; Porotsky, S.; Rubinstein, R.Y. The cross-entropy method for continuous multi-extremal optimization. Methodol. Comput. Appl. Probab. 2006, 8, 383–407. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, Levy flights and global optimization. In Research and Development in Intelligent Systems XXVI; Bramer, M., Ellis, R., Petridis, M., Eds.; Springer: London, UK, 2010; pp. 209–218. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 IEEE Congress on Evolutionary Computation (CEC), Portland, OR, USA, 19–23 June 2004; pp. 325–331. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A.; Sadiq, A.S. Autonomous particles groups for particle swarm optimization. Arab. J. Sci. Eng. 2014, 39, 4683–4697. [Google Scholar] [CrossRef]
- Cui, Z.; Zeng, J.; Yin, Y. An improved PSO with time-varying accelerator coefficients. In Proceedings of the 2008 IEEE Eighth International Conference on Intelligent Systems Design and Applications (ISDA), Kaohsiung, Taiwan, 26–28 November 2008; pp. 638–643. [Google Scholar]
- Bao, G.; Mao, K. Particle swarm optimization algorithm with asymmetric time varying acceleration coefficients. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 2134–2139. [Google Scholar]
- Tang, Z.; Zhang, D. A modified particle swarm optimization with an adaptive acceleration coefficients. In Proceedings of the 2009 IEEE Asia-Pacific Conference on Information Processing (APCIP), Shenzhen, China, 18–19 July 2009; pp. 330–332. [Google Scholar]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Cruz, C., González, J.R., Krasnogor, N., Pelta, D.A., Terrazas, G., Eds.; Springer: Berlin, Germany, 2010; pp. 65–74. [Google Scholar]
- Ünveren, A.; Acan, A. Multi-objective optimization with cross entropy method: Stochastic learning with clustered pareto fronts. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation (CEC), Singapore, 25–29 September 2007; pp. 3065–3071. [Google Scholar]
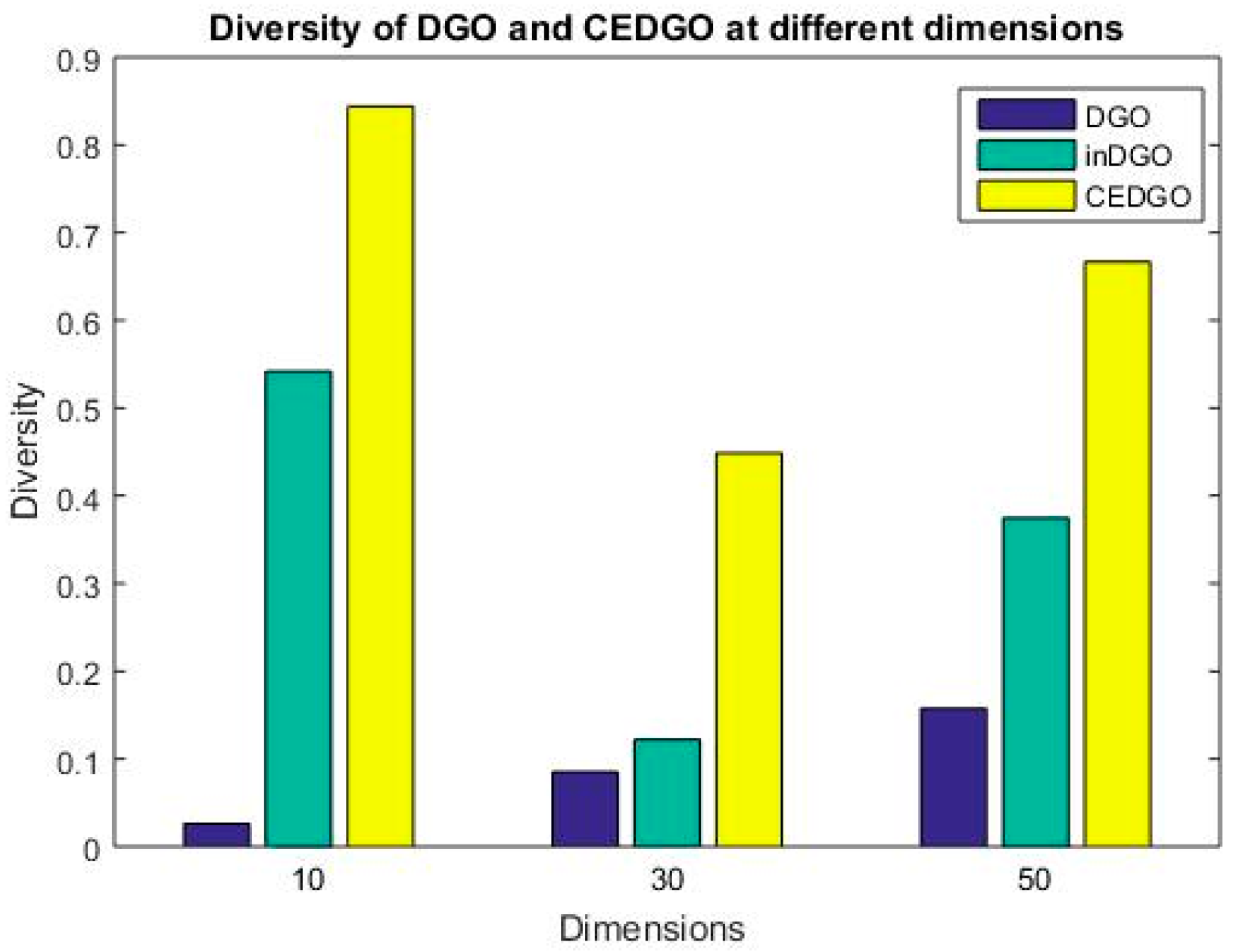
| D = 10 | D = 30 | D = 50 | |
|---|---|---|---|
| DGO | 0.0261 | 0.0852 | 0.1577 |
| inDGO | 0.542 | 0.1221 | 0.3747 |
| D = 10 | D = 30 | D = 50 | |
|---|---|---|---|
| DGO | 0.0261 | 0.0852 | 0.1577 |
| inDGO | 0.542 | 0.1221 | 0.3747 |
| CEDGO | 0.84402 | 0.4485 | 0.6667 |
| Property | Value |
|---|---|
| CPU | Intel i7, 3.60 GHz |
| RAM | 8.00 GB |
| Software | MATLAB R2015a |
| Function | DGO | p Value | CEDGO | |
|---|---|---|---|---|
| AVGr ± SDr | AVGr ± SDr | |||
| F1 | 3.68 × 10−133 ± 7.59 × 10−133 | 7.94 × 10−03 | + | 0.00 × 10+00 ± 0.00 × 10+00 |
| F2 | 2.09 × 10−19 ± 4.67 × 10−19 | 7.94 × 10−03 | + | 4.23 × 10−254 ± 0.00 × 10+00 |
| F3 | 5.59 × 10−05 ± 1.25 × 10−04 | 2.22 × 10−03 | + | 3.02 × 10−18 ± 6.64 × 10−18 |
| F4 | 2.29 × 10−02 ± 5.96 × 10−03 | 7.94 × 10−03 | + | 2.92 × 10−34 ± 2.71 × 10−34 |
| F5 | 1.20 × 10+01 ± 8.96 × 10+00 | 4.21 × 10−01 | = | 6.92 × 10+00 ± 7.76 × 10+00 |
| F6 | 1.83 × 10−22 ± 3.44 × 10−22 | 7.94 × 10−03 | + | 1.73 × 10−32 ± 1.65 × 10−32 |
| F7 | 4.85 × 10−03 ± 3.99 × 10−03 | 3.17 × 10−02 | - | 1.61 × 10−02 ± 6.24 × 10−03 |
| F8 | −1.04 × 10+04 ± 3.27 × 10+02 | 2.22 × 10−01 | - | −8.70 × 10+03 ± 2.36 × 10+03 |
| F9 | 3.98 × 10−01 ± 5.45 × 10−01 | 7.94 × 10−03 | - | 9.52 × 10+01 ± 8.43 × 10+01 |
| F10 | 2.07 × 10−12 ± 2.72 × 10−12 | 7.94 × 10−03 | + | 6.57 × 10−15 ± 1.95 × 10−15 |
| F11 | 2.41 × 10−02 ± 1.66 × 10−02 | 3.17 × 10−02 | + | 1.89 × 10−08 ± 2.69 × 10−08 |
| F12 | 1.87 × 10−19 ± 4.19 × 10−19 | 6.51 × 10−01 | = | 1.51 × 10−02 ± 2.07 × 10−02 |
| F13 | 3.31 × 10−21 ± 5.06 × 10−21 | 1.35 × 10−01 | = | 2.20 × 10−03 ± 4.91 × 10−03 |
| F14 | 3.74 × 10+00 ± 4.05 × 10+00 | 2.86 × 10−01 | + | 9.98 × 10−01 ± 1.24 × 10−11 |
| F15 | 4.34 × 10−03 ± 8.96 × 10−03 | 5.48 × 10−01 | + | 4.95 × 10−04 ± 4.07 × 10−04 |
| F16 | −1.03 × 10+00 ± 0.00 × 10+00 | 1.00 × 10+00 | = | −1.03 × 10+00 ± 0.00 × 10+00 |
| F17 | 3.98 × 10−01 ± 0.00 × 10+00 | 1.00 × 10+00 | = | 3.98 × 10−01 ± 1.04 × 10−07 |
| F18 | 3.00 × 10+00 ± 4.44 × 10−16 | 1.19 × 10−01 | = | 3.00 × 10+00 ± 5.44 × 10−16 |
| F19 | −3.86 × 10+00 ± 0.00 × 10+00 | 1.00 × 10+00 | = | −3.86 × 10+00 ± 2.22 × 10−16 |
| F20 | −3.27 × 10+00 ± 6.51 × 10−02 | 6.83 × 10−01 | = | −3.32 × 10+00 ± 6.51 × 10−02 |
| F21 | −6.13 × 10+00 ± 3.80 × 10+00 | 9.37 × 10−01 | = | −6.62 × 10+00 ± 2.21 × 10+00 |
| F22 | −3.23 × 10+00 ± 1.23 × 10+00 | 7.94 × 10−03 | + | −8.19 × 10+00 ± 2.26 × 10+00 |
| F23 | −3.04 × 10+00 ± 1.18 × 10+00 | 1.59 × 10−02 | + | −8.68 × 10+00 ± 2.24 × 10+00 |
| +/=/- | 11/9/3 | |||
| Function | AGPSO | IPSO | TACPSO | MPSO | CEDGO |
|---|---|---|---|---|---|
| AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | |
| F1 | 4.39 × 10−31 ± 9.52 × 10−31 | 1.34 × 10−73 ± 3.01 × 10−73 | 2.78 × 10−56 ± 6.22 × 10−56 | 1.68 × 10−42 ± 3.75 × 10−42 | 0.00 × 10+00 ± 0.00 × 10+00 |
| F2 | 2.05 × 10−11 ± 4.02 × 10−11 | 4.00 × 10+00 ± 8.94 × 10+00 | 2.18 × 10−15 ± 3.70 × 10−15 | 3.20 × 10+01 ± 2.49 × 10+01 | 4.23 × 10−254 ± 0.00 × 10+00 |
| F3 | 1.00 × 10+03 ± 2.24 × 10+03 | 2.00 × 10+03 ± 2.74 × 10+03 | 2.56 × 10−09 ± 3.11 × 10−09 | 1.40 × 10+04 ± 5.60 × 10+03 | 3.02 × 10−18 ± 6.64 × 10−18 |
| F4 | 3.48 × 10+00 ± 2.02 × 10+00 | 1.73 × 10−05 ± 1.91 × 10−05 | 6.30 × 10−04 ± 6.83 × 10−04 | 1.81 × 10−02 ± 1.71 × 10−02 | 2.92 × 10−34 ± 2.71 × 10−34 |
| F5 | 6.15 × 10+02 ± 1.35 × 10+03 | 2.89 × 10+00 ± 2.64 × 10+00 | 1.80 × 10+04 ± 4.02 × 10+04 | 3.60 × 10+04 ± 4.93 × 10+04 | 6.92 × 10+00 ± 7.76 × 10+00 |
| F6 | 2.82 × 10−25 ± 6.27 × 10−25 | 1.71 × 10−30 ± 3.54 × 10−30 | 1.43 × 10−30 ± 3.10 × 10−30 | 8.50 × 10−32 ± 1.27 × 10−31 | 1.73 × 10−32 ± 1.65 × 10−32 |
| F7 | 4.55 × 10−03 ± 1.02 × 10−03 | 6.36 × 10−03 ± 2.75 × 10−03 | 5.06 × 10−03 ± 3.90 × 10−03 | 1.08 × 10+00 ± 1.47 × 10+00 | 1.61 × 10−02 ± 6.24 × 10−03 |
| F8 | −9.62 × 10+03 ± 5.08 × 10+02 | −9.69 × 10+03 ± 4.64 × 10+02 | −9.91 × 10+03 ± 4.36 × 10+02 | −9.16 × 10+03 ± 8.20 × 10+02 | −8.70 × 10+03 ± 2.36 × 10+03 |
| F9 | 1.53 × 10+01 ± 3.89 × 10+00 | 5.35 × 10+01 ± 2.99 × 10+01 | 3.64 × 10+01 ± 1.09 × 10+01 | 9.52 × 10+01 ± 4.62 × 10+01 | 9.52 × 10+01 ± 8.43 × 10+01 |
| F10 | 7.55 × 10−14 ± 1.13 × 10−13 | 5.31 × 10−01 ± 7.38 × 10−01 | 8.20 × 10−01 ± 8.51 × 10−01 | 9.75 × 10−14 ± 1.14 × 10−13 | 6.57 × 10−15 ± 1.95 × 10−15 |
| F11 | 4.96 × 10−02 ± 3.01 × 10−02 | 2.36 × 10−02 ± 3.02 × 10−02 | 2.95 × 10−02 ± 5.65 × 10−02 | 2.01 × 10−02 ± 3.31 × 10−02 | 1.89 × 10−08 ± 2.69 × 10−08 |
| F12 | 2.07 × 10−02 ± 4.64 × 10−02 | 6.22 × 10−02 ± 5.68 × 10−02 | 1.04 × 10−01 ± 2.32 × 10−01 | 2.49 × 10−01 ± 5.01 × 10−01 | 1.51 × 10−02 ± 2.07 × 10−02 |
| F13 | 4.39 × 10−03 ± 6.02 × 10−03 | 2.20 × 10−03 ± 4.91 × 10−03 | 2.39 × 10−02 ± 4.15 × 10−02 | 2.20 × 10−03 ± 4.91 × 10−03 | 2.20 × 10−03 ± 4.91 × 10−03 |
| F14 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01 ± 1.24 × 10−11 |
| F15 | 4.91 × 10−04 ± 4.10 × 10−04 | 3.07 × 10−04 ± 5.41 × 10−19 | 3.07 × 10−04 ± 9.46 × 10−19 | 4.93 × 10−03 ± 8.63 × 10−03 | 4.95 × 10−04 ± 4.07 × 10−04 |
| F16 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 0.00 × 10+00 |
| F17 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 1.04 × 10−07 |
| F18 | 3.00 × 10+00 ± 9.93 × 10−16 | 3.00 × 10+00 ± 0.00 × 10+00 | 3.00 × 10+00 ± 0.00 × 10+00 | 3.00 × 10+00 ± 0.00 × 10+00 | 3.00 × 10+00 ± 5.44 × 10−16 |
| F19 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 2.22 × 10−16 |
| F20 | −3.32 × 10+00 ± 0.00 × 10+00 | −3.30 × 10+00 ± 5.32 × 10−02 | −3.32 × 10+00 ± 0.00 × 10+00 | −3.25 × 10+00 ± 6.64 × 10−02 | −3.32 × 10+00 ± 6.51 × 10−02 |
| F21 | −8.13 × 10+00 ± 2.77 × 10+00 | −8.13 × 10+00 ± 2.77 × 10+00 | −9.14 × 10+00 ± 2.26 × 10+00 | −9.14 × 10+00 ± 2.26 × 10+00 | −6.62 × 10+00 ± 2.21 × 10+00 |
| F22 | −1.04 × 10+01 ± 0.00 × 10+00 | −1.04 × 10+01 ± 1.26 × 10−15 | −9.35 × 10+00 ± 2.36 × 10+00 | −8.29 × 10+00 ± 2.90 × 10+00 | −8.19 × 10+00 ± 2.26 × 10+00 |
| F23 | −1.05 × 10+01 ± 8.88 × 10−16 | −1.05 × 10+01 ± 8.88 × 10−16 | −9.46 × 10+00 ± 2.40 × 10+00 | −1.05 × 10+01 ± 8.88 × 10−16 | −8.68 × 10+00 ± 2.24 × 10+00 |
| Algorithm | Parameter Setting |
|---|---|
| BA | P = 30, loudness = 0.5, pulse rate = 0.5 |
| WSA | P = 30, pa = 0.25 |
| PSO | P = 30, c1 = 1.49, c2 = 1.49 |
| GA | P = 30, Cr = 0.8, Mr = 0.2 |
| Function | BA | PSO | GA | WSA | CEDGO |
|---|---|---|---|---|---|
| AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | |
| F1 | 1.12 × 10−05 ± 8.86 × 10−07 | 3.67 × 10−158 ± 8.21 × 10−158 | 7.73 × 10−19 ± 2.36 × 10-19 | 2.44 × 10−03 ± 6.51 × 10−04 | 0.00 × 10+00 ± 0.00 × 10+00 |
| F2 | 2.07 × 10+02 ± 2.62 × 10+02 | 1.62 × 10−73 ± 3.62 × 10−73 | 2.60 × 10−08 ± 1.98 × 10−08 | 9.78 × 10+07 ± 1.42 × 10+08 | 4.23 × 10−254 ± 0.00 × 10+00 |
| F3 | 2.92 × 10−05 ± 8.16 × 10−06 | 1.11 × 10−06 ± 1.97 × 10−06 | 4.04 × 10−05 ± 2.55 × 10−05 | 1.58 × 10−02 ± 6.81 × 10−03 | 3.02 × 10−18 ± 6.64 × 10−18 |
| F4 | 1.75 × 10+00 ± 3.97 × 10−01 | 5.26 × 10+00 ± 3.26 × 10+00 | 7.98 × 10−02 ± 1.90 × 10−02 | 1.00 × 10+01 ± 0.00 × 10+00 | 2.92 × 10−34 ± 2.71 × 10−34 |
| F5 | 7.44 × 10+00 ± 1.16 × 10+00 | 3.33 × 10+02 ± 7.39 × 10+02 | 2.36 × 10+01 ± 6.35 × 10−01 | 1.75 × 10+01 ± 5.42 × 10+00 | 6.92 × 10+00 ± 7.76 × 10+00 |
| F6 | 1.13 × 10−05 ± 8.20 × 10−07 | 6.27 × 10−31 ± 6.38 × 10−31 | 5.00 × 10−19 ± 1.54 × 10−19 | 2.31 × 10−03 ± 3.89 × 10−04 | 1.73 × 10−32 ± 1.65 × 10−32 |
| F7 | 5.63 × 10+00 ± 8.14 × 10−01 | 5.42 × 10+00 ± 8.40 × 10+00 | 2.24 × 10−01 ± 2.29 × 10−02 | 6.73 × 10−03 ± 1.59 × 10−03 | 1.61 × 10−02 ± 6.24 × 10−03 |
| F8 | −8.52 × 10+09 ± 4.57 × 10+07 | −1.23 × 10+03 ± 5.80 × 10+03 | −7.27 × 10+02 ± 6.14 × 10+01 | −1.34 × 10+02 ± 1.68 × 10+01 | −8.70 × 10+03 ± 2.36 × 10+03 |
| F9 | 2.26 × 10+02 ± 9.35 × 10+01 | 1.71 × 10+02 ± 7.48 × 10+01 | 7.36 × 10+00 ± 3.42 × 10+00 | 4.22 × 10+02 ± 8.93 × 10+01 | 9.52 × 10+01 ± 8.43 × 10+01 |
| F10 | 8.28 × 10+00 ± 1.40 × 10+00 | 2.03 × 10+01 ± 1.75 × 10−01 | 8.81 × 10−11 ± 3.67 × 10−11 | 1.73 × 10+01 ± 0.00 × 10+00 | 6.57 × 10−15 ± 1.95 × 10−15 |
| F11 | 1.08 × 10−02 ± 6.40 × 10−03 | 5.91 × 10−03 ± 6.18 × 10−03 | 2.22 × 10−07 ± 4.97 × 10−17 | 2.69 × 10−04 ± 5.52 × 10−05 | 1.89 × 10−08 ± 2.69 × 10−08 |
| F12 | 4.15 × 10−02 ± 9.27 × 10−02 | 9.11 × 10−01 ± 1.47 × 10+00 | 2.07 × 10−02 ± 4.64 × 10−02 | 1.11 × 10+02 ± 2.70 × 10−02 | 1.51 × 10−02 ± 2.07 × 10−02 |
| F13 | 9.46 × 10+00 ± 5.65 × 10+00 | 1.76 × 10+00 ± 1.80 × 10+00 | 1.54 × 10−02 ± 1.67 × 10−02 | 4.18 × 10+00 ± 1.96 × 10+00 | 2.20 × 10−03 ± 4.91 × 10−03 |
| F14 | 1.17 × 10+01 ± 2.15 × 10+00 | 1.20 × 10+00 ± 4.45 × 10−01 | 0.00 × 10+00 ± 2.10 × 10+00 | 1.74 × 10+01 ± 4.55 × 10+00 | 9.98 × 10−01 ± 1.24 × 10−11 |
| F15 | 2.95 × 10−02 ± 5.89 × 10−02 | 1.33 × 10−03 ± 4.20 × 10−04 | 1.15 × 10−03 ± 3.86 × 10−04 | 3.07 × 10−04 ± 1.48 × 10−05 | 4.95 × 10−04 ± 4.07 × 10−04 |
| F16 | −8.68 × 10−01 ± 3.65 × 10−01 | −1.03 × 10+00 ±1.92 × 10−16 | −1.03 × 10+00 ± 1.11 × 10−16 | −1.03 × 10+00 ± 2.53 × 10−10 | −1.03 × 10+00 ± 0.00 × 10+00 |
| F17 | 3.98 × 10−01 ± 2.29 × 10−11 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 0.00 × 10+00 | −1.03 × 10+00 ± 1.82 × 10−10 | 3.98 × 10−01 ± 1.04 × 10−07 |
| F18 | 8.40 × 10+00 ± 1.21 × 10+01 | 2.46 × 10+01 ± 3.52 × 10+01 | 1.92 × 10+01 ± 3.62 × 10+01 | 3.00 × 10+00 ± 1.00 × 10−08 | 3.00 × 10+00 ± 5.44 × 10−16 |
| F19 | −3.29 × 10+00 ± 1.28 × 10+00 | −7.73 × 10−01 ± 1.73 × 10+00 | −3.86 × 10+00 ± 3.14 × 10−16 | −3.86 × 10+00 ± 2.09 × 10+00 | −3.86 × 10+00 ± 2.22 × 10−16 |
| F20 | −3.27 × 10+00 ± 6.51 × 10−02 | 0.00 × 10+00 ± 0.00 × 10+00 | −3.25 × 10+00 ± 6.51 × 10−02 | −3.32 × 10+00 ± 0.00 × 10+00 | −3.32 × 10+00 ± 6.51 × 10−02 |
| F21 | −5.12 × 10+00 ± 3.06 × 10+00 | −6.57 × 10+00 ± 3.38 × 10+00 | −4.58 × 10+00 ± 1.06 × 10+00 | −5.67 × 10+00 ± 2.62 × 10−03 | −6.62 × 10+00 ± 2.21 × 10+00 |
| F22 | −7.82 × 10+00 ± 3.64 × 10+00 | −4.76 × 10+00 ± 3.32 × 10+00 | −6.28 × 10+00 ± 3.88 × 10+00 | −7.35 × 10+00 ± 3.94 × 10−03 | −8.19 × 10+00 ± 2.26 × 10+00 |
| F23 | −4.09 × 10+00 ± 3.63 × 10+00 | −4.27 × 10+00 ± 3.59 × 10+00 | −8.37 × 10+00 ± 2.96 × 10+00 | −7.29 × 10+00 ± 2.00 × 10−04 | −8.68 × 10+00 ± 2.24 × 10+00 |
| Function | GA | PSO | BA | WSA | DGO | CEDGO |
|---|---|---|---|---|---|---|
| AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | |
| F1 | 1.87 × 10−03 ± 3.05 × 10−04 | 5.04 × 10+05 ± 3.47 × 10+05 | 1.66 × 10−03 ± 5.61 × 10−05 | 1.59 × 10+00 ± 4.46 × 10−02 | 9.71 × 10−04 ± 1.56 × 10−05 | 3.93 × 10−28 ± 4.17 × 10−28 |
| F2 | 2.83 × 10+01 ± 2.75 × 10+00 | - | 5.63 × 10+00 ± 1.18 × 10+00 | 4.43 × 10+21 ± 1.49 × 10+22 | 1.69 × 10−01 ± 3.07 × 10−01 | 1.44 × 10−17 ± 3.21 × 10−17 |
| F3 | 3.09 × 10+02 ± 2.11 × 10+02 | 4.53 × 10+07 ± 1.10 × 10+07 | 6.42 × 10+00 ± 2.86 × 10+00 | 4.95 × 10+03 ± 3.83 × 10+02 | 1.89 × 10+05 ± 1.13 × 10+05 | 9.36 × 10+05 ± 1.81 × 10+05 |
| F4 | 2.09 × 10+00 ± 1.66 × 10−01 | 7.55 × 10+02 ± 5.15 × 10+01 | 8.63 × 10−01 ± 1.25 × 10−01 | 2.00 × 10+00 ± 0.00 × 10+00 | 6.88 × 10+00 ± 3.35 × 10+00 | 9.83 × 10+01 ± 4.34 × 10−01 |
| F5 | 5.33 × 10+02 ± 8.41 × 10+01 | 1.47 × 10+13 ± 3.25 × 10+13 | 2.95 × 10+02 ± 1.45 × 10+00 | 8.58 × 10+02 ± 2.44 × 10+01 | 8.36 × 10+01 ± 1.78 × 10+01 | 3.63 × 10+02 ± 5.59 × 10+01 |
| F6 | 1.97 × 10−03 ± 4.18 × 10−04 | 4.43 × 10+05 ± 3.13 × 10+05 | 1.67 × 10−03 ± 5.81 × 10−05 | 1.62 × 10+00 ± 4.16 × 10−02 | 5.80 × 10−04 ± 4.80 × 10−03 | 2.31 × 10−28 ± 6.93 × 10−29 |
| F7 | 4.01 × 10+00 ± 5.19 × 10−01 | 3.16 × 10+13 ± 1.11 × 10+14 | 5.39 × 10+00 ± 6.79 × 10−01 | 8.29 × 10+00 ± 6.21 × 10−01 | 1.40 × 10+00 ± 3.70 × 10−01 | 8.49 × 10−01 ± 3.56 × 10−01 |
| F8 | −5.62 × 10+03 ± 1.69 × 10+03 | - | - | −1.21 × 10+03 ± 1.61 × 10+01 | −9.04 × 10+04 ± 2.60 × 10+04 | −3.74 × 10+04 ± 1.53 × 10+04 |
| F9 | 2.89 × 10+02 ± 4.93 × 10+01 | 7.58 × 10+05 ± 4.84 × 10+05 | 3.34 × 10+02 ± 1.49 × 10+02 | 1.20 × 10+03 ± 0.00 × 10+00 | 9.60 × 10+01 ± 1.75 × 10+01 | 2.23 × 10+03 ± 3.12 × 10+02 |
| F10 | 2.86 × 10+00 ± 1.47 × 10−01 | 2.11 × 10+01 ± 2.97 × 10−01 | 2.17 × 10+00 ± 2.50 × 10−01 | 6.59 × 10+00 ± 9.11 × 10−16 | 1.94 × 10+00 ± 2.35 × 10+00 | 1.78 × 10+00 ± 8.06 × 10−01 |
| F11 | 1.64 × 10−03 ± 2.14 × 10−03 | 1.30 × 10+02 ± 1.18 × 10+02 | 1.80 × 10−05 ± 1.29 × 10−06 | 2.14 × 10−02 ± 9.15 × 10−04 | 1.70 × 10−05 ± 1.86 × 10−06 | 1.48 × 10−03 ± 3.31 × 10−03 |
| F12 | 1.09 × 10−03 ± 3.21 × 10−03 | 4.69 × 10+13 ± 1.76 × 10+14 | 2.07 × 10−03 ± 5.42 × 10−03 | 2.99 × 10+00 ± 1.98 × 10−01 | 1.11 × 10−04 ± 2.45 × 10−05 | 4.20 × 10+06 ± 4.67 × 10+06 |
| F13 | 1.05 × 10+01 ± 2.47 × 10+00 | 1.02 × 10+13 ± 1.57 × 10+13 | 1.55 × 10+01 ± 5.58 × 10+00 | 3.00 × 10+01 ± 0.00 × 10+00 | 1.21 × 10+00 ± 2.03 × 10+00 | 4.88 × 10+05 ± 7.71 × 10+05 |
| Function | 0.25 | 0.5 | 0.65 | 0.8 |
|---|---|---|---|---|
| AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | AVGr ± SDr | |
| F1 | 4.04 × 10−05 ± 9.04 × 10−05 | 4.61 × 10−07 ± 9.17 × 10−07 | 3.63 × 10−28 ± 8.04 × 10−28 | 0.00 × 10+00 ± 0.00 × 10+00 |
| F2 | 8.96 × 10−09 ± 1.38 × 10−08 | 2.91 × 10−05 ± 6.50 × 10−05 | 1.83 × 10−27 ± 4.04 × 10−27 | 7.54 × 10−221 ± 0.00 × 10+00 |
| F3 | 4.73 × 10−02 ± 3.69 × 10−02 | 1.30 × 10+00 ± 2.88 × 10+00 | 2.02 × 10+02 ± 4.35 × 10+02 | 7.07 × 10+01 ± 1.23 × 10+02 |
| F4 | 3.32 × 10−03 ± 4.85 × 10−03 | 6.92 × 10−02 ± 1.55 × 10−01 | 4.16 × 10+00 ± 4.49 × 10+00 | 5.59 × 10−30 ± 1.21 × 10−29 |
| F5 | 2.74 × 10+01 ± 1.30 × 10+00 | 2.65 × 10+01 ± 1.68 × 10+00 | 1.36 × 10+02 ± 1.01 × 10+02 | 1.26 × 10+01 ± 2.74 × 10+01 |
| F6 | 2.29 × 10+00 ± 1.14 × 10+00 | 3.70 × 10−01 ± 3.89 × 10−01 | 2.47 × 10−03 ± 3.70 × 10−03 | 2.47 × 10−34 ± 1.95 × 10−34 |
| F7 | 3.92 × 10−04 ± 3.60 × 10−04 | 2.60 × 10−03 ± 1.14 × 10−03 | 1.00 × 10−02 ± 4.45 × 10−03 | 1.61 × 10−02 ± 9.23 × 10−03 |
| F8 | −6.29 × 10+03 ± 7.21 × 10+02 | −7.37 × 10+03 ± 3.95 × 10+02 | −9.37 × 10+03 ± 8.64 × 10+02 | −7.25 × 10+03 ± 2.15 × 10+03 |
| F9 | 1.15 × 10+02 ± 3.47 × 10+01 | 9.67 × 10+01 ± 2.66 × 10+01 | 6.41 × 10+01 ± 2.44 × 10+01 | 1.19 × 10+02 ± 4.93 × 10+01 |
| F10 | 2.19 × 10−11 ± 1.99 × 10−11 | 2.74 × 10−03 ± 6.12 × 10−03 | 4.44 × 10−15 ± 0.00 × 10+00 | 5.86 × 10−15 ± 1.95 × 10−15 |
| F11 | 2.58 × 10−15 ± 5.76 × 10−15 | 8.10 × 10−03 ± 1.78 × 10−02 | 6.23 × 10−02 ± 1.39 × 10−01 | 3.30 × 10−05 ± 7.08 × 10−05 |
| F12 | 1.03 × 10−01 ± 5.93 × 10−02 | 1.93 × 10−02 ± 2.68 × 10−02 | 3.40 × 10−01 ± 6.64 × 10−01 | 1.13 × 10−32 ± 3.53 × 10−34 |
| F13 | 2.04 × 10+00 ± 3.12 × 10−01 | 9.08 × 10−01 ± 6.49 × 10−01 | 1.22 × 10−01 ± 2.61 × 10−01 | 4.39 × 10−03 ± 6.02 × 10−03 |
| F14 | 9.98 × 10−01 ± 7.70 × 10−10 | 9.98 × 10−01 ± 9.28 × 10−10 | 9.98 × 10−01 ± 1.11 × 10−16 | 9.98 × 10−01 ± 2.22 × 10−16 |
| F15 | 3.33 × 10−04 ± 5.24 × 10−05 | 7.79 × 10−04 ± 4.29 × 10−04 | 4.31 × 10−04 ± 1.59 × 10−04 | 6.84 × 10−04 ± 5.13 × 10−04 |
| F16 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 1.11 × 10−16 | −1.03 × 10+00 ± 0.00 × 10+00 | −1.03 × 10+00 ± 6.15 × 10−09 |
| F17 | 3.98 × 10−01 ± 3.18 × 10−12 | 3.98 × 10−01 ± 6.12 × 10−06 | 3.98 × 10−01 ± 3.56 × 10−06 | 3.98 × 10−01± 7.42 × 10−05 |
| F18 | 3.00 × 10+00 ± 6.51 × 10−08 | 3.00 × 10+00 ± 1.75 × 10−15 | 3.00 × 10+00 ± 2.01 × 10−15 | 3.00 × 10+00 ± 1.02 × 10−15 |
| F19 | −3.86 × 10+00 ± 7.02 × 10−05 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 0.00 × 10+00 | −3.86 × 10+00 ± 0.00 × 10+00 |
| F20 | −3.27 × 10+00 ± 6.47 × 10−02 | −3.32 × 10+00 ± 1.17 × 10−05 | −3.25 × 10+00 ± 6.51 × 10−02 | −3.27 × 10+00 ± 6.51 × 10−02 |
| F21 | −7.91 × 10+00 ± 2.62 × 10+00 | −8.19 × 10+00 ± 2.28 × 10+00 | −6.40 × 10+00 ± 2.69 × 10+00 | −7.20 × 10+00 ± 2.96 × 10+00 |
| F22 | −9.08 × 10+00 ± 2.24 × 10+00 | −8.55 × 10+00 ± 1.16 × 10+00 | −7.47 × 10+00 ± 2.93 × 10+00 | −8.80 × 10+00 ± 1.94 × 10+00 |
| F23 | −9.18 × 10+00 ± 2.27 × 10+00 | −9.93 × 10+00 ± 8.52 × 10−01 | −6.93 × 10+00 ± 1.83 × 10+00 | −9.06 × 10+00 ± 1.65 × 10+00 |
| ACODE | CODE | jDE | SaDE | CEDGO | |
|---|---|---|---|---|---|
| F1 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 |
| F2 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 4.87 × 10−104 ± 2.11 × 10−103 | 4.23 × 10−254 ± 0.00 × 10+00 |
| F3 | 4.60 × 10−17 ± 6.85 × 10−17 | 6.24 × 10−16 ± 1.79 × 10−15 | 1.38 × 10−12 ± 3.74 × 10−12 | 3.74 × 10−06 ± 6.45 × 10−06 | 3.02 × 10−18 ± 6.64 × 10−18 |
| F4 | 8.34 × 10−18 ± 5.55 × 10−18 | 7.81 × 10−16 ± 6.52 × 10−16 | 1.81 × 10+01 ± 6.48 × 10+00 | 5.51 × 10−05 ± 2.35 × 10−04 | 2.92 × 10−34 ± 2.71 × 10−34 |
| F5 | 3.99 × 10−01 ± 1.23 × 10+00 | 3.43 × 10−11 ± 9.25 × 10−11 | 9.97 × 10−01 ± 1.77 × 10+00 | 2.49 × 10+01 ± 2.42 × 10+01 | 6.92 × 10+00 ± 7.76 × 10+00 |
| F6 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 5.24 × 10−33 ± 8.25 × 10−33 | 1.08 × 10−33 ± 1.08 × 10−33 | 1.73 × 10−32 ± 1.65 × 10−32 |
| F7 | 2.30 × 10−03 ± 8.57 × 10−04 | 2.70 × 10−03 ± 7.69 × 10−04 | 2.85 × 10−03 ± 2.95 × 10−03 | 4.70 × 10−03 ± 1.90 × 10−03 | 1.61 × 10−02 ± 6.24 × 10−03 |
| F8 | −1.26 × 10+04 ± 1.87 × 10−12 | −1.26 × 10+04 ± 1.87 × 10−12 | −1.25 × 10+04 ± 9.80 × 10+01 | −1.26 × 10+04 ± 2.65 × 10+01 | −8.70 × 10+03 ± 2.36 × 10+03 |
| F9 | 0.00 × 10+00 ± 0.00 × 10+00 | 4.97 × 10−-02± 2.23 × 10−01 | 1.49 × 10−01 ± 3.65 × 10−01 | 7.96 × 10−01 ± 8.90 × 10−01 | 9.52 × 10+01 ± 8.43 × 10+01 |
| F10 | 4.44 × 10−15 ± 0.00 × 10+00 | 4.44 × 10−15 ± 0.00 × 10+00 | 1.24 × 10−14 ± 1.59 × 10−14 | 1.09 × 10+00 ± 7.21 × 10−01 | 6.57 × 10−15 ± 1.95 × 10−15 |
| F11 | 0.00 × 10+00 ± 0.00 × 10+00 | 0.00 × 10+00 ± 0.00 × 10+00 | 4.06 × 10−03 ± 8.89 × 10−03 | 1.04 × 10−02 ± 1.69 × 10−02 | 1.89 × 10−08 ± 2.69 × 10−08 |
| F12 | 1.57 × 10−32 ± 2.81 × 10−48 | 1.57 × 10−32 ± 2.81 × 10−48 | 6.80 × 10−02 ± 2.80 × 10−01 | 6.22 × 10−02 ± 1.63 × 10−01 | 1.51 × 10−02 ± 2.07 × 10−02 |
| F13 | 1.35 × 10−32 ± 2.81 × 10−48 | 1.35 × 10−32 ± 2.81 × 10−48 | 5.49 × 10−04 ± 2.46 × 10−03 | 7.99 × 10−02 ± 7.99 × 10−02 | 2.20 × 10-03 ± 4.91 × 10−03 |
| F14 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01± 5.09 × 10−17 | 1.05 × 10+00 ± 2.22 × 10−01 | 9.98 × 10−01 ± 0.00 × 10+00 | 9.98 × 10−01 ± 1.24 × 10−11 |
| F15 | 3.07 × 10−04 ±1.03 × 10−19 | 3.07 × 10−04 ± 1.27 × 10−19 | 3.07 × 10−04 ± 1.09 × 10−19 | 3.07 × 10−04 ± 9.79 × 10−20 | 4.95 × 10−04 ± 4.07 × 10−04 |
| F16 | −1.03 × 10+00 ± 2.10 × 10−16 | −1.03 × 10+00 ± 2.04 × 10−16 | −1.03 × 10+00 ± 2.28 × 10−16 | −1.03 × 10+00 ± 2.28 × 10−16 | −1.03 × 10+00 ± 0.00 × 10+00 |
| F17 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 0.00 × 10+00 | −1.03 × 10+00 ± 2.28 × 10−16 | 3.98 × 10−01 ± 0.00 × 10+00 | 3.98 × 10−01 ± 1.04 × 10−07 |
| F18 | 3.00 × 10+00 ± 9.77 × 10−16 | 3.00 × 10+00 ± 9.11 × 10−16 | 3.00 × 10+00 ± 7.42 × 10−16 | 3.00 × 10+00 ± 2.04 × 10−16 | 3.00 × 10+00 ± 5.44 × 10−16 |
| F19 | −3.86 × 10+00 ± 2.28 × 10-15 | −3.86 × 10+00 ± 2.28 × 10−15 | −3.86 × 10+00 ± 2.28 × 10−15 | −3.86 × 10+00 ± 2.28 × 10−15 | −3.86 × 10+00 ± 2.22 × 10−16 |
| F20 | −3.32 × 10+00 ± 5.49 × 10-16 | −3.31 × 10+00 ± 3.66 × 10−02 | −3.29 × 10+00 ± 5.59 × 10−02 | −3.32 × 10+00 ± 6.98 × 10−16 | −3.32 × 10+00 ± 6.51 × 10−02 |
| F21 | −1.02 × 10+01 ± 3.51 × 10−15 | −1.02 × 10+01 ± 3.58 × 10−15 | −9.53 × 10+00 ± 1.97 × 10+00 | −9.90 × 10+00 ± 1.13 × 10+00 | −6.62 × 10+00 ± 2.21 × 10+00 |
| F22 | −1.04 × 10+01 ± 3.05 × 10−15 | −1.04 × 10+01± 3.05 × 10−15 | −1.04 × 10+01 ± 2.41 × 10−15 | −1.01 × 10+01 ± 1.18 × 10+00 | −8.19 × 10+00 ± 2.26 × 10+00 |
| F23 | −1.05 × 10+01 ± 1.78 × 10−15 | −1.05 × 10+01 ± 1.82 × 10−15 | −1.01 × 10+01 ± 1.81 × 10+00 | −1.05 × 10+01 ± 1.95 × 10−15 | −8.68 × 10+00 ± 2.24 × 10+00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Fong, S.; Dey, N.; Wong, R.K.; Mohammed, S. Cross Entropy Method Based Hybridization of Dynamic Group Optimization Algorithm. Entropy 2017, 19, 533. https://doi.org/10.3390/e19100533
Tang R, Fong S, Dey N, Wong RK, Mohammed S. Cross Entropy Method Based Hybridization of Dynamic Group Optimization Algorithm. Entropy. 2017; 19(10):533. https://doi.org/10.3390/e19100533
Chicago/Turabian StyleTang, Rui, Simon Fong, Nilanjan Dey, Raymond K. Wong, and Sabah Mohammed. 2017. "Cross Entropy Method Based Hybridization of Dynamic Group Optimization Algorithm" Entropy 19, no. 10: 533. https://doi.org/10.3390/e19100533






