Backtracking and Mixing Rate of Diffusion on Uncorrelated Temporal Networks
Abstract
:1. Introduction
2. Random Walk on Temporal Network
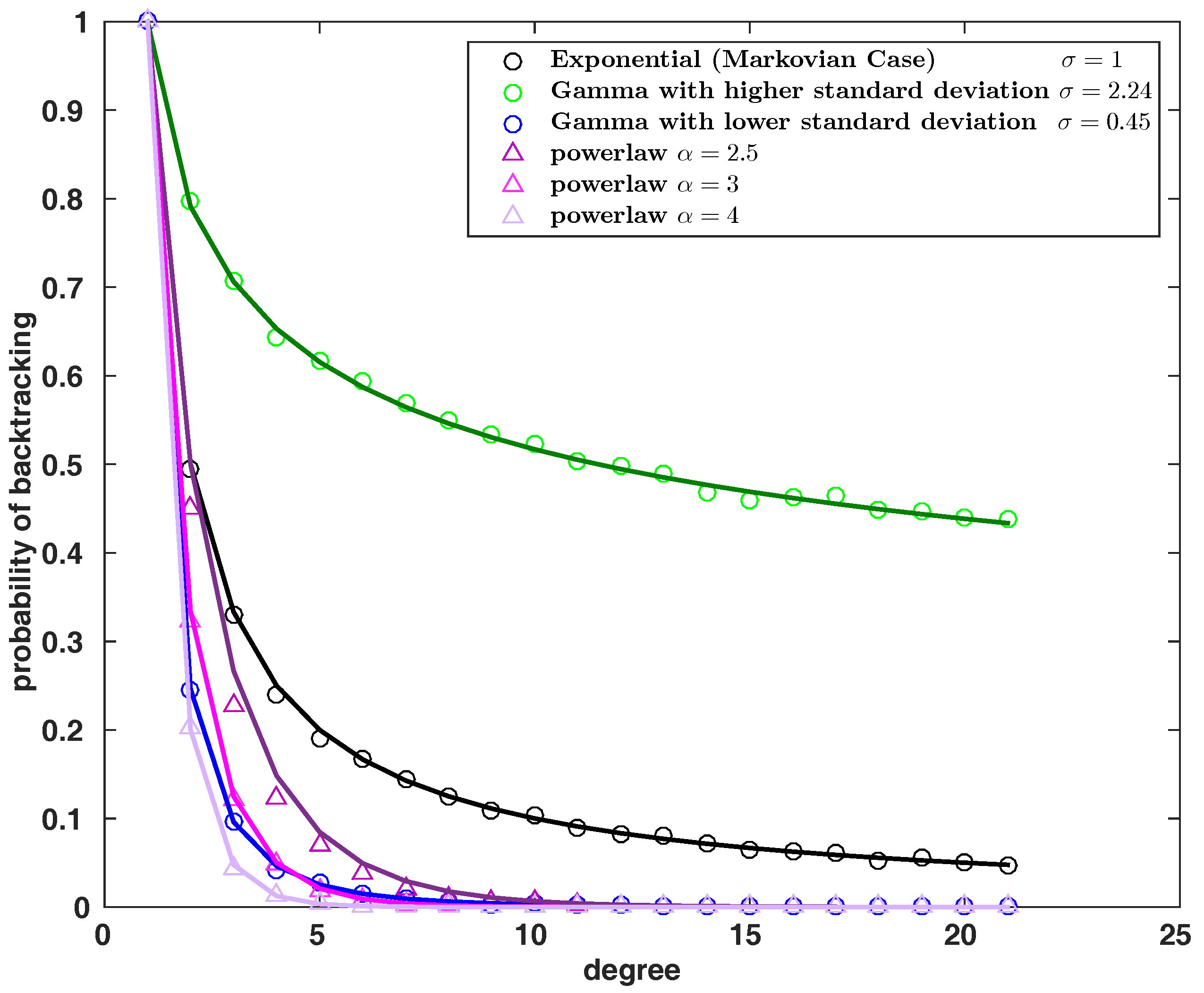
2.1. Bias on the Probability of Backtracking
2.2. Impact of Backtracking on the Mixing Rate of the Random Walk
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Shared Eigenvalues of the Transition Matrix and Its Associated Transition Line Graph
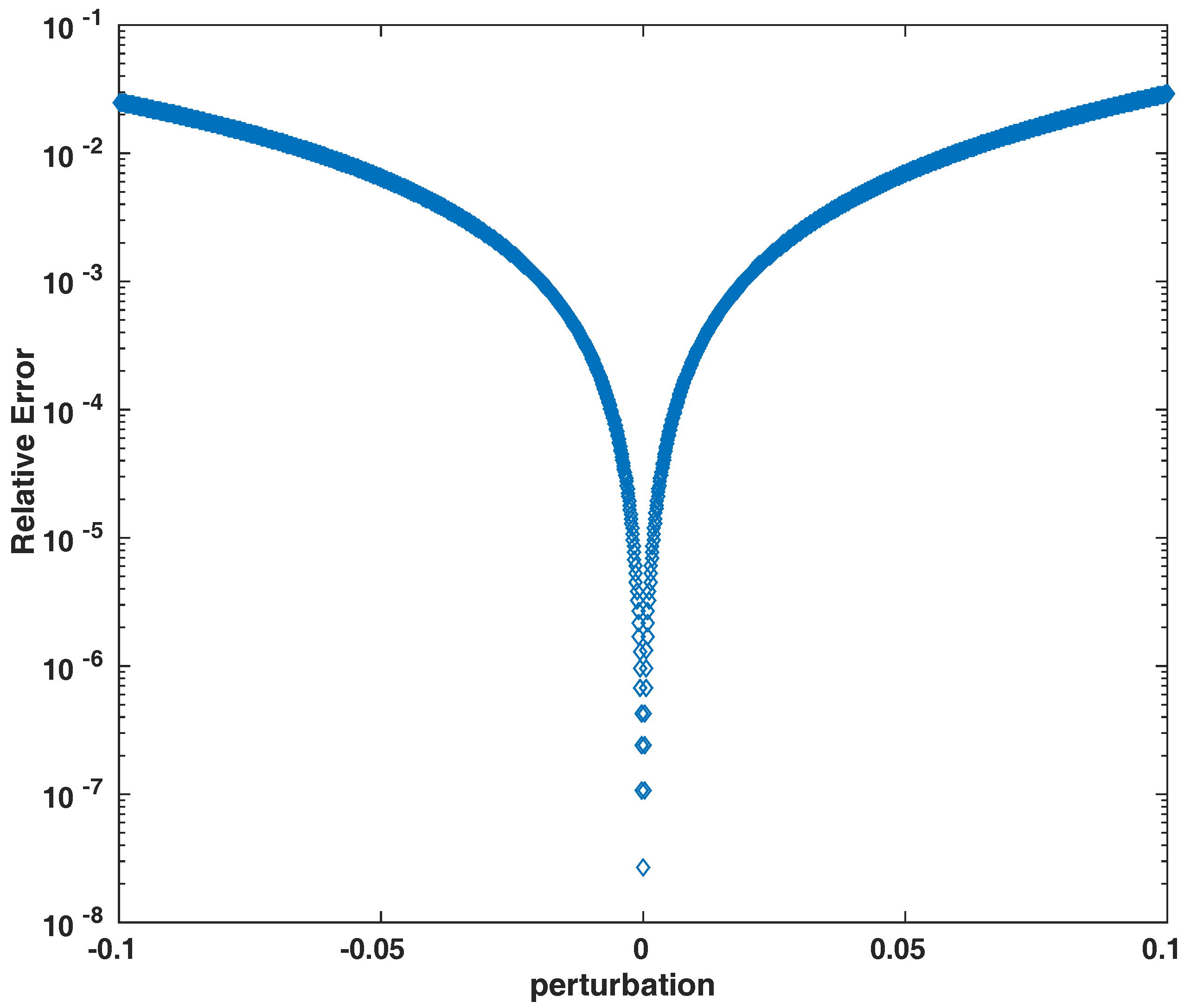
Appendix B. First Order Approximation of the Spectral Gap for Regular Network
References
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. arXiv 2016, arXiv:1612.03281. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Gleich, D.F. PageRank Beyond the Web. SIAM Rev. 2015, 57, 321–363. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Delvenne, J.C.; Yaliraki, S.N.; Barahona, M. Stability of graph communities across time scales. Proc. Natl. Acad. Sci. USA 2010, 107, 12755–12760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, F.R.K. Spectral Graph Theory. In CBMS Regional Conference Series in Mathematics; American Mathematical Society: Providence, RI, USA, 1996; Volume 92. [Google Scholar]
- Holme, P.; Saramäki, J. Temporal networks. Phys. Rep. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Masuda, N.; Lambiotte, R. A Guide to Temporal Networks; World Scientific Publishing Europe Ltd.: London, UK, 2016. [Google Scholar]
- Jo, H.H.; Karsai, M.; Kertész, J.; Kaski, K. Circadian pattern and burstiness in mobile phone communication. New J. Phys. 2012, 14, 013055. [Google Scholar] [CrossRef]
- Lambiotte, R.; Salnikov, V.; Rosvall, M. Effect of memory on the dynamics of random walks on networks. J. Complex Netw. 2014, 3, 177–188. [Google Scholar] [CrossRef]
- Karsai, M.; Kaski, K.; Barabási, A.L.; Kertész, J. Universal features of correlated bursty behaviour. Sci. Rep. 2012, 2, 397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scholtes, I.; Wider, N.; Pfitzner, R.; Garas, A.; Tessone, C.J.; Schweitzer, F. Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef]
- Barabasi, A.L. Bursts: The Hidden Patterns Behind Everything We Do, from Your E-mail to Bloody Crusades; Plume: New York, NY, USA, 2010. [Google Scholar]
- Starnini, M.; Baronchelli, A.; Barrat, A.; Pastor-Satorras, R. Random walks on temporal networks. Phys. Rev. E 2012, 85, 056115. [Google Scholar] [CrossRef] [PubMed]
- Karsai, M.; Kivelä, M.; Pan, R.K.; Kaski, K.; Kertész, J.; Barabási, A.L.; Saramäki, J. Small but slow world: How network topology and burstiness slow down spreading. Phys. Rev. E 2011, 83, 025102. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, T.; Porter, M.A.; Lambiotte, R. Random Walks on Stochastic Temporal Networks. In Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 295–313. [Google Scholar]
- Speidel, L.; Lambiotte, R.; Aihara, K.; Masuda, N. Steady state and mean recurrence time for random walks on stochastic temporal networks. Phys. Rev. E 2015, 91, 012806. [Google Scholar] [CrossRef] [PubMed]
- Saramäki, J.; Holme, P. Exploring temporal networks with greedy walks. Eur. Phys. J. B 2015, 88. [Google Scholar] [CrossRef]
- Lambiotte, R.; Tabourier, L.; Delvenne, J.C. Burstiness and spreading on temporal networks. Eur. Phys. J. B 2013, 86. [Google Scholar] [CrossRef]
- Delvenne, J.C.; Lambiotte, R.; Rocha, L.E.C. Diffusion on networked systems is a question of time or structure. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Génois, M.; Vestergaard, C.L.; Fourner, J.; Panisson, A.; Bonmarin, I.; Barrat, A. Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers. Netw. Sci. 2015, 3, 326–347. [Google Scholar] [CrossRef] [Green Version]
- Gemmetto, V.; Barrat, A.; Cattuto, C. Mitigation of infectious disease at school: Targeted class closure vs. school closure. BMC Infect. Dis. 2014, 14, 695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stehlé, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Isella, L.; Pinton, J.F.; Quaggiotto, M.; den Broeck, W.V.; Régis, C.; Lina, B.; et al. High-Resolution Measurements of Face-to-Face Contact Patterns in a Primary School. PLoS ONE 2011, 6, e23176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mastrandrea, R.; Fournet, J.; Barrat, A. Contact Patterns in a High School: A Comparison between Data Collected Using Wearable Sensors, Contact Diaries and Friendship Surveys. PLoS ONE 2015, 10, e0136497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanhems, P.; Barrat, A.; Cattuto, C.; Pinton, J.F.; Khanafer, N.; Régis, C.; Kim, B.; Comte, B.; Voirin, N. Estimating Potential Infection Transmission Routes in Hospital Wards Using Wearable Proximity Sensors. PLoS ONE 2013, 8, e73970. [Google Scholar] [CrossRef]
- Rosvall, M.; Esquivel, A.V.; Lancichinetti, A.; West, J.D.; Lambiotte, R. Memory in network flows and its effects on spreading dynamics and community detection. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
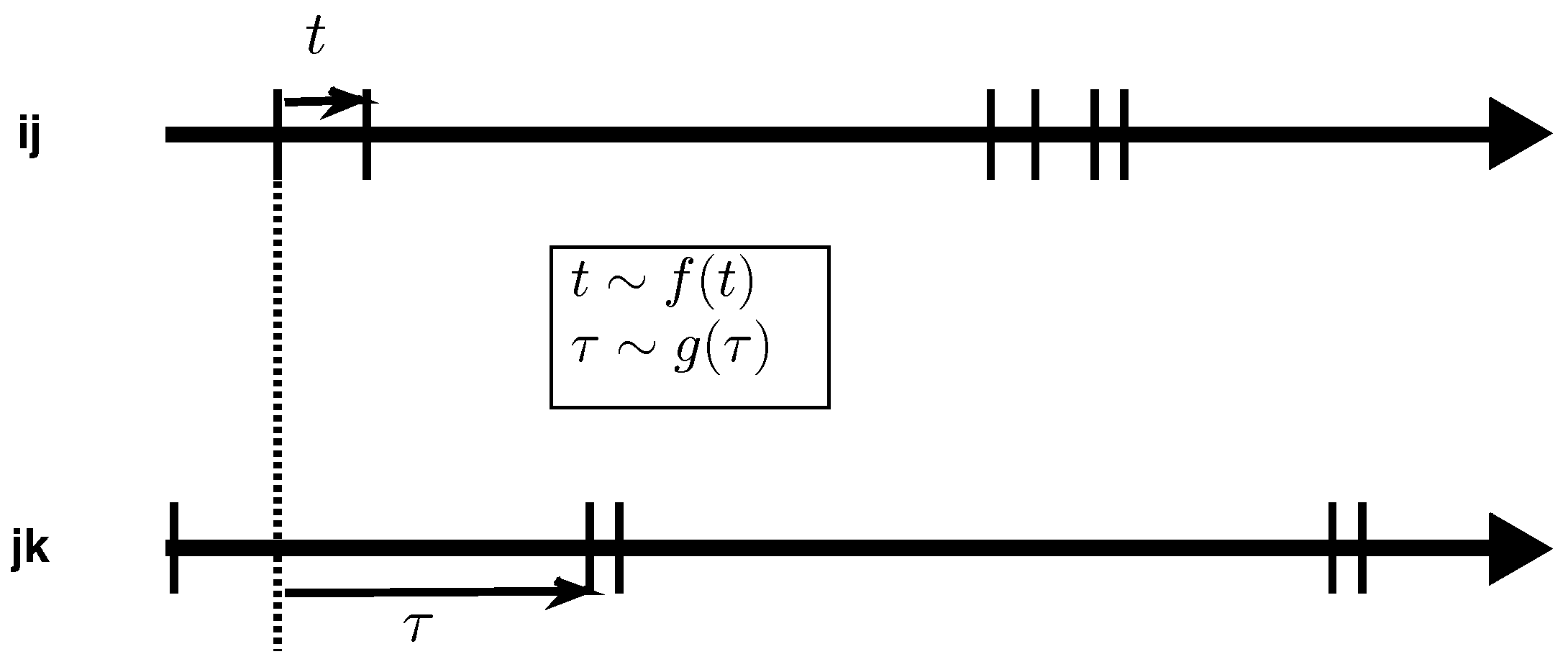

| Spectral Gap of Markovian RW | Spectral Gap of Backtracking RW | |
|---|---|---|
| Primary | 0.4151 | 0.2738 |
| Work | 0.3057 | 0.0569 |
| Highschool | 0.1349 | 0.0396 |
| Hospital | 0.5695 | 0.2105 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gueuning, M.; Lambiotte, R.; Delvenne, J.-C. Backtracking and Mixing Rate of Diffusion on Uncorrelated Temporal Networks. Entropy 2017, 19, 542. https://doi.org/10.3390/e19100542
Gueuning M, Lambiotte R, Delvenne J-C. Backtracking and Mixing Rate of Diffusion on Uncorrelated Temporal Networks. Entropy. 2017; 19(10):542. https://doi.org/10.3390/e19100542
Chicago/Turabian StyleGueuning, Martin, Renaud Lambiotte, and Jean-Charles Delvenne. 2017. "Backtracking and Mixing Rate of Diffusion on Uncorrelated Temporal Networks" Entropy 19, no. 10: 542. https://doi.org/10.3390/e19100542






