Entropy Production in Stochastics
Abstract
:1. Introduction
- It is dimensionless as d(ln t) = dt/t and thus, given that entropy is a dimensionless quantity per se (see next section), the EPLT remains a dimensionless quantity.
- It is consistent with the notion of the ‘arrow of time’. Usually entropy per se is related to the time asymmetry and the Second Law is regarded as the origin of the arrow. However, it may be simpler to think that it is the action of observation that creates time asymmetry. In this respect, we can set t = 0 for the observation time, i.e., the present, while t < 0 denotes the observable past and t > 0 denotes the unknown future. The fact that the past is observable, but the future not, generates the asymmetry. It is clarified that when the future becomes observable, it is no longer future; rather it has become present or past. Once the future (t > 0) is treated separately from the past, it is legitimate to differentiate with respect to the logarithm of time.
- It makes extremization of entropy production easier, particularly for asymptotic times t → 0 and t → ∞, as it avoids infinite or zero values of entropy production [22]; indeed, the asymptotic values of EPLT are always bounded (see Section 2.4).
- It provides the means to study or even explain the scaling behaviour often observed in geophysical processes (see Section 2.2 and Section 2.4).
2. Methods
2.1. General Context
2.2. Entropy and Entropy Production
- For a discrete random variable x with probability mass function Pj ≔ P{x = xj}, j = 1, …, w:
- For a continuous random variable z with probability density function f(z):where m(x) is the density of a background measure (usually Lebesgue, i.e., m(x) = 1, with dimensions [x−1]).
2.3. Scaling
- For local scaling:
- For global scaling:
2.4. Bounds of Scaling and Entropy Production
3. Results
3.1. Revisiting Earlier Results
- (a)
- Lebesgue background measure;
- (b)
- constrained mean μ and variance γ(1) at a specified (observation) time scale;
- (c)
- constrained lag-one autocorrelation ρ at the specified time scale;
- (d)
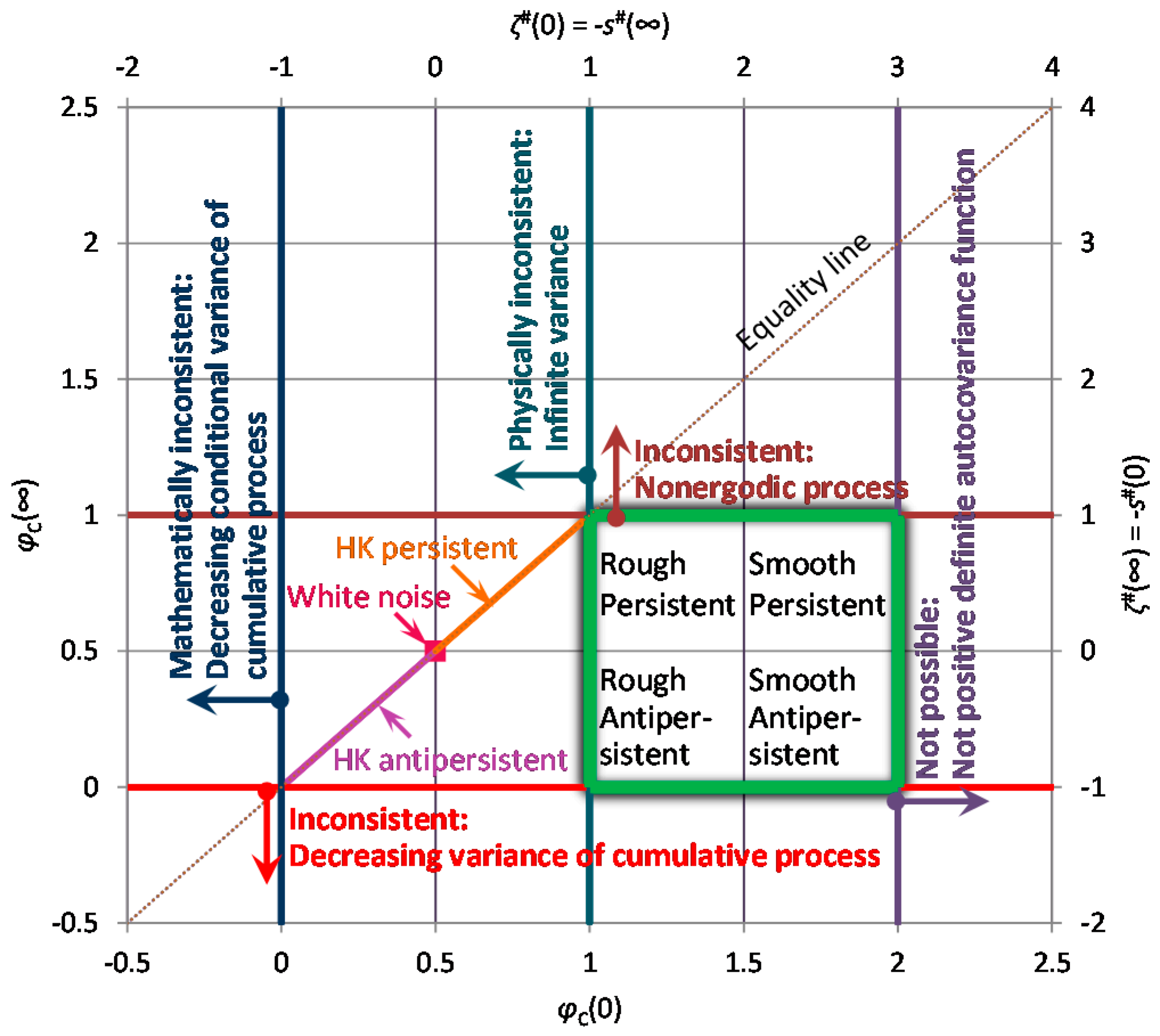
- an inequality constraint φC(t) ≥ φ(t) to ensure physical realism as, naturally, by observing the present and past state of a process, the future entropy is reduced, whereas as t → ∞ conditional and unconditional entropies should tend to be equal, which, however, cannot happen if the entropy production is consistently lower in the conditional than in the unconditional case;
- (e)
- extremization of entropy production at asymptotic time scales, i.e., t → 0 and t → ∞.
- A Markov process:maximizes entropy production for small times (t → 0) but minimizes it for large times (t → ∞).
- A Hurst-Kolmogorov (HK) process:maximizes entropy production for large times (t → ∞) but minimizes it for small times (t → 0).
- The minimal entropy production of the HK process at small times may not be plausible for complex processes; rather we should generally expect that complex processes maximize entropy production at both small and large times (asymptotically as t → 0 and ∞).
- The HK process is characterized by infinite variance (, which, as discussed in the previous section, makes it physically inconsistent.
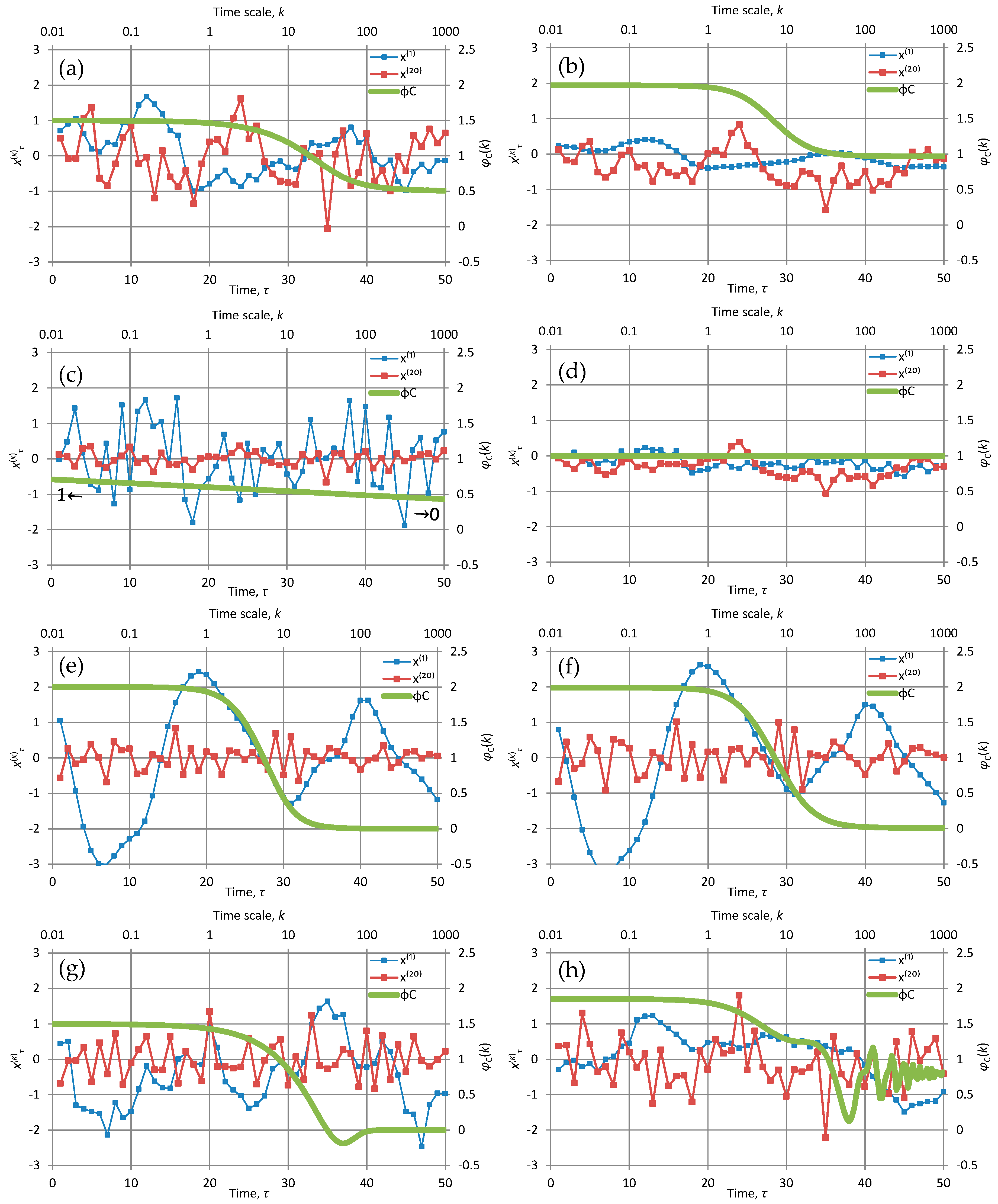
- The premise φC(t) ≥ φ(t) should certainly hold asymptotically (for t → 0 and t → ∞) but not necessarily at intermediate times. A specific example is the process shown in Figure 4h which includes a periodic component where the curve of φC(t) intersects that of φ(t) (the latter is not shown in the figure), even though asymptotically the inequality holds. It can thus be conjectured that if a process incorporates a deterministic component (e.g., periodic) while it is treated stochastically without separating the deterministic component, the inequality for EPLT and CEPLT could be violated at intermediate times.
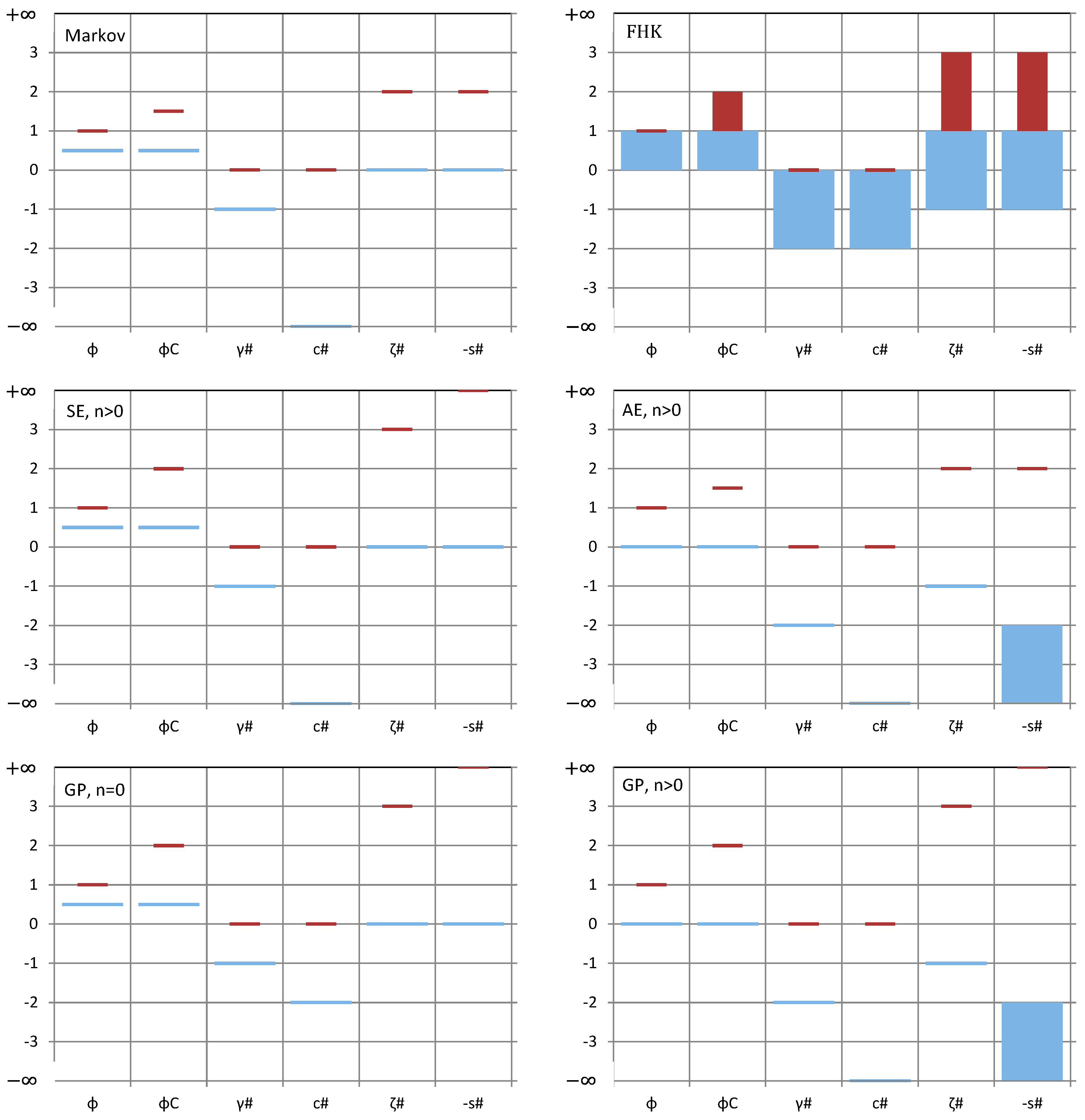
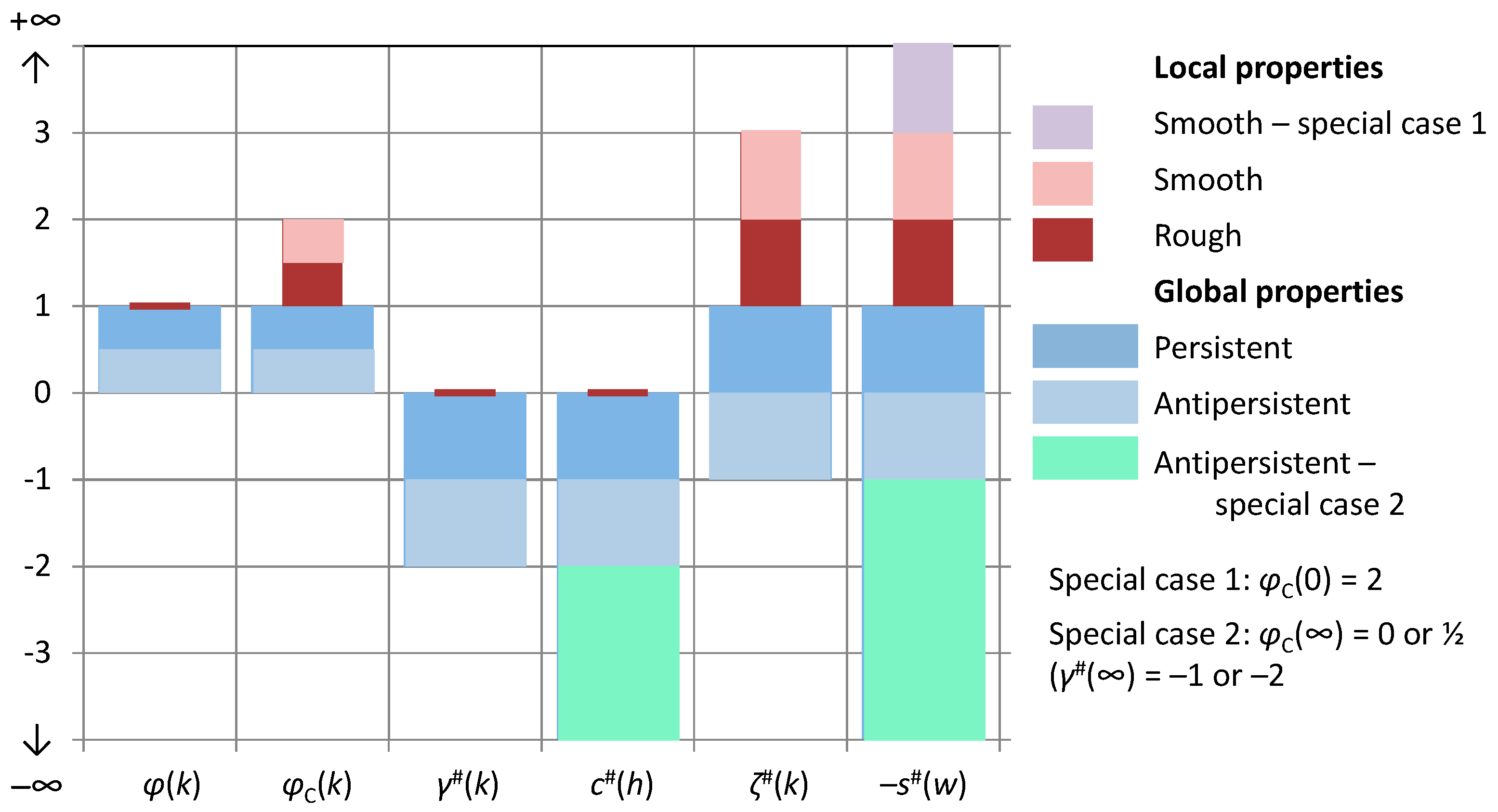
- While the Markov process represents the maximal EPLT as t → 0 (φ(0) = 1), this property is shared by many other processes (see next subsection). Furthermore, in terms of CEPLT, while the Markov process corresponds to φC(0) = 3/2, there are processes which have higher CEPLT than the Markov, up to φC(0) = 2. These are smoother than the Markov process and have structure function with v#(0) = ξ#(0) > 1, where the value 1 corresponds to the Markov process.
3.2. Specific Processes
3.3. Comparison of Asymptotic Properties
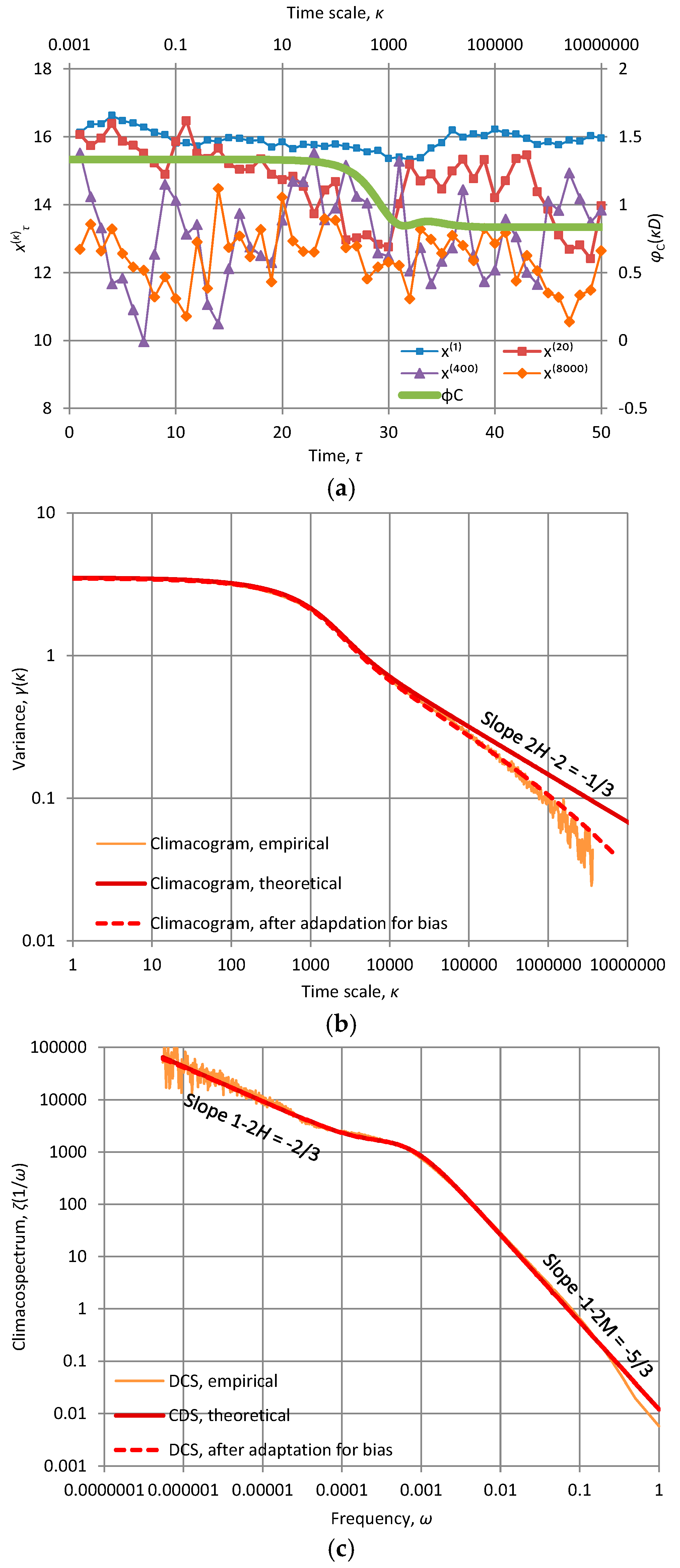
3.4. Real World Case Study
4. Discussion and Conclusions
- Definition of entropy production with respect to logarithmic time has some attractive characteristics and is consistent with the notion of the time arrow.
- The asymptotic values of entropy production for time zero and infinity seem to be crucial for its extremization and define important features of a process.
- In particular, the asymptotic value of CEPLT for zero time defines the roughness (fractality) of the stochastic process while the common asymptotic value of EPLT and CEPLT for infinite time defines the (long-term) persistence of the process and equals the Hurst parameter.
- Both ELPT and CEPLT are finite and constrained within specific theoretically justified bounds. The scaling laws of all second order characteristics of stochastic processes are a result of these finite values and are also subject to bounds (with few exceptions fully described). The proofs of existence of these bounds offer the means to fight common misunderstanding, misuse, false reporting and inconsistent estimation of characteristics of geophysical processes, as well as to develop consistent estimation algorithms.
- The climacogram and its derivative tools introduced here, namely, the differenced climacogram and the climacospectrum are very powerful and support the estimation of entropy production, in either of its forms, from data series.
- The broad family of models for stochastic processes investigated here covers the entire admissible range of asymptotic behaviours and offers the means for modelling any type of processes, either using a single model or a combination of more than one model.
- The real-world application presented with the extraordinary long time series of turbulent velocity shows how a parsimonious stochastic model can be identified and fitted using the tools developed.
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Derivations and Theoretical Details
Appendix A.1.1. Properties of the LLD
Appendix A.1.2. Proof of the Positive Definiteness of the Climacogram
Appendix A.1.3. Proof that the Differenced Climacogram Is Nonnegative
Appendix A.1.4. Determination of the Characteristic Constant ε of CEPLT
Appendix A.1.5. Asymptotic Properties of CEPLT
Appendix A.1.6. Area of Climacospectrum
Appendix A.1.7. Details and Derivation of the Inverse Transformation of Climacospectrum
Appendix A.1.8. Remarks on Asymptotic Scaling
- We find . If then we replace f(x) with , otherwise we keep it as it is. Clearly then, .
- We find . If then we replace f(x) with ln|f(x)| (which preserves the property ); if necessary, we make iterations so that eventually and .
- Given the properties in point 2, there exists a unique b, 0 < b < ∞ satisfying:so that for any b′ ≠ b:
- The constant b defines an asymptotic power law with exponent b (cf. Hausdorff dimension; the case b = 0 signifies an improper scaling).
Appendix A.1.9. Asymptotic Scaling of the Different Second Order Tools
- The asymptotic behaviour of the autocovariance function is the same with that of the climacogram.
- The asymptotic behaviour of the structure function is the same with that of the climacostructure function.
- The asymptotic behaviour of the power spectrum is the same with that of the climacospectrum.
- and : Markov, Smooth Exponential models
- and : Generalized Planck model for n = 0
- and , also while −1: Antipersistent Exponential model for n > 0
- and , also while : Generalized Planck model for n > 0
- and while : Generalized Planck model
- = 2 and while : Smooth Exponential for n > 0
Appendix A.1.10. Proof of Physical Inconsistency of too Mild Slopes at High Frequencies in Power Spectrum
Appendix A.1.11. Proof of the Inconsistency of too Steep Slopes at High Frequencies in Power Spectrum
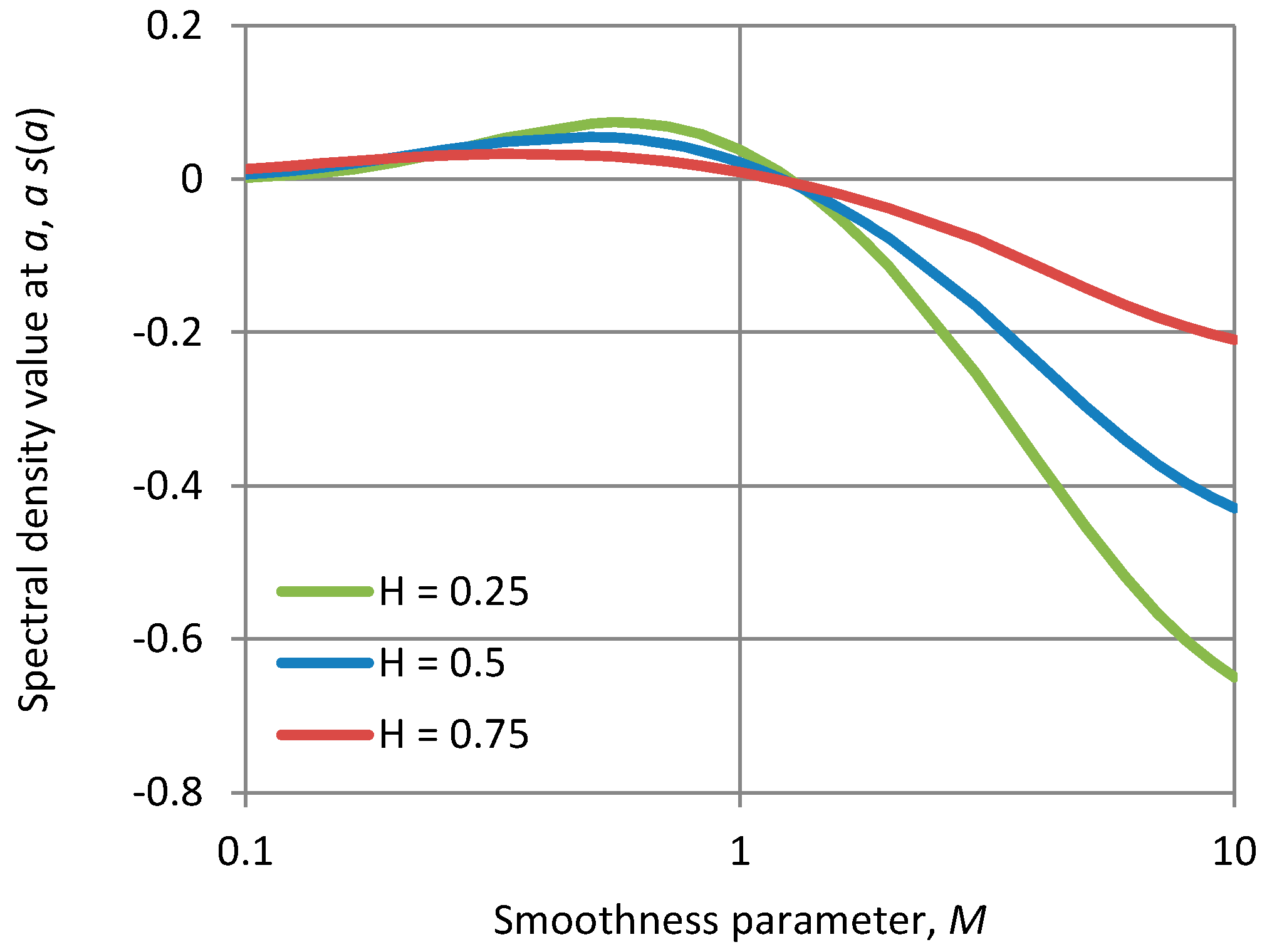
Appendix A.2. Specific Stochastic Models and Their Behaviour
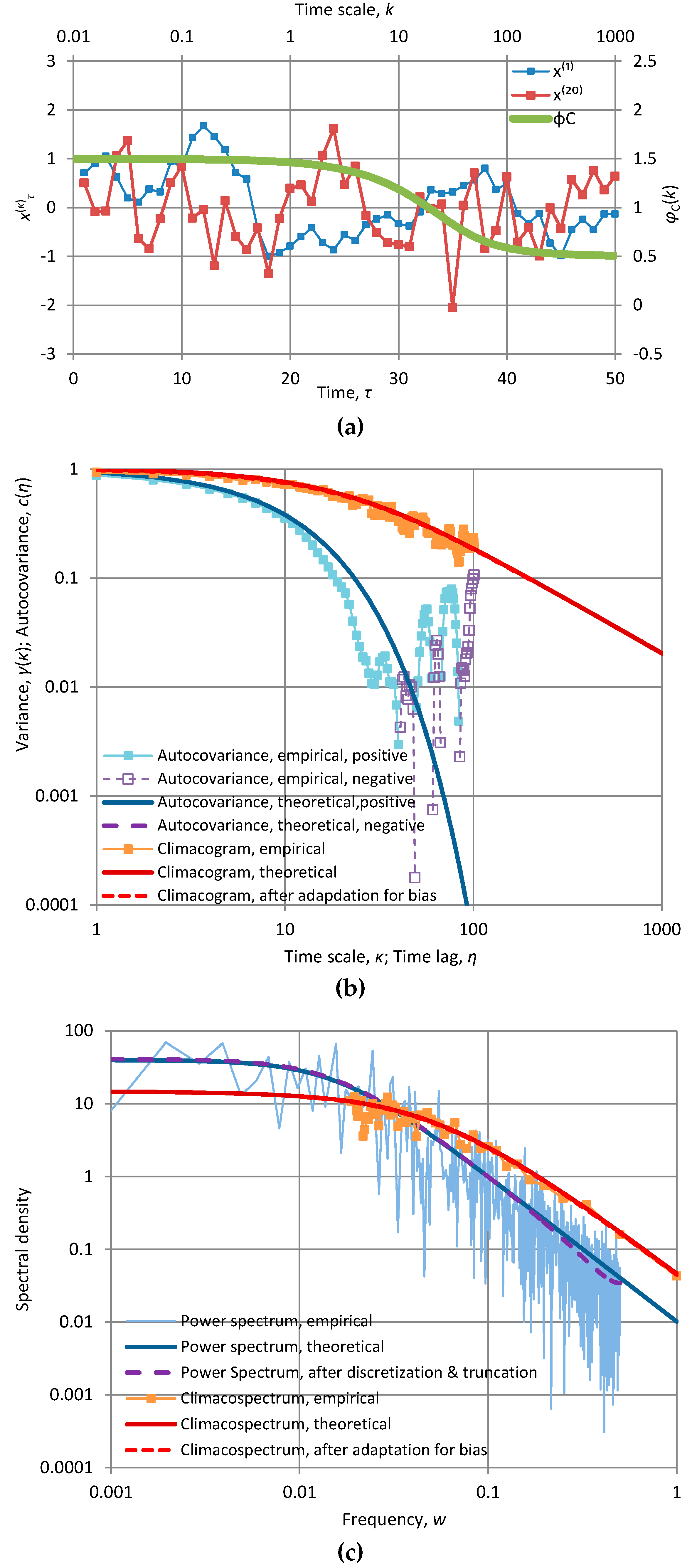
Appendix A.2.1. Markov Process
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | (A70) | |||
| Climacospectrum | (A71) | |||
| Entropy production | (A72) | |||
| Autocovariance function | 0 | (A73) | ||
| Power spectrum | (A74) |
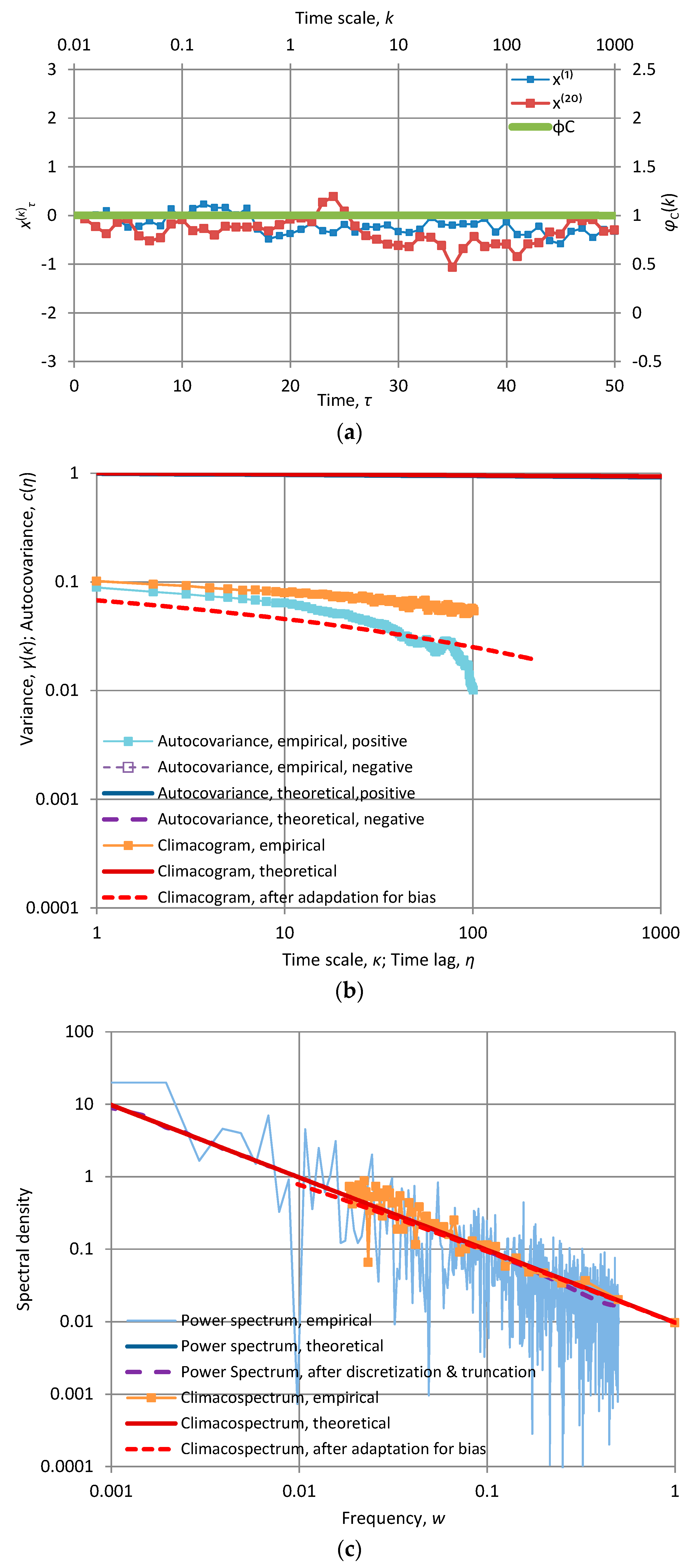
Appendix A.2.2. FHK Process with Cauchy-Type Climacogram (FHK-C)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | (A75) | |||
| Climacospectrum | (A76) | |||
| Entropy production | (A77) | |||
| Autocovariance function | 0 | (A78) | ||
| Power spectrum | Analytical expression not possible except in special cases; numerical solution easily derived from (10) | (A79) |


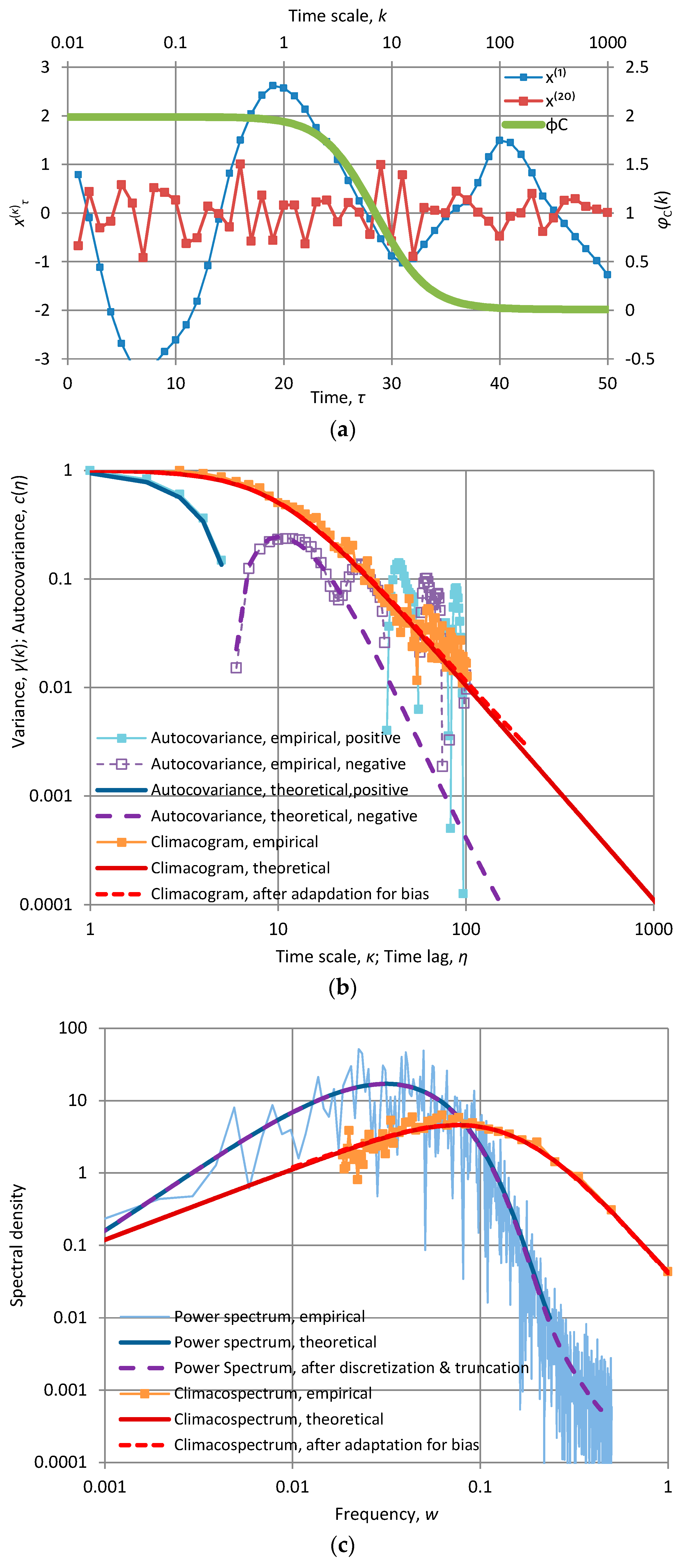
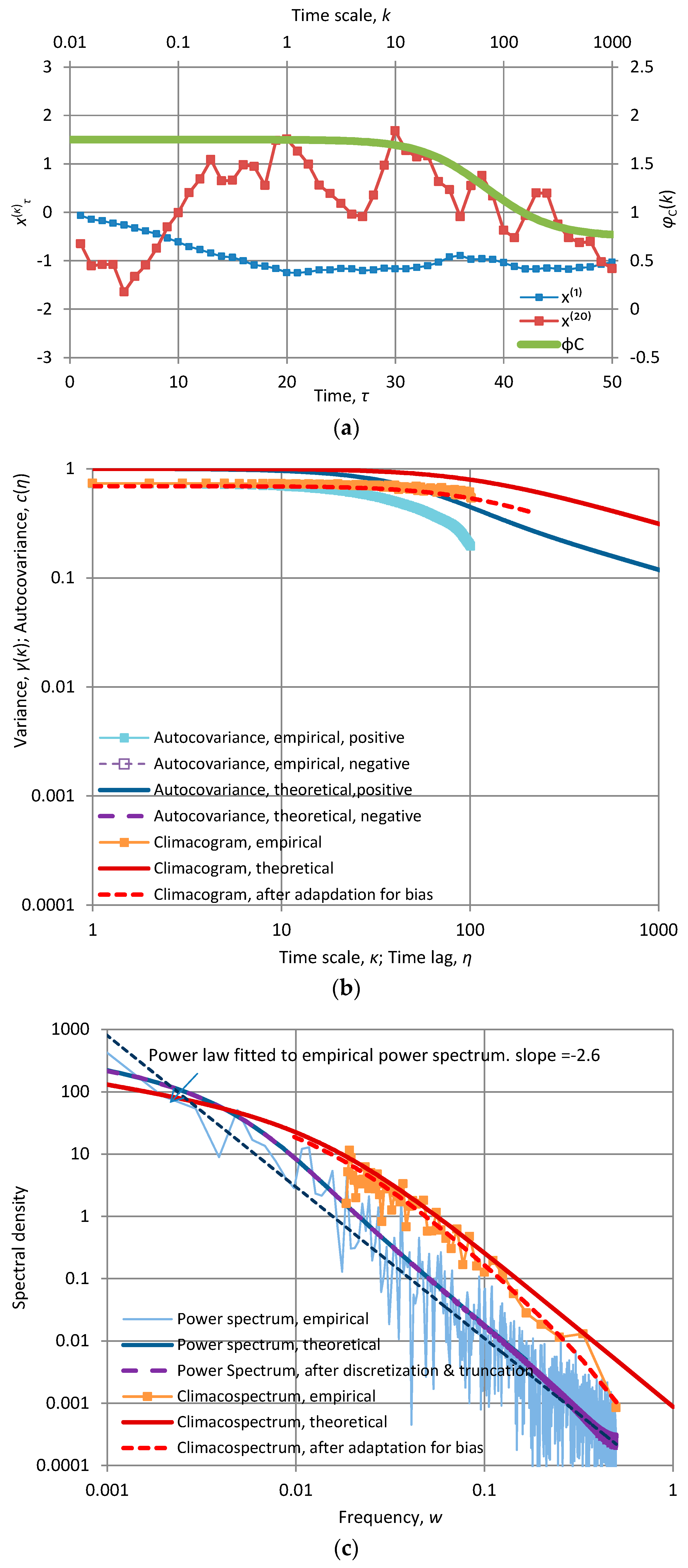
Appendix A.2.3. FHK Process with Dagum-Type Climacogram (FHK-D)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | (A82) | |||
| Climacospectrum | (A83) | |||
| Entropy production | (A84) | |||
| Autocovariance function | 0 | (A85) | ||
| Power spectrum | Analytical expression not possible except in special cases; numerical solution easily derived from (10) | (A86) |
Appendix A.2.4. FHK Process with Climacogram Equal to the Sum of a Cauchy and a Dagum Climacograms (FHK-CD)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | (A88) | |||
| Climacospectrum | (A89) | |||
| Entropy production | (A90) | |||
| Autocovariance function | 0 | (A91) | ||
| Power spectrum | Analytical expression too complex, derived from (10) | (A92) |
Appendix A.2.5. Smooth Process with Generalized Exponential-Type Autocovariance (SE)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | where n = 0, 1, 2, …, is a polynomial and a coefficient, both determined using (23); the first five are: | (A93) | ||
| Climacospectrum | (A94) | |||
| Entropy production | where are coefficients as above and are polynomials determined using (39); the first five are: | (A95) | ||
| Autocovariance function | where is a polynomial determined by the power spectrum (see below) using (22); the first five are: | 0 | (A96) | |
| Power spectrum | (A97) |
Appendix A.2.6. Antipersistent Process with Generalized Exponential-Type Autocovariance (AE)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | where n = 0, 1, 2…, while for n > 0 is a polynomial determined using (23); the first four are: | (A98) | ||
| Climacospectrum | (A99) | |||
| Entropy production | where , while for n > 0 are polynomials determined using (39); the first four are: | (A100) | ||
| Autocovariance function | where is a polynomial determined by the power spectrum (see below) using (22); the first five are:1 | 0 | (A101) | |
| Power spectrum | (A102) |
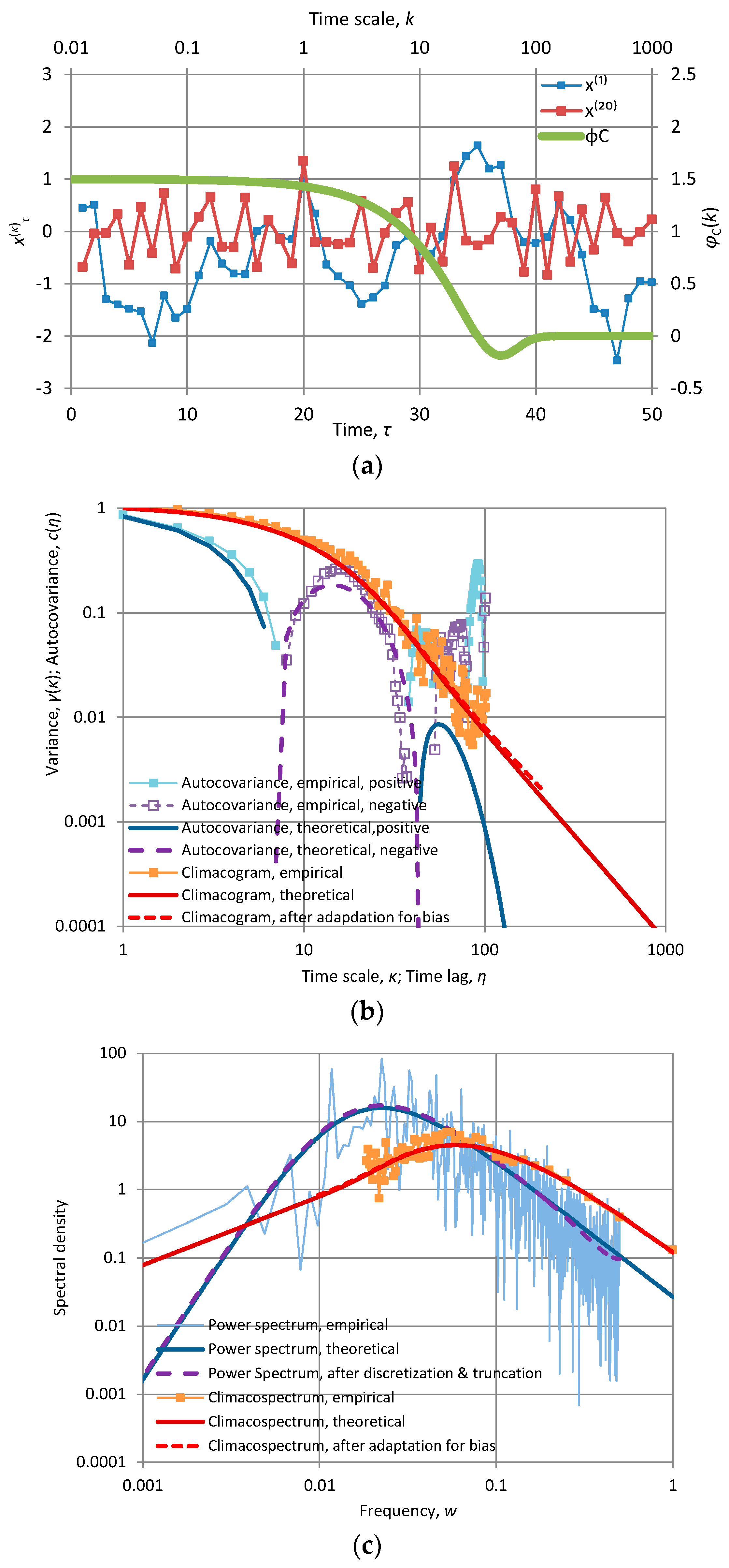
Appendix A.2.7. Generalized Planck Model (GP)
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | where n = 0, 1, 2, …, is a function determined using (23) the first three are: | n = 0 n > 0 | (A103) | |
| Climacospectrum | n = 0 n > 0 | (A104) | ||
| Entropy production | φ(k) is determined from (39); the first three terms are: | φ(0) = 1 φC(0) = 2 | φ(∞) = φC(∞) = 1/2, n = 0 φ(∞) = φC(∞) = 0, n > 0 | (A105) |
| Autocovariance function | where is a function determined from (22); the first three are: | 0 | (A106) | |
| Power spectrum | where cn is a normalizing constant making the area of the power spectrum ; the first three are c0 = 24, c1 = 240, c2 = 504 | (A107) | ||
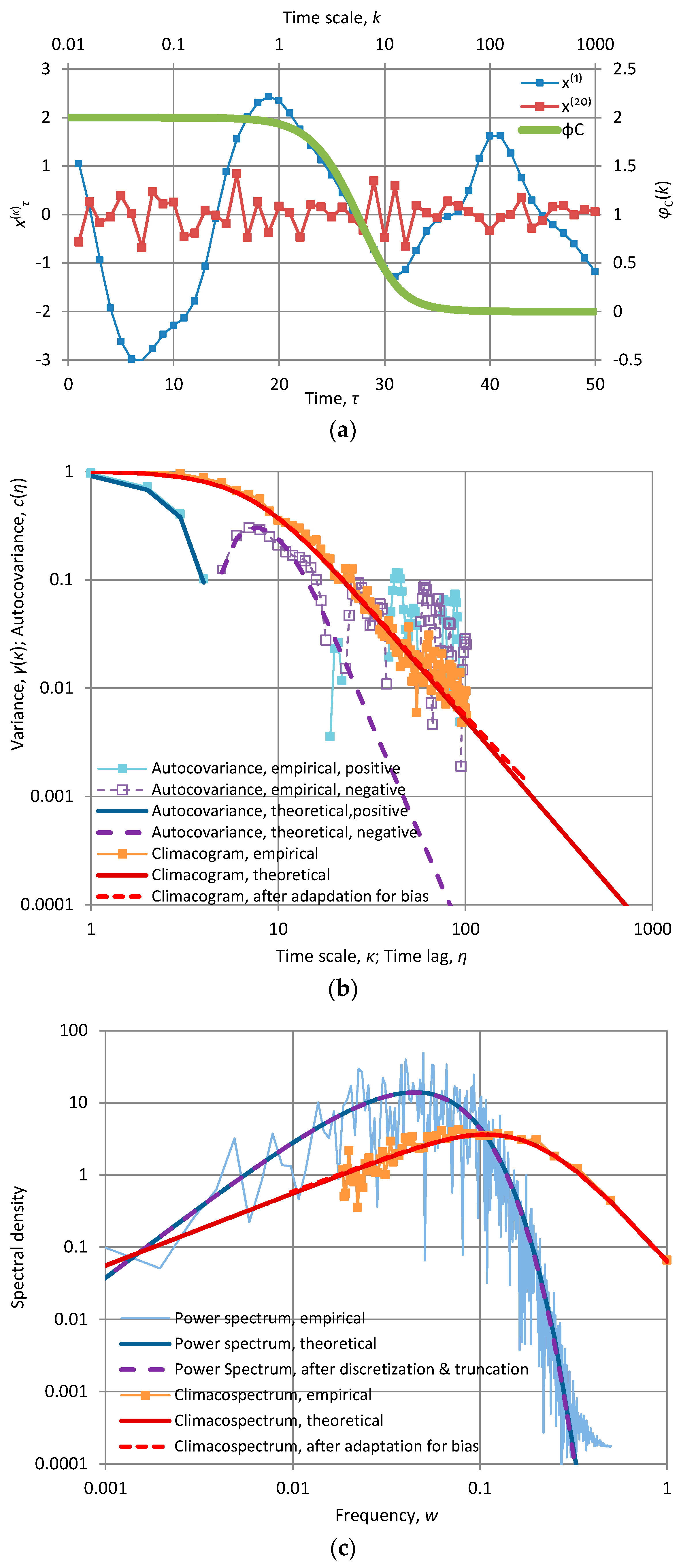
Appendix A.2.8. Harmonic Oscillation Treated as a Stochastic Process
| Characteristic | Mathematical Expression | Local Asymptotic Properties | Global Asymptotic Properties | Equation |
|---|---|---|---|---|
| Climacogram | where T is the period, m ∈ N0 and the harmonic oscillation is described by , 0 ≤ b ≤ T | (A109) | ||
| Climacospectrum | does not converge as k → | (A110) | ||
| Entropy production | (for ) | and do not converge as k → | (A111) | |
| Autocovariance function | 0 | does not converge as k → | (A112) | |
| Power spectrum | (not applicable) | (A113) | ||
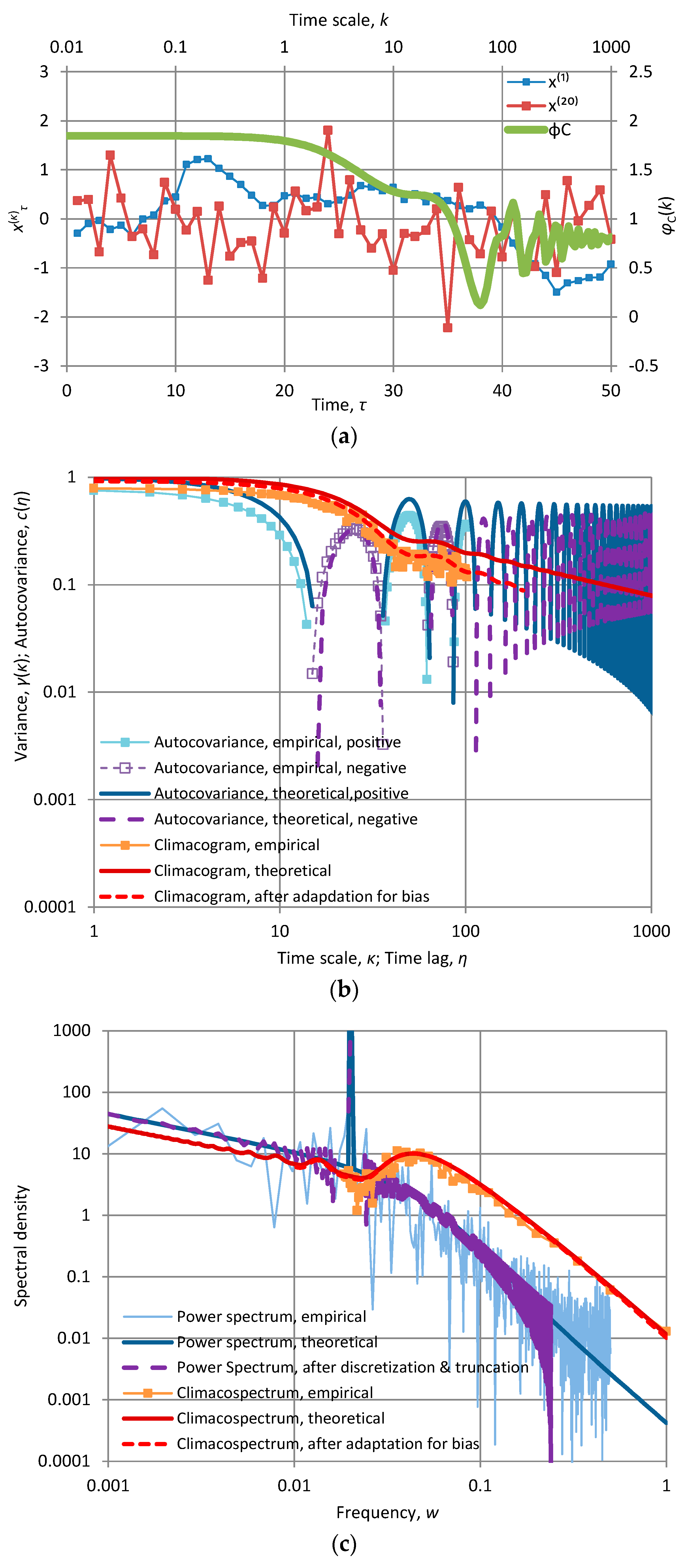
References
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien. Ber. 1877, 76, 373–435. (In German) [Google Scholar]
- Shannon, C.E. The mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Sonuga, J.O. Principle of maximum entropy in hydrologic frequency analysis. J. Hydrol. 1972, 17, 177–191. [Google Scholar] [CrossRef]
- Jackson, D.R.; Aron, G. Parameter estimation in hydrology: The state of the art. J. Am. Water Resour. Assoc. 1971, 7, 457–472. [Google Scholar] [CrossRef]
- Singh, V.P.; Fiorentino, M. A Historical Perspective of Entropy Applications in Water Resources. In Entropy and Energy Dissipation in Water Resources; Singh, V.P., Fiorentino, M., Eds.; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process. 1997, 11, 587–626. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic synthesis using entropy theory: review. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H. Entropy Theory for Groundwater Modeling. Available online: http://www.aggs.in/Issues/JGWR-2015101.pdf (accessed on 24 October 2017).
- Singh, V.P.; Cui, H. Entropy theory for streamflow forecasting. Environ. Process. 2015, 2, 449–460. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw Hill: New York, NY, USA, 2017. [Google Scholar]
- Porporato, A.; Rigby, J.R.; Daly, E. Irreversibility and fluctuation theorem in stationary time series. Phys. Rev. Lett. 2007, 98, 94101. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; Wiley: Chichester, UK, 1998. [Google Scholar]
- Pujol, T.; Llebot, J.E. Extremal principle of entropy production in the climate system. Q. J. R. Meteorol. Soc. 1999, 125, 79–90. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Prigogine, I. Moderation et transformations irreversibles des systemes ouverts. Bull. Classe Sci. Acad. R. Belg. 1945, 31, 600–606. [Google Scholar]
- Ziegler, H. Progress in Solid Mechanics; Sneddon, I.N., Hill, R., Eds.; North-Holland: Amsterdam, The Netherlands, 1963; Volume 4. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426. [Google Scholar] [CrossRef]
- Niven, R. Entropy production extremum principles. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw Hill: New York, NY, USA, 2017. [Google Scholar]
- Koutsoyiannis, D. HESS Opinions: A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res. 2012, 48, W09555. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst-Kolmogorov dynamics as a result of extremal entropy production. Phys. A Stat. Mech. Appl. 2011, 390, 1424–1432. [Google Scholar] [CrossRef]
- Hemelrijk, J. Underlining random variables. Stat. Neerl. 1966, 20. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A simplified proof of the Birkhoff-Khinchin ergodic theorem. Uspekhi Mat. Nauk 1938, 5, 52–56. [Google Scholar]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst–Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Physics of uncertainty, the Gibbs paradox and indistinguishable particles. Stud. Hist. Philos. Mod. Phys. 2013, 44, 480–489. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Entropy: from thermodynamics to hydrology. Entropy 2014, 16, 1287–1314. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Dimitriadis, P.; Lombardo, F.; Stevens, S. From fractals to stochastics: Seeking theoretical consistency in analysis of geophysical data. In Advances in Nonlinear Geosciences; Tsonis, A., Ed.; Springer: New York, NY, USA, 2018. [Google Scholar]
- Dechant, A.; Lutz, E. Wiener-Khinchin theorem for nonstationary scale-invariant processes. Phys. Rev. Lett. 2015, 115, 80603. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B. Gaussian Self-Affinity and Fractals: Globality, the Earth, 1/f Noise, and R/S (Vol. 8); Springer: New York, NY, USA, 2002. [Google Scholar]
- Kitanidis, P.K. Geostatistics. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Gaetan, C.; Guyon, X. Spatial Statistics and Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
- Clark, I. Statistics or geostatistics? Sampling error or nugget effect? J. South. Afr. Inst. Min. Metall. 2010, 110, 307–312. [Google Scholar]
- Gneiting, T.; Schlather, M. Stochastic models that separate fractal dimension and the Hurst effect. SIAM Rev. 2004, 46, 269–282. [Google Scholar] [CrossRef]
- Keshner, M.S. 1/f noise. Proc. IEEE 1982, 70, 212–218. [Google Scholar] [CrossRef]
- Wornell, G.W. Wavelet-based representations for the 1/f family of fractal processes. Proc. IEEE 1993, 81, 1428–1450. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Climatic variability over time scales spanning nine orders of magnitude: Connecting Milankovitch cycles with Hurst–Kolmogorov dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- Pappas, C.; Mahecha, M.D.; Frank, D.C.; Babst, F.; Koutsoyiannis, D. Ecosystem functioning is enveloped by hydrometeorological variability. Nat. Ecol. Evol. 2017, 1, 1263–1270. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.S.; Chester, S.; Meneveau, C. Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 2003, 480, 129–160. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Stochastic synthesis approximating any process dependence and distribution. Stoch. Environ. Res. Risk Assess. 2017. submitted. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003; p. 728. [Google Scholar]
- Swendsen, R.H. How physicists disagree on the meaning of entropy. Am. J. Phys. 2011, 79, 342–348. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data; Springer: New York, NY, USA, 1999. [Google Scholar]
- Beran, J. Statistics for Long-Memory Processes; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Taqqu, M.S. Fractional Brownian motion and long-range dependence. In Theory and Applications of Long-Range Dependence; Doukhan, P., Oppenheim, G., Taqqu, M.S., Eds.; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
| Name of Quantity or Characteristic | Symbol and Definition | Remarks | Equation |
|---|---|---|---|
| Stochastic process of interest | x(t) | Assumed stationary | |
| Time, continuous | t | Dimensional quantity | |
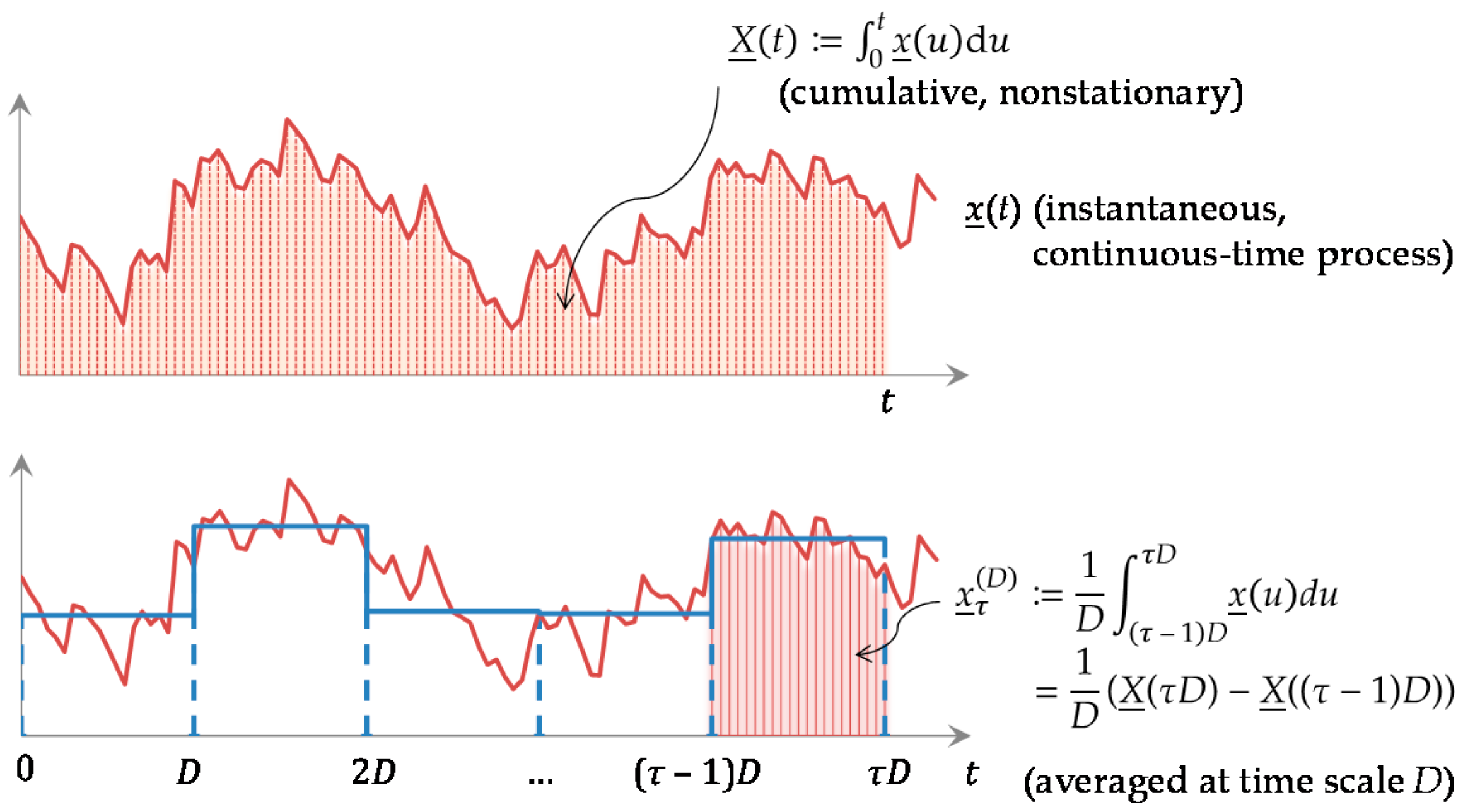
| Cumulative process | Nonstationary | (3) | |
| Variance, instantaneous | γ0 ≔ Var[x(t)] | Constant (not a function of t) | (4) |
| Cumulative climacogram | Γ(t) ≔ Var[X(t)] | A function of t, Γ(0) = 0 | (5) |
| Climacogram | γ(k) ≔ Var[(1/k)(X(t + k) − X(t))] = Var[X(k)/k] = Γ(k)/k2 | Not a function of t, γ(0) = γ0 | (6) |
| Time scale, continuous | k | Units of time | |
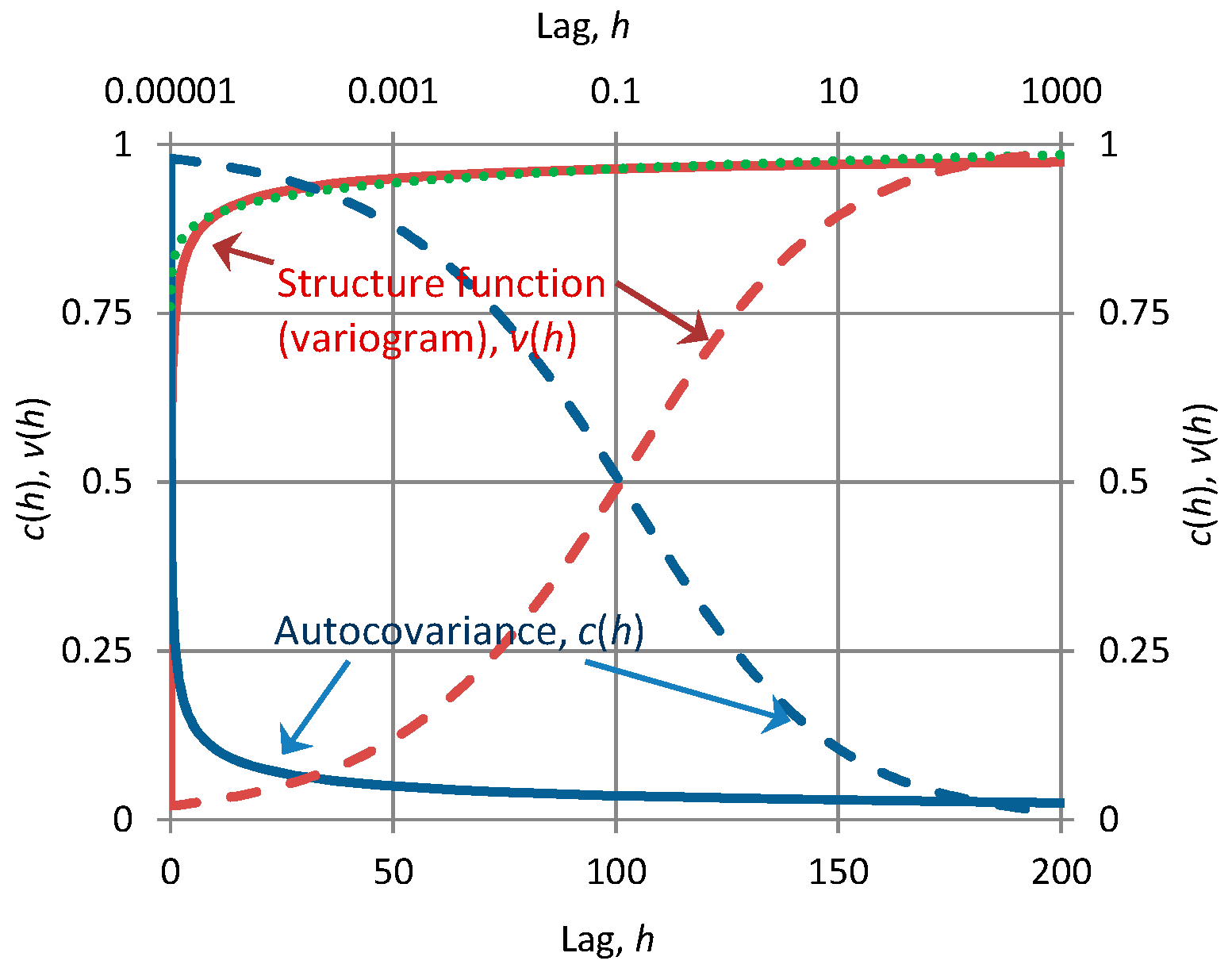
| Autocovariance function | c(h) := Cov[x(t), x(t + h)] | c(0) = γ0 | (7) |
| Time lag, continuous | h | Units of time | |
| Structure function (or semivariogram or variogram) | [x(t) − x(t + h)] | (8) | |
| Climacostructure function | ξ(k) ≔ γ0 − γ(k) | (9) | |
| Power spectrum (or spectral density) | (10) | ||
| Frequency, continuous | w = 1/k | Units of inverse time | (11) |
| Name of Quantity or Characteristic | Symbol and Definition | Remarks | Equation |
|---|---|---|---|
| Stochastic process, discrete time | (12) | ||
| Time unit = discretization time step | D | Time step or length of time window of averaging | |
| Time, discrete | τ := t/D | Dimensionless quantity, integer | (13) |
| Characteristic variance | Var[ ] = γ(D) | (14) | |
| Climacogram | = γ(D) | (15) | |
| Time scale, discrete | κ := k/D | Dimensionless quantity | (16) |
| Autocovariance function | ≔ Cov[] | ||
| Time lag, discrete | η := h/D | Dimensionless quantity | (17) |
| Structure function | (18) | ||
| Power spectrum | (19) | ||
| Frequency, discrete | ω := wD = 1/κ | Dimensionless quantity | (20) |
| Related Characteristics | Direct Relationship | Inverse Relationship | Equation |
|---|---|---|---|
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| ξ(k) ≔ γ0 − γ(k) | γ(k) = ξ(∞) − ξ(k) ( | (25) | |
| (26) | |||
Alternatively, where, in recursive mode, with , | (27) | ||
| (28) | |||
| (29) |
| Persistence | Smoothness | ||
|---|---|---|---|
| Maximal Roughness | Neutral Smoothness | Maximal Smoothness | |
| Maximal Persistence, | ~FHK | ~FHK | ~FHK |
| Neutral Persistence | ~FHK | Markov, FHK | SE, GP, FHK |
| Maximal Antipersistence | ~FHK | AE, FHK | GP, FHK |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoyiannis, D. Entropy Production in Stochastics. Entropy 2017, 19, 581. https://doi.org/10.3390/e19110581
Koutsoyiannis D. Entropy Production in Stochastics. Entropy. 2017; 19(11):581. https://doi.org/10.3390/e19110581
Chicago/Turabian StyleKoutsoyiannis, Demetris. 2017. "Entropy Production in Stochastics" Entropy 19, no. 11: 581. https://doi.org/10.3390/e19110581





