Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy
Abstract
:1. Introduction
No one is considered scientifically literate today who does not know what a Gaussian distribution is or the meaning and scope of the concept of entropy. It is possible to believe that no one will be considered scientifically literate tomorrow who is not equally familiar with fractals.—Attributed to John A. Wheeler (1983)
2. Theoretical Models
2.1. The Relation of Fractal Dimension to Entropy
2.2. Entropy and Fractal Dimension Indicating Geo-Spatial Development
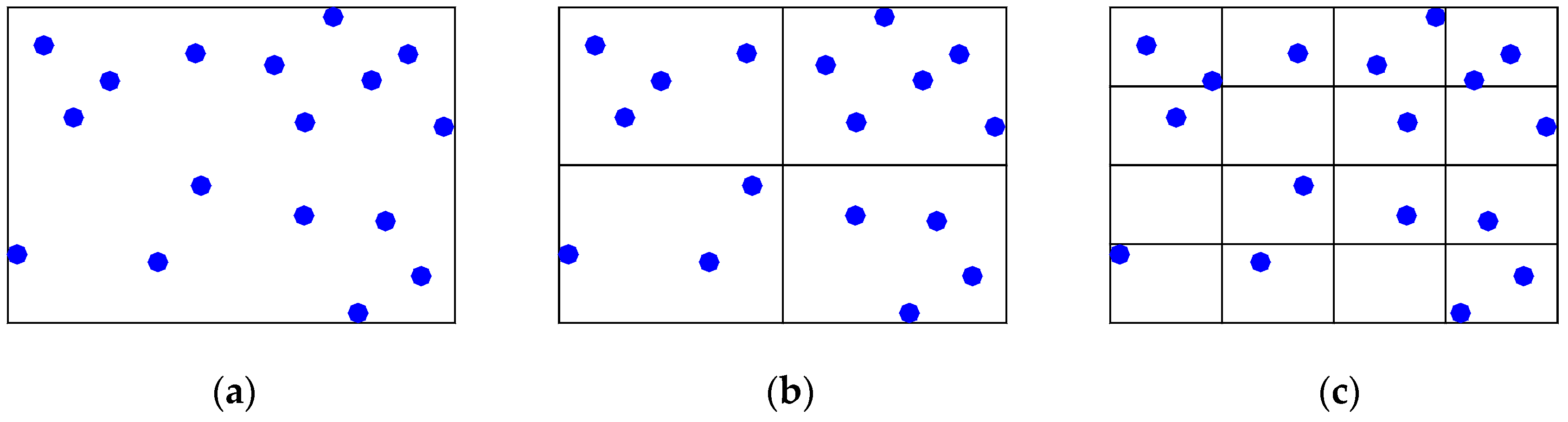
3. Materials and Methods
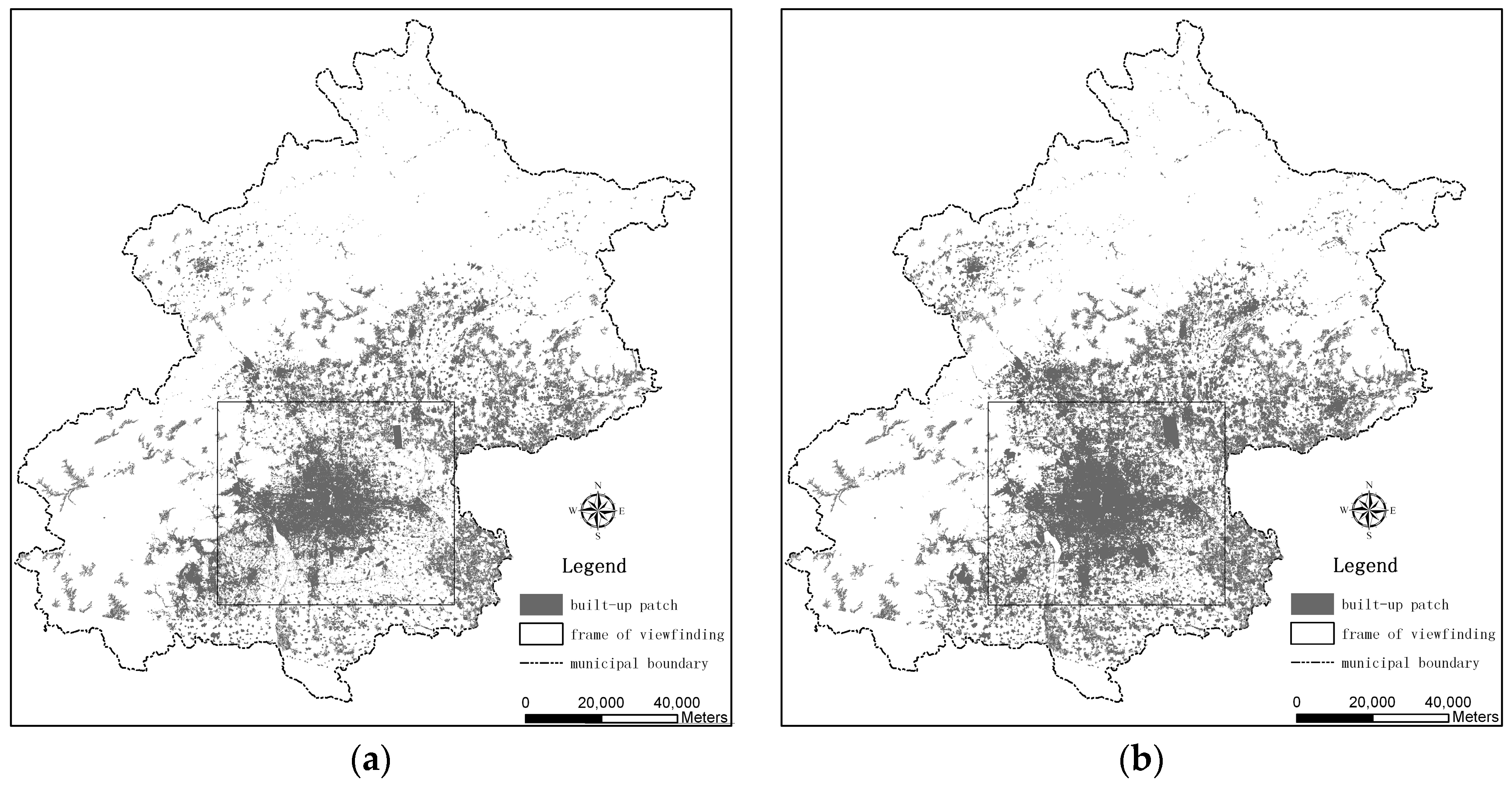
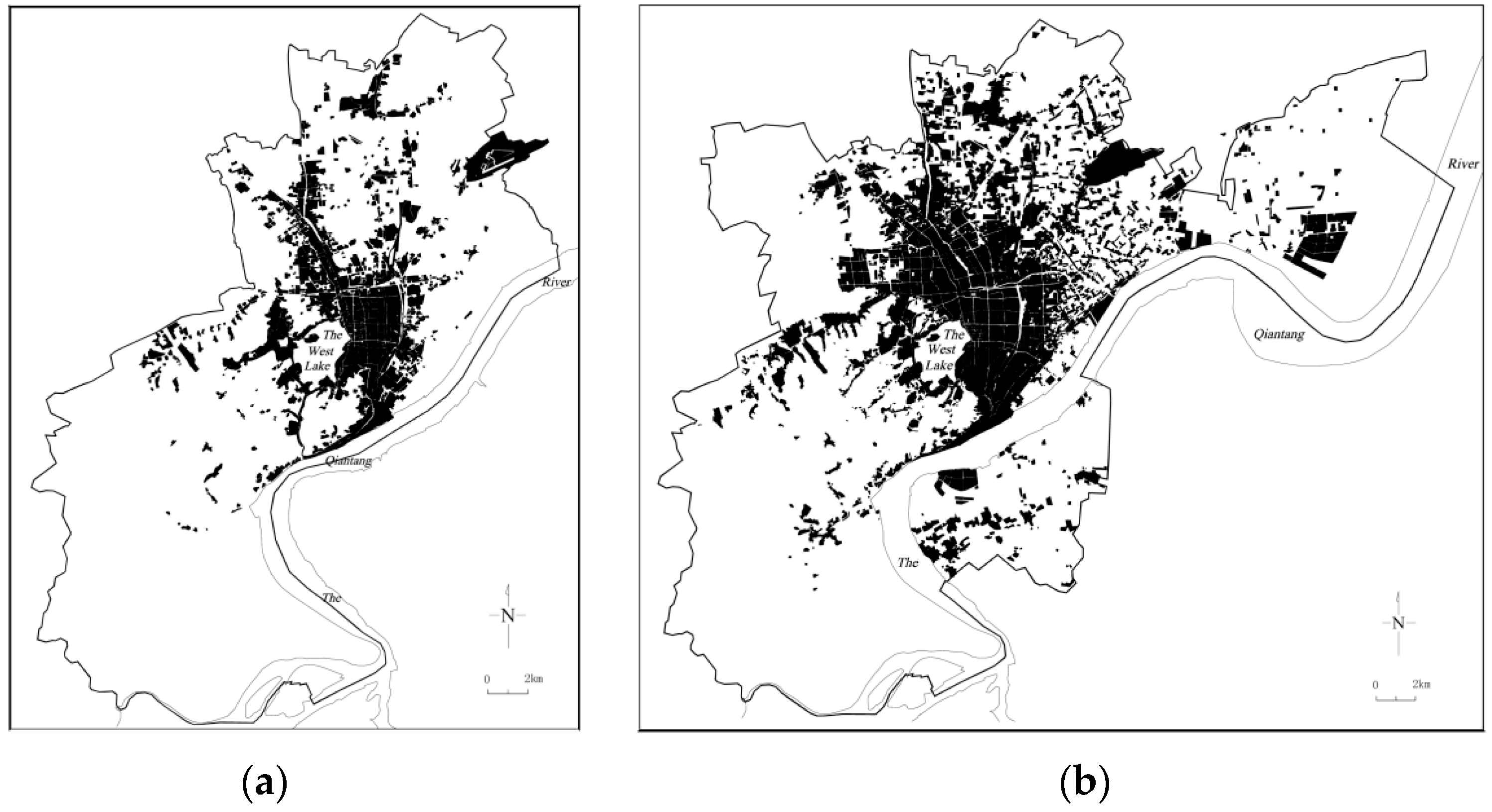
3.1. Study Area, Data, and Approaches
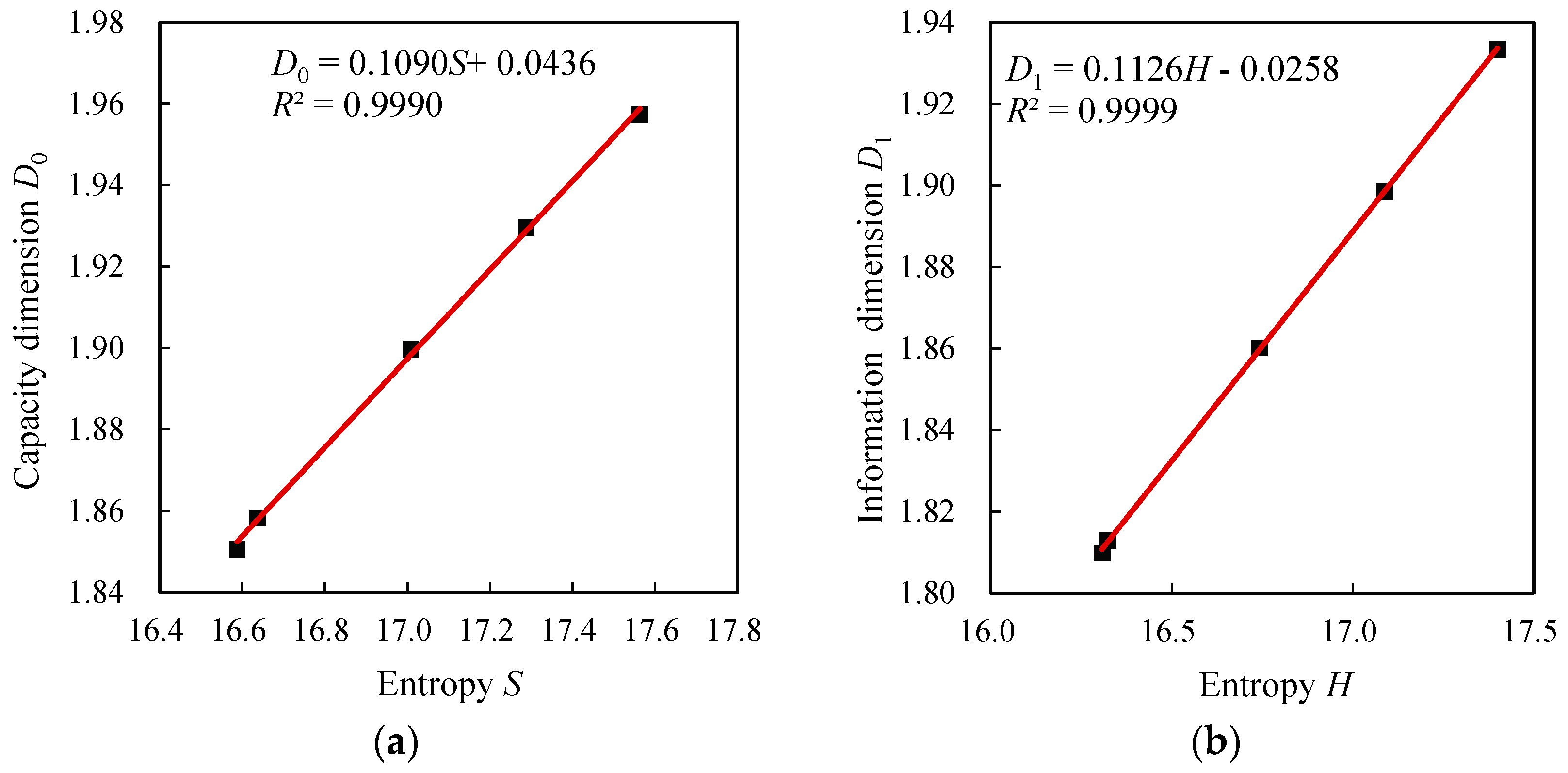
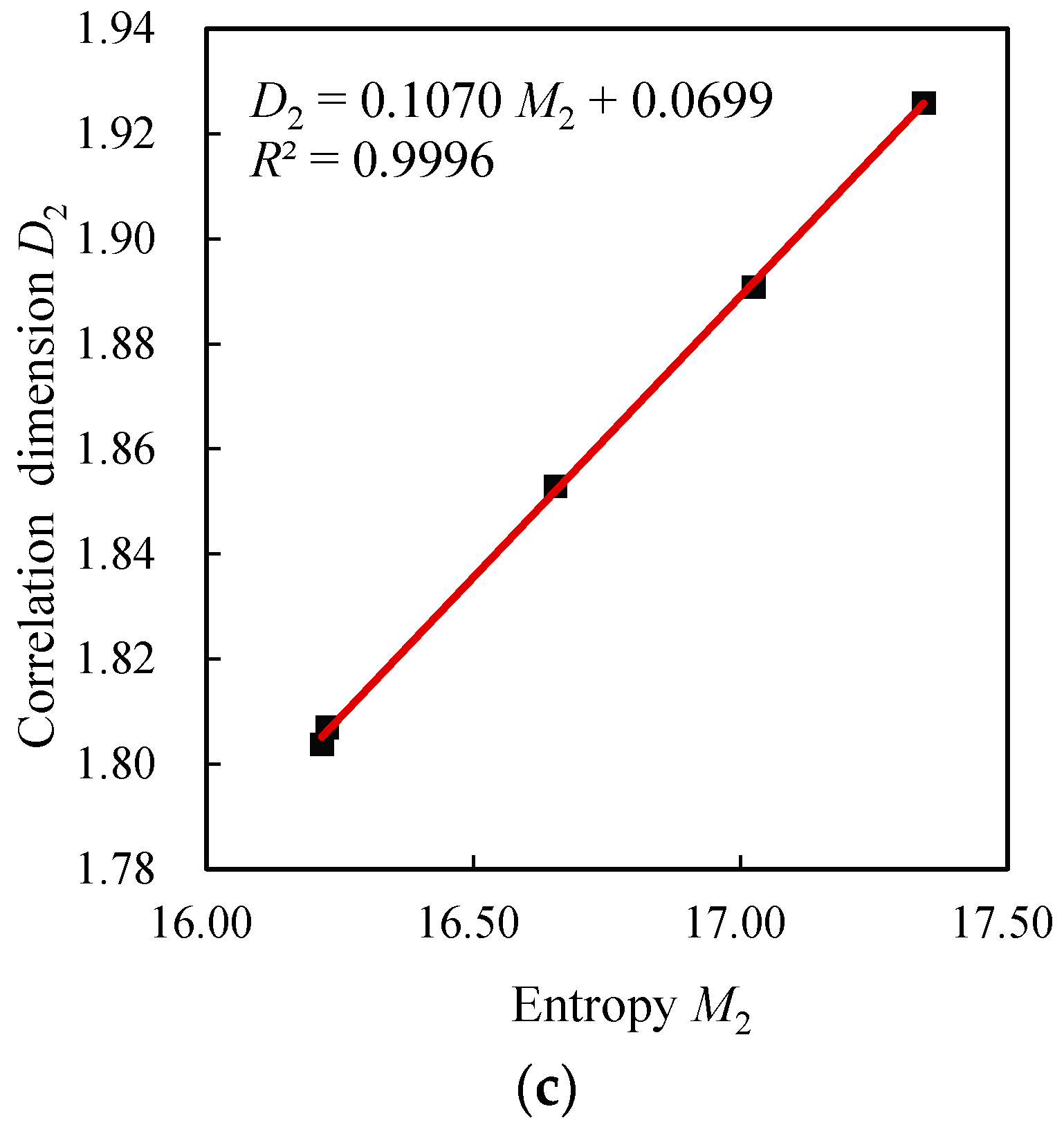
3.2. Results and Findings Based on Fixed Box Method
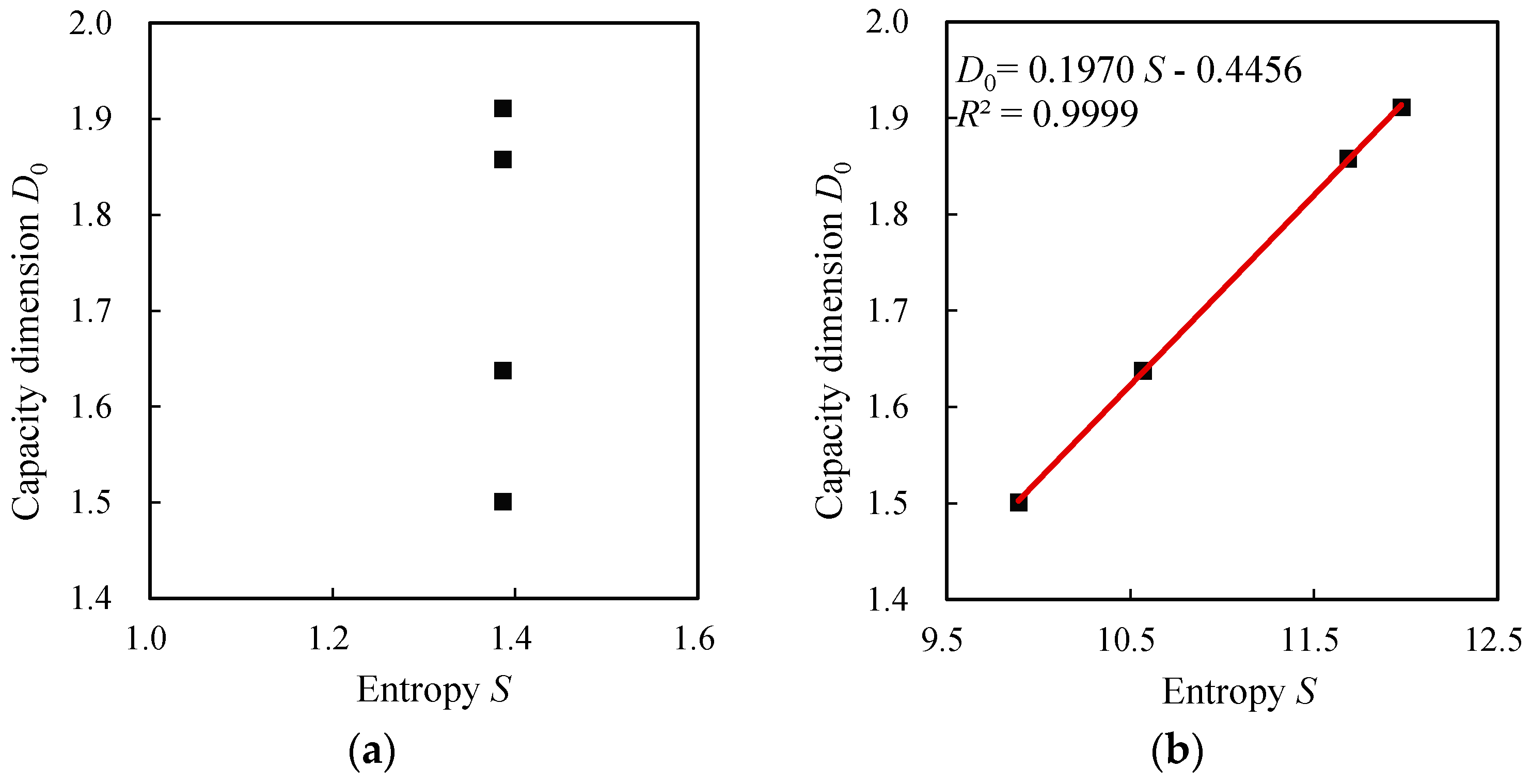
3.3. Observational Evidences and Findings Based on Unfixed Box Method
4. Discussion
- (1)
- The problem of methods. It is hard to find solutions to this kind of problem. In fact, for a random system or based on random variables, it is unlikely to find the true parameter values for a mathematical model. Even for the simplest linear regression model, it is impossible to evaluate the real parameters by empirical analysis. A number of algorithms such as least squares method, maximum likelihood method, major axis, and reduced major axis can be used to estimate the regression coefficients, but different methods result in different parameter values. Scientists then look for comparable parameter values instead of real parameter values.
- (2)
- The problems of fractal objects. The real fractals in geometry are just like the high-dimensional spaces in linear algebra, which can be imagined but can never be observed. All the fractal images we encounter in books and articles represent prefractals rather than real fractals. A real fractal has infinite levels, but a prefractal is a limited hierarchy. The basic property of a random prefractal object is that its scaling is limited. For a given aspect (area or boundary) of a regular monofractal, its fractal dimension value is unique, and the real fractal dimension can be calculated through its prefractal structure. However, for a regular multifractal object, different parts have different local fractal dimension values, and the real fractal dimension values cannot be computed by applying a geometric method to its prefractal structure. We can compute its actual fractal parameter values by finding the numerical solutions to its multifractal transcendental equation. A city in the real world is actually a complex random multifractal system with prefractal structure. Different sizes of study area bear different global fractal dimensions, and different parts bear different local fractal dimensions. As a result, changing the scope or central location of study area will yield different fractal parameter values. We never know the real fractal dimension value set. Fortunately, as indicated above, we need comparable parameter values rather than real parameter values, and we can utilize multifractal dimension spectrums to make global and local analyses for complex urban morphology.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gould, P.R. Pedagogic review: Entropy in urban and regional modelling. Ann. Assoc. Am. Geogr. 1972, 62, 689–700. [Google Scholar] [CrossRef]
- Batty, M. Spatial entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Batty, M. Entropy in spatial aggregation. Geogr. Anal. 1976, 8, 1–21. [Google Scholar] [CrossRef]
- Chen, Y.-G. The distance-decay function of geographical gravity model: Power law or exponential law? Chaos Solitons Fractals 2015, 77, 174–189. [Google Scholar] [CrossRef]
- Wilson, A.G. Complex Spatial Systems: The Modelling Foundations of Urban and Regional Analysis; Pearson Education: Singapore, 2000. [Google Scholar]
- Anastassiadis, A. New derivations of the rank-size rule using entropy-maximising methods. Environ. Plan. B Plan. Des. 1986, 13, 319–334. [Google Scholar] [CrossRef]
- Bussiere, R.; Snickers, F. Derivation of the negative exponential model by an entropy maximizing method. Environ. Plan. A 1970, 2, 295–301. [Google Scholar] [CrossRef]
- Chen, Y.-G. A wave-spectrum analysis of urban population density: Entropy, fractal, and spatial localization. Discret. Dyn. Nat. Soc. 2008. [Google Scholar] [CrossRef]
- Chen, Y.-G. The rank-size scaling law and entropy-maximizing principle. Phys. A Stat. Mech. Appl. 2012, 391, 767–778. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Liu, J.-S. Derivations of fractal models of city hierarchies using entropy-maximization principle. Prog. Nat. Sci. 2002, 12, 208–211. [Google Scholar]
- Curry, L. The random spatial economy: An exploration in settlement theory. Ann. Assoc. Am. Geogr. 1964, 54, 138–146. [Google Scholar] [CrossRef]
- Wilson, A.G. Modelling and systems analysis in urban planning. Nature 1968, 220, 963–966. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.G. Entropy in Urban and Regional Modelling; Pion Press: London, UK, 1970. [Google Scholar]
- Cressie, N.A. Change of support and the modifiable areal unit problem. Geogr. Syst. 1996, 3, 159–180. [Google Scholar]
- Kwan, M.P. The uncertain geographic context problem. Ann. Assoc. Am. Geogr. 2012, 102, 958–968. [Google Scholar] [CrossRef]
- Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwick, UK, 1983. [Google Scholar]
- Unwin, D.J. GIS, spatial analysis and spatial statistics. Prog. Hum. Geogr. 1996, 20, 540–551. [Google Scholar] [CrossRef]
- Chen, Y.-G. Simplicty, complexity, and mathematical modeling of geographical distributions. Prog. Geogr. 2015, 34, 321–329. (In Chinese) [Google Scholar]
- Jiang, B.; Brandt, S.A. A Fractal perspective on scale in geography. Int. J. Geo-Inf. 2016, 5, 95. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Batty, M. New ways of looking at cities. Nature 1995, 377, 574. [Google Scholar] [CrossRef]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Frankhauser, P. The fractal approach: A new tool for the spatial analysis of urban agglomerations. Popul. Engl. Sel. 1998, 10, 205–240. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Ryabko, B.Y. Noise-free coding of combinatorial sources, Hausdorff dimension and Kolmogorov complexity. Probl. Pereda. Inf. 1986, 22, 16–26. [Google Scholar]
- Chen, T. Studies on Fractal Systems of Cities and Towns in the Central Plains of China. Master’s Thesis, Northeast Normal University, Changchun, China, 15 June 1995. (In Chinese). [Google Scholar]
- Chen, Y.-G. Fractal analytical approach of urban form based on spatial correlation function. Chaos Solitons Fractals 2013, 49, 47–60. [Google Scholar] [CrossRef]
- Jullien, R.; Botet, R. Aggregation and Fractal Aggregates; World Scientific Publishing Co.: Singapore, 1987. [Google Scholar]
- Vicsek, T. Fractal Growth Phenomena; World Scientific Publishing Co.: Singapore, 1989. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- Chen, Y.-G. Fractal dimension evolution and spatial replacement dynamics of urban growth. Chaos Solitons Fractals 2012, 45, 115–124. [Google Scholar] [CrossRef]
- Longley, P.A.; Batty, M.; Shepherd, J. The size, shape and dimension of urban settlements. Trans. Inst. Br. Geogr. (New Ser.) 1991, 16, 75–94. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modeling approach to the evolution of urban land-use patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960. [Google Scholar]
- Fan, Y.; Yu, G.-M.; He, Z.-Y.; Yu, H.-L.; Bai, R.; Yang, L.R.; Wu, D. Entropies of the Chinese land use/cover change from 1990 to 2010 at a county level. Entropy 2017, 19, 51. [Google Scholar] [CrossRef]
- Padmanaban, R.; Bhowmik, A.K.; Cabral, P.; Zamyatin, A.; Almegdadi, O.; Wang, S.G. Modelling urban sprawl using remotely sensed data: A case study of Chennai City, Tamilnadu. Entropy 2017, 19, 163. [Google Scholar] [CrossRef]
- Grassberger, P. Generalizations of the Hausdorff dimension of fractal measures. Phys. Lett. A 1985, 107, 101–105. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Multifractals and 1/f Noise: Wild Self-Affinity in Physics (1963–1976); Springer: New York, NY, USA, 1999. [Google Scholar]
- Grassberger, P. Generalized dimensions of strange attractors. Phys. Lett. A 1983, 97, 227–230. [Google Scholar] [CrossRef]
- Batty, M. The fractal nature of geography. Geogr. Mag. 1992, 64, 33–36. [Google Scholar]
- Wheeler, J.A. Review on the Fractal Geometry of Nature by Benoit B. Mandelbrot. Am. J. Phys. 1983, 51, 286–287. [Google Scholar]
- Chen, Y.-G.; Wang, J.-J. Multifractal characterization of urban form and growth: The case of Beijing. Environ. Plan. B Plan. Des. 2013, 40, 884–904. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Tsonis, A.A. Functional box-counting and multiple elliptical dimensions in rain. Science 1987, 235, 1036–1038. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Chen, Y.G. Spatiotemporal evolution of urban form and land use structure in Hangzhou, China: Evidence from fractals. Environ. Plan. B Plan. Des. 2010, 37, 838–856. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Mark, D.M. The fractal nature of geographical phenomena. Ann. Assoc. Am. Geogr. 1987, 77, 265–278. [Google Scholar] [CrossRef]
- Benguigui, L.; Czamanski, D.; Marinov, M.; Portugali, Y. When and where is a city fractal? Environ. Plan. B Plan. Des. 2000, 27, 507–519. [Google Scholar] [CrossRef]
- Clark, C. Urban population densities. J. R. Stat. Soc. 1951, 114, 490–496. [Google Scholar] [CrossRef]
- Takayasu, H. Fractals in the Physical Sciences; Manchester University Press: Manchester, UK, 1990. [Google Scholar]
- Feng, J. Modeling the spatial distribution of urban population density and its evolution in Hangzhou. Geogr. Res. 2002, 21, 635–646. (In Chinese) [Google Scholar]
- Cramer, F. Chaos and Order: The Complex Structure of Living Systems; Loewus, D.I., Translator; VCH Publishers: New York, NY, USA, 1993. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Bar-Yam, Y. Multiscale complexity/entropy. Adv. Complex Syst. 2004, 7, 47–63. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Multiscale variety in complex systems. Complexity 2004, 9, 37–45. [Google Scholar] [CrossRef]
- Carroll, C. National city-size distributions: What do we know after 67 years of research? Prog. Hum. Geogr. 1982, 6, 1–43. [Google Scholar] [CrossRef]
- Barabasi, A.-L.; Bonabeau, E. Scale-free networks. Sci. Am. 2003, 288, 50–59. [Google Scholar] [CrossRef]
- Smeed, R.J. Road development in urban area. J. Inst. Highw. Eng. 1963, 10, 5–30. [Google Scholar]
- Chen, Y.-G. Defining urban and rural regions by multifractal spectrums of urbanization. Fractals 2016, 24, 1650004. [Google Scholar] [CrossRef]
- Moore, G.E. Cramming more components onto integrated circuits. Proc. IEEE 1998, 86, 82–85, (Reprinted from Electronics, pp. 114–117, 19 April 1965). [Google Scholar] [CrossRef]
- Arbesman, S. The Half-Life of Facts: Why Everything We Know Has an Expiration Date; Penguin Group: New York, NY, USA, 2012. [Google Scholar]
- Moore, G.E. Moore’s law at 40. In Understanding Moore’s Law: Four Decades of Innovation; Brock, D., Ed.; Chemical Heritage Foundation: Philadelphia, PA, USA, 2006; pp. 67–84. [Google Scholar]
- Ariza-Villaverde, A.B.; Jimenez-Hornero, F.J.; De Rave, E.G. Multifractal analysis of axial maps applied to the study of urban morphology. Comput. Environ. Urban Syst. 2013, 38, 1–10. [Google Scholar] [CrossRef]
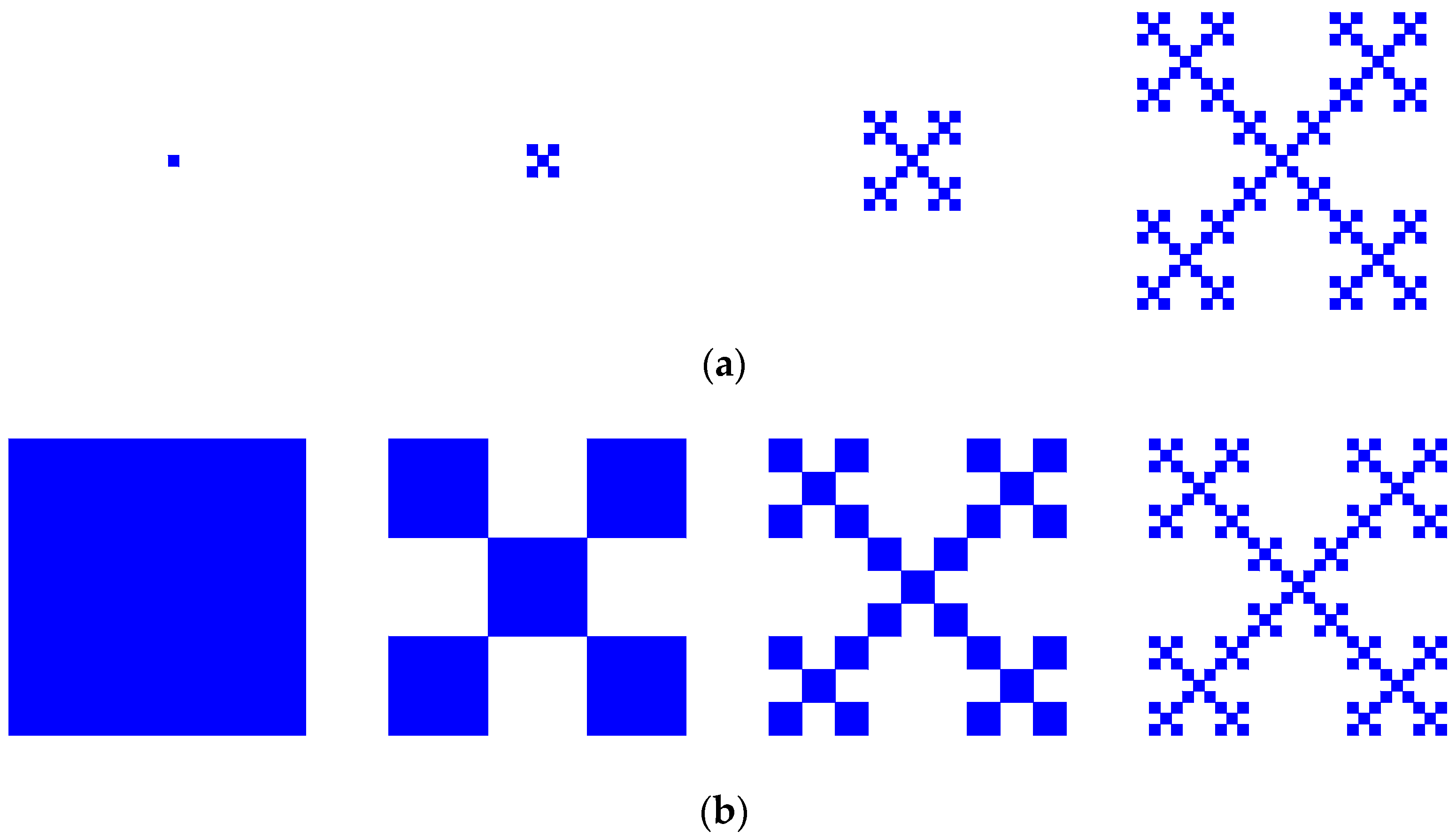
| Step m | Linear Size of Fractal Copies εm | Number of Fractal Copies Nm(ε) | Entropy H (nat) | Fractal Dimension D |
|---|---|---|---|---|
| 1 | 1/30 | 50 | 0.000 | (0, or 2) |
| 2 | 1/31 | 51 | 1.609 | 1.465 |
| 3 | 1/32 | 52 | 3.219 | 1.465 |
| 4 | 1/33 | 53 | 4.828 | 1.465 |
| 5 | 1/34 | 54 | 6.438 | 1.465 |
| 6 | 1/35 | 55 | 8.047 | 1.465 |
| 7 | 1/36 | 56 | 9.657 | 1.465 |
| 8 | 1/37 | 57 | 11.266 | 1.465 |
| 9 | 1/38 | 58 | 12.876 | 1.465 |
| 10 | 1/39 | 59 | 14.485 | 1.465 |
| … | … | … | … | … |
| m | 1/3m−1 | 5m−1 | (m − 1)ln(5) | ln(5)/ln(3) |
| Scale (ε) | Three Types of Entropy Values (Mq) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 1992 | 1999 | 2006 | 2009 | |||||||||||
| M0 (q = 0) | M1 (q = 1) | M2 (q = 2) | M0 (q = 0) | M1 (q = 1) | M2 (q = 2) | M0 (q = 0) | M1 (q = 1) | M2 (q = 2) | M0 (q = 0) | M1 (q = 1) | M2 (q = 2) | M0 (q = 0) | M1 (q = 1) | M2 (q = 2) | |
| 1/20 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1/21 | 2.0000 | 1.9672 | 1.9364 | 2.0000 | 1.9775 | 1.9569 | 2.0000 | 1.9650 | 1.9279 | 2.0000 | 1.9964 | 1.9928 | 2.0000 | 1.9942 | 1.9886 |
| 1/22 | 4.0000 | 3.5770 | 3.2749 | 4.0000 | 3.4693 | 3.1363 | 4.0000 | 3.6850 | 3.4668 | 4.0000 | 3.8306 | 3.6976 | 4.0000 | 3.9231 | 3.8617 |
| 1/23 | 6.0000 | 5.3986 | 5.0152 | 6.0000 | 5.2657 | 4.8831 | 6.0000 | 5.5608 | 5.2991 | 6.0000 | 5.7431 | 5.5816 | 6.0000 | 5.8783 | 5.7959 |
| 1/24 | 7.9944 | 7.2654 | 6.8736 | 7.9887 | 7.1303 | 6.7571 | 7.9887 | 7.4614 | 7.1875 | 7.9887 | 7.6778 | 7.5024 | 7.9944 | 7.8342 | 7.7421 |
| 1/25 | 9.9233 | 9.1260 | 8.7581 | 9.9672 | 9.0084 | 8.6618 | 9.9556 | 9.3590 | 9.0951 | 9.9672 | 9.6112 | 9.4351 | 9.9701 | 9.7897 | 9.6896 |
| 1/26 | 11.7224 | 10.9502 | 10.6430 | 11.8986 | 10.8623 | 10.5656 | 11.8431 | 11.2301 | 10.9973 | 11.8986 | 11.5117 | 11.3460 | 11.9263 | 11.7163 | 11.6131 |
| 1/27 | 13.3201 | 12.7152 | 12.4926 | 13.7249 | 12.6723 | 12.4488 | 13.5868 | 13.0592 | 12.8761 | 13.7249 | 13.3678 | 13.2316 | 13.8404 | 13.6112 | 13.5160 |
| 1/28 | 14.9124 | 14.4897 | 14.3423 | 15.5017 | 14.4859 | 14.3320 | 15.2798 | 14.8915 | 14.7582 | 15.5017 | 15.2185 | 15.1195 | 15.7081 | 15.4972 | 15.4202 |
| 1/29 | 16.5871 | 16.3073 | 16.2155 | 17.2877 | 16.3234 | 16.2255 | 17.0079 | 16.7416 | 16.6532 | 17.2877 | 17.0879 | 17.0245 | 17.5632 | 17.3994 | 17.3428 |
| Type | Parameter/Statistic | 1988 | 1992 | 1999 | 2006 | 2009 |
|---|---|---|---|---|---|---|
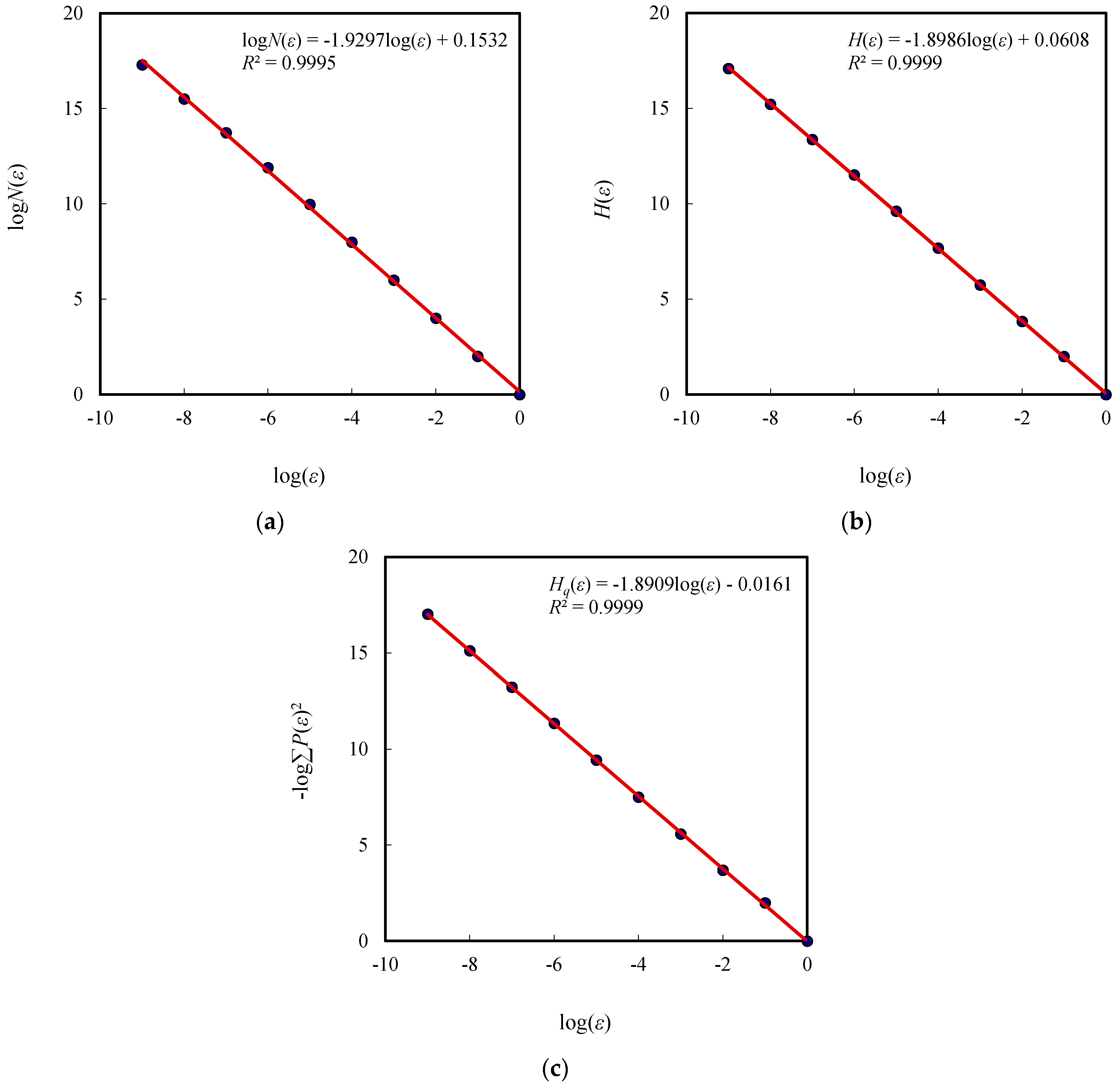
| Capacity dimension D0 | Parameter D0 | 1.8507 | 1.8584 | 1.8998 | 1.9297 | 1.9575 |
| Standard error δ | 0.0310 | 0.0299 | 0.0222 | 0.0160 | 0.0095 | |
| R Square R2 | 0.9978 | 0.9979 | 0.9989 | 0.9995 | 0.9998 | |
| Information dimension D1 | Parameter D1 | 1.8099 | 1.8130 | 1.8602 | 1.8986 | 1.9335 |
| Standard error δ | 0.0070 | 0.0114 | 0.0050 | 0.0053 | 0.0051 | |
| R Square R2 | 0.9999 | 0.9997 | 0.9999 | 0.9999 | 0.9999 | |
| Correlation dimension D2 | Parameter D2 | 1.8039 | 1.8071 | 1.8530 | 1.8909 | 1.9259 |
| Standard error δ | 0.0201 | 0.0271 | 0.0130 | 0.0065 | 0.0027 | |
| R Square R2 | 0.9990 | 0.9982 | 0.9996 | 0.9999 | 1.0000 |
| Moment Order q | Correlation Coefficient Square (R2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ε = 1/21 | ε = 1/22 | ε = 1/23 | ε = 1/24 | ε = 1/25 | ε = 1/26 | ε = 1/27 | ε = 1/28 | ε = 1/29 | |
| q = 0 | -- | -- | -- | 0.0095 | 0.9330 | 0.9786 | 0.9963 | 1.0000 | 0.9990 |
| q = 1 | 0.5909 | 0.9460 | 0.9549 | 0.9641 | 0.9768 | 0.9877 | 0.9963 | 0.9994 | 0.9999 |
| q = 2 | 0.5460 | 0.9640 | 0.9780 | 0.9846 | 0.9893 | 0.9925 | 0.9966 | 0.9989 | 0.9996 |
| Type | Box Size | Parameter and Statistic | R Square R2 | |||
|---|---|---|---|---|---|---|
| 1949 | 1959 | 1980 | 1996 | |||
| Entropy | 1/21 | 1.3863 | 1.3863 | 1.3863 | 1.3863 | -- |
| 1/22 | 2.7081 | 2.7081 | 2.7726 | 2.7726 | 0.8992 | |
| 1/23 | 3.6376 | 3.7842 | 4.1431 | 4.1431 | 0.9812 | |
| 1/24 | 4.3820 | 4.7536 | 5.4161 | 5.4765 | 0.9943 | |
| 1/25 | 5.3132 | 5.8201 | 6.6631 | 6.7979 | 0.9981 | |
| 1/26 | 6.3244 | 6.9048 | 7.8793 | 8.0983 | 0.9997 | |
| 1/27 | 7.3896 | 8.0446 | 9.1344 | 9.2927 | 0.9975 | |
| 1/28 | 8.5704 | 9.2595 | 10.3984 | 10.6780 | 0.9999 | |
| 1/29 | 9.8901 | 10.5666 | 11.6846 | 11.9757 | 0.9999 | |
| Capacity dimension | Parameter D0 | 1.5013 | 1.6379 | 1.8581 | 1.9115 | |
| R Square R2 | 0.9953 | 0.9983 | 0.9995 | 0.9997 | ||
| Standard error δ | 0.0365 | 0.0236 | 0.0148 | 0.0112 | ||
| Eigen entropy | Parameter b | 0.6630 | 0.6095 | 0.5379 | 0.5230 | |
| R Square R2 | 0.9953 | 0.9983 | 0.9995 | 0.9997 | ||
| Entropy 1/b | 1.5084 | 1.6406 | 1.8591 | 1.9120 | ||
| Year | Average Density (ρ) | Characteristic Radius (r0) | Entropy (H) | Entropy Ratio (H/Hmax) |
|---|---|---|---|---|
| 1964 | 4721.3643 | 3.5644 | 2.4593 | 0.7548 |
| 1982 | 5702.7587 | 3.6713 | 2.4843 | 0.7625 |
| 1990 | 6774.3742 | 3.6285 | 2.5486 | 0.7822 |
| 2000 | 8411.6099 | 3.9457 | 2.7251 | 0.8364 |
| Year | a | b | R2 | 1/b | Dq |
|---|---|---|---|---|---|
| 1988 | 1.1183 | 0.5391 | 0.9978 | 1.8549 | 1.8507 |
| 1.0132 | 0.5525 | 0.9999 | 1.8101 | 1.8099 | |
| 0.9367 | 0.5538 | 0.9990 | 1.8057 | 1.8039 | |
| 1992 | 1.1122 | 0.5370 | 0.9979 | 1.8622 | 1.8584 |
| 0.9842 | 0.5514 | 0.9997 | 1.8136 | 1.8130 | |
| 0.9088 | 0.5524 | 0.9982 | 1.8103 | 1.8071 | |
| 1999 | 1.0787 | 0.5258 | 0.9989 | 1.9018 | 1.8998 |
| 1.0089 | 0.5375 | 0.9999 | 1.8603 | 1.8602 | |
| 0.9577 | 0.5395 | 0.9996 | 1.8537 | 1.8530 | |
| 2006 | 1.0547 | 0.5179 | 0.9995 | 1.9308 | 1.9297 |
| 1.0222 | 0.5267 | 0.9999 | 1.8987 | 1.8986 | |
| 0.9938 | 0.5288 | 0.9999 | 1.8911 | 1.8909 | |
| 2009 | 1.0324 | 0.5108 | 0.9998 | 1.9578 | 1.9575 |
| 1.0229 | 0.5172 | 0.9999 | 1.9336 | 1.9335 | |
| 1.0109 | 0.5192 | 1.0000 | 1.9260 | 1.9259 |
| Type | Entropy | Fractal Dimension |
|---|---|---|
| Distribution | Gaussian (normal) distribution | Pareto-Mandelbrot (power-law) distribution |
| Scale | Based on characteristic scale | Based on scaling (scale-free) |
| System | Determinate systems | Complex systems |
| Symmetry | Spatio-temporal translational symmetry | Scaling symmetry (invariance under contraction or dilation) |
| Variation | Different types of entropy | Different types of fractal dimension |
| State | Order or chaos | Edge of chaos |
| Spatial measurement | The results depend on the method, the scope of the study area, and the linear size | The results depend on the method and the scope of the study area, but not on the linear size |
| Sphere of application | (1) The patterns and processes with characteristic scale (determinate length, size, mean, eigen value ); (2) Global analysis | (1) The patterns and processes without characteristic scale (indeterminate length, size, mean, eigen value ); (2) Both global and local analysis. |
| Example 1 | Urban population density (Table 6) | Urban land use pattern (Table 4 and Table 5) |
| Example 2 | Size distributions of road lengths | Urban traffic network |
| Example 3 | Lognormal distribution of city size | Power-law distribution of city size |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, J.; Feng, J. Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy. Entropy 2017, 19, 600. https://doi.org/10.3390/e19110600
Chen Y, Wang J, Feng J. Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy. Entropy. 2017; 19(11):600. https://doi.org/10.3390/e19110600
Chicago/Turabian StyleChen, Yanguang, Jiejing Wang, and Jian Feng. 2017. "Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy" Entropy 19, no. 11: 600. https://doi.org/10.3390/e19110600





