Revealing Tripartite Quantum Discord with Tripartite Information Diagram
Abstract
:1. Introduction
2. Quantum Discord
3. Revealing Tripartite Quantum Discord with Tripartite Information Diagram
4. Tripartite Quantum Discord Focused on One Subsystem for Pure States
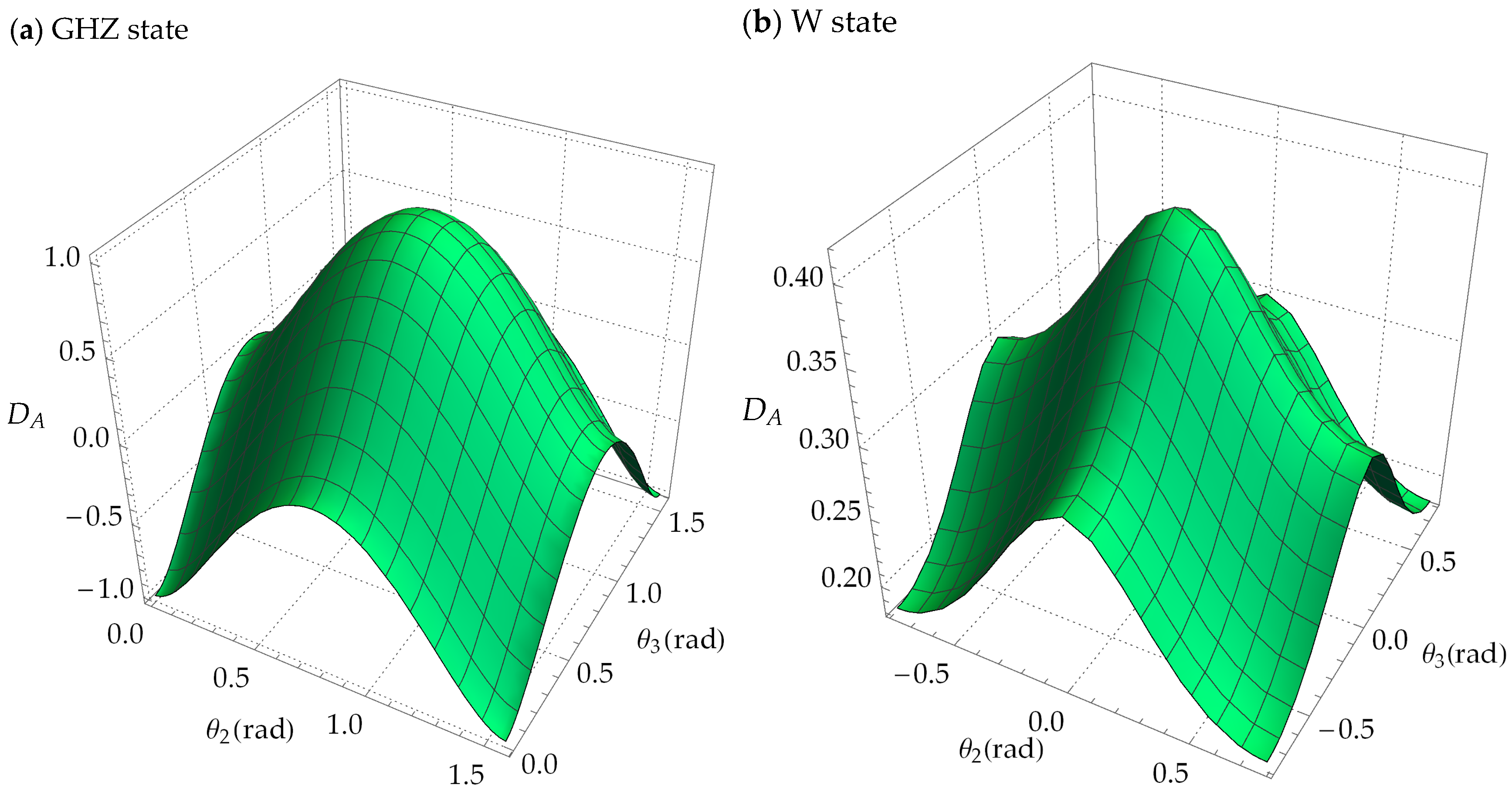
4.1. Tripartite Quantum Discord Focused on One Subsystem for GHZ State
4.2. Tripartite Quantum Discord Focused on One Subsystem for W State
5. Tripartite Quantum Discord Focused on One Subsystem for the Mixed States
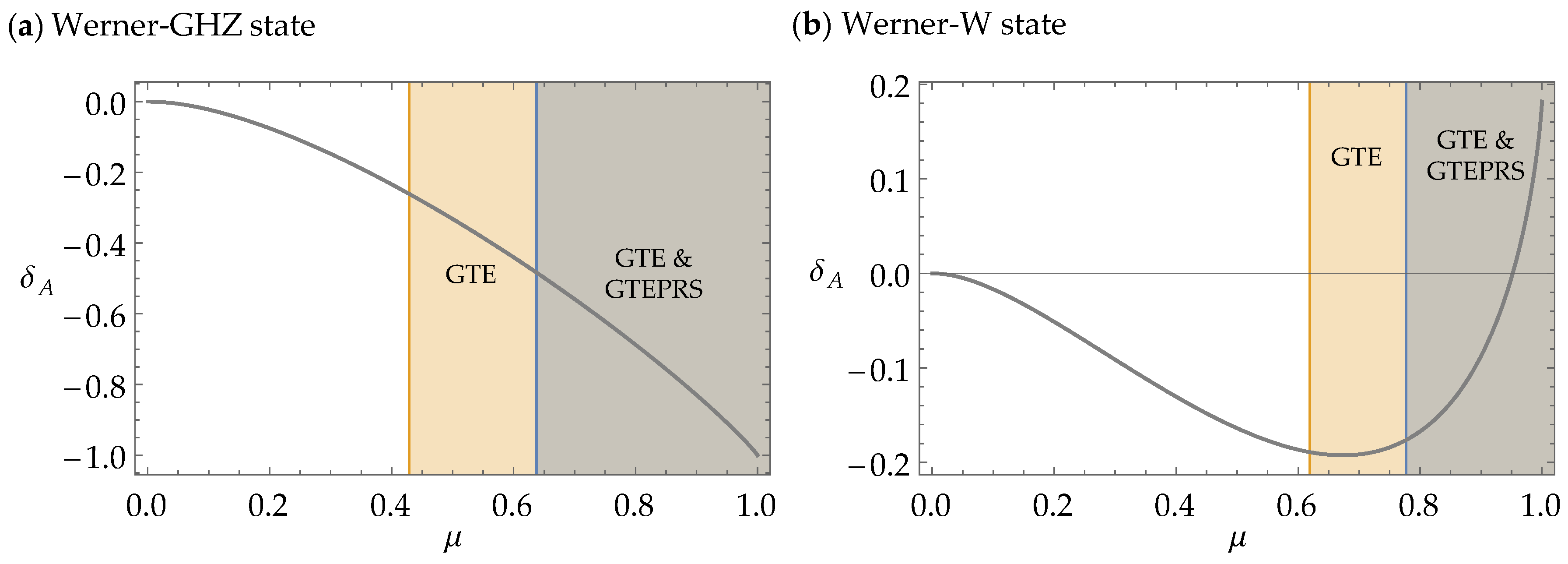
5.1. Tripartite Quantum Discord Focused on One Subsystem for the Werner-GHZ States
5.2. Tripartite Quantum Discord Focused on One Subsystem for the Werner-W States
5.3. Relation with Genuine Tripartite Entanglement and Einstein–Podolsky–Rosen (EPR) Steering
5.4. Tripartite Quantum Discord Focused on One Subsystem for Biseparable States
6. Comparison with Other Measures
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Werlang, T.; Trippe, C.; Ribeiro, G.A.P.; Rigolin, G. Quantum correlations in spin chains at finite temperatures and quantum phase transitions. Phys. Rev. Lett. 2010, 105, 095702. [Google Scholar] [CrossRef] [PubMed]
- Mazzola, L.; Piilo, J.; Maniscalco, S. Sudden transition between classical and quantum decoherence. Phys. Rev. Lett. 2010, 104, 200401. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2002, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34, 6899. [Google Scholar] [CrossRef]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Koashi, M.; Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 2004, 69. [Google Scholar] [CrossRef]
- Fanchini, F.; Castelano, L.; Cornelio, M.; de Oliveira, M. Locally inaccessible information as a fundamental ingredient to quantum information. New J. Phys. 2012, 14, 013027. [Google Scholar] [CrossRef]
- Rulli, C.C.; Sarandy, M.S. Global quantum discord in multipartite systems. Phys. Rev. A 2011, 84, 042109. [Google Scholar] [CrossRef]
- Chakrabarty, I.; Agrawal, P.; Pati, A.K. Quantum dissension: Generalizing quantum discord for three-qubit states. Eur. Phys. J. D 2011, 65, 605–612. [Google Scholar] [CrossRef]
- Bourennane, M.; Eibl, M.; Kurtsiefer, C.; Gaertner, S.; Weinfurter, H.; Gühne, O.; Hyllus, P.; Bruß, D.; Lewenstein, M.; Sanpera, A. Experimental detection of multipartite entanglement using witness operators. Phys. Rev. Lett. 2004, 92, 087902. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-M.; Chen, K.; Chen, Y.-N.; Zhang, Q.; Chen, Y.-A.; Pan, J.-W. Genuine high-order Einstein–Podolsky– Rosen steering. Phys. Rev. Lett. 2015, 115, 010402. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; J. Wiley: New York, NY, USA, 1991. [Google Scholar]
- Ghahramani, S. Fundamental of Probability, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2004; pp. 100–105. [Google Scholar]
- Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Going beyond bell’s theorem. arXiv, 2007; arXiv:0712.0921. [Google Scholar]
- Werner, R.F. Quantum states with einstein-podolsky-rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef]
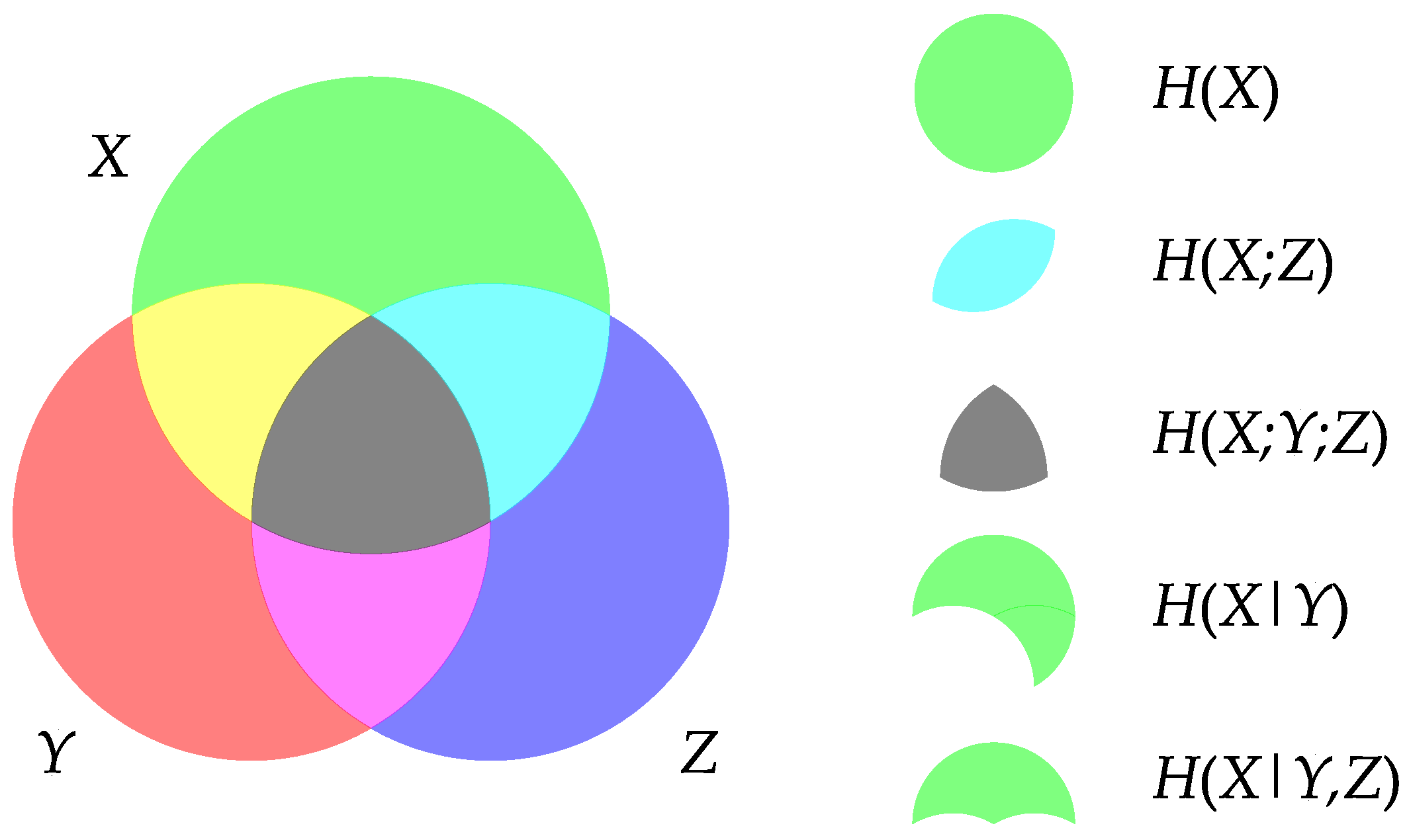
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.-T.; Li, C.-M. Revealing Tripartite Quantum Discord with Tripartite Information Diagram. Entropy 2017, 19, 602. https://doi.org/10.3390/e19110602
Lee W-T, Li C-M. Revealing Tripartite Quantum Discord with Tripartite Information Diagram. Entropy. 2017; 19(11):602. https://doi.org/10.3390/e19110602
Chicago/Turabian StyleLee, Wei-Ting, and Che-Ming Li. 2017. "Revealing Tripartite Quantum Discord with Tripartite Information Diagram" Entropy 19, no. 11: 602. https://doi.org/10.3390/e19110602




