Properties of Risk Measures of Generalized Entropy in Portfolio Selection
Abstract
:1. Introduction
2. Some Basic Properties of Risk Measures
- (1)
- Sub-additivity. For , , we have .
- (2)
- Consistency. For , , we have .
- (3)
- Monotonicity. For , , with , we have .
- (4)
- Translation Invariance. For , , we havewhere the particular risk-free asset is modeled as having an initial price of 1 and a strictly positive price, (or total return), in any state at date, .
- (5)
- Positive Homogeneity. For , , we have .
- (6)
- Convexity. For , and , , we have
3. Properties of Risk Measures of Generalized Entropy
3.1. Information Entropy
3.2. Cumulative Residual Entropy
3.3. Fuzzy Entropy
3.4. Credibility Entropy
- (1)
- If , then the left and right inverse membership functions of are , . Then
- (2)
- If , we have .
- (3)
- If , then the left and right inverse membership functions of are , . Then
3.5. Sine Entropy
3.6. Hybrid Entropy
3.7. Comparing the Properties of Risk Measures of Generalized Entropy
4. Empirical Comparisons of Seven Models
4.1. The Portfolio Selection Models Based on Generalized Entropy
4.2. Empirical Comparisons among the Portfolio Selection Models
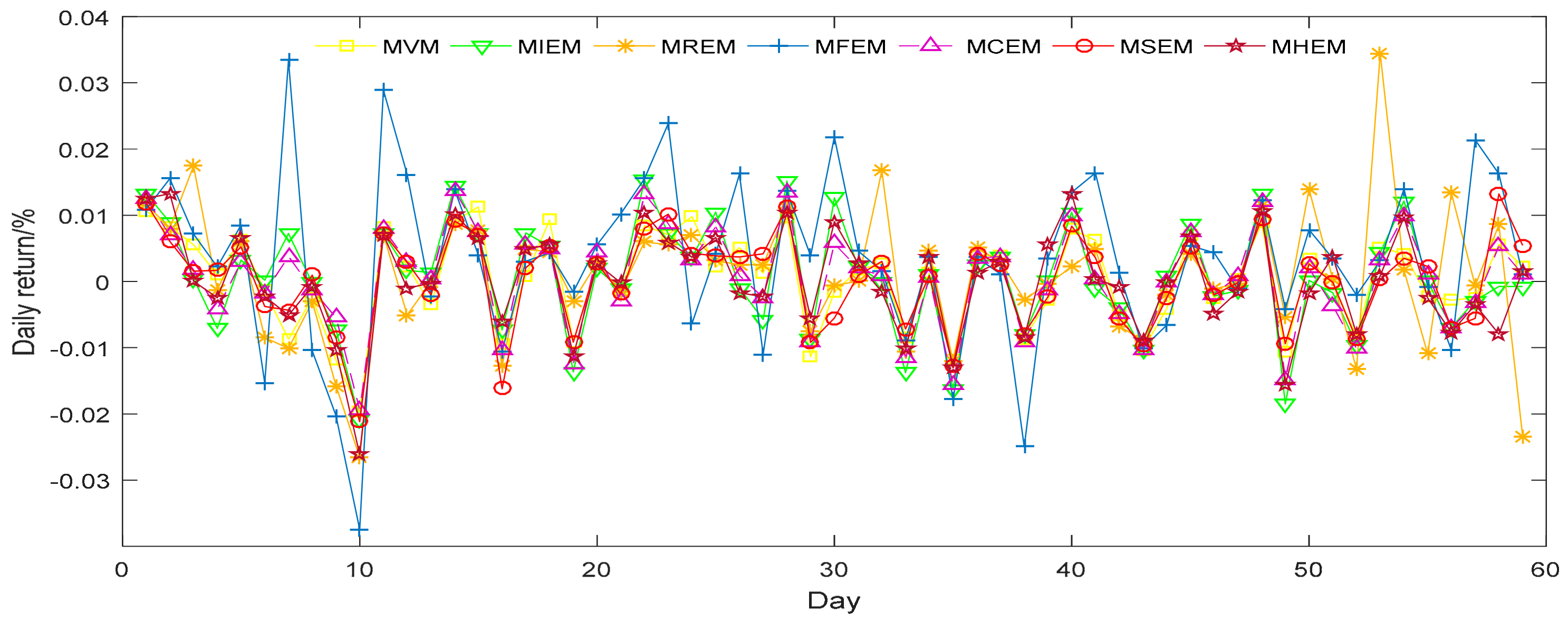
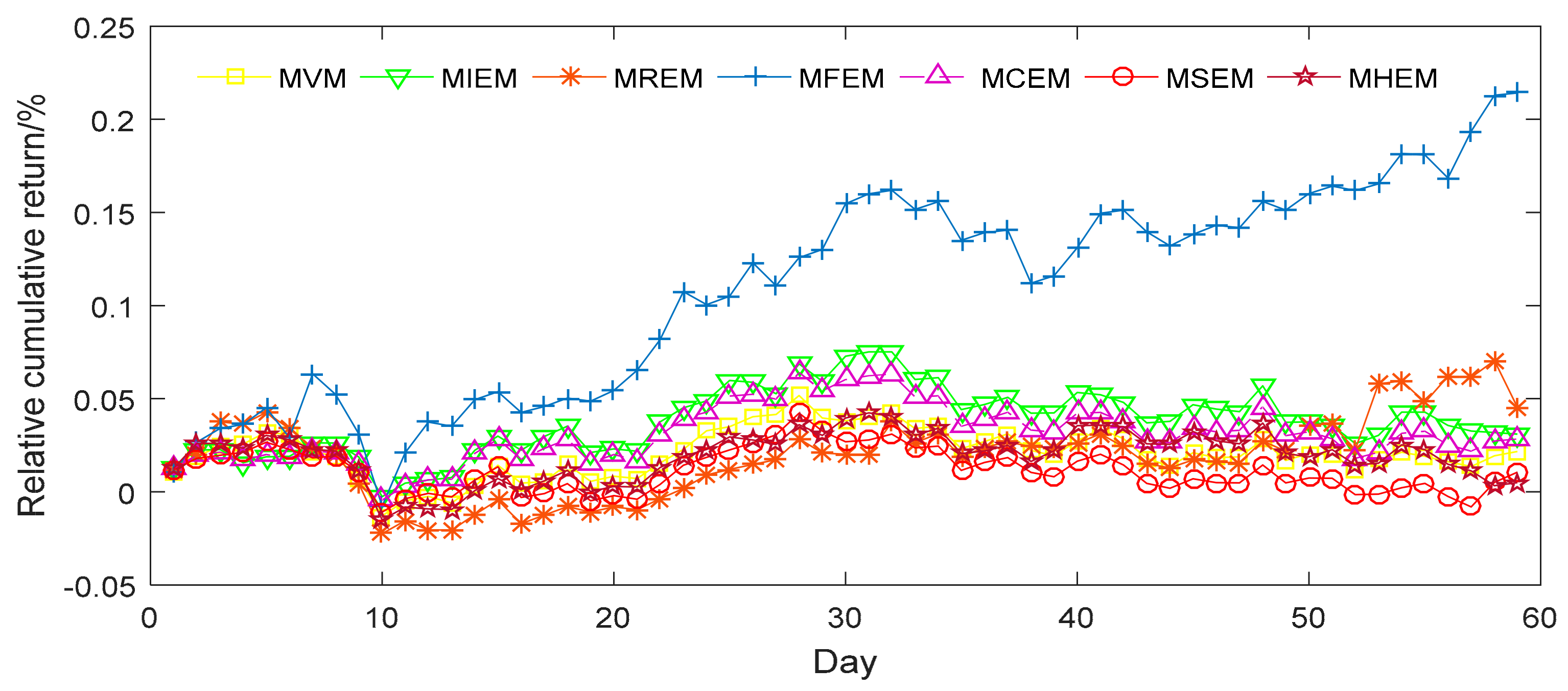
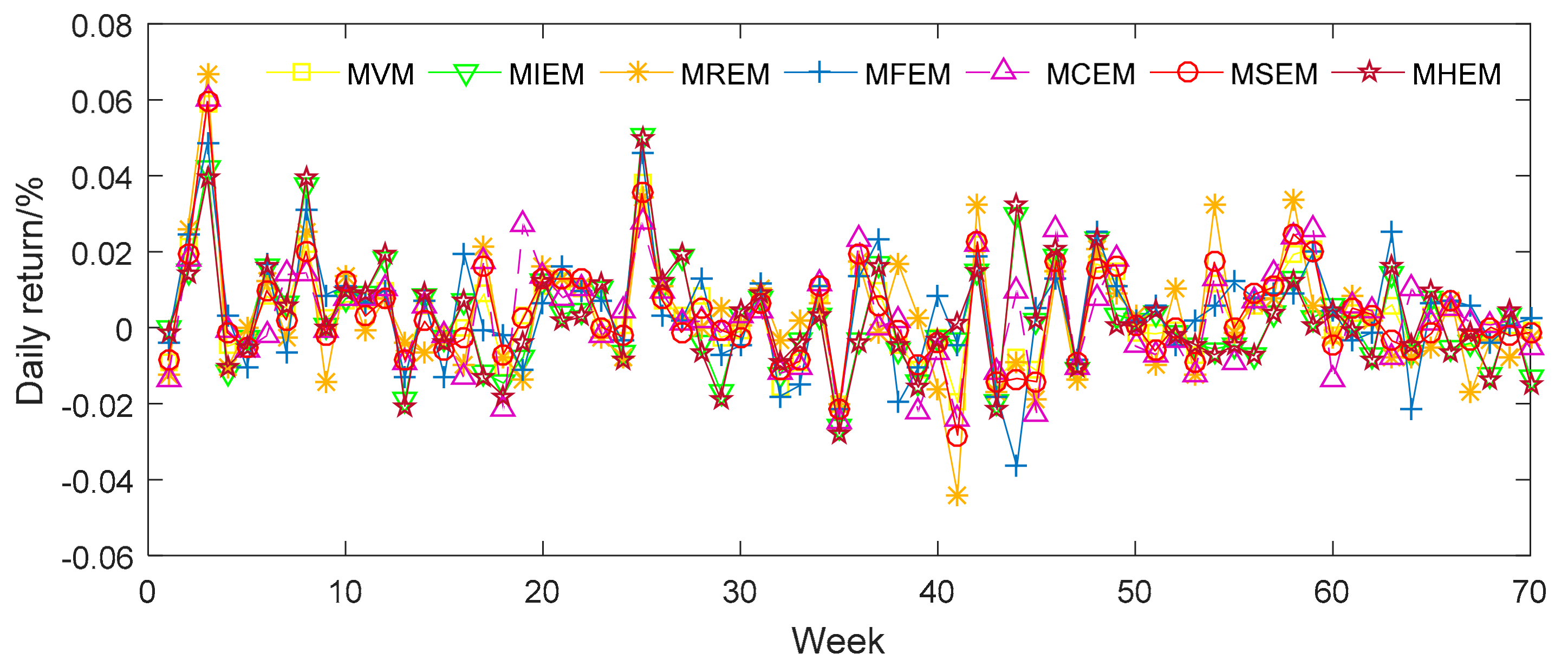
4.2.1. Empirical Analysis from Chinese Sample Data
4.2.2. Empirical Analysis from American Sample Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Markowitz, H.M. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investment; John Wiley: New York, NY, USA, 1959. [Google Scholar]
- Philippatos, G.C.; Wilson, C.J. Entropy, market risk, and the selection of efficient portfolios. Appl. Econ. 1972, 4, 209–220. [Google Scholar] [CrossRef]
- Konno, H.; Yamazaki, H. Mean-absolute deviation portfolio optimization model and its application to Tokyo stock market. Manag. Sci. 1991, 37, 519–531. [Google Scholar] [CrossRef]
- Cai, X.Q.; Teo, K.L.; Yang, X.Q.; Zhou, X.Y. Portfolio optimization under a minimax rule. Manag. Sci. 2000, 46, 957–972. [Google Scholar] [CrossRef]
- Jorion, P. Measure the risk in value at risk. Financ. Anal. J. 1996, 52, 47–55. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of Conditional value at risk. J. Risk. 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Acerbi, C.; Tasche, D. On the coherence of expected shortfall. J. Bank. Financ. 2002, 26, 1487–1503. [Google Scholar] [CrossRef]
- Zhou, R.X.; Cai, R.; Tong, G.Q. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Philippatos, G.C.; Gressis, N. Conditions of equivalence among E-V, SSD, and E-H portfolio selection criteria: The case for uniform, normal and lognormal distributions. Manag. Sci. 1975, 21, 617–625. [Google Scholar] [CrossRef]
- Nawrocki, D.N.; Harding, W.H. State-value weighted entropy as a measure of investment risk. Appl. Econ. 1986, 18, 411–419. [Google Scholar] [CrossRef]
- Smimou, K.; Bector, C.R.; Jacoby, G. A subjective assessment of approximate probabilities with a portfolio application. Res. Int. Bus. Financ. 2007, 21, 134–160. [Google Scholar] [CrossRef]
- Huang, X.X. Mean-Entropy Models for Fuzzy Portfolio Selection. IEEE Trans. Fuzzy Syst. 2008, 16, 1096–1101. [Google Scholar] [CrossRef]
- Xu, J.P.; Zhou, X.; Wu, D.D. Portfolio selection using λ mean and hybrid entropy. Ann. Oper Res. 2011, 185, 213–229. [Google Scholar] [CrossRef]
- Usta, I.; Kantar, Y.M. Mean-Variance-Skewness-Entropy Measures: A Multi-Objective Approach for Portfolio Selection. Entropy 2011, 13, 117–133. [Google Scholar] [CrossRef]
- Zhang, W.G.; Liu, Y.J.; Xu, W.J. A possibilistic mean-semivariance- entropy model for multi-period portfolio selection with transaction costs. Eur. J. Oper. Res. 2012, 222, 341–349. [Google Scholar] [CrossRef]
- Zhou, R.X.; Wang, X.G.; Dong, X.F.; Zong, Z. Portfolio Selection Model with the Measures of Information Entropy-Incremental Entropy-Skewness. Adv. Inf. Sci. Serv. Sci. 2013, 5, 853–864. [Google Scholar]
- Zhang, W.G.; Liu, Y.J.; Xu, W.J. A new fuzzy programming approach for multi-period portfolio optimization with return demand and risk control. Fuzzy Set. Syst. 2014, 246, 107–126. [Google Scholar] [CrossRef]
- Yao, K. Sine entropy of uncertain set and its applications. Appl. Soft Comput. 2014, 22, 432–442. [Google Scholar] [CrossRef]
- Yu, J.R.; Lee, W.Y.; Chiou, W.J.P. Diversified portfolios with different entropy measures. Appl. Math. Comput. 2014, 241, 47–63. [Google Scholar] [CrossRef]
- Zhou, R.X.; Zhan, Y.; Cai, R.; Tong, G.Q. A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns. Entropy 2015, 17, 3319–3331. [Google Scholar] [CrossRef]
- Gao, J.W.; Liu, H.C. A Risk-Free Protection Index Model for Portfolio Selection with Entropy Constraint under an Uncertainty Framework. Entropy 2017, 19, 1–12. [Google Scholar] [CrossRef]
- Ramsay, C.M. Loading gross premiums for risk without using utility theory. Trans. Soc. Actuar. 1993, 45, 305–349. [Google Scholar]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Coherent Measures of Risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Follmer, H.; Schied, A. Convex measures of risk and trading constraints. Financ. Stoch. 2002, 6, 429–447. [Google Scholar] [CrossRef]
- Bali, T.G.; Cakici, N.; Fousseni, C.Y. A Generalized Measure of Riskiness. Manag. Sci. 2011, 57, 1406–1423. [Google Scholar] [CrossRef]
- Zheng, C.L.; Chen, Y. Coherent risk measure based on relative entropy. Appl. Math. Inform. Sci. 2012, 6, 233–238. [Google Scholar]
- Gaivoronski, A.; Pflug, G. Value at Risk in Portfolio Optimization; Properties and Computational Approach; Technical Report; University of Vienna: Wien, Austria, 2001. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cao, X.H. Information Theory and Coding; Tsinghua University Press: Beijing, China, 2009. [Google Scholar]
- Rao, M.; Chen, Y.; Vemuri, B.; Fei, W. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Liu, B.D. Uncertain logic for modeling human language. J. Uncertain Syst. 2011, 5, 3–20. [Google Scholar]
- Liu, B.D. A Survey of Entropy of Fuzzy Variables. J. Uncertain Syst. 2007, 1, 4–13. [Google Scholar]
- Liu, B.D. Membership functions and operational law of uncertain sets. Fuzzy Optim. Decis. Mak. 2012, 11, 387–410. [Google Scholar] [CrossRef]
- Yao, K.; Ke, H. Entropy operator for membership function of uncertain set. Appl. Math. Comput. 2014, 242, 898–906. [Google Scholar] [CrossRef]
- Li, P.K.; Liu, B.D. Entropy of credibility distributions for fuzzy variables. IEEE Trans. Fuzzy Syst. 2008, 16, 123–129. [Google Scholar]
- Yao, K. Sine entropy of uncertain variables. Int. J. Uncertain. 2013, 21, 743–753. [Google Scholar] [CrossRef]
- Shang, X.G.; Jiang, W.S. Rationality Analysis and Promotion of De Luca-Termini Hybrid Entropy. J. East China Univ. Sci. Technol. 1996, 23, 590–595. [Google Scholar]

| Information Entropy | Cumulative Residual Entropy | Fuzzy Entropy | Credibility Entropy | Sine Entropy | Hybrid Entropy | |
|---|---|---|---|---|---|---|
| Monotonicity | × | × | × | × | × | × |
| Translation Invariance | × | × | × | × | × | × |
| Sub-additivity | √ | √ | √ * | √ * | √ * | √ * |
| Positive Homogeneity | × | √ | √ | √ | √ | × |
| Consistency | √ | × | √ | √ | √ | √ |
| Convexity | × | √ | √ * | √ * | √ * | × |
| Model Name | Risk Measure |
|---|---|
| Mean and Variance Model (MVM) | |
| Mean Information Entropy Model (MIEM) | |
| Mean Residual Entropy Model (MREM) | |
| Mean Fuzzy Entropy Model (MFEM) | |
| Mean Credibility Entropy Model (MCEM) | |
| Mean Sine Entropy Model (MSEM) | |
| Mean Hybrid Entropy Model (MHEM) |
| Stock Code | Industry | Company Name |
|---|---|---|
| 002116 | Scientific research and technology service | China Haisum Engineering Co Ltd |
| 000966 | Utilities | Guodian Changyuan Electric Power Co Ltd |
| 000005 | Water resources, environment and public facilities management | Shenzhen Fountain Corporation |
| 000937 | Mining | Jizhong Energy Resources Co Ltd |
| 000882 | Leasing and business services | Beijing Hualian Department Store Co Ltd |
| 000776 | Finance | GF Securities Co Ltd |
| 000010 | Construction | Beijing Shenhuaxin Co Ltd |
| 000022 | Transportation, warehousing and postal services | Shenzhen Chiwan Wharf Holdings Co Ltd |
| 000592 | Agriculture, forestry, livestock farming, fishery | Zhongfu Straits (Pingtan) Development Co Ltd |
| 000837 | Manufacturing | Qinchuan Machinery Development Co Ltd of Shaanxi |
| Stock Code | Expected Value | Variance | Information Entropy | Cumulative Residual Entropy |
| 002116 | 0.000358 | 0.000684 | 0.522250 | 0.014387 |
| 000966 | 0.000106 | 0.000411 | 0.522197 | 0.010422 |
| 000005 | 0.000583 | 0.000771 | 0.495046 | 0.018321 |
| 000937 | 0.002914 | 0.000879 | 0.541494 | 0.020575 |
| 000882 | 0.001688 | 0.000690 | 0.517706 | 0.014476 |
| 000776 | 0.001089 | 0.000443 | 0.486794 | 0.013178 |
| 000010 | 0.001764 | 0.000831 | 0.536057 | 0.018320 |
| 000022 | 0.001292 | 0.000717 | 0.555807 | 0.015292 |
| 000592 | –0.001478 | 0.000942 | 0.529302 | 0.019134 |
| 000837 | 0.000007 | 0.000784 | 0.524759 | 0.020385 |
| Stock Code | Fuzzy Entropy | Credibility Entropy | Sine Entropy | Hybrid Entropy |
| 002116 | 0.917527 | 0.017518 | 0.022316 | 0.768799 |
| 000966 | 0.909969 | 0.012838 | 0.016354 | 0.798535 |
| 000005 | 0.925415 | 0.018119 | 0.023081 | 0.752247 |
| 000937 | 0.921937 | 0.023726 | 0.030225 | 0.825716 |
| 000882 | 0.923970 | 0.020318 | 0.025883 | 0.767248 |
| 000776 | 0.907789 | 0.014732 | 0.018767 | 0.752970 |
| 000010 | 0.923278 | 0.017534 | 0.022336 | 0.812668 |
| 000022 | 0.894561 | 0.020841 | 0.026549 | 0.829238 |
| 000592 | 0.922229 | 0.017690 | 0.022535 | 0.794126 |
| 000837 | 0.832758 | 0.016749 | 0.021337 | 0.802894 |
| Stock Code | MVM | MIEM | MREM | MFEM | MCEM | MSEM | MHEM |
|---|---|---|---|---|---|---|---|
| 002116 | 0.0662 | 0.0189 | 0.450 | 0.0149 | 0.0181 | 0.0106 | 0.0077 |
| 000966 | 0.4994 | 0.0341 | 0.4056 | 0.1194 | 0.2561 | 0.6104 | 0.0508 |
| 000005 | 0.0349 | 0.0911 | 0.0011 | 0.0605 | 0.0043 | 0.0110 | 0.3407 |
| 000937 | 0.1124 | 0.0005 | 0.0006 | 0.0009 | 0.0015 | 0.0016 | 0.0011 |
| 000882 | 0.0518 | 0.0621 | 0.0007 | 0.0167 | 0.0017 | 0.0008 | 0.0547 |
| 000776 | 0.1368 | 0.7124 | 0.1315 | 0.0767 | 0.5738 | 0.2742 | 0.4900 |
| 000010 | 0.0380 | 0.0089 | 0.0013 | 0.0258 | 0.0754 | 0.0241 | 0.0146 |
| 000022 | 0.0392 | 0.0016 | 0.0050 | 0.1899 | 0.0037 | 0.0013 | 0.0188 |
| 000592 | 0.0202 | 0.0125 | 0.0029 | 0.1069 | 0.0089 | 0.0516 | 0.0132 |
| 000837 | 0.0011 | 0.0579 | 0.0005 | 0.3883 | 0.0565 | 0.0144 | 0.0084 |
| MVM | MIEM | MREM | MFEM | MCEM | MSEM | MHEM | |
|---|---|---|---|---|---|---|---|
| DR | 0.00039 | 0.00055 | 0.00080 | 0.00338 | 0.00050 | 0.00020 | 0.00011 |
| RCR | 0.02074 | 0.03744 | 0.01912 | 0.10800 | 0.03087 | 0.01128 | 0.01937 |
| Stock Code | Industry | Company Name |
|---|---|---|
| XOM | Basic Materials | Exxon Mobil Corporation |
| NEE | Utilities | NextEra Energy, Inc. |
| PG | Consumer Goods | The Procter & Gamble Company |
| JNJ | Healthcare | Johnson & Johnson |
| T | Technology | AT&T Inc. |
| BCH | Financial | Banco de Chile |
| WMT | Services | Wal-Mart Stores, Inc. |
| GE | Industrial Goods | General Electric Company |
| HRG | Conglomerates | HRG Group, Inc. |
| Stock Code | Expected Value | Variance | Information Entropy | Cumulative Residual Entropy |
| XOM | 0.000684 | 0.000667 | 0.579663 | 0.009051 |
| NEE | 0.002050 | 0.000476 | 0.617725 | 0.007630 |
| PG | 0.001078 | 0.000382 | 0.597884 | 0.006739 |
| JNJ | 0.001719 | 0.000333 | 0.595278 | 0.006417 |
| T | 0.000886 | 0.000472 | 0.582108 | 0.007338 |
| BCH | –0.001058 | 0.000906 | 0.547013 | 0.009808 |
| WMT | 0.001595 | 0.000533 | 0.622009 | 0.008027 |
| GE | 0.001872 | 0.000858 | 0.546699 | 0.010659 |
| HRG | 0.001702 | 0.001756 | 0.625417 | 0.014955 |
| Stock Code | Fuzzy Entropy | Credibility Entropy | Sine Entropy | Hybrid Entropy |
| XOM | 0.954630 | 0.018010 | 0.022943 | 0.856335 |
| NEE | 0.935999 | 0.016779 | 0.021374 | 0.891082 |
| PG | 0.929912 | 0.014469 | 0.018432 | 0.876359 |
| JNJ | 0.946126 | 0.014319 | 0.018241 | 0.877410 |
| T | 0.963329 | 0.016518 | 0.021042 | 0.862157 |
| BCH | 0.939306 | 0.022284 | 0.028387 | 0.829200 |
| WMT | 0.960407 | 0.015609 | 0.019883 | 0.894488 |
| GE | 0.909638 | 0.020336 | 0.025906 | 0.838212 |
| HRG | 0.943969 | 0.036577 | 0.046594 | 0.890792 |
| Stock Code | MVM | MIEM | MREM | MFEM | MCEM | MSEM | MHEM |
|---|---|---|---|---|---|---|---|
| XOM | 0.0081 | 0.0492 | 0.0007 | 0.0011 | 0.0019 | 0.0022 | 0.0679 |
| NEE | 0.1468 | 0.0010 | 0.0033 | 0.4415 | 0.0263 | 0.2012 | 0.0010 |
| PG | 0.2469 | 0.0902 | 0.7990 | 0.0816 | 0.2990 | 0.3991 | 0.0834 |
| JNJ | 0.2063 | 0.0839 | 0.1713 | 0.0451 | 0.1509 | 0.1537 | 0.0150 |
| T | 0.0938 | 0.1074 | 0.0185 | 0.1128 | 0.1000 | 0.0826 | 0.0737 |
| BCH | 0.1289 | 0.2412 | 0.0012 | 0.2363 | 0.0001 | 0.0002 | 0.2515 |
| WMT | 0.1652 | 0.0014 | 0.0037 | 0.0159 | 0.4201 | 0.1598 | 0.0278 |
| GE | 0.0009 | 0.4248 | 0.0012 | 0.0423 | 0.0011 | 0.0003 | 0.4671 |
| HRG | 0.0031 | 0.0009 | 0.0011 | 0.0234 | 0.0006 | 0.0009 | 0.0126 |
| MVM | MIEM | MREM | MFEM | MCEM | MSEM | MHEM | |
|---|---|---|---|---|---|---|---|
| DR | 0.00372 | 0.00268 | 0.00289 | 0.00422 | 0.00321 | 0.00334 | 0.00256 |
| RCR | 0.18683 | 0.16366 | 0.16107 | 0.20296 | 0.15893 | 0.17101 | 0.15561 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Liu, X.; Yu, M.; Huang, K. Properties of Risk Measures of Generalized Entropy in Portfolio Selection. Entropy 2017, 19, 657. https://doi.org/10.3390/e19120657
Zhou R, Liu X, Yu M, Huang K. Properties of Risk Measures of Generalized Entropy in Portfolio Selection. Entropy. 2017; 19(12):657. https://doi.org/10.3390/e19120657
Chicago/Turabian StyleZhou, Rongxi, Xiao Liu, Mei Yu, and Kyle Huang. 2017. "Properties of Risk Measures of Generalized Entropy in Portfolio Selection" Entropy 19, no. 12: 657. https://doi.org/10.3390/e19120657





