On the Binary Input Gaussian Wiretap Channel with/without Output Quantization
Abstract
:1. Introduction
- Both the legitimate receiver and the wiretapper have unquantized outputs;
- Both the legitimate receiver and the wiretapper have binary quantized outputs;
- The legitimate receiver has binary quantized outputs, while the wiretapper has unquantized outputs;
- The legitimate receiver has unquantized outputs, while the wiretapper has binary quantized outputs.
2. System Model
2.1. Gaussian Channel with Binary Inputs
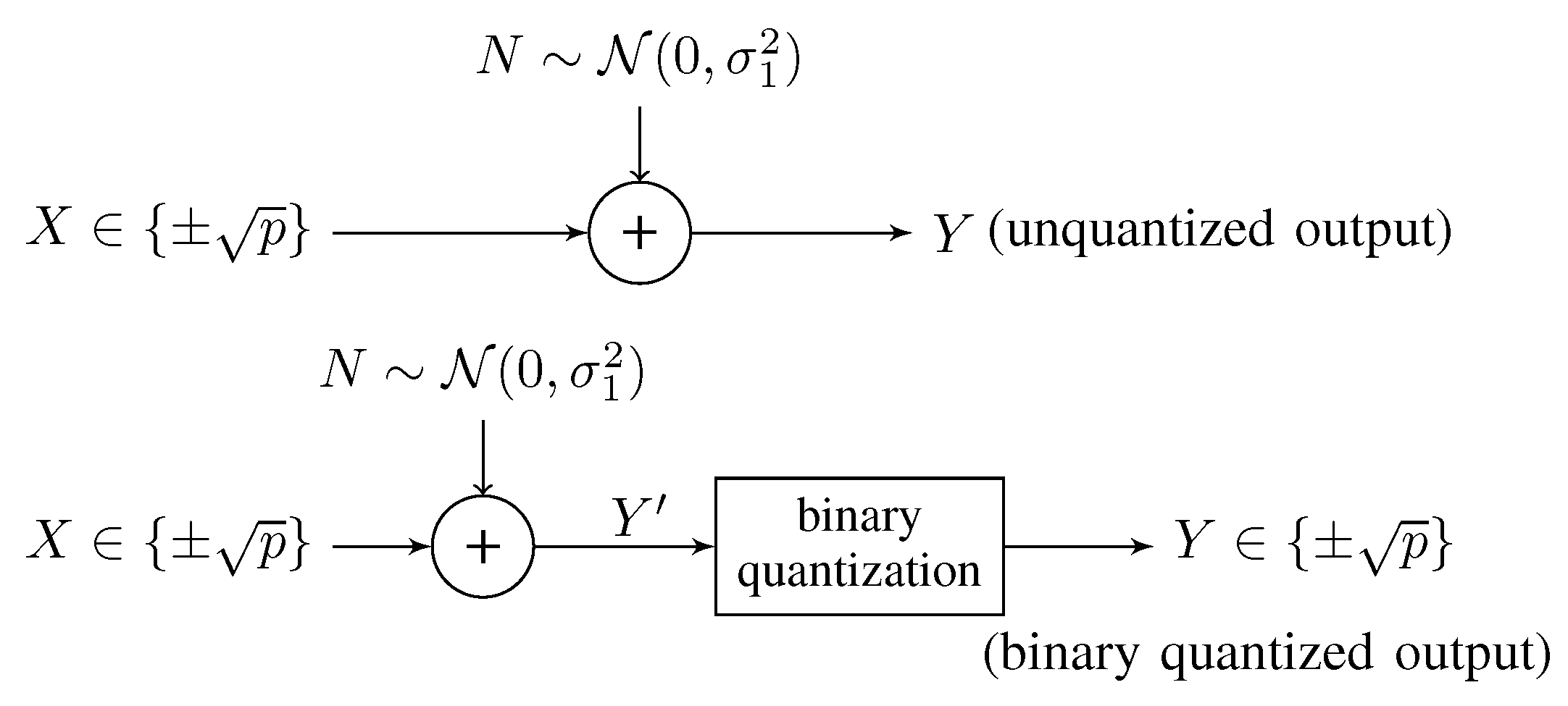
- Unquantized outputs:If the channel output signal is directly processed by the receiver without binary quantization as shown in Figure 1, we call it the unquantized output. The channel output Y is a continuous signal, having the conditional probability density functionWith the unquantized output, a closed-form expression of the channel capacity for the BI-GWC was given in [11] aswhere . This channel capacity is achieved if and only if the input signal is uniformly distributed [11].For the sake of simplifying computation in what follows, the channel capacity can be approximated by keeping the first m terms of the summation as [11]
- Binary quantized outputs:Through a binary quantization, the binary quantized output iswhere is the original continuous channel output signal.In fact, this case can be modeled as the a binary symmetric channel with transition probability [10]. By means of the results for binary symmetric channel [12], we can obtain the channel capacity for the BI-GWC with binary quantized outputs aswhere is the binary entropy function. Note that is achieved iff the binary input distribution is uniform [12].
2.2. Gaussian Wiretap Channel with Binary Inputs
3. BI-GWC with/without Output Quantization
3.1. Both the Legitimate Receiver and the Eavesdropper Have Unquantized Outputs or Both Have Binary Quantized Outputs
3.1.1. BI-GWC: Secrecy Capacity When the Legitimate Receiver and the Eavesdropper Have Unquantized Outputs
3.1.2. BI-GWC: Secrecy Capacity When the Legitimate Receiver and the Eavesdropper Have Binary Quantized Outputs
3.2. One of the Legitimate Receiver and the Eavesdropper Has Binary Quantized Outputs and the Other Has Unquantized Outputs
3.2.1. BI-GWC: Secrecy Capacity When the Legitimate Receiver Has Binary Quantized Outputs and the Eavesdropper Has Unquantized Outputs
3.2.2. BI-GWC: Secrecy Capacity When the Legitimate Receiver Has Unquantized Outputs and the Eavesdropper Has Binary Quantized Outputs
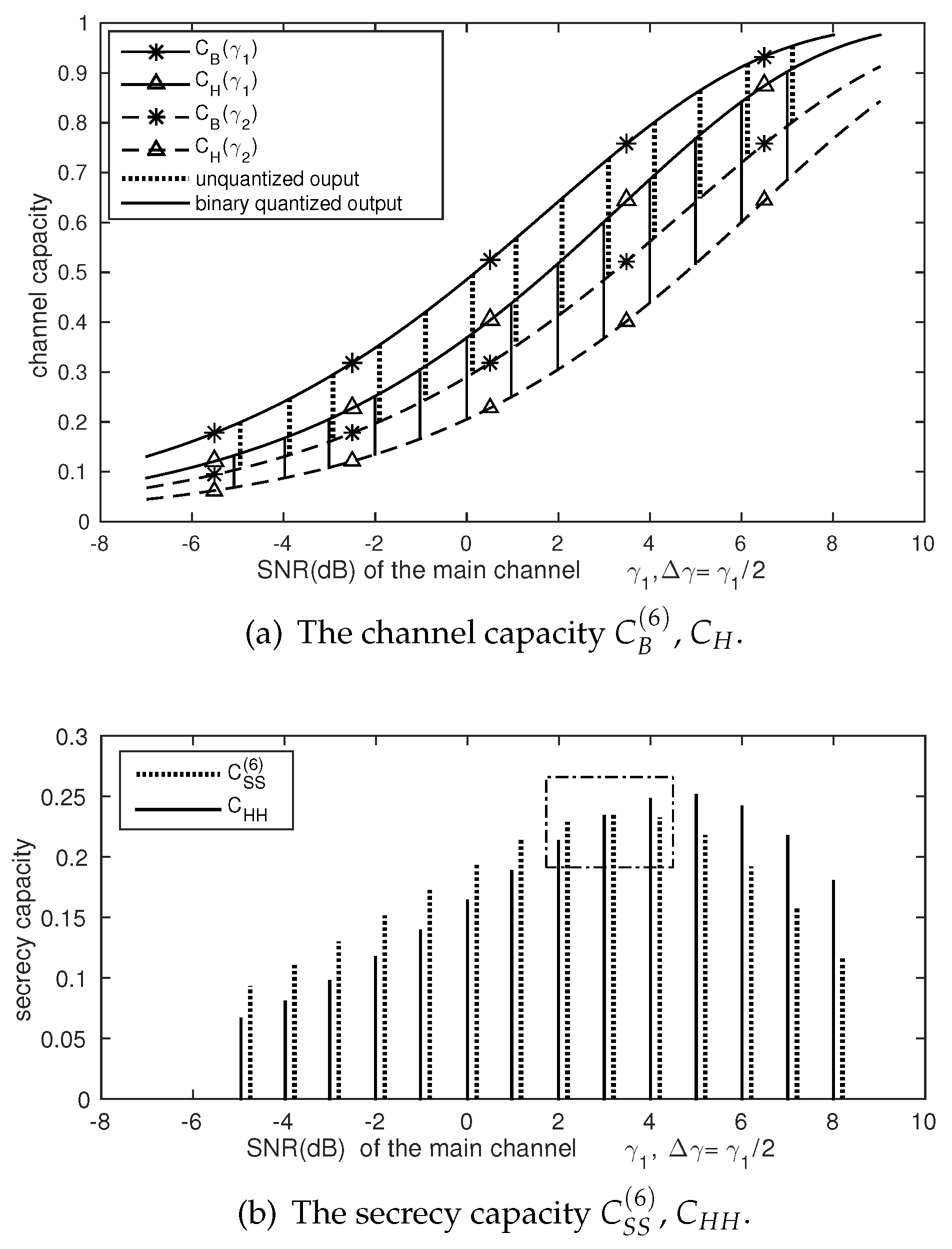
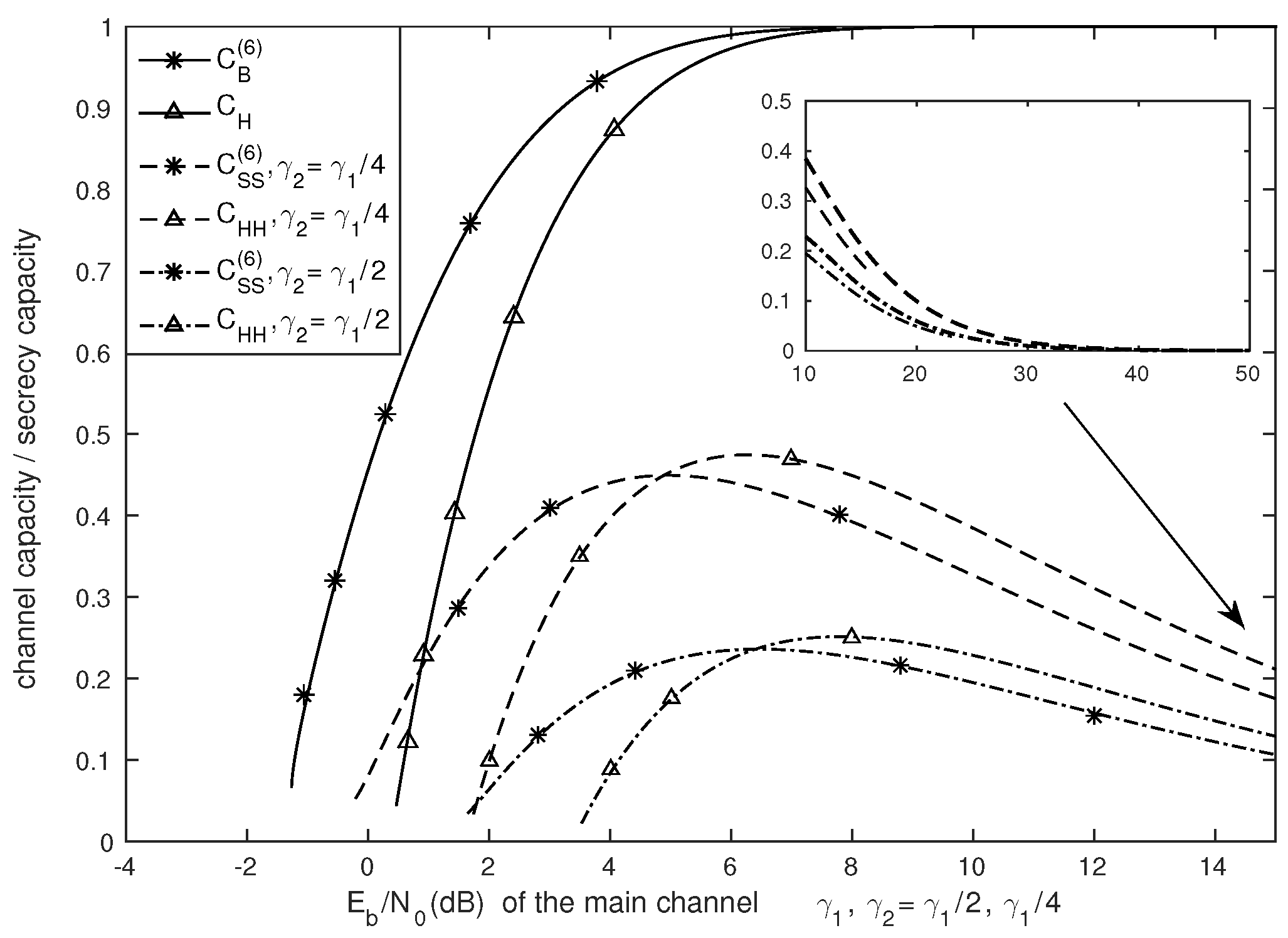
4. Numerical Results
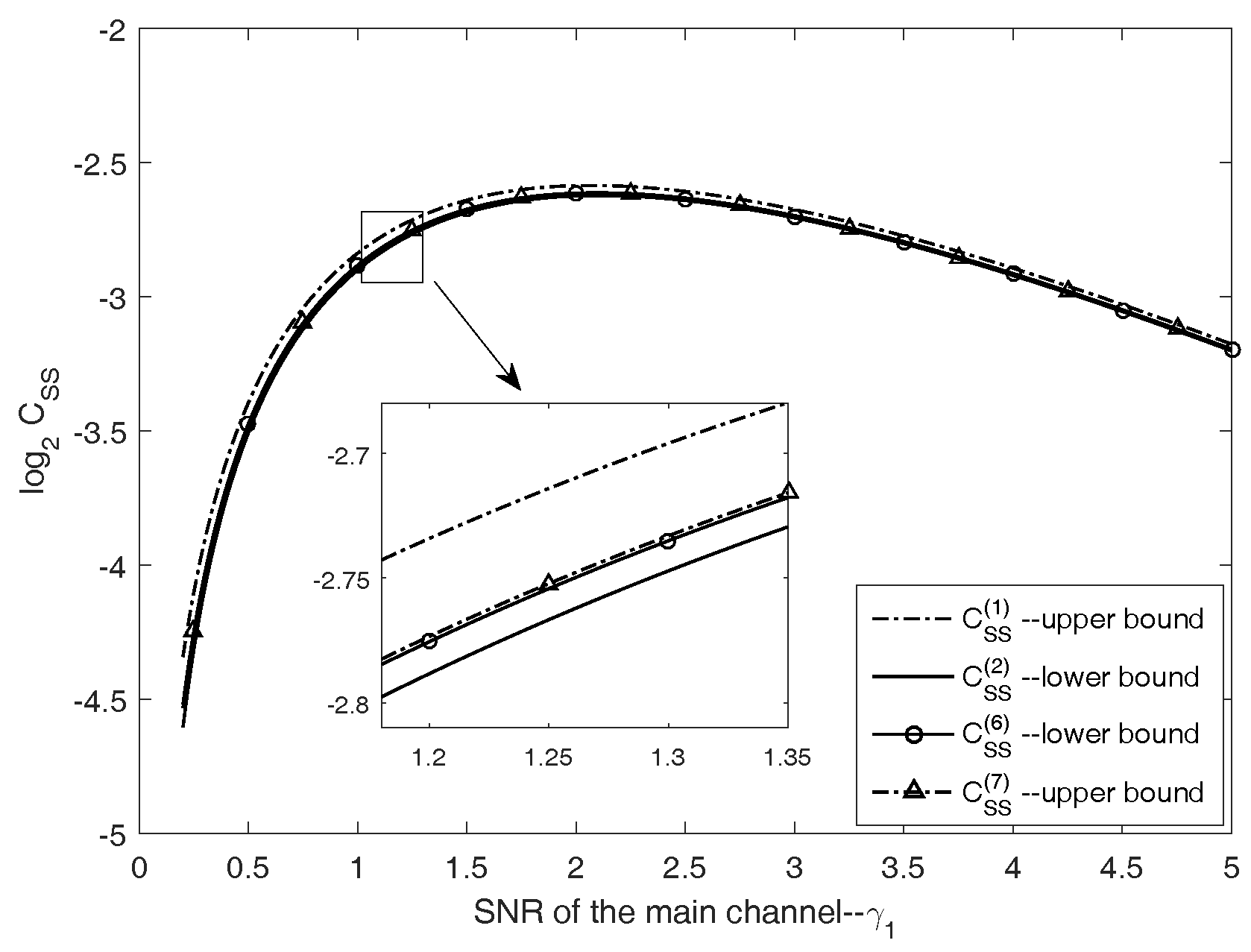
4.1. Comparison of , , and
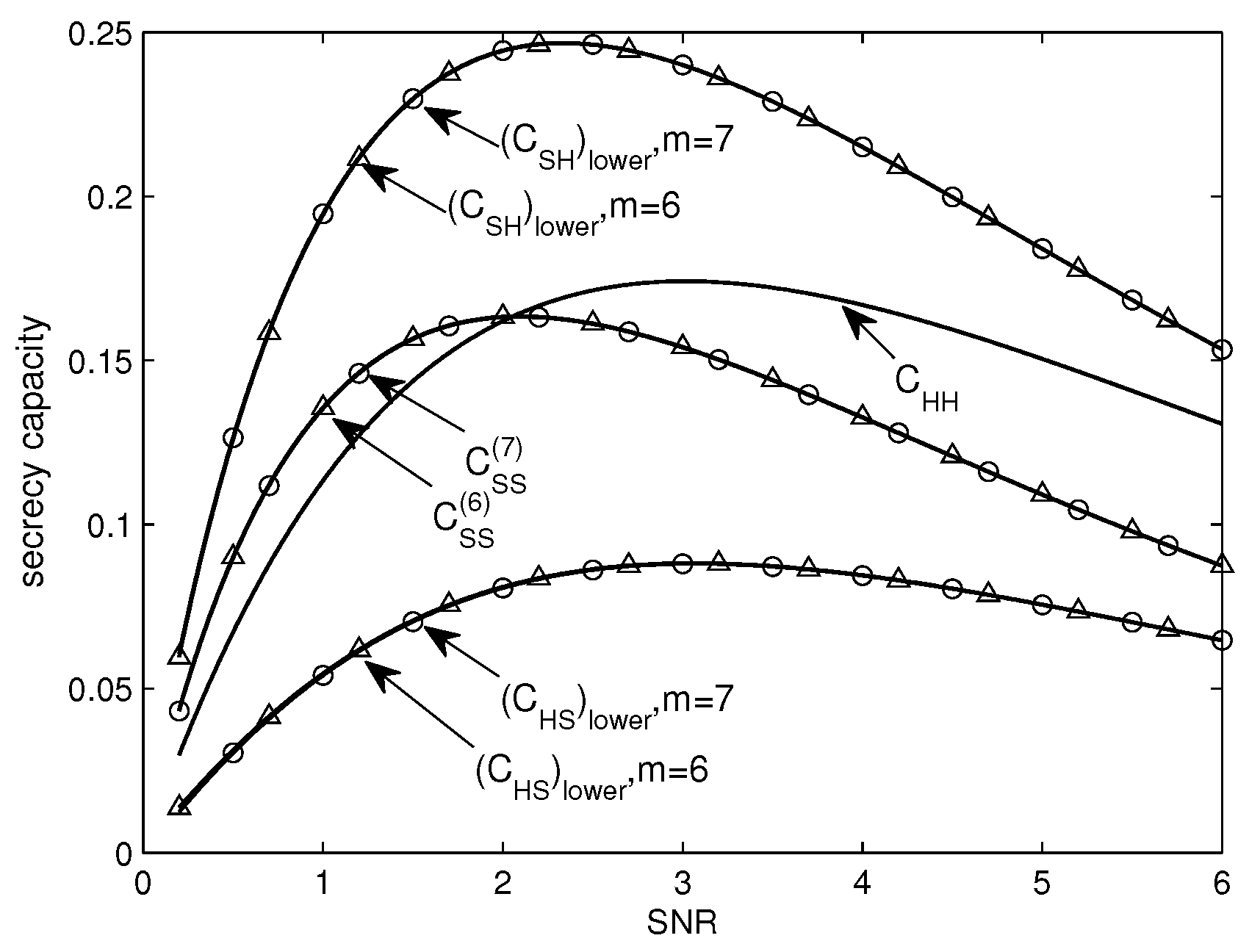
4.2. Comparison from the Perspectives of SNR and SNR/bit
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Property 1
References
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wyner, A. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Rodrigues, M.R.D.; Somekh-Baruch, A.; Bloch, M. On Gaussian wiretap channels with M-PAM inputs. In Proceedings of the 2010 European Wireless Conference, Lucca, Italy, 12–15 April 2010; pp. 774–781.
- Bashar, S.; Ding, Z.; Xiao, C. On the secrecy rate of multi-antenna wiretap channel under finite-alphabet input. IEEE Commun. Lett. 2011, 15, 527–529. [Google Scholar] [CrossRef]
- Bashar, S.; Ding, Z.; Xiao, C. On secrecy rate analysis of MIMO wiretap channels driven by finite-alphabet input. IEEE Trans. Commun. 2012, 60, 3816–3825. [Google Scholar] [CrossRef]
- Wong, C.W.; Wong, T.F.; Shea, J.M. Secret-sharing LDPC codes for the BPSK-constrained Gaussian wiretap channel. IEEE Trans. Inf. Forensics Secur. 2011, 6, 551–564. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Leung-Yan-Cheong, S.; Hellman, M.E. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 1978, 24, 451–456. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2007. [Google Scholar]
- Nasif, A.; Karystinos, G.N. Binary transmissions over additive Gaussian noise: A closed-form expression for the channel capacity. In Proceedings of the 2005 Conference on Information Sciences and Systems (CISS), Dayton, OH, USA, 16–18 March 2005.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Leung-Yan-Cheong, S. On a special class of wiretap channels. IEEE Trans. Inf. Theory 1977, 23, 625–627. [Google Scholar] [CrossRef]
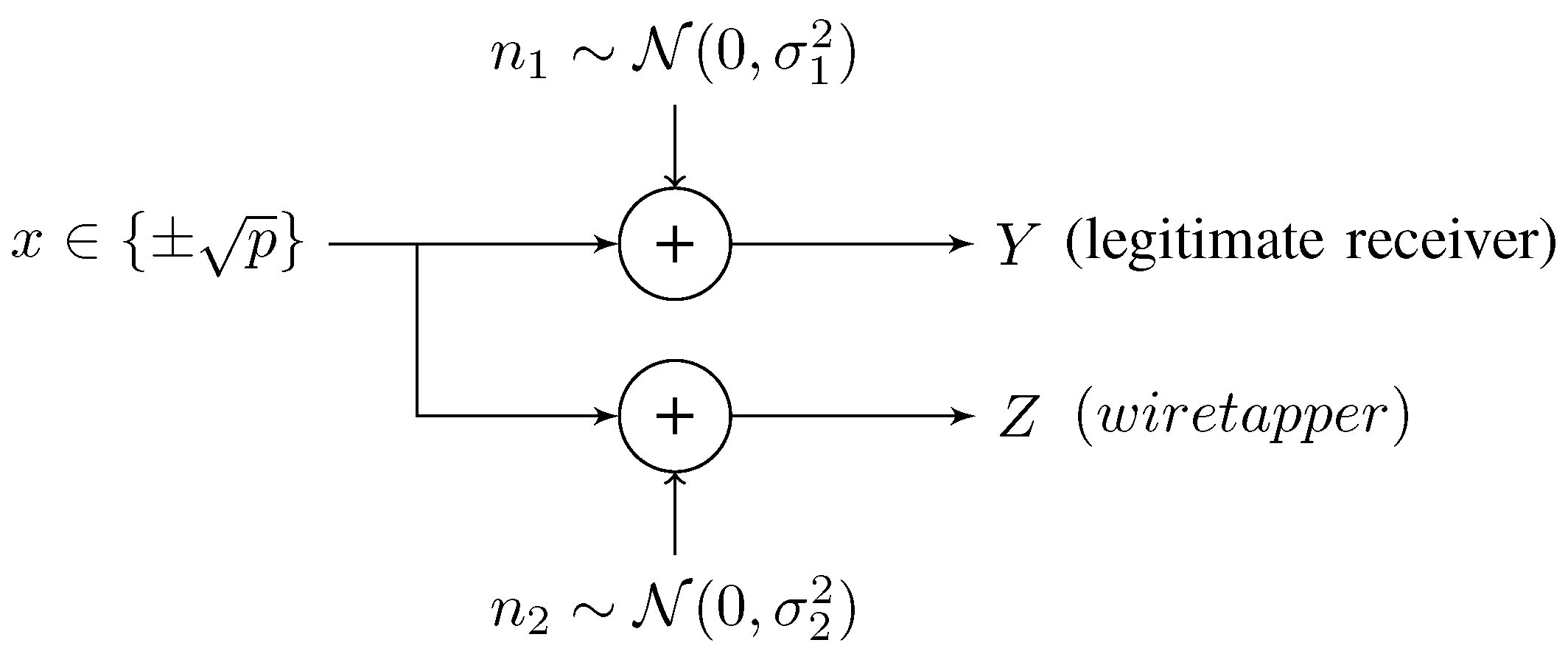
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, C.; Chen, Y.; Vinck, A.J.H. On the Binary Input Gaussian Wiretap Channel with/without Output Quantization. Entropy 2017, 19, 59. https://doi.org/10.3390/e19020059
Qi C, Chen Y, Vinck AJH. On the Binary Input Gaussian Wiretap Channel with/without Output Quantization. Entropy. 2017; 19(2):59. https://doi.org/10.3390/e19020059
Chicago/Turabian StyleQi, Chao, Yanling Chen, and A. J. Han Vinck. 2017. "On the Binary Input Gaussian Wiretap Channel with/without Output Quantization" Entropy 19, no. 2: 59. https://doi.org/10.3390/e19020059




