Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field

Abstract

Entropy generation for a paramagnetic fluid in a square enclosure with thermomagnetic convection is numerically investigated under the influence of a magnetic quadrupole field. The magnetic field is calculated using the scalar magnetic potential approach. The finite-volume method is applied to solve the coupled equation for flow, energy, and entropy generation. Simulations are conducted to obtain streamlines, isotherms, Nusselt numbers, entropy generation, and the Bejan number for various magnetic forces (1 ≤ γ ≤ 100) and Rayleigh numbers (10⁴ ≤ Ra ≤ 10⁶). In the absence of gravity, the total entropy generation increases with the increasing magnetic field number, but the average Bejan number decreases. In the gravitational field, the total entropy generation respects the insensitive trend to the change of the magnetic force for low Rayleigh numbers, while it changes significantly for high Rayleigh numbers. When the magnetic field enhances, the share of viscous dissipation in energy losses keeps growing.

1. Introduction

With the development of superconducting magnets providing strong magnetic induction, the study of thermomagnetic convection is becoming attractive. Many studies have been published in the fields of fluid mechanics and heat transfer over several decades [1,2,3,4,5,6]. The application of strong magnetic fields on the control of natural convection of non-ferrous materials (i.e., paramagnetic air or diamagnetic water) has received considerable attention [7,8,9,10,11,12]. Braithwaite et al. [3] reported the control of thermal-convection of paramagnetic fluids by the relative orientation of the magnetic field gradient and the temperature gradient. Qi et al. [13] investigated, numerically and theoretically, the effect of a vertical magnetic field gradient on thermal convection. Ozoe and co-workers [14,15] studied the magnetizing force effect for air under thermal and magnetic field gradients. They observed that the thermomagnetic convection could be controlled by different combinations of the gravitational force and magnetic forces. Kaneda et al. [16] studied the effect of a cusp-shaped magnetic field on air in a cube enclosure. Yang et al. [17,18] performed experimental and numerical studies on the free convection of air or oxygen in an enclosure. They found that the thermomagnetic convection was enhanced or suppressed by an outward radial magnetic field. Jiang et al. [19] used the local thermal non-equilibrium models to solve the thermomagnetic convection problem of air in a porous square enclosure under a magnetic quadrupole field. Bednarz et al. [8,20,21] analyzed the effect of the Rayleigh number, inclined angle, and the location of the electric coil on heat transfer of the paramagnetic fluid. Kenjeres et al. [22,23], numerically and experimentally, studied the flow and heat transfer of a paramagnetic fluid under various strong non-uniform magnetic field gradients. The combined effects of thermal buoyancy force and magnetic force were considered. Akamatsu et al. [7] and Naffouti et al. [9] studied the effect of magnetic fields on Rayleigh-Benard convection of paramagnetic air. Purusothaman et al. [24] simulated the 3D natural convection for mercury, air, and dielectric liquid in a cubical cavity with a thermally-active heater and revealed that heat transfer and flow patterns depended strongly on the strength of the magnetic field.

In the investigations mentioned above, the thermomagnetic convection of air is based on the viewpoint of the first law of thermodynamics. The contemporary trend in the field of heat transfer and thermal design is from the second law (of thermodynamics) analysis and its design-related concept of entropy generation and its minimization [25]. Entropy generation is used to quantify thermodynamics irreversibility, which exists in all heat transfer and fluid flow processes. Such irreversibilities may be caused by heat transfer across the finite temperature gradient, viscous dissipation and magnetic field effects, etc. The magnetic field influence on entropy generation in nanofluid-filled cavities has been exposed in the recent literature [26,27,28]. The results showed that the magnetic field and the presence of nanoparticle had a substantial influence on flow pattern, heat transfer, and entropy generation. Kolsi et al. [29] and Sathiyamoorthy et al. [30] investigated the effect of magnetic fields on entropy generation in three-dimensional natural convection for an electrically-conducting liquid metal under the different thermal boundary conditions. Kolsi et al. [29] pointed out that the entropy produced by friction and the Joule effect is more influenced by the magnetic field than that produced by thermal dissipation. Sathiyamoorthy et al. [30] found that the entropy generation rate decreased in magnitude with an increase in magnetic force. Jery et al. [31] numerically investigated the influence of an inclination angle of the magnetic field on entropy generation in natural convection for air and liquid gallium. Bouabid et al. [32] studied the thermosolutal convection in a square cavity filled with a binary gas mixture under an inclined magnetic field. It was found that the magnetic field induced the decrease of entropy generation. Mahmud and Fraser [33] studied entropy generation in a porous cavity for laminar natural convection in the presence of the magnetic field acted towards the direction of gravity. They found that the entropy generation reached a minimum when walls are cooled in an asymmetrical way.

In our previously published paper, the scalar magnetic potential and finite-volume method were applied to investigate thermomagnetic convection and heat transfer of paramagnetic air under a magnetic quadrupole field within porous media. The numerical results in a porous square enclosure showed the magnetic field intensity and Rayleigh number, as well as the Darcy number, have a significant influence on flow field and heat transfer [19,34]. Except for the flow and heat transfer characteristics, efficient utilization of energy is also considered as one of the main concerns in thermal engineering applications. It can be achieved with the calculation of entropy generation since it clarifies the distribution of irreversibility.

In order to further obtain the influence of thermomagnetic convection on energy loss, the current paper is to analyze the influence of a magnetic quadrupole field on entropy generation in thermomagnetic convection of paramagnetic fluid in a square cavity. Simulations are carried out for a range of parameters, Ra = 10⁴–10⁶ and γ = 1–100, and the results are presented in the form of isotherms (θ), streamlines (ψ) and entropy generation maps (S_θ and S_ψ). The effects of Rayleigh number and magnetic force number on the total entropy generation (S_total), average Bejan number (Be_av), and average Nusselt number (Nu_m) are also studied to analyze the relative importance of heat transfer and fluid friction irreversibilities.

2. Mathematical Model

2.1. Physical Description

The schematic of the studied system is shown in Figure 1. Four permanent magnets are used to generate a magnetic field. Both left and right walls are maintained at the uniform temperature T_h and T_c, where T_c < T_h. The horizontal walls are insulated. The gravitational force acts in the −Y direction. In the present study, the length of the enclosure L, the length of the permanent magnet L₁ and the distance of the permanent magnets L₂ are 0.024 m, 0.02 m and 0.03 m, respectively.

2.2. Governing Equations

The flow is assumed as steady, incompressible, Newtonian, and laminar. In addition, all thermophysical properties are assumed as constant except the density for the buoyancy force term. Boussinesq approximation is used to simplify the variation of density with temperature. The viscous heat dissipation and magnetic dissipation are small enough to be ignored.

The magnetizing force in an inhomogeneous field is given as follows according to Braithwaite et al. [3]:

$$f_{\mathrm{m}}=\frac{{\chi }_{\mathrm{m}}}{2{\mu }_{\mathrm{m}}}\nabla b^2=\frac{\rho \chi }{2{\mu }_{\mathrm{m}}}\nabla b^2$$

(1)

The Navier-Stokes equation which includes the magnetic force term can be presented as:

$$\rho U\cdot \nabla U=-\nabla p+\mu {\nabla }^{2}U+\frac{\rho \chi }{2{\mu }_{\mathrm{m}}}\nabla b^2+\rho g$$

(2)

At the reference state of the isothermal state, there will be no convection. Therefore, Equation (2) becomes:

$$0=-\nabla p_0+\frac{{\rho }_0{\chi }_0}{2{\mu }_{\mathrm{m}}}\nabla b^2+{\rho }_{0}g$$

(3)

subtracting Equation (3) from (2) gives:

$$\rho U\cdot \nabla U=-\nabla p^{\text{'}}+\mu {\nabla }^{2}U+\frac{(\rho \chi -{\rho }_0{\chi }_0)}{2{\mu }_{\mathrm{m}}}\nabla b^2+(\rho -{\rho }_0)g$$

(4)

where $p=p_0+p^{\prime }$, $p\text{'}$ is the pressure difference due to the perturbed state. Since $\rho$ and $\chi$ are functions of the temperature, so $\rho \chi$ and $\rho$ can be indicated as according to Taylor expansion method, respectively:

$$\rho \chi ={(\rho \chi )}_0+{(\frac{\partial (\rho \chi )}{\partial T})}_0(T-T_0)+\cdots ,$$

(5)

$$\rho ={\rho }_0+{(\frac{\partial \rho }{\partial T})}_0(T-T_0)+\cdots$$

(6)

For the paramagnetic fluid, the mass magnetic susceptibility is inversely proportional to absolute temperature, according to the Curie’s law:

$$\chi =\frac{m}{T}$$

(7)

So Equation (5) can be written as:

$$\begin{array}{l}\rho \chi -{(\rho \chi )}_0={\left(\frac{\partial \rho }{\partial T}\chi -\rho \frac{\chi }{T}\right)}_0(T-T_0)+\cdots \\ ={\left(-\rho \beta \chi -\rho \frac{\chi }{T}\right)}_0(T-T_0)+\cdots =-{\rho }_0{\chi }_0\beta (1+\frac{1}{T_0\beta })(T-T_0)+\cdots \end{array}$$

(8)

The higher order small amount in Equation (8) is omitted and generated by Equation (9):

$$U\cdot \nabla U=-\frac{\nabla p^{\text{'}}}{{\rho }_0}+\frac{\mu }{{\rho }_0}{\nabla }^{2}U-\frac{{\chi }_0\beta }{2{\mu }_{\mathrm{m}}}(1+\frac{1}{T_0\beta })(T-T_0)\nabla b^2+\beta (T-T_0)g$$

(9)

The governing equations can be written as:

• Continuity equation:

  $$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

  (10)
• Momentum equation:

  $$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\nu (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2})-(1+\frac{1}{T_0\beta })\frac{{\chi }_0\beta (T-T_0)}{2{\mu }_{\mathrm{m}}}\frac{\partial (b^2)}{\partial x}$$

  (11)

  $$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\nu (\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2})-(1+\frac{1}{T_0\beta })\frac{{\chi }_0\beta (T-T_0)}{2{\mu }_{\mathrm{m}}}\frac{\partial (b^2)}{\partial y}+\rho g\left(T-T_0\right)$$

  (12)
• Energy equation:

  $$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha (\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2})$$

  (13)

The above Equations (10)–(13) can be non-dimensionalized into the following forms, respectively.

• Continuity equation:

  $$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

  (14)
• Momentum equation:

  $$U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+Pr(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2})-\frac{C}{2}\gamma RaPr\theta \frac{\partial (B^2)}{\partial X}$$

  (15)

  $$U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+Pr(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2})-\frac{C}{2}\gamma RaPr\theta \frac{\partial (B^2)}{\partial Y}+RaPr\theta$$

  (16)
• Energy equation:

  $$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2}$$

  (17)

The dimensionless variables and parameters in the above equations are defined as:

$X=\frac{x}{L}$, $Y=\frac{y}{L}$, $U=\frac{uL}{\alpha }$, $V=\frac{vL}{\alpha }$, $\theta =\frac{T-T_0}{T_{\mathrm{h}}-T_{\mathrm{c}}}$, $P=\frac{p{L}^2}{\rho {\alpha }^2}$, $Pr=\frac{\nu }{\alpha }$, $Ra=\frac{g\beta (T_{\mathrm{h}}-T_{\mathrm{c}})L^3}{\alpha \nu }$, $B=\frac{b}{b_0}$, $T_0=\frac{T_{\mathrm{h}}+T_{\mathrm{c}}}{2}$, $b_0=Br$, $C=1+\frac{1}{T_0\beta }$, $\gamma =\frac{{\chi }_0{b}_0^2}{{\mu }_{\mathrm{m}}gL}$.

2.3. Magnetic Field Calculation

Maxwell’s equations are applied to describe the magnetic quadrupole field:

$$\nabla \cdot \mathbf{B}=0$$

(18)

$$\nabla \times \mathbf{H}=0$$

(19)

The constitutive relation that describes the behavior of the magnetic material is:

$$\mathbf{B}=\mu \mathbf{H}$$

(20)

The scalar magnetic potential, ϕ_m, is used to calculate the magnetic field:

$$\mathbf{H}=-\nabla {\phi }_{\mathrm{m}}$$

(21)

Therefore, the scalar magnetic potential satisfies:

$${\nabla }^2{\phi }_{\mathrm{m}}=0$$

(22)

2.4. Boundary Conditions

The no-slip condition is imposed on the two velocity components on solid walls. The temperature boundary conditions are given by:

• U = V = 0 for all walls;
• Left and right vertical wall: $\theta =1$, 0 for X = 0, 1; and
• Top and bottom horizontal adiabatic walls: $\partial \theta /\partial Y=0$ for Y = 0 and 1.

2.5. Entropy Generation Calculation

The irreversible nature of heat transfer and viscous dissipation causes continuous production of entropy in a natural convection system. In the case of the existence of a magnetic field, the rate of entropy generation can be quantified for a two-dimensional flow as follows [35]:

$$S_{\mathrm{gen}}^{‴}=\frac{k}{T^2}\left[{\left(\frac{\partial T}{\partial x}\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{\mu }{T}\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)}^2\right]+\frac{\left(\mathbf{J}-Q\mathbf{U}\right)\left(\mathbf{E}+\mathbf{U}\times \mathbf{B}\right)}{T}$$

(23)

where: $\mathbf{J}=\sigma \left(\mathbf{E}+\mathbf{U}\times \mathbf{B}\right)$.

Neglecting QU compared to J and disregarding E in comparison with U × B, the entropy generation rate, Equation (23) is reduced in this case as:

$$S_{\mathrm{gen}}^{‴}=\frac{k}{T^2}\left[{\left(\frac{\partial T}{\partial x}\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{\mu }{T}\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)}^2\right]+\frac{\sigma {\left(\mathbf{U}\times \mathbf{B}\right)}^2}{T}$$

(24)

The first term on the right-hand side of Equation (24) represents entropy generation due to heat transfer, and the second and third terms are the result of fluid friction and the magnetic field, respectively. It is assumed that the irreversibility due to the magnetic field is ignored because the electrical conductivity of the paramagnetic fluid is infinitely small.

The dimensionless total local entropy generation is given as:

$$S_{\mathrm{G}}=\left[{\left(\frac{\partial \theta }{\partial X}\right)}^2+{\left(\frac{\partial \theta }{\partial Y}\right)}^2\right]+\varphi \left\{2\left[{\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial V}{\partial Y}\right)}^2\right]+{\left(\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}\right)}^2\right\}$$

(25)

From this dimensionless expression of local entropy generation, local irreversibility due to heat transfer and fluid dissipation are written respectively by:

$$S_{\mathsf{\theta }}=\left[{\left(\frac{\partial \theta }{\partial X}\right)}^2+{\left(\frac{\partial \theta }{\partial Y}\right)}^2\right]$$

(26)

$$S_{\mathsf{\psi }}=\varphi \left\{2\left[{\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial V}{\partial Y}\right)}^2\right]+{\left(\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}\right)}^2\right\}$$

(27)

where the irreversibility distribution ratio $\varphi$ is defined as:

$$\varphi =\frac{\mu T_0}{k}{\left(\frac{\alpha }{L\mathsf{\Delta }T}\right)}^2$$

(28)

In this work, $\varphi$ is taken as 10⁻⁴. A similar value for $\varphi$ was considered by Ilis et al. [34].

Integrating Equation (25), the total entropy generation (S_total) over the domain Ω can be defined as:

$$S_{\mathrm{G},\mathrm{total}}={\displaystyle {\int }_{\mathsf{\Omega }}{S}_{\mathsf{\theta }}}\mathrm{d}\mathsf{\Omega }+{\displaystyle {\int }_{\mathsf{\Omega }}{S}_{\mathsf{\psi }}}\mathrm{d}\mathsf{\Omega }=S_{\mathsf{\theta },\mathrm{total}}+S_{\mathsf{\psi },\mathrm{total}}$$

(29)

In addition, an important dimensionless number regarding the entropy is Bejan number, which is defined as the ratio of the heat transfer irreversibility to the total entropy generation and can be written as:

$$B{e}_{\mathrm{av}}=\frac{S_{\mathsf{\theta },\mathrm{total}}}{S_{\mathsf{\theta },\mathrm{total}}+S_{\mathsf{\psi },\mathrm{total}}}=\frac{S_{\mathsf{\theta },\mathrm{total}}}{S_{\mathrm{total}}}$$

(30)

It is clear that Be ranges from 0 to 1. Therefore, Be < 0.5, indicating that the fluid friction irreversibility dominates; while Be > 0.5 illustrates that the heat transfer irreversibility dominates. For Be = 0.5, heat transfer entropy generation is equal to fluid friction entropy generation [36].

2.6. Nusselt Number Calculation

The average Nusselt number at the hot wall is given by:

$$N{u}_{\mathrm{m}}=-{\displaystyle {\int }_0^1{\frac{\partial \theta }{\partial X}|}_{X=0}}\mathrm{d}Y$$

(31)

3. Numerical Procedures and Code Verification

The finite-volume method (FVM) and the SIMPLE (semi-implicit method for pressure-linked equations) algorithm developed in our previous work [19,34] are adopted to the governing Equations (14)–(17).

Considering the accuracy of numerical results and efficiency of computing simultaneously, a grid-independence examination is conducted, and results are shown in

Table 1. Comparison of the average Nusselt number Nu_m for different grid resolutions at γRa = 5 × 10⁵, Pr = 0.71 without a gravitational field.

Grid Dimension	Num
30 × 30	3.8762
40 × 40	3.5539
50 × 50	3.4814
60 × 60	3.4647
70 × 70	3.4642

. It was found that a 60 × 60 grid size is sufficient to produce accurate results.

The entropy generation is compared with those reported by Ilis et al. [37], showing excellent agreement, as shown in Figure 2.

4. Results and Discussion

The vector of the magnetizing force that is induced by a magnetic quadrupole field points radially outwards. The details are given in our previous work [19].

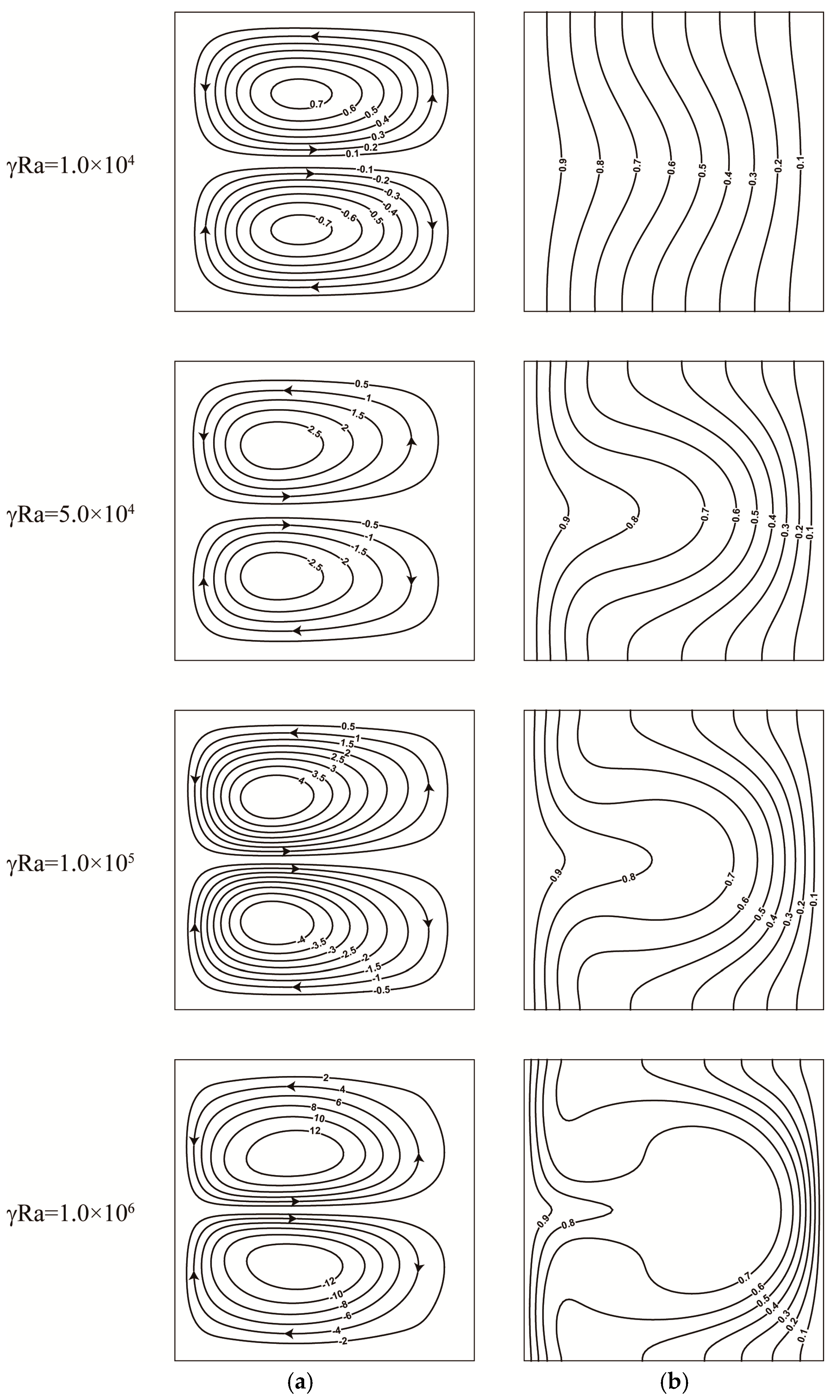
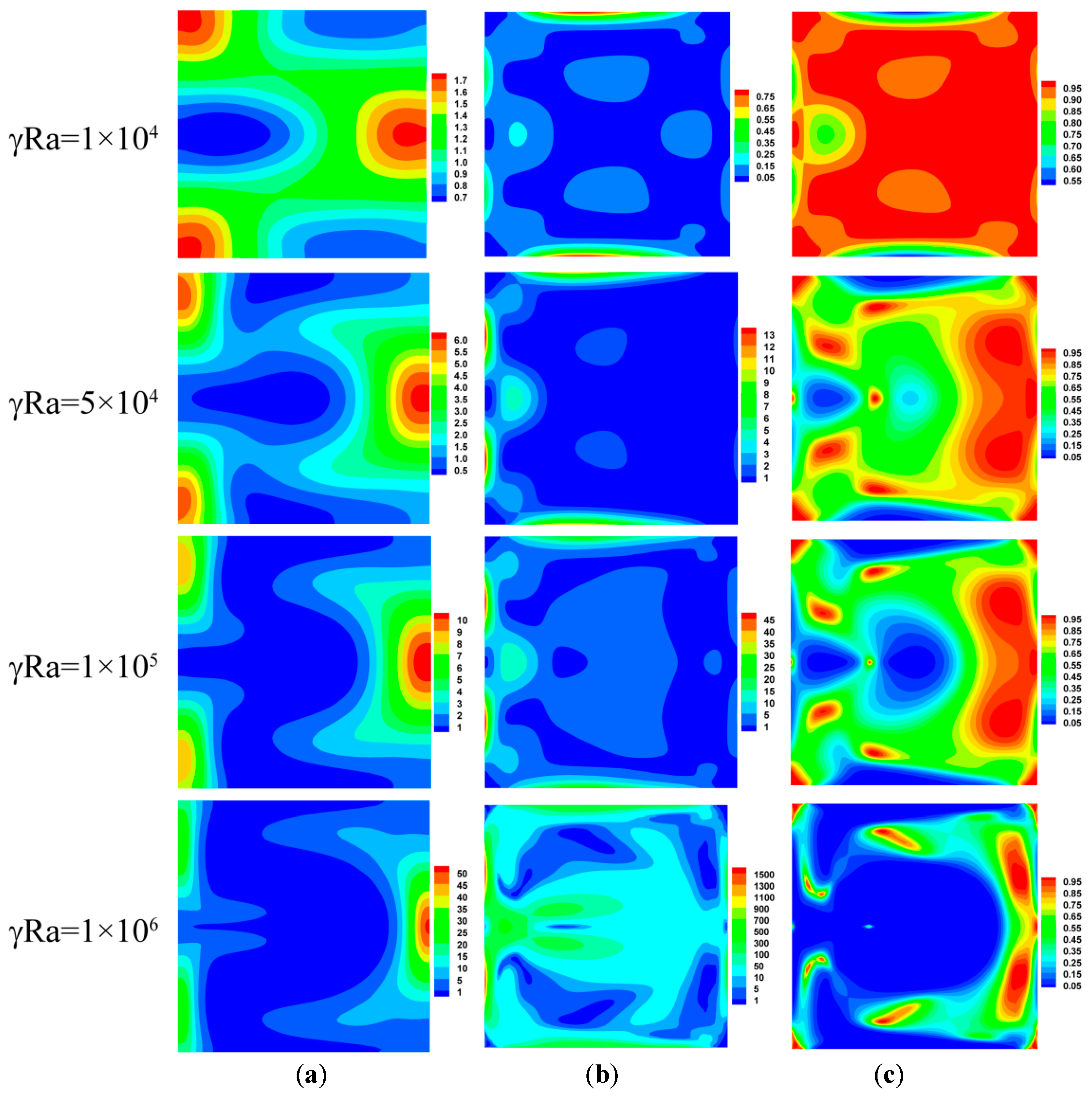
4.1. Numerical Results without a Gravitational Field

Since Ra becomes zero, and γ becomes infinity when g = 0. The product γRa, which is finite, is used as the governing parameter in the absence of a gravitational field.

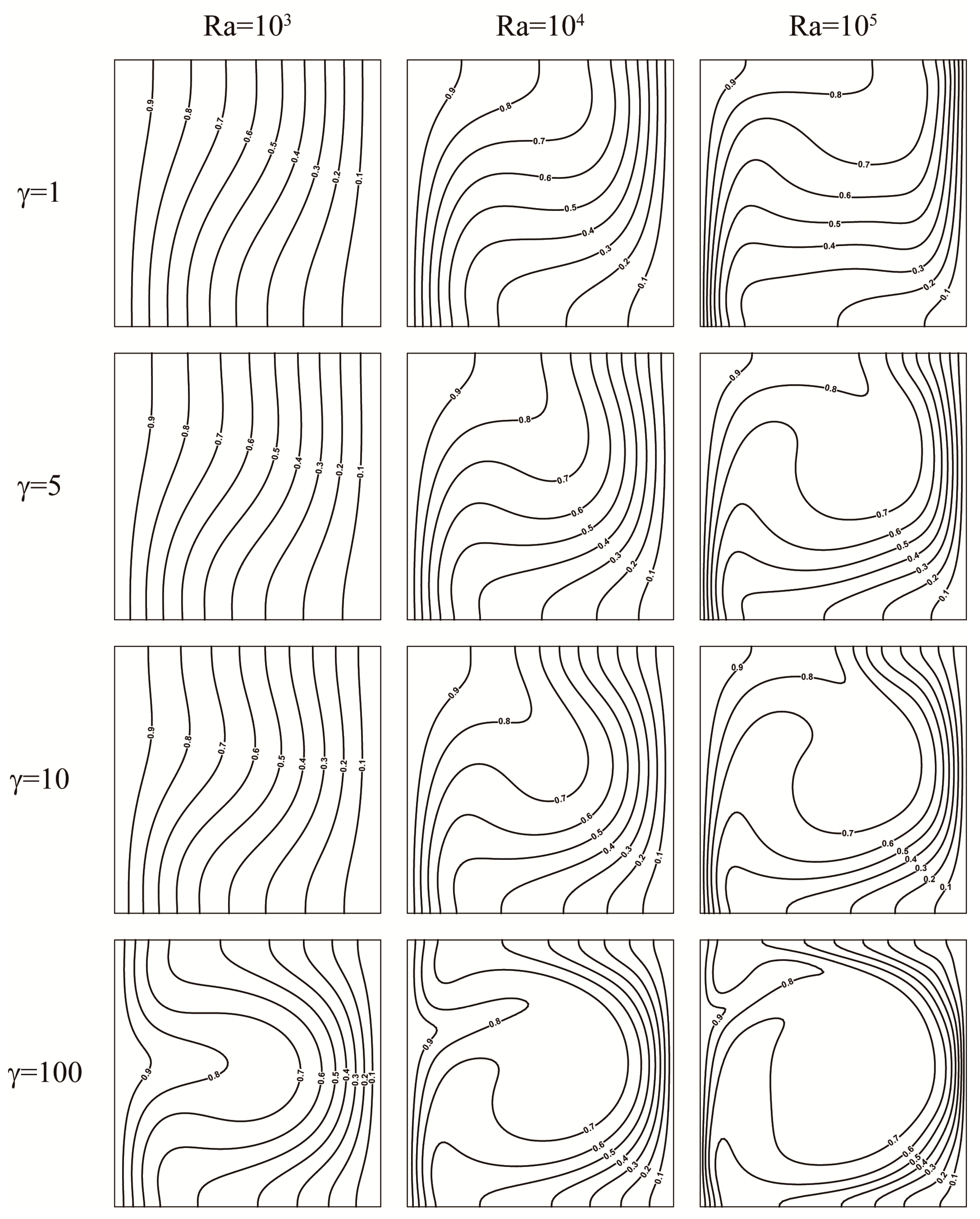
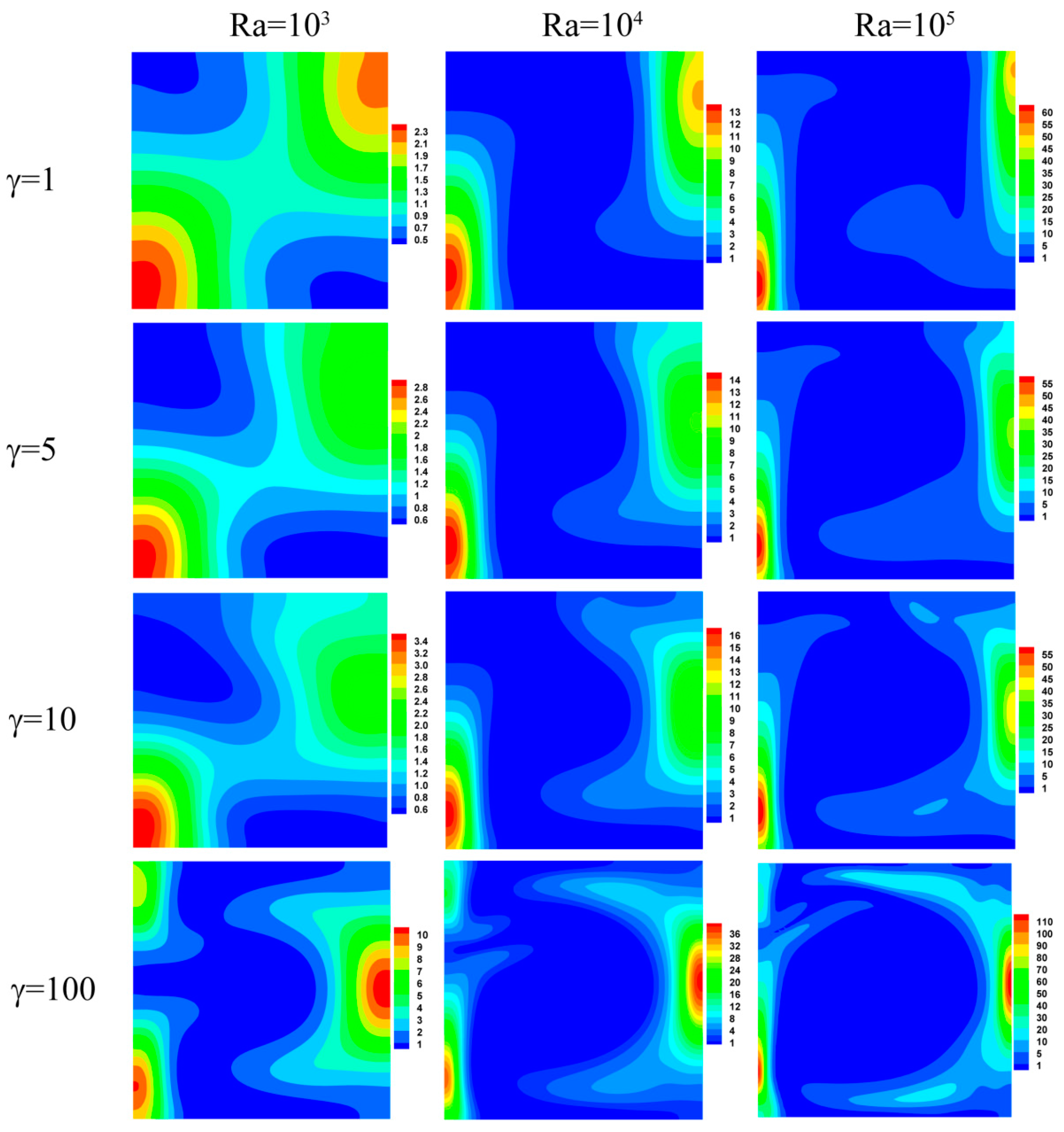
4.1.1. Streamlines, Isotherms, and Entropy Generation Characteristics

Figure 3 shows the streamlines and isotherms for paramagnetic fluid at various γRa numbers. Streamlines display two symmetric cells within the cavity. One circulates in the counterclockwise direction, and the other circulates in the clockwise direction with the same strength. This characteristic is strengthened by increasing γRa. According to the Curie law, the colder fluid becomes more magnetized. Thus, it is drawn to regions with a stronger field (Y = 0 and 1) displacing warmer and less magnetized fluid.

For the isotherm contours (Figure 3b), they are symmetric about the horizontal middle line of the enclosure. For γRa = 1 × 10⁴, isotherms are almost parallel with the hot and the cold walls, which indicates that conduction dominates heat transfer. With increasing γRa, the isotherms deformed from the hot wall to the cold wall by the strong convection. On the other hand, an increase in γRa causes the temperature gradient in the center of the enclosure to decrease, and the whole fluid cavity tends to a uniform temperature.

Figure 4 illustrates local Bejan number (Be), entropy generation maps due to heat transfer (S_θ), and fluid friction (S_ψ) for a paramagnetic fluid with γRa = 10⁴–10⁶. The maximums of local entropy generation due to heat transfer and fluid friction increase with the ascending of γRa. From the entropy generation map, due to heat transfer (S_θ), it can be found that S_θ is higher at the top and the bottom left corner of the cold wall, as well as the mid-sections of the hot wall due to the steep thermal gradient near those regions. At the midplane, the thermal entropy is at a minimum due to two opposing vortices’ energy transfer which causes the minimum thermal gradient. It is noted that zones with significant entropy generation due to heat transfer also become narrower with γRa, although the strength of S_θ is strengthened. For entropy generation due to flow friction depicted by S_ψ, the effect of S_ψ is almost negligible over the whole enclosure at γRa = 1 × 10⁴. With increasing γRa, the peak values of S_ψ emerge near the left top and bottom portions of the hot wall. In the core of the cavity, a higher fluid friction irreversibility is observed, which is more likely to be generated by the interface of the two opposite vortices. Comparisons of S_θ and S_ψ for γRa from 10⁴ to 10⁶, the magnitude of S_ψ,max is increased approximately by one-hundred times, whereas S_ψ,max is 1500 for γRa = 10⁶ and 13 for γRa = 10⁴.

The distributions of local Bejan numbers are almost symmetric on the horizontal middle line of the cavity. When γRa = 10⁴, the irreversibility due to heat transfer dominates the entire region, except for two thin layers near the top and bottom center of the adiabatic walls. The minimum Bejan number appears in the vicinity of the adiabatic wall. At higher γRa (i.e., γRa = 10⁵ and 10⁶), the motion of the fluid is strengthened. The area dominated by irreversibility due to viscous friction is enlarged. When γRa = 10⁶, the dominant contribution of fluid friction on entropy generation appears in a large zone.

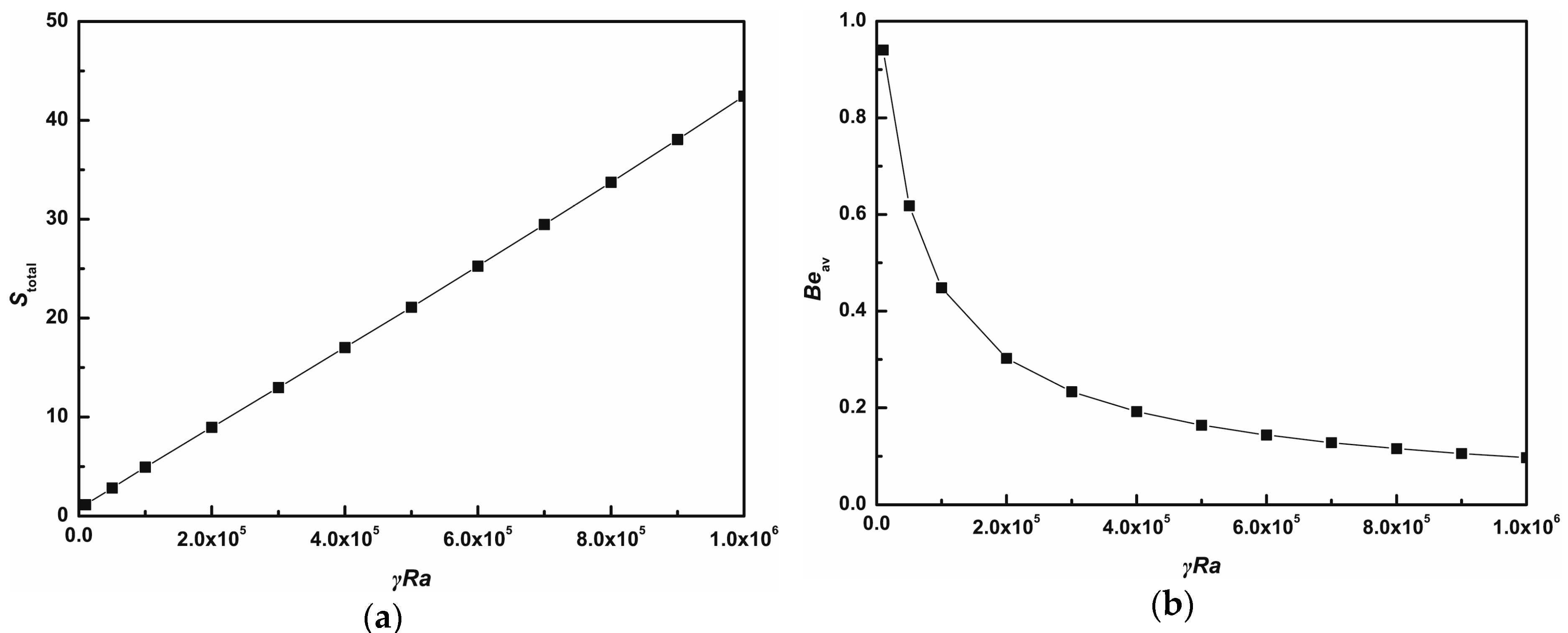
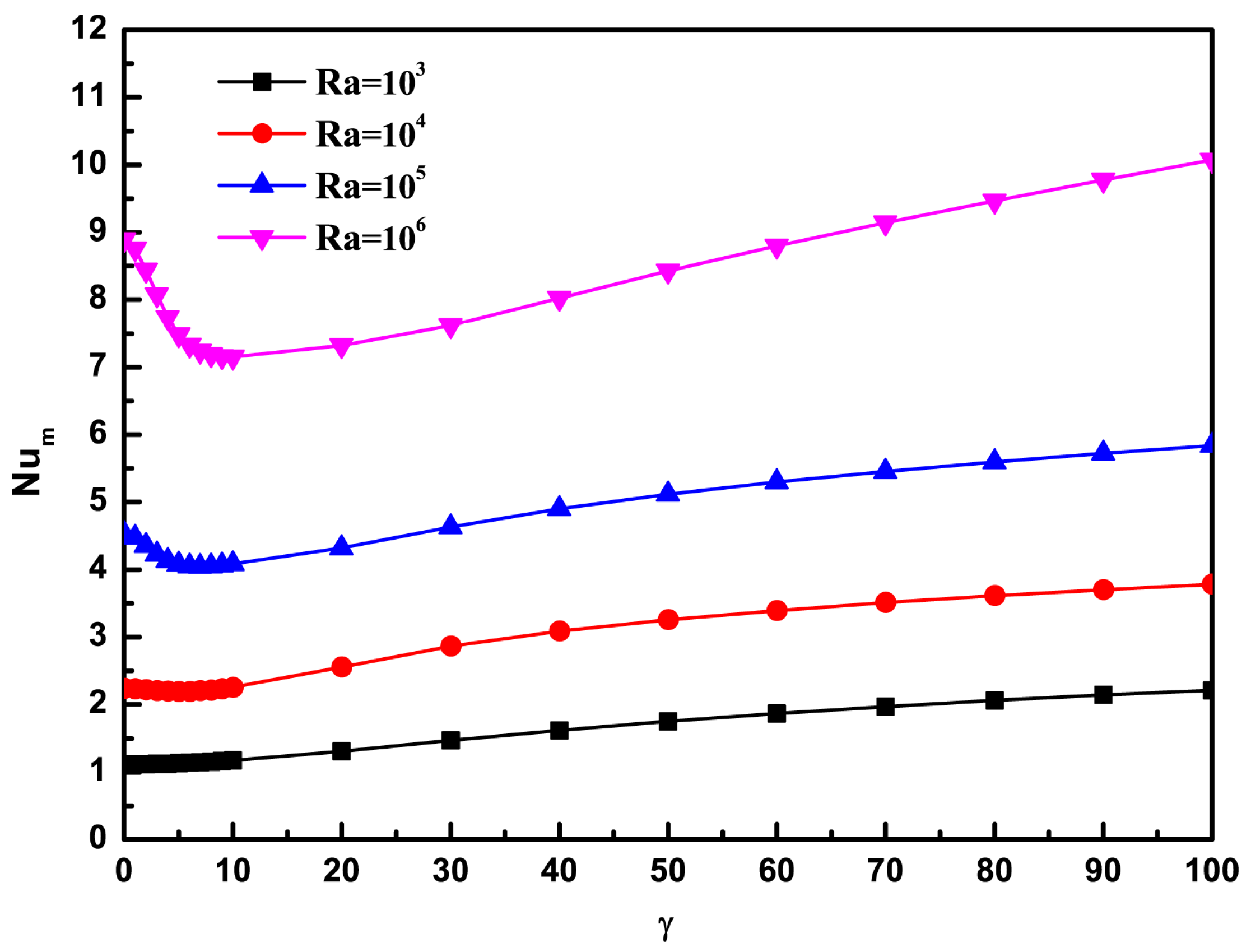
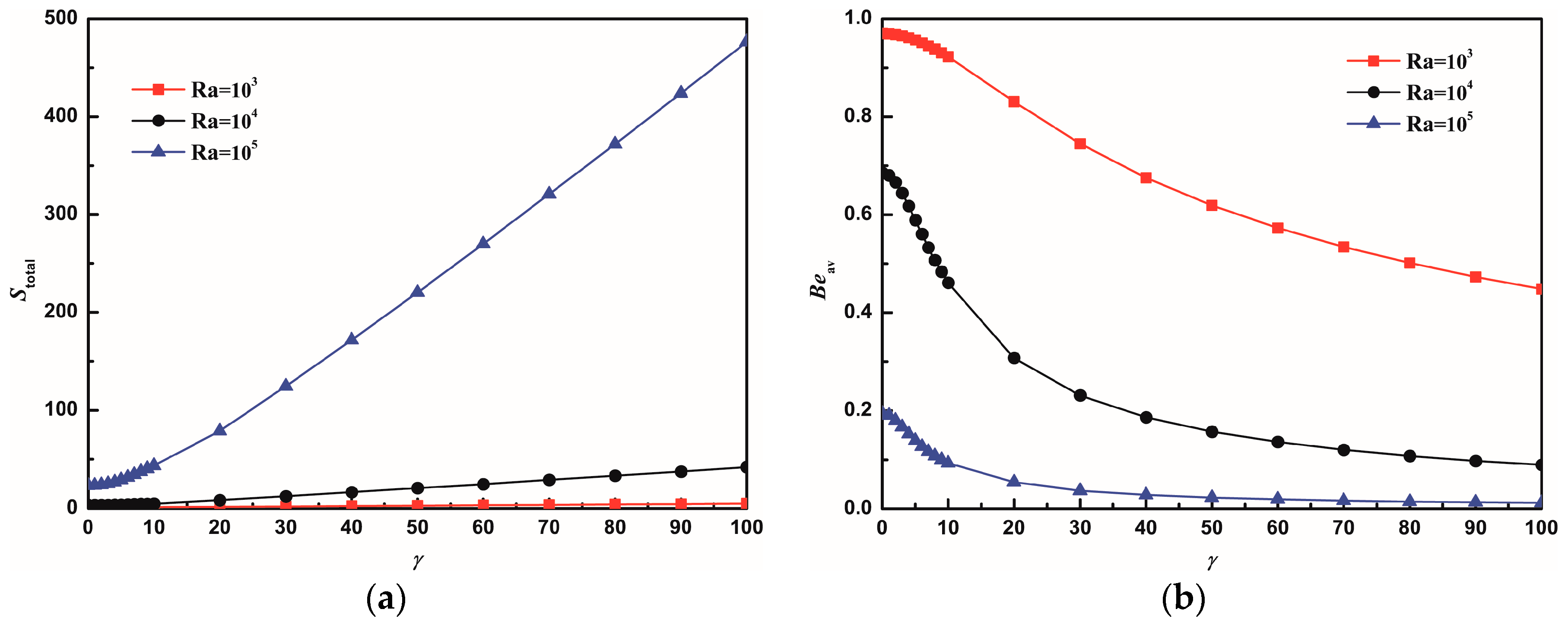
4.1.2. Average Nusselt Number, Total Entropy Generation, and Average Bejan Number

Figure 5 shows variations of the average Nusselt number (Nu_m) of the enclosure for different values of γRa. One can observe that the presence of a magnetic field is associated with an increase in the heat transfer and Nu_m is monotonically increased with γRa. Especially, the increment of Nu_m becomes much slower at higher Ra.

Figure 6 illustrates the variation of total entropy generation (S_total) and average Bejan number (Be_av) versus γRa. The distribution of total entropy generation (S_total) increases almost linearly with γRa. This implies that the intensification of γRa leads to an acceleration of the flow, which increases the temperature and velocity gradients. This causes the increase of total entropy generation. Figure 6b illustrates the corresponding average Bejan number (Be_av), which indicates the contribution of irreversibility due to thermal diffusion to the total entropy generation number. A common decreasing trend in Be_av with γRa is observed. The maximum value for Be_av occurs at the low γRa, indicating that the heat transfer irreversibility predominates the domain at the dominant conduction mode. When γRa = 10⁵, Be_av approaches 0.5, which implies that the irreversibility due to viscous dissipation will supersede the other and become a leading contributor to entropy generation. At higher γRa, the increment of γRa causes the dominance of fluid friction to entropy generation. Consequently, the vast amount of available energy is utilized to overcome the fluid friction irreversibility at a high γRa.

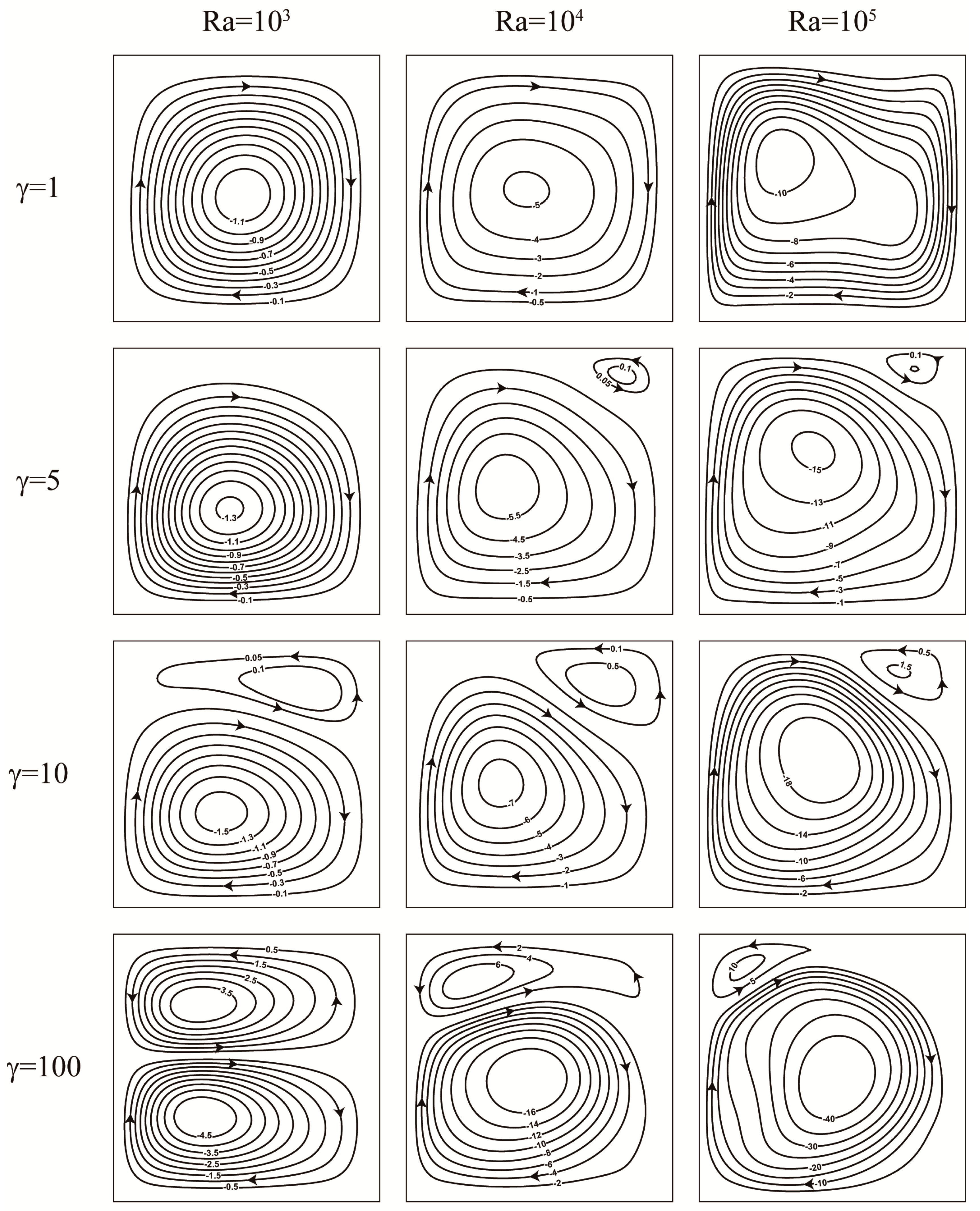
4.2. Numerical Results with a Gravitational Filed

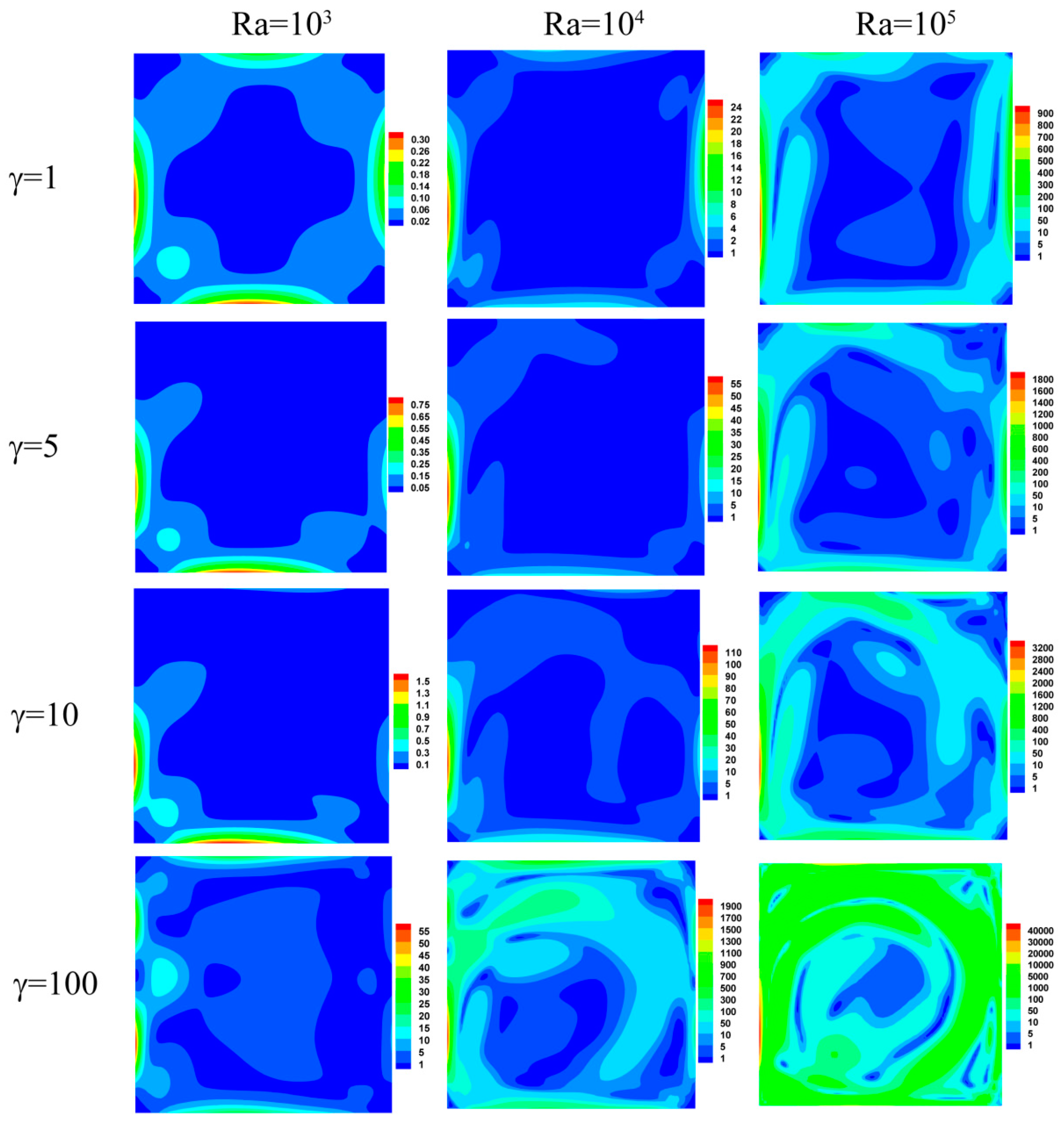
4.2.1. Streamlines, Isotherms, and Entropy Generation Characteristics

Figure 7 shows the effect of magnetic force number on streamlines of a paramagnetic fluid for different Rayleigh numbers in the gravitational field. The fluid is driven by the combination of magnetic buoyancy force with a radial direction outwards and gravity buoyancy force. In the lower part of the cavity, the Y component of magnetic acceleration is identical in direction with that of gravitational acceleration. The synergy of magnetic buoyancy force and gravitational buoyancy force improves the paramagnetic fluid flow. In the upper part of the cavity, the Y component of magnetic acceleration is opposite to the direction with that of gravitational acceleration. A small counter-acting vortex forms at the top. Therefore, the flow field undergoes a bifurcation where two inner vortices merge. For the same Rayleigh number, the natural convection induced by the magnetic buoyancy force is strengthened with increasing magnetic field number. As a result, the counterclockwise vortex under the top part gradually grows, while the clockwise under the bottom part of the enclosure shrinks.

Figure 8 presents the distribution of isotherms in the range Ra = 10³–10⁵ and γ = 1–100. With increasing Rayleigh numbers, the influence of the gravity buoyancy force on the flow field is observed. Due to the influence of the gravity buoyancy force directed in a negative Y direction, isotherms are more deformed in the middle region, and the area of compression about the horizontal center symmetry deflects downwards.

To understand the magnitudes of entropy generation due to heat transfer and fluid flow, the entropy generations are plotted for magnetic field number (γ) 1 to 100 and Rayleigh number (Ra) 10³ to 10⁶, as depicted in Figure 9 and Figure 10. It is observed that for low values of Ra and γ, maximum entropy generation due to both fluid flow and heat transfer is small and the irreversibility related to the process is negligible. From Figure 9, the entropy generation contours due to the heat transfer are concentrated strongly adjacent to the middle right and bottom left wall; however, S_θ is almost insignificant at the core of the cavity because of the negligible thermal gradient in that regime. When Rayleigh numbers and magnetic force numbers increase, the entropy generated from the heat transfer is almost zero in most parts due to the growth of heat transfer by convection.

It is worth noting from Figure 10 that S_ψ reaches the maximum value at the interface between the primary circulation cell and the hot wall as a result of the no-slip boundary condition on the solid side. With the increase of Ra and γ, the entropy generation due to fluid friction increases significantly and the significant zones of S_ψ extend deeply into the cavity. This implies that the interaction of the magnetic and gravity forces strengthens the fluid movement and leads to a substantial increase in S_ψ. Compared S_θ with S_ψ, S_θ,max increases marginally; while S_ψ,max increases significantly with increasing Rayleigh numbers or magnetic field numbers.

4.2.2. Average Nusselt Number, Total Entropy Generation, and Average Bejan Number

Figure 11 shows the variations of the average Nusselt number (Nu_m) with magnetic force number (γ) for various Rayleigh numbers (Ra). The average Nusselt number increases with increasing Ra. However, Nu_m shows different dependence on the change of γ. At a low Ra, such as Ra = 10³, heat transfer rate respects a slowly monotonic increasing function of γ. At higher Ra, Nu_m changes non-monotonically because of the synergy and counteraction between the magnetic force and the gravity force. In other words, the increase of the magnetic field number makes the average Nusselt number decrease firstly, and then increase.

Figure 12 represents the variations total entropy generation (S_total) and the average Bejan number (Be_av) versus the magnetic force number for various Rayleigh numbers. S_total is very small and remains almost constant as the value of magnetic field number increases at Ra = 10³ and 10⁴. It can be found that the effect of magnetic field on entropy generation is more pronounced at high Rayleigh numbers. To explain this phenomenon, at low Rayleigh numbers the heat transfer is dominated by conduction, while at high Rayleigh numbers the heat transfer is controlled by convection. The S_total increases because of the strong effect of the natural convection with respect to the influence of the magnetic field.

A common decreasing trend in Be_av with Ra is observed for all γ in Figure 12b. The decrease of Be_av with increasing values of magnetic field number shows the augmentation of the friction irreversibility rate because of the increase of the velocity gradient by applying a magnetic quadrupole field. At lower Ra, the entropy generation is controlled by conduction. The heat transfer irreversibility is much larger than the fluid friction irreversibility. In this regime, even increasing the magnetic field number to 100, S_θ dominates over S_ψ, resulting Be_av > 0.5. When Ra increases to 10⁴, entropy generation due to the viscous effects becomes dominant against the heat transfer ones, from γ close to 10. For Ra = 10⁵, Be ≤ 0.2 occurs for all γ because of enhanced magnetic and gravity convection resulting in the dominance of fluid friction entropy generation.

5. Conclusions

Entropy generation for thermomagnetic convection of a paramagnetic fluid under a magnetic quadrupole field with and without gravity is analyzed. The effect of the Rayleigh number and magnetic field number are evaluated. The following conclusions are drawn:

• In the absence of gravity, the flow field with two cellular structures is symmetric about the horizontal centerline. As the Nusslet number increases, the total entropy generation (S_total) increases linearly as well with increasing γRa. When γRa < 1 × 10⁵, entropy generation due to heat transfer is relatively dominant. However, when γRa > 1 × 10⁵, the leading contributor to the irreversibility comes from fluid friction because the flow is enhanced by convection.
• In the presence of gravity, with an increase in the magnetic force number, a clockwise vortex reinforces and splitting phenomenon occurs, which results in two vortices with opposite circulating directions and strength. Fluid friction irreversibility begins to surpass heat transfer irreversibility for increasing Rayleigh numbers and magnetic field numbers. Entropy generation spreads throughout the domain at high Rayleigh numbers, but is restricted to the vicinity of the boundaries at small Rayleigh numbers. The total entropy generation is insensitive to the variation of the magnetic field number for low Rayleigh numbers; while the magnitude of the total entropy generation changes significantly for high Rayleigh numbers. Higher magnetic field numbers lead to lower Bejan numbers.