1. Introduction
In 1922, Stern and Gerlach published a paper [
1] reporting experimental findings on how silver atoms could be deflected when travelling through a magnet with a field gradient in the direction of the main component of the field. They observed that the silver atoms followed one of two paths corresponding to a deflection of equal size but of opposite sign.
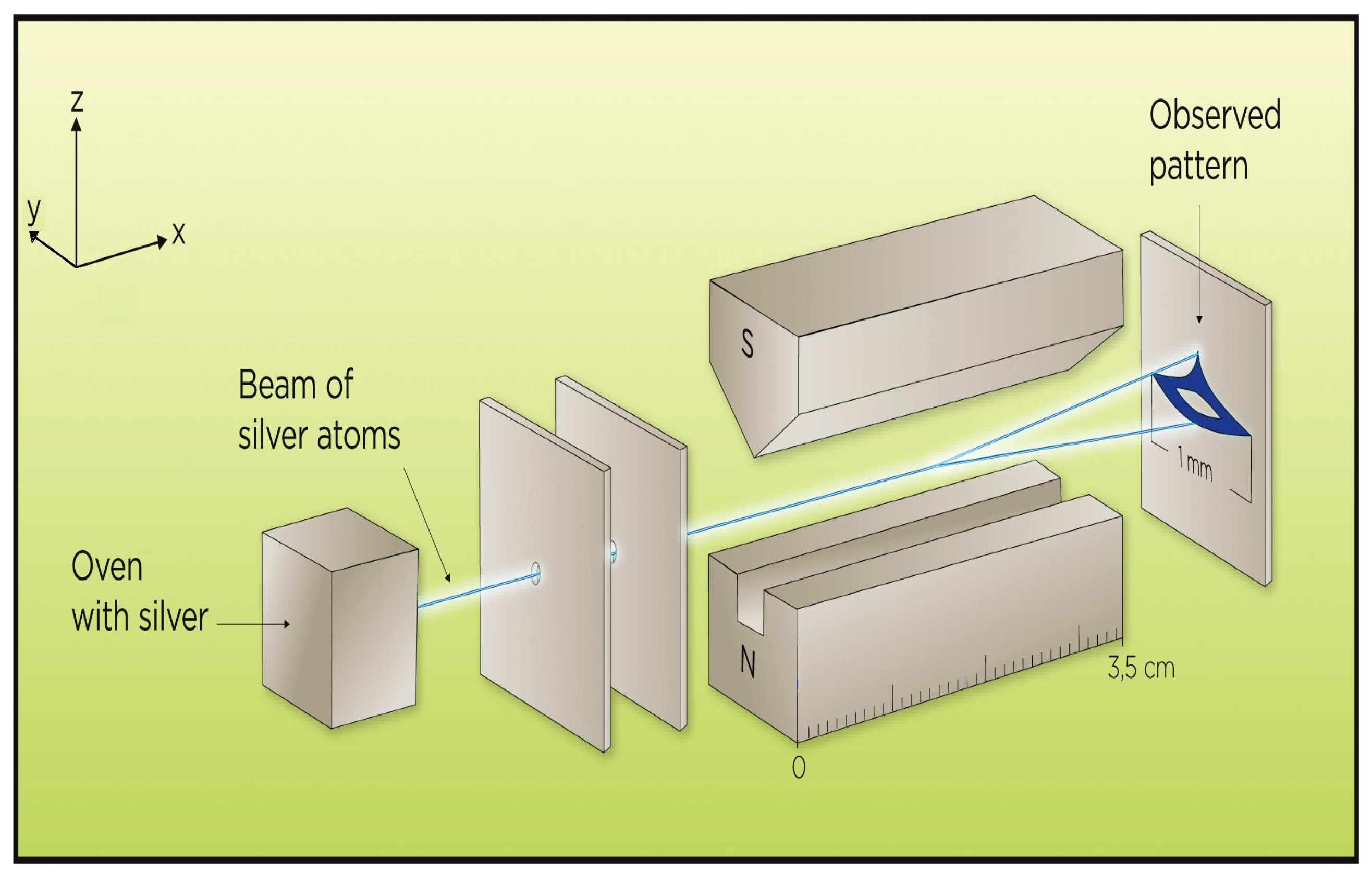
Figure 1 shows a schematic view of the experiment. The result was surprising to the authors, but they immediately understood that they had observed another manifestation of the quantum world that was in the process of being unraveled at that time. Stern even sent a postcard to Bohr the day after the observation to congratulate him for a successful theoretical prediction! It would soon turn out, however, that Bohr’s analysis didn’t provide the correct explanation of the observation. A fascinating historical account of the Stern–Gerlach (SG) experiment and the scientific discussion it initiated was recently published by Schmidt-Böcking et al. [
2]. It was later realized that the observation of a splitting into two paths was due to an interaction between the spin of the unpaired electron in the ground s state of the silver atom. It was also concluded that the measured deflection was consistent with a
g-factor of 2 for the electron spin. The calculation was based on treating the interaction spin–magnetic field in a quantum formalism, while treating the dynamics of the atom using classical mechanics.
The report by Stern and Gerlach was soon followed by other investigations using the same concept. Studies were made on alkali and hydrogen atoms [
3,
4] and the experimental results followed the established expectations supporting the original interpretations. At this stage, the SG experiment was scientifically established and was no longer a part of the research front. It was, however, one of the rare experiments that were considered to be fundamental enough to take a role in forming a conceptual understanding. Consequently, a large fraction of textbooks of quantum mechanics makes use of the experiment to illustrate the spin concept in quantum theory [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. In these textbook accounts, one typically keeps the classical description of the translational motion and remarks that the fundamental quantum effect is that the silver atoms behave as if their spin takes one of two possible values. Some authors point out [
13,
14] that there is a question of how the initially unpolarized spins transform into adopting one of two possible states. A further complication addressed by D. Bohm [
5], for example, is that a gradient in the field must, according to Maxwell’s equations, have at least two vectorial components so one along the
z-direction requires one also along the
y-direction.
Considering its conceptual importance, it took a long time before the SG experiment was analyzed using a more complete quantum description. A. Bohm [
17], Scully et al. [
18,
19] and Utz et al. [
20] and Gomis and Perez [
21] have shown that, using a Hamiltonian accounting for translation and a field in the
z-direction, it is possible to derive the basic SG observation of a splitting into two separate signals at the detector without invoking further approximations. Even though the authors of these papers provide a formal description of the experiment, they refrain from addressing some of the interpretation problems. How is the polarization of the spin created? For a spin polarized in the
-plane, there is no force generated on the atom. There is, however, still a force transmitted by the gradient. What happens with the spin on the entry to the magnetic field? What is the effect of the gradient in the perpendicular direction? In the present paper, we aim at getting more insight into these questions by combining a more realistic description of the magnetic field with an ambition to push the quantum treatment of the problem as far as is feasible. The final description is developed in three steps. In
Section 2, we first present a formally exact solution to the problem of a spin one half particle traveling initially in the
x-direction in a magnet with a field
B = (0, 0,
). This problem has been solved previously [
18,
19,
20,
21,
22], but we present an alternative formally simple derivation. It has the dual advantage of providing both a more obvious connection to the semi-classical text-book description and a basis for a generalization including also the effect of the field gradient in the
y-direction. In
Section 3, the latter case is analyzed considering the extra term in the Hamiltonian as a perturbation. The third step is in
Section 4 where we consider the dynamics of the particle and its spin associated with the entrance of the particle into the magnet. The magnetic field has a complex space dependence in this region, and we consider explicitly only the situation when a particle enters the magnet with
strictly. In
Section 5, the formal results are then discussed in terms of possible interpretations. The observations of the original SG experiment are quantitatively accounted for, including the role of the spread in the initial position and momentum in the
y-direction.
Section 6 concludes that the formal results are consistent with the validity of the adiabatic approximation applied to spin dynamics from the point where the spin enters the magnetic field, to its exit from the magnet.
Section 7 gives a discussion of alternative descriptions based on spin relaxation and decoherence concepts and final conclusions are summarized in
Section 8 .
2. Silver Atom inside a Magnet with Field Exclusively in the z-Direction
Discussions of the SG experiment are typically based on the simplifying assumption that the magnetic field, B, is strictly along the
z-axes, with a main component and a gradient
which is a measure of the strength of the gradient:
The Hamiltonian of the silver atom in the field is then
Here, , where the electron gyromagnetic ratio for the 5 s electron is sT, and is the dimensionless spin angular momentum operator. In the following derivations, we simplify the notation using .
This is valid inside the magnet
, where
L is the length of the magnet. In order to obtain manageable boundary conditions, it is assumed that, at
the silver atoms enter the magnet with a momentum,
, solely along the
x-direction. In reality, there has to be a distribution of momenta also in the other directions. In the original experiment, two slits were used to keep
and
small, while simultaneously having
and
as well-defined as possible. The Hamiltonian Equation (
2) and the initial conditions specifies a quantum mechanical problem.
Below, we present a solution to this problem that differs formally, but not fundamentally, from previously reported solutions [
17,
18,
19,
20,
21,
22]. The starting point is the general equation of motion of an observable
involving the commutator of
and
HSince the spin operator
in the
z-direction commutes with
H it follows that
and
is a constant of the motion. The other central operator in the problem is the momentum
describing the translational motion in the
z-direction. One has
Since
is a constant of the motion it follows that the derivative
is time independent. This describes the time evolution of the mean value of
. However, to have a more complete description, we need information on how the distribution of
develops. Thus, consider
It follows that the evolution of
is determined by the correlation between
and
, which could appear difficult to calculate. However,
This operator has a constant time derivative and
Inserting this result into Equation (
7) yields, since
Note that this result is independent of the initial state of the spin system. Equations (6) and (8) give explicit expressions for how the mean and the root mean square values of
change during the passage through the magnet. In Equation (
6), there is a dependence on the initial state of the spin. Consider first a spin that is polarized in the
z-direction so that
and use
and then
Thus, if there is no initial spread in the distribution of
, the motion through the magnet doesn’t give rise to such a spread since
Note that the expression for
in Equation (
11) is identical to the one obtained in a semi-classical description. For the case when
and there is no spin polarization in the
z-direction, Equation (
6) shows that the average momentum
remains at zero if it is initially zero. For
, on the other hand, Equation (
10) still applies and the mean square average of
evolves as for the fully polarized case. Experimentally, one never observes deviations in the
z-direction that exceed those for fully polarized spins. On both experimental and theoretical grounds, one has the relation
. Combined with the two conditions
this can only be realized by a distribution
Equation (
14) implies that a spin system, initially with no net polarization, behaves with a probability
as does a system with
and with the same probability as a system with
. This conclusion is consistent with the textbook account of the SG experiment. There is, however, a remaining question of how to interpret these probabilities. For a pure spin state,
implies that the spin is polarized in the
-plane. The magnetic field in the
z-direction gives rise to an in plane Larmor precession and there is formally no net force on the silver atom. The formalism still gives that
is time dependent according to Equation (
10). This issue will be discussed more in
Section 5. To obtain a better basis for the discussion of this conceptual problem and to get a more complete description of the SG experiment, we consider two circumstances that have been ignored by the use of the Hamiltonian of Equation (
2).
3. Silver Atom inside a Magnet Including Also the y-Component of the Field
A virtue of the formalism used in the previous section is that it can provide a basis for a feasible treatment of a more general case. To make the magnetic field of Equation (
1) consistent with Maxwell’s equations, it is necessary to add a gradient also in the
y-direction. Then, there is an additional term in the Hamiltonian
With this term in the Hamiltonian, the spin
is no longer a constant of the motion and
Equation (
5) for the time derivative of the momentum
remains the same as well as Equation (
7) for the evolution of
. We no longer get a closed set of equations, however, since, instead of Equation (
8), one has
To make progress, it seems necessary to introduce approximations into the calculations utilizing the fact that deviations of
y from zero are small making
a weak perturbation. Consider the case where initially
. There is a force on the atom in the
y-direction, but it is much smaller than the force in the
z-direction, and it is assumed that one can ignore the change in the
y-coordinate during passage through the magnet. Then, one can replace
y by
y(0) in the equations. The time dependence of
is no longer linear and, to find the correction, one can take the time derivative of Equation (
5)
The time variation in
is
By assumption, we have
. If one then neglects the last term in Equation (
19), one is back to a normal Larmor precession in a magnetic field
and
Using this relation, Equation (
18) can be integrated to yield
There is, thus, in addition to the leading term proportional to
t, also an oscillating correction term in the expression for
. We can now evaluate the correction term in Equation (
17) as approximately
Here, the last equality follows from the circumstance that
oscillates rapidly so it averages to zero over a short time. Using Equation (
22), the derivative in Equation (
17)
is time independent as in the absence of a
y-component of the field, but with a somewhat smaller value. After integrating the equation using the initial condition
one has
Thus, the presence of a gradient in the
y-direction has only a limited influence on the dynamics of the silver atoms. This conclusion was reached by more qualitative arguments by Bohm [
5] and Le Bellac [
14]. However, as not shown previously, a deviation in the initial
y-value from zero has the effect of reducing
and thus the deviation in the
z-coordinate of the atoms during the passage. Integration of Equation (
24) results in our final expression for the dynamics of the silver atoms in a realistic magnetic field
This result is, as for the corresponding Equation (
10), independent of the initial spin polarization.
In
Section 2, it was concluded that Equation (
10) was only compatible with a delta function distribution of
. Is a similar argument valid for Equation (
25)? For a position with
, the magnetic field is not along the
z-direction. If one assumes that there initially is a perfect polarization of the spin along the
z-direction
there will be a rapid precession and
will have a component that averages to zero over a short time. The net force on the atom in the
z-direction is then reduced by a factor
, where
is the angle between the field and the
z-axes. Similarly, if one assumes that the spin is polarized along the direction of the field, the net force in the
z-direction is also reduced by a factor
. For
it follows that
Thus, the maximum/minimum value of
is
Comparing Equations (25) and (27), it follows that, to the leading order,
Thus, also for the case the atoms move as if they follow one of two trajectories where the force is maximal. This behavior is independent of the initial condition for the spin.
4. Spin Dynamics on Entering the SG Magnet
In the previous sections, the description was focused on the events once the silver atoms had entered the magnet. The initial conditions were chosen at and . A somewhat bewildering formal result was that the behavior inside the magnet was partly independent of the initial condition for the spin state. This concerns in particular how the square of the momentum in the z-direction developed.
In most accounts of the SG experiment, one avoids an explicit discussion of the behavior of the system prior to the entry into the magnet. It is remarked that there is a narrow zone of the same order as the gap width where the magnetic field goes from essentially zero to the value inside the magnet. The magnetic field outside the magnet isn’t controlled explicitly. The experimental result can, however, be accounted for solely on the basis of the events inside the magnet, and this suggests that what happens outside the magnet is irrelevant. Below, we scrutinize this somewhat optimistic assumption.
The fact that the outcome of the experiment seems to be independent of the detailed properties of the entrance magnetic field suggests that one can use a model magnetic field in the discussion of entrance effects. The field inside the magnet is known from Equations (1) and (15). Outside the magnet, the field can be estimated (see
Appendix A) by integrating the dipolar contribution from a magnet with uniform gap
D. Then, for
,
Due to the presence of the gradient in the plane inside the magnet, there is not a perfect fit between the expressions for the field around , but we ignore this complication.
It is a substantial challenge to solve the dynamic quantum equations for a silver atom moving across such a field. Even though the transition zone is narrow, the residence time of the silver atoms is still much larger than the inverse of the varying Larmor frequency. There is no obvious basis for assuming that the spin state is, in general, conserved during the entrance into the magnet.
To obtain some information on what can happen to the spins in the entrance zone, consider the idealized case where silver atoms enter along
. In this limit, Equation (
29) shows that there is only a field in the
z-direction. It varies strongly with the position
x and there is a coupling between the
component of the spin and the translational motion along the
x-direction. In a semi-classical approximation, the Hamiltonian is
where the varying Larmor frequency is given by
. If the spin is initially polarized along the the
z-direction in the spin up state, Equation (
30) implies that the spin energy is
. It is increasing in time as
x increases and, by conservation of energy, there has to be a corresponding loss of kinetic energy of the atoms. With a spin in the opposite state, the spin energy decreases, resulting in an increase of the kinetic energy of the atoms. For the case of an initial polarization of the spin in the
-plane so that
= 0, it follows from the Hamiltonian of Equation (
30) that the average spin energy
is zero throughout the entrance phase. Analogous with the analysis of the properties of the momentum
in the previous section, it is revealing to consider the mean square energy of the spin system and
This value is independent of the character of the spin state. For a pure spin up, or spin down, this is fully consistent with the value for . All other initial spin states behave as if they were either spin up or spin down with probabilities given by the diagonal elements of the spin density matrix. Note that, by making the semi-classical approximation by treating the translational motion classically, the spin state, for example, represented by a density matrix, need not correspond to a pure state.
5. Quantitative Interpretation of the SG Observations
In
Section 2,
Section 3 and
Section 4, we have derived a number of exact and approximate relations valid for the SG experiment, but without explicitly addressing the question concerning the pattern observed on the detector. Equation (
11) in
Section 2 shows how the momentum in the
z-direction evolves in time for a spin system that is initially spin polarized along the
z-direction. This dependence is derived from a quantum formalism. To find a predicted pattern on the detector placed at the exit of the magnet, a relation between position and momentum is needed. This, in turn, involves an interpretation step. By inserting the quantum result for the momentum into a classical trajectory calculation, one obtains the prediction that the silver atom with mass
m is deflected to
in full accordance with observations and with the standard description. It thus appears that the position-momentum relation for the atoms can be seen as fully classical in this particular case. For a system that is initially unpolarized in the
z-direction, the mean of
is zero, but, according to Equation (
14), this reflects the fact that
is distributed into two values corresponding to the ones found for the two fully polarized states. There are two main possibilities for interpreting this situation. One possibility (see, for example, Utz et al. [
20]) is to see the particle state as a superposition of the two space/spin combinations and there is then a reduction of the wavefunction on the detector. The other possibility (see, for example, Schmidt-Böcking et al. [
2] is to, analogously with the case for an initially polarized situation, consider two separate classical trajectories where each particular atom follows one of these trajectories with equal probability. Schmidt-Böcking et al. argue in detail in favor of this interpretation.
The main result of
Section 3 was the conclusion that an initial deviation of the position in the
y-direction, from zero, results in a reduction of the increase in momentum during the passage through the magnet. If one also in this case applies a classical relation between momentum and position, one has at the detector in position
Thus, as the
-value increases, the gradient in the
y-direction consequently decreases the gap between the two final
z-positions. This conclusion explains semi-quantitatively the observed “mouth-like” pattern on the detector in the original experiment. In reality, we expect that there is also a contribution from an initial spread in the momentum
around its average value of zero. First, when this effect is also considered, it is possible to determine the initial deviations in
y and
from their mean value of zero based on the observed pattern on the detector. It emerges from the calculations, however, that the observed “mouth-like” pattern on the detector (see
Figure 1) is a generic consequence of the necessary presence of a magnetic field gradient also in the
y-direction [
23].
In
Section 2, it was concluded that the evolution of the momentum in the
z-direction squared
has a time evolution that is independent of the initial spin state. This poses the question whether the system behaves is if it was in either a spin up or a spin down state or if the spin actually is in both of these states. The calculations in
Section 4 gave further insight into this question. It was concluded that the same dilemma appears also for the conditions in the entry zone just outside the magnet. It was further concluded that there is a covariation between spin coordinate and the momentum in the
x-direction. In this situation, there is also a choice between seeing the state of a particular silver atom as a superposition of two spin/momentum combinations or considering the atom as adopting one of two possible states with equal probability.
6. Applying the Adiabatic Approximation
A virtue of considering the dynamics of the silver atoms from a position clearly outside the SG magnet to the point of exit is that it provides a basis for considering all events from preparation to detection. Above it was found, from the point of entrance into the magnetic field to the exit at the detector, the spin of the silver atoms has the property of behaving as if it was polarized along the
z-direction. This property was found to apply irrespective of the initial state of the spin before entering the magnetic field. It was deducted that this was the case, however, at an early stage based on the outcome of the experiment. The first to formulate the conceptual problem were Einstein and Ehrenfest [
24], in a paper from 1922 [
25]. In addition, Stern expressed concerns, even late in life [
2] that such a property is hard to understand conceptually. Similar remarks also appear in textbooks.
A main conclusion from
Section 4 is that, in general, the state of the spin evolves already when entering the magnetic field. Even though one can account for the experimental outcome by considering the dynamics for position
and on using an empirical rule for the spin state, this leaves out a conceptually important aspect. In
Section 4, the entry of the silver atoms into the field was described using a time-dependent magnetic field, which implies a semi-classical approximation. For such a case, one can apply the adiabatic approximation, which states that a system in an eigenstate will remain in an eigenstate if the time variation of the Hamiltonian is slow enough. Except at the very entrance to the field, the Larmor frequency is large relative to the time variation of the Hamiltonian as measured by
s
. The criterion for applying the adiabatic approximation thus seems to be fulfilled, except at positions clearly outside the magnet. What are the consequences of applying the adiabatic approximation for the SG experiment?
Consider first the case of an atom with a spin in the
state before entering the magnet. Assume also, as in
Section 4, that the atoms come in along the
x-axis with
. The spin will then interact with a field along the
z-axes. Since it is initially in an eigenstate of the spin Hamiltonian, it will remain so. It will then follow a trajectory and reach the detector at
. This behavior is consistent with the calculations in
Section 2 and
Section 4 as well as with the conventional analysis of the SG experiment. If we introduce now the complication that the
y-coordinate is slightly off center so that
, but we still have the spin polarized along the
z-direction. If we assume a field as in Equation (
15) and adopt the adiabatic approximation, the spin enters the magnet unchanged. There a
y-component to the field appears and, according to the adiabatic approximation, the polarization changes slightly to follow the direction of the field. Then, the force in the
z-direction on the atom is reduced leading to a smaller deviation in
z at the exit. This deviation is quantitatively consistent with the finding in
Section 3. A third case is when the spin outside the magnet is polarized in the
x-direction with
. Since the field is zero, it is in a ( degenerate) spin eigenstate, but, on entering the field, this is no longer the case. There is a change from a degenerate state into a situation with two nondegenerate states. The adiabatic approximation doesn’t provide a rule for which of the two possible states will be populated. Lacking such an explicit rule one can apply a symmetry argument using the fact that there is no inherent preference for either state connecting it to a possible final state. The natural assumption is then that they are populated with equal probability. The prediction is then that the silver atoms reach the detector at
or
with equal probability of
. In addition, for this case, the prediction is consistent with observations using two SG magnet in series, but with the field direction rotated
.
In the original SG experiment, there was no active preparation of the spin state of the silver atoms leaving the oven. The initial spin state can then be represented by a spin density matrix of the form
but with a unknown reference direction
. To apply the adiabatic approximation, one first transforms the spin density matrix to a coordinate system along the magnetic field at the entrance
An equation was derived for evolution of the momentum
and its relation to the expectation value of
. If one now assumes that also during the entry phase the atoms experience a field strictly along the
z-axis, consistency with the application of the adiabatic approximation is achieved by reducing the density matrix of Equation (
35) to a diagonal form:
This no longer refers to a pure spin state and it can be interpreted as if the spin up state is adopted with probability and the spin down state with probability . For the ensemble of silver atoms, all occurs with equal probability. Thus, on average, spin up and spin down occur with equal probability and one should have with equal probability at the detector, which is consistent with the observations.
The main conclusion of the present section is that one can account for the observations in the original SG experiment and closely analogous ones by explicitly considering the spin dynamics during the full passage from oven to detector by adopting the adiabatic approximation. The problem of finding a selection rule for connecting an initially doubly degenerate spin state with one of two nondegenerate states inside the field was solved by requiring consistency with exact equations derived for special conditions of the field. A second implication of the use of the adiabatic approximation is that the silver atom follows one of two possible trajectories during the passage through the detector. There is no need to invoke a superposition of the two alternatives.
7. The Relation to Other Interpretations of the SG Experiment
In a previous paper [
23], we have analyzed the SG experiment in terms of the motion of the silver atoms inside the magnet by considering the effects of the spin relaxation. It was concluded that, by assuming a very rapid
-relaxation, it was possible to account for the experimental findings. This includes the qualitative observation that a deviation in the initial
y-coordinate,
, gives rise to a decrease in the
z-coordinate at the detector resulting in a “mouth-like” pattern. The effect of the
relaxation is to reduce a spin density matrix of the form in Equation (
35) to the diagonal one in Equation (
36). The thermal fluctuations of the magnetic field were considered to be the main cause of this relaxation. The effect to reduce the density matrix to a diagonal form is, however, the same as achieved by applying the adiabatic approximation. It is the conclusion of the present paper that the coupling between the translational motion and the spin dynamics is more essential for understanding the SG experiment than the coupling spin–thermally fluctuating field. A complete description would require considerations of both aspects. In [
21], Gomis and Perez discuss the reduction of the spin density matrix from the form in Equation (
35) to the one of Equation (
36) in terms of a decoherence process [
26]. They use a Calderia–Legett master equation to describe the coupling between the spin and a thermal bath. Although formally different, this is conceptually closely analogous to the approach of [
23], where the coupling to the thermal bath was described using the relaxation concept.
In their recent thorough account of the SG experiment and its historical context, Schmidt- Böcking et al. [
2] also discuss how to describe the motion of the silver atoms in the magnet. They conclude based on a careful argumentation the atom dynamics can, with a good approximation, be described in terms of classical trajectories. In
Section 2, we have provided additional support to this conclusion, by showing within an exact quantum description that the evolution of the momentum
is consistent with the semi-classical picture.
Scully et al. [
19], Bohm [
17], Utz et al. [
20], Gomis et al. [
21] and Reddy et al. [
22] all treat the case considered in
Section 2 within a full quantum description of spin and translation, but not of the magnetic field. The specific formalisms differ between these authors, but the main results are the same and they are in accordance with the formal results of
Section 2. Utz et al. also discuss specifically how the polarization of the spin occurs. They find, starting from
and
, in the notation used in
Section 2, that an initial spin polarized in the
-plane is rapidly polarized into a state with a spin density matrix as in Equation (
36), where the off-diagonal elements have decayed to zero. They make an interpretation that each silver atom travels as a wave packet with nonzero amplitude around the two positions of the classical trajectory. At the detector, there is then a “reduction of the wave packet”. The difficulties associated with this view are discussed in the paper by Schmidt-Böcking et al. [
2].
One important application of the SG experiment has been in discussions of coincidence effects involving the study of an entangled spin system. For two atoms in an initial combined spin singlet state that are entering two separate SG magnets, one expects a correlation between the measured deviations at the two detectors. Such a case was analyzed by Bell who arrived at a conclusion, now referred to as Bell’s theorem [
27]. One basis for the argument leading to the theorem is an assumption that the singlet character of the spin state is preserved during the passage through the magnet. For the special case of two magnets with the same direction of the field, this implies that if a spin up is observed at one magnet, this implies that one would observe spin down for the other atom. A consequence of the discussion in
Section 4 above is that the spin state evolves during the entry to the magnet. Is the singlet character preserved during this evolution? The characteristic feature of the singlet state is that it is antisymmetric with respect to particle exchange. This symmetry is preserved only if the two atoms experience identical fields during the entry of the magnet. This can’t be the case in general. There is thus no conservation rule ensuring the preservation of the singlet character. It can still be approximately valid, but a theorem based on such an approximation appears a bit unsatisfactory. By adopting the view expressed in
Section 5, that the SG experiment can be understood by applying the adiabatic approximation, a basis for an analysis of the coincidence measurement is provided. It was concluded that an atom with an initially polarized spin in the direction of the field would pass the whole SG device with an unchanged spin state. For the other extreme with a spin polarized perpendicular to the direction of the field, there is a change of the spin state into one of two possibilities with equal probability. Lacking an explicit description of this dynamic event, the most natural way is to consider it as a stochastic event. There is no basis for assuming that there is a correlation between two such stochastic events in the two magnets of a coincidence measurement. There is no conservation rule that would ensure such a correlation. When the arguments for these two limiting cases are applied to an initial singlet system analyzed in two SG devices of the same orientation, the predicted correlation is −1/3 rather than −1 as assumed by Bell. We have previously published a more detailed analysis of this argument elsewhere [
28].