Criticality and Information Dynamics in Epidemiological Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Description
2.2. Information Dynamics
2.3. Measuring Information Dynamics in the SIS Model
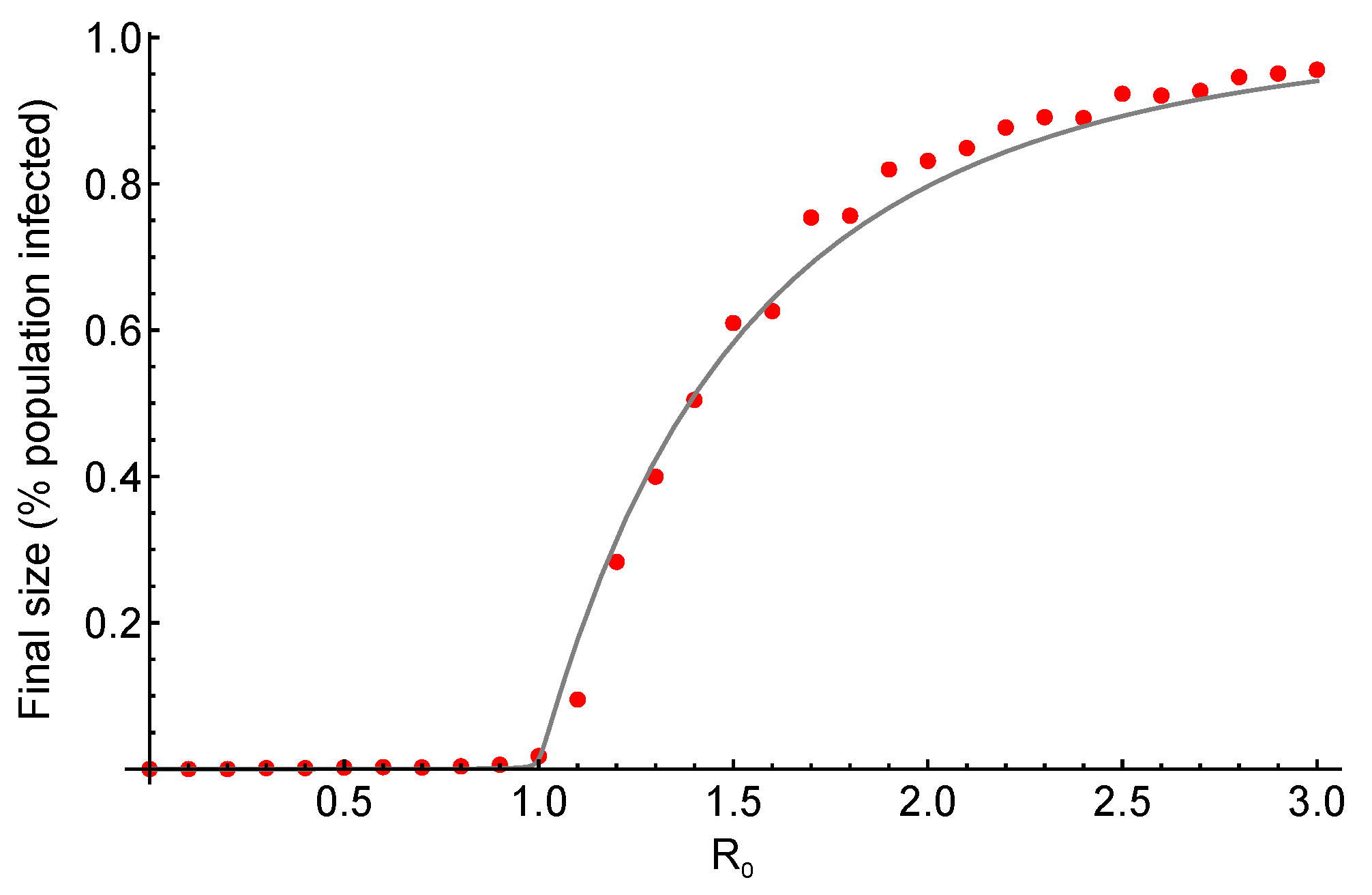
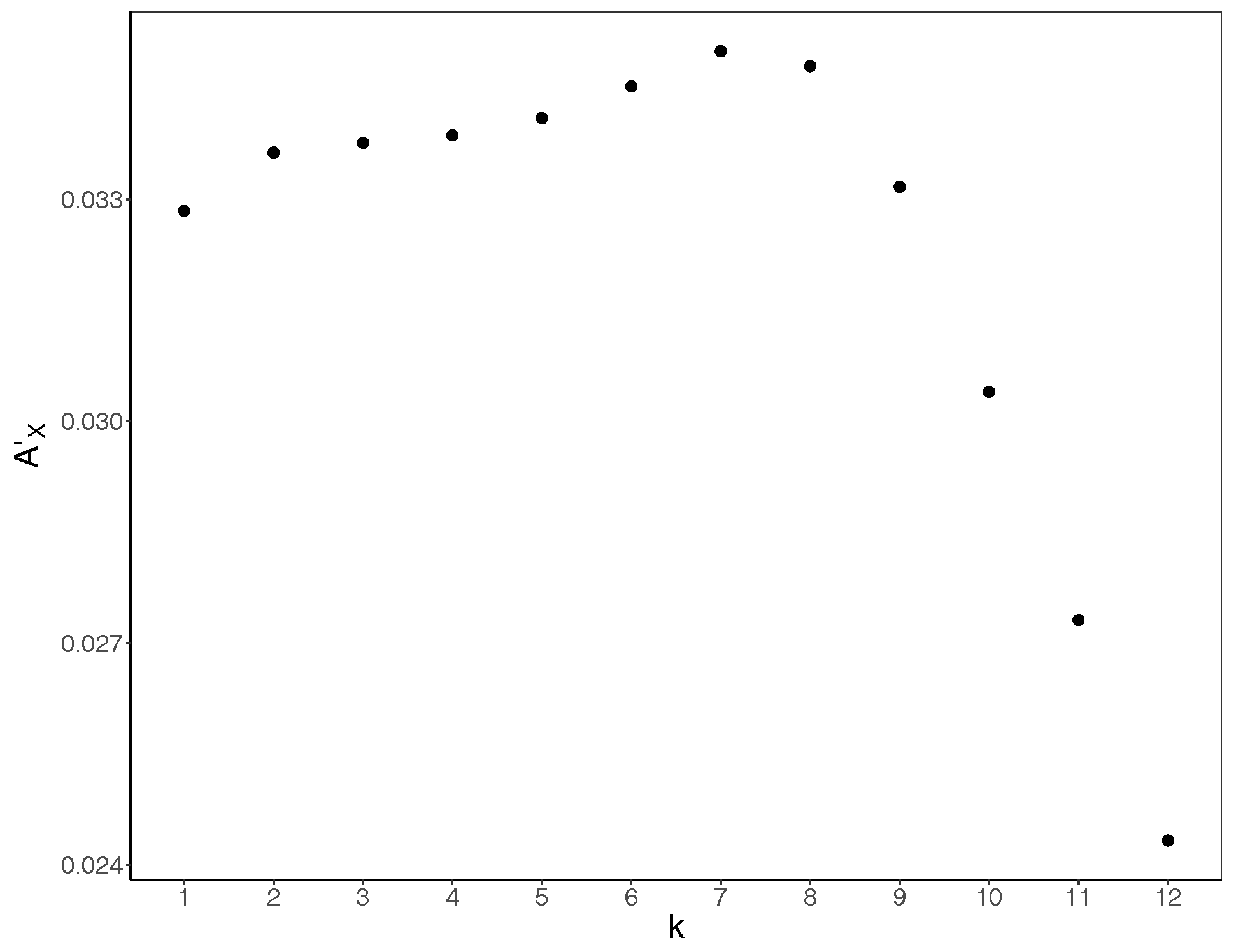
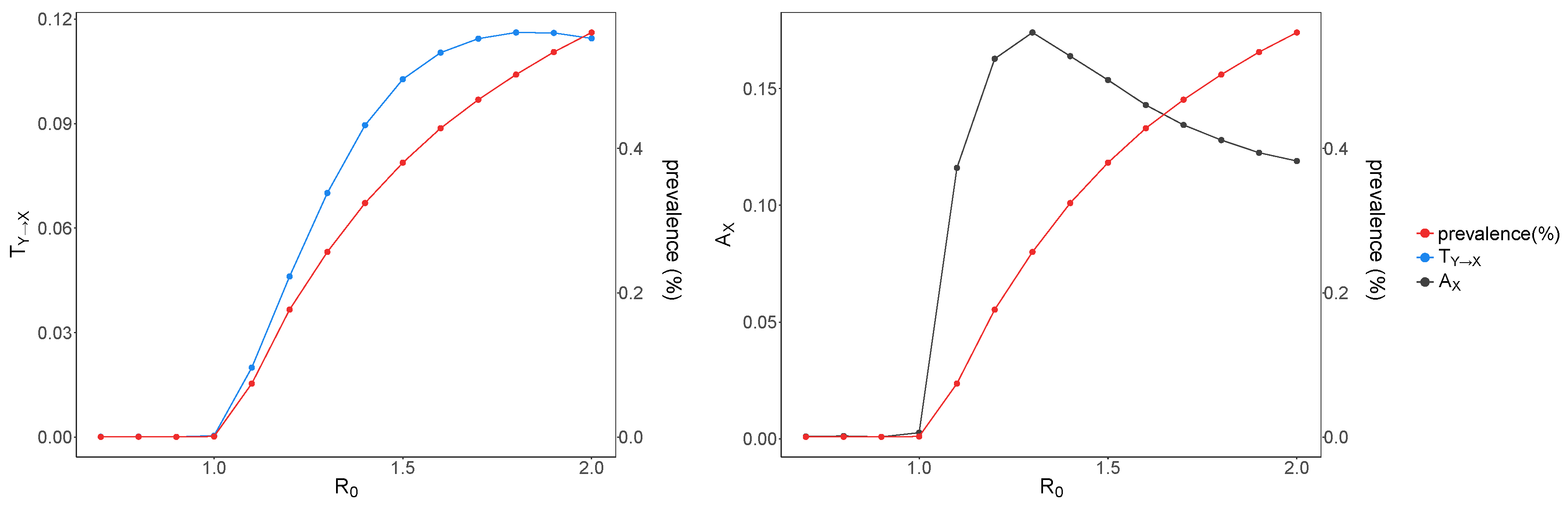
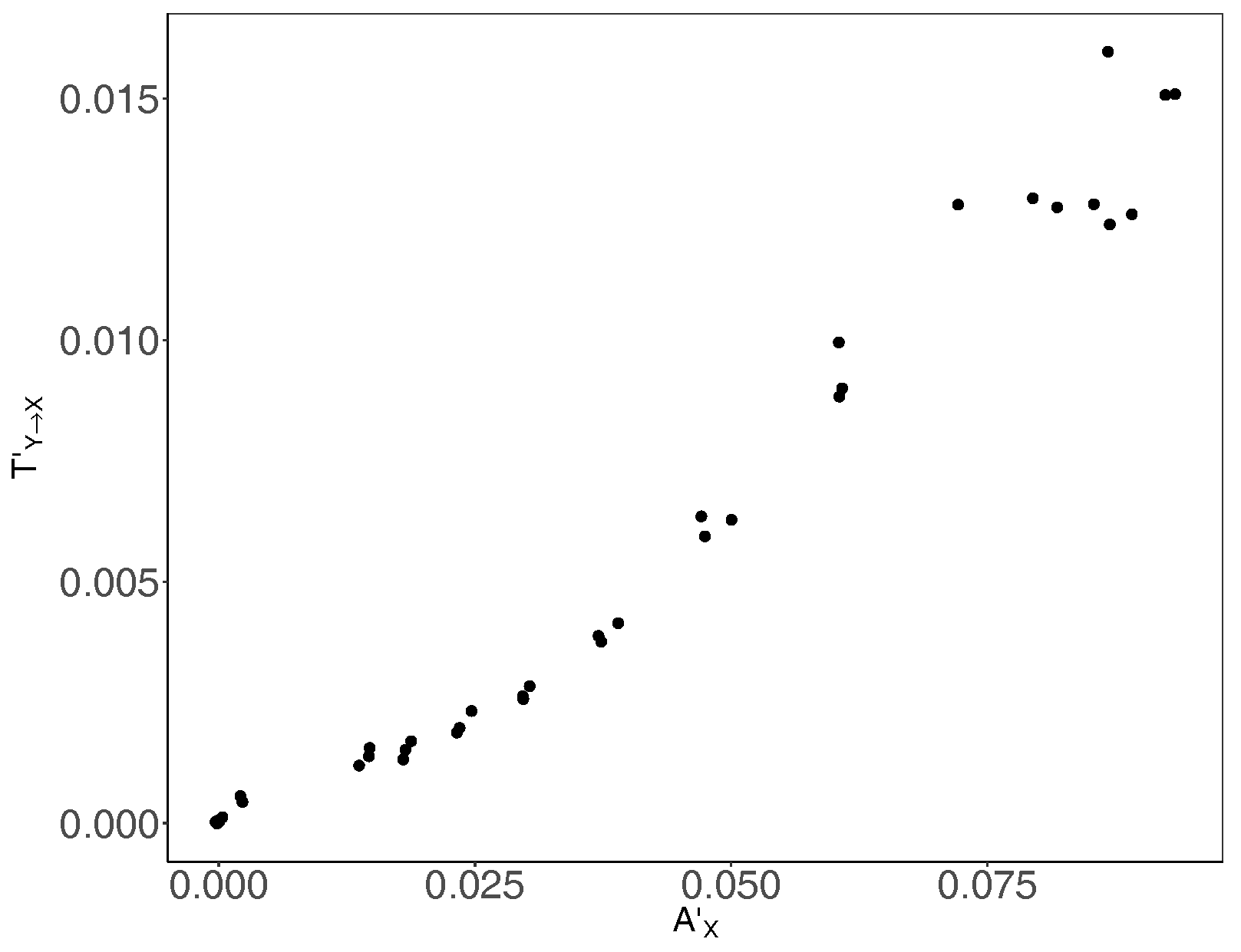
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bernoulli, D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir. Hist. Acad. R. Sci. Mém. Math. Phys. 1766, 1–45. (In French) [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Leventhal, G.E.; Hill, A.L.; Nowak, M.A.; Bonhoeffer, S. Evolution and emergence of infectious diseases in theoretical and real-world networks. Nat. Commun. 2015, 6, 6101. [Google Scholar] [CrossRef] [PubMed]
- Bauer, F.; Lizier, J.T. Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach. Europhys. Lett. 2012, 99, 68007. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M.; Anderson, B. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992; Volume 28. [Google Scholar]
- Heesterbeek, J.; Dietz, K. The concept of Ro in epidemic theory. Stat. Neerl. 1996, 50, 89–110. [Google Scholar] [CrossRef]
- Artalejo, J.; Lopez-Herrero, M. Stochastic epidemic models: New behavioral indicators of the disease spreading. Appl. Math. Model. 2014, 38, 4371–4387. [Google Scholar] [CrossRef]
- Heffernan, J.; Smith, R.; Wahl, L. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Artalejo, J.R.; Lopez-Herrero, M.J. On the Exact Measure of Disease Spread in Stochastic Epidemic Models. Bull. Math. Biol. 2013, 75, 1031–1050. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- Yeomans, J.M. Statistical Mechanics of Phase Transitions; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Antia, R.; Regoes, R.R.; Koella, J.C.; Bergstrom, C.T. The role of evolution in the emergence of infectious diseases. Nature 2003, 426, 658–661. [Google Scholar] [CrossRef] [PubMed]
- O’Regan, S.M.; Drake, J.M. Theory of early warning signals of disease emergenceand leading indicators of elimination. Theor. Ecol. 2013, 6, 333–357. [Google Scholar] [CrossRef]
- Wang, X.R.; Lizier, J.T.; Prokopenko, M. Fisher Information at the Edge of Chaos in Random Boolean Networks. Artif. Life 2011, 17, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Prokopenko, M.; Lizier, J.T.; Obst, O.; Wang, X.R. Relating Fisher information to order parameters. Phys. Rev. E 2011, 84, 041116. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Information modification and particle collisions in distributed computation. Chaos 2010, 20, 037109. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inf. Sci. 2012, 208, 39–54. [Google Scholar] [CrossRef]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. A Framework for the Local Information Dynamics of Distributed Computation in Complex Systems. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 9, pp. 115–158. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. The Information Dynamics of Phase Transitions in Random Boolean Networks. Artif. Life 2008, 11, 374–381. [Google Scholar]
- Lizier, J.T.; Pritam, S.; Prokopenko, M. Information dynamics in small-world Boolean networks. Artif. Life 2011, 17, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Harré, M.; Lizier, J.; Seth, A.K.; Bossomaier, T. Information Flow in a Kinetic Ising Model Peaks in the Disordered Phase. Phys. Rev. Lett. 2013, 111, 177203. [Google Scholar] [CrossRef] [PubMed]
- Boedecker, J.; Obst, O.; Lizier, J.T.; Mayer, N.M.; Asada, M. Information processing in echo state networks at the edge of chaos. Theory Biosci. 2012, 131, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Coherent information structure in complex computation. Theory Biosci. 2012, 131, 193–203. [Google Scholar] [CrossRef] [PubMed]
- Cliff, O.M.; Lizier, J.T.; Wang, P.; Wang, X.R.; Obst, O.; Prokopenko, M. Quantifying Long-Range Interactions and Coherent Structure in Multi-Agent Dynamics. Artif. Life 2017, 23, 34–57. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Cornforth, D.J. The information dynamics of cascading failures in energy networks. In Proceedings of the European Conference on Complex Systems (ECCS), Warwick, UK, 21–25 September 2009; p. 54. [Google Scholar]
- Amador, J.; Artalejo, J.R. Stochastic modeling of computer virus spreading with warning signals. J. Frankl. Inst. 2013, 350, 1112–1138. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans; Oxford University Press: Oxford, UK, 1991; Volume 1. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Scarpino, S.V.; Petri, G. On the predictability of infectious disease outbreaks. arXiv, 2017; arXiv:1703.07317. [Google Scholar]
- Artalejo, J.; Lopez-Herrero, M. The SIS and SIR stochastic epidemic models: A maximum entropy approach. Theor. Popul. Biol. 2011, 80, 256–264. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T. Measuring the Dynamics of Information Processing on a Local Scale in Time and Space. In Directed Information Measures in Neuroscience; Wibral, M., Vicente, R., Lizier, J.T., Eds.; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 161–193. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Meier, J.; Zhou, X.; Hillebrand, A.; Tewarie, P.; Stam, C.J.; Mieghem, P.V. The Epidemic Spreading Model and the Direction of Information Flow in Brain Networks. NeuroImage 2017, 152, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Garland, J.; James, R.G.; Bradley, E. Leveraging information storage to select forecast-optimal parameters for delay-coordinate reconstructions. Phys. Rev. E 2016, 93, 022221. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T. JIDT: An Information-Theoretic Toolkit for Studying the Dynamics of Complex Systems. arXiv, 2014; arXiv:1408.3270. [Google Scholar]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Spinney, R.E.; Prokopenko, M.; Lizier, J.T. Transfer entropy in continuous time, with applications to jump and neural spiking processes. Phys. Rev. E 2017, 95, 032319. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the effect of individual variation on disease emergence. Nature 2005, 438, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Schneeberger, A.; Mercer, C.H.; Gregson, S.A.; Ferguson, N.M.; Nyamukapa, C.A.; Anderson, R.M.; Johnson, A.M.; Garnett, G.P. Scale-free networks and sexually transmitted diseases: A description of observed patterns of sexual contacts in Britain and Zimbabwe. Sex. Transm. Dis. 2004, 31, 380–387. [Google Scholar] [CrossRef] [PubMed]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [PubMed]
- Priesemann, V.; Munk, M.; Wibral, M. Subsampling effects in neuronal avalanche distributions recorded in vivo. BMC Neurosci. 2009, 10, 40. [Google Scholar] [CrossRef] [PubMed]
- Priesemann, V.; Wibral, M.; Valderrama, M.; Pröpper, R.; Le Van Quyen, M.; Geisel, T.; Triesch, J.; Nikolić, D.; Munk, M.H.J. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 2014, 8, 108. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O.; Thivierge, J.P.; Breakspear, M. Neurobiologically Realistic Determinants of Self-Organized Criticality in Networks of Spiking Neurons. PLoS Comput. Biol. 2011, 7, e1002038. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value |
|---|---|
| Time steps (t) | |
| Population size (N) | |
| Number of contacts | 4 |
| Transmission rate () | 0.7–2.0 (with step size 0.1) |
| Coefficient for per contact transmission rate (c) | 0.33 |
| Recovery rate () | 1.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erten, E.Y.; Lizier, J.T.; Piraveenan, M.; Prokopenko, M. Criticality and Information Dynamics in Epidemiological Models. Entropy 2017, 19, 194. https://doi.org/10.3390/e19050194
Erten EY, Lizier JT, Piraveenan M, Prokopenko M. Criticality and Information Dynamics in Epidemiological Models. Entropy. 2017; 19(5):194. https://doi.org/10.3390/e19050194
Chicago/Turabian StyleErten, E. Yagmur, Joseph T. Lizier, Mahendra Piraveenan, and Mikhail Prokopenko. 2017. "Criticality and Information Dynamics in Epidemiological Models" Entropy 19, no. 5: 194. https://doi.org/10.3390/e19050194








