Measures of Qualitative Variation in the Case of Maximum Entropy
Abstract
:1. Introduction
2. Entropy and Qualitative Variation
2.1. Common Entropy Measures
2.1.1. Shannon Entropy
2.1.2. Rényi Entropy
2.1.3. Tsallis Entropy
2.1.4. Asymptotic Sampling Distributions of Entropy Measures
2.2. Qualitative Variation Statistics
2.2.1. Axiomatizing Qualitative Variation
- Variation is between zero and one;
- When all of the observations are identical, variation is zero;
- When all of the observations are different, the variation is one.
2.2.2. Selected Indices of Qualitative Variation
2.2.3. Normalizing (Standardizing) an Index
2.2.4. Power-Divergence Statistic and Qualitative Variation
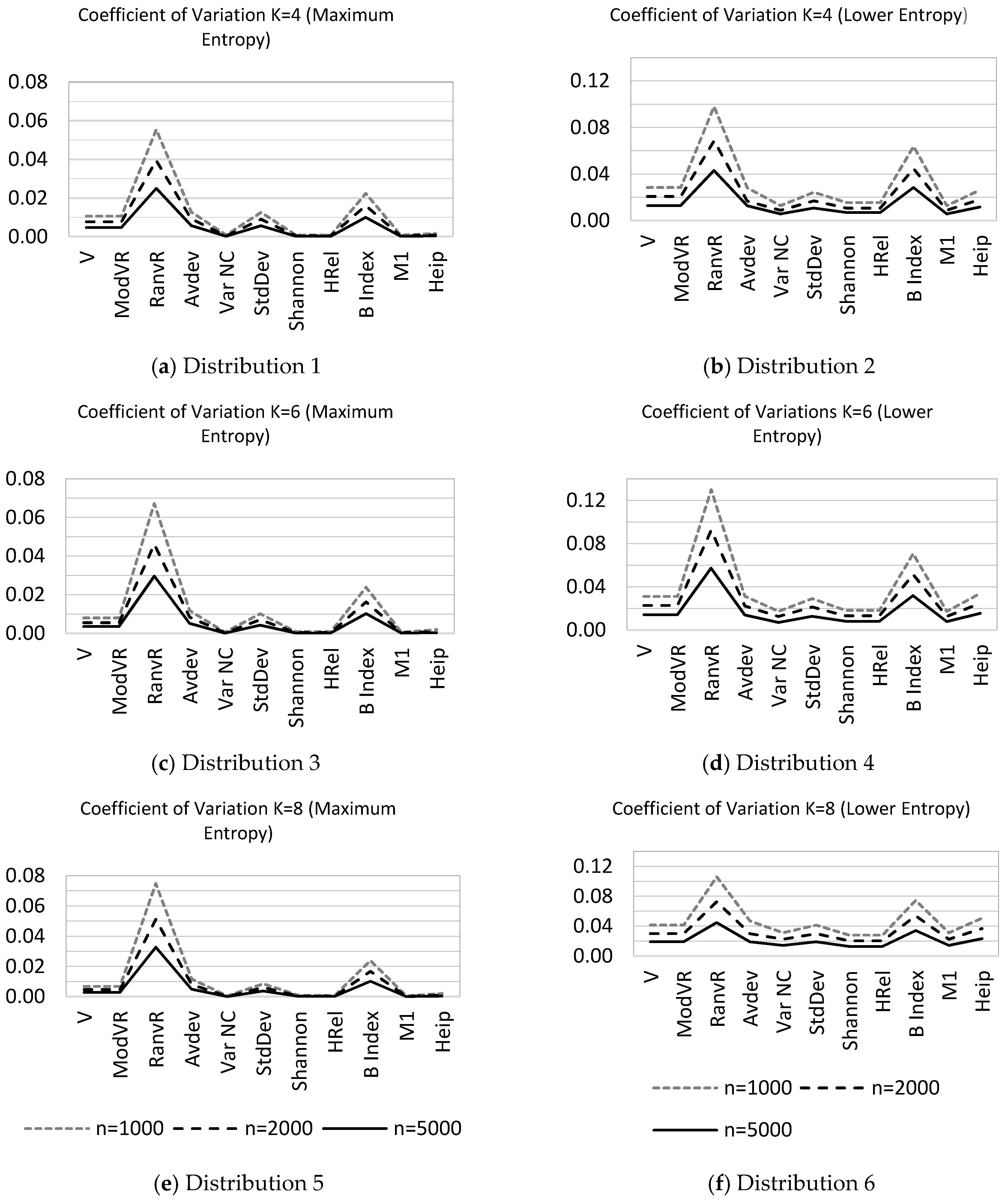
3. Normality Tests for the Various Measures of Qualitative Variation
3.1. Tests for Normality and Scenarios Used for the Evaluation
3.2. Test Results for General Parent Distributions
3.3. Test Results for Cases of Maximum Entropy
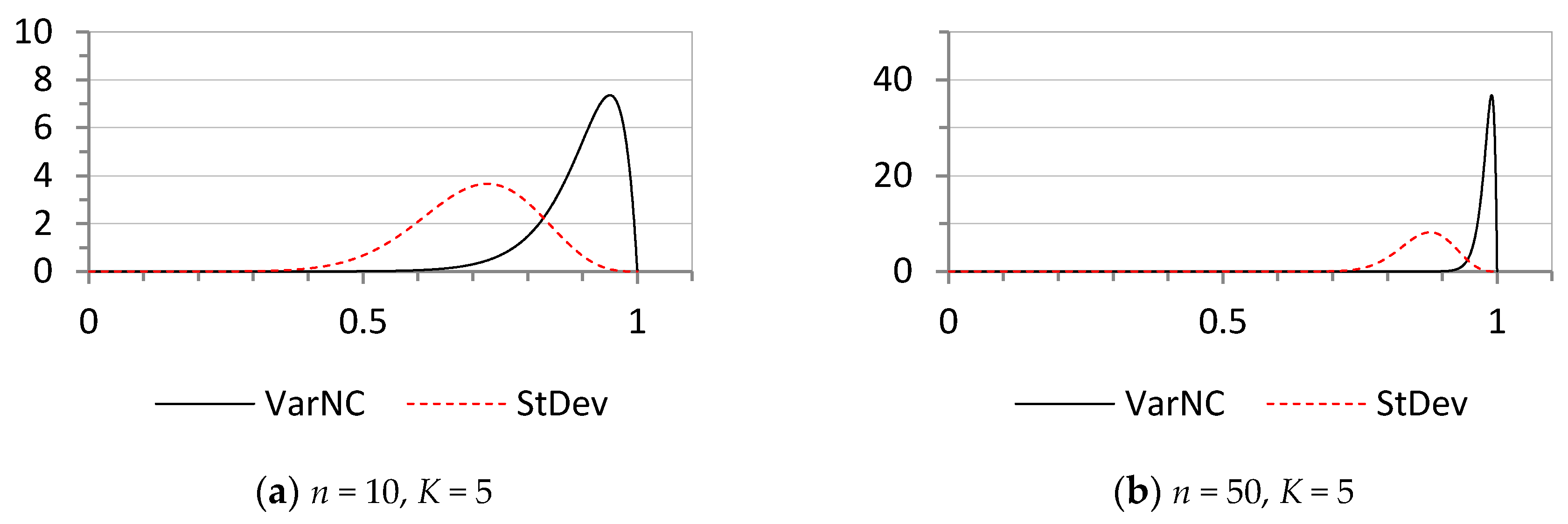
4. Sampling Properties
4.1. VarNC Statistic
4.2. StDev Statistic
4.3. Probability Distribution of VarNC and StDev under Maximum Entropy
5. Discussion
Author Contributions
Conflicts of Interest
References
- Wilcox, A.R. Indices of Qualitative Variation; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1967. [Google Scholar]
- Swanson, D.A. A sampling distribution and significance test for differences in qualitative variation. Soc. Forces. 1976, 55, 182–184. [Google Scholar] [CrossRef]
- Gregorius, H.R. Linking diversity and differentiation. Diversity 2010, 2, 370–394. [Google Scholar] [CrossRef]
- McDonald, D.G.; Dimmick, J. The Conceptualization and Measurement of Diversity. Commun. Res. 2003, 30, 60–79. [Google Scholar] [CrossRef]
- Heip, C.H.R.; Herman, P.M.J.; Soetaert, K. Indices of diversity and evenness. Oceanis 1998, 24, 61–88. [Google Scholar]
- Hill, T.C.; Walsh, K.A.; Harris, J.A.; Moffett, B.F. Using ecological diversity measures with bacterial communities. FEMS Microbiol. Ecol. 2003, 43, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Jost, L. Entropy and Diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Fattorini, L. Statistical analysis of ecological diversity. In Environmetrics; El-Shaarawi, A.H., Jureckova, J., Eds.; EOLSS: Paris, France, 2009; Volume 1, pp. 18–29. [Google Scholar]
- Frosini, B.V. Descriptive measures of biological diversity. In Environmetrics; El-Shaarawi, A.H., Jureckova, J., Eds.; EOLSS: Paris, France, 2009; Volume 1, pp. 29–57. [Google Scholar]
- Justus, J. A case study in concept determination: Ecological diversity. In Handbook of the Philosophy of Science: Philosophy of Ecology; Gabbay, D.M., Thagard, P., Woods, J., Eds.; Elsevier: San Diego, CA, USA, 2011; pp. 147–168. [Google Scholar]
- Rényi, A. Foundations of Probability; Dover Publications: New York, NY, USA, 2007; p. 23. [Google Scholar]
- Ben-Naim, A. Entropy Demystified; World Scientific Publishing: Singapore, 2008; pp. 196–208. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2002; p. 350. [Google Scholar]
- Pardo, L. Statistical Inference Measures Based on Divergence Measures; CRC Press: London, UK, 2006; pp. 87–93. [Google Scholar]
- Esteban, M.D.; Morales, D. A summary on entropy statistics. Kybernetika 1995, 31, 337–346. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell. Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Zhang, X. Asymptotic Normality of Entropy Estimators. Ph.D. Thesis, The University of North Carolina, Charlotte, NC, USA, 2013. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Los Angeles, CA, USA, 20–30 June 1961; Volume 1, pp. 547–561. [Google Scholar]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Everitt, B.S.; Skrondal, A. The Cambridge Dictionary of Statistics, 4th ed.; The Cambridge University Press: New York, NY, USA, 2010; p. 187. [Google Scholar]
- Agresti, A.; Agresti, B.F. Statistical analysis of qualitative variation. Sociol. Methodol. 1978, 9, 204–237. [Google Scholar] [CrossRef]
- Magurran, A.E. Ecological Diversity and Its Measurement; Princeton University Press: Princeton, NJ, USA, 1988; pp. 145–149. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2002; pp. 575–587. [Google Scholar]
- Evren, A.; Ustaoglu, E. On asymptotic normality of entropy estimators. Int. J. Appl. Sci. Technol. 2015, 5, 31–38. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing-an annotated biography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Bhatia, B.K.; Singh, S. On A New Csiszar’s F-divergence measure. Cybern. Inform. Technol. 2013, 13, 43–57. [Google Scholar] [CrossRef]
- Cressie, N.; Read, T.R.C. Pearson’s χ2 and the loglikelihood ratio statistic G2: A comparative review. Int. Stat. Rev. 1989, 57, 19–43. [Google Scholar] [CrossRef]
- Chen, H.-S.; Lai, K.; Ying, Z. Goodness of fit tests and minimum power divergence estimators for Survival Data. Stat. Sin. 2004, 14, 231–248. [Google Scholar]
- Harremoës, P.; Vajda, I. On the Bahadur-efficient testing of uniformity by means of the entropy. IEEE Trans. Inform. Theory 2008, 54, 321–331. [Google Scholar]
- Mood, A.M.; Graybill, F.A.; Boes, D.C. Introduction to the Theory of Statistics, 3rd ed.; McGraw Hill International Editions: New York, NY, USA, 1974; pp. 294–296. [Google Scholar]

| Index | Defining Formula | Min | Max | Explanation |
|---|---|---|---|---|
| Variation ratio or Freeman’s index (VR) | 0 | is the frequency of the modal class. | ||
| Index of deviations from the mode (ModVR) | 0 | 1 | Normalized form of the variation ratio. | |
| Index based on a range of frequencies (RanVR) | 0 | 1 | are minimum and maximum frequencies. | |
| Average deviation (AVDEV) | 0 | 1 | Analogous to mean deviation. K is the number of categories. | |
| Variation index based on the variance of cell frequencies (VarNC) | 0 | 1 | Normalized form of Tsallis entropy when . Analogous to variance. | |
| Std deviation (StDev) | 0 | 1 | Analogous to standard deviation. | |
| Shannon entropy (H) | 0 | logK | The base of the logarithm is immaterial. | |
| Normalized entropy (HRel) | 0 | 1 | Normalization is used to force the index between 0 and 1. | |
| B index | 0 | 1 | B index considers the geometric mean of cell probabilities. | |
| M1 (Tsallis entropy for | 0 | It is also known as Gini Concentration Index. | ||
| Heip Index (HI) | 0 | 1 | If Shannon entropy is based on natural logarithms. |
| Distribution | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| X | f(x) | f(x) | f(x) | f(x) | f(x) | f(x) |
| 1 | 0.25 | 0.35 | 0.166 | 0.5 | 0.125 | 0.05 |
| 2 | 0.25 | 0.1 | 0.166 | 0.2 | 0.125 | 0.65 |
| 3 | 0.25 | 0.45 | 0.166 | 0.1 | 0.125 | 0.05 |
| 4 | 0.25 | 0.1 | 0.166 | 0.1 | 0.125 | 0.05 |
| 5 | - | - | 0.166 | 0.05 | 0.125 | 0.05 |
| 6 | - | - | 0.166 | 0.05 | 0.125 | 0.05 |
| 7 | - | - | - | - | 0.125 | 0.05 |
| 8 | - | - | - | - | 0.125 | 0.05 |
| Index | Distribution 2 | Distribution 4 | Distribution 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n = 1000 | n = 2000 | n = 5000 | n = 1000 | n = 2000 | n = 5000 | n = 1000 | n = 2000 | n = 5000 | |
| Variation ratio | 71 | 86 | 100 | 100 | 100 | 100 | 86 | 100 | 100 |
| ModVR | 71 | 86 | 100 | 100 | 100 | 100 | 86 | 100 | 100 |
| RanVR | 100 | 71 | 100 | 100 | 71 | 100 | 100 | 86 | 43 |
| Average Deviation | 100 | 71 | 100 | 86 | 100 | 100 | 86 | 100 | 100 |
| VarNC | 57 | 100 | 100 | 14 | 100 | 100 | 100 | 100 | 100 |
| StDev | 100 | 100 | 100 | 86 | 100 | 100 | 100 | 100 | 100 |
| Shannon entropy | 71 | 100 | 100 | 14 | 100 | 100 | 100 | 100 | 100 |
| HRel | 71 | 100 | 100 | 14 | 100 | 100 | 100 | 100 | 100 |
| B index | 100 | 71 | 100 | 100 | 100 | 100 | 100 | 100 | 57 |
| M1 | 57 | 100 | 100 | 14 | 100 | 100 | 100 | 100 | 100 |
| Heip index | 28 | 100 | 100 | 57 | 100 | 100 | 100 | 100 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evren, A.; Ustaoğlu, E. Measures of Qualitative Variation in the Case of Maximum Entropy. Entropy 2017, 19, 204. https://doi.org/10.3390/e19050204
Evren A, Ustaoğlu E. Measures of Qualitative Variation in the Case of Maximum Entropy. Entropy. 2017; 19(5):204. https://doi.org/10.3390/e19050204
Chicago/Turabian StyleEvren, Atif, and Erhan Ustaoğlu. 2017. "Measures of Qualitative Variation in the Case of Maximum Entropy" Entropy 19, no. 5: 204. https://doi.org/10.3390/e19050204





