Information Content Based Optimal Radar Waveform Design: LPI’s Purpose
Abstract
:1. Introduction
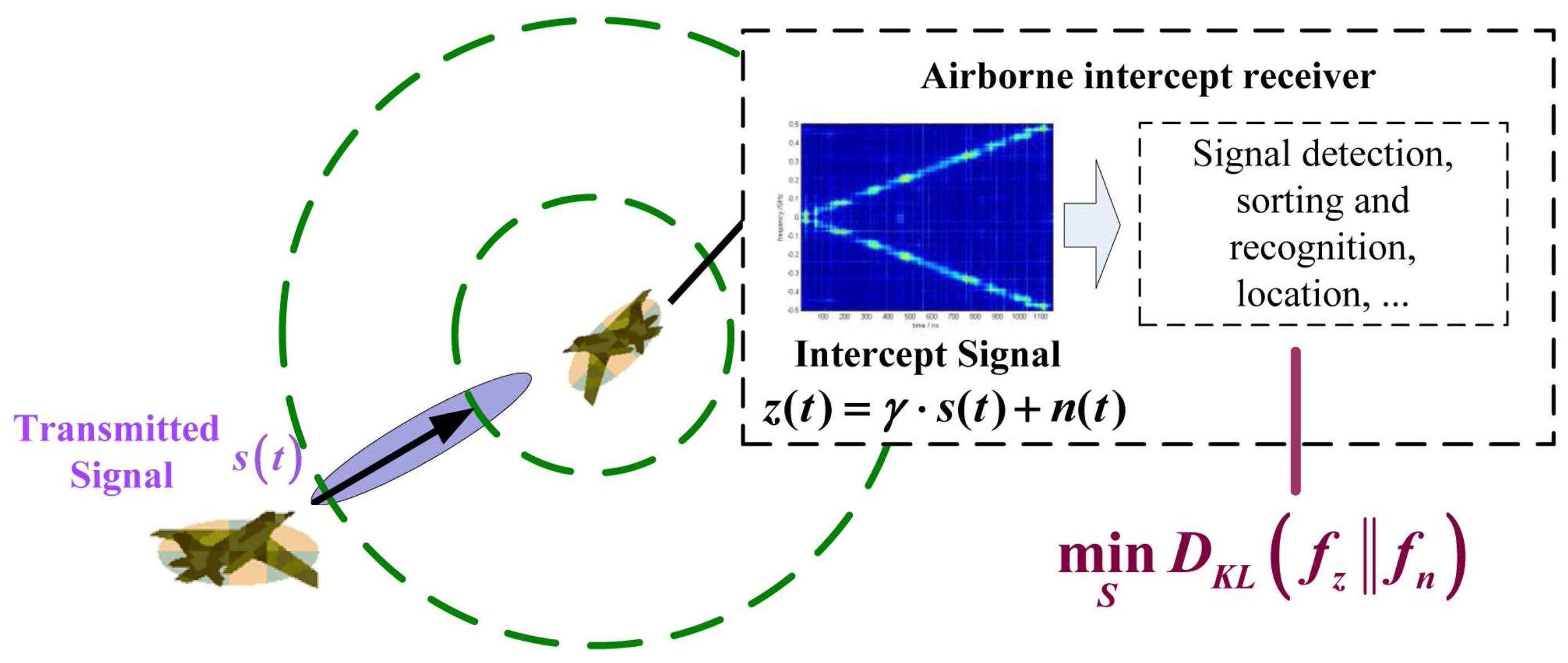
2. Information Theoretic Analyses of Radar and Intercept Receiver
2.1. Mutual Information in Radar System
2.2. Kullback–Leibler Divergence in the Intercept Receiver
3. Optimization of Radar Waveform for the Purpose of LPI
3.1. Solution of the OP1
3.2. Solution of the OP2
3.3. Solution for the Optimization Problem of LPI Waveform Design
| Algorithm 1: Radar waveform optimization for the purpose of LPI |
|
4. Simulation Results
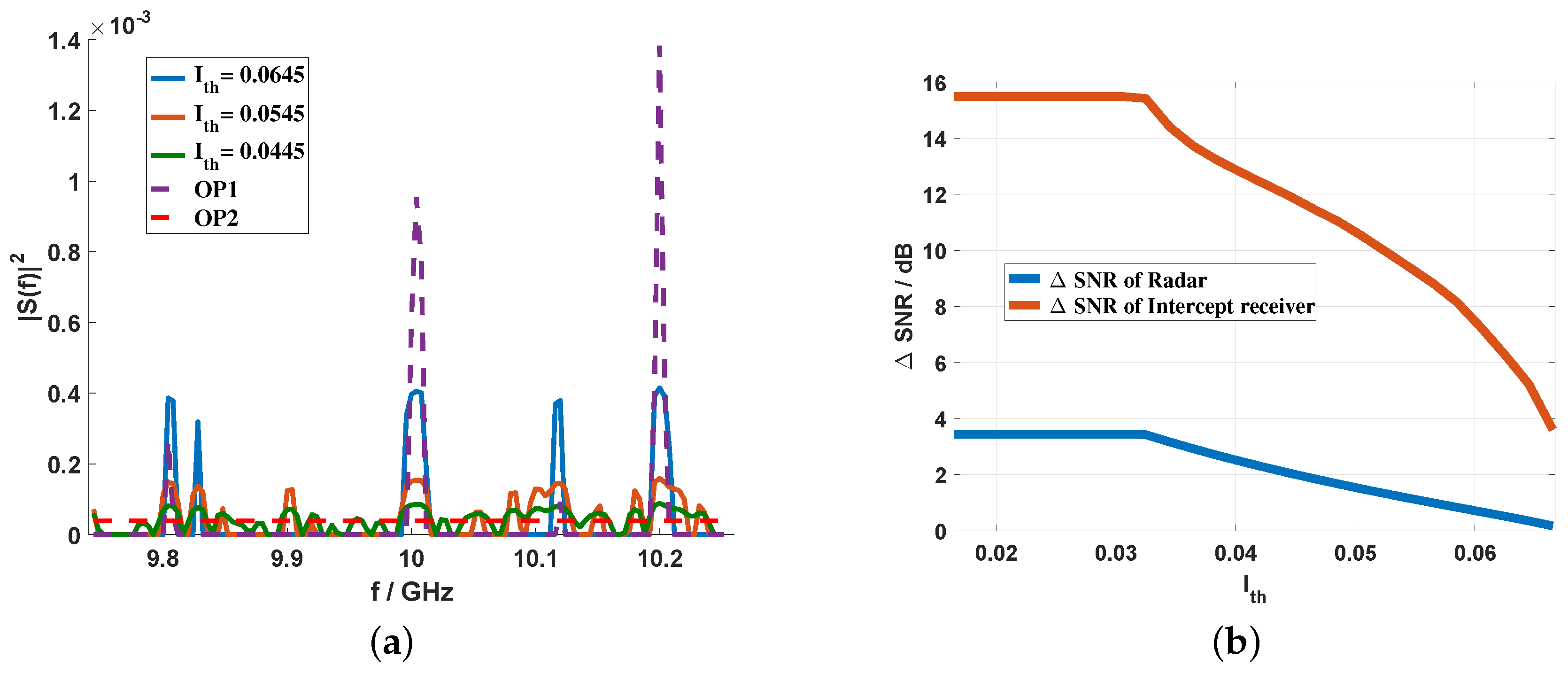
4.1. Both Radar and Intercept Receiver are under White Gaussian Noise Background
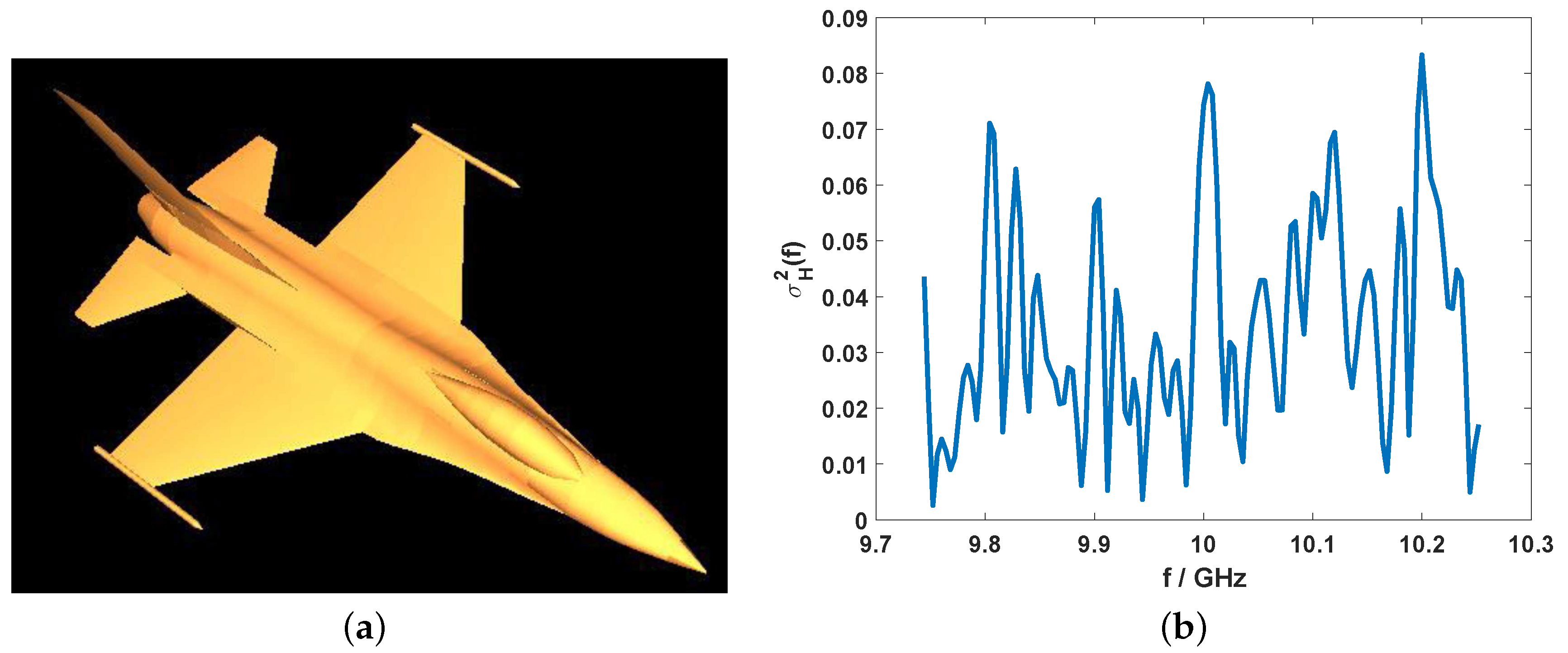
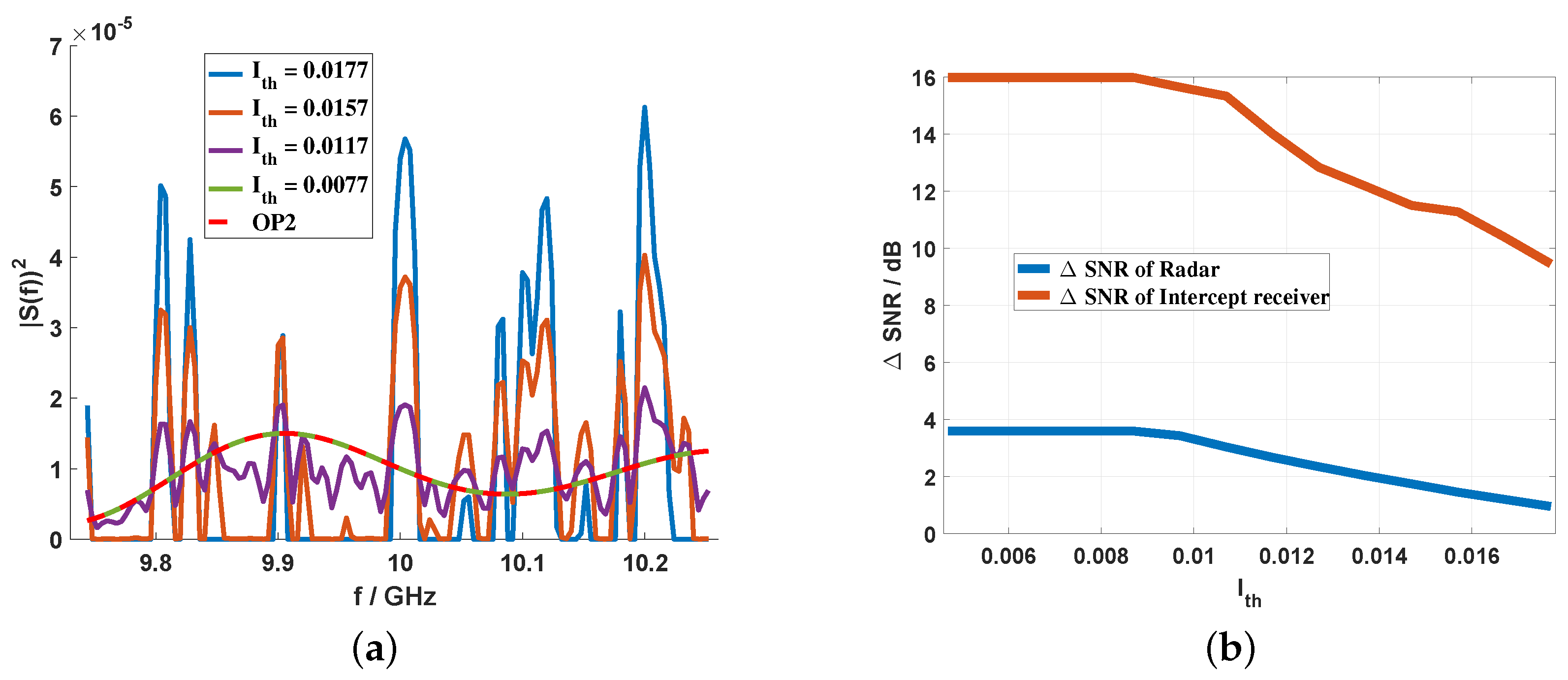
4.2. Only Radar or Intercept Receiver is under a Colored Gaussian Noise Background
4.3. Both Radar and Intercept Receiver are under Colored Gaussian Noise
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- David, L.J. Introduction to stealth systems. In Introduction to RF Stealth; SciTec Publishing Inc.: Raleigh, NC, USA, 2004; pp. 1–59. [Google Scholar]
- Schleher, D.C. LPI radar: Fact or fiction. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 3–6. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.; Xia, W.; Zhou, J. LPI Airborne Radar Signal Processing; Science Press: Beijing, China, 2015; pp. 1–19. [Google Scholar]
- Stove, A.G.; Hume, A.L.; Baker, C.J. Low probability of intercept radar strategies. IEE Proc. Radar Sonar Navig. 2004, 151, 249–260. [Google Scholar] [CrossRef]
- Schrick, G.; Wiley, R.G. Interception of LPI radar signals. In Proceedings of the IEEE International Conference on Radar, Arlington, VA, USA, 7–10 May 1990; pp. 108–111. [Google Scholar]
- Van der Merwe, J.R.; du Plessis, W.P.; Maasdorp, F.D.; Cilliers, J.E. Introduction of low probability of recognition to radar system classification. In Proceedings of the IEEE International Conference on Radar, Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Pace, P.E. Detecting and Classifying Low Probability of Intercept Radar, 2nd ed.; Artech House: Norwood, MA, USA, 2009; pp. 81–247. [Google Scholar]
- Gini, F.; De Maio, A.; Patton, L. Waveform Design and Diversity for Advanced Radar Systems; IET Radar and Sonar Navigation: London, UK, 2011. [Google Scholar]
- Bell, M.R. Information theory and radar waveform design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
- Yang, Y.; Blum, R.S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 330–343. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Farina, A.; Wicks, M. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal dependent clutter. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 93–117. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Naghsh, M. MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE J. Sel. Topics Signal Process. 2015, 9, 1387–1399. [Google Scholar] [CrossRef]
- Zhou, W.; Fei, M.; Zhou, H.; Li, K. A sparse representation based fast detection method for surface defect detection of bottle caps. Neurocomputing 2014, 123, 406–414. [Google Scholar] [CrossRef]
- Zhou, H.; Yuan, Y.; Lin, F.; Liu, T. Level set image segmentation with Bayesian analysis. Neurocomputing 2008, 71, 1994–2000. [Google Scholar] [CrossRef]
- Chen, Z.M. Stealth Waveform for Airborn Radar. Modern Radar 2006, 9, 1–7. [Google Scholar]
- Wang, F.; Sellathurai, M.; Liu, W.; Zhou, J. Security information factor based airborne radar RF stealth. J. Syst. Eng. Electron. 2015, 26, 258–266. [Google Scholar] [CrossRef]
- Fancey, C.; Alabaster, C.M. The metrication of low probability of intercept waveforms. In Proceedings of the IEEE International Conference on Waveform Diversity and Design (WDD), Niagara Falls, ON, Canada, 8–13 August 2010; pp. 58–62. [Google Scholar]
- Chen, J.; Wang, F.; Zhou, J. The metrication of LPI radar waveforms based on the asymptotic spectral distribution of wigner matrices. In Proceedings of the IEEE International Symposium Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 331–335. [Google Scholar]
- Chen, J.; Wang, F.; Zhou, J.; Dai, C. Information content-based low probability of interception waveforms selection against channelized receivers. In Proceedings of the International Symposium Signal, Image, Video and Communications (ISIVC), Tunis, Tunisia, 21–23 Novmber 2016; pp. 115–119. [Google Scholar]
- Cha, S.H. Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Models Methods Appl. Sci. 2007, 4, 300–307. [Google Scholar]
- Tumminello, M.; Lillo, F.; Mantegna, R. N. Kullback–Leibler distance as a measure of the information filtered from multivariate data. Phys. Rev. E 2007, 76, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]



| Parameter Name | Parameter Value | Parameter Name | Parameter Value |
|---|---|---|---|
| Radar transmitting antenna gain | 30 dB | Radar Receiving antenna gain | 30 dB |
| Intercept receiver antenna gain | 0 dB | emitter wavelength | 0.03 m |
| Waveform bandwidth | 512 MHz | Waveform duration | 25 ns |
| Average transmitted power | 20 KW | Path loss | −10 dB |
| Path loss | −10 dB | Detection distance R | 100 Km |
| LFM OW | Frank OW | P1 OW | P2 OW | P3 OW | P4 OW | |
|---|---|---|---|---|---|---|
| of radar (dB) | 3.1150 | 3.4526 | 3.4526 | 3.4096 | 3.4526 | 3.4526 |
| 3.1150 | 3.4450 | 3.4450 | 3.4096 | 3.4450 | 3.4450 | |
| of intercept receiver (dB) | 4.5985 | 12.4808 | 12.4808 | 11.4856 | 12.4808 | 12.4808 |
| 14.0591 | 15.4911 | 15.4911 | 14.3828 | 15.4911 | 15.4911 |
| LFM OW | Frank OW | P1 OW | P2 OW | P3 OW | P4 OW | |
|---|---|---|---|---|---|---|
| of radar (dB) | 2.9966 | 3.3342 | 3.3342 | 3.2912 | 3.3342 | 3.3342 |
| 2.9966 | 3.3266 | 3.3266 | 3.2912 | 3.3266 | 3.3266 | |
| of intercept receiver (dB) | 3.1807 | 11.0629 | 11.0629 | 10.0678 | 11.0629 | 11.0629 |
| 12.6468 | 14.0732 | 14.0732 | 13.8503 | 14.0732 | 14.0732 |
| LFM OW | Frank OW | P1 OW | P2 OW | P3 OW | P4 OW | |
|---|---|---|---|---|---|---|
| of radar (dB) | 3.3256 | 3.6632 | 3.6632 | 3.6203 | 3.6632 | 3.6632 |
| 3.3256 | 3.6632 | 3.6632 | 3.6203 | 3.6632 | 3.6632 | |
| of intercept receiver (dB) | 7.8518 | 15.8298 | 15.8298 | 14.8673 | 15.8298 | 15.8298 |
| 16.8611 | 17.4032 | 17.4032 | 17.3344 | 17.4032 | 17.4032 |
| LFM OW | Frank OW | P1 OW | P2 OW | P3 OW | P4 OW | |
|---|---|---|---|---|---|---|
| of radar (dB) | 3.2133 | 3.5509 | 3.5509 | 3.5079 | 3.5509 | 3.5509 |
| 3.2133 | 3.5509 | 3.5509 | 3.5079 | 3.5509 | 3.5509 | |
| of intercept receiver (dB) | 6.3629 | 14.3410 | 14.3410 | 13.3782 | 14.3410 | 14.3410 |
| 15.4731 | 15.8928 | 15.8928 | 15.8032 | 15.8928 | 15.8928 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, F.; Zhou, J. Information Content Based Optimal Radar Waveform Design: LPI’s Purpose. Entropy 2017, 19, 210. https://doi.org/10.3390/e19050210
Chen J, Wang F, Zhou J. Information Content Based Optimal Radar Waveform Design: LPI’s Purpose. Entropy. 2017; 19(5):210. https://doi.org/10.3390/e19050210
Chicago/Turabian StyleChen, Jun, Fei Wang, and Jianjiang Zhou. 2017. "Information Content Based Optimal Radar Waveform Design: LPI’s Purpose" Entropy 19, no. 5: 210. https://doi.org/10.3390/e19050210





