On the Convergence and Law of Large Numbers for the Non-Euclidean L^p -Means

Abstract

This paper describes and proves two important theorems that compose the Law of Large Numbers for the non-Euclidean ${\mathcal{L}}^p$-means, known to be true for the Euclidean ${\mathcal{L}}^2$-means: Let the ${\mathcal{L}}^p$-mean estimator, which constitutes the specific functional that estimates the ${\mathcal{L}}^p$-mean of N independent and identically distributed random variables; then, (i) the expectation value of the ${\mathcal{L}}^p$-mean estimator equals the mean of the distributions of the random variables; and (ii) the limit $N\to \infty$ of the ${\mathcal{L}}^p$-mean estimator also equals the mean of the distributions.

1. Introduction: Definition of ${\mathcal{L}}^{\mathit{p}}$-Means and Their Basic Properties

In [1,2,3], a generalized characterization of means was introduced, namely, the non-Euclidean means, based on metrics induced by ${\mathcal{L}}^p$-norms, wherein the median is included as a special case for $p=1$ (${\mathcal{L}}^1$) and the ordinary Euclidean mean for $p=2$ (${\mathcal{L}}^2$) (see also: [4,5]). Let the set of y-values ${\left\{y_k\right\}}_{k=1}^W$ ($y_k\in D_y\subseteq \Re$), associated with the probabilities ${\left\{{\mathit{p}}_k\right\}}_{k=1}^W$; then, the non-Euclidean means ${\mu }_p$, based on ${\mathcal{L}}^p$-norms, are defined by

$$\sum _{k=1}^W{\mathit{p}}_k{|y_k-{\mu }_p|}^{p-1}sign(y_k-{\mu }_p)=0,$$

(1)

where the median ${\mu }_1$ and the arithmetic mean ${\mu }_2$ follow as special cases when the Taxicab ${\mathcal{L}}^1$ and Euclidean ${\mathcal{L}}^2$-norms are respectively considered. Both the median ${\mu }_1$ and arithmetic ${\mu }_2$ means can be implicitly written in the form of Equation (1) as ${\sum }_{k=1}^W{\mathit{p}}_{k}sign(y_k-{\mu }_1)=0$ and ${\sum }_{k=1}^W{\mathit{p}}_k|y_k-{\mu }_2|sign(y_k-{\mu }_2)=0$ ($\iff {\mu }_2={\sum }_{k=1}^W{\mathit{p}}_k{y}_k$), respectively.

Note that the solution of Equation (1) is a specific case of the so-called M-estimators [6], while it is also related to the Fréchet Means [7]. The Euclidean norm ${\mathcal{L}}^2$ is also known as “Pythagorean” norm. In [3], we preferred referring to the non-Pythagorean norms as non-Euclidean, inheriting the same characterization to Statistics. One may adopt the more explicit characterizations of “Non-Euclidean-normed” Statistics, for avoiding any confusion with the non-Euclidean metric of the (Euclidean-normed) Riemannian Geometry. As an example of an application in physics, the ${\mathcal{L}}^p$ expectation value of an energy spectrum ${\left\{{\epsilon }_k\right\}}_{k=1}^W$ is defined by representing the non-Euclidean adaptation of internal energy $U_p$ [8].

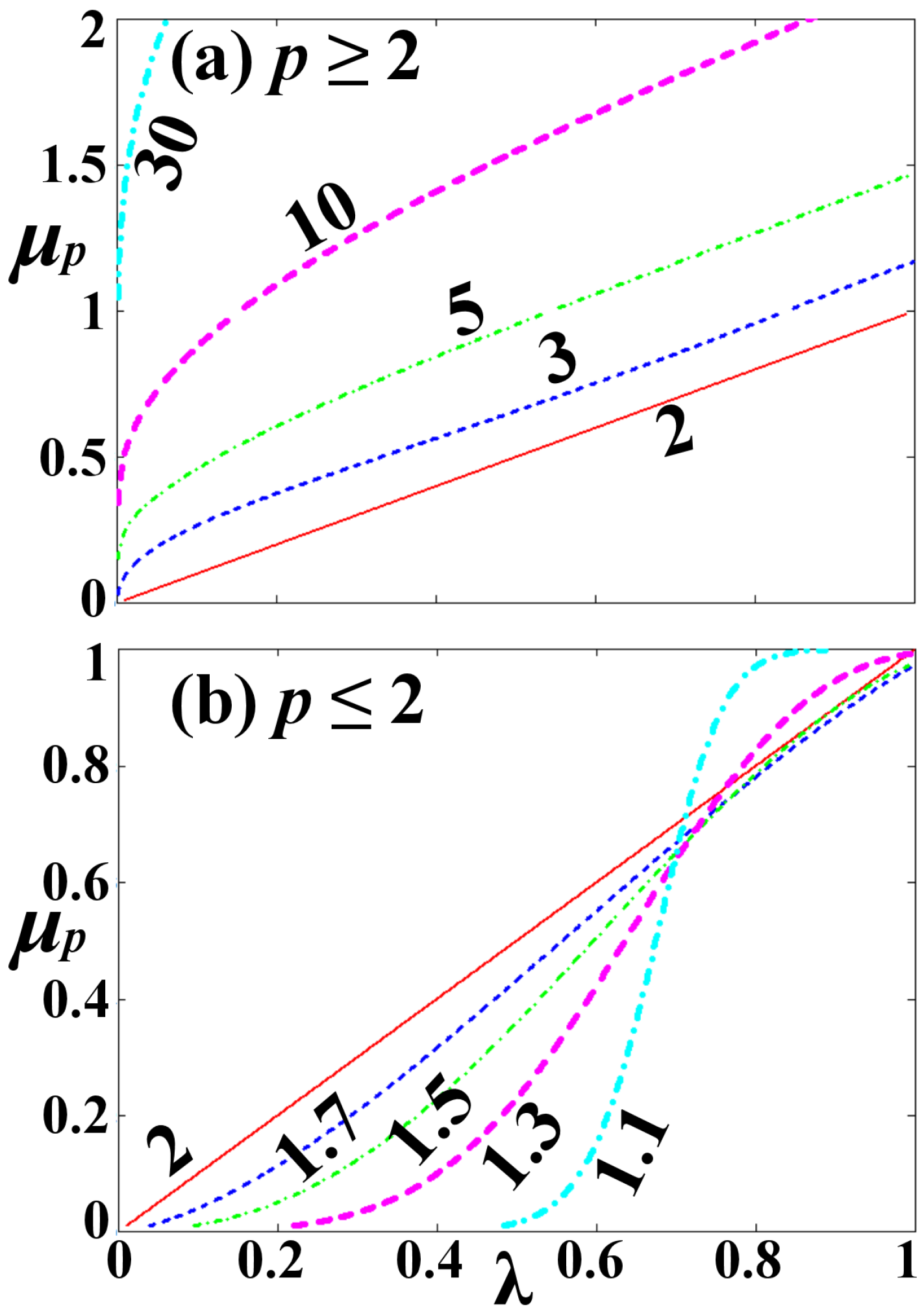
Figure 1 illustrates an example of ${\mathcal{L}}^p$-means. We use the Poisson distribution ${\mathit{p}}_k=e^{-\lambda }{\lambda }^k/k!$ and the dataset $y_k=k$, for $k=1,\dots ,W$; hence, the ${\mathcal{L}}^p$-means are implicitly given by ${\sum }_{k=1}^W\frac{{\lambda }^k}{k!}{|k-{\mu }_p|}^{p-1}sign(k-{\mu }_p)=0$ (note that the constant term $e^{-\lambda }$ can be ignored). The function ${\mu }_p={\mu }_p\left(\lambda \right)$ is examined for various values of the p-norm, either (a) super-Euclidean, $p>2$, or (b) sub-Euclidean $p<2$. The mean value for the Euclidean case, $p=2$, is ${\mu }_2=\lambda$, which is represented by the diagonal line in both panels. We observe that for $p>2$ we always have ${\mu }_p>\lambda$, while for $p<2$ there is a critical value ${\lambda }^{*}\left(p\right)$, for which ${\mu }_p>\lambda$ for $\lambda >{\lambda }^{*}$ and ${\mu }_p<\lambda$ for $\lambda <{\lambda }^{*}$. The critical value ${\lambda }^{*}\left(p\right)$ increases with p, and as $p\to 2$, ${\mu }_p\to \lambda$. For $\lambda =1$, ${\mu }_p=1$ for any $p\le 2$, while for $\lambda =0$, ${\mu }_p=0$ for any values of p.

The Law of Large Numbers is a theorem that guarantees the stability of long-term averages of random events, but is valid only for Euclidean metrics based on $L^2$-norms. The purpose of this paper is to extend the theorem of the “Law of Large Numbers” to the non-Euclidean, ${\mathcal{L}}^p$-means. Namely, (i) the expectation value of the ${\mathcal{L}}^p$-mean estimator (that corresponds to Equation (1)) equals the mean of the distribution of each of the random variables; and (ii) the limit $N\to \infty$ of the ${\mathcal{L}}^p$-mean estimator also equals the mean of the distributions. These are numbered as Theorems 2 and 3, respectively. The paper is organized as follows: In Section 2, we prove the theorem of uniqueness of the ${\mathcal{L}}^p$-means (Theorem 1). This will be used in the proofs of Theorems 2 and 3, shown in Section 3 and Section 4, respectively. Finally, Section 5 briefly summarizes the conclusions. Several examples are used to illustrate the validity of the Theorems 1–3, that is, the Poisson distribution (discrete description) and a superposition of normal distributions (continuous description).

2. Uniqueness of ${\mathcal{L}}^{\mathit{p}}$-Means

Here, we show the theorem of uniqueness of the ${\mathcal{L}}^p$-means for any $p>1$. The theorem will be used in the Theorem 2 and 3 of the next sections.

Theorem 1.

The curve ${\mu }_p\left(p\right)$ is univalued, namely, for each $p>1$, there is a unique value of the ${\mathcal{L}}^p$-mean ${\mu }_p\left(p\right)$.

Proof of Theorem 1.

Using the implicit function theorem [9], we can easily show the uniqueness in a sufficiently small neighbourhood of p = 2. Indeed, there is at least one point, that is the Euclidean point $(p=2,{\mu }_p={\mu }_2)$, for which the function ${\mu }_p\left(p\right)$ exists and is univalued. Then, the values of ${\mu }_p\left(p\right)$, $\forall p>1$, can be approximated to any accuracy, starting from the Euclidean point. The implicit function $F(p,{\mu }_p)=0$, defined by Equation (1), is continuous and $\partial F(p,{\mu }_p)/\partial {\mu }_p=\left(\mathrm{p}-1\right){\sum }_{k=1}^W{\mathit{p}}_k{|y_k-{\mu }_p|}^{p-2}\ne 0$; then ${\mu }_p\left(p\right)$ is univalued in some domain around $p=2$. The first derivative ${\mu }_{\acute{p}}\left(p\right)$ is finite $\forall p>1$ (e.g., for $p=2$ we have ${\mu }_{\acute{\mathrm{2}}}={[\partial {\mu }_p\left(p\right)/\partial p]}_{p=2}={\sum }_{k=1}^W{\mathit{p}}_k(y_k-{\mu }_2)ln\left(\right|y_k-{\mu }_2\left|\right)$). Indeed, the inverse derivative is non-zero for any p, i.e.,

$$\frac{\partial p}{\partial {\mu }_p}=\frac{(p-1){\sum }_{k=1}^W{\mathit{p}}_k{|y_k-{\mu }_p|}^{p-2}}{{\sum }_{k=1}^W{\mathit{p}}_k|y_k-{\mu }_p{|}^{p-1}sign(y_k-{\mu }_p)ln\left(\right|y_k-{\mu }_p\left|\right)},\forall p>1.$$

(2)

  ☐

The inverse function, $p\left({\mu }_p\right)$, should be continuous and differentiable according to Equation (2). If ${\mu }_p\left(p\right)$ were multi-valued, then, it should have local minima or maxima. However, the derivative $dp/d{\mu }_p$ is non-zero. Therefore, we conclude that $p\left({\mu }_p\right)$ cannot be multi-valued, and there is a unique curve ${\mu }_p\left(p\right)$ that passes through $(p=2,{\mu }_p={\mu }_2)$.

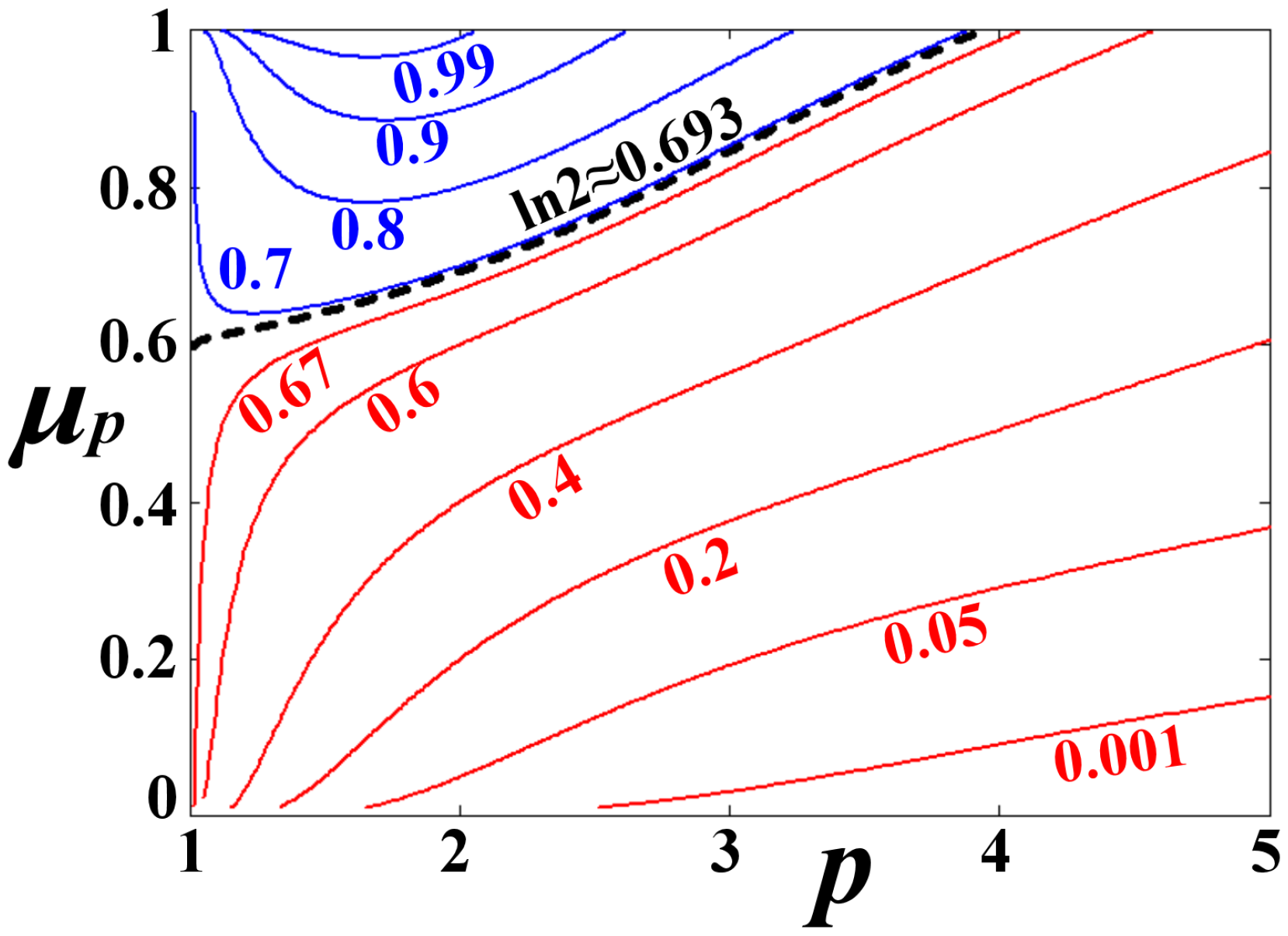
As an example, Figure 2 plots the ${\mathcal{L}}^p$-means of the Poisson distribution shown in Figure 1, but now as a function of the p-norm, and for various values of $0<\lambda <1$. For $\lambda <ln2$, the function ${\mu }_p\left(p\right)$ is monotonically increasing with p. On the contrary, for $\lambda >ln2$, the function ${\mu }_p\left(p\right)$ is not monotonic, having a minimum in the region of sub-Euclidean norms, $1<p<2$. The separatrix between these two behaviors of ${\mu }_p\left(p\right)$ is given for $\lambda =ln2$. We observe that the function ${\mu }_p\left(p\right)$ is differentiable, $\partial {\mu }_p/\partial p$ is always finite or $\partial p/\partial {\mu }_p$ is always non-zero, thus ${\mu }_p\left(p\right)$ is unique for any value of p.

Finally, we note that the uniqueness of ${\mu }_p$ for a given p does not ensure monotonicity, as different values of p may lead to the same ${\mathcal{L}}^p$-mean. Such an example is the ${\mathcal{L}}^p$-means of the Poisson distribution for $\lambda >ln2$, shown in Figure 2. As stated and illustrated in [3], when the examined probability distribution is symmetric, then the whole set of ${\mathcal{L}}^p$-means degenerates to one single value, while when it is asymmetric, a spectrum-like range of ${\mathcal{L}}^p$-means is rather generated.

3. The Concept of ${\mathcal{L}}^{\mathit{p}}$-Expectation Values

Given the sampling ${\left\{y_i\right\}}_{i=1}^N$, the ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}={\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$ is implicitly expressed by

$$\sum _{i=1}^N{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]=0.$$

(3)

Then, the ${\mathcal{L}}^p$ expectation value of ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$, namely ${\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p\equiv {\widehat{E}}_p\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]$, is implicitly given by

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p\right|}^{p-1}sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0,\end{array}$$

(4)

where $\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)$ is the normalized joint probability density, so that

$$\begin{array}{c}\hfill \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=1.\end{array}$$

(5)

Definition 1.

Let the sampling ${\left\{y_i\right\}}_{i=1}^N$, $y_i\in D_y\subseteq \Re ,\forall i=1,\dots ,N$, of the set of random variables ${\left\{Y_i\right\}}_{i=1}^N$. This set is called symmetrically distributed if the joint distribution density has the property $\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)=\mathcal{P}(y_1...y_k...y_i...y_N)=\mathcal{P}(y_1...y_i...y_k...y_N)$, $\forall i,k(\ne i)=1,\dots ,N$. This property is formally called Exchange-ability [10] and will be used in Lemmas 1 and 2.

Next, we postulate and prove Lemmas a and 2, which are necessary for the following Theorem 2 about the expectation value of the ${\mathcal{L}}^p$-mean estimator.

Lemma 1.

The symmetrically distributed random variables ${\left\{Y_i\right\}}_{i=1}^N$ are characterized by the same ${\mathcal{L}}^p$ expectation value, namely, ${\langle Y_i\rangle }_p={\widehat{E}}_p\left(Y_i\right)={\mu }_p\in \Re ,\forall i=1,\dots ,N$, which is implicitly given by

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\mu }_p\right|}^{p-1}sign\left(y_i-{\mu }_p\right)\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\hfill \\ ={\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}sign\left(y_i-{\mu }_p\right){\mathcal{P}}_y\left(y_i\right)d{y}_i=0,\hfill \end{array}$$

(6)

where ${\mathcal{P}}_{y_i}\left(u\right)\equiv {\mathcal{P}}_y\left(u\right)$, $\forall i=1,\dots ,N$, is the marginal distribution density, that is identical for all the random variables ${\left\{Y_i\right\}}_{i=1}^N$.

Proof of Lemma 1.

The $y_i$-marginal probability density, ${\mathcal{P}}_{y_i}\left(y_i\right)$, is

$$\begin{array}{c}\hfill {\mathcal{P}}_{y_i}\left(y_i\right)=\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1,j\ne i}^N}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_{i-1}d{y}_{i+1}\dots d{y}_N,\end{array}$$

(7)

so that

$$\begin{array}{c}\hfill {\int }_{y_i\in D_y}{\mathcal{P}}_{y_i}\left(y_i\right)d{y}_i=1.\end{array}$$

(8)

Given the symmetrical joint distribution, we have

$$\begin{array}{c}{\mathcal{P}}_{y_i}\left(y_i\right)=\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1,j\ne i}^N}\mathcal{P}(y_1...y_i...y_k...y_N)d{y}_1...d{y}_{i-1}d{y}_{i+1}...d{y}_N\hfill \\ ={\left\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1,j\ne i}^N}\mathcal{P}(y_1...y_k...y_i...y_N)d{y}_1...d{y}_{k-1}d{y}_{k+1}...d{y}_N\right\}}_{y_k=y_i}\hfill \\ ={\left\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1,j\ne i}^N}\mathcal{P}(y_1...y_i...y_k...y_N)d{y}_1...d{y}_{k-1}d{y}_{k+1}...d{y}_N\right\}}_{y_k=y_i}\hfill \\ ={\mathcal{P}}_{y_k}\left(y_i\right)\forall i,k(\ne i)=1,\dots ,N.\hfill \end{array}$$

(9)

Hence, the expression of the marginal distribution density ${\mathcal{P}}_{y_i}\left(u\right)$ is identical $\forall i=1,\dots ,N$, i.e., for all the random variables, ${\mathcal{P}}_{y_i}\left(u\right)\equiv {\mathcal{P}}_y\left(u\right)$.

Then, we readily derive that the random variables ${\left\{Y_i\right\}}_{i=1}^N$ are characterized by the same ${\mathcal{L}}^p$ expectation value, namely, ${\langle Y_i\rangle }_p={\widehat{E}}_p\left(Y_i\right)={\mu }_p\in \Re ,\forall i=1,\dots ,N$, which is implicitly expressed by

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\mu }_p\right|}^{p-1}sign\left(y_i-{\mu }_p\right)\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\hfill \\ ={\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}sign\left(y_i-{\mu }_p\right){\mathcal{P}}_y\left(y_i\right)d{y}_i=0.\hfill \end{array}$$

(10)

Indeed, if we had ${\langle Y_i\rangle }_p={\mu }_{\mathit{pi}}\in \Re ,\forall i=1,\dots ,N$, then

$$\begin{array}{c}\hfill {\int }_{y_i\in D_y}{\left|y_i-{\mu }_{\mathit{pi}}\right|}^{p-1}sign\left(y_i-{\mu }_{\mathit{pi}}\right){\mathcal{P}}_y\left(y_i\right)d{y}_i=0,\end{array}$$

(11)

and for $k\ne i$,

$$\begin{array}{c}{\int }_{y_k\in D_y}{\left|y_k-{\mu }_p{}_k\right|}^{p-1}sign\left(y_k-{\mu }_p{}_k\right){\mathcal{P}}_y\left(y_k\right)d{y}_k=0,\hfill \\ \Rightarrow {\int }_{y_i\in D_y}{\left|y_i-{\mu }_p{}_k\right|}^{p-1}sign\left(y_i-{\mu }_p{}_k\right){\mathcal{P}}_y\left(y_i\right)d{y}_i=0.\hfill \end{array}$$

(12)

However, given the uniqueness of the ${\mathcal{L}}^p$-means, Equations (11) and (12) lead to ${\mu }_{\mathit{pi}}={\mu }_{\mathit{pk}}\forall i,k(\ne i)$ = $1,\dots ,N$, or ${\mu }_{\mathit{pi}}={\mu }_p$, $\forall i=1,\dots ,N$. ☐

Lemma 2.

Let the auxiliary functionals ${\left\{G_i\right\}}_{i=1}^N$, with $G_i=G_i({\left\{y_j\right\}}_{j=1}^N;p)\equiv y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$, $\forall i=1,\dots ,N$. Then, their ${\mathcal{L}}^p$ expectation values are zero, namely, ${\langle G_i\rangle }_p={\widehat{E}}_p\left(G_i\right)=0$, $\forall i=1,\dots ,N$.

Proof of Lemma 2.

The ${\mathcal{L}}^p$ expectation value of ${\langle G_i\rangle }_p$ is implicitly given by

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\langle G_i\rangle }_p\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\langle G_i\rangle }_p\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0.\end{array}$$

(13)

If ${\langle G_i\rangle }_p=0$, then

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0,\end{array}$$

(14)

while if ${\langle G_i\rangle }_p\ne 0$, then the above functional has to be non-zero, because of the uniqueness of ${\mathcal{L}}^p$ expectation values, namely,

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=C_i(p,N)\ne 0,\end{array}$$

(15)

Now, rewriting Equation (15) for an index $k(\ne i)$, we have

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_k-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_k-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\hfill \\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=C_k(p,N)\hfill \\ =\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_k-{\widehat{\mu }}_{{p,}_N}(y_1...y_i...y_k...y_N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}(y_1...y_i...y_k...y_N;p)\right]\hfill \\ \times \mathcal{P}(y_1...y_i...y_k...y_N)d{y}_1...d{y}_i...d{y}_k...d{y}_N\hfill \\ =\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}(y_1...y_k...y_i...y_N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}(y_1...y_i...y_k...y_N;p)\right]\hfill \\ \times \mathcal{P}(y_1...y_k...y_i...y_N)d{y}_1...d{y}_k...d{y}_i...d{y}_N\hfill \\ =\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}(y_1...y_i...y_k...y_N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}(y_1...y_k...y_i...y_N;p)\right]\hfill \\ \times \mathcal{P}(y_1...y_i...y_k...y_N)d{y}_1...d{y}_i...d{y}_k...d{y}_N=C_i(p,N),\hfill \end{array}$$

(16)

because of the symmetrical distribution of random variables ${\left\{y_j\right\}}_{j=1}^N$, i.e., $\mathcal{P}(y_1...y_k...y_i...y_N)=\mathcal{P}(y_1...y_i...y_k...y_N)$, $\forall i,k(\ne i)=1,\dots ,N$, (the same symmetry holds also for the estimator ${\widehat{\mu }}_{{p,}_N}$, while the integration on each $y_i$ spans the same integral $D_y$. Hence, $C_i(p,N)=C_k(p,N)\equiv C(p,N)$. Then, by summing both sides of Equation (15) with ${\sum }_{i=1}^N$, we conclude in

$$\begin{array}{c}\hfill \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}\sum _{i=1}^N{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\\ \hfill \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0=\sum _{i=1}^N{C}_i(p,N)=NC(p,N),\end{array}$$

or $C(p,N)=0$. Thus, Equation (14) holds, and given the uniqueness of ${\mathcal{L}}^p$ expectation values, we conclude in ${\langle G_i\rangle }_p=0$, $\forall i=1,\dots ,N$. ☐

Theorem 2.

Consider the sampling ${\left\{y_i\right\}}_{i=1}^N$, $y_i\in D_y\subseteq \Re ,\forall i=1,\dots ,N$, of the symmetrically distributed random variables ${\left\{Y_i\right\}}_{i=1}^N$. According to Lemma 1, the random variables are characterized by the same ${\mathcal{L}}^p$ expectation value (assuming that this exists), namely, ${\langle Y_i\rangle }_p={\widehat{E}}_p\left(Y_i\right)={\mu }_p\in \Re ,\forall i=1,\dots ,N$, which is implicitly expressed by Equation (6). Then, the ${\mathcal{L}}^p$ expectation value of the ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$ is equal to ${\mu }_p$, i.e., ${\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p={\widehat{E}}_p\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]={\mu }_p$ or

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0.\end{array}$$

(17)

Proof of Theorem 2.

(For useful inequalities, see [11]) Apparently, the following integral inequalities hold:

$$\begin{array}{c}0=|\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}sign\left[y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\hfill \\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N|\hfill \\ \le \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,\hfill \end{array}$$

(18)

and, $\forall i=1,\dots ,N$,

$$\begin{array}{c}0=\left|{\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}sign(y_i-{\mu }_p){\mathcal{P}}_y\left(y_i\right)d{y}_i\right|\hfill \\ \le {\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i.\hfill \end{array}$$

(19)

Furthermore, we consider the ${\mathcal{L}}^p$ expectation value of the functional $g({\left\{y_j\right\}}_{j=1}^N;p)\equiv {\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p$, namely, ${\langle g\rangle }_p={\widehat{E}}_p\left(g({\left\{y_j\right\}}_{j=1}^N;p)\right)$, which is implicitly given by

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p-{\langle g\rangle }_p\right|}^{p-1}\\ \times sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p-{\langle g\rangle }_p\right]\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0.\end{array}$$

(20)

If ${\langle g\rangle }_p=0$, then,

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=0,\end{array}$$

(21)

while if ${\langle g\rangle }_p\ne 0$, then the above functional has to be non-zero, because of the uniqueness of ${\mathcal{L}}^p$ expectation values, namely,

$$\begin{array}{c}\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right]\\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N=D(p,N)\ne 0,\end{array}$$

(22)

or

$$\begin{array}{c}\left|D(p,N)\right|=|\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}sign\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right]\hfill \\ \times \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N|\hfill \\ \le \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N.\hfill \end{array}$$

(23)

 ☐

First case, $p\le 2$: Hence, $p-1\le 1$, and from the power inequality $\left(\right|f|+{\left|g\right|)}^s\le {\left|f\right|}^s+{\left|g\right|}^s$ holding $\forall s\le 1$, we have the following:

The triangle inequality gives $|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p|\le |{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i|+|y_i-{\mu }_p|$. Then, applying the above power inequality for $s=p-1$, $f={\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i$, and $g=y_i-{\mu }_p$, we have $|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p{|}^{p-1}\le \left(\right|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i|+|y_i-{\mu }_p{\left|\right)}^{p-1}\le |{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i{|}^{p-1}+{|y_i-{\mu }_p|}^{p-1}$. Thereafter, Equation (23) becomes

$$\begin{array}{c}\left|D\right(p,N\left)\right|\le \hfill \\ \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\hfill \\ +\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|y_i-{\mu }_p\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,\hfill \\ \Rightarrow \left|D\right(p,N\left)\right|\le \hfill \\ \int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\hfill \\ +{\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i,\hfill \end{array}$$

(24)

or

$$\begin{array}{c}\frac{1}{2}\left|D(p,N)\right|\le Max\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\\ \mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,{\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i\}.\end{array}$$

(25)

Second case, $p\ge 2$: Hence, $p-1\ge 1$, and applying the Minkowski inequality on Equation (23), we have

$$\begin{array}{c}{\left|D(p,N)\right|}^{\frac{1}{p-1}}\le \hfill \\ {\left[\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\right]}^{\frac{1}{p-1}}\hfill \\ \le {\left[\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N\right]}^{\frac{1}{p-1}}\hfill \\ +{\left[{\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)\right]}^{\frac{1}{p-1}}d{y}_i.\hfill \end{array}$$

(26)

or

$$\begin{array}{c}\frac{1}{2^{p-1}}\left|D(p,N)\right|\le \hfill \\ Max\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,\hfill \\ {\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i\}.\hfill \end{array}$$

(27)

Combining Equations (25) and (27), we conclude in an inequality that holds $\forall p\ge 1$,

$$\begin{array}{c}0\ne Min\left\{{\left[\frac{1}{2}\left|D(p,N)\right|\right]}_{p\le 2},{\left[\frac{1}{2^{p-1}}\left|D(p,N)\right|\right]}_{p\ge 2}\right\}\equiv \tilde{D}(p,N)\le \hfill \\ Max\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,\hfill \\ {\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i\}.\hfill \end{array}$$

(28)

On the other hand, Equations (18) and (19) imply that

$$\begin{array}{c}0\le Max\{\int \cdots {\int }_{{\{y_j\in D_y\}}_{j=1}^N}{\left|{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-y_i\right|}^{p-1}\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N,\hfill \\ {\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}{\mathcal{P}}_y\left(y_i\right)d{y}_i\}.\hfill \end{array}$$

(29)

We construct the auxiliary random variables ${\left\{X_i\right\}}_{i=1}^N$, defined by $X_i=f_x\left(Y_i\right)\equiv Y_i·\tilde{D}{(p,N)}^{-\frac{1}{p-1}}$, having values ${\{x_i=f_x\left(y_i\right)\}}_{i=1}^N$ in the domain $x_i\in D_x\equiv \{f_x\left(y_{Min}\right)\le x\le f_x\left(y_{Max}\right)\}\subseteq \Re ,\forall i=1,\dots ,N$ (where $y_{Min}\equiv D_{y,Min}\in D_y$ is the infimum of $D_y$, while $y_{Max}\equiv D_{y,Max}\in D_y$ is the supremum of $D_y$). The ${\mathcal{L}}^p$-mean estimator of the set ${\left\{x_i\right\}}_{i=1}^N$ is given by the functional ${\mu }_{{p,}_N}^X={\mu }_{{p,}_N}^X({\left\{x_j\right\}}_{j=1}^N;p)={\widehat{\mu }}_{{p,}_N}({\{y_j=x_j\tilde{D}{(p,N)}^{\frac{1}{p-1}}\}}_{j=1}^N;p)\tilde{D}{(p,N)}^{-\frac{1}{p-1}}$, while the random variables ${\left\{X_i\right\}}_{i=1}^N$ have the common ${\mathcal{L}}^p$ expectation value ${\langle X_i\rangle }_p\equiv {\widehat{E}}_p\left(X_i\right)={\mu }_p^X={\mu }_p\tilde{D}{(p,N)}^{-\frac{1}{p-1}}\in \Re ,\forall i=1,\dots ,N$. The respective joint probability density is given by ${\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)=\mathcal{P}\left[{\{y_j=x_j\tilde{D}{(p,N)}^{\frac{1}{p-1}}\}}_{j=1}^N\right]·\tilde{D}{(p,N)}^{\frac{N}{p-1}}$, so that, ${\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)d{x}_1\dots d{x}_N=\mathcal{P}\left({\left\{y_j\right\}}_{j=1}^N\right)d{y}_1\dots d{y}_N$. Then, Equations (28) and (29) become

$$\begin{array}{c}1\le Max\{\int \cdots {\int }_{{\{x_j\in D_x\}}_{j=1}^N}{\left|{\mu }_{{p,}_N}^X({\left\{x_j\right\}}_{j=1}^N;p)-x_i\right|}^{p-1}{\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)d{x}_1\dots d{x}_N,\hfill \\ {\int }_{x_i\in D_x}{\left|x_i-{\mu }_p^X\right|}^{p-1}{\mathcal{P}}_x^X\left(x_i\right)d{x}_i\},\hfill \end{array}$$

(30)

and

$$\begin{array}{c}0\le Max\{\int \cdots {\int }_{{\{x_j\in D_x\}}_{j=1}^N}{\left|{\mu }_{{p,}_N}^X({\left\{x_j\right\}}_{j=1}^N;p)-x_i\right|}^{p-1}{\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)d{x}_1\dots d{x}_N,\hfill \\ {\int }_{x_i\in D_x}{\left|x_i-{\mu }_p^X\right|}^{p-1}{\mathcal{P}}_x^X\left(x_i\right)d{x}_i\},\hfill \end{array}$$

(31)

respectively (where ${\mathcal{P}}_{x_i}^X\left(u\right)={\mathcal{P}}_x^X\left(u\right),\forall i=1,\dots ,N$ is the identical marginal distribution density for all the random variables ${\left\{X_i\right\}}_{i=1}^N$).

Moreover, we define the nonnegative quantities ${\ell }_p^X$, determined by the integral operator ${\widehat{I}}_p^X$, given by

$$\begin{array}{c}{\widehat{I}}_p^X\equiv Max\{\int \cdots {\int }_{{\{x_j\in D_x\}}_{j=1}^N}{\left|{\mu }_{{p,}_N}^X({\left\{x_j\right\}}_{j=1}^N;p)-x_i\right|}^{p-1}\widehat{1}d{x}_1\dots d{x}_N,\hfill \\ {\int }_{x_i\in D_x}{\left|x_i-{\mu }_p^X\right|}^{p-1}\widehat{1}d{x}_i\},\hfill \end{array}$$

(32)

which acts on the probability densities ${\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)$ so that

$${\ell }_p^X={\widehat{I}}_p^X\left[{\mathcal{P}}^X\left({\left\{x_j\right\}}_{j=1}^N\right)\right].$$

(33)

Now consider the subset $\mathcal{M}\subseteq \Re$ of all the possible values of ${\ell }_p^X$. Equation (30) yields $1\le {\ell }_p^X$, so that the infimum $\mathcal{I}\left(\mathcal{M}\right)=1$ (Note that, in this case, the infimum is element of $\mathcal{M}$, obtained for $p=1$). On the other hand, Equation (31) yields $0\le {\ell }_p^X$, which reads that the nonnegative quantities ${\ell }_p^X$ can be arbitrary small, even zero, so that the infimum is now given by $\mathcal{I}\left(\mathcal{M}\right)=0$.

However, the infimum is unique. The false by contradiction comes from the statement $D(p,N)\ne 0$. Hence, $D(p,N)=0$, and Equation (20) yields ${\langle g\rangle }_p=0$, i.e., ${\langle {\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)-{\mu }_p\rangle }_p=0$, or ${\langle {\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\rangle }_p={\mu }_p={\langle y_i\rangle }_p,\forall i=1,\dots ,N$.

4. Limit of the ${\mathcal{L}}^{\mathit{p}}$-Mean Estimator

The following theorem derives the limit of ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$.

Theorem 3.

Let the sampling ${\left\{y_i\right\}}_{i=1}^N$, $y_i\in D_y\subseteq \Re ,\forall i=1,\dots ,N$, of the independent and identically distributed random variables ${\left\{Y_i\right\}}_{i=1}^N$. The ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$ converges to its ${\mathcal{L}}^p$ expectation value, ${\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p={\widehat{E}}_p\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]\equiv {\mu }_p$, as $N\to \infty$, namely, ${lim}_{N\to \infty }{\widehat{\mu }}_{{p,}_N}={\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p\equiv {\mu }_p$.

Notes:

• Obviously, the independent and identically distributed random variables are also symmetrically distributed. Thus, according to Theorem 2, we have ${\langle {\widehat{\mu }}_{{p,}_N}\rangle }_p={\widehat{E}}_p\left[{\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)\right]={\langle Y_i\rangle }_p={\widehat{E}}_p\left(Y_i\right)={\mu }_p$.
• The ${\mathcal{L}}^p$ expectation value ${\langle Y_i\rangle }_p={\mu }_p$ should be calculated given the marginal distribution density ${\mathcal{P}}_y\left(y_i\right)$, $\forall i=1,\dots ,N$. However, the expression of this distribution is usually unknown, and thus, we estimate ${\mu }_p$ by means of ${lim}_{N\to \infty }{\widehat{\mu }}_{{p,}_N}$.

Proof of Theorem 3.

We construct the set of auxiliary random variables ${\left\{X_i\right\}}_{i=1}^N$, defined by $X_i=f_x\left(Y_i\right)\equiv {|Y_i-{\mu }_p|}^{p-1}sign(Y_i-{\mu }_p)$, and having the relevant sampling values ${\{x_i=f_x\left(y_i\right)\}}_{i=1}^N$, with domain $x_i\in D_x\equiv \{-|f_x\left(y_{Min}\right)|\le x\le |f_x\left(y_{Max}\right)\left|\right\}\subseteq \Re ,\forall i=1,\dots ,N$. Apparently, ${\left\{X_i\right\}}_{i=1}^N$ are also independent and identically distributed random variables, and let ${\mathcal{P}}_{x_i}^X\left(u\right)={\mathcal{P}}_x^X\left(u\right),\forall i=1,\dots ,N$ be the identical marginal distribution density for all the random variables ${\left\{X_i\right\}}_{i=1}^N$. ☐

Then, the Euclidean expectation value of each of the random variables is

$${\langle x_i\rangle }_2={\int }_{x_i\in D_x}{x}_i{\mathcal{P}}_x\left(x_i\right)d{x}_i={\int }_{y_i\in D_y}{\left|y_i-{\mu }_p\right|}^{p-1}sign(y_i-{\mu }_p){\mathcal{P}}_y\left(y_i\right)d{y}_i=0,$$

(34)

$\forall i=1,\dots ,N$. Thereafter, from the “Law of Large Numbers” we have that ${\sum }_{i=1}^N(x_i-{\langle x_i\rangle }_2)$ converges to zero, as $N\to \infty$ [12,13,14]. Thus,

$$\begin{array}{c}\hfill \sum _{i=1}^{\infty }{\left|y_i-{\mu }_p\right|}^{p-1}sign(y_i-{\mu }_p)=0.\end{array}$$

(35)

On the other hand, Equation (3), for $N\to \infty$ (assuming the convergence of the sum at this limit), is written as

$$\begin{array}{c}\hfill \sum _{i=1}^{\infty }{\left|y_i-\underset{N\to \infty }{lim}{\widehat{\mu }}_{{p,}_N}\right|}^{p-1}sign\left(y_i-\underset{N\to \infty }{lim}{\widehat{\mu }}_{{p,}_N}\right)=0,\end{array}$$

(36)

while, given the uniqueness of ${\mu }_p$, we conclude in ${lim}_{N\to \infty }{\widehat{\mu }}_{{p,}_N}={\mu }_p$.

As an application, we examine the probability distribution $\mathcal{P}\left(x\right)$, constructed by the superposition of two different normal distributions ${\mathcal{N}}_1(y;\mu =1,\sigma =1)$ and ${\mathcal{N}}_2(y;\mu =1+\delta a,\sigma =2)$ with $\delta a>0$; namely, $\mathcal{P}(y;\delta a;\lambda )=[{\mathcal{N}}_1\left(y\right)+\lambda {\mathcal{N}}_2(y;\delta a)]/(1+\lambda )$. For $\delta a=0$, the constructed probability distribution is symmetric, and as explained in Section 3 and [3], the whole set of ${\mathcal{L}}^p$-means degenerates to one single value—in our case ${\mu }_p=1$, $\forall p>1$. First, we derive the ${\mathcal{L}}^p$-mean of the distribution, ${\langle y\rangle }_p={\mu }_p$, where ${\int }_{-\infty }^{+\infty }{\left|y-{\mu }_p\right|}^{p-1}sign(y-{\mu }_p)\mathcal{P}\left(y\right)dy=0$. Then, we compute the ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$, where the y-values, ${\left\{y_j\right\}}_{j=1}^N$, follow the probability distribution constructed above, $\mathcal{P}(y;\delta a;\lambda )$. The Ny-values are generated as follows: we derive the cumulative distribution of $\mathcal{P}$, that is $\mathcal{F}(y;\delta a;\lambda )=\frac{1}{2}+\left[\mathrm{erf}\left(\frac{y-1}{\sqrt{2}}\right)+\lambda ·\mathrm{erf}\left(\frac{y-1-\delta a}{2\sqrt{2}}\right)\right]/\left[2(1+\lambda )\right]$, and then we set the parametrization $\mathcal{F}(y_i;\delta a;\lambda )=i/N$, from where we solve for $y_i$. The estimator ${\widehat{\mu }}_{{p,}_N}({\left\{y_j\right\}}_{j=1}^N;p)$ is implicitly given by ${\sum }_{i=1}^N{\left|y_i-{\widehat{\mu }}_{{p,}_N}\right|}^{p-1}sign\left(y_i-{\widehat{\mu }}_{{p,}_N}\right)=0$; then, we demonstrate Theorem 3 showing the equality ${lim}_{N\to \infty }{\widehat{\mu }}_{{p,}_N}={\mu }_p$; in particular, we construct the sum $S\left(N\right)\equiv {\sum }_{i=1}^N{\left|y_i-{\mu }_p\right|}^{p-1}sign\left(y_i-{\mu }_p\right)$, and show that $li{m}_{N\to \infty }S\left(N\right)\to 0$, satisfying Equation (35).

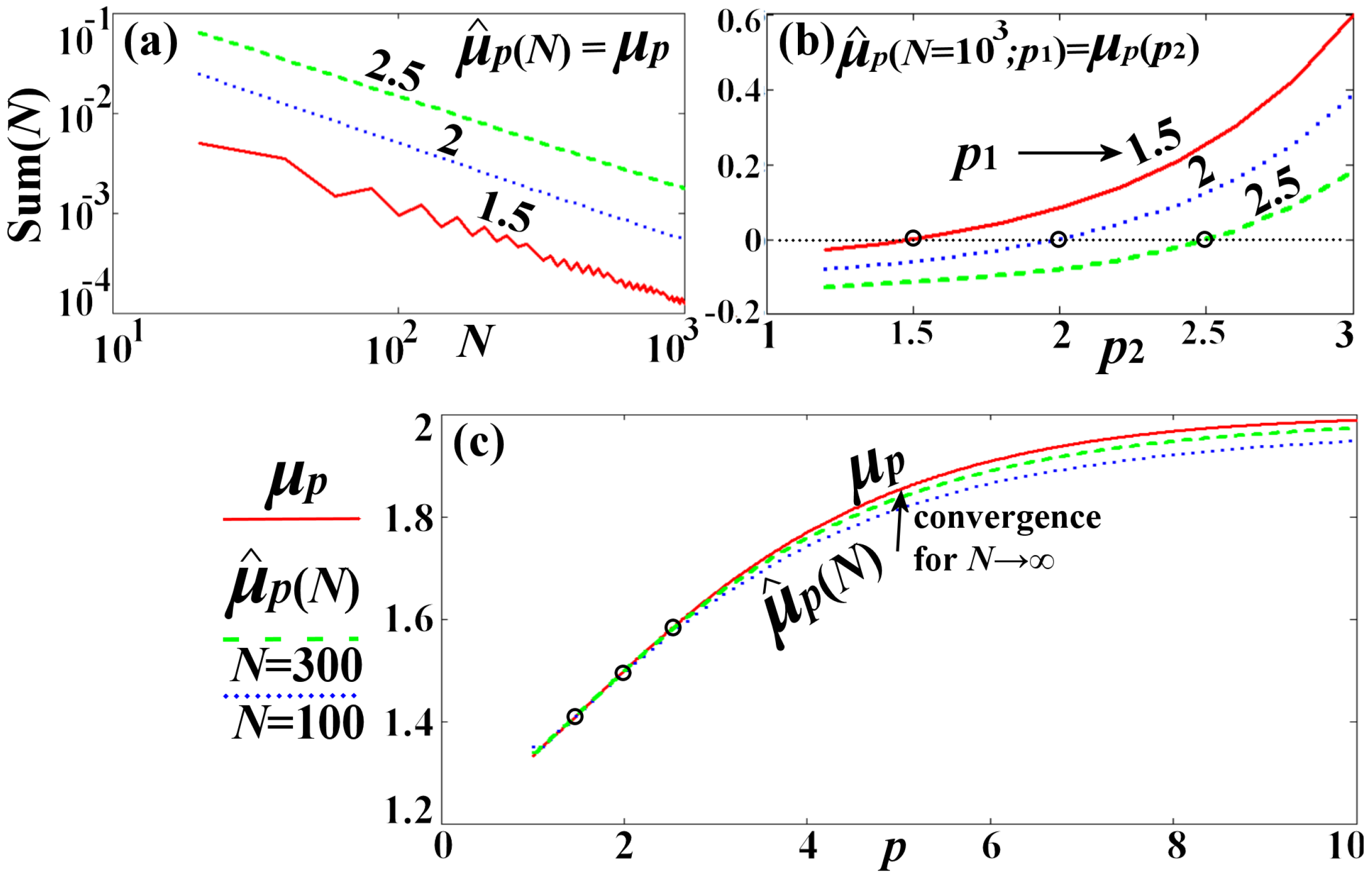
Figure 3 illustrates the convergence ${lim}_{N\to \infty }{\widehat{\mu }}_{{p,}_N}={\mu }_p$. Panel (a) plots the sum $S\left(N\right)$ as a function of N and for the norms $p=1.5$, 2, and $2.5$; we find a convergence rate of $S\left(N\right)\sim 1/N$. Panel (b) plots the summation $S\left(N\right)$ for large N$(={10}^3)$, which becomes zero only if the p-norm used by the estimator ${\widehat{\mu }}_{{p,}_N}$, that is $p=p_1$, equals the p-norm used by the mean ${\mu }_p$, that is $p=p_2$. Finally, panel (c) plots the value of the estimator ${\widehat{\mu }}_{{p,}_N}$, as a function of the norm p, for two data numbers $N=100$ and $N=300$, showing the convergence to ${\mu }_p$, which is co-plotted as a function of p.

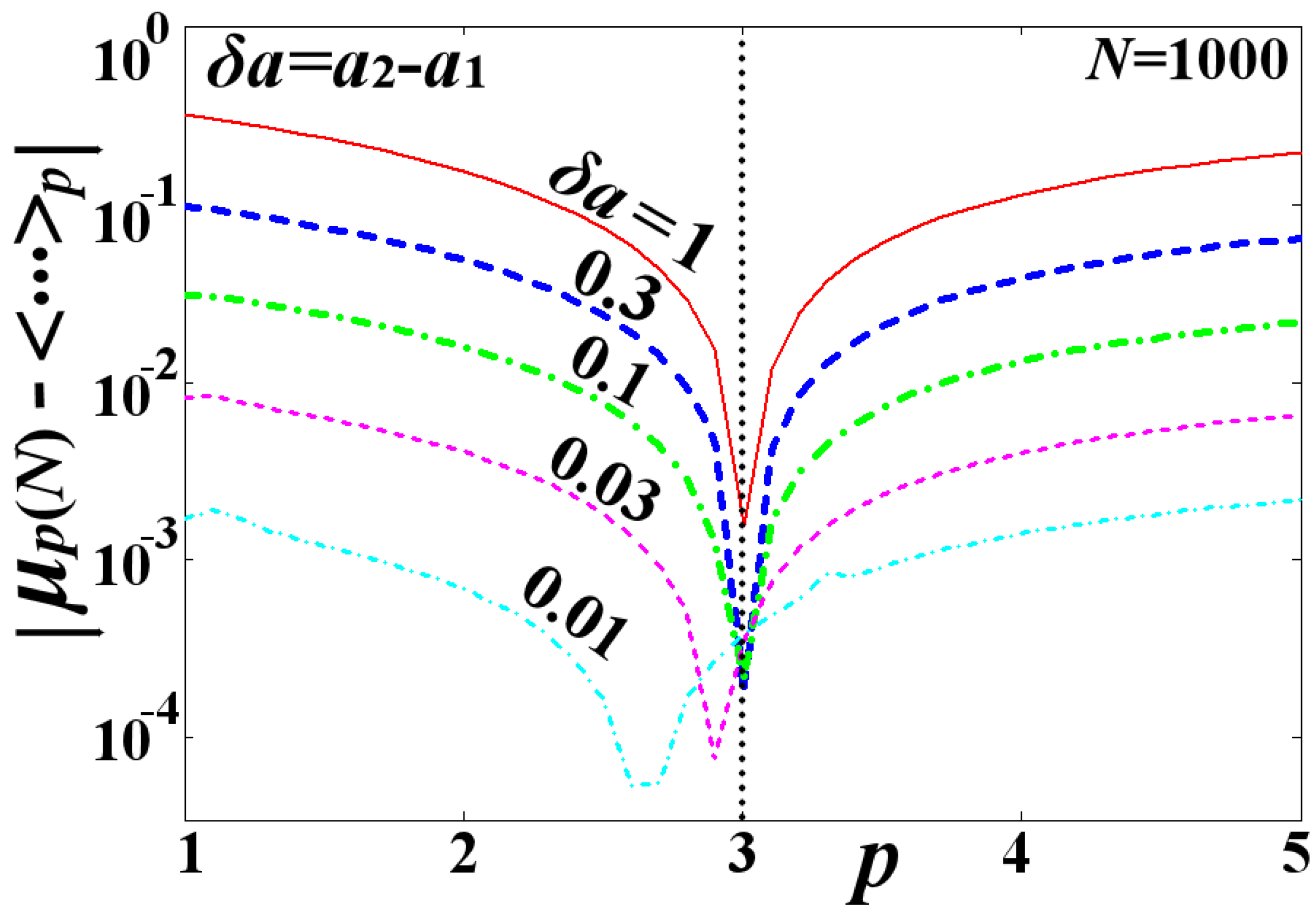
Figure 4 plots the deviation between the ${\mathcal{L}}^p$-mean estimator ${\widehat{\mu }}_{{p,}_N}$ and the mean ${\mu }_p$, that is, $|{\widehat{\mu }}_{{p,}_N}-{\mu }_p|$, and for a large number of data ($N={10}^3$). The mean ${\mu }_p$ is taken for the norm $p=3$, while the deviation is plotted as a function of the norm p of the estimator. We observe that the deviation is minimized, tending to zero, when the norm is $p\cong 3$. However, this result holds if the distribution is not symmetric. Once the parameter $\delta a$ decreases approaching zero, the distribution $\mathcal{P}(y;\delta a\to 0;\lambda )$ becomes symmetric and the deviation $|{\widehat{\mu }}_{{p,}_N}-{\mu }_p|$ obtains small values (while its minimization at a certain p loses its meaning). We observe that for $\delta a\approx 0.01$ or smaller, the deviation is small enough—of the order of ${10}^{-4}-{10}^{-3}$ (it is non-zero because of the computation errors caused by the finite N), so that ${\widehat{\mu }}_{{p,}_N}\approx {\mu }_p$.

5. Conclusions

The Euclidean ${\mathcal{L}}^2$ means are derived by minimizing the sum of the total square deviations, i.e., the Euclidean variance. In a similar way, the non-Euclidean ${\mathcal{L}}^p$ means were developed by minimizing the sum of the ${\mathcal{L}}^p$ deviations, that is proportional to the ${\mathcal{L}}^p$ variance [3]. The main advantage of the new statistical approach is that the p-norm is a free parameter, thus both the ${\mathcal{L}}^p$-normed expectation values and their variance are flexible to analyze new phenomena that cannot be described under the notions of classical statistics based on Euclidean norms. The least square method based on the Euclidean norm, $p=2$, and the least absolute deviations method based on the “Taxicab” norm, $p=1$, are some cases of the general fitting methods based on the ${\mathcal{L}}^p$ -norms (e.g., [15]; for more applications on the fitting methods based on Lp norms, see: [2,4,16,17]; several other applications can be in signal processing optimization and block entropy analysis, e.g., [2]; in image processing, e.g., [18]; in general data analysis, e.g., [5]; in statistical mechanics, e.g., [3,8,19]. The Law of Large Numbers is a theorem that guarantees the stability of long-term averages of random events, but is valid only for metrics induced by the Euclidean ${\mathcal{L}}^2$ norm. The importance of this paper is in extending this theorem for ${\mathcal{L}}^p$-norms. Other interesting applications will be to establish a central limit theorem applied for the ${\mathcal{L}}^p$-means.