Multiscale Information Theory and the Marginal Utility of Information

Abstract

Complex systems display behavior at a range of scales. Large-scale behaviors can emerge from the correlated or dependent behavior of individual small-scale components. To capture this observation in a rigorous and general way, we introduce a formalism for multiscale information theory. Dependent behavior among system components results in overlapping or shared information. A system’s structure is revealed in the sharing of information across the system’s dependencies, each of which has an associated scale. Counting information according to its scale yields the quantity of scale-weighted information, which is conserved when a system is reorganized. In the interest of flexibility we allow information to be quantified using any function that satisfies two basic axioms. Shannon information and vector space dimension are examples. We discuss two quantitative indices that summarize system structure: an existing index, the complexity profile, and a new index, the marginal utility of information. Using simple examples, we show how these indices capture the multiscale structure of complex systems in a quantitative way.

1. Introduction

The field of complex systems seeks to identify, understand and predict common patterns of behavior across the physical, biological and social sciences [1,2,3,4,5,6,7]. It succeeds by tracing these behavior patterns to the structures of the systems in question. We use the term “structure” to mean the totality of quantifiable relationships, or dependencies, among the components comprising a system. Systems from different domains and contexts can share key structural properties, causing them to behave in similar ways. For example, the central limit theorem tells us that the sum over many independent random variables yields an aggregate value whose probability distribution is well-approximated as a Gaussian. This helps us understand systems composed of statistically independent components, whether those components are molecules, microbes or human beings. Likewise, different chemical elements and compounds display essentially the same behavior near their respective critical points. The critical exponents which encapsulate the thermodynamic properties of a substance are the same for all substances in the same universality class, and membership in a universality class depends upon structural features such as dimensionality and symmetry properties, rather than on details of chemical composition [8].

Outside of known universality classes, identifying the key structural features that dictate the behavior of a system or class of systems often relies upon an ad hoc leap of intuition. This becomes particularly challenging for complex systems, where the set of system components is not only large, but also interwoven and resistant to decomposition. Information theory [9,10] holds promise as a general tool for quantifying the dependencies that comprise a system’s structure [11]. We can consider the amount of information that would be obtained from observations of any component or set of components. Dependencies mean that one observation can be fully or partially inferred from another, thereby reducing the amount of joint information present in a set of components, compared to the amount that would be present without those dependencies. Information theory allows one to quantify not only fixed or rigid relationships among components, but also “soft” relationships that are not fully determinate, e.g., statistical or probabilistic relationships.

However, traditional information theory is primarily concerned with amounts of independent bits of information. Consequently, each bit of non-redundant information is regarded as equally significant, and redundant information is typically considered irrelevant, except insofar as it provides error correction [10,12]. These features of information theory are natural in applications to communication, but present a limitation when characterizing the structure of a physical, biological, or social system. In a system of celestial bodies, the same amount of information might describe the position of a moon, a planet, or a star. Likewise, the same amount of information might describe the velocity of a solitary grasshopper, or the mean velocity of a locust swarm. A purely information-theoretic treatment has no mechanism to represent the fact that these observables, despite containing the same amount of information, differ greatly in their significance.

Overcoming this limitation requires a multiscale approach to information theory [13,14,15,16,17,18]—one that identifies not only the amount of information in a given observable but also its scale, defined as the number or volume of components to which it applies. Information describing a star’s position applies at a much larger scale than information describing a moon’s position. In shifting from traditional information theory to a multiscale approach, redundant information becomes not irrelevant but crucial: Redundancy among smaller-scale behaviors gives rise to larger-scale behaviors. In a locust swarm, measurements of individual velocity are highly redundant, in that the velocity of all individuals can be inferred with reasonable accuracy by measuring the velocity of just one individual. The multiscale approach, rather than collapsing this redundant information into a raw number of independent bits, identifies this information as large-scale and significant precisely because it is redundant across many individuals.

The multiscale approach to information theory also sheds light on a classic difficulty in the field of complex systems: to clarify what a “complex system” actually is. Naïvely, one might think to define complex systems as those that display the highest complexity, as quantified using Shannon information or other standard measures. However, the systems deemed the most “complex” by these measures are those in which the components behave independently of each other, such as ideal gases. Such systems lack the multiscale regularities and interdependencies that characterize the systems typically studied by complex systems researchers. Some theorists have argued that true complexity is best viewed as occupying a position between order and randomness [19,20,21]. Music is, so the argument goes, intermediate between still air and white noise. But although complex systems contain both order and randomness, they do not appear to be mere blends of the two. A more satisfying answer is that complex systems display behavior across a wide range of scales. For example, stock markets can exhibit small-scale behavior, as when an individual investor sells a small number of shares for reasons unrelated to overall market activity. They can also exhibit large-scale behavior, e.g., a large institutional investor sells many shares [22], or many individual investors sell shares simultaneously in a market panic [23].

Formalizing these ideas requires a synthesis of statistical physics and information theory. Statistical physics [24,25,26,27]—in particular the renormalization group of phase transitions [28,29]—provides a notion of scale in which individual components acting in concert can be considered equivalent to larger-scale units. Information theory provides the tool of multivariate mutual information: the information shared among an arbitrary number of variables (also called interaction information or co-information) [13,14,15,16,17,30,31,32,33,34,35,36,37,38,39]. These threads were combined in the complexity profile [13,14,15,16,17,18], a quantitative index of structure that characterizes the amount of information applying at a given scale or higher. In the context of the complexity profile, the multivariate mutual information of a set of n variables is considered to have scale n. In this way, information is understood to have scale equal to the multiplicity (or redundancy) at which it arises—an idea which is also implicit in other works on multivariate mutual information [40,41].

Here we present a mathematical formalism for multiscale information theory, for use in quantifying the structure of complex systems. Our starting point is the idea discussed in the previous paragraph, that information has scale equal to the multiplicity at which it arises. We formalize this idea mathematically and generalize it in two directions: First, we allow each system component to have an arbitrary intrinsic scale, reflecting its inherent size, volume, or multiplicity. For example, the mammalian muscular system includes both large and small muscles, corresponding to different scales of environmental challenge (e.g., pursuing prey and escaping from predators versus chewing food) [42]. Scales are additive in our formalism, in the sense that a set of components acting in perfect coordination is formally equivalent to a single component with scale equal to the sum of the scales of the individual components. This equivalence can greatly simplify the representation of a system. Consider, for example, an avalanche consisting of differently-sized rocks. To represent this avalanche within the framework of traditional (single-scale) information theory, one must either neglect the differences in size (thereby diminishing the utility of the representation) or else model each rock by a collection of myriad statistical variables, each corresponding to a equally-sized portion. Our formalism, by incorporating scale as a fundamental quantity, allows each rock to be represented in a direct and physically meaningful way.

Second, in the interest of generality, we use a new axiomatized definition of information, which encompasses traditional measures such as Shannon information as well as other quantifications of freedom or indeterminacy. In this way, our formalism is applicable to system representations for which traditional information measures cannot be used.

Using these concepts of information and scale, we identify how a system’s joint information is distributed across each of its irreducible dependencies—relationships among some components conditional on all others. Each irreducible dependency has an associated scale, equal to the sum of the scales of the components included in this dependency. This formalizes the idea that any information pertaining to a system applies at a particular scale or combination of scales. Multiplying quantities of information by the scales at which they apply yields the scale-weighted information, a quantity that is conserved when a system is reorganized or restructured.

We use this multiscale formalism to develop quantitative indices that summarize important aspects of a system’s structure. We generalize the complexity profile to allow for arbitrary intrinsic scales and a variety of information measures. We also introduce a new index, the marginal utility of information (MUI), which characterizes the extent to which a system can be described using limited amounts of information. The complexity profile and the MUI both capture a tradeoff of complexity versus scale that is present in all systems.

Our basic definitions of information, scale, and systems are presented in Section 2, Section 3 and Section 4, respectively. Section 5 formalizes the multiscale approach to information theory by defining the information and scale of each of a system’s dependencies. Section 6 and Section 7 discuss our two indices of structure. Section 8 establishes a mathematical relationship between these two indices for a special class of systems. Section 9 applies our indices of structure to the noisy voter model [43]. We conclude in Section 10 and Section 11 by discussing connections between our formalism and other work in information theory and complex systems science.

2. Information

We begin by introducing a generalized, axiomatic notion of information. Conceptually, information specifies a particular entity out of a set of possibilities and thus enables us to describe or characterize that entity. Information measures such as Shannon information quantify the amount of resources needed in this specification. Rather than adopting a specific information measure, we consider that the amount of information may be quantified in different ways, each appropriate to different contexts.

Let A be the set of components in a system. An information function, H, assigns a nonnegative real number to each subset $U\subset A$, representing the amount of information needed to describe the components in U. (Throughout, the subset notation $U\subset A$ includes the possibility that $U=A$.) We require that an information function satisfy two axioms:

• Monotonicity: The information in a subset U that is contained in a subset V cannot have more information than V, that is, $U\subset V\Rightarrow H(U)\le H(V)$.
• Strong subadditivity: Given two subsets, the information contained in both cannot exceed the information in each of them separately minus the information in their intersection:

  $$H(U\cup V)\le H(U)+H(V)-H(U\cap V).$$

  (1)

Strong subadditvity expresses how information combines when parts of a system (U and V) are regarded as a whole ($U\cup V$). Information regarding U may overlap with information regarding V for two reasons. First, U and V may share components; this is corrected for by subtracting $H(U\cap V)$. Second, constraints in the behavior of non-shared components may reduce the information needed to describe the whole. Thus, information describing the whole may be reduced due to overlaps or redundancies in the information applying to different parts, but it cannot be increased.

In contrast to other axiomatizations of information, which uniquely specify the Shannon information [9,44,45,46] or a particular family of measures [47,48,49,50], the two axioms above are compatible with a variety of different measures that quantify information or complexity:

• Microcanonical or Hartley entropy: For a system with a finite number of joint states, $H_0(U)=logm$ is an information function, where m is the number of joint states available to the subset U of components. Here, information content measures the number of yes-or-no questions which must be answered to identify one joint state out of m possibilities.
• Shannon entropy: For a system characterized by a probability distribution over all possible joint states, $H(U)=-{\sum }_{i=1}^m{p}_{i}log{p}_i$ is an information function, where $p_1,\dots ,p_m$ are the probabilities of the joint states available to the components in U [9]. Here, information content measures the number of yes-or-no questions which must be answered to identify one joint state out of all the joint states available to U, where more probable states can be identified more concisely.
• Tsallis entropy: The Tsallis entropy [51,52] is a generalization of the Shannon entropy with applications to nonextensive statistical mechanics. For the same setting as in Shannon entropy, Tsallis entropy is defined as $H_q(U)=-{\sum }_{i=1}^m{p}_i^q(p_i^{1-q}-1)/(1-q)$ for some parameter $q\ge 0$. Shannon entropy is recovered in the limit $q\to 1$. Tsallis entropy is an information function for $q\ge 1$ (but not for $q<1$); this follows from Proposition 2.1 and Theorem 3.4 of [53].
• Logarithm of period: For a deterministic dynamic system with periodic behavior, an information function $L(U)$ can be defined as the logarithm of the period of a set U of components (i.e., the time it takes for the joint state of these components to return to an initial joint state) [54]. This information function measures the number of questions which one should expect to answer in order to locate the position of those components in their cycle.
• Vector space dimension: Consider a system of n components, each of whose state is described by a real number. Then the joint states of any subset U of $m\le n$ components can be described by points in some linear subspace of ${\mathbb{R}}^m$. The minimal dimension $d(U)$ of such a subspace is an information function, equal to the number of coordinates one must specify in order to identify the joint state of U.
• Matroid rank: A matroid consists of a set of elements called the ground set, together with a rank function that takes values on subsets of the ground set. Rank functions are defined to include the monotonicity and strong subadditivity properties [55], and generalize the notion of vector subspace dimension. Consequently, the rank function of a matroid is an information function, with the ground set identified as the set of system components.

In principle, measurements of algorithmic complexity may also be regarded as information functions. For example, when a subset U can be encoded as a binary string, the algorithmic complexity $H(U)$ can be quantified as the length of the shortest self-delimiting program producing this string, with respect to some universal Turing machine [56]. Information content then measures the number of machine-language instructions which must be given to reconstruct U. Algorithmic complexity—at least under certain formulations—obeys versions of the monotonicity and strong subadditivity axioms [56,57]. However, while conceptually clean, this definition is difficult to apply quantitatively. First, the algorithmic complexity is only defined up to a constant which depends on the choice of universal Turing machine. Second, as a consequence of the halting problem, algorithmic complexity can only be bounded, not computed exactly.

3. Scale

A defining feature of complex systems is that they exhibit nontrivial behavior on multiple scales [1,13,14]. While the term “scale” has different meanings in different scientific contexts, we use the term scale here in the sense of the number of entities or units acting in concert, with each involved entity potentially weighted according to a measure of importance.

For many systems, it is reasonable to regard all components as having a priori equal scale. In this case we may choose the units of scale so that each component has scale equal to 1. This convention was used in previous work on the complexity profile [13,14,15,16,17]. However, it is in many cases necessary to represent the components of a system as having different intrinsic scales, reflecting their built-in size, multiplicity or redundancy. For example, in a system of many physical bodies, it may be natural to identify the scale of each body as a function of its mass, reflecting the fact that each body comprises many molecules moving in concert. In a system of investment banks [58,59,60], it may be desirable to assign weight to each bank according to its volume of assets. In these cases, we denote the a priori scale of a system component a by a positive real number $\sigma (a)$, defined in terms of some meaningful scale unit.

Scales are additive, in the sense that a set of completely interdependent components can be replaced by a single component whose scale is equal to the sum of the scales of the individual components. We describe this property formally in Section 5.4 and in Appendix B.

4. Systems

We formally define a system $\mathcal{A}$ to comprise three elements:

• A finite set A of components,
• An information function $H_{\mathcal{A}}$, giving the information in each subset $U\subset A$,
• A scale function ${\sigma }_{\mathcal{A}}$, giving the intrinsic scale of each compoent $a\in A$.

The choice of information and scale functions will reflect how the system is modeled mathematically, and the kind of statements we can make about its structure. We omit the subscripts from H and $\sigma$ when only one system is under consideration.

In this work, we treat the three elements of a system as unchanging, even though the system itself may be dynamic (existing in a sequence of states through time). A dynamic system can be represented as a set of time histories, or—using the approach of ergodic theory—by defining a probability distribution over states with probabilities corresponding to frequencies of occupancy over extended periods of time. The methods outlined here could also be used to explore the dynamics or histories of a system’s structure, using information and scale functions whose values vary as relationships change within a system over time. However, our current work focuses only on the static or time-averaged properties of a system.

In requiring that the set A of components be finite, we exclude, for example, systems represented as continuum fields, in which each point in a continuous space might be regarded as a component. While the concepts of multiscale information theory may still be useful in thinking about such systems, the mathematical representation of these concepts presents challenges that are beyond the scope of this work.

We shall use four simple systems as running examples. Each consists of three binary random variables, each having intrinsic scale one.

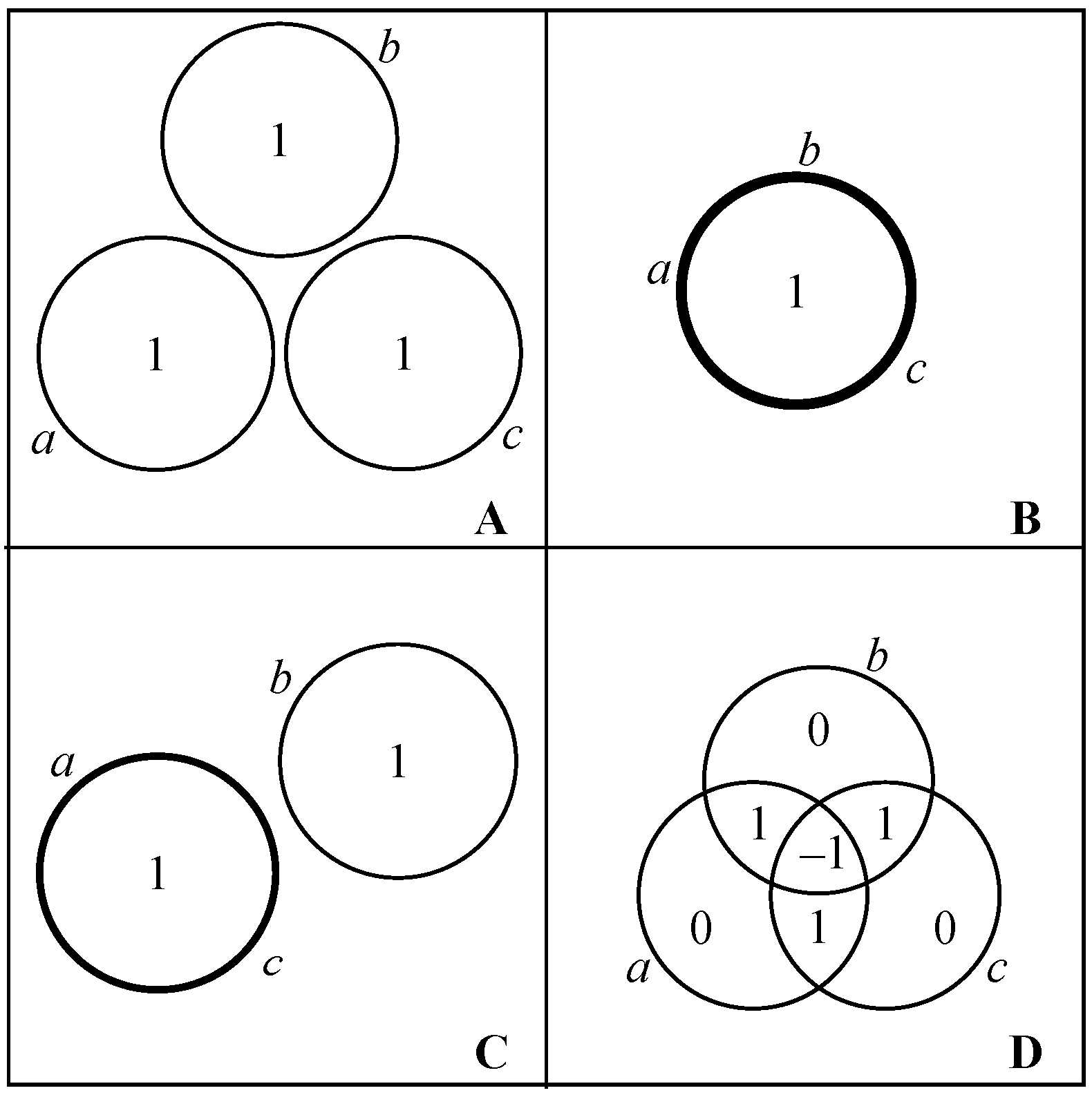
• Example A: Three independent components. Each component is equally likely to be in state 0 or state 1, and the system as a whole is equally likely to be in any of its eight possible states.
• Example B: Three completely interdependent components. Each component is equally likely to be in state 0 or state 1, but all three components are always in the same state.
• Example C: Independent blocks of dependent components. Each component is equally likely to take the value 0 or 1; however, the first two components always take the same value, while the third can take either value independently of the coupled pair.
• Example D: The $2+1$ parity bit system. The components can exist in the states 110, 101, 011, or 000 with equal probability. In each state, each component is equal to the parity (0 if even; 1 if odd) of the sum of the other two. Any two of the component are statistically independent of each other, but the three as a whole are constrained to have an even sum.

We define a subsystem of $\mathcal{A}=(A,H_{\mathcal{A}},{\sigma }_{\mathcal{A}})$ as a triple $\mathcal{B}=(B,H_{\mathcal{B}},{\sigma }_{\mathcal{B}})$, where B is a subset of A, $H_{\mathcal{B}}$ is the restriction of $H_{\mathcal{A}}$ to subsets of B, and ${\sigma }_{\mathcal{B}}$ is the restriction of ${\sigma }_{\mathcal{A}}$ to elements of B.

5. Multiscale Information Theory

Here we formalize the multiscale approach to information theory. We begin by introducing notation for dependencies. We then identify how information is shared across irreducible dependencies, generalizing the notion of multivariate mutual information [13,14,15,16,17,30,31,32,33,34,35,36,37,38,39] to an arbitrary information function. We then define the scale of a dependency and introduce the quantity of scale-weighted information. Finally, we formalize the key concepts of independence and complete interdependence.

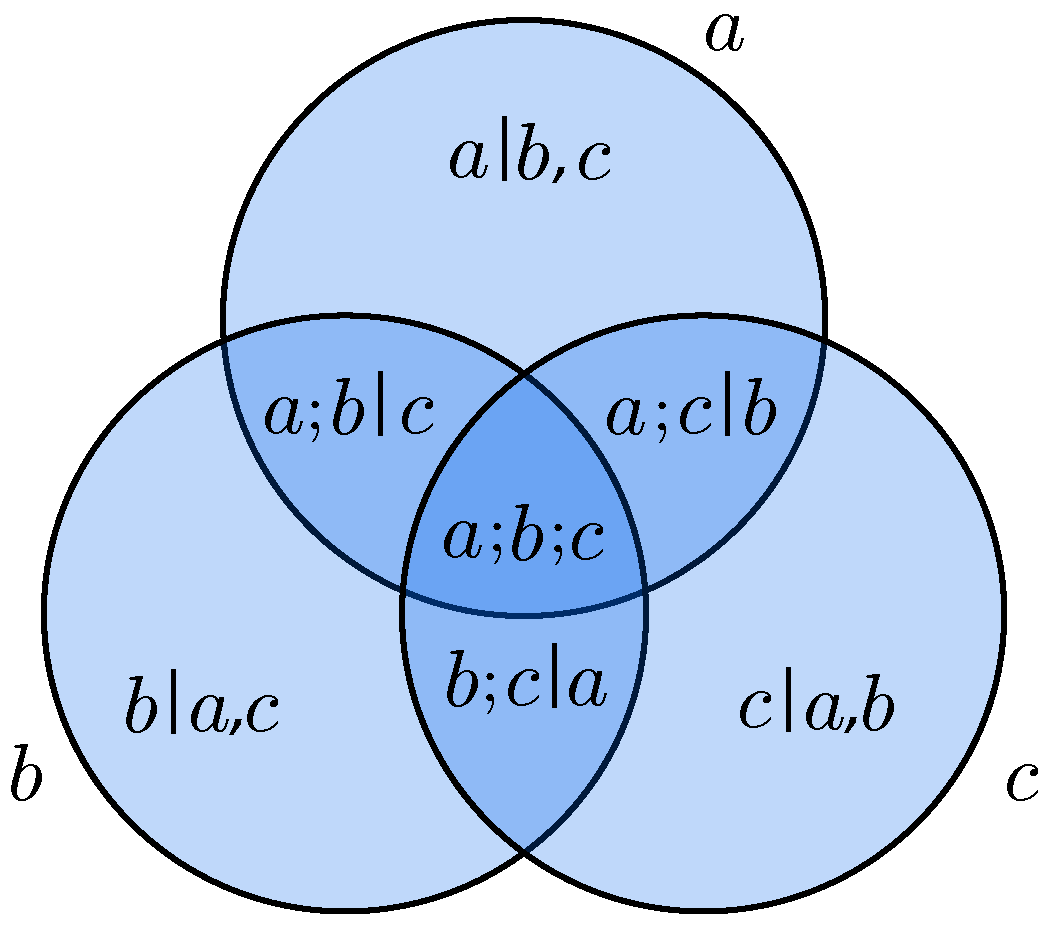
5.1. Dependencies

A dependency among a collection of components $a_1,\dots ,a_m$ is the relationship (if any) among these components such that the behavior of some of the components is in part obtainable from the behavior of others. We denote this dependency by the expression $a_1;\dots ;a_m$. This expression represents a relationship, rather than a number or quantity. We use a semicolon to keep our notation consistent with information theory (in particular, with multivariate mutual information; see Section 5.2).

We can identify a more general concept of conditional dependencies. Consider two disjoint sets of components $a_1,\dots ,a_m$ and $b_1,\dots ,b_k$. The conditional dependency $a_1;\dots ;a_m|b_1,\dots ,b_k$ represents the relationship (if any) between $a_1,\dots ,a_m$ such that the behavior of some of these components can yield improved inferences about the behavior of others, relative to what could be inferred from the behavior of $b_1,\dots ,b_k$. We call this the dependency of $a_1,\dots ,a_m$ given $b_1,\dots ,b_k$, and we say $a_1,\dots ,a_m$ are included in this dependency, while $b_1,\dots ,b_k$ are excluded.

We call a dependency irreducible if every system component is either included or excluded. We denote the set of all irreducible dependencies of a system $\mathcal{A}$ by ${\mathfrak{D}}_{\mathcal{A}}$. A system’s dependencies can be organized in a Venn diagram, which we call a dependency diagram (Figure 1).

The relationship between the components and dependencies of $\mathcal{A}$ can be captured by a mapping, which we denote by $\delta$, from A to subsets of ${\mathfrak{D}}_{\mathcal{A}}$. A component $a\in A$ maps to the set of irreducible dependencies that include a (or in visual terms, the region of the dependency diagram that corresponds to component a). For example, in a system of three components a, b, c, we have

$$\delta (a)=\{a;b;c,a;b|c,a;c|b,a|b,c\}.$$

(2)

We extend the domain of $\delta$ to subsets of components, by mapping each subset $U\subset A$ onto to the set of all irreducible dependencies that include at least one element of U; for example,

$$\delta (\{a,b\})=\{a;b;c,a;b|c,a;c|b,b;c|a,a|b,c,b|a,c\}.$$

(3)

Visually, $\delta (\{a,b\})$ is the union of the circles representing a and b in the dependency diagram. Finally, we extend the domain of $\delta$ to dependencies, by mapping the dependency $a_1;\dots ;a_m|b_1,\dots ,b_k$ onto the set of all irreducible dependencies that include $a_1,\dots ,a_m$ and exclude $b_1,\dots ,b_k$; for example,

$$\delta (a|c)=\{a;b|c,a|b,c\}.$$

(4)

Visually, $\delta (a|c)$ consists of the regions corresponding to a but not to c.

5.2. Information Quantity in Dependencies

Here we define the shared information, $I_{\mathcal{A}}(x)$, of a dependency x in a system $\mathcal{A}$. I generalizes the multivariate mutual information [13,14,15,16,17,30,31,32,33,34,35,36,37,38,39] to an arbitrary information function H. We note that H and I characterize the same quantity—information—but are applied to different kinds of arguments: H is applied to subsets of components of $\mathcal{A}$, while I is applied to dependencies.

The values of I on irreducible dependencies x of $\mathcal{A}$ are uniquely determined by the system of equations

$$\sum _{x\in \delta (U)}I(x)=H(U)\mathrm{for}\mathrm{all}\mathrm{subsets}U\subset A$$

(5)

As U runs over all subsets of A, the resulting system of equations determines the values $I(x)$, $x\in {\mathfrak{D}}_{\mathcal{A}}$, in terms of the values $H(U)$, $U\subset A$. The solution is an instance of the inclusion-exclusion principle [61], and can also be obtained by Gaussian elimination. An explicit formula obtained in the context of Shannon information [32] applies as well to any information function. Figure 2 shows the information in each irreducible dependecy for our four running examples.

We extend I to dependencies that are not irreducible by defining the shared information $I(x)$ to be equal to the sum of the values of $I(y)$ for all irreducible dependencies y encompassed by a dependency x:

$$I(x)=\sum _{y\in \delta (x)}I(y).$$

(6)

Our notation corresponds to that of Shannon information theory. For example, in a system of two components a and b, solving (5) yields

$$I(a;b)=H(a)+H(b)-H(a,b).$$

(7)

Above, $H(a,b)$ is shorthand for $H(\{a,b\})$; we use similar shorthand throughout. Equation (7) coincides with the classical definition of mutual information [9,10], with H representing joint Shannon information. Similarly, $I(a_1|b_1,\dots ,b_k)$ is the conditional entropy of $a_1$ given $b_1,\dots ,b_k$, and $I(a_1;a_2|b_1,\dots ,b_k)$ is the conditional mutual information of $a_1$ and $a_2$ given $b_1,\dots ,b_k$. For a dependency including more than two components, $I(x)$ is the multivariate mutual information (also called interaction information or co-information) of the dependency x [30,31,32,33,36,37,38,39].

For any information function H, we observe that the information of one component conditioned on others, the conditional information $I(a_1|b_1,\dots ,b_k)$ is nonnegative due to the monotonicity axiom. Likewise, the mutual information of two components conditioned on others, $I(a_1;a_2|b_1,\dots ,b_k)$, is nonnegative due to the strong subadditivity axiom. However, the information shared among three or more components can be negative. This is illustrated in running Example D, for which the tertiary shared information $I(a;b;c)$ is negative (Figure 2D). Such negative values appear to capture an important property of dependencies, but their interpretation is the subject of continuing discussion [34,36,37,62,63].

5.3. Scale-Weighted Information

Multiscale information theory is based on the principle that any information about a system should be understood as applying at a specific scale. Information shared among a set of components—arising from dependent behavior among these components—has scale equal to the sum of the scales of these components. This principle was first discussed in the context of the complexity profile [13,14,15,16,17], and is also implicit in other works on multivariate information theory [40,41], as we discuss in Section 10.2.

To formalize this principle, we define the scale $s(x)$ of an irreducible dependency $x\in {\mathfrak{D}}_{\mathcal{A}}$ to be equal to the total scale of all components included in x:

$$s(x)=\sum _{\begin{array}{c}a\in A\\ x\mathrm{includes}a\end{array}}\sigma (a).$$

(8)

The information in an irreducible dependency $x\in {\mathfrak{D}}_{\mathcal{A}}$ is understood to apply at scale $s(x)$. Large-scale information pertains to many components and/or to components of large intrinsic scale; whereas small-scale information pertains to few components, and/or components of small intrinsic scale. In running Example C (Figure 2C), the bit of information that applies to components a and c has scale 2, while the bit applying to component b has scale 1.

The overall significance of a dependency in a system depends on both its information and its scale. It therefore natural to weight quantities of information by their scale. We define the scale-weighted information $S(x)$ of an irreducible dependency x to be the scale of x times its information quantity

$$S(x)=s(x)I(x).$$

(9)

Extending this definition, we define the scale-weighted information of any subset $U\subset {\mathfrak{D}}_{\mathcal{A}}$ of the dependence space to be the sum of the scale-weighted information of each irreducible-dependency in this subset:

$$S(U)=\sum _{x\in U}S(x)=\sum _{x\in U}s(x)I(x).$$

(10)

The scale-weighted information of the entire dependency space ${\mathfrak{D}}_{\mathcal{A}}$—that is, the scale-weighted information of the system $\mathcal{A}$—is equal to the sum of the scale-weighted information of each component:

$$S({\mathfrak{D}}_{\mathcal{A}})=\sum _{a\in A}\sigma (a)H(a).$$

(11)

As we show in Appendix A, this property arises directly from the fact that scale-weighted information counts redundant information according to its multiplicity or total scale.

According to Equation (11), the total scale-weighted information $S({\mathfrak{D}}_{\mathcal{A}})$ does not change if the system is reorganized or restructured, as long as the information $H(a)$ and scale $\sigma (a)$ of each individual component $a\in A$ is maintained. The value $S({\mathfrak{D}}_{\mathcal{A}})$ can therefore be considered a conserved quantity. The existence of this conserved quantity implies a tradeoff of information versus scale, which can be illustrated using the example of a stock market. If investors act largely independently of each other, information overlaps are minimal. The total amount of information is large, but most of this information is small-scale—applying only to a single investor at a time. On the other hand, in a market panic, there is much overlapping or redundant information in their actions—the behavior of one can be largely inferred from the behavior of others [23]. Because of this redundancy, the amount of information needed to describe their collective behavior is low. This redundancy also makes this collective behavior large-scale and highly significant.

5.4. Independence and Complete Interdependence

Components $a_1,\dots ,a_k\in A$ are independent if their joint information is equal to the sum of the information in each separately:

$$H(a_1,\cdots ,a_k)=H(a_1)+\dots +H(a_k).$$

(12)

In running Example C, components a, b, and c are independent. This definition generalizes standard notions of independence in information theory, linear algebra, and matroid theory.

We extend the notion of independence to subsystems: subsystems ${\mathcal{B}}_i=(B_i,H_{{\mathcal{B}}_i},{\sigma }_{{\mathcal{B}}_i})$ of $\mathcal{A}$, for $i=1,\dots ,k$, are defined to be independent of one another if

$$H_{\mathcal{A}}(B_1\cup \dots \cup B_k)=H_{{\mathcal{B}}_1}(B_1)+\dots +H_{{\mathcal{B}}_k}(B_k).$$

(13)

We recall from Section 4 that $H_{{\mathcal{B}}_i}$ is the restriction of $H_{\mathcal{A}}$ to subsets of $B_i$. In running Example C, the subsystem comprised of components a and c is independent of the subsystem comprised of component b.

Independence has the following hereditary property [64]: if subsystems ${\mathcal{B}}_1,\dots ,{\mathcal{B}}_k$ are independent, then all components and subsystems of ${\mathcal{B}}_i$ are independent of all components and subsystems of ${\mathcal{B}}_j$, for all $j\ne i$. We prove the hereditary property of independence from our axioms in Appendix C.

At the opposite extreme, we define a set of components $U\subset A$ to be completely interdependent if $H(a)=H(U)$ for any component $a\in U$. In words, any information applying to any component in U applies to all components in U.

A set $U\subset A$ of completely interdependent components can be replaced by a single component of scale ${\sum }_{a\in U}\sigma (a)$ to obtain an equivalent, reduced representation of the system. Thus, in running Example C, the set $\{a,c\}$ is completely interdependent, and can be replaced by a single component of scale two. We show in Appendix B that replacements of this kind preserve all relevant quantities of information and scale.

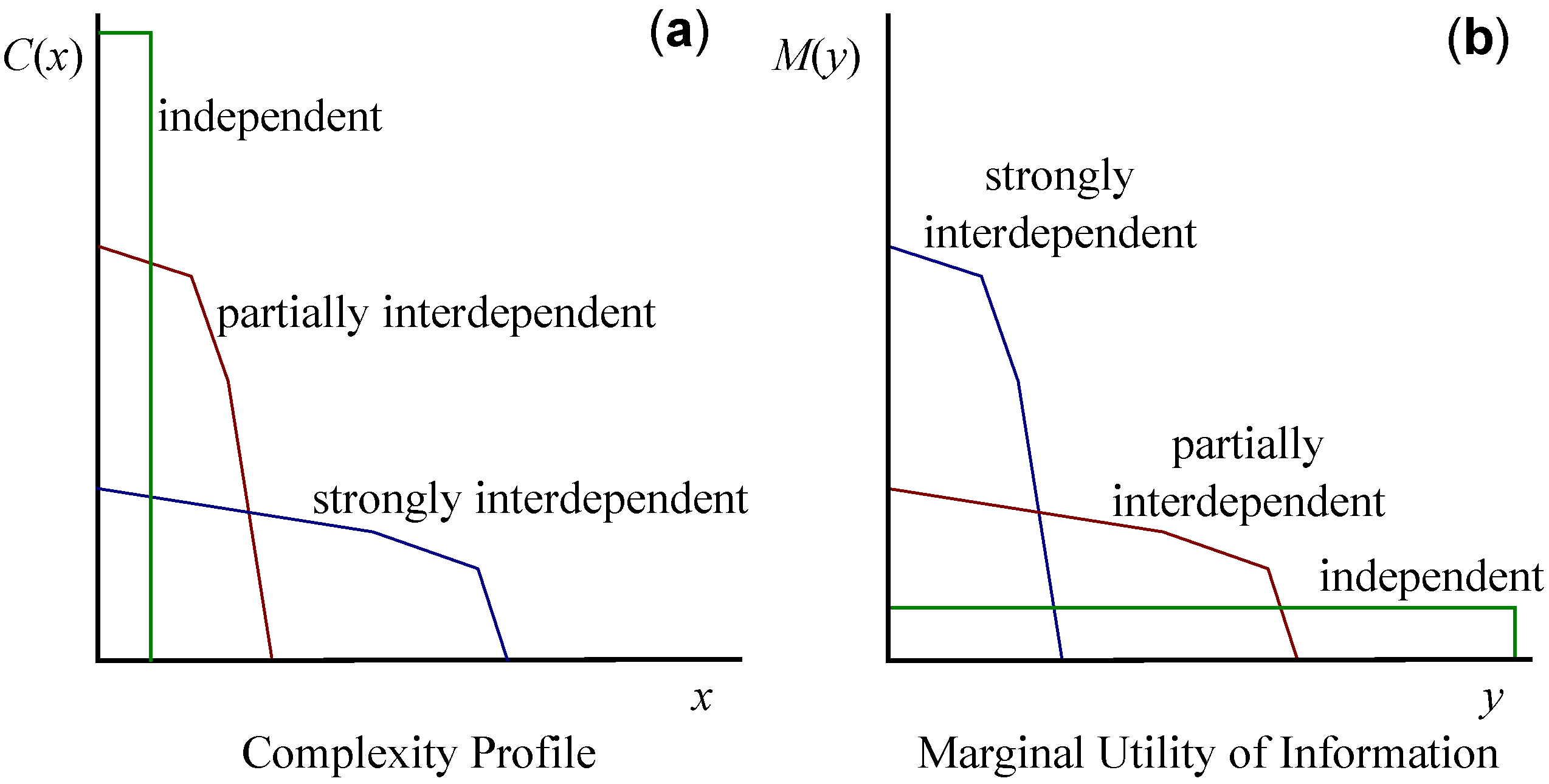
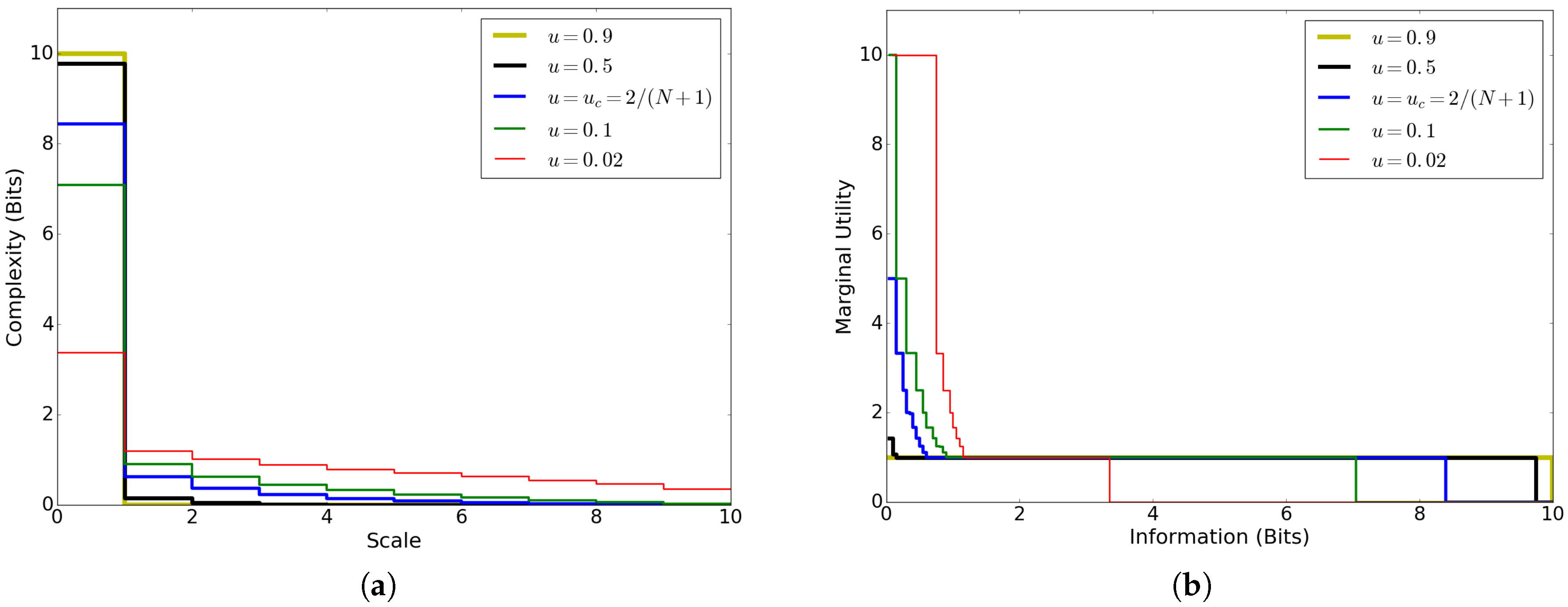
6. Complexity Profile

We now turn to quantitative indices that summarize a system’s structure. One such index is the complexity profile [13,14,15,16,17], which concretizes the observation that a complex system exhibits structure at multiple scales. We define the complexity profile of a system $\mathcal{A}$ to be a real-valued function $C_{\mathcal{A}}(y)$ of a positive real number y, equal to the total amount of information at scale y or higher in $\mathcal{A}$:

$$C_{\mathcal{A}}(y)=I\left(\{x\in {\mathfrak{D}}_{\mathcal{A}}:s(x)\ge y\}\right).$$

(14)

Equation (14) generalizes previous definitions of the complexity profile [13,14,15,16,17], which use Shannon information as the information function and consider all components to have scale one.

The complexity profile reveals the levels of interdependence in a system. For systems where components are highly independent, $C(0)$ is large and $C(y)$ decreases sharply in y, since only small amounts of information apply at large scales in such a system. Conversely, in rigid or strongly interdependent systems, $C(0)$ is small and the decrease in $C(y)$ is shallower, reflecting the prevalence of large-scale information, as shown in in Figure 3. We plot the complexity profiles of our four running examples in Figure 4.

Previous works have developed and applied an explicit formula for the complexity profile [13,14,16,17,35] for cases where all components have equal intrinsic scales, $\sigma (a)=1$ for all $a\in A$. To construct this formula, we first define the quantity $Q(j)$ as the sum of the joint information of all collections of j components:

$$Q(j)=\sum _{i_1,\dots ,i_j}H(a_{i_1},\dots ,a_{i_j}).$$

(15)

The complexity profile can then be expressed as

$$C(k)=\sum _{j=N-k}^{N-1}{(-1)}^{j+k-N}\left(\genfrac{}{}{0pt}{}{j}{j+k-N}\right)Q(j+1),$$

(16)

where $N=\left|A\right|$ is the number of components in $\mathcal{A}$ [13,14]. The coefficients in this formula can be inferred from the inclusion-exclusion principle [61]; see [13] for a derivation.

The complexity profile has the following properties:

• Conservation law: The area under $C(y)$ is equal to the total scale-weighted information of the system, and is therefore independent of the way the components depend on each other [13]:

  $${\int }_0^{\infty }C(y)dy=S({\mathfrak{D}}_{\mathcal{A}}).$$

  (17)

  This result follows from the conservation law for scale-weighted information, Equation (11), as shown in Appendix A.
• Total system information: At the lowest scale $y=0$, $C(y)$ corresponds to the overall joint information: $C(0)=H(A)$. For physical systems with the Shannon information function, this is the total entropy of the system, in units of information rather than the usual thermodynamic units.
• Additivity: If a system $\mathcal{A}$ is the union of two independent subsystems $\mathcal{B}$ and $\mathcal{C}$, the complexity profile of the full system is the sum of the profiles for the two subsystems, $C_{\mathcal{A}}(y)=C_{\mathcal{B}}(y)+C_{\mathcal{C}}(y)$. We prove this property Appendix D.

Due to the combinatorial number of dependencies for an arbitrary system, calculation of the complexity profile may be computationally prohibitive; however, computationally tractable approximations to the complexity profile have been developed [15].

The complexity profile has connections to a number of other information-theoretic characterizations of structure and dependencies among sets of random variables [38,40,41,65,66,67], as we discuss in Section 10.2. What distinguishes the complexity profile from these other approaches is the explicit inclusion of scale as an axis complementary to information.

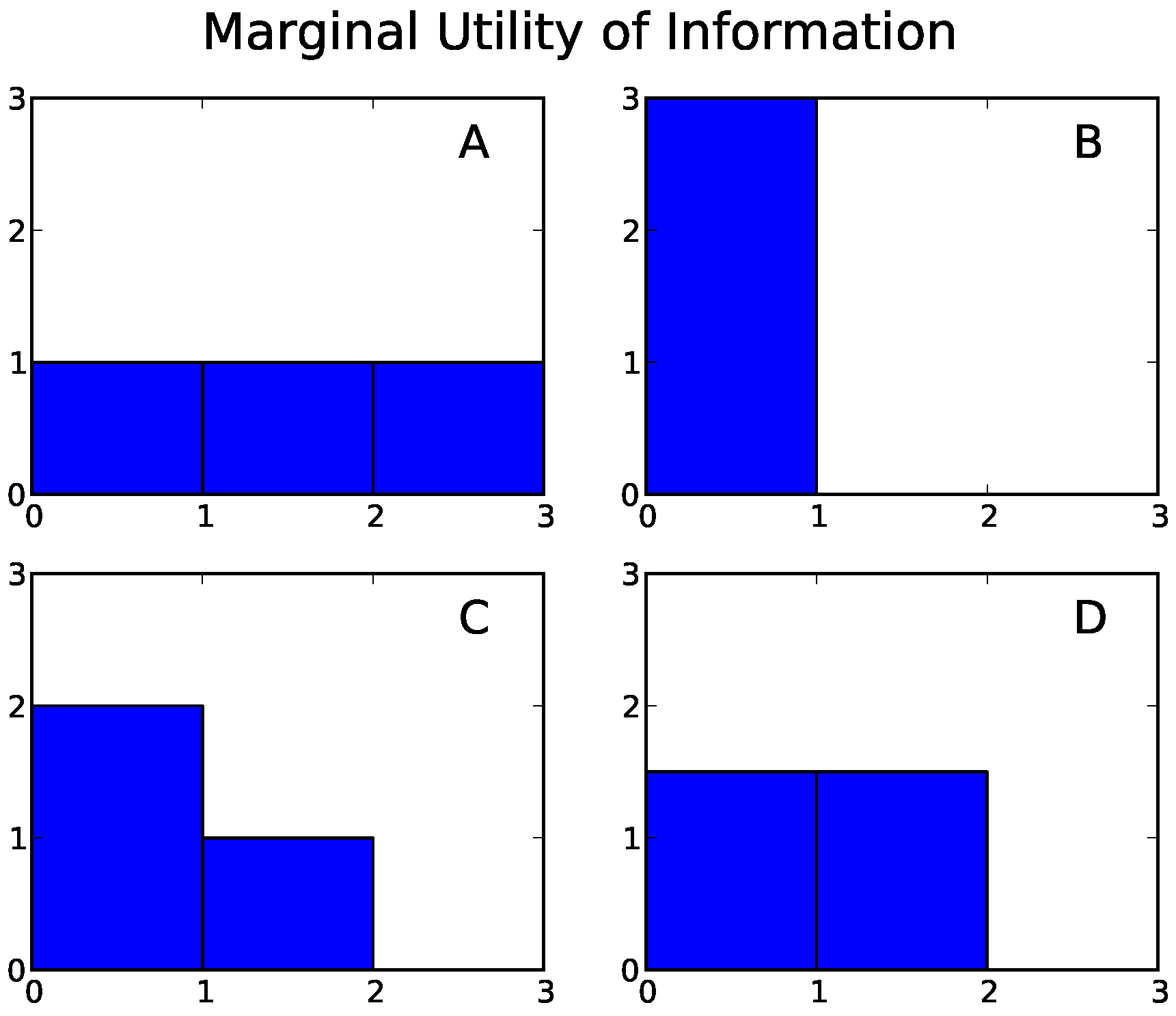
7. Marginal Utility of Information

Here we introduce an new index characterizing multiscale structure: the marginal utility of information (MUI), denoted $M(y)$. The MUI quantifies how well a system can be characterized using a limited amount of information.

To obtain this index, we first ask how much scale-weighted information (as defined in Section 5.3) can be represented using y or fewer units of information. We call this quantity the maximal utility of information, denoted $U(y)$. For small values of y, an optimal characterization will convey only large-scale features of the system. As y increases, smaller-scale features will be progressively included. For a given system $\mathcal{A}$, the maximal amount of scale-weighted information that can be represented, $U(y)$, is constrained not only by the information limit y, but also by the pattern of information overlaps in $\mathcal{A}$—that is, the structure of $\mathcal{A}$. More strongly interdependent systems allow for larger amounts of scale-weighted information to be described using the same amount of information y.

We define the marginal utility of information as the derivative of maximal utility: $M(y)=U^{\prime }(y)$. $M(y)$ quantifies how much scale-weighted information each additional unit of information can impart. The value of $M(y)$, being the derivative of scale-weighted information with respect to information, has units of scale. $M(y)$ declines steeply for rigid or strongly interdependent systems, and shallowly for weakly interdependent systems.

We now develop the formal definition of $U(y)$. We call any entity d that imparts information about system $\mathcal{A}$ a descriptor of $\mathcal{A}$. The utility of a descriptor will be defined as a quantity of the form

$$u=\sum _{a\in A}\sigma (a)I(d;a).$$

(18)

For this to be a meaningful expression, we consider each descriptor d to be an element of an augmented system ${\mathcal{A}}^{†}=(A^{†},H_{{\mathcal{A}}^{†}})$, whose components include d as well as the original components of $\mathcal{A}$, which is a subsystem of ${\mathcal{A}}^{†}$. The amount of information that d conveys about any subset $V\subset A$ of components is given by

$$\begin{array}{cc}\hfill I(d;V)& =I_{{\mathcal{A}}^{†}}(d;V)\hfill \\ & =H_{{\mathcal{A}}^{†}}(d)+H_{{\mathcal{A}}^{†}}(V)-H_{{\mathcal{A}}^{†}}\left(\{d\}\cup V\right).\hfill \end{array}$$

(19)

For example, the amount that d conveys about a component $a\in A$ can be written $I(d;a)=H(d)+H(a)-H(d,a)$. $I(d;A)$ is the total information d imparts about the system. Because the original system $\mathcal{A}$ is a subsystem of ${\mathcal{A}}^{†}$, the augmented information function $H_{{\mathcal{A}}^{†}}$ coincides with $H_{\mathcal{A}}$ on subsets of A.

The quantities $I(d;V)$ are constrained by the structure of $\mathcal{A}$ and the axioms of information functions. Applying these axioms, we arrive at the following constraints on $I(d;V)$:

(i)

$0\le I(d;V)\le H(V)$ for all subsets $V\subset A$.

(ii)

For any pair of nested subsets $W\subset V\subset A$, $0\le I(d;V)-I(d;W)\le H(V)-H(W)$.

(iii)

For any pair of subsets $V,W\subset A$,

$$I(d;V)+I(d;W)-I(d;V\cup W)-I(d;V\cap W)\le H(V)+H(W)-H(V\cup W)-H(V\cap W).$$

To obtain the maximum utility of information, we interpret the values $I(d;V)$ as variables subject to the above constraints. We define $U(y)$ as the maximum value of the utility expression, Equation (18), as $I(d;V)$ vary subject to constraints (i)–(iii) and that the total information d imparts about $\mathcal{A}$ is less than or equal to y: $I(d;A)\le y$.

$U(y)$ characterizes the maximal amount of scale-weighted information that could in principle be conveyed about $\mathcal{A}$ using y or less units of information, taking into account the information-sharing in $\mathcal{A}$ and the fundamental constraints on how information can be shared. $U(y)$ is well-defined since it is the maximal value of a linear function on a bounded set. Moreover, elementary results in linear programming theory [68] imply that $U(y)$ is piecewise linear, increasing and concave in y.

The above results imply that the marginal utility of information, $M(y)=U^{\prime }(y)$, is piecewise constant, positive and nonincreasing. The MUI thus avoids the issue of counterintuitive negative values. The value of $M(y)$ can be understood as the additional scale units that can be described by an additional bit of information, given that the first y bits have been optimally utilized. Code for computing the MUI has been developed and is available online [69].

The marginal utility of information has the following additional properties:

1.

Conservation law: The total area under the curve $M(y)$ equals the total scale-weighted information of the system:

$${\int }_0^{\infty }M(y)dy=S({\mathfrak{D}}_{\mathcal{A}}).$$

(20)

This property follows from the observation that, since $M(y)$ is the derivative of $U(y)$, the area under this curve is equal to the maximal utility of any descriptor, which is equal to $S({\mathfrak{D}}_A)$ since utility is defined in terms of scale-weighted information.

2.

Total system information: The marginal utility vanishes for information values larger than the total system information, $M(y)=0$ for $y>H(A)$, since, for higher values, the system has already been fully described.

3.

Additivity: If $\mathcal{A}$ separates into independent subsystems $\mathcal{B}$ and $\mathcal{C}$, then

$$U_{\mathcal{A}}(y)=\underset{\begin{array}{c}{y}_1+y_2=y\\ y_1,y_2\ge 0\end{array}}{max}\left(U_{\mathcal{B}}(y_1)+U_{\mathcal{C}}(y_2)\right).$$

(21)

The proof follows from recognizing that, since information can apply either to $\mathcal{B}$ or to $\mathcal{C}$ but not both, an optimal description allots some amount $y_1$ of information to subsystem $\mathcal{B}$, and the rest, $y_2=y-y_1$, to subsystem $\mathcal{C}$. The optimum is achieved when the total maximal utility over these two subsystems is maximized. Taking the derivative of both sides and invoking the concavity of U yields a corresponding formula for the marginal utility M:

$$M_{\mathcal{A}}(y)=\underset{\begin{array}{c}{y}_1+y_2=y\\ y_1,y_2\ge 0\end{array}}{min}max\left\{M_{\mathcal{B}}(y_1),M_{\mathcal{C}}(y_2)\right\}.$$

(22)

Equations (21) and (22) are proven in Appendix E. This additivity property can also be expressed as the reflection (generalized inverse) of M. For any piecewise-constant, nonincreasing function f, we define the reflection $\tilde{f}$ as

$$\tilde{f}(x)=max\{y:f(y)\le x\}.$$

(23)

A generalized inverse [15] is needed since, for piecewise constant functions, there exist x-values for which there is no y such that $f(y)=x$. For such values, $\tilde{f}(x)$ is the largest y such that $f(y)$ does not exceed x. This operation is a reflection about the line $f(y)=y$, and applying it twice recovers the original function. If $\mathcal{A}$ comprises independent subsystems $\mathcal{B}$ and $\mathcal{C}$, the additivity property, Equation (22), can be written in terms of the reflection as

$${\tilde{M}}_{\mathcal{A}}(x)={\tilde{M}}_{\mathcal{B}}(x)+{\tilde{M}}_{\mathcal{C}}(x).$$

(24)

Equation (24) is proven in Appendix E.

Plots of the MUI for our four running examples are shown in Figure 5. The most interesting case is the parity bit system, Example D, for which the marginal utility is

$$M(y)=\left\{\begin{array}{cc}\frac{3}{2}\hfill & 0\le y\le 2\hfill \\ 0\hfill & y>2.\hfill \end{array}\right.$$

(25)

The optimal description scheme leading to this marginal utility is shown in Figure 6. The marginal utility of information $M(y)$ captures the intermediate level of interdependency among components in Example D, in contrast to the maximal independence and maximal interdependence in Examples A and B, respectively (Figure 5). For an N-component generalization of Example D, in which each component acts as a parity bit for all others, we show in Appendix F that the MUI is given by

$$M(y)=\left\{\begin{array}{cc}\frac{N}{N-1}\hfill & 0\le y\le N-1\hfill \\ 0\hfill & y>N-1.\hfill \end{array}\right.$$

(26)

The MUI is similar in spirit to, and can be approximated by, principal components analysis, Information Bottleneck methods [70,71,72,73], and other methods that characterize the best possible description of a system using limited resources [66,74,75,76,77,78,79]. We discuss these connections in Section 10.3.

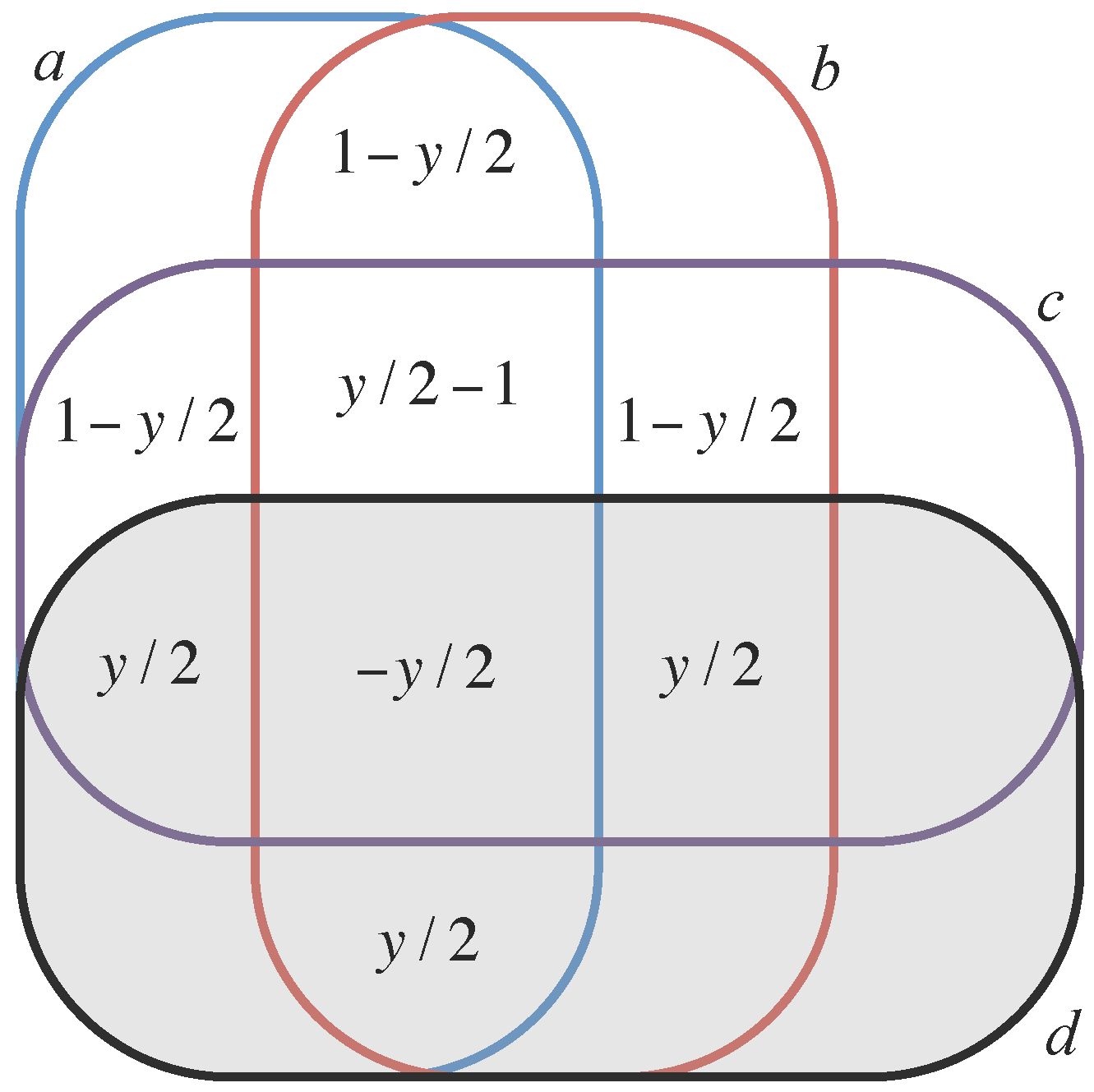
8. Reflection Principle for Systems of Independent Blocks

For systems with a particularly simple structure, the complexity profile and the MUI turn out to be reflections (generalized inverses) of each other. The simplest case is a system consisting of a single component a. In this case, according to Equation (14), the complexity profile $C(x)$ has value $H(a)$ for $0\le x\le \sigma (a)$ and zero for $x>\sigma (a)$:

$$C(x)=H(a)\Theta \left(\sigma (a)-x\right).$$

(27)

Above, $\Theta (y)$ is a step function with value 1 for $y\ge 0$ and 0 otherwise. To compute the marginal utility of information for this system, we observe that a descriptor with maximal utility has $I(d;a)=min\{y,H(a)\}$ for each value of the informational constraint y, and it follows that

$$M(y)=\sigma (a)\Theta \left(H(a)-y\right).$$

(28)

We observe that $C(x)$ and $M(x)$ are reflections of each other: $C(x)=\tilde{M}(x)$, where $\tilde{M}(x)$ is defined in Equation (23).

We next consider a system whose components are all independent of each other. Additivity over independent subsystems (Property 3 in Section 6 and Section 7), together with Equations (27) and (28), implies

$$C(x)=\tilde{M}(x)=\sum _{a\in A}H(a)\Theta \left(\sigma (a)-x\right).$$

(29)

Thus the reflection principle holds for systems of independent components.

More generally, one can consider a system of “independent blocks”—that is, a system that can be partitioned into independent subsystems, where the components of each subsystem are completely interdependent (see Section 5.4 for definitions.) Running example C is such a system, in that it can be partitioned into independent subsystems with component sets $\{a,c\}$ and $\{b\}$, and each of these sets is completely interdependent. We show in Appendix B that any set of completely interdependent components can be replaced by a single component, with scale equal to the sum of the scales of the replaced components, without altering the complexity profile or MUI. Thus, for systems of independent blocks, each block can be collapsed into a single component, whereupon Equation (29) applies and the reflection principle holds.

We have thus established that for any system of independent blocks, the complexity profile and the MUI are reflections of each other $C(x)=\tilde{M}(x)$. However, this relationship does not hold for every system. $C(x)$ and $M(y)$ are not reflections of each other in the case of Example D, and, more generally, for a class of systems that exhibit negative information, as shown in Equation (26).

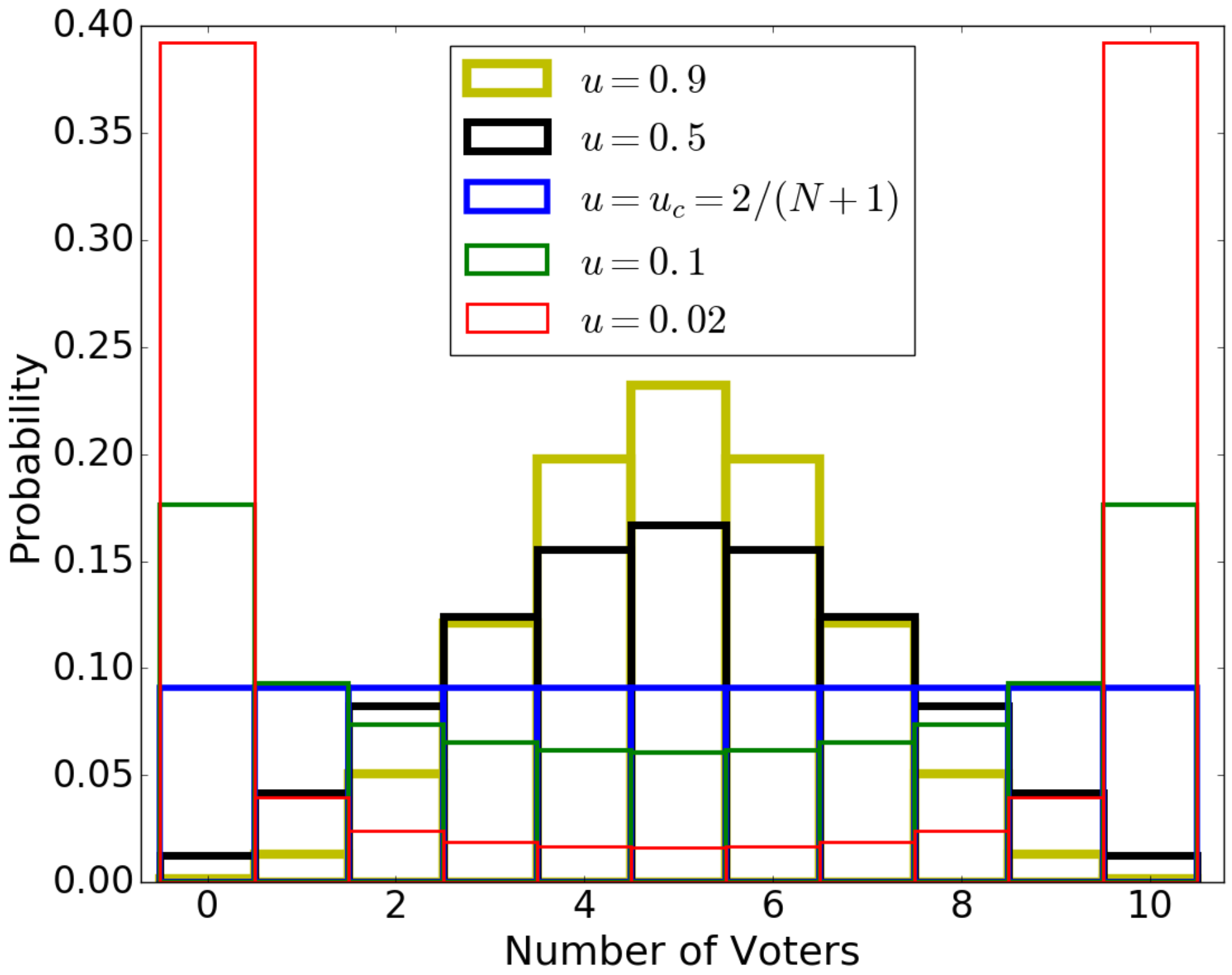
9. Application to Noisy Voter Model

As an application of our framework, we compute the marginal utility of information for the noisy voter model [43] on a complete graph. This model is a stochastic process with N “voters”. Each voter, $i=1,\dots ,N$, can exist in one of two states, which we label ${\eta }_i\in \{-1,1\}$. Each voter updates its state at Poisson rate 1. With probability u it chooses $\pm 1$ with equal probability; otherwise, with probability $1-u$, it copies a random other individual. Here $u\in [0,1]$ is noise (or mutation) parameter that mediates the level of interdependence among voters. It follows that voter i flips its state (from $+1$ to $-1$ or vice versa) at Poisson rate

$${\lambda }_i=\frac{u}{2}+\frac{1-u}{N-1}\sum _{j=1}^N\frac{|{\eta }_j-{\eta }_i|}{2}.$$

(30)

For $u\ll 1$, voters are typically in consensus; for $u=1$, all voters behave independently. The noisy voter model is mathematically equivalent to the Moran model [80] of neutral drift with mutation, and to a model of financial behavior on networks [23,81].

This model has a stationary distribution in which the number m of voters in the $+1$ state has a beta-binomial distribution (Figure 7) [18,82]:

$$P(m)\propto \frac{\Gamma (N+M-m)\Gamma (M+m)}{\Gamma (N+1-m)\Gamma (1+m)},M=\frac{(N-1)u}{2(1-u)}.$$

(31)

For small u, P is concentrated on the “consensus” states 0 and N, converging to the uniform distribution on these states as $u\to 0$. For large u, P exhibits a central tendency around $m=N/2$, and converges to the binomial distribution with $p=1/2$ as $u\to 1$. These two modes are separated by the critical value of $u_c=2/(N+1)$, at which $M=1$ and P becomes the uniform distribution on $\{0,\dots ,N\}$. This is the scenario in which mutation exactly balances the uniformizing effect of faithful copying. As $u\to 0$, P converges to the uniform distribution on the states 0 and N.

The noisy voter model on a complete graph possesses exchange symmetry, meaning its behavior is preserved under permutation of its components. As a consequence, if subsets U and V have the same cardinality, $\left|U\right|=\left|V\right|$, then they have the same information, $H(U)=H(V)$. The information function is therefore fully characterized by the quantities $H_1,\dots ,H_N$, where $H_n$ is the information in each subset with $n\le N$ components.

To calculate the MUI for systems with exchange symmetry, it suffices to consider descriptors that also possess exchange symmetry, so that $I(d;U)=I(d;V)$ whenever $\left|U\right|=\left|V\right|$. Denoting by $I_n$ the information that a descriptor imparts about a subset of size n, constraints (i)–(iii) of Section 7 reduce to

(i)

$0\le I_n\le H_n$ for all $n\in \{1,\dots ,N\}$,

(ii)

$0\le I_n-I_{n-1}\le H_n-H_{n-1}$ for all $n\in \{1,\dots ,N\}$,

(iii)

$I_n+I_m-I_{n+m-\ell }-I_{\ell }\le H_n+H_m-H_{n+m-\ell }-H_{\ell }$ for all $n,m,\ell \in \{1,\dots ,N\}$.

The maximum utility of information $U(y)$ is the maximum value of $N{I}_1$, subject to (i)–(iii) above and $I_N\le y$. Since the number of constraints is polynomial in N, the maximum utility—and therefore the MUI—are readily computable.

The complexity profile and MUI for this model (Figure 8) both capture how the interdependence of voters is mediated by the noise parameter u. For small u, conformity among voters leads to large-scale information (positive $C(x)$ for large x) and enables efficient partial descriptions of the system (large $M(y)$ for small y). For large u, weak dependence among voters means that most information applies at small scale ($C(x)$ decreases rapidly) and optimal descriptions cannot do much better than to describe each component singly ($M(y)=1$ for most values of y). Unlike the case of independent block systems (Section 8), the complexity profile and MUI are not reflections of each other for this model, but the reflection of each is qualitatively similar to the other.

10. Discussion

10.1. Potential Applications

Here we have presented a multiscale extension of information theory, along with two quantitative indices, as tools the analysis of structure in complex systems. Our generalized, axiomatic definition of information enables this framework to be applied to a variety of physical, biological, social, and economic systems. In particular, we envision applications to spin systems [1,17,83,84], gene regulatory systems [85,86,87,88,89,90,91], neural systems [92,93,94], biological swarming [95,96,97], spatial evolutionary dynamics [82,98,99], and financial markets [22,59,81,100,101,102,103,104,105].

In each of these systems, multiscale information theory enables the analysis of such questions as: Do components (genes, neurons, investors, etc.) behave largely independently, or are their behaviors strongly interdependent? How significant are intermediate scales of organization such as the genetic pathway, the cerebral lobe, or the financial sector? Can other “hidden” scales of organization be identified? Do the scales of behavior vary across different instances of a particular kind of system (e.g., gene regulation in stem versus differentiated cells; neural systems across taxa)? And how do the scales of organization in these systems compare to the scales of challenges they face?

The realization of these applications faces a computational hurdle: a full characterization of a system’s structure requires the computation of $2^N$ informational quantities. Thus for large real-world systems, efficient approximations must be developed. Fortunately, there already exist efficient approximations to the complexity profile [15], and approximations to the MUI can be obtained using restricted description schemes as we discuss in Section 10.3 below.

10.2. Multivariate and Multiscale Information

The idea of using entropy or information to quantify a system’s structure has deep roots. One of the earliest and most influential attempts was Schrödinger’s concept of negative entropy or negentropy [106,107], which he introduced to quantify the extent to which a living system deviates from maximum entropy. Negentropy can be expressed in our formalism as $J={\sum }_{a\in A}H(a)-H(A)$. This same quantity is known in other contexts as multi-information [38,65,66], integration [40] or intrinsic information [67], and is used to characterize the extent of statistical dependence among a set of random variables. Supposing that each component of our system has scale one, we have the following equivalent characterizations of this quantity:

$$J=S({\mathfrak{D}}_{\mathcal{A}})-I({\mathfrak{D}}_{\mathcal{A}})=\sum _{k=1}^{\infty }C(k)-C(1)=\sum _{k=2}^{\infty }C(k).$$

(32)

Equation (32) makes clear that while J quantifies the deviation of a system from full independence, it does not identify the scale at which this deviation arises: all information at scales 2 and higher is subsumed into a single quantity.

Other proposed information-theoretic measures of structure also aggregate over scales in various ways. For example, the excess entropy, as defined by Ay et al. [41], is equal to $C(2)$, the amount of information that applies at scales 2 and higher. Another example is the complexity measure of Tononi et al. [40], which is defined for an N-component system as

$$T=\sum _{k=1}^N\left(\frac{1}{\left(\genfrac{}{}{0pt}{}{N}{k}\right)}\sum _{\begin{array}{c}U\subset A\\ \left|U\right|=k\end{array}}H(U)-\frac{k}{N}H(A)\right).$$

(33)

Using Equation (5), we can re-express T as a weighted sum of the information in each irreducible dependency, where each dependency x is weighted by a particular combinatorial function of its scale $s(x)$:

$$T=\sum _{x\in {\mathfrak{D}}_{\mathcal{A}}}I(x)\left(\sum _{k=1}^{N-s(x)}\frac{\left(\genfrac{}{}{0pt}{}{N-s(x)}{k}\right)}{\left(\genfrac{}{}{0pt}{}{N}{k}\right)}-\frac{N-1}{2}\right).$$

(34)

In this equation it is assumed that each it is assumed that each component has scale 1, so that $s(x)$ equals the number of components included in dependency x.

These previous measures can be understood as attempts to capture the idea that complex systems are not merely the sums of their parts—that is, they exhibit multiple scales of organization. We argue that this idea is best captured by making the notion of scale explicit, as a complementary axis to information. Doing so provides a formal basis for ideas that are implicit in earlier approaches.

The amount of information I that we assign to each of a system’s dependencies is known in the context of Shannon information as the multivariate mutual information or interaction information [30,31,32,33,37,38,39]. The use of multivariate mutual information is sometimes criticized [36,62], in part because it yields negative values that may be difficult to interpret. Such negative values arise for the complexity profile, but are avoided by the MUI. The value of $M(y)$ is always nonnegative and has a consistent interpretation as the additional scale units describable by an additional bit of information. The notion of descriptors also avoids negative values, since the information that a descriptor d provides about a subset U of components is always nonnegative: $I(d;U)\ge 0$.

Finally, some recent work raises the important question of whether measures based on shared information suffice to characterize the structure of a system. James and Crutchfield [63] exhibit pairs of systems of random variables that have qualitatively different probabilistic relationships, but the same joint Shannon information $H(U)$ for each subset U of variables. As a consequence, the shared information I, complexity profile C, and marginal utility of information M, are the same for the two systems in such a pair. These examples demonstrate that probabilistic relationships among variables need not be determined by their information-theoretic measures, raising the question as to whether structure can be defined in terms of those measures. This conclusion, however, is dependent on the definition of the variables that are used to identify system states. To illustrate, if we take a particular system and combine variables into fewer ones with more states, the fewer information-theoretic measures that are obtained in the usual way become progressively less distinguishing of system probabilities. In the extreme case of a single variable having all of the possible states of the system, there is only one information measure. In the reverse direction, we have found [108] that a given system of random variables can be augmented with additional variables, the values of which are completely determined by the original system, in such a way that the probabilistic structure of the original system is uniquely determined by information overlaps in the augmented system. Thus, in this sense, moving to a more detailed representation can reveal relationships that are obscured in higher-level representations, and information theory may be sufficient to define structure in a general way.

10.3. Relation of the MUI to Other Measures

Our new index of structure, the MUI, is philosophically similar to data-reduction or dimensionality reduction techniques like principal component analysis, multidimensional scaling and detrended fluctuation analysis [74,76]; to the Information Bottleneck methods of Shannon information theory [70,71,72,73]; to Kolmogorov structure functions and algorithmic statistics in Turing-machine-based complexity theory [77,78,79]; to Gell-Mann and Lloyd’s “effective complexity” [75]; and to Schneiderman et al.’s “connected information” [66]. All of these methods are mathematical techniques for characterizing the most important behaviors of the system under study. Each is an implementation of the idea of finding the best possible partial description of a system, where the resources available for this description (bits, coordinates, etc.) are constrained.

The essential difference from these previous measures is that the MUI is not tied to any particular method for generating partial descriptions. Rather, the MUI is defined in terms of optimally effective descriptors: for each possible amount of information invested in describing the system, the MUI considers the descriptor that provides the best possible theoretical return (in terms of scale-weighted information) on that investment. These returns are limited only by the structure of the system being described and the the fundamental constraints on information as encapsulated by our axioms.

In some applied contexts, it may be difficult or impossible to realize these theoretical maxima, due to constraints beyond those imposed by the axioms of information functions. It is often useful in these contexts to consider a particular “description scheme”, in which descriptors are restricted to be of a particular form. Many of the data reduction and dimensionality reduction techniques described above can be understood as finding an optimal description of limited information using a specified description scheme. In these cases, the maximal utility found using the specified description scheme is in general less than the theoretical optimum. Calculating the marginal utility under a particular description scheme yields an approximation to the MUI.

10.4. Multiscale Requisite Variety

The discipline of cybernetics, an ancestor to modern control theory, used Shannon’s information theory to quantify the difficulty of performing tasks, a topic of relevance both to organismal survival in biology and to system regulation in engineering. Ashby [109] considered scenarios in which a regulator device must protect some important entity from the outside environment and its disruptive influences. Successful regulation implies that if one knows only the state of the protected component, one cannot deduce the environmental influences; i.e., the job of the regulator is to minimize mutual information between the protected component and the environment. This is an information-theoretic statement of the idea of homeostasis. Ashby’s “Law of Requisite Variety” states that the regulator’s effectiveness is limited by its own information content, or variety in cybernetic terminology. An insufficiently flexible regulator will not be able to cope with the environmental variability.

Multiscale information theory enables us to overcome a key limitation of the requisite variety concept. In the framework of traditional cybernetics [109], each action of the environment requires a specific, unique reaction on the part of the regulator. This framework neglects the important difference between large-scale and fine-scale impacts. Systems may be able to absorb fine-scale impacts without any specific response, whereas responses to large-scale impacts are potentially critical to survival. For example, a human being can afford to be indifferent to the impact of a single molecule, whereas a falling rock (which may be regarded as the collective motion of many molecules) cannot be neglected. Ashby’s Law does not make this distinction; indeed, there is no framework for this distinction in traditional information theory, since the molecule and the rock can be specified using the same amount of information.

This limitation can be overcome by a multiscale generalization of Ashby’s Law [14], in which the responses of the system must occur at a scale appropriate to the environmental challenge. To protect against infection, for example, organisms have physical barriers (e.g., skin), generic physiological responses (e.g., clotting, inflammation) and highly specific adaptive immune responses, involving interactions among many cell types, evolved to identify pathogens at the molecular level. The evolution of immune systems is the evolution of separate large- and small-scale countermeasures to threats, enabled by biological mechanisms for information transmission and preservation [110]. By allowing for arbitrary intrinsic scales of components, and a range of different information functions, our work provides an expanded mathematical foundation for the multiscale generalization of Ashby’s Law.

10.5. Mechanistic versus Informational Dependencies

Information-theoretic measures of a system’s structure are essentially descriptive in nature. The tools we have proposed are aimed at identifying the scales of behavior of a system, but not necessarily the causes of this behavior. Importantly, causal influences at one scale can produce correlations at another. For example, the interactions in an Ising spin system are pairwise in character: the energy of a state depends only on the relative spins of neighboring pairs. These pairwise couplings can, however, give rise to long-range patterns [27]. Similarly, in models of coupled oscillators, dyadic physical interactions can lead to global synchronization [111]. Thus local interactions can create large-scale collective behavior.

11. Conclusions

Information theory has made, and will continue to make, formidable contributions to all areas of science. We argue that, in applying information theory to the study of complex systems, it is crucial to identify the scales at which information applies, rather than collapsing redundant or overlapping information into a raw number of independent bits. The multiscale approach to information theory falls squarely within the tradition of statistical physics—itself born of a marriage between probability theory and classical mechanics. By providing a general axiomatic framework for multiscale information theory, along with quantitative indices, we hope to deepen, clarify, and expand the mathematical foundations of complex systems theory.