On the Reliability Function of Variable-Rate Slepian-Wolf Coding ^†

Abstract

The reliability function of variable-rate Slepian-Wolf coding is linked to the reliability function of channel coding with constant composition codes, through which computable lower and upper bounds are derived. The bounds coincide at rates close to the Slepian-Wolf limit, yielding a complete characterization of the reliability function in that rate region. It is shown that variable-rate Slepian-Wolf codes can significantly outperform fixed-rate Slepian-Wolf codes in terms of rate-error tradeoff. Variable-rate Slepian-Wolf coding with rate below the Slepian-Wolf limit is also analyzed. In sharp contrast with fixed-rate Slepian-Wolf codes for which the correct decoding probability decays to zero exponentially fast if the rate is below the Slepian-Wolf limit, the correct decoding probability of variable-rate Slepian-Wolf codes can be bounded away from zero.

1. Introduction

Consider the problem (see Figure 1) of compressing $X^n=(X_1,X_2,\cdots ,X_n)$ with side information $Y^n=(Y_1,Y_2,\cdots ,Y_n)$ available only at the decoder. Here ${\left\{(X_i,Y_i)\right\}}_{i=1}^{\infty }$ is a joint memoryless source with zero-order joint probability distribution $P_{XY}$ on finite alphabet $\mathcal{X}\times \mathcal{Y}$. Let $P_X$ and $P_Y$ be the marginal probability distributions of X and Y induced by the joint probability distribution $P_{XY}$. Without loss of generality, we shall assume $P_X\left(x\right)>0,P_Y\left(y\right)>0$ for all $x\in \mathcal{X},y\in \mathcal{Y}$. This problem was first studied by Slepian and Wolf in their landmark paper [1]. They proved a surprising result that the minimum rate for reconstructing $X^n$ at the decoder with asymptotically zero error probability (as block length n goes to infinity) is $H\left(X\right|Y)$, which is the same as the case where the side information $Y^n$ is also available at the encoder. The fundamental limit $H\left(X\right|Y)$ is often referred to as the Slepian-Wolf limit. We shall assume $H\left(X\right|Y)>0$ throughout this paper.

Different from conventional lossless source coding, where most effort has been devoted to variable-rate coding schemes, research on Slepian-Wolf coding has almost exclusively focused on fixed-rate codes (see, e.g., [2,3,4,5] and the references therein). This phenomenon can be partly explained by the influence of channel coding. It is well known that there is an intimate connection between channel coding and Slepian-Wolf coding. Intuitively, one may view $Y^n$ as the channel output generated by channel input $X^n$ through discrete memoryless channel $P_{Y|X}$, where $P_{Y|X}$ is the probability transition matrix from $\mathcal{X}$ to $\mathcal{Y}$ induced by the joint probability probability distribution $P_{XY}$. Since $Y^n$ is not available at the encoder, Slepian-Wolf coding is, in a certain sense, similar to channel coding without feedback. In a channel coding system, there is little incentive to use variable-rate coding schemes if no feedback link exists from the receiver to the transmitter. Therefore, it seems justifiable to focus on fixed-rate codes in Slepian-Wolf coding.

This viewpoint turns out to be misleading. We shall show that variable-rate Slepian-Wolf codes can significantly outperform fixed-rate codes in terms of rate-error tradeoff. Specifically, it is revealed that variable-rate Slepian-Wolf codes can beat the sphere-packing bound for fixed-rate Slepian-Wolf codes at rates close to the Slepian-Wolf limit. It is known [6] that the correct decoding probability of fixed-rate Slepian-Wolf codes decays to zero exponentially fast if the rate is below the Slepian-Wolf limit. Somewhat surprisingly, the decoding error probability of variable-rate Slepian-Wolf codes can be bounded away from one even when they are operated below the Slepian-Wolf limit, and the performance degrades gracefully as the rate goes to zero. Therefore, variable-rate Slepian-Wolf coding is considerably more robust.

The rest of this paper is organized as follows. In Section 2, we review the existing bounds on the reliability function of fixed-rate Slepian-Wolf coding, and point out the intimate connections with their counterparts in channel coding. In Section 3, we characterize the reliability function of variable-rate Slepian-Wolf coding by leveraging the reliability function of channel coding with constant composition codes. Computable lower and upper bounds are derived. The bounds coincide at rates close to the Slepian-Wolf limit. The correct decoding probability of variable-rate Slepian-Wolf coding with rate below the Slepian-Wolf limit is studied in Section 4. An illustrative example is given in Section 5. We conclude the paper in Section 6. Throughout this paper, we assume the logarithm function is to base e unless specified otherwise.

2. Fixed-Rate Slepian-Wolf Coding and Channel Coding

To facilitate the comparisons between the performances of fixed-rate Slepian-Wolf coding and variable-rate coding, we shall briefly review the existing bounds on the reliability function of fixed-rate Slepian-Wolf coding. It turns out that a most instructive way is to first consider their counterparts in channel coding. The reason is two-fold. First, it provides the setup to introduce several important definitions. Second and more important, it will be clear that the reliability function of fixed-rate Slepian-Wolf coding is closely related to that of channel coding; indeed, such a connection will be further explored in the context of variable-rate Slepian-Wolf coding.

For any probability distributions $P,Q$ on $\mathcal{X}$ and probability transition matrices $V,W:\mathcal{X}\to \mathcal{Y}$, we use $H\left(P\right)$, $I(P,V)$, $D(Q\parallel P)$, and $D(W\parallel V|P)$ to denote the standard entropy, mutual information, divergence, and conditional divergence functions; specifically, we have

$$\begin{array}{c}H\left(P\right)=-\sum _{x}P\left(x\right)\log P\left(x\right),\hfill \\ I(P,V)=\sum _{x,y}P\left(x\right)V\left(y\right|x)\log \frac{V\left(y\right|x)}{{\sum }_{x^{\prime }}P\left(x^{\prime }\right)V\left(y\right|x^{\prime })},\hfill \\ D(Q\parallel P)=\sum _{x}Q\left(x\right)\log \frac{Q\left(x\right)}{P\left(x\right)},\hfill \\ D(W\parallel V|P)=\sum _{x,y}P\left(x\right)W\left(y\right|x)\log \frac{W\left(y\right|x)}{V\left(y\right|x)}.\hfill \end{array}$$

The main technical tool we need is the method of types. First, we shall quote a few basic definitions from [7]. Let $\mathcal{P}\left(\mathcal{X}\right)$ denote the set of all probability distributions on $\mathcal{X}$. The type of a sequence $x^n\in {\mathcal{X}}^n$, denoted as $P_{x^n}$, is the empirical probability distribution of $x^n$. Let ${\mathcal{P}}_n\left(\mathcal{X}\right)$ denote the set consisting of the possible types of sequences $x^n\in {\mathcal{X}}^n$. For any $P\in {\mathcal{P}}_n\left(\mathcal{X}\right)$, the type class ${\mathcal{T}}_n\left(P\right)$ is the set of sequences in ${\mathcal{X}}^n$ of type P. We will make frequent use of the following elementary results:

$$|{\mathcal{P}}_n{\left(\mathcal{X}\right)|\le (n+1)}^{\left|\mathcal{X}\right|},$$

(1)

$$\frac{1}{{(n+1)}^{\left|\mathcal{X}\right|}}{e}^{nH\left(P\right)}\le \left|{\mathcal{T}}_n\left(P\right)\right|\le e^{nH\left(P\right)},P\in {\mathcal{P}}_n\left(\mathcal{X}\right),$$

(2)

$$\prod _{i=1}^{n}P\left(x_i\right)=e^{-n\left[D(Q\parallel P)+H\left(Q\right)\right]},x^n\in {\mathcal{T}}_n\left(Q\right),Q\in {\mathcal{P}}_n\left(\mathcal{X}\right),P\in \mathcal{P}\left(\mathcal{X}\right).$$

(3)

A block code ${\mathcal{C}}_n$ is an ordered collection of sequences in ${\mathcal{X}}^n$. We allow ${\mathcal{C}}_n$ to contain identical sequences. Moreover, for any set $\mathcal{A}\subseteq {\mathcal{X}}^n$, we say that ${\mathcal{C}}_n\subseteq \mathcal{A}$ if $x^n\in \mathcal{A}$ for all $x^n\in {\mathcal{C}}_n$. Note that ${\mathcal{C}}_n\subseteq \mathcal{A}$ does not imply $|{\mathcal{C}}_n|\le |\mathcal{A}|$. The rate of ${\mathcal{C}}_n$ is defined as

$$\begin{array}{c}\hfill R\left({\mathcal{C}}_n\right)=\frac{1}{n}\log \left|{\mathcal{C}}_n\right|.\end{array}$$

Given a channel $W_{Y|X}:\mathcal{X}\to \mathcal{Y}$, a block code ${\mathcal{C}}_n\subseteq {\mathcal{X}}^n$, and channel output $Y^n\in {\mathcal{Y}}^n$, the output of the optimal maximum likelihood (ML) decoder is

$$\begin{array}{c}\hfill {\widehat{X}}^n=\arg \underset{x^n\in {\mathcal{C}}_n}{\min }-\sum _{i=1}^n\log W_{Y|X}\left(Y_i\right|x_i),\end{array}$$

where the ties are broken in an arbitrary manner. The average decoding error probability of block code ${\mathcal{C}}_n$ over channel $W_{Y|X}$ is defined as

$$P_e({\mathcal{C}}_n,W_{Y|X})=\frac{1}{|{\mathcal{C}}_n|}\sum _{x^n\in {\mathcal{C}}_n}\mathrm{Pr}\{{\widehat{X}}^n\ne x^n|x^n\mathrm{is} \mathrm{transmitted}\}.$$

The maximum decoding error probability of block code ${\mathcal{C}}_n$ over channel $W_{Y|X}$ is defined as

$$P_{e,\max }({\mathcal{C}}_n,W_{Y|X})=\underset{x^n\in {\mathcal{C}}_n}{\max }\mathrm{Pr}\{{\widehat{X}}^n\ne x^n|x^n\mathrm{is} \mathrm{transmitted}\}.$$

The average correct decoding probability of block code ${\mathcal{C}}_n$ over channel $W_{Y|X}$ is defined as

$$P_c({\mathcal{C}}_n,W_{Y|X})=1-P_e({\mathcal{C}}_n,W_{Y|X}).$$

Definition 1.

Given a channel $W_{Y|X}:\mathcal{X}\to \mathcal{Y}$, we say that an error exponent $E\ge 0$ is achievable with block codes at rate R if for any $\delta >0$, there exists a sequence of block codes $\left\{{\mathcal{C}}_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_n\right)\ge R-\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_e({\mathcal{C}}_n,W_{Y|X})\ge E-\delta .\hfill \end{array}$$

(4)

The largest achievable error exponent at rate R is denoted by $E(W_{Y|X},R)$. The function $E(W_{Y|X},·)$ is referred to as the reliability function of channel $W_{Y|X}$.

Similarly, we say that a correct decoding exponent $E^c\ge 0$ is achievable with block channel codes at rate R if for any $\delta >0$, there exists a sequence of block codes $\left\{{\mathcal{C}}_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_n\right)\ge R-\delta ,\hfill \\ \underset{n\to \infty }{\lim \inf }-\frac{1}{n}\log P_c({\mathcal{C}}_n,W_{Y|X})\le E^c+\delta .\hfill \end{array}$$

The smallest achievable correct decoding exponent at rate R is denoted by $E^c(W_{Y|X},R)$. It will be seen that $E^c(W_{Y|X},R)$ is positive if and only if $R>C\left(W_{Y|X}\right)$, where $C\left(W_{Y|X}\right)\triangleq {\max }_{Q_X}I(Q_X,W_{Y|X})$ is the capacity of channel $W_{Y|X}$. Therefore, we shall refer to the function $E^c(W_{Y|X},·)$ as the reliability function of channel $W_{Y|X}$ above the capacity.

Remark 1.

Given any block code ${\mathcal{C}}_n$ of average decoding error probability $P_e({\mathcal{C}}_n,W_{Y|X})$, we can expurgate the worst half of the codewords so that the maximum decoding error probability of the resulting code is bounded above by $2P_e({\mathcal{C}}_n,W_{Y|X})$. Therefore, the reliability function $E(W_{Y|X},·)$ is unaffected if we replace $P_e({\mathcal{C}}_n,W_{Y|X})$ by $P_{e,\max }({\mathcal{C}}_n,W_{Y|X})$ in (4).

Definition 2.

Given a probability distribution $Q_X\in \mathcal{P}\left(\mathcal{X}\right)$ and a channel $W_{Y|X}:\mathcal{X}\to \mathcal{Y}$, we say that an error exponent $E\ge 0$ is achievable at rate R with constant composition codes of type approximately $Q_X$ if for any $\delta >0$, there exists a sequence of block codes $\left\{{\mathcal{C}}_n\right\}$ with ${\mathcal{C}}_n\subseteq {\mathcal{T}}_n\left(P_n\right)$ for some $P_n\in {\mathcal{P}}_n\left(\mathcal{X}\right)$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim }\parallel P_n-Q_X\parallel =0,\hfill \\ \underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_n\right)\ge R-\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_e({\mathcal{C}}_n,W_{Y|X})\ge E-\delta ,\hfill \end{array}$$

where $\parallel ·\parallel$ is the $l_1$ norm.

The largest achievable error exponent at rate R for constant composition codes of type approximately $Q_X$ is denoted by $E(Q_X,W_{Y|X},R)$. The function $E(Q_X,W_{Y|X},·)$ is referred to as the reliability function of channel $W_{Y|X}$ for constant composition codes of type approximately $Q_X$.

Similarly, we say that a correct decoding exponent $E^c\ge 0$ is achievable at rate R with constant composition codes of type approximately $Q_X$ if for any $\delta >0$, there exists a sequence of block codes $\left\{{\mathcal{C}}_n\right\}$ with ${\mathcal{C}}_n\subseteq {\mathcal{T}}_n\left(P_n\right)$ for some $P_n\in {\mathcal{P}}_n\left(\mathcal{X}\right)$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim }\parallel P_n-Q_X\parallel =0,\hfill \\ \underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_n\right)\ge R-\delta ,\hfill \\ \underset{n\to \infty }{\lim \inf }-\frac{1}{n}\log P_c({\mathcal{C}}_n,W_{Y|X})\le E^c+\delta .\hfill \end{array}$$

(5)

The smallest achievable correct decoding exponent at rate R for constant composition codes of type approximately $Q_X$ is denoted by $E^c(Q_X,W_{Y|X},R)$.

Remark 2.

The reliability function $E(Q_X,W_{Y|X},·)$ is unaffected if we replace $P_e({\mathcal{C}}_n,W_{Y|X})$ by $P_{e,\max }({\mathcal{C}}_n,W_{Y|X})$ in (5).

Let ${\left|t\right|}^{+}=\max \{0,t\}$ and $d_{W_{Y|X}}(x,\tilde{x})=-\log {\sum }_y\sqrt{W_{Y|X}\left(y\right|x)W_{Y|X}\left(y\right|\tilde{x})}$. Define

$$\begin{array}{c}{E}_{ex}(Q_X,W_{Y|X},R)=\underset{Q_{\tilde{X}|X}:Q_X=Q_{\tilde{X}},I(Q_X,Q_{\tilde{X}|X})\le R}{\min }\left[{\mathbb{E}}_{Q_{X\tilde{X}}}{d}_{W_{Y|X}}(X,\tilde{X})+I(Q_X,Q_{\tilde{X}|X})-R\right],\hfill \end{array}$$

(6)

$$\begin{array}{c}{E}_{rc}(Q_X,W_{Y|X},R)=\underset{V_{Y|X}}{\min }\left[D(V_{Y|X}\parallel W_{Y|X}|Q_X)+|I(Q_X,V_{Y|X}){-R|}^{+}\right],\hfill \end{array}$$

(7)

$$\begin{array}{c}{E}_{sp}(Q_X,W_{Y|X},R)=\underset{V_{Y|X}:I(Q_X,V_{Y|X})\le R}{\min }D(V_{Y|X}\parallel W_{Y|X}\left|Q_X\right),\hfill \end{array}$$

(8)

where in (6), $Q_{\tilde{X}}$ and $Q_{X\tilde{X}}$ are respectively the marginal probability distribution of $\tilde{X}$ and the joint probability distribution of X and $\tilde{X}$ induced by $Q_X$ and $Q_{\tilde{X}|X}$.

Let $R_{ex}^{\infty }(Q_X,W_{Y|X})$ be the smallest $R\ge 0$ with $E_{ex}(Q_X,W_{Y|X},R)<\infty$. We have

$$\begin{array}{c}\hfill R_{ex}^{\infty }(Q_X,W_{Y|X})=\underset{Q_{\tilde{X}|X}:Q_X=Q_{\tilde{X}},{\mathbb{E}}_{Q_{X\tilde{X}}}{d}_{W_{Y|X}}(X,\tilde{X})<\infty }{\min }I(Q_X,Q_{\tilde{X}|X}).\end{array}$$

(9)

It is known ([7], Exercise 5.18) that $E_{ex}(Q_X,W_{Y|X},R)$ is a decreasing convex function of R for $R\ge R_{ex}^{\infty }(Q_X,W_{Y|X})$; moreover, the minimum in (9) is achieved at $Q_{X\tilde{X}}$ if and only if

$$Q_{X\tilde{X}}(x,\tilde{x})=\left\{\begin{array}{cc}cQ\left(x\right)Q\left(\tilde{x}\right)\hfill & \mathrm{if} d_{W_{Y|X}}(x,\tilde{x})<\infty ,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where the probability distribution Q and the constant c are uniquely determined by the condition $Q_X=Q_{\tilde{X}}$.

It is shown in ([8], Lemma 3) that, for some $R^{*}(Q_X,W_{Y|X})\in [0,I(Q_X,W_{Y|X})]$, we have

$$\begin{array}{cc}\hfill \max \left\{E_{ex}(Q_X,W_{Y|X},R),E_{rc}(Q_X,P_{Y|X},R)\right\}=\left\{\begin{array}{cc}{E}_{ex}(Q_X,W_{Y|X},R)\hfill & \mathrm{if} R\le R^{*}(Q_X,W_{Y|X}),\hfill \\ E_{rc}(Q_X,W_{Y|X},R)\hfill & \mathrm{if} R>R^{*}(Q_X,W_{Y|X}).\hfill \end{array}\right.& \hfill \end{array}$$

(10)

It is also known ([7], Corollary 5.4) that

$$\begin{array}{cc}\hfill E_{rc}(Q_X,W_{Y|X},R)=\left\{\begin{array}{cc}{E}_{sp}(Q_X,W_{Y|X},R)\hfill & \mathrm{if} R\ge R_{cr}(Q_X,W_{Y|X}),\hfill \\ E_{sp}(Q_X,W_{Y|X},R_{cr})+R_{cr}-R\hfill & \mathrm{if} 0\le R\le R_{cr}(Q_X,W_{Y|X}),\hfill \end{array}\right.& \hfill \end{array}$$

(11)

where $R_{cr}\triangleq R_{cr}(Q_X,W_{Y|X})$ is the smallest R at which the convex curve $E_{sp}(Q_X,W_{Y|X},R)$ meets its supporting line of slope −1. It is obvious that $R_{cr}(Q_X,W_{Y|X})\le I(Q_X,W_{Y|X})$.

Proposition 1.

$R_{cr}(Q_X,W_{Y|X})=I(Q_X,W_{Y|X})$ if and only if the value of

$$\begin{array}{c}\hfill \frac{W_{Y|X}\left(y\right|x)}{{\sum }_{x^{\prime }}{Q}_X\left(x^{\prime }\right)W_{Y|X}\left(y\right|x^{\prime })}\end{array}$$

does not depend on y for all $x,y$ such that $Q_X\left(x\right)W_{Y|X}\left(y\right|x)>0$.

Proof. 

See Appendix A ☐

Define $R_{sp}^{\infty }(Q_X,W_{Y|X})=\inf \{R>0:E_{sp}(Q_X,W_{Y|X},R)<\infty \}$. It is known ([7], Exercise 5.3) that

$$\begin{array}{c}\hfill R_{sp}^{\infty }(Q_X,W_{Y|X})=\min I(Q_X,V_{Y|X}),\end{array}$$

(12)

where the minimum is taken over those $V_{Y|X}$’s for which $V_{Y|X}\left(y\right|x)=0$ whenever $W_{Y|X}\left(y\right|x)=0$; in particular, $R_{sp}^{\infty }(Q_X,W_{Y|X})>0$ if and only if for every $y\in \mathcal{Y}$ there exists an $x\in \mathcal{X}$ with $Q_X\left(x\right)>0$ and $W_{Y|X}\left(y\right|x)=0$.

Proposition 2.

The minimum in (12) is achieved at $V_{Y|X}=W_{Y|X}$ if and only if the value of

$$\begin{array}{c}\hfill \frac{W_{Y|X}\left(y\right|x)}{{\sum }_{x^{\prime }}{Q}_X\left(x^{\prime }\right)W_{Y|X}\left(y\right|x^{\prime })}\end{array}$$

does not depend on y for all $x,y$ such that $Q_X\left(x\right)W_{Y|X}\left(y\right|x)>0$.

Proof. 

The proof is similar to that of Proposition 1. The details are omitted. ☐

One can readily prove the following result by combining Propositions 1 and 2.

Proposition 3.

The following statements are equivalent:

• $R_{cr}(Q_X,P_{Y|X})=I(Q_X,W_{Y|X})$;
• $R_{sp}^{\infty }(Q_X,P_{Y|X})=I(Q_X,W_{Y|X})$;
• the value of

  $$\begin{array}{c}\hfill \frac{W_{Y|X}\left(y\right|x)}{{\sum }_{x^{\prime }}{Q}_X\left(x^{\prime }\right)W_{Y|X}\left(y\right|x^{\prime })}\end{array}$$

  does not depend on y for all $x,y$ such that $Q_X\left(x\right)W_{Y|X}\left(y\right|x)>0$.

Proposition 4.

• $E(Q_X,W_{Y|X},R)\ge \max \{E_{ex}(Q_X,W_{Y|X},R),E_{rc}(Q_X,W_{Y|X},R)\}$;
• $E(Q_X,P_{Y|X},R)\le E_{sp}(Q_X,W_{Y|X},R)$ with the possible exception of $R=R_{sp}^{\infty }(Q_X,W_{Y|X})$ at which point the inequality not necessarily holds;
• $E^c(Q_X,W_{Y|X},R)={\min }_{V_{Y|X}}\left[D(V_{Y|X}\parallel W_{Y|X}|Q_X)+|R-I(Q_X;V_{Y|X}){|}^{+}\right]$.

Remark 3.

$E_{ex}(Q_X,W_{Y|X},R)$, $E_{rc}(Q_X,W_{Y|X},R)$, and $E_{sp}(Q_X,W_{Y|X},R)$ are respectively the expurgated exponent, the random coding exponent, and the sphere packing exponent of channel $W_{Y|X}$ for constant composition codes of type approximately $Q_X$. The results in Proposition 4 are well known [7,9]. However, bounding the decoding error probability of constant composition codes often serves as an intermediate step in characterizing the reliability function for general block codes; as a consequence, the reliability function for constant composition codes is rarely explicitly defined. Moreover, $E_{ex}(Q_X,W_{Y|X},R)$, $E_{rc}(Q_X,W_{Y|X},R)$, and $E_{sp}(Q_X,W_{Y|X},R)$ are commonly used to bound the decoding error probability of constant composition codes for a fixed block length n; therefore, it is implicitly assumed that $Q_X$ is taken from ${\mathcal{P}}_n\left(\mathcal{X}\right)$ (see, e.g., [7]). In contrast, we consider a sequence of constant composition codes with block length increasing to infinity and type converging to $Q_X$ for some $Q_X\in \mathcal{P}\left(\mathcal{X}\right)$ (see Definition 2). A continuity argument is required for passing $Q_X$ from ${\mathcal{P}}_n\left(\mathcal{X}\right)$ to $\mathcal{P}\left(\mathcal{X}\right)$. For completeness, we supply the proof in Appendix B. Note that different from $E(Q_X,W_{Y|X},·)$, the function $E^c(Q_X,W_{Y|X},·)$ has been completely characterized.

Proposition 5.

• $E(W_{Y|X},R)={\sup }_{Q_X}E(Q_X,W_{Y|X},R)$,
• $E^c(W_{Y|X},R)={\inf }_{Q_X}{E}^c(Q_X,W_{Y|X},R)$.

Remark 4.

In view of the fact that $E^c(Q_X,W_{Y|X},R)$ is a continuous function of $Q_X$ defined on a compact set, we can replace “inf" with “min" in the above equation, i.e.,

$$\begin{array}{c}\hfill E^c(W_{Y|X},R)=\underset{Q_X}{\min }{E}^c(Q_X,W_{Y|X},R).\end{array}$$

(13)

Proof. 

It is obvious that $E(W_{Y|X},R)\ge {\sup }_{Q_X}E(Q_X,W_{Y|X},R)$; the other direction follows from the fact that every block code ${\mathcal{C}}_n$ contains a constant composition code ${\mathcal{C}}_n^{\prime }$ with $P_{e,\max }({\mathcal{C}}_n^{\prime },W_{Y|X})\le P_{e,\max }({\mathcal{C}}_n,W_{Y|X})$ and $R\left({\mathcal{C}}_n^{\prime }\right)\ge R\left({\mathcal{C}}_n\right)-\left|\mathcal{X}\right|\frac{\log (n+1)}{n}$. Similarly, it is clear that $E^c(W_{Y|X},R)\le {\inf }_{Q_X}{E}^c(Q_X,W_{Y|X},R)$; the other direction follows from the fact that given any block code ${\mathcal{C}}_n$, one can construct a constant composition code ${\mathcal{C}}_n^{\prime }$ with $P_c({\mathcal{C}}_n^{\prime },W_{Y|X})\le {(n+1)}^{\left|\mathcal{X}\right|}{P}_c({\mathcal{C}}_n,W_{Y|X})$ and $R\left({\mathcal{C}}_n^{\prime }\right)=R\left({\mathcal{C}}_n\right)$ [9]. ☐

The expurgated exponent, random coding exponent, and sphere packing exponent of channel $W_{Y|X}$ for general block codes are defined as follows:

• expurgated exponent

  $$\begin{array}{c}\hfill E_{ex}(W_{Y|X},R)=\underset{Q_X}{\max }{E}_{ex}(Q_X,W_{Y|X},R),\end{array}$$

  (14)
• random coding exponent

  $$\begin{array}{c}\hfill E_{rc}(W_{Y|X},R)=\underset{Q_X}{\max }{E}_{rc}(Q_X,W_{Y|X},R),\end{array}$$

  (15)
• sphere packing exponent

  $$\begin{array}{c}\hfill E_{sp}(W_{Y|X},R)=\underset{Q_X}{\max }{E}_{sp}(Q_X,W_{Y|X},R).\end{array}$$

  (16)

Let $R_{sp}^{\infty }\left(W_{Y|X}\right)$ be the smallest R to the right of which $E_{sp}(W_{Y|X},R)$ is finite. It is known ([7], Exercise 5.3) and [10] that

$$\begin{array}{cc}\hfill R_{sp}^{\infty }\left(W_{Y|X}\right)& =\underset{Q_X}{\max }{R}_{sp}^{\infty }(Q_X,W_{Y|X})\hfill \\ & =-\log \left[\underset{Q_X}{\min }\underset{y}{\max }\sum _{x\in \mathcal{X}:W_{Y|X}\left(y\right|x)>0}{Q}_X\left(x\right)\right].\hfill \end{array}$$

By Propositions 4 and 5, we recover the following well-known result [7,10]:

$$\begin{array}{c}\hfill \max \{E_{ex}(W_{Y|X},R),E_{rc}(W_{Y|X},R)\}\le E(W_{Y|X},R)\le E_{sp}(W_{Y|X},R)\end{array}$$

(17)

with the possible exception of $R=R_{sp}^{\infty }\left(W_{Y|X}\right)$ at which point the second inequality in (17) not necessarily holds.

Now we proceed to review the results on the reliability function of fixed-rate Slepian-Wolf coding. A fixed-rate Slepian-Wolf code ${\varphi }_n(·)$ is a mapping from ${\mathcal{X}}^n$ to a set ${\mathcal{A}}_n$. The rate of ${\varphi }_n(·)$ is defined as

$$\begin{array}{c}\hfill R\left({\varphi }_n\right)=\frac{1}{n}\log \left|{\mathcal{A}}_n\right|.\end{array}$$

Given ${\varphi }_n\left(X^n\right)$ and $Y^n$, the output of the optimal maximum a posteriori (MAP) decoder is

$$\begin{array}{cc}\hfill {\widehat{X}}^n& =\arg \underset{x^n:{\varphi }_n\left(x^n\right)={\varphi }_n\left(X^n\right)}{\min }-\sum _{i=1}^n\log P_{X|Y}\left(x_i\right|Y_i)\hfill \\ & =\arg \underset{x^n:{\varphi }_n\left(x^n\right)={\varphi }_n\left(X^n\right)}{\min }-\sum _{i=1}^n\log P_{XY}(x_i,Y_i),\hfill \end{array}$$

where the ties are broken in an arbitrary manner. The decoding error probability of Slepian-Wolf code ${\varphi }_n(·)$ is defined as

$$\begin{array}{c}\hfill P_e({\varphi }_n,P_{XY})=\mathrm{Pr}\{{\widehat{X}}^n\ne X^n\}.\end{array}$$

The correct decoding probability of Slepian-Wolf code ${\varphi }_n(·)$ is defined as

$$\begin{array}{c}\hfill P_c({\varphi }_n,P_{XY})=1-P_e({\varphi }_n,P_{XY}).\end{array}$$

Definition 3.

Given a joint probability distribution $P_{XY}$, we say that an error exponent $E\ge 0$ is achievable with fixed-rate Slepian-Wolf codes at rate R if for any $\delta >0$, there exists a sequence of fixed-rate Slepian-Wolf codes $\left\{{\varphi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R\left({\varphi }_n\right)\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_e({\varphi }_n,P_{XY})\ge E-\delta .\hfill \end{array}$$

The largest achievable error exponent at rate R is denoted by $E_f(P_{XY},R)$. The function $E_f(P_{XY},·)$ is referred to as the reliability function of fixed-rate Slepian-Wolf coding.

Similarly, we say that a correct decoding exponent $E^c\ge 0$ is achievable with fixed-rate Slepian-Wolf codes at rate R if for any $\delta >0$, there exists a sequence of fixed-rate Slepian-Wolf codes $\left\{{\varphi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R\left({\varphi }_n\right)\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \inf }-\frac{1}{n}\log P_c({\varphi }_n,P_{XY})\le E^c+\delta .\hfill \end{array}$$

The smallest achievable correct decoding exponent at rate R is denoted by $E_f^c(P_{XY},R)$. It will be seen that $E_f^c(P_{XY},R)$ is positive if and only if $R<H\left(X\right|Y)$. Therefore, we shall refer to the function $E_f^c(P_{XY},·)$ as the reliability function of fixed-rate Slepian-Wolf coding below the Slepian-Wolf limit.

The expurgated exponent, random coding scheme, and sphere packing exponent of fixed-rate Slepian-Wolf coding are defined as follows:

• expurgated exponent

  $$\begin{array}{c}\hfill E_{f,ex}(P_{XY},R)=\underset{Q_X}{\min }\left[D(Q_X\parallel P_X)+E_{ex}(Q_X,P_{Y|X},H\left(Q_X\right)-R)\right],\end{array}$$

  (18)
• random coding exponent

  $$\begin{array}{c}\hfill E_{f,rc}(P_{XY},R)=\underset{Q_X}{\min }\left[D(Q_X\parallel P_X)+E_{rc}(Q_X,P_{Y|X},H\left(Q_X\right)-R)\right],\end{array}$$

  (19)
• sphere packing exponent

  $$\begin{array}{c}\hfill E_{f,sp}(P_{XY},R)=\underset{Q_X}{\min }\left[D(Q_X\parallel P_X)+E_{sp}(Q_X,P_{Y|X},H\left(Q_X\right)-R)\right].\end{array}$$

  (20)

Equivalently, the random coding exponent and sphere packing exponent of fixed-rate Slepian-Wolf coding can be written as [11]:

$$\begin{array}{c}{E}_{f,rc}(P_{XY},R)=\underset{0\le \rho \le 1}{\max }\left\{-\log \sum _y{\left[\sum _x{P}_{XY}{(x,y)}^{\frac{1}{1+\rho }}\right]}^{1+\rho }+\rho R\right\},\hfill \\ E_{f,sp}(P_{XY},R)=\underset{\rho >0}{sup}\left\{-\log \sum _y{\left[\sum _x{P}_{XY}{(x,y)}^{\frac{1}{1+\rho }}\right]}^{1+\rho }+\rho R\right\}.\hfill \end{array}$$

To see the connection between the random coding exponent and the sphere packing exponent, we shall write them in the following parametric forms [11]:

$$\begin{array}{c}R=H(X^{\left(\rho \right)}|Y^{\left(\rho \right)}),\hfill \\ E_{f,sp}(P_{XY},R)=D(P_{X^{\left(\rho \right)}{Y}^{\left(\rho \right)}}\parallel P_{XY}),\hfill \end{array}$$

and

$$\begin{array}{c}\hfill E_{f,rc}(P_{XY},R)=\left\{\begin{array}{cc}D(P_{X^{\left(\rho \right)}{Y}^{(\rho })}\parallel P_{XY})\hfill & \mathrm{if} {\left.H\left(X\right|Y)\le R\le H\left(X_{\rho }\right|Y_{\rho })\right|}_{\rho =1},\hfill \\ -\log {\displaystyle \sum _y}{\left[{\displaystyle \sum _x}\sqrt{P_{XY}(x,y)}\right]}^2+R\hfill & \mathrm{if} R>{\left.H\left(X^{\left(\rho \right)}\right|Y^{\left(\rho \right)})\right|}_{\rho =1},\hfill \end{array}\right.\end{array}$$

where the joint distribution of $(X^{\left(\rho \right)},Y^{\left(\rho \right)})$ is $P_{X^{\left(\rho \right)}{Y}^{\left(\rho \right)}}$, which is specified by

$$\begin{array}{c}{P}_{Y^{\left(\rho \right)}}\left(y\right)=\frac{P_Y\left(y\right){\left[{\sum }_x{P}_{X|Y}{\left(x\right|y)}^{\frac{1}{1+\rho }}\right]}^{1+\rho }}{{\sum }_{y^{\prime }}{P}_Y\left(y^{\prime }\right){\left[{\sum }_x{P}_{X|Y}{\left(x\right|y^{\prime })}^{\frac{1}{1+\rho }}\right]}^{1+\rho }},y\in \mathcal{Y},\hfill \end{array}$$

(21)

$$\begin{array}{c}{P}_{X^{\left(\rho \right)}|Y^{\left(\rho \right)}}\left(x\right|y)=\frac{P_{X|Y}{\left(x\right|y)}^{\frac{1}{1+\rho }}}{{\sum }_{x^{\prime }}{P}_{X|Y}{\left(x^{\prime }\right|y)}^{\frac{1}{1+\rho }}},x\in \mathcal{X},y\in \mathcal{Y}.\hfill \end{array}$$

(22)

Define the critical rate

$$\begin{array}{c}\hfill R_{f,cr}\left(P_{XY}\right)={\left.H(X^{\left(\rho \right)}|Y^{\left(\rho \right)})\right|}_{\rho =1}.\end{array}$$

Note that $E_{rc}(P_{XY},R)$ and $E_{sp}(P_{XY},R)$ coincide when $R\in [H\left(X\right|Y),R_{f,cr}\left(P_{XY}\right)]$. Let $R_{f,sp}^{\infty }\left(P_{XY}\right)=\sup \{R:E_{f,sp}(P_{XY},R)<\infty \}$. It is shown in [12] that

$$\begin{array}{c}\hfill R_{f,sp}^{\infty }\left(P_{XY}\right)=\underset{y}{\max }\log \left|\{x\in \mathcal{X}:P_{X|Y}\left(x\right|y)>0\}\right|.\end{array}$$

It is well known [8,11,13] that the reliability function $E_f(P_{XY},·)$ is upper-bounded by $E_{f,sp}(P_{XY},·)$ and lower-bounded by $E_{f,rc}(P_{XY},·)$ and $E_{f,ex}(P_{XY},·)$, i.e.,

$$\begin{array}{c}\hfill \max \{E_{f,rc}(P_{XY},R),E_{f,ex}(P_{XY},R)\}\le E_f(P_{XY},R)\le E_{f,sp}(P_{XY},R)\end{array}$$

(23)

with the possible exception of $R=R_{f,sp}^{\infty }\left(P_{XY}\right)$ at which point the second inequality in (23) not necessarily holds. Note that $E_f(P_{XY},R)$ is completely characterized for $R\in [H\left(X\right|Y),R_{f,cr}\left(P_{XY}\right)]$.

Unlike $E_f(P_{XY},·)$, the function $E_f^c(P_{XY},·)$ has been characterized for all R. Specifically, it is shown in [6,14] that

$$\begin{array}{c}\hfill E_f^c(P_{XY},R)=\underset{Q_X}{\min }\left[D(Q_X\parallel P_X)+E^c(Q_X,P_{Y|X},H\left(Q_X\right)-R)\right].\end{array}$$

(24)

Comparing (14) with (18), (15) with (19), (16) with (20), and (13) with (24), one can easily see that there exists an intimate connection between fixed-rate Slepian-Wolf coding for source distribution $P_{XY}$ and channel coding for channel $P_{Y|X}$. This connection can be roughly interpreted as the manifestation of the following facts [15].

• Given, for each type $Q_X\in {\mathcal{P}}_n\left(\mathcal{X}\right)$, a constant composition code ${\mathcal{C}}_n\left(Q_X\right)\subseteq {\mathcal{T}}_n\left(Q_X\right)$ with $R\left({\mathcal{C}}_n\left(Q_X\right)\right)\approx H\left(Q_X\right)-R$ and $P_{e,\max }({\mathcal{C}}_n\left(Q_X\right),P_{Y|X})\approx e^{-nE\left(Q_X\right)}$, one can use ${\mathcal{C}}_n\left(Q_X\right)$ to partition type class ${\mathcal{T}}_n\left(Q_X\right)$ into approximately $e^{nR}$ disjoint subsets such that each subset is a constant composition code of type $Q_X$ with the maximum decoding error probability over channel $P_{Y|X}$ approximately equal to or less than that of ${\mathcal{C}}_n\left(Q_X\right)$. Note that these partitions, one for each type class, yield a fixed-rate Slepian-Wolf code of rate approximately R with $\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n\left(Q_X\right)\}⪅e^{-nE\left(Q_X\right)}$. Since $\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(Q_X\right)\}\approx e^{-nD(Q_X\parallel P_X)}$ (cf. (2) and (3)), it follows that $\mathrm{Pr}\{{\widehat{X}}^n\ne X^n,X^n\in {\mathcal{T}}_n\left(Q_X\right)\}⪅e^{-n[D(Q_X\parallel P_X)+E\left(Q_X\right)]}$. The overall decoding error probability $\mathrm{Pr}\{{\widehat{X}}^n\ne X^n\}$ of the resulting Slepian-Wolf code can be upper-bounded, on the exponential scale, by $e^{-n[D(Q_X^{*}\parallel P_X)+E\left(Q_X^{*}\right)]}$, where $Q_X^{*}=\arg {\min }_{Q_X}D(Q_X\parallel P_X)+E\left(Q_X\right)$. In contrast, one has the freedom to choose $Q_X$ in channel coding, which explains why maximization (instead of minimization) is used in (14)–(16).
• Given a fixed-rate Slepian-Wolf code ${\varphi }_n(·)$ with $R\left({\varphi }_n\right)\approx R$ and $P_e({\varphi }_n,P_{XY})\approx e^{-nE}$, one can, for each type $Q_X\in {\mathcal{P}}_n\left(\mathcal{X}\right)$, lift out a constant composition code ${\mathcal{C}}_n\left(Q_X\right)\subseteq {\mathcal{T}}_n\left(Q_X\right)$ with $R\left({\mathcal{C}}_n\left(Q_X\right)\right)⪆H\left(Q_X\right)-R$ and $P_e({\mathcal{C}}_n\left(Q_X\right),P_{Y|X})⪅e^{-n[E-D(Q_X\parallel P_X)]}$.
• The correct decoding exponents for channel coding and fixed-rate Slepian-Wolf coding can be interpreted in a similar way. Note that in channel coding, to maximize the correct decoding probability one has to minimize the correct decoding exponent; this is why in (13) minimization (instead of maximization) is used.

Therefore, it should be clear that to characterize the reliability functions for channel coding and fixed-rate Slepian-Wolf coding, it suffices to focus on constant composition codes. It will be shown in the next section that a similar reduction holds for variable-rate Slepian-Wolf coding. Indeed, the reliability function for constant component codes plays a predominant role in determining the fundamental rate-error tradeoff in variable-rate Slepian-Wolf coding.

3. Variable-Rate Slepian-Wolf Coding: Above the Slepian-Wolf Limit

A variable-rate Slepian-Wolf code ${\phi }_n(·)$ is a mapping from ${\mathcal{X}}^n$ to a binary prefix code ${\mathcal{B}}_n$. Let $l\left({\varphi }_n\left(x^n\right)\right)$ denote the length of binary string ${\varphi }_n\left(x^n\right)$. The rate of variable-rate Slepian-Wolf code ${\varphi }_n(·)$ is defined as

$$\begin{array}{c}\hfill R({\phi }_n,P_{XY})=\frac{1}{n{\log }_{2}e}\mathbb{E}\left[l\left({\phi }_n\left(X^n\right)\right)\right].\end{array}$$

It is worth noting that $R({\phi }_n,P_{XY})$ depends on $P_{XY}$ only through $P_X$.

Given ${\phi }_n\left(X^n\right)$ and $Y^n$, the output of the optimal maximum a posteriori (MAP) decoder is

$$\begin{array}{cc}\hfill {\widehat{X}}^n& =\arg \underset{x^n:{\phi }_n\left(x^n\right)={\phi }_n\left(X^n\right)}{\min }-\sum _{i=1}^n\log P_{X|Y}\left(x_i\right|Y_i)\hfill \\ & =\arg \underset{x^n:{\phi }_n\left(x^n\right)={\phi }_n\left(X^n\right)}{\min }-\sum _{i=1}^n\log P_{XY}(x_i,Y_i),\hfill \end{array}$$

where the ties are broken in an arbitrary manner. The decoding error probability of variable-rate Slepian-Wolf code ${\phi }_n(·)$ is defined as

$$\begin{array}{c}\hfill P_e({\phi }_n,P_{XY})=\mathrm{Pr}\{{\widehat{X}}^n\ne X^n\}.\end{array}$$

The correct decoding probability of Slepian-Wolf code ${\phi }_n(·)$ is defined as

$$\begin{array}{c}\hfill P_c({\varphi }_n,P_{XY})=1-P_e({\phi }_n,P_{XY}).\end{array}$$

Definition 4.

Given a joint probability distribution $P_{XY}$, we say that an error exponent $E\ge 0$ is achievable with variable-rate Slepian-Wolf codes at rate R if for any $\delta >0$, there exists a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_e({\phi }_n,P_{XY})\ge E-\delta .\hfill \end{array}$$

The largest achievable error exponent at rate R is denoted by $E_v(P_{XY},R)$. The function $E_v(P_{XY},·)$ is referred to as the reliability function of variable-rate Slepian-Wolf coding.

The power of variable-rate Slepian-Wolf coding results from its flexibility in rate allocation. Since there are only polynomial number of types for any given n (cf. (1)), the encoder can convey the type information to the decoder using negligible amount of rate when n is large enough. Therefore, without loss of much generality, we can assume that the type of $X^n$ is known to the decoder. Under this assumption, an optimal fixed-rate Slepian-Wolf encoder of rate R should partition ${\mathcal{T}}_n\left(P\right)$ into $\min \left\{\right|{\mathcal{T}}_n\left(P\right)|,e^{nR}\}$ disjoint subsets for each $P\in {\mathcal{P}}_n$. It can be seen that the rate allocated to ${\mathcal{T}}_n\left(P\right)$ is always R if $|{\mathcal{T}}_n\left(P\right)|\ge e^{nR}$. In general, the type $Q_X^{*}$ that dominates the error probability of fixed-rate Slepian-Wolf coding is different from $P_X$. In contrast, for variable-rate Slepian-Wolf coding, we can losslessly compress the sequences of types that are bounded away $P_X$ by allocating enough rate to those type classes (but its contribution to the overall rate is still negligible since the probability of those type classes are extremely small), and therefore, effectively eliminate the dominant error event in fixed-rate Slepian-Wolf coding. As a consequence, the types that can cause decoding error in variable-rate Slepian-Wolf coding must be very close to $P_X$. This is the main intuition underlying the proof of the following theorem. A similar argument has been used in the context of variable-rate Slepian-Wolf coding under mismatched decoding [16].

Theorem 1.

$E_v(P_{XY},R)=E(P_X,P_{Y|X},H\left(P_X\right)-R)$.

Proof. 

The proof is divided into two parts. Firstly, we shall show that $E_v(P_{XY},R)\ge E(P_X,P_{Y|X},H\left(P_X\right)-R)$. The main idea is that one can use a constant composition code ${\mathcal{C}}_n$ of type approximately $P_X$ and rate approximately $H\left(P_X\right)-R$ to construct a variable-rate Slepian-Wolf code ${\phi }_{n^{\prime }}(·)$ with $n^{\prime }\approx n$, $R({\phi }_{n^{\prime }},P_{XY})\approx R$, and $P_e({\phi }_{n^{\prime }},P_{XY})\le P_{e,\max }({\mathcal{C}}_n,P_{Y|X})$.

By Definition 2, for any $\delta >0$, there exists a sequence of constant composition codes $\left\{{\mathcal{C}}_n\right\}$ with ${\mathcal{C}}_n\subseteq {\mathcal{T}}_n\left(P_n\right)$ for some $P_n\in {\mathcal{P}}_n\left(\mathcal{X}\right)$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim }\parallel P_n-P_X\parallel =0,\hfill \\ \underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_n\right)\ge H\left(P_X\right)-R-\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_{e,\max }({\mathcal{C}}_n,P_{Y|X})\ge E(P_X,P_{Y|X},H\left(P_X\right)-R)-\delta .\hfill \end{array}$$

Since $P_X\left(x\right)>0$ for all $x\in \mathcal{X}$, we have

$$\begin{array}{c}\hfill \underset{P\in {\mathcal{P}}_n\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}{\max }\underset{x}{\max }\frac{P_n\left(x\right)}{P\left(x\right)}\le {(1+\delta )}^2\end{array}$$

for all sufficiently n, where

$$\begin{array}{c}\hfill \mathcal{E}\left(\delta \right)=\left\{P\in \mathcal{P}\left(\mathcal{X}\right):\underset{x}{\max }\frac{P_X\left(x\right)}{P\left(x\right)}\le 1+\delta ,H\left(P\right)\le H\left(P_X\right)+\delta ,D(P\parallel P_X)\le \delta \right\}.\end{array}$$

Let $k_n=\lceil {(1+\delta )}^{2}n\rceil$. When n is large enough, we can, for each $P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)$, construct a constant composition code ${\mathcal{C}}_{k_n}^{\prime }\left(P\right)$ of length $k_n$ and type P by appending a fixed sequence in ${\mathcal{X}}^{k_n-n}$ to each codeword in ${\mathcal{C}}_n$. It is easy to see that

$$\begin{array}{c}|{\mathcal{C}}_{k_n}^{\prime }\left(P\right)|=|{\mathcal{C}}_n|,\hfill \end{array}$$

(25)

$$\begin{array}{c}{P}_{e,\max }({\mathcal{C}}_{k_n}^{\prime }\left(P\right),P_{Y|X})=P_{e,\max }({\mathcal{C}}_n,P_{Y|X})\hfill \end{array}$$

(26)

for all $P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)$. One can readily show by invoking the covering lemma in [17] that for each $P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)$, there exist $L\left(k_n\right)$ permutations ${\pi }_1,\cdots ,{\pi }_{L\left(k_n\right)}$ of the integers $1,\cdots ,k_n$ such that

$$\begin{array}{c}\hfill \bigcup _{i=1}^{L\left(k_n\right)}{\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right))={\mathcal{T}}_{k_n}\left(P\right),\end{array}$$

where

$$\begin{array}{c}\hfill L\left(k_n\right)\triangleq \underset{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}{\max }⌊|{\mathcal{C}}_{k_n}^{\prime }{\left(P\right)|}^{-1}|{\mathcal{T}}_{k_n}\left(P\right)\left|\log \right|{\mathcal{T}}_{k_n}\left(P\right)|+1⌋.\end{array}$$

In view of (25), we can rewrite $L\left(k_n\right)$ as

$$\begin{array}{c}\hfill L\left(k_n\right)=\underset{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}{\max }⌊|{\mathcal{C}}_n{|}^{-1}|{\mathcal{T}}_{k_n}\left(P\right)\left|\log \right|{\mathcal{T}}_{k_n}\left(P\right)|+1⌋.\end{array}$$

Note that

$$\begin{array}{c}\hfill P_{e,\max }({\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),P_{Y|X})=P_{e,\max }({\mathcal{C}}_{k_n}^{\prime }\left(P\right),P_{Y|X}),i=1,2,\cdots ,L\left(k_n\right).\end{array}$$

(27)

Given ${\pi }_1({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),\cdots ,{\pi }_{L\left(k_n\right)}({\mathcal{C}}_{k_n}^{\prime }\left(P\right))$, we can partition ${\mathcal{T}}_{k_n}\left(P\right)$ into $L\left(k_n\right)$ disjoint subsets:

$$\begin{array}{c}{\mathcal{T}}_{k_n}(P,1)={\pi }_1({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),\hfill \\ {\mathcal{T}}_{k_n}(P,i)={\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right))∖\bigcup _{j=1}^{i-1}{\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),i=2,\cdots ,L\left(k_n\right).\hfill \end{array}$$

It is clear that

$$\begin{array}{c}\hfill P_{e,\max }({\mathcal{T}}_{k_n}(P,i),P_{Y|X})\le P_{e,\max }({\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),P_{Y|X}),i=1,2,\cdots ,L\left(k_n\right).\end{array}$$

(28)

Now construct a sequence of variable-rate Slepian-Wolf codes $\left\{{\varphi }_{k_n}(·)\right\}$ as follows.

• The encoder sends the type of $x^{k_n}$ to the decoder, where each type is uniquely represented by a binary sequence of length $m_1\left(k_n\right)$.
• If $x^{k_n}\in {\mathcal{T}}_{k_n}\left(P\right)$ for some $P\notin \mathcal{E}\left(\delta \right)$, the encoder sends $x^{k_n}$ losslessly to the decoder, where each $x^{k_n}\in {\mathcal{T}}_{k_n}\left(P\right)$ is uniquely represented by a binary sequence of length $m_2\left(k_n\right)$.
• If $x^{k_n}\in {\mathcal{T}}_{k_n}\left(P\right)$ for some $P\in \mathcal{E}\left(\delta \right)$, the encoder finds the set ${\pi }_{i^{*}}({\mathcal{C}}_{k_n}^{\prime }\left(P\right))$ that contains $x^{k_n}$ and sends the index $i^{*}$ to the decoder, where each index in $\{1,2,\cdots ,L\left(k_n\right)\}$ is uniquely represented by a binary sequence of length $m_3\left(k_n\right)$.

Specifically, we choose

$$\begin{array}{c}{m}_1\left(k_n\right)=\lceil {\log }_2|{\mathcal{P}}_{k_n}\left(\mathcal{X}\right)|\rceil ,\hfill \\ m_2\left(k_n\right)=\underset{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)}{\max }\lceil {\log }_2|{\mathcal{T}}_{k_n}\left(P\right)|\rceil ,\hfill \\ m_3\left(k_n\right)=\lceil {\log }_{2}L\left(k_n\right)\rceil .\hfill \end{array}$$

Note that

$$\begin{array}{c}\hfill R({\phi }_{k_n},P_{XY})=\frac{m_1\left(k_n\right)+(1-\theta )m_2\left(k_n\right)+\theta m_3\left(k_n\right)}{k_n{\log }_{2}e},\end{array}$$

where

$$\begin{array}{c}\hfill \theta =\sum _{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}\mathrm{Pr}\{X^{k_n}\in {\mathcal{T}}_{k_n}\left(P\right)\}.\end{array}$$

It is easy to verify (cf. (1)–(3)) that

$$\begin{array}{c}{m}_1\left(k_n\right)\le \left|\mathcal{X}\right|{\log }_2(k_n+1)+1,\hfill \\ m_2\left(k_n\right)\le k_n{\log }_2\left|\mathcal{X}\right|+1,\hfill \\ 1-\theta \le {(k_n+1)}^{\left|\mathcal{X}\right|}{e}^{-k_n\delta }.\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim \sup }R({\varphi }_{k_n},P_{XY})& =\underset{n\to \infty }{\lim \sup }\frac{m_3\left(k_n\right)}{k_n{\log }_{2}e}\hfill \\ & \le \underset{P\in \mathcal{E}\left(\delta \right)}{\max }H\left(P\right)-\frac{1}{{(1+\delta )}^2}\underset{n\to \infty }{lim\; inf}R\left({\mathcal{C}}_n\right)\hfill \\ & \le H\left(P_X\right)+\delta -\frac{H\left(P_X\right)-R-\delta }{{(1+\delta )}^2}.\hfill \end{array}$$

(29)

By (26)–(28) and the construction of ${\phi }_{k_n}(·)$, it is clear that

$$\begin{array}{cc}\hfill P_e({\phi }_{k_n},P_{XY})& =\sum _{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}\sum _{i=1}^{L\left(k_n\right)}\mathrm{Pr}\{X^{k_n}\in {\mathcal{T}}_{k_n}(P,i)\}\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^{k_n}\in {\mathcal{T}}_{k_n}(P,i)\}\hfill \\ & \le \sum _{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}\sum _{i=1}^{L\left(k_n\right)}\mathrm{Pr}\{X^{k_n}\in {\mathcal{T}}_{k_n}(P,i)\}{P}_{e,\max }({\mathcal{T}}_{k_n}(P,i),P_{Y|X})\hfill \\ & \le \sum _{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}\sum _{i=1}^{L\left(k_n\right)}\mathrm{Pr}\{X^{k_n}\in {\mathcal{T}}_{k_n}(P,i)\}{P}_{e,\max }({\pi }_i({\mathcal{C}}_{k_n}^{\prime }\left(P\right)),P_{Y|X})\hfill \\ & =\sum _{P\in {\mathcal{P}}_{k_n}\left(\mathcal{X}\right)\cap \mathcal{E}\left(\delta \right)}\sum _{i=1}^{L\left(k_n\right)}\mathrm{Pr}\{X^{k_n}\in {\mathcal{T}}_{k_n}(P,i)\}{P}_{e,\max }({\mathcal{C}}_n,P_{Y|X})\hfill \\ & \le P_{e,\max }({\mathcal{C}}_n,P_{Y|X}),\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim \sup }-\frac{1}{k_n}\log P_e({\phi }_{k_n},P_{XY})& \ge \underset{n\to \infty }{\lim \sup }-\frac{1}{k_n}\log P_{e,\max }({\mathcal{C}}_n,P_{Y|X})\hfill \\ & \ge \frac{E(P_X,P_{Y|X},H\left(P_X\right)-R)-\delta }{{(1+\delta )}^2}.\hfill \end{array}$$

(30)

In view of (29), (30), and the fact that $\delta >0$ is arbitrary, we must have $E_v(P_{XY},R)\ge E(P_X,P_{Y|X},H\left(P_X\right)-R)$ (cf. Definition 4).

Now we proceed to show that $E_v(P_{XY},R)\le E(P_X,P_{Y|X},H\left(P_X\right)-R)$. The main idea is that one can extract a constant composition code of type approximately $P_X$ and rate approximately $H\left(X\right)-R$ or greater from a given variable-rate Slepian-Wolf code ${\phi }_n(·)$ of rate approximately R such that the average decoding error probability of this constant composition code over channel $P_{Y|X}$ is bounded from above by $\gamma P_e({\phi }_n,P_{XY})$, where $\gamma$ is a constant that does not depend on n.

By Definition 4, for any $\delta >0$, there exists a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})\le R+\delta ,\hfill \end{array}$$

(31)

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup }-\frac{1}{n}\log P_e({\phi }_n,P_{XY})\ge E_v(P_{XY},R)-\delta .\hfill \end{array}$$

(32)

Suppose ${\phi }_n(·)$ induces a partition of ${\mathcal{T}}_n\left(P\right)$, $P\in {\mathcal{P}}_n\left(\mathcal{X}\right)$, into $N_n\left(P\right)$ disjoint subsets ${\mathcal{T}}_n(P,1),\cdots ,{\mathcal{T}}_n(P,N_n\left(P\right))$. Here the partition is defined as follows: ${\phi }_n\left(x^n\right)={\phi }_n\left({\tilde{x}}^n\right)$ if $x^n,{\tilde{x}}^n\in {\mathcal{T}}_n(P,i)$ for some i, and ${\phi }_n\left(x^n\right)\ne {\phi }_n\left({\tilde{x}}^n\right)$ if $x^n\in {\mathcal{T}}_n(P,i),{\tilde{x}}^n\in {\mathcal{T}}_n(P,j)$ for $i\ne j$. Let

$$\begin{array}{c}\hfill r\left({\mathcal{T}}_n\left(P\right)\right)=\frac{1}{n{\log }_{2}e}\mathbb{E}\left[l\left({\phi }_n\left(X^n\right)\right)\right|X^n\in {\mathcal{T}}_n\left(P\right)],P\in {\mathcal{P}}_n\left(\mathcal{X}\right).\end{array}$$

It follows from the source coding theorem that

$$\begin{array}{cc}\hfill r\left({\mathcal{T}}_n\left(P\right)\right)& \ge \frac{1}{n}\sum _{i=1}^{N_n\left(P\right)}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}.\hfill \end{array}$$

(33)

Define

$$\begin{array}{c}{\mathcal{F}}_n\left(\delta \right)=\left\{(P,i):\frac{1}{n}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\le R+2\delta ,P\in {\mathcal{P}}_n\left(\mathcal{X}\right),i=1,2,\cdots ,N_n\left(P\right)\right\},\hfill \\ {\mathcal{F}}_n^c\left(\delta \right)=\left\{(P,i)\notin {\mathcal{F}}_n\left(\delta \right):P\in {\mathcal{P}}_n\left(\mathcal{X}\right),i=1,2,\cdots ,N_n\left(P\right)\right\},\hfill \\ {\mathcal{G}}_n\left(\gamma \right)=\left\{(P,i):\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n(P,i)\}\le \gamma P_e({\phi }_n,P_{XY}),P\in {\mathcal{P}}_n\left(\mathcal{X}\right),i=1,2,\cdots ,N_n\left(P\right)\right\},\hfill \\ {\mathcal{G}}_n^c\left(\gamma \right)=\left\{(P,i)\notin {\mathcal{G}}_n\left(\gamma \right):P\in {\mathcal{P}}_n\left(\mathcal{X}\right),i=1,2,\cdots ,N_n\left(P\right)\right\},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill \gamma >\frac{R+2\delta }{\delta }.\end{array}$$

(34)

Note that

$$\begin{array}{cc}\hfill R({\phi }_n,P_{XY})& =\sum _{P\in {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}r\left({\mathcal{T}}_n\left(P\right)\right)\hfill \\ \left(35\right)& & \ge \frac{1}{n}\sum _{P\in {\mathcal{P}}_n\left(\mathcal{X}\right)}\sum _{i=1}^{N_n\left(P\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\hfill & \ge \frac{1}{n}\sum _{(P,i)\in {\mathcal{F}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\hfill \\ \left(36\right)& & \ge (R+2\delta )\sum _{(P,i)\in {\mathcal{F}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\},\hfill \end{array}$$

where (35) is due to (33). Combing (31) and (36) yields

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim \sup }\sum _{(P,i)\in {\mathcal{F}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\le \frac{R+\delta }{R+2\delta }.\end{array}$$

(37)

Moreover, we have

$$\begin{array}{c}\hfill \sum _{(P,i)\in {\mathcal{G}}_n^c\left(\gamma \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\le \frac{1}{\gamma }\end{array}$$

(38)

since otherwise

$$\begin{array}{cc}\hfill P_e({\phi }_n,P_{XY})& =\sum _{P\in {\mathcal{P}}_n\left(\mathcal{X}\right)}\sum _{i=1}^{N_n\left(P\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n(P,i)\}\hfill \\ & \ge \sum _{(P,i)\in {\mathcal{G}}_n^c\left(\gamma \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n(P,i)\}\hfill \\ & >\gamma P_e({\phi }_n,P_{XY})\sum _{(P,i)\in {\mathcal{G}}_n^c\left(\gamma \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\hfill \\ & \ge P_e({\phi }_n,P_{XY}),\hfill \end{array}$$

which is absurd.

Define

$$\begin{array}{c}{\mathcal{S}}_n\left(\delta \right)=\left\{P\in {\mathcal{P}}_n\left(\mathcal{X}\right):H\left(P\right)\ge H\left(P_X\right)-\delta ,\underset{x}{\max }\frac{P\left(x\right)}{P_X\left(x\right)}\le 1+\delta \right\},\hfill \\ {\mathcal{S}}_n^c\left(\delta \right)={\mathcal{P}}_n\left(\mathcal{X}\right)\setminus {\mathcal{S}}_n\left(\delta \right),\hfill \\ {\mathcal{D}}_n(\delta ,\gamma )=\left\{(P,i):(P,i)\in {\mathcal{F}}_n\left(\delta \right)\cap {\mathcal{G}}_n\left(\gamma \right),P\in {\mathcal{S}}_n\left(\delta \right)\right\},\hfill \\ {\mathcal{D}}_n^c(\delta ,\gamma )=\left\{(P,i)\notin {\mathcal{D}}_n(\delta ,\gamma ):P\in {\mathcal{P}}_n\left(\mathcal{X}\right),i=1,2,\cdots ,N_n\left(P\right)\right\}.\hfill \end{array}$$

It follows from the weak law of large numbers that

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\sum _{P\in {\mathcal{S}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}=0.\end{array}$$

(39)

We have

$$\begin{array}{c}\underset{n\to \infty }{\lim \inf }\sum _{(P,i)\in {\mathcal{D}}_n(\delta ,\gamma )}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\hfill \\ =\underset{n\to \infty }{\lim \inf }\left\{1-\sum _{(P,i)\in {\mathcal{D}}_n^c(\delta ,\gamma )}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\right\}\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\left\{1-\sum _{(P,i)\in {\mathcal{F}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}-\sum _{(P,i)\in {\mathcal{G}}_n^c\left(\gamma \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n(P,i)\}\right.\hfill \\ \left.-\sum _{P\in {\mathcal{S}}_n^c\left(\delta \right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\right\}\hfill \\ \left(40\right)& \ge 1-\frac{R+\delta }{R+2\delta }-\frac{1}{\gamma }\hfill \left(41\right)& >0,\hfill \end{array}$$

where (40) is due to (37)–(39), and (41) is due to (34). Therefore, ${\mathcal{D}}_n(\delta ,\gamma )$ is non-empty for all sufficiently large n. Pick an arbitrary $(P_n^{*},i^{*})$ from ${\mathcal{D}}_n(\delta ,\gamma )$ for each sufficiently large n. We can construct a constant composition code ${\mathcal{C}}_{m_n}$ of length $m_n=\lceil (1+\delta )n\rceil$ and type $P_{m_n}$ for some $P_{m_n}\in {\mathcal{P}}_{m_n}\left(\mathcal{X}\right)$ by concatenating a fixed sequence in ${\mathcal{X}}^{m_n-n}$ to each sequence in ${\mathcal{T}}_n(P_n^{*},i^{*})$ such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\parallel P_{m_n}-P_X\parallel =0.\end{array}$$

(42)

Note that

$$\begin{array}{cc}\underset{n\to \infty }{\lim \inf } R\left({\mathcal{C}}_{m_n}\right)\hfill & =\underset{n\to \infty }{\lim \inf }\frac{1}{m_n}\log \left|{\mathcal{T}}_n(P_n^{*},i^{*})\right|\hfill \\ & \ge \underset{n\to \infty }{\lim \inf }\frac{n}{m_n}\left[\frac{1}{n}\log \left|{\mathcal{T}}_n\left(P_n^{*}\right)\right|-R-2\delta \right]\hfill \\ & \ge \frac{H\left(P_X\right)-R-3\delta }{1+\delta }.\hfill \end{array}$$

(43)

Moreover, since

$$\begin{array}{c}\hfill P_e({\mathcal{C}}_{m_n},P_{Y|X})=\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n(P_n^{*},i^{*})\}\le \gamma P_e({\phi }_n,P_{XY}),\end{array}$$

it follows from (32) that

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim \sup }-\frac{1}{m_n}\log P_e({\mathcal{C}}_{m_n},P_{Y|X})\ge \frac{E_v(P_{XY},R)-\delta }{1+\delta }.\end{array}$$

(44)

In view of (42)–(44) and the fact that $\delta >0$ is arbitrary, we must have $E_v(P_{XY},R)\le E(P_X,P_{Y|X},H\left(P_X\right)-R)$ (cf. Definition 2). The proof is complete. ☐

The following result is an immediate consequence of Theorem 1 and Proposition 4.

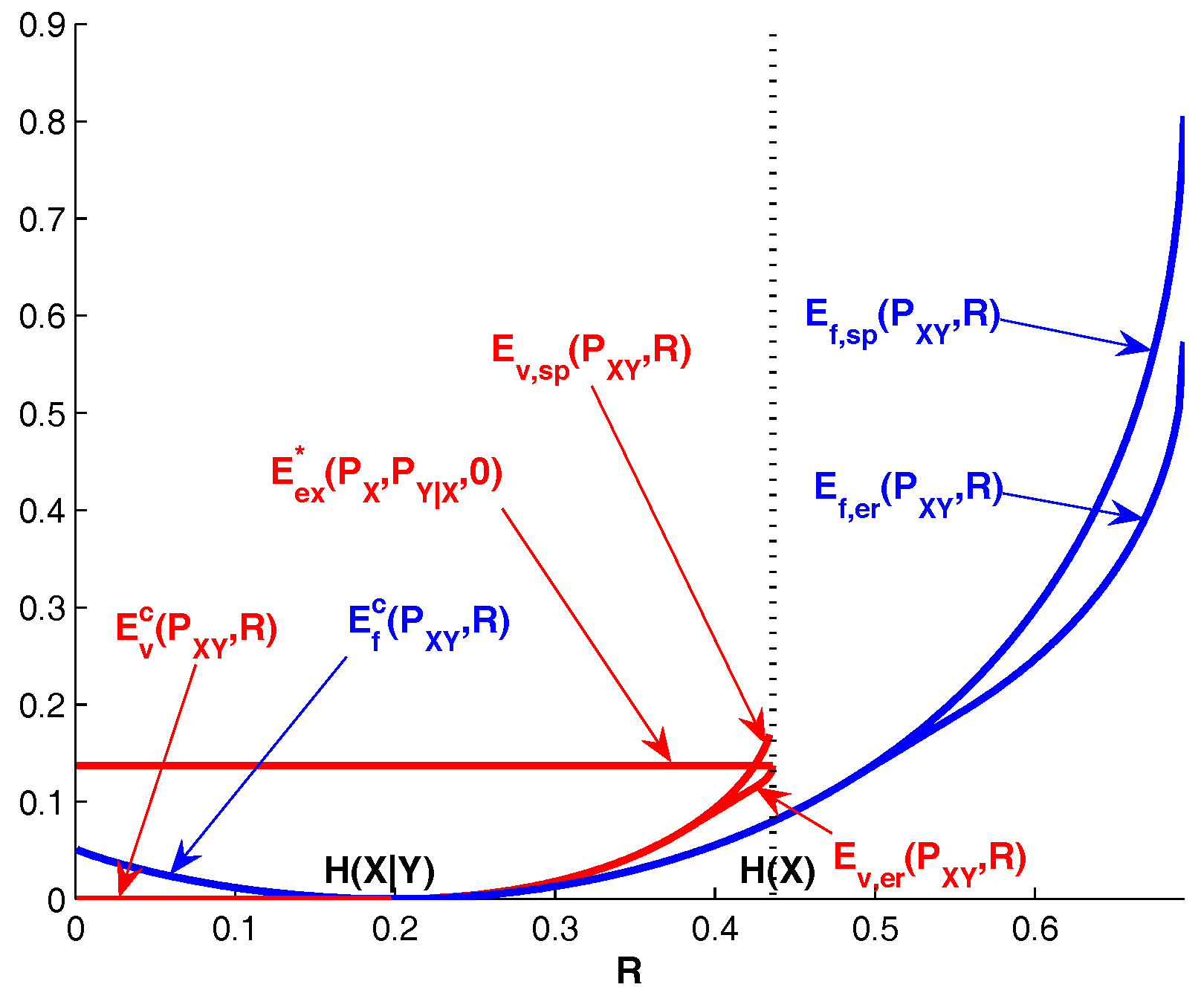
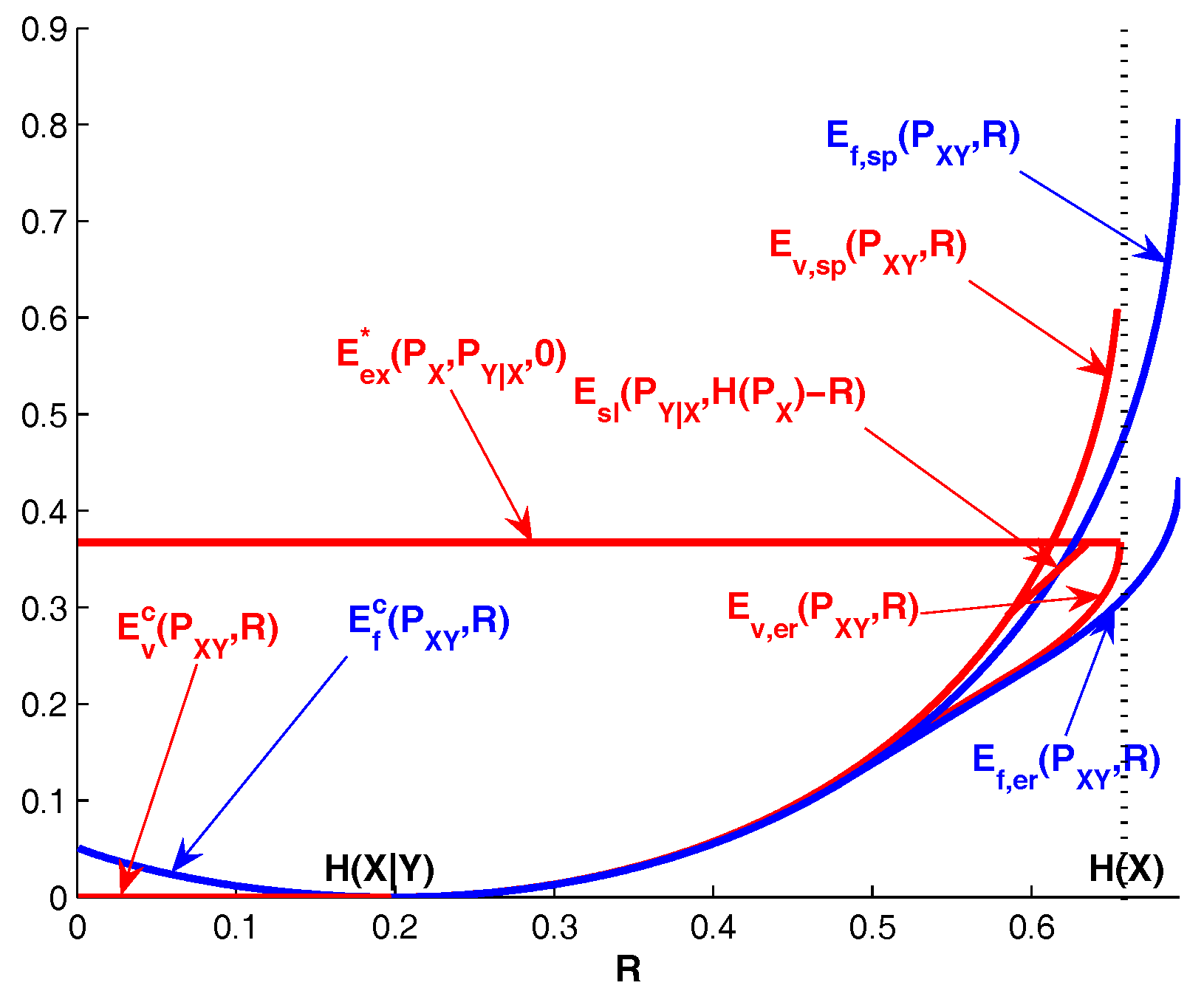
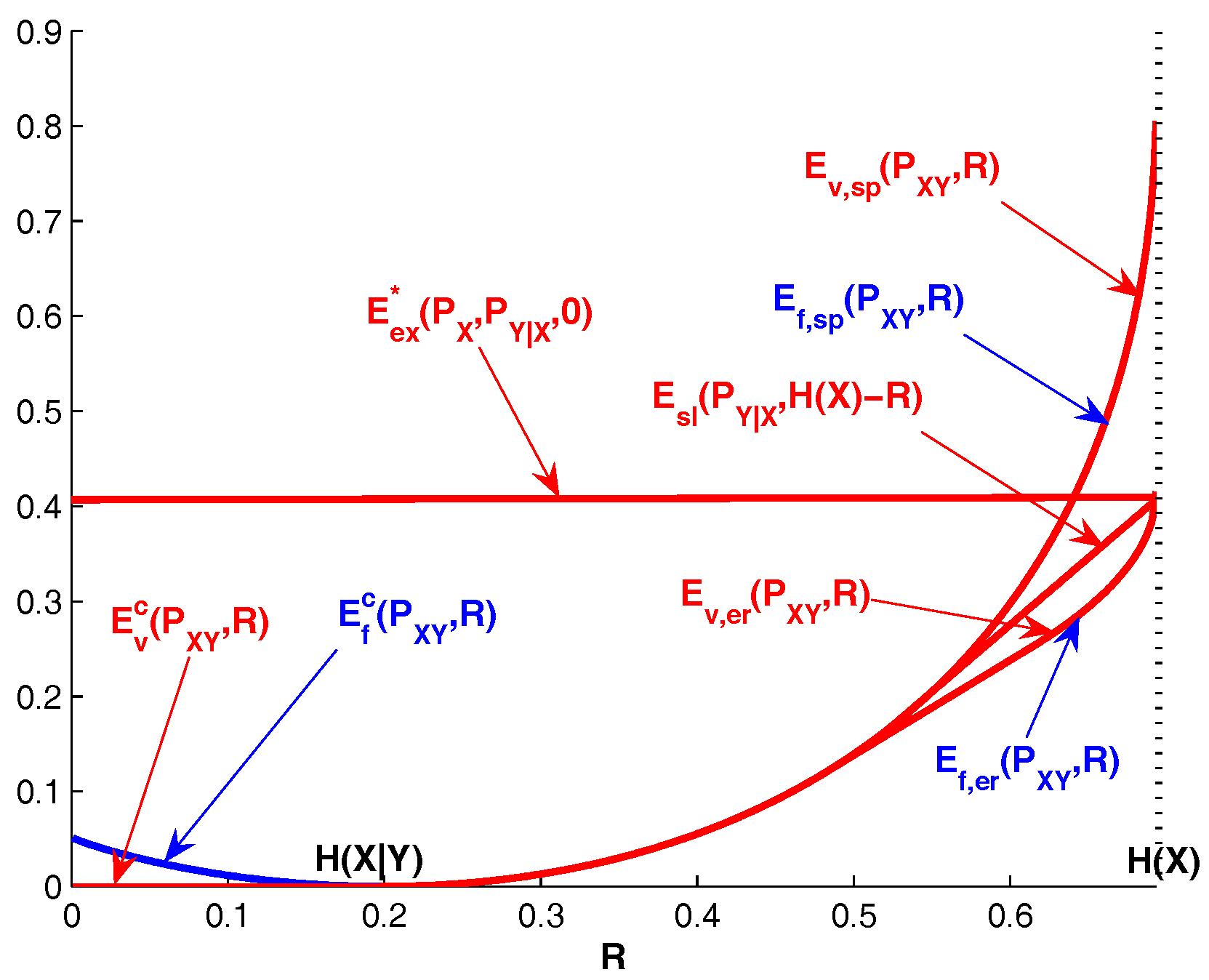
Corollary 1.

Define

$$\begin{array}{c}{E}_{v,ex}(P_{XY},R)=E_{ex}(P_X,P_{Y|X},H\left(P_X\right)-R),\hfill \\ E_{v,rc}(P_{XY},R)=E_{rc}(P_X,P_{Y|X},H\left(P_X\right)-R),\hfill \\ E_{v,sp}(P_{XY},R)=E_{sp}(P_X,P_{Y|X},H\left(P_X\right)-R).\hfill \end{array}$$

We have

• $E_v(P_{XY},R)\ge \max \{E_{v,ex}(P_{XY},R),E_{v,rc}(P_{XY},R)\}$;
• $E_v(P_{XY},R)\le E_{v,sp}(P_{XY},R)$ with the possible exception of $R=H\left(P_X\right)-R_{sp}^{\infty }(P_X,P_{Y|X})$ at which point the inequality not necessarily holds.

Remark 5.

• We have $E_v(P_{XY},R)=\infty$ for $R>H\left(P_X\right)-R_{ex}^{\infty }(P_X,P_{Y|X})$, and $E_v(P_{XY},R)<\infty$ for $R<H\left(P_X\right)-R_{sp}^{\infty }(P_X,P_{Y|X})$. Therefore, $H\left(P_X\right)-R_{ex}^{\infty }(P_X,P_{Y|X})$ and $H\left(P_X\right)-R_{sp}^{\infty }(P_X,P_{Y|X})$ are respectively the upper bound and the lower bound on the zero-error rate of variable-rate Slepian-Wolf coding.
• In view of (11), we have

  $$\begin{array}{c}\hfill E_v(P_{XY},R)=E_{v,sp}(P_{XY},R)=E_{sp}(P_X,P_{Y|X},H\left(P_X\right)-R)\end{array}$$

  for $R\in [H\left(X\right|Y),H\left(P_X\right)-R_{cr}(P_X,P_{Y|X})]$. Note that

  $$\begin{array}{c}\hfill E_{v,sp}(P_{XY},R)\ge E_{f,sp}(P_{XY},R)\ge E_f(P_{XY},R),\end{array}$$

  where the first inequality is strict unless the minimum in (20) is achieved at $Q_X=P_X$, (i.e., $P_{X^{\left(\rho \right)}}=P_X$, where $P_{X^{\left(\rho \right)}}$ is the marginal distribution of $X^{\left(\rho \right)}$ induced by $P_{Y^{\left(\rho \right)}}$ and $P_{X^{\left(\rho \right)}|Y^{\left(\rho \right)}}$ in (21) and (22)). Therefore, variable-rate Slepian-Wolf coding can outperform fixed-rate Slepian-Wolf coding in terms of rate-error tradeoff.

For $R>H\left(P_X\right)-R_{cr}(P_X,P_{Y|X})$, it is possible to obtain upper bounds on $E_v(P_{XY},R)$ that are tighter than $E_{v,sp}(P_{XY},R)$. Let $E_{ex}(P_{Y|X},R)$ and $E_{sp}(P_{Y|X},R)$ be respectively the expurgated exponent and the sphere packing exponent of channel $P_{Y|X}$. The straight-line exponent $E_{sl}(P_{Y|X},R)$ of channel $P_{Y|X}$ [10] is the smallest linear function of R which touches the curve $E_{sp}(P_{Y|X},R)$ and also satisfies

$$\begin{array}{c}\hfill E_{sl}(P_{Y|X},0)=E_{ex}(P_{Y|X},0),\end{array}$$

where $E_{ex}(P_{Y|X},0)$ is assumed to be finite. Let $R_{sl}\left(P_{Y|X}\right)$ be the point at which $E_{sl}(P_{Y|X},R)$ and $E_{sp}(P_{Y|X},R)$ coincide. It is well known [10] that $E(P_{Y|X},R)\le E_{sl}(P_{Y|X},R)$ for $R\in (0,R_{sl}\left(P_{Y|X}\right)]$. Since $E(P_X,P_{Y|X},R)\le E(P_{Y|X},R)$, it follows from Theorem 1 that

$$\begin{array}{c}\hfill E_v(P_{XY},R)\le E_{sl}(P_{Y|X},H\left(P_X\right)-R)\end{array}$$

for $R\in [\max \{H\left(P_X\right)-R_{sl}\left(P_{Y|X}\right),0\},H\left(P_X\right))$.

Note that the straight-line exponent holds for arbitrary block codes; one can obtain further improvement at high rates by leveraging bounds tailored to constant composition codes. Let $E_{ex}^{*}(Q_X,P_{Y|X},0)$ be the concave upper envelope of $E_{ex}(Q_X,P_{Y|X},0)$ considered as a function of $Q_X$. In view of ([7], Exercise 5.21), we have

$$\begin{array}{c}\hfill E(Q_X,P_{Y|X},R)\le E_{ex}^{*}(Q_X,P_{Y|X},0)\end{array}$$

for any $Q_X\in \mathcal{P}\left(\mathcal{X}\right)$ and $R>0$. Now it follows from Theorem 1 that

$$\begin{array}{c}\hfill E_v(P_{XY},R)\le E_{ex}^{*}(P_X,P_{Y|X},0)\end{array}$$

for $R<H\left(P_X\right)$.

The following theorem provides the second order expansion of $E_v(P_{XY},R)$ at the Slepian-Wolf limit.

Theorem 2.

Assuming $R_{cr}(P_X,P_{X|Y})<I(P_X,P_{Y|X})$ (see Proposition 1 for the necessary and sufficient condition), we have

$$\begin{array}{c}\hfill \underset{r\downarrow 0}{\lim }\frac{E_v(P_{XY},H\left(X\right|Y)+r)}{r^2}=\frac{1}{2}{\left[\sum _{x,y}{P}_{XY}(x,y){\tau }^2(x,y)-\sum _x{P}_X\left(x\right){\left(\sum _y\tau (x,y)P_{Y|X}\left(y\right|x)\right)}^2\right]}^{-1},\end{array}$$

where $\tau (x,y)=\log P_Y\left(y\right)-\log P_{Y|X}\left(y\right|x)$.

Remark 6.

If $R_{cr}(P_X,P_{Y|X})=I(P_X,P_{Y|X})$, then we have $E_{v,rc}(P_{XY},R)=R-H\left(X\right|Y)$ for $R\ge H\left(X\right|Y)$, which implies

$$\begin{array}{c}\hfill \underset{r\downarrow 0}{\lim }\frac{E_v(P_{XY},H\left(X\right|Y)+r)}{r^2}=\infty .\end{array}$$

It is also worth noting that the second order expansion of $E_v(P_{XY},R)$ at the Slepian-Wolf limit yields the redundancy-error tradeoff constant of variable-rate Slepian-Wolf coding derived in [18].

Proof. 

Since $R_{cr}(P_X,P_{X|Y})<I(P_X;P_{Y|X})$, it follows that $H\left(X\right|Y)+r\in (H\left(X\right|Y),H\left(P_X\right)-R_{cr}(P_X,P_{Y|X}))$ when r $(r>0)$ is sufficiently close to zero. In this case, we have

$$\begin{array}{cc}\hfill \frac{E_v(P_{XY},H\left(X\right|Y)+r)}{r^2}& =\frac{E_{sp}(P_X,P_{Y|X},I(P_X,P_{Y|X})-r)}{r^2}\hfill \\ & =\underset{Q_{Y|X}:I(P_X,Q_{Y|X})\le I(P_X,P_{Y|X})-r}{\min }\frac{D(Q_{Y|X}\parallel P_{Y|X}|P_X)}{r^2}\hfill \\ & =\underset{Q_{Y|X}:I(P_X,Q_{Y|X})=I(P_X,P_{Y|X})-r}{\min }\frac{D(Q_{Y|X}\parallel P_{Y|X}|P_X)}{r^2},\hfill \end{array}$$

where the last equality follows from the fact that $E_{sp}(P_X,P_{Y|X},R)$ is a strictly decreasing convex function of R for $R\in (R_{sp}^{\infty }(P_X,P_{Y|X}),I(P_X,P_{Y|X})]$.

Let $\Delta (x,y)=Q_{Y|X}\left(y\right|x)-P_{Y|X}\left(y\right|x)$ for $x\in \mathcal{X}$, $y\in \mathcal{Y}$. Let $\Delta \left(y\right)={\sum }_x{P}_X\left(x\right)\Delta (x,y)$ for $y\in \mathcal{Y}$. By the Taylor expansion,

$$\begin{array}{cc}\hfill I(P_X,Q_{Y|X})& =\sum _{x,y}{P}_X\left(x\right)(P_{Y|X}\left(y\right|x)+\Delta (x,y))\log (P_{Y|X}\left(y\right|x)+\Delta (x,y))\hfill \\ & -\sum _y(P_Y\left(y\right)+\Delta \left(y\right))\log (P_Y\left(y\right)+\Delta \left(y\right))\hfill \\ & =\sum _{x,y}{P}_X\left(x\right)(P_{Y|X}\left(y\right|x)+\Delta (x,y))\left(\log P_{Y|X}\left(y\right|x)+\frac{\Delta (x,y)}{P_{Y|X}\left(y\right|x)}+o(\Delta (x,y))\right)\hfill \\ & -\sum _y(P_Y\left(y\right)+\Delta \left(y\right))\left(\log P_Y\left(y\right)+\frac{\Delta \left(y\right)}{P_Y\left(y\right)}+o(\Delta \left(y\right))\right)\hfill \\ & =I(P_X,P_{Y|X})-\sum _y(\Delta \left(y\right)+\Delta \left(y\right)\log P_Y\left(y\right)+o\left({\Delta }_y\right))\hfill \\ & +\sum _{x,y}{P}_X\left(x\right)(\Delta (x,y)+\Delta (x,y)\log P_{Y|X}\left(y\right|x)+o(\Delta (x,y)))\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill D(Q_{Y|X}\parallel P_{Y|X}|P_X)& =\sum _{x,y}{P}_X\left(x\right)Q_{Y|X}\left(y\right|x)\log \frac{Q_{Y|X}\left(y\right|x)}{P_{Y|X}\left(y\right|x)}\hfill \\ & =\sum _{x,y}{P}_X\left(x\right)(P_{Y|X}\left(y\right|x)+\Delta (x,y))\log \left(1+\frac{\Delta (x,y)}{P_{Y|X}\left(y\right|x)}\right)\hfill \\ & =\sum _{x,y}{P}_X\left(x\right)(P_{Y|X}\left(y\right|x)+\Delta (x,y))\left(\frac{\Delta (x,y)}{P_{Y|X}\left(y\right|x)}-\frac{{\Delta }^2(x,y)}{2P_{Y|X}^2\left(y\right|x)}+o\left({\Delta }^2(x,y)\right)\right)\hfill \\ & =\sum _{x,y}{P}_X\left(x\right)\left(\frac{{\Delta }^2(x,y)}{2P_{Y|X}\left(y\right|x)}+o\left({\Delta }^2(x,y)\right)\right).\hfill \end{array}$$

Here $f\left(z\right)=o\left(z\right)$ means ${\lim }_{z\to 0}\frac{f\left(z\right)}{z}=0$.

As $r\downarrow 0$, we have $\Delta \left(y\right)\to 0$, $\Delta (x,y)\to 0$ for all $x\in \mathcal{X},y\in \mathcal{Y}$. Therefore, by ignoring the high order terms which do not affect the limit, we get

$$\begin{array}{c}\hfill \underset{r\downarrow 0}{\lim }\frac{E_v(P_{XY},H\left(X\right|Y)+r)}{r^2}=\underset{r\downarrow 0}{\lim }\min \sum _{x,y}\frac{P_X\left(x\right){\Delta }^2(x,y)}{2P_{Y|X}\left(y\right|x)r^2},\end{array}$$

(45)

where the minimization is over $\Delta (x,y)$ ($x\in \mathcal{X},y\in \mathcal{Y}$) subject to the constraints

• ${\sum }_y\Delta (x,y)=0$ for all $x\in \mathcal{X}$,
• ${\sum }_{x,y}{P}_X\left(x\right)\tau (x,y)\Delta (x,y)=r$.

Introduce the Lagrange multipliers $\alpha \left(x\right)$ $(x\in \mathcal{X})$ and $\beta$ for these constraints, and define

$$\begin{array}{c}\hfill G=\sum _{x,y}\frac{P_X\left(x\right){\Delta }^2(x,y)}{2P_{Y|X}\left(y\right|x)}-\sum _{x,y}\alpha \left(x\right)\Delta (x,y)-\beta \sum _{x,y}{P}_X\left(x\right)\tau (x,y)\Delta (x,y).\end{array}$$

The Karush-Kuhn-Tucker conditions yield

$$\begin{array}{c}\hfill \frac{\partial G}{\partial \Delta (x,y)}=-\alpha \left(x\right)-\beta P_X\left(x\right)\tau (x,y)+\frac{P_X\left(x\right)\Delta (x,y)}{P_{Y|X}\left(y\right|x)}=0,x\in \mathcal{X},y\in \mathcal{Y}.\end{array}$$

Therefore, we have

$$\begin{array}{c}\hfill \Delta (x,y)=\beta \tau (x,y)P_{Y|X}\left(y\right|x)+\frac{P_{Y|X}\left(y\right|x)}{P_X\left(x\right)}\alpha \left(x\right).\end{array}$$

(46)

Substituting (46) into constraint 1, we obtain

$$\begin{array}{c}\hfill \alpha \left(x\right)=-\beta P_X\left(x\right)\sum _y\tau (x,y)P_{Y|X}\left(y\right|x),\end{array}$$

which, together with (46), yields

$$\begin{array}{c}\hfill \Delta (x,y)=\beta \tau (x,y)P_{Y|X}\left(y\right|x)-\beta P_{Y|X}\left(y\right|x)\sum _{y^{\prime }}\tau (x,y^{\prime })P_{Y|X}\left(y^{\prime }\right|x).\end{array}$$

(47)

Therefore, we have

$$\begin{array}{c}\sum _{x,y}\frac{P_X\left(x\right){\Delta }^2(x,y)}{2P_{Y|X}\left(y\right|x)}\hfill \\ =\frac{{\beta }^2}{2}\sum _{x,y}{P}_{XY}(x,y){\left[\tau (x,y)-\sum _{y^{\prime }}\tau (x,y^{\prime })P_{Y|X}\left(y^{\prime }\right|x)\right]}^2\hfill \\ =\frac{{\beta }^2}{2}\sum _{x,y}{P}_{XY}(x,y)\left[{\tau }^2(x,y)-2\tau (x,y)\sum _{y^{\prime }}\tau (x,y^{\prime })P_{Y|X}\left(y^{\prime }\right|x)+{\left(\sum _{y^{\prime }}\tau (x,y^{\prime })P_{Y|X}\left(y^{\prime }\right|x)\right)}^2\right]\hfill \\ =\frac{{\beta }^2}{2}\left[\sum _{x,y}{P}_{XY}(x,y){\tau }^2(x,y)-\sum _x{P}_X\left(x\right){\left(\sum _y\tau (x,y)P_{Y|X}\left(y\right|x)\right)}^2\right].\hfill \end{array}$$

(48)

Constraint 2 and (47) together yield

$$\begin{array}{cc}\hfill \frac{r^2}{{\beta }^2}& =\frac{1}{{\beta }^2}{\left(\sum _{x,y}{P}_X\left(x\right)\tau (x,y)\Delta (x,y)\right)}^2\hfill \\ & ={\left[\sum _{x,y}{P}_X\left(x\right)\tau (x,y)\left(\tau (x,y)P_{Y|X}\left(y\right|x)-P_{Y|X}\left(y\right|x)\sum _{y^{\prime }}\tau (x,y^{\prime })P_{Y|X}\left(y^{\prime }\right|x)\right)\right]}^2\hfill \\ & ={\left[\sum _{x,y}{P}_{XY}(x,y){\tau }^2(x,y)-\sum _x{P}_X\left(x\right){\left(\sum _y\tau (x,y)P_{Y|X}\left(y\right|x)\right)}^2\right]}^2.\hfill \end{array}$$

(49)

The proof is complete by substituting (48) and (49) back into (45). ☐

4. Variable-Rate Slepian-Wolf Coding: Below the Slepian-Wolf Limit

Definition 5.

Given a joint probability distribution $P_{XY}$, we say that a correct decoding exponent $E^c\ge 0$ is achievable with variable-rate Slepian-Wolf codes at rate R if for any $\delta >0$, there exists a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \inf }-\frac{1}{n}\log P_c({\phi }_n,P_{XY})\le E^c+\delta .\hfill \end{array}$$

The smallest achievable correct decoding exponent at rate R is denoted by $E_v^c(P_{XY},R)$.

In view of Theorem 1, it is tempting to conjecture that $E_v^c(P_{XY},R)=E^c(P_X,P_{Y|X},H\left(P_X\right)-R)$. It turns out this is not true. We shall show that $E_v^c(P_{XY},R)=0$ for all R. Actually we have a stronger result—the correct decoding probability of variable-rate Slepian-Wolf coding can be bounded away from zero even when $R<H\left(X\right|Y)$. This is in sharp contrast with fixed-rate Slepian-Wolf coding for which the correct decoding probability decays to zero exponentially fast if the rate is below the Slepian-Wolf limit. To make the statement more precise, we need the following definition.

Definition 6.

Given a joint probability distribution $P_{XY}$, we say that a correct decoding probability $P_{c,v}(P_{XY},R)$ is achievable with variable-rate Slepian-Wolf codes at rate R if for any $\delta >0$, there exists a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n\right\}$ such that

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup } P_c({\phi }_n,P_{XY})\ge P_{c,v}(P_{XY},R)-\delta .\hfill \end{array}$$

The largest achievable correct decoding probability at rate R is denoted by $P_{c,v}^{\max }(P_{XY},R)$.

Theorem 3.

$P_{c,v}^{\max }(P_{XY},R)=\frac{R}{H\left(X\right|Y)}$ for $R\in (0,H(X\left|Y\right)]$.

Remark 7.

It is obvious that $P_{c,v}^{\max }(P_{XY},R)=1$ for $R>H\left(X\right|Y)$. Moreover, since $P_{c,v}^{\max }(P_{XY},R)$ is a monotonically increasing function of R, it follows that $P_{c,v}^{\max }(P_{XY},0)=0$.

Proof. 

The intuition underlying the proof is as follows. Assume the rate is below the Slepian-Wolf limit, i.e., $R<H\left(X\right|Y)$. For each type P in the neighborhood of $P_X$, the rate allocated to the type class ${\mathcal{T}}_n\left(P\right)$ should be no less than $H\left(X\right|Y)$ in order to correctly decode the sequences in ${\mathcal{T}}_n\left(P\right)$. However, since almost all the probability are captured by the type classes whose types are in the neighborhood of $P_X$, there is no enough rate to protect all of them. Note that if the rate is evenly allocated among these type classes, none of them can get enough rate; consequently, the correct decoding probability goes to zero. A good way is to protect only a portion of them to accumulate enough rate. Specifically, we can protect $\frac{R}{H\left(X\right|Y)}$ fraction of these type classes so that the rate allocated to each of them is about $H\left(X\right|Y)$ and leave the remaining type classes unprotected. It turns out this strategy achieves the maximum correct decoding probability as the block length n goes to infinity. Somewhat interestingly, although $E_v^c(P_{XY},R)\ne E^c(P_X,P_{Y|X},H\left(P_X\right)-R)$, the function $E^c(P_X,P_{Y|X},·)$ does play a fundamental role in establishing the correct result.

The proof is divided into two parts. Firstly, we shall show that $P_{c,v}^{\max }(P_{XY},R)\ge \frac{R}{H\left(X\right|Y)}$. For any $ϵ>0$, define

$$\begin{array}{c}\hfill \mathcal{U}\left(ϵ\right)=\left\{P\in \mathcal{P}\left(\mathcal{X}\right):\parallel P-P_X\parallel \le ϵ\right\}.\end{array}$$

Since $P_X\left(x\right)>0$ for all $x\in \mathcal{X}$, we can choose $ϵ$ small enough so that

$$\begin{array}{c}\hfill q_{\min }\left(ϵ\right)\triangleq \underset{P\in \mathcal{U}\left(ϵ\right),x\in \mathcal{X}}{\min }P\left(x\right)>0.\end{array}$$

Using Stirling’s approximation

$$\begin{array}{c}\hfill \sqrt{2\pi m}{\left(\frac{m}{e}\right)}^m{e}^{\frac{1}{12m+1}}<m!<\sqrt{2\pi m}{\left(\frac{m}{e}\right)}^m{e}^{\frac{1}{12m}},\end{array}$$

we have, for any $P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)$,

$$\begin{array}{cc}\hfill \mathrm{Pr}(X^n\in {\mathcal{T}}_n\left(P\right))& =\frac{n!}{{\prod }_x\left(nP\left(x\right)\right)!}\prod _x{\left[P_X\left(x\right)\right]}^{nP\left(x\right)}\hfill \\ & \le \frac{\sqrt{2\pi n}{e}^{\frac{1}{12n}}}{{\prod }_x\sqrt{2\pi nP\left(x\right)}}{e}^{-nD(P\parallel P_X)}\hfill \\ & \le \frac{\sqrt{2\pi }{e}^{\frac{1}{12n}}}{{\prod }_x\sqrt{2\pi P\left(x\right)}}{n}^{-\frac{\left|\mathcal{X}\right|-1}{2}}\hfill \\ & \le \frac{\sqrt{2\pi }{e}^{\frac{1}{12n}}}{{\prod }_x\sqrt{2\pi q_{\min }\left(ϵ\right)}}{n}^{-\frac{\left|\mathcal{X}\right|-1}{2}},\hfill \end{array}$$

which implies that $\mathrm{Pr}(X^n\in {\mathcal{T}}_n\left(P\right))$ converges uniformly to zero as $n\to \infty$ for all $P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)$. Moreover, it follows from the weak law of large numbers that

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}(X^n\in {\mathcal{T}}_n\left(P\right))=1.\end{array}$$

Therefore, for any $\delta >0$, $R\in (0,H(X\left|Y\right)]$, and sufficiently large n, we can find a set ${\mathcal{S}}_n\subseteq \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)$ such that

$$\begin{array}{c}\hfill \frac{R}{H\left(X\right|Y)}-\delta \le \sum _{P\in {\mathcal{S}}_n}\mathrm{Pr}(X^n\in {\mathcal{T}}_n\left(P\right))\le \frac{R}{H\left(X\right|Y)}.\end{array}$$

Now consider a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n(·)\right\}$ specified as follows.

• The encoder sends of type of $X^n$ to the decoder, where each type is uniquely represented by a binary sequence of length $\lceil {\log }_2\left|{\mathcal{P}}_n\left(\mathcal{X}\right)\right|\rceil$.
• For each $P\in {\mathcal{S}}_n$, the encoder partitions the type class ${\mathcal{T}}_n\left(P\right)$ into $L_n$ subsets ${\mathcal{T}}_n(P,1),{\mathcal{T}}_n(P,2),\cdots ,{\mathcal{T}}_n(P,L_n)$. If $X^n\in {\mathcal{T}}_n\left(P\right)$ for some $P\in {\mathcal{S}}_n$, the encoder finds the subset ${\mathcal{T}}_n(P,i^{*})$ that contains $X^n$ and sends the index $i^{*}$ to the decoder, where each index in $\{1,2,\cdots ,L_n\}$ is uniquely represented by a binary sequence of length $\lceil {\log }_2{L}_n\rceil$.
• The remaining type classes are left uncoded.

Specifically, we let

$$\begin{array}{c}\hfill L_n=⌈\left(2{(n+1)}^{{\left|\mathcal{X}\right|}^2}{e}^{n\left(H\right(X\left|Y\right)+\delta )}\right)⌉.\end{array}$$

It follows from ([8], Theorem 2) that for each $P\in {\mathcal{S}}_n$, it is possible to partition the type class ${\mathcal{T}}_n\left(P\right)$ into $L_n$ disjoint subsets ${\mathcal{T}}_n(P,1),{\mathcal{T}}_n(P,2),\cdots ,{\mathcal{T}}_n(P,L_n)$ so that

$$\begin{array}{c}\hfill -\frac{1}{n}\log \mathrm{Pr}({\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n\left(P\right))\ge \underset{Q_X\in \mathcal{U}\left(ϵ\right)}{\min }\left[E_{rc}(Q_X,P_{Y|X},H\left(Q_X\right)-H\left(X\right|Y)-\delta )-ϵ\right]\end{array}$$

uniformly for all $P\in {\mathcal{S}}_n$ when n is sufficiently large. In view of the fact that $E_{rc}(P_X,P_{Y|X},I(P_X,P_{Y|X})-\delta )>0$ and that $E_{rc}(Q_X,P_{Y|X},R)$ as a function of the pair $(Q_X,R)$ is uniformly equicontinuous, we have

$$\begin{array}{c}\hfill \underset{Q_X\in \mathcal{U}\left(ϵ\right)}{\min }\left[E_{rc}(Q_X,P_{Y|X},H\left(Q_X\right)-H\left(X\right|Y)-\delta )-ϵ\right]\triangleq {\kappa }_1>0\end{array}$$

for sufficiently small $ϵ$.

For this sequence of constructed variable-rate Slepian-wolf codes $\left\{{\phi }_n(·)\right\}$, it can be readily verified that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})& =\underset{n\to \infty }{\lim \sup }\frac{1}{n{\log }_{2}e}\left[\lceil {\log }_2|{\mathcal{P}}_n\left(\mathcal{X}\right)|\rceil +\sum _{P\in {\mathcal{S}}_n}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\lceil {\log }_2{L}_n\rceil \right]\hfill \\ & \le \frac{R}{H\left(X\right|Y)}(H\left(X\right|Y)+\delta )\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim \sup } P_c({\phi }_n,R)& \ge \underset{n\to \infty }{\lim \sup }\sum _{P\in {\mathcal{S}}_n}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\left[1-\mathrm{Pr}\{{\widehat{X}}^n\ne X^n|X^n\in {\mathcal{T}}_n\left(P\right)\}\right]\hfill \\ & \ge \underset{n\to \infty }{\lim \sup }\sum _{P\in {\mathcal{S}}_n}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\left(1-e^{-n{\kappa }_1}\right)\hfill \\ & \ge \frac{R}{H\left(X\right|Y)}-\delta .\hfill \end{array}$$

Since $\delta >0$ is arbitrary, it follows from Definition 6 that $P_{c,v}^{\max }(P_{XY},R)\ge \frac{R}{H\left(X\right|Y)}$.

Now we proceed to prove the other direction. It follows from Definition 6 that for any $\delta >0$, there exists a sequence of variable-rate Slepian-Wolf codes $\left\{{\phi }_n(·)\right\}$ with

$$\begin{array}{c}\underset{n\to \infty }{\lim \sup } R({\phi }_n,P_{XY})\le R+\delta ,\hfill \\ \underset{n\to \infty }{\lim \sup } P_c({\phi }_n,P_{XY})\ge P_{c,v}^{\max }\left(R\right)-\delta .\hfill \end{array}$$

Recall the definition of ${\mathcal{T}}_n(P,1),\cdots ,{\mathcal{T}}_n(P,N_n\left(P\right))$ as well as $r\left({\mathcal{T}}_n\left(P\right)\right)$ in the proof of Theorem 1. For $P\in {\mathcal{P}}_n\left(\mathcal{X}\right)$, define

$$\begin{array}{c}{\mathcal{I}}_n(P,\delta )=\left\{i:\frac{1}{n}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\le H\left(X\right|Y)-\delta ,i=1,2,\cdots ,N_n\left(P\right)\right\},\hfill \\ {\mathcal{I}}_n^c(P,\delta )=\left\{i:\frac{1}{n}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}>H\left(X\right|Y)-\delta ,i=1,2,\cdots ,N_n\left(P\right)\right\}.\hfill \end{array}$$

Note that

$$\begin{array}{c}\hfill \sum _{i\in {\mathcal{I}}_n(P,\delta )}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}\ge 1-\frac{r\left({\mathcal{T}}_n\left(P\right)\right)}{H\left(X\right|Y)-\delta }\end{array}$$

since

$$\begin{array}{cc}\hfill r\left({\mathcal{T}}_n\left(P\right)\right)& \ge \frac{1}{n}\sum _{i=1}^{N_n\left(P\right)}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\hfill \\ & \ge \frac{1}{n}\sum _{i\in {\mathcal{I}}_n^c(P,\delta )}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}\log \frac{|{\mathcal{T}}_n\left(P\right)|}{|{\mathcal{T}}_n(P,i)|}\hfill \\ & \ge (H\left(X\right|Y)-\delta )\sum _{i\in {\mathcal{I}}_n^c(P,\delta )}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|},\hfill \end{array}$$

(50)

where (50) is due to (33).

Each ${\mathcal{T}}_n(P,i)$ can be viewed as a constant composition code of type P and we have

$$\begin{array}{c}\hfill \mathrm{Pr}\{{\widehat{X}}^n=X^n|X^n\in {\mathcal{T}}_n(P,i)\}=P_c({\mathcal{T}}_n(P,i),P_{Y|X}).\end{array}$$

Note that for $P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)$ and $i\in {\mathcal{I}}_n(P,\delta )$,

$$\begin{array}{cc}\hfill \frac{1}{n}\log \left|{\mathcal{T}}_n(P,i)\right|& \ge \frac{1}{n}\log \left|{\mathcal{T}}_n\left(P\right)\right|-H\left(X\right|Y)+\delta \hfill \\ & \ge H\left(P\right)-H\left(X\right|Y)+\delta -\left|\mathcal{X}\right|\frac{\log (n+1)}{n}.\hfill \end{array}$$

Therefore, it follows from ([9], Lemma 5) that

$$\begin{array}{c}\hfill -\frac{1}{n}\log P_c({\mathcal{T}}_n(P,i),P_{Y|X})\ge \underset{Q_X\in \mathcal{U}\left(ϵ\right)}{\min }{E}^c(Q_X,P_{Y|X},H\left(Q_X\right)-H\left(X\right|Y)+\delta -ϵ)-ϵ\end{array}$$

uniformly for all $P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)$ and $i\in {\mathcal{I}}_n(P,\delta )$ when n is sufficiently large. In view of the fact that $E^c(P_X,P_{Y|X},I(P_X,P_{Y|X})+\delta )>0$ and that $E^c(Q_X,P_{Y|X},R)$ as a function of the pair $(Q_X,R)$ is uniformly equicontinuous, we have

$$\begin{array}{c}\hfill \underset{Q_X\in \mathcal{U}\left(ϵ\right)}{\min }\left[E^c(Q_X,P_{Y|X},H\left(Q_X\right)-H\left(X\right|Y)+\delta -ϵ)-ϵ\right]\triangleq {\kappa }_2>0\end{array}$$

for sufficiently small $ϵ$.

Now it is easy to see that

$$\begin{array}{c}\underset{n\to \infty }{\lim \inf } P_e({\phi }_n,P_{XY})\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\sum _{i\in {\mathcal{I}}_n(P,\delta )}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}\left(1-\mathrm{Pr}\{{\widehat{X}}^n=X^n|X^n\in {\mathcal{T}}_n(P,i)\}\right)\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\sum _{i\in {\mathcal{I}}_n(P,\delta )}\frac{|{\mathcal{T}}_n(P,i)|}{|{\mathcal{T}}_n\left(P\right)|}(1-e^{-n{\kappa }_2})\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\left(1-\frac{r\left({\mathcal{T}}_n\left(P\right)\right)}{H\left(X\right|Y)-\delta }\right)(1-e^{-n{\kappa }_2})\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}(1-e^{-n{\kappa }_2})\hfill \\ -\underset{n\to \infty }{\lim \sup }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\frac{r\left({\mathcal{T}}_n\left(P\right)\right)}{H\left(X\right|Y)-\delta }(1-e^{-n{\kappa }_2})\hfill \\ \ge \underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}(1-e^{-n{\kappa }_2})\hfill \\ -\underset{n\to \infty }{\lim \sup }\sum _{P\in {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}\frac{r\left({\mathcal{T}}_n\left(P\right)\right)}{H\left(X\right|Y)-\delta }(1-e^{-n{\kappa }_2})\hfill \\ =\underset{n\to \infty }{\lim \inf }\sum _{P\in \mathcal{U}\left(ϵ\right)\cap {\mathcal{P}}_n\left(\mathcal{X}\right)}\mathrm{Pr}\{X^n\in {\mathcal{T}}_n\left(P\right)\}(1-e^{-n{\kappa }_2})\hfill \\ -\underset{n\to \infty }{\lim \sup }\frac{R({\phi }_n,P_{XY})}{H\left(X\right|Y)-\delta }(1-e^{-n{\kappa }_2})\hfill \\ =1-\frac{R+\delta }{H\left(X\right|Y)-\delta },\hfill \end{array}$$

which implies

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim \sup } P_c({\phi }_n,P_{XY})\le \frac{R+\delta }{H\left(X\right|Y)-\delta }.\end{array}$$

Therefore, we have

$$\begin{array}{c}\hfill P_{c,v}^{\max }(P_{XY},R)-\delta \le \frac{R+\delta }{H\left(X\right|Y)-\delta }.\end{array}$$

Since $\delta >0$ is arbitrary, this completes the proof. ☐

5. Example

Consider the joint distribution $P_{XY}$ over ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ with $P_{X|Y}\left(1\right|0)=P_{X|Y}\left(0\right|1)=p$ and $P_Y\left(0\right)=\tau$. We assume $p\in (0,\frac{1}{2})$, $\tau \in (0,\frac{1}{2}]$. It is easy to compute that

$$\begin{array}{c}{P}_X\left(0\right)=1-P_X\left(1\right)=\tau (1-p)+(1-\tau )p,\hfill \\ P_{Y|X}\left(1\right|0)=1-P_{Y|X}\left(0\right|0)=\frac{(1-\tau )p}{\tau (1-p)+(1-\tau )p},\hfill \\ P_{Y|X}\left(0\right|1)=1-P_{Y|X}\left(1\right|1)=\frac{\tau p}{\tau p+(1-\tau )(1-p))}.\hfill \end{array}$$

For this joint distribution, we have $H\left(X\right|Y)=H_b\left(p\right)$, where $H_b(·)$ is the binary entropy function (i.e., $H_b\left(p\right)=-p\log p-(1-p)\log (1-p)$). Given $R\in [0,\log 2]$, let q be the unique number satisfying $H_b\left(q\right)=R$ and $q\le \frac{1}{2}$. It can be verified that

$$\begin{array}{c}{E}_{f,sp}(P_{XY},R)=D(q\parallel p),R\in [H_b\left(p\right),\log 2],\hfill \\ E_f^c(P_{XY},R)=D(q\parallel p),R\in [0,H_b\left(p\right)].\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill E_{ex}(Q_X,P_{Y|X},0)& =-\sum _{x,x^{\prime }}{Q}_X\left(x\right)Q_X\left(x^{\prime }\right)\log \left[\sum _y\sqrt{P_{Y|X}\left(y\right|x)P_{Y|X}\left(y\right|x^{\prime })}\right]\hfill \\ & =-2Q_X\left(0\right)Q_X\left(1\right)\log \left[\sum _y\sqrt{P_{Y|X}\left(y\right|0)P_{Y|X}\left(y\right|1)}\right],\hfill \end{array}$$

which is a concave function of $Q_X$. Therefore,

$$\begin{array}{c}\hfill E_{ex}^{*}(P_X,P_{Y|X},0)=E_{ex}(P_X,P_{Y|X},0).\end{array}$$

Moreover, we have

$$\begin{array}{cc}\hfill E_{ex}(P_{Y|X},0)& =\underset{Q_X}{\max }{E}_{ex}(Q_X,P_{Y|X},0)\hfill \\ & =-\frac{1}{2}\log \left[\sum _y\sqrt{P_{Y|X}\left(y\right|0)P_{Y|X}\left(y\right|1)}\right].\hfill \end{array}$$

It is easy to show that

$$\begin{array}{cc}\hfill E_{v,sp}(P_{XY},H\left(P_X\right))& =E_{sp}(P_X,P_{X|Y},0)\hfill \\ & =\underset{Q_Y}{\min }\sum _x{P}_X\left(x\right)\sum _y{Q}_Y\left(y\right)\log \frac{Q_Y\left(y\right)}{P_{Y|X}\left(y\right|x)},\hfill \end{array}$$

where the minimizer $Q_Y^{*}$ is given by

$$\begin{array}{c}\hfill Q_Y^{*}\left(y\right)=\frac{{\prod }_x{P}_{Y|X}{\left(y\right|x)}^{P_X\left(x\right)}}{{\sum }_{y^{\prime }}{\prod }_x{P}_{Y|X}{\left(y^{\prime }\right|x)}^{P_X\left(x\right)}},y\in \mathcal{Y}.\end{array}$$

Define

$$\begin{array}{c}{E}_{f,er}(P_{XY},R)=\max \{E_{f,ex}(P_{XY},R),E_{f,rc}(P_{XY},R)\},\hfill \\ E_{v,er}(P_{XY},R)=\max \{E_{v,ex}(P_{XY},R),E_{v,rc}(P_{XY},R)\}.\hfill \end{array}$$

We have

$$\begin{array}{c}{E}_f(P_{XY},R)\ge E_{f,er}(P_{XY},R),\hfill \\ E_v(P_{XY},R)\ge E_{v,er}(P_{XY},R).\hfill \end{array}$$

It can be seen from Figure 2 that the achievable error exponent $E_{v,er}(P_{XY},R)$ of variable-rate Slepian-Wolf coding can completely dominate the sphere packing exponent $E_{f,sp}(P_{XY},R)$ of fixed-rate Slepian-Wolf coding. The gain of variable-rate coding gradually diminishes as $\tau \to \frac{1}{2}$ (see Figure 3 and Figure 4).

6. Concluding Remarks

We have studied the reliability function of variable-rate Slepian-Wolf coding. An intimate connection between variable-rate Slepian-Wolf codes and constant composition codes has been revealed. It is shown that variable-rate Slepian-Wolf coding can outperform fixed-rate Slepian-Wolf coding in terms of rate-error tradeoff. Finally, we would like to mention that Theorem 1 has been generalized by Weinberger and Merhav in their recent paper on the optimal tradeoff between the error exponent and the excess-rate exponent of variable-rate Slepian-Wolf coding [19].