A Thermodynamic Point of View on Dark Energy Models
Abstract
:1. Introduction
2. Dark Energy Models
2.1. The BA Parameterization
2.2. The Hobbit Model
3. Constraining Model Parameters
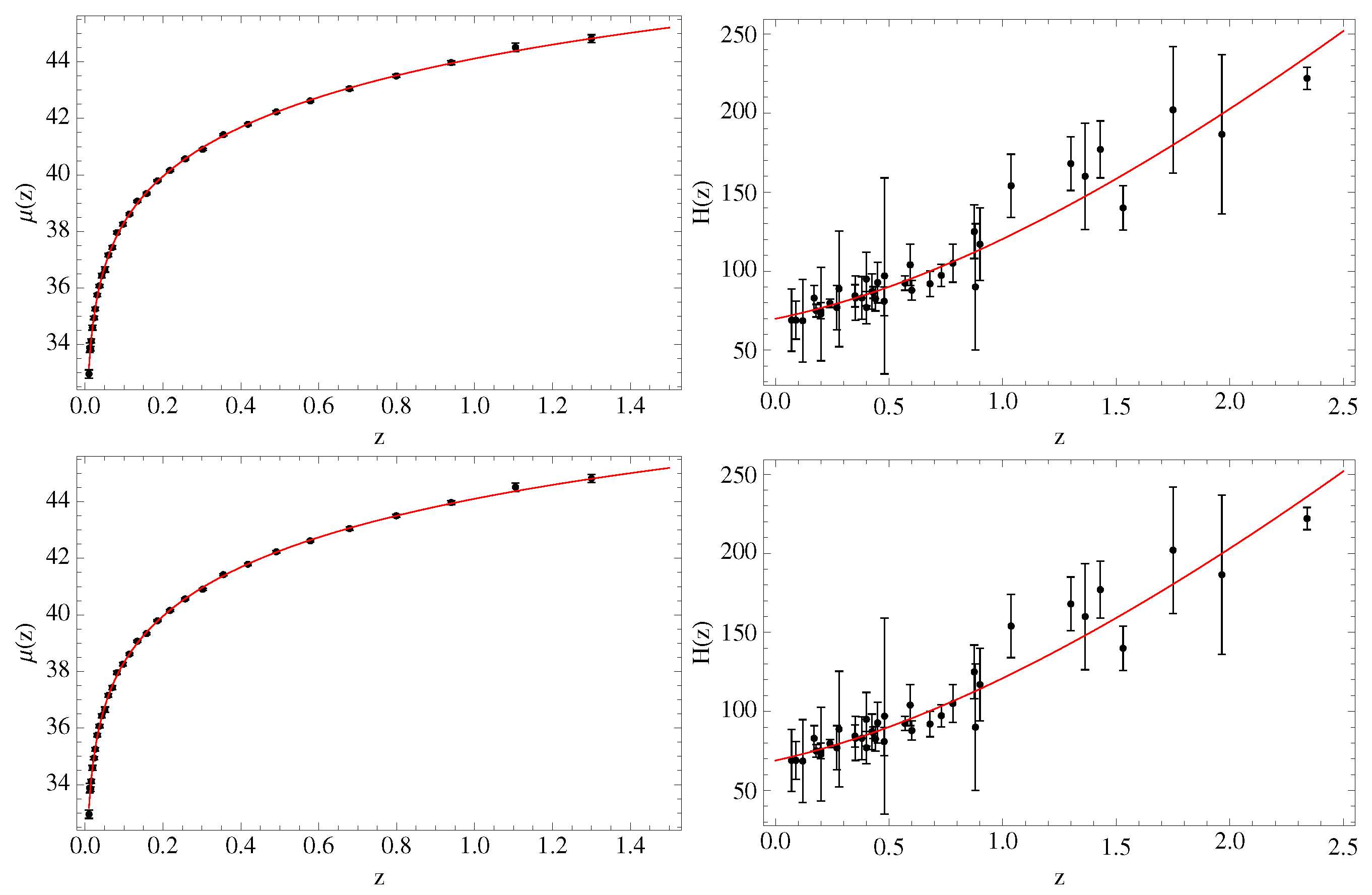
3.1. Data and Fitting Method
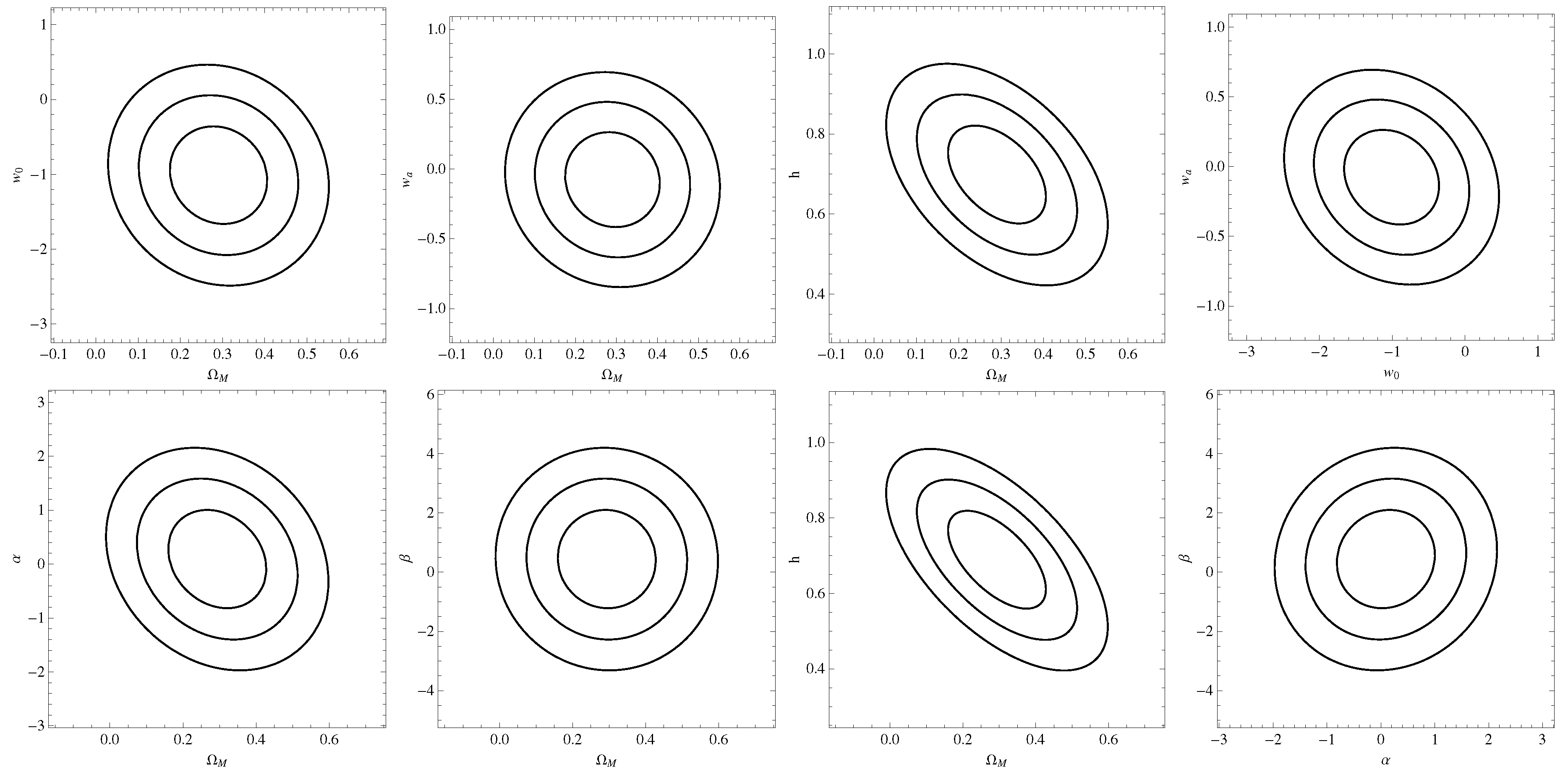
3.2. Results
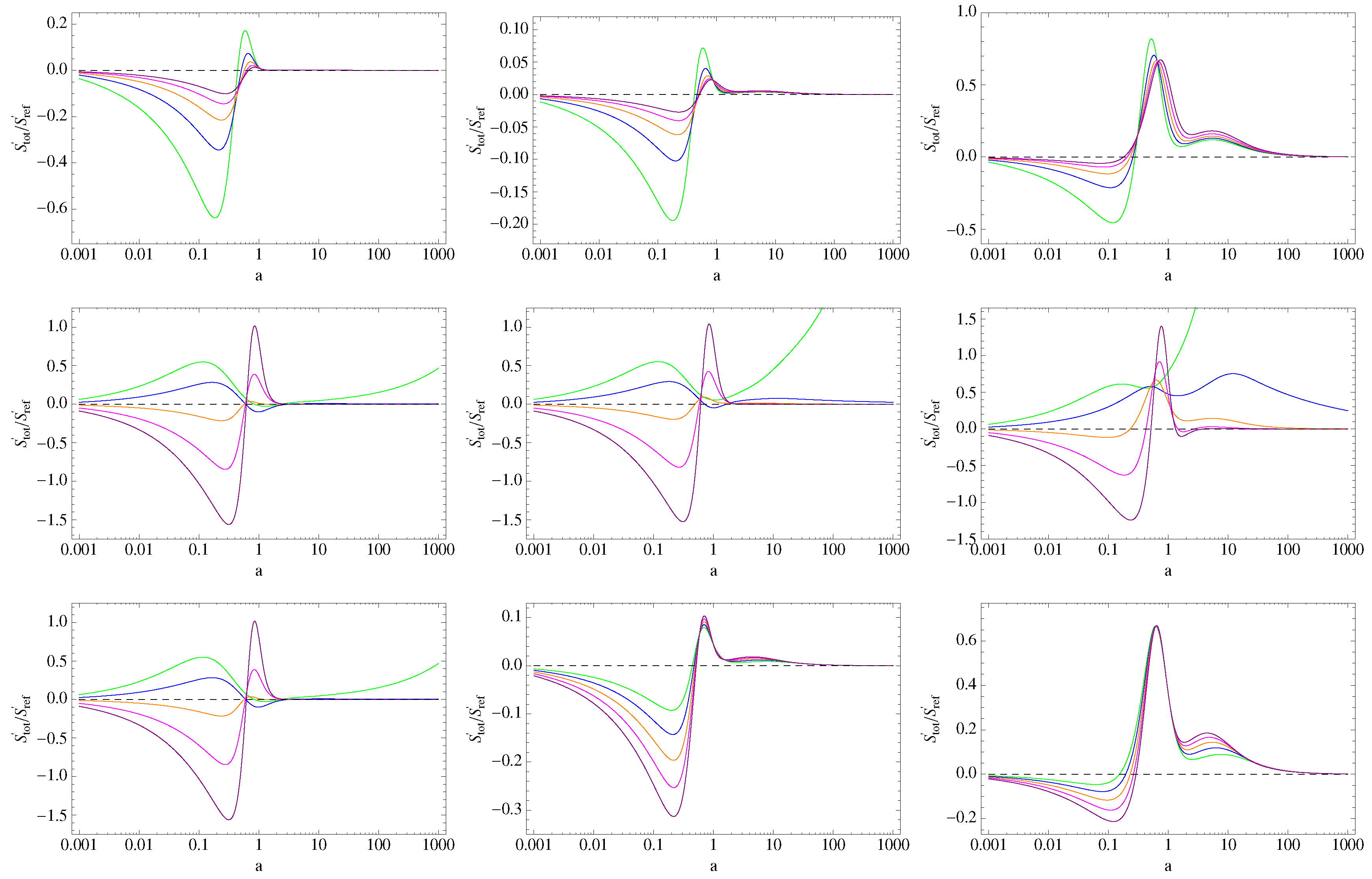
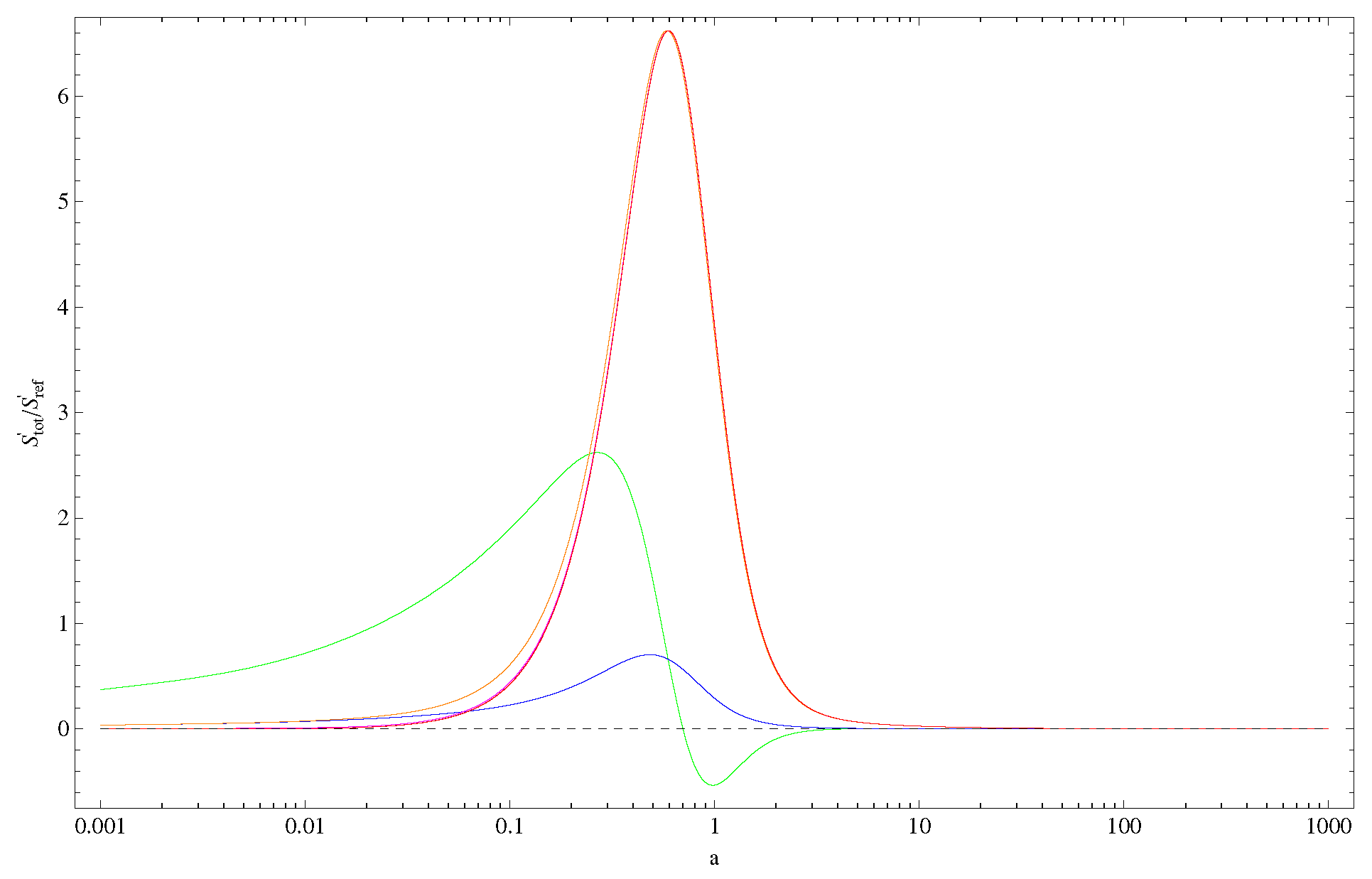
4. Thermodynamic Analysis
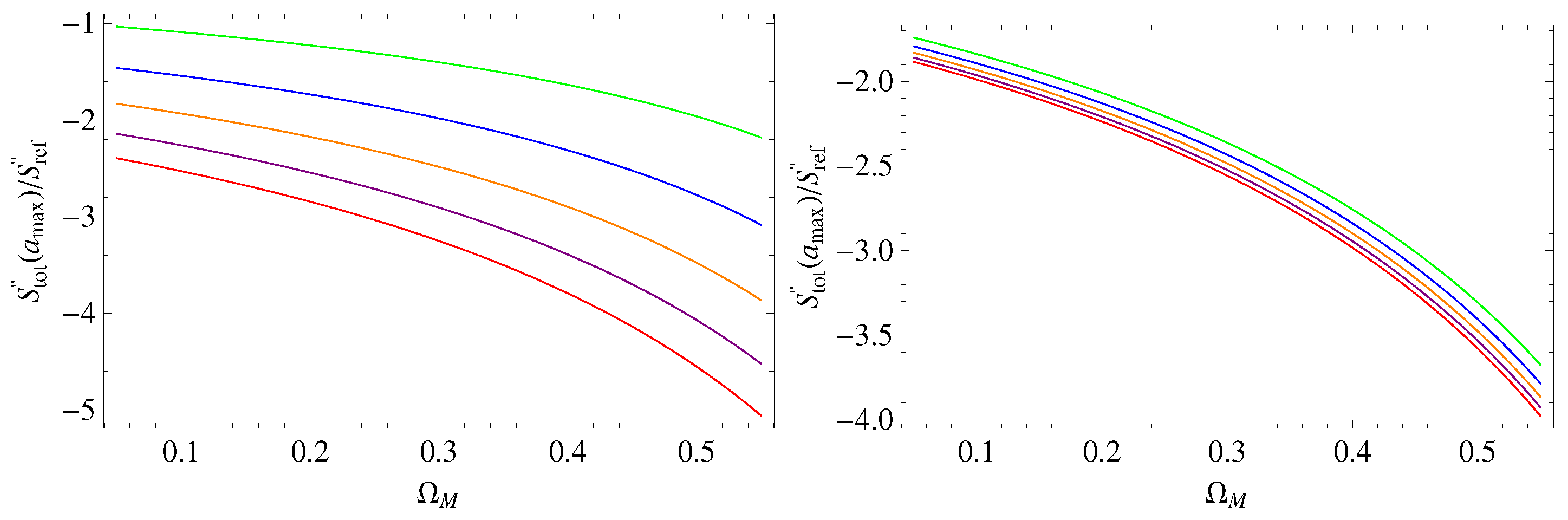
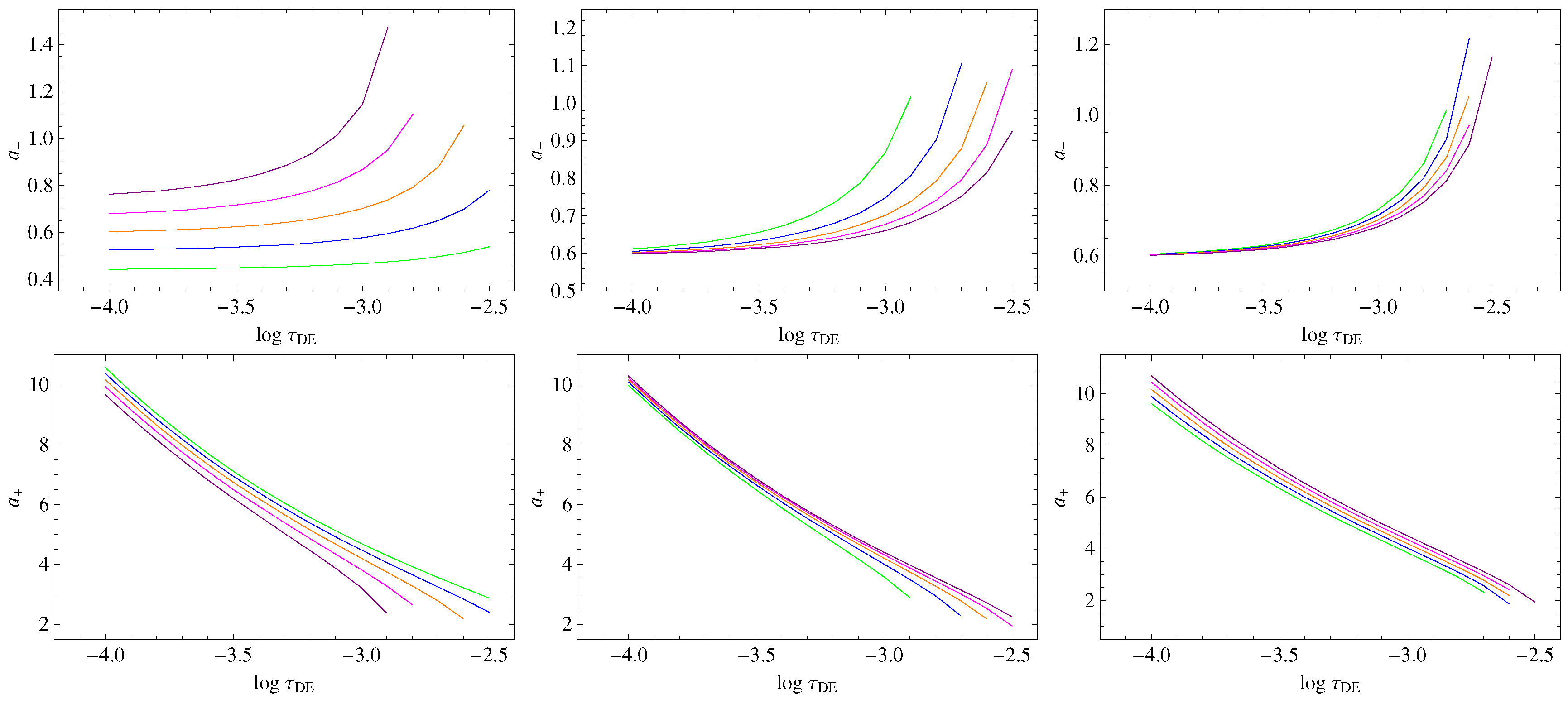
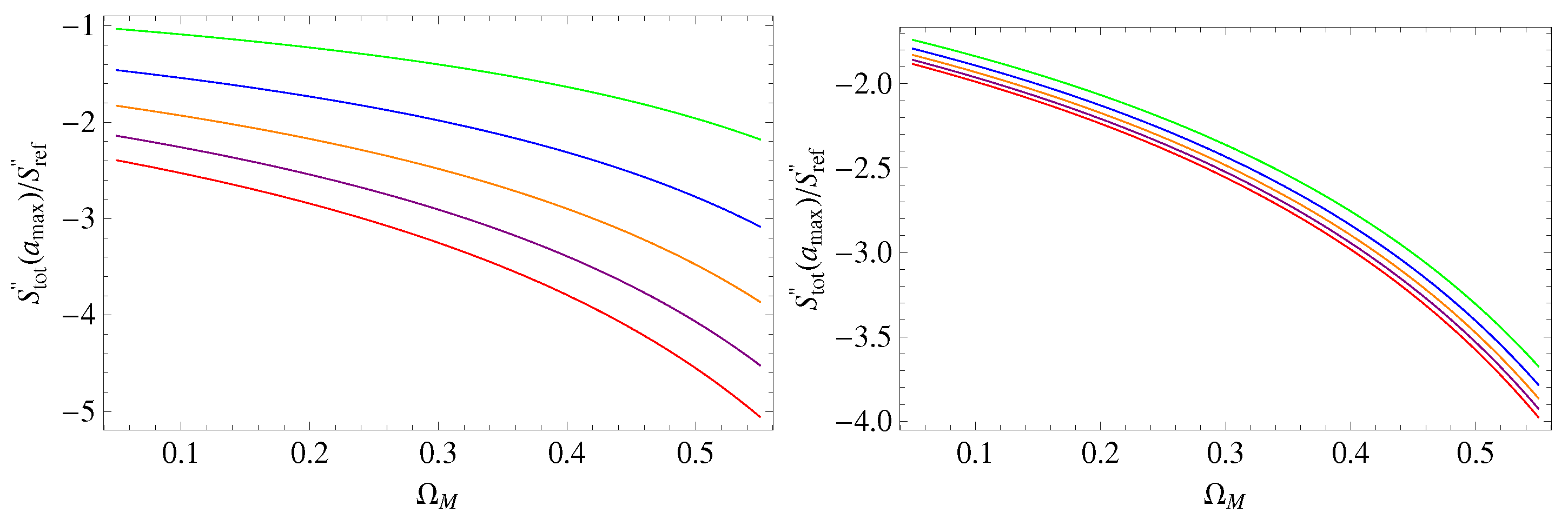
5. Thermodynamic Constraints
5.1. BA Model
5.2. Hobbit Model
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Garnavich, P.M.; Jha, S.; Challis, P.; Clocchiatti, A.; Diercks, A.; Filippenko, A.V.; Gilliland, R.L.; Hogan, C.J.; Kirshner, R.P.; Leibundgut, B.; et al. Supernova Limits on the Cosmic Equation of State. Astrophys. J. 1998, 509, 74–79. [Google Scholar] [CrossRef]
- Rebolo, R.; Battye, R.A.; Carreira, P.; Cleary, K.; Davies, R.D.; Davis, R.J.; Dickinson, C.; Genova-Santos, R.; Grainge, K.; Gutirrez, C.M.; et al. Cosmological parameter estimation using Very Small Array data out to ℓ = 1500. MNRAS 2004, 353, 747–759. [Google Scholar] [CrossRef]
- Pope, A.C.; Matsubara, T.; Szalay, A.S.; Blanton, M.R.; Eisenstein, D.J.; Gray, J.; Jain, B.; Bahcall, N.A.; Brinkmann, J.; Budavari, T.; et al. Cosmological Parameters from Eigenmode Analysis of Sloan Digital Sky Survey Galaxy Redshifts. Astrophys. J. 2004, 607, 655–660. [Google Scholar] [CrossRef]
- Tegmark, M.; Eisenstein, D.; Strauss, M.; Weinberg, D.; Blanton, M.; Frieman, J.; Fukugita, M.; Gunn, J.; Hamilton, A.; Knapp, G.; et al. Cosmological Constraints from the SDSS Luminous Red Galaxies. Phys. Rev. D 2006, 74, 123507. [Google Scholar] [CrossRef]
- Percival, W.J.; Cole, S.; Eisenstein, D.J.; Nichol, R.C.; Peacock, J.A.; Pope, A.C.; Szalay, A.S. Measuring the Baryon Acoustic Oscillation scale using the Sloan Digital Sky Survey and 2dF Galaxy Redshift Survey. MNRAS 2007, 381, 1053–1066. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2015 results. XVIII. Background geometry & topology. Astron. Astrophys. 2016, 594, A18. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Burgess, C.P. The Cosmological Constant Problem: Why it’s hard to get Dark Energy from Micro-physics. arXiv, 2013; arXiv:1309.4133. [Google Scholar]
- De Putter, R.; Huterer, D.; Linder, E.V. Measuring the Speed of Dark: Detecting Dark Energy Perturbations. Phys. Rev. D 2010, 81, 103513. [Google Scholar] [CrossRef]
- Yoo, J.; Watanabe, Y. Theoretical Models of Dark Energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relat. 2013, 16, 6. [Google Scholar] [CrossRef]
- Joyce, A.; Schmidt, L.; Schmidt, F. Dark Energy vs. Modified Gravity. Annu. Rev. Nucl. Part. Sci. 2016, 66, 95–122. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2013, 10, 213–224. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
- Cardone, V.F.; Troisi, A.; Capozziello, A. Unified dark energy models: A Phenomenological approach. Phys. Rev. D 2004, 69, 083517. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. Polytropic dark matter flows illuminate dark energy and accelerated expansion. Astron. Astrophys. 2015, 576, A23. [Google Scholar]
- Kleidis, K.; Spyrou, N.K. Dark Energy: The Shadowy Reflection of Dark Matter? Entropy 2016, 18, 94. [Google Scholar] [CrossRef]
- Akarsu, O.; Bouhmadi-López, M.; Brilenkov, M.; Brilenkov, R.; Eingorn, M.; Zhuk, A. Are dark energy models with variable EoS parameter ww compatible with the late inhomogeneous Universe? JCAP 2015. [Google Scholar] [CrossRef]
- Rivera, A.B.; Farieta, J.G. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. arXiv, 2016; arXiv:1605.01984. [Google Scholar]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292–3300. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Gravity and the Thermodynamics of Horizons. Phys. Rep. 2005, 406, 49–125. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics and particle creation. Phys. Rev. D 1977, 15, 2738. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Thermodynamics of an accelerated expanding universe. Phys. Rev. D 2006, 74, 083520. [Google Scholar] [CrossRef]
- Izquierdo, G.; Pavón, D. The generalized second law in phantom dominated universes in the presence of black holes. Phys. Lett. B 2006, 633, 420. [Google Scholar] [CrossRef]
- Visser, M. Essential and inessential features of Hawking radiation. Int. J. Mod. Phys. D 2003, 12, 649–661. [Google Scholar] [CrossRef]
- Cai, R.-G.; Kim, S.P. First law of Thermodynamics and Friedmann equations of Friedmann–Robertson–Walker Universe. JHEP 2005, 0502, 050. [Google Scholar] [CrossRef]
- Cai, R.-G.; Cao, L.-M.; Hu, W.-P. Hawking Radiation of Apparent Horizon in a FRW Universe. Class. Quant. Grav. 2009, 26, 155018. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, B.; Gong, Y.; Abdalla, E. The generalized second law of thermodynamics in the accelerating universe. Phys. Lett. B 2007, 652, 86–91. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, B.; Wang, A. Thermodynamical properties of the Universe with dark energy. JCAP 2007, 01, 024. [Google Scholar] [CrossRef]
- Yang, R.J.; Qi, R.J.; Feng, L. Bound on the Equation of State of Dark Energy from the Generalized Second Law of Thermodynamics. Int. J. Theor. Phys. 2012, 51, 1692–1697. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics; John Wiley: New York, NY, USA, 1960. [Google Scholar]
- Radicella, N.; Pavón, D. A thermodynamic motivation for dark energy. Gen. Rel. Grav. 2012, 44, 685–702. [Google Scholar] [CrossRef]
- Radicella, N.; Pavón, D. The generalized second law in universes with quantum corrected entropy relations. Phys. Lett. B 2010, 691, 121–126. [Google Scholar] [CrossRef]
- Radicella, N.; Pavón, D. Thermodynamical analysis on a braneworld scenario with curvature corrections. Phys. Lett. B 2011, 7041, 260–264. [Google Scholar] [CrossRef]
- Pavón, D.; Radicella, N. Does the entropy of the Universe tend to a maximum? Gen. Rel. Grav. 2013, 45, 63–68. [Google Scholar] [CrossRef]
- Radicella, N.; Pavón, D. Thermodynamics of the unified dark fluid with fast transition. Phys. Rev. D 2014, 89, 067302. [Google Scholar] [CrossRef]
- Barboza, E.M.; Alcaniz, J.S. Probing the time dependence of dark energy. JCAP 2012, 2012, 042. [Google Scholar] [CrossRef]
- Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. MNRAS 2011, 416, 3017–3032. [Google Scholar]
- Eisenstein, D.J.; Hu, W. Baryonic features in the matter transfer function. Astrophys. J. 1998, 496, 605. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezic, Z.; Knapp, G.R.; et al. Baryon Acoustic Oscillations in the Sloan Digital Sky Survey Data Release 7 Galaxy Sample. MNRAS 2010, 401, 2148–2168. [Google Scholar] [CrossRef] [Green Version]
- Beutler, F.; Blake, C.; Koda, J.; Marin, F.; Seo, H.; Cuesta, A.J.; Schneider, D.P. The BOSS-WiggleZ overlap region I. Baryon acoustic oscillations. MNRAS 2016, 455, 3230–3248. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Duan, X.; Zhou, M.; Zhang, T. Testing consistency of general relativity with kinematic and dynamical probes preprint. arXiv, 2016; arXiv:1605.03947. [Google Scholar]
- Efstathiou, G. H0 Revisited. MNRAS 2014, 440, 1138–1152. [Google Scholar] [CrossRef]
- Bruni, M.; Lazkoz, R.; Rozas-Fernández, A. Phenomenological models for Unified Dark Matter with fast transition. MNRAS 2013, 431, 2907–2916. [Google Scholar] [CrossRef]
- Sandvik, H.B.; Tegmark, M.; Zaldarriaga, M.; Waga, I. The end of unified dark matter? Phys. Rev. D 2004, 69, 123524. [Google Scholar] [CrossRef]
- Bak, D.; Rey, S.-J. Cosmic holography. Class. Quant. Grav. 2000, 17, L83. [Google Scholar] [CrossRef]

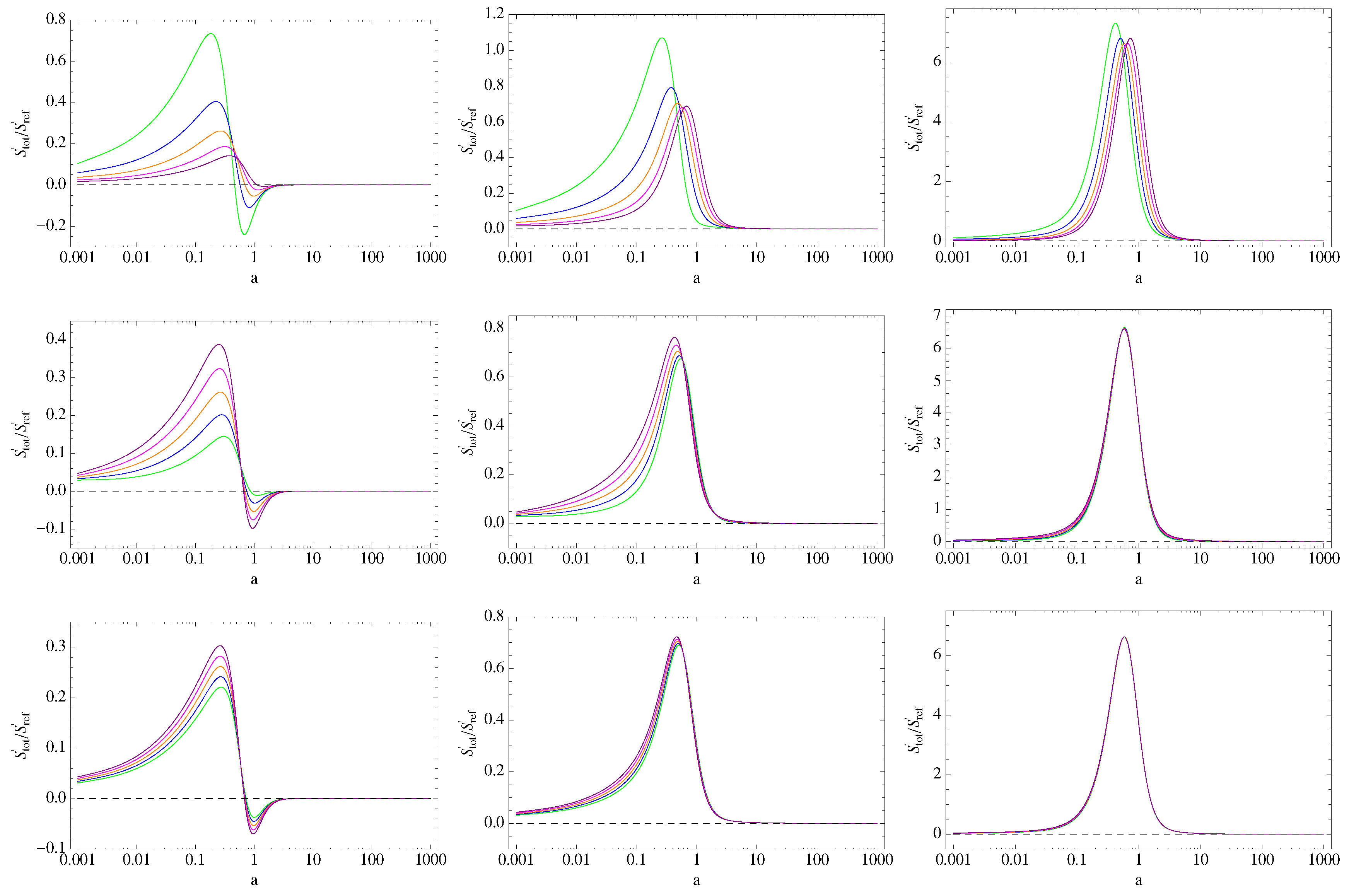
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardone, V.F.; Radicella, N.; Troisi, A. A Thermodynamic Point of View on Dark Energy Models. Entropy 2017, 19, 392. https://doi.org/10.3390/e19080392
Cardone VF, Radicella N, Troisi A. A Thermodynamic Point of View on Dark Energy Models. Entropy. 2017; 19(8):392. https://doi.org/10.3390/e19080392
Chicago/Turabian StyleCardone, Vincenzo F., Ninfa Radicella, and Antonio Troisi. 2017. "A Thermodynamic Point of View on Dark Energy Models" Entropy 19, no. 8: 392. https://doi.org/10.3390/e19080392



