Intrinsic Losses Based on Information Geometry and Their Applications
Abstract
:1. Introduction
2. The Riemannian Geometry and Dual Geometry of Exponential Family
2.1. The Fisher Metric and the -Connections
- (1)
- It is invariant under one-to-one reparameterizations.
- (2)
- It is invariant under reduction to sufficient statistics.
2.2. Geometric Structure of Exponential Family
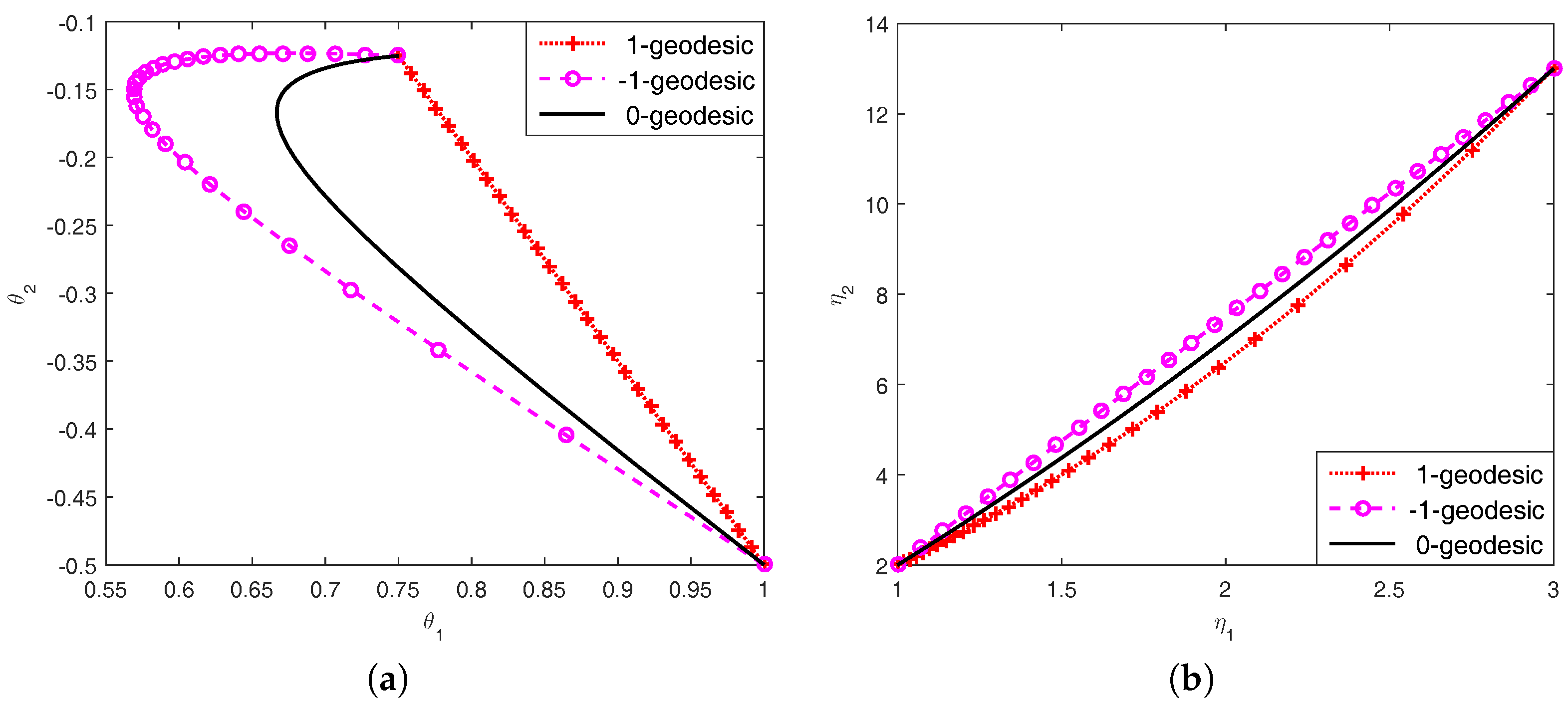
2.3. -Geodesics
2.4. The Length and Energy of a Curve
3. Intrinsic Bayesian Analysis
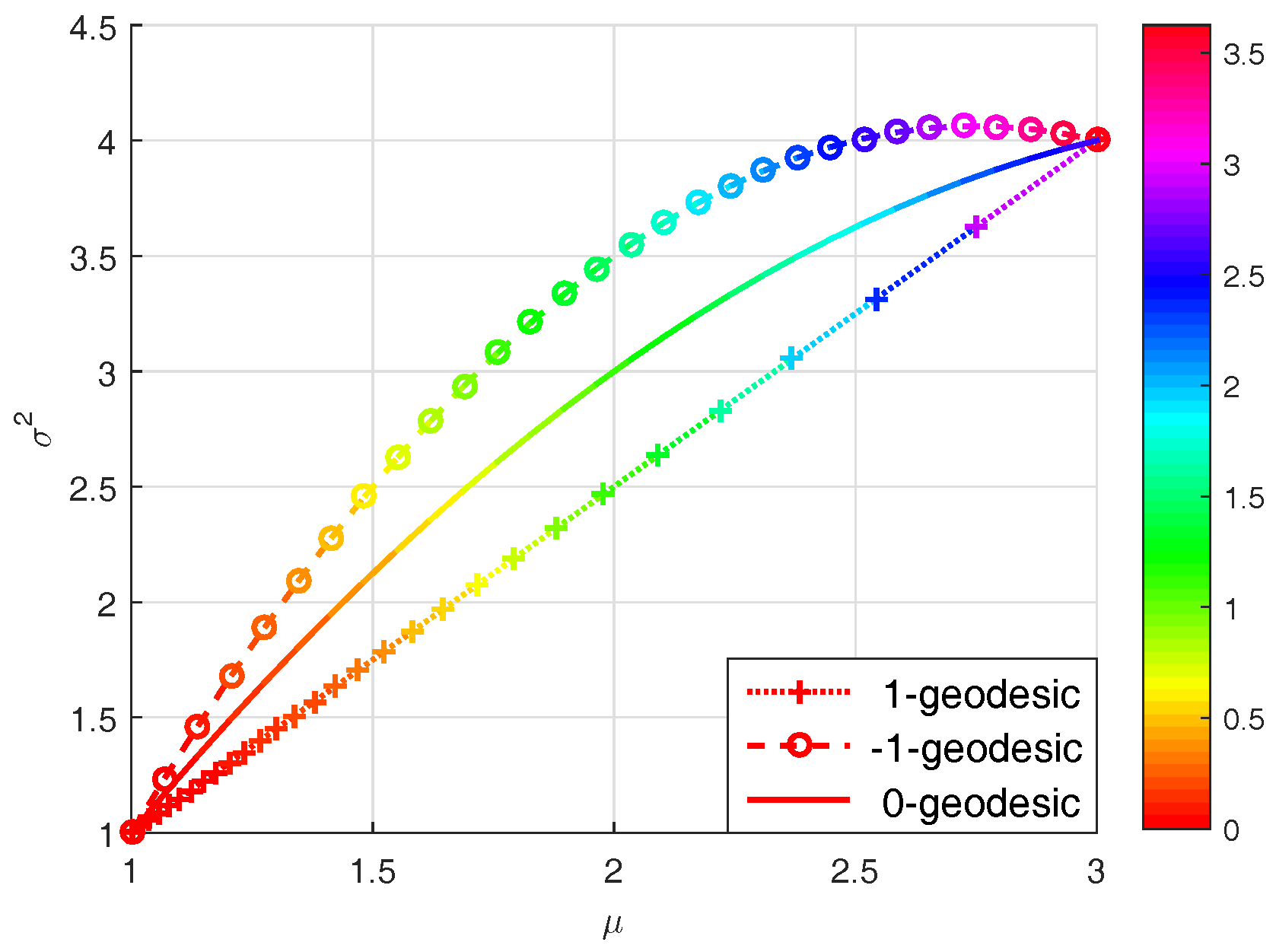
3.1. Two Intrinsic Losses
- (i)
- Intrinsic loss based on the squared Rao distance (hereafter referred to as the Rao loss):which stands for the energy difference along a 0-geodesic connecting and on S and parameterized by .
- (ii)
- Intrinsic loss based on the Jeffreys divergence (hereafter referred to as the Jeffreys loss):which stands for the energy difference along a - or 1-geodesic connecting and on S and parameterized by if S is an exponential family.
3.2. Priors
3.3. Intrinsic Bayesian Analysis
4. Applications
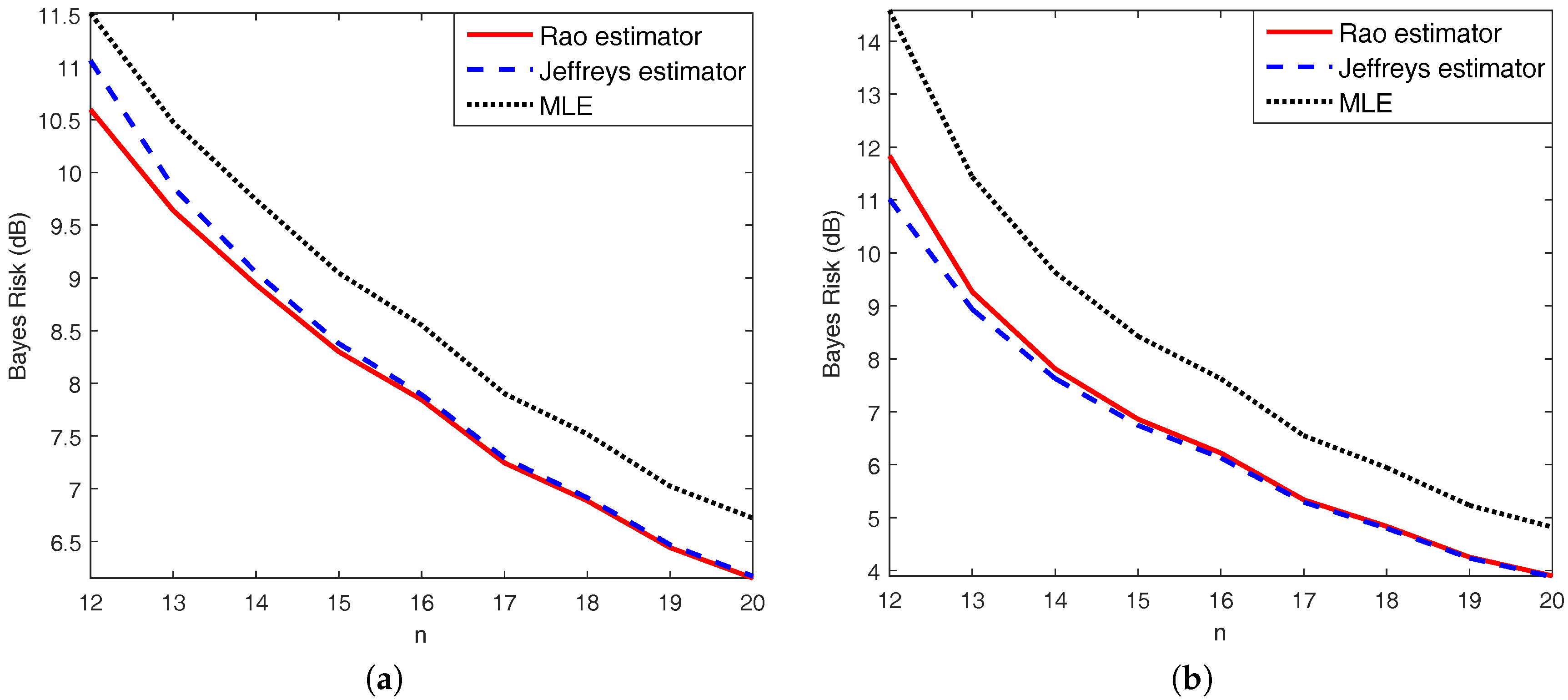
4.1. Covariance Estimation
4.2. Range-Spread Target Detection
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Robert, C.P. Intrinsic losses. Theor. Decis. 1996, 40, 191–214. [Google Scholar] [CrossRef]
- Bernardo, J.M. Intrinsic credible regions: An objective Bayesian approach to interval estimation. Test 2005, 14, 317–384. [Google Scholar] [CrossRef]
- Bernardo, J.M. Nested hypothesis testing: The Bayesian reference criterion. In Bayesian Statistics 6; Bernardo, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 101–130. [Google Scholar]
- Bernardo, J.M. Integrated objective Bayesian estimation and hypothesis testing. In Bayesian Statistics 9; Bernardo, J.M., Bayarri, M.J., Berger, J.O., Dawid, A.P., Heckerman, D., Eds.; Oxford University Press: Oxford, UK, 2010; pp. 1–68. [Google Scholar]
- Bernardo, J.M.; Juárez, M. Intrinsic estimation. In Bayesian Statistics 7; Bernardo, J.M., Bayarri, M.J., Berger, J.O., Dawid, A.P., Heckerman, D., Smith, A.F.M., West, M., Eds.; Oxford University Press: Oxford, UK, 2003; pp. 465–476. [Google Scholar]
- Bernardo, J.M. Intrinsic point estimation of the normal variance. In Bayesian Statistics and Its Applications; Upadhyay, S.K., Singhand, U., Dey, D.K., Eds.; Anamaya Publication: New Delhi, India, 2006; pp. 110–121. [Google Scholar]
- Bernardo, J.M.; Bernardo, J.M. Objective Bayesian point and region estimation in location-scale models. Stat. Oper. Res. Trans. 2007, 31, 3–44. [Google Scholar]
- Calin, O.; Udrişte, C. Geometric Modeling in Probability and Statistics; Springer: Basel, Switzerland, 2014. [Google Scholar]
- Amari, S.I.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Čencov, N.N. Statistical Decision Rules and Optimal Inference; Ametrican Mathematical Society: Providence, RI, USA, 1982. [Google Scholar]
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- García, G.; Oller, J.M. What does intrinsic mean in statistical estimation? Stat. Oper. Res. Trans. 2006, 30, 125–170. [Google Scholar]
- Darling, R.W.R. Geometrically intrinsic nonlinear recursive filters II: Foundations. Available online: https://arxiv.org/ftp/math/papers/9809/9809029.pdf (accessed on 4 August 2017).
- Ilea, I.; Bombrun, L.; Terebes, R.; Borda, M.; Germain, C. An M-estimator for robust centroid estimation on the manifold of covariance matrices. IEEE Signal Process. Lett. 2016, 23, 1255–1259. [Google Scholar] [CrossRef]
- Tang, M.; Rong, Y.; Zhou, J. Information-geometric methods for distributed multi-sensor estimation fusion. In Proceedings of the 19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016; pp. 1585–1592. [Google Scholar]
- Cheng, Y.; Wang, X.; Morelande, M.; Moran, B. Information geometry of target tracking sensor network. Inf. Fusion 2013, 14, 311–326. [Google Scholar] [CrossRef]
- Oller, J.M.; Corcuera, J.M. Intrinsic analysis of statistical estimation. Ann. Stat. 1995, 23, 1562–1581. [Google Scholar] [CrossRef]
- Smith, S.T. Covariance, subspace, and intrinsic Cramér-Rao bounds. IEEE Trans. Signal Process. 2005, 53, 1610–1630. [Google Scholar] [CrossRef]
- Amari, S.I. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.I. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Amari, S.I. Differential-Geometrical Methods in Statistics; Vol. 28, Lecture Notes in Statistics; Springer: New York, NY, USA, 1985. [Google Scholar]
- Amari, S.I. Information geometry of the EM and em algorithms for neural networks. Neural Netw. 1995, 8, 1379–1408. [Google Scholar] [CrossRef]
- Amari, S.I. Information geometry of statistical inference–an overview. In Proceedings of the IEEE Information Theory Workshop, Bangalore, India, 25 October 2002; pp. 86–89. [Google Scholar]
- Ay, N.; Jost, J.; Vân Lê, H.; Schwachhöfer, L. Information geometry and sufficient statistics. Probab. Theory Related Fields 2015, 162, 327–364. [Google Scholar] [CrossRef]
- Skovgaard, L.T. A Riemannian geometry of the multivariate normal model. Scand. J. Stat. 1984, 11, 211–223. [Google Scholar]
- Postnikov, M.M. Geometry VI: Riemannian Geometry; Vol. 91, Encyclopaedia of Mathematical Sciences; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Calvo, M.; Oller, J.M. An explicit solution of information geodesic equations for the multivariate normal model. Stat. Decis. 1991, 9, 119–138. [Google Scholar] [CrossRef]
- Imai, T.; Takaesu, A.; Wakayama, M. Remarks on geodesics for multivariate normal models. J. Math. Industry 2011, 3, 125–130. [Google Scholar]
- do Carmo, M.P. Riemannian Geometry; Birkhäuser: Boston, MA, USA, 1992. [Google Scholar]
- Magnant, C.; Grivel, E.; Giremus, A.; Joseph, B.; Ratton, L. Jeffrey’s divergence for state-space model comparison. Signal Process. 2015, 114, 61–74. [Google Scholar] [CrossRef]
- Legrand, L.; Grivel, E. Evaluating dissimilarities between two moving-average models: A comparative study between Jeffrey’s divergence and Rao distance. In Proceedings of the 24th European Signal Processing Conference, Budapest, Hungary, 29 August–2 September 2016; pp. 205–209. [Google Scholar]
- Bernardo, J.M. Reference posterior distributions for Bayesian inference. J. R. Stat. Soc. Series B Stat. Methodol. 1979, 41, 113–147. [Google Scholar]
- Yang, R.; Berger, J.O. Estimation of a covariance matrix using the reference prior. Ann. Stat. 1994, 22, 1195–1211. [Google Scholar] [CrossRef]
- Sun, D.; Berger, J.O. Objective Bayesian analysis for the multivariate normal model. Proceedings of Valencia / ISBA 8th World Meeting on Bayesian Statistics, Alicante, Spain, 1–6 June 2006; pp. 525–547. [Google Scholar]
- Barrau, A.; Bonnabel, S. A note on the intrinsic Cramer-Rao bound. In Geometric Science of Information; Springer: Berlin/Heidelberg, Germany, 2013; pp. 377–386. [Google Scholar]
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Costa, S.I.; Santos, S.A.; Strapasson, J.E. Fisher information distance: A geometrical reading. Discrete Appl. Math. 2015, 197, 59–69. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Arellano-Valle, R.B. Kullback–Leibler divergence measure for multivariate skew-normal distributions. Entropy 2012, 14, 1606–1626. [Google Scholar] [CrossRef]
- Protter, M.H.; Morrey, C.B., Jr. Intermediate Calculus; Springer: New York, NY, USA, 1985. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Moakher, M. A differential geometric approach to the geometric mean of symmetric positive-definite matrices. SIAM J. Matrix Anal. Appl. 2005, 26, 735–747. [Google Scholar] [CrossRef]
- Kelly, E.J. An adaptive detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, 22, 115–127. [Google Scholar] [CrossRef]
- Atkinson, C.; Mitchell, A.F. Rao’s distance measure. Sankhya 1981, 43, 345–365. [Google Scholar]
- Conte, E.; De Maio, A.; Galdi, C. CFAR detection of multidimensional signals: An invariant approach. IEEE Trans. Signal Process. 2003, 51, 142–151. [Google Scholar] [CrossRef]
- Liu, W.; Xie, W.; Wang, Y. Rao and Wald tests for distributed targets detection with unknown signal steering. IEEE Signal Process. Lett. 2013, 20, 1086–1089. [Google Scholar]

| n | n | ||||
|---|---|---|---|---|---|
| 12 | 50 | ||||
| 13 | 100 | ||||
| 14 | 200 | ||||
| 16 | 500 | ||||
| 18 | |||||
| 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, Y.; Tang, M.; Zhou, J. Intrinsic Losses Based on Information Geometry and Their Applications. Entropy 2017, 19, 405. https://doi.org/10.3390/e19080405
Rong Y, Tang M, Zhou J. Intrinsic Losses Based on Information Geometry and Their Applications. Entropy. 2017; 19(8):405. https://doi.org/10.3390/e19080405
Chicago/Turabian StyleRong, Yao, Mengjiao Tang, and Jie Zhou. 2017. "Intrinsic Losses Based on Information Geometry and Their Applications" Entropy 19, no. 8: 405. https://doi.org/10.3390/e19080405





