Effect of Slip Conditions and Entropy Generation Analysis with an Effective Prandtl Number Model on a Nanofluid Flow through a Stretching Sheet
Abstract
:1. Introduction
2. Mathematical Formulation
3. Thermophysical Properties of γAl2O3-H2O and Al2O3-C2H6O2 Nanofluids
- (i)
- Dynamic viscosity model:
- (ii)
- Effective thermal conductivity model:
- (iii)
- Effective Prandtl number model:
4. Important Physical Quantities
5. Entropy Generation Analysis
6. Numerical Method
7. Results and Discussion
8. Conclusions
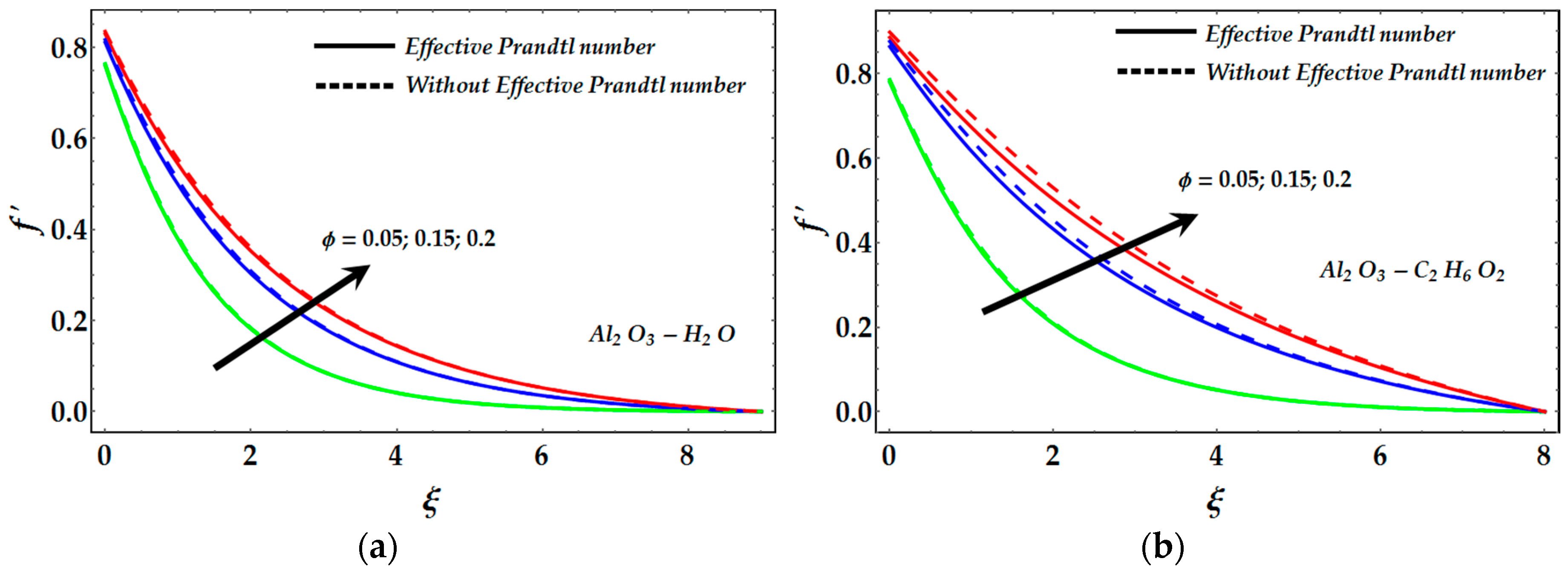
- An increment in nanoparticle volume fraction causes a marked increment in the velocity of nanofluids.
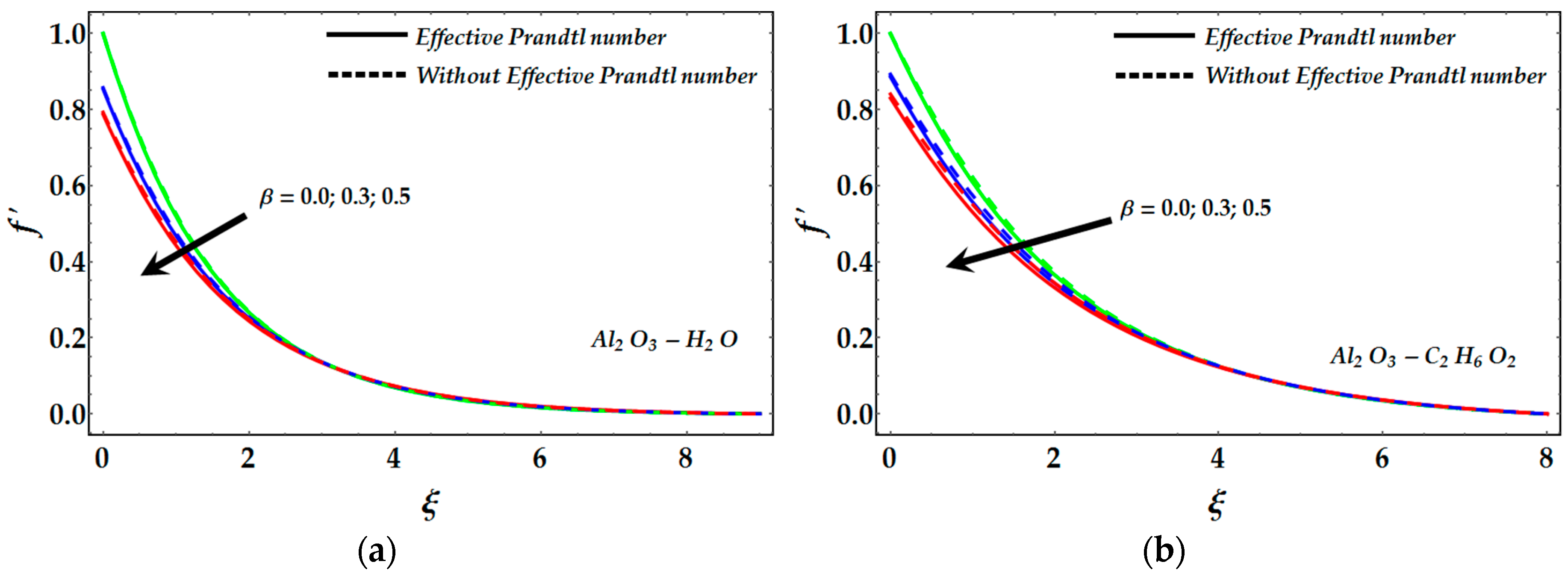
- Slip effects tend to provide a significant resistance in the velocity profile for both γAl2O3-C2H6O2 and γAl2O3-H2O nanofluids. The existence of Prandtl number tends to diminish the velocity profile.
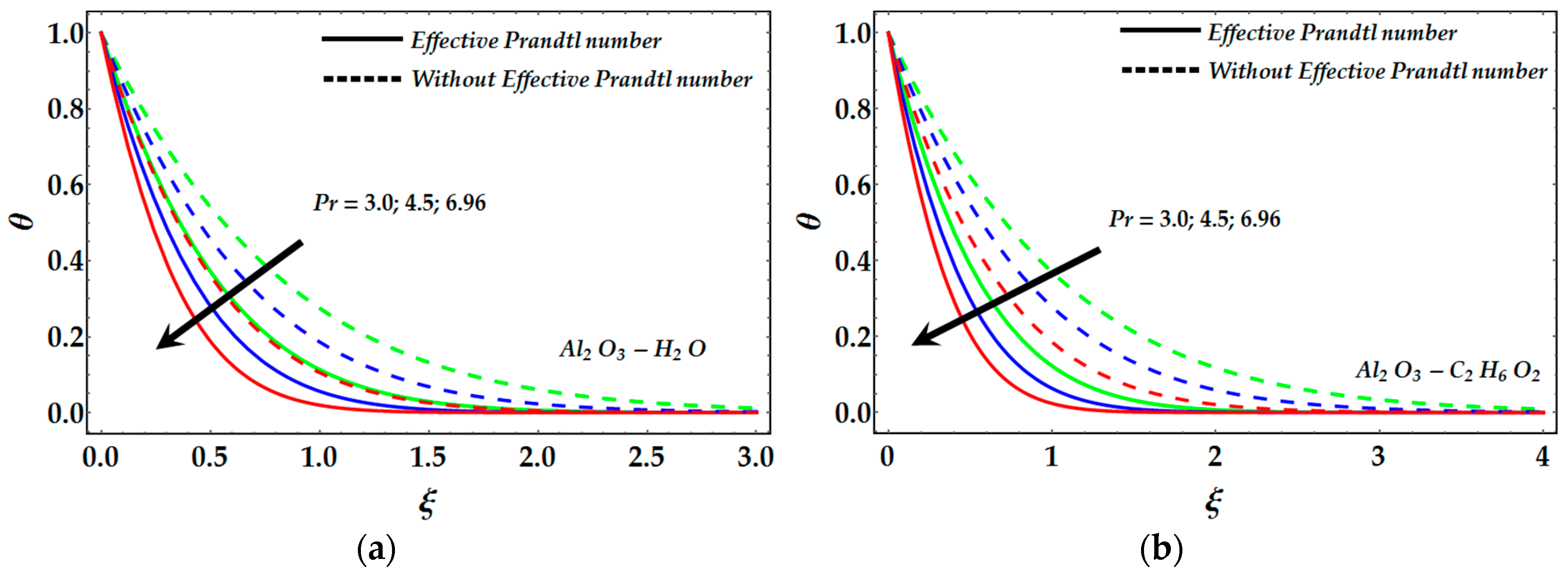
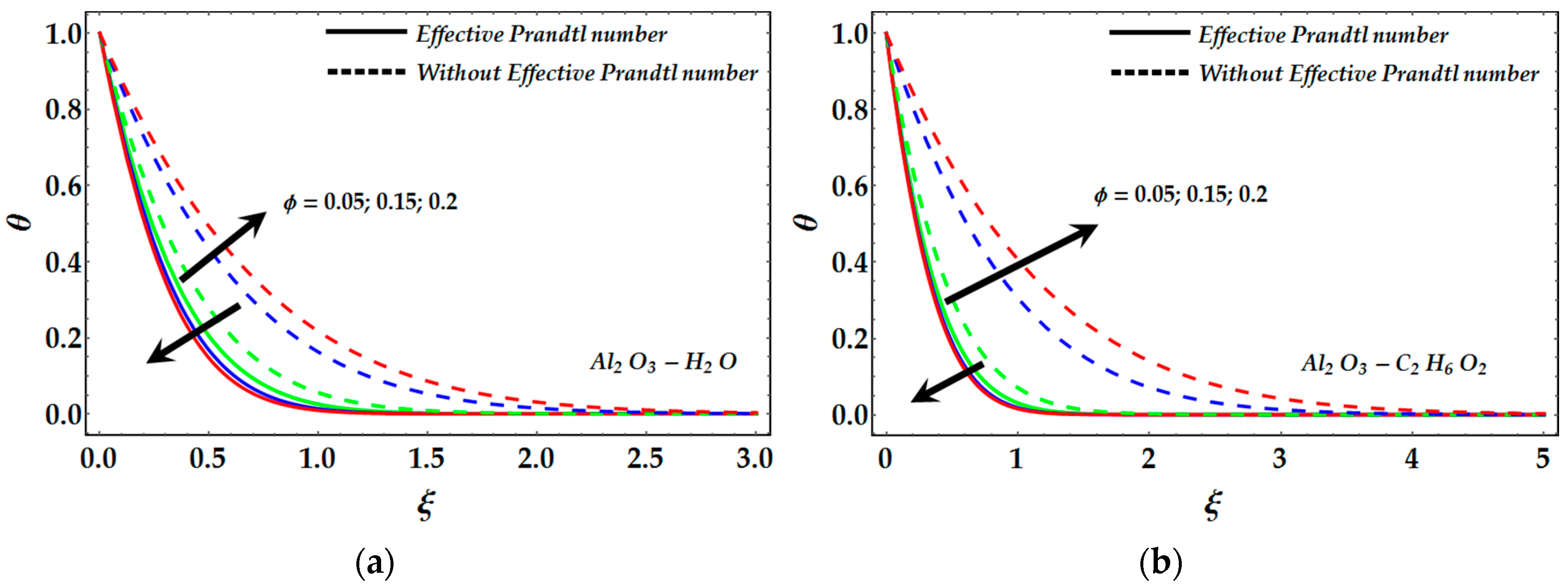
- A remarkable reduction occurs in the temperature profile by increasing the Prandtl number for both γAl2O3-C2H6O2 and γAl2O3-H2O nanofluids.
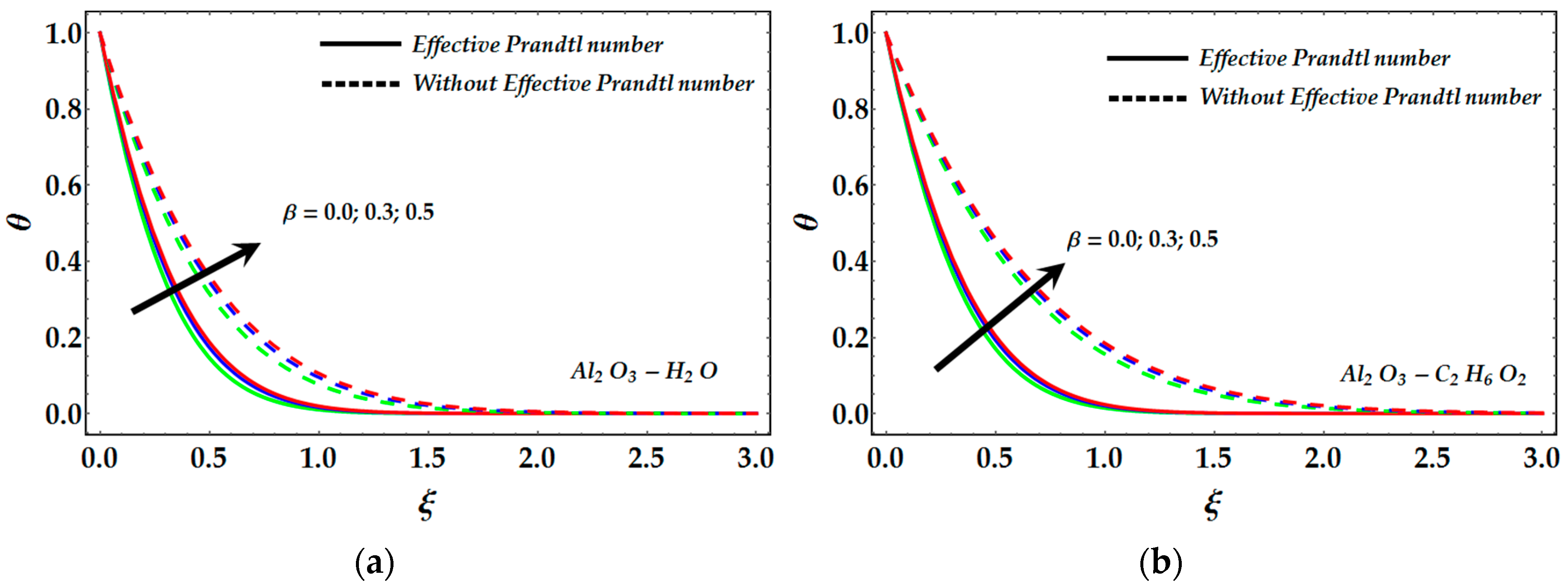
- The impact of slip conditions significantly enhances the temperature profile in the presence and absence of an effective Prandtl number.
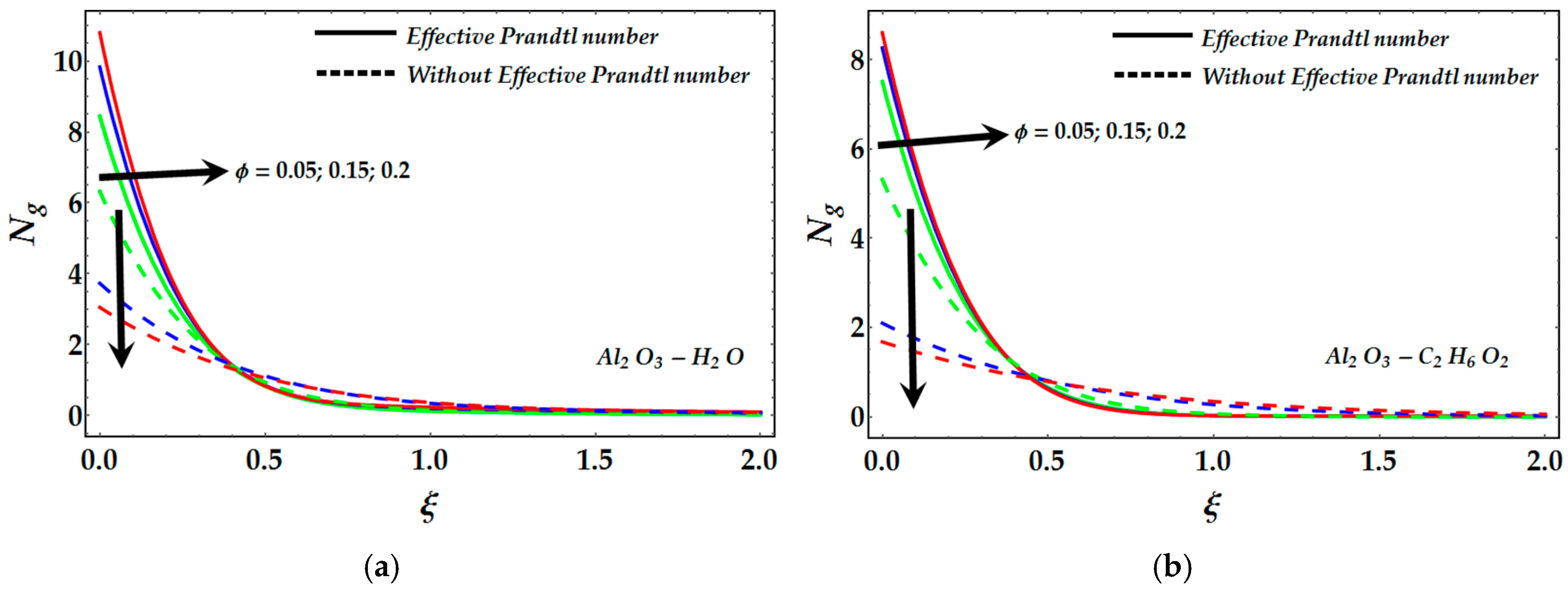
- The temperature profile is enhanced due to nanoparticle volume fraction in the absence of an effective Prandtl number, whereas the converse behavior is seen in the presence of an effective Prandtl number.
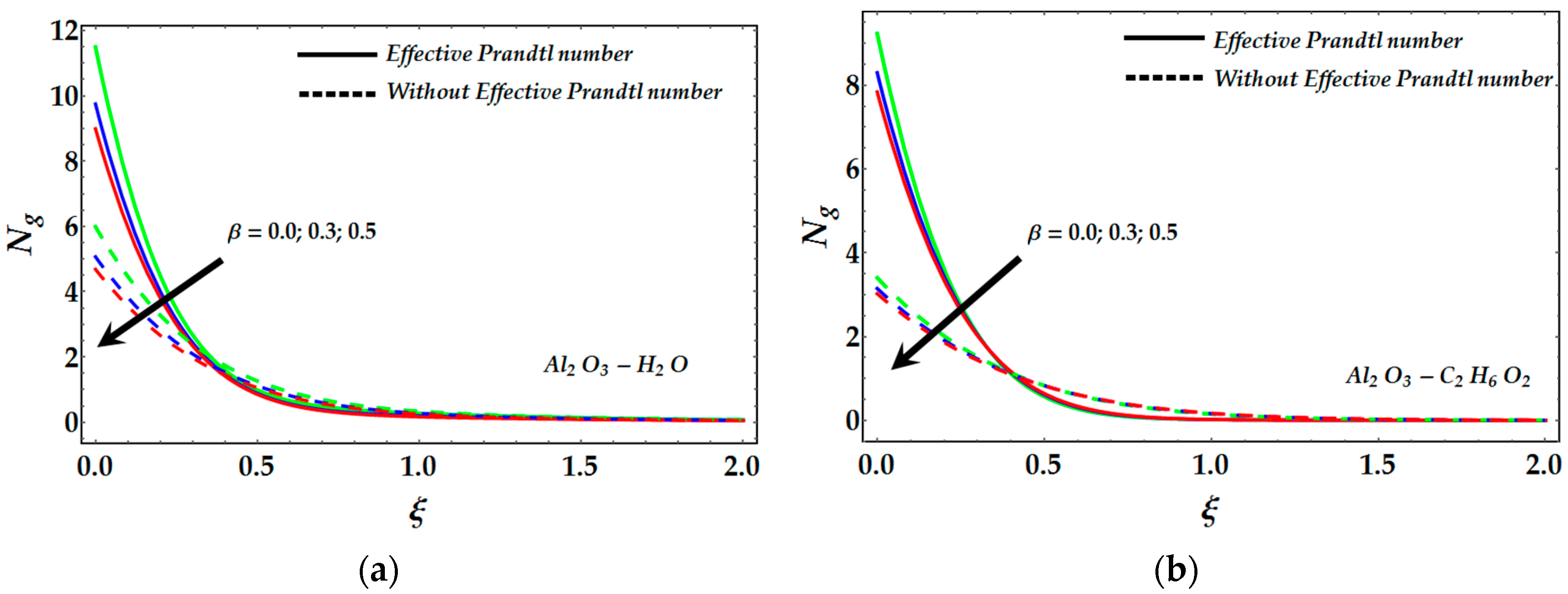
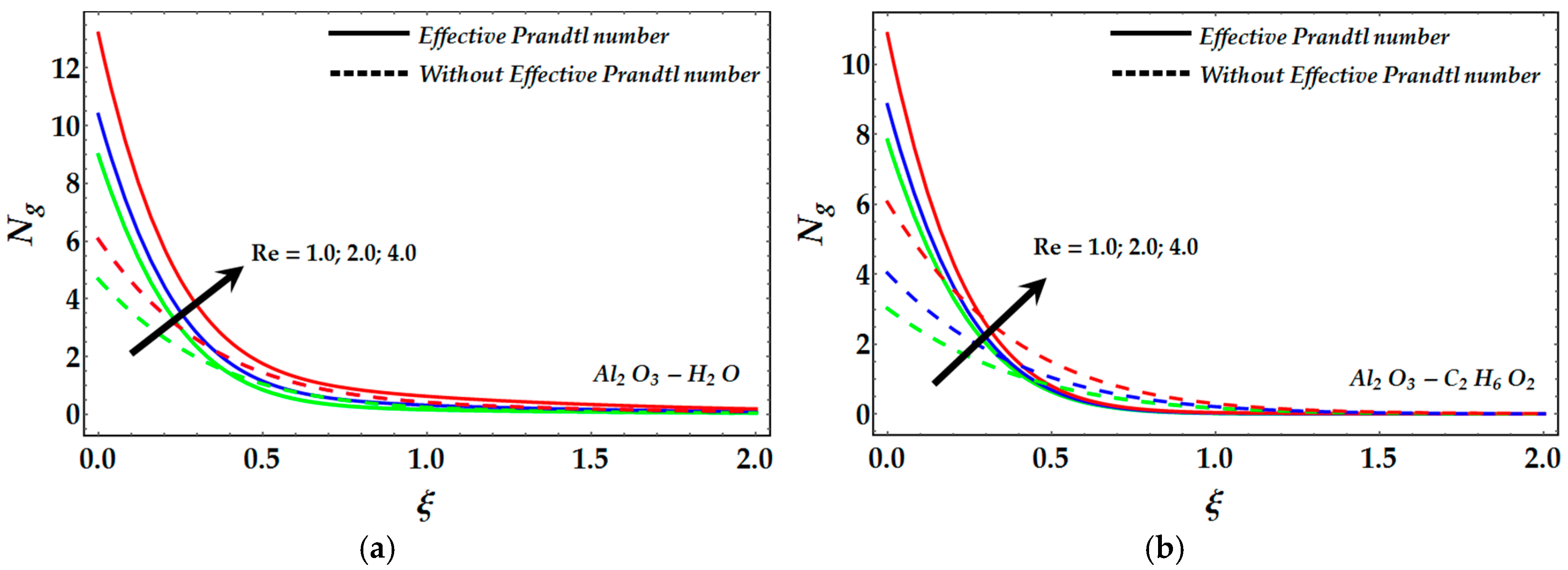
- Due to the increment in slip parameter the entropy profile decreases whereas an effective Prandtl number enhances entropy generation.
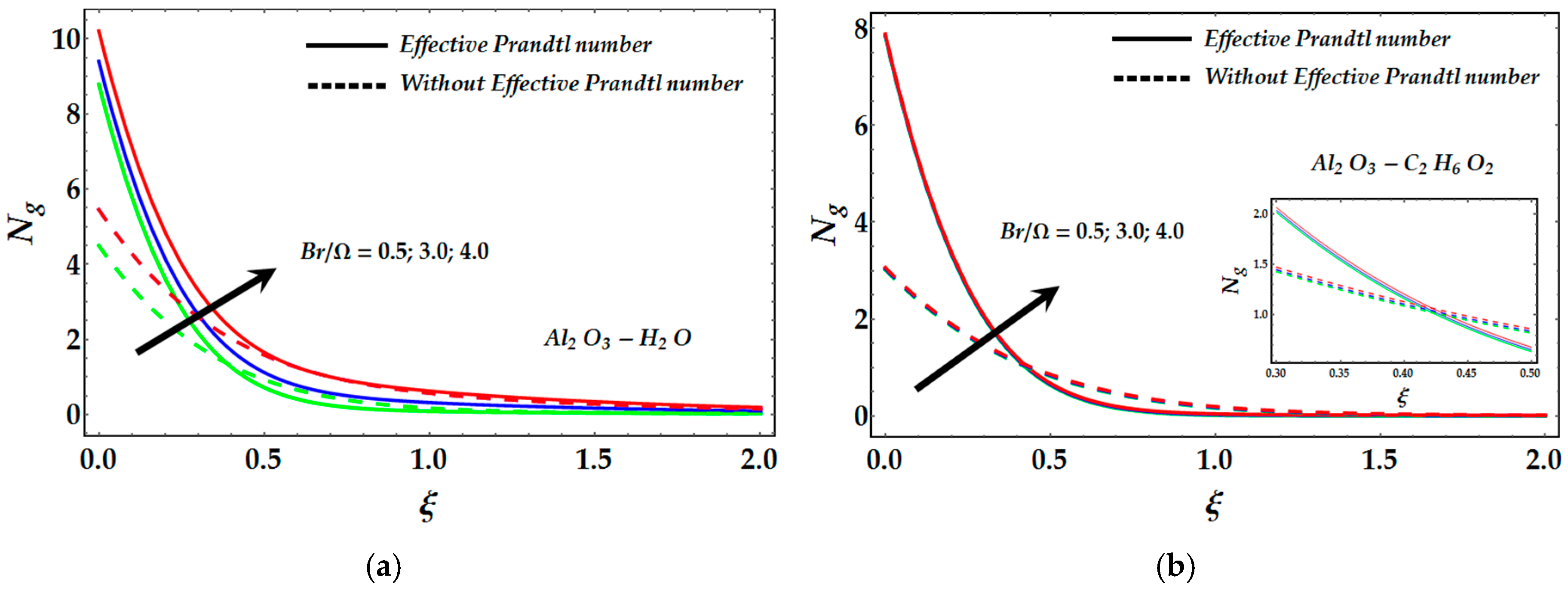
- Reynolds number and Brinkmann number also enhance the entropy profile and a similar relation has been observed in the presence of an effective Prandtl number.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Temperature of wall | |
| Nanofluid, Prandtl number | |
| g,m/ | Gravity |
| Nanofluid, thermal conductivity | |
| Nanofluid temperature | |
| Base fluid Prandtl number | |
| Nusselt number of nano fluid | |
| skin friction coefficient | |
| Base fluid, thermal conductivity | |
| ambient temperature | |
| m/s | Expression of velocity in horizontal and vertical directions, Respectively |
| Nanoparticles, thermal conductivity |
Greek Symbols
| parameter of mixed convection | |
| volume fraction of the model | |
| nanofluid effective density | |
| viscosity of the nanofluid effective dynamic | |
| coefficient of Nanoparticles thermal expansion | |
| the base fluid dynamic viscosity | |
| Base fluid thermal expansion coefficient | |
| Nanoparticles density | |
| base fluid density | |
| nanofluid thermal expansion coefficient | |
| variable of space |
References
- Chol, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed 1995, 231, 99–106. [Google Scholar]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinunma, N.; Ebata, Y. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles (dispersion of γ-Al2O3, SiO2 and TiO2 ultra-fine particles). Netsu Bussei 1993, 7, 227–233. (In Janpanese) [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.; Khan, Z.H. Numerical study of MHD boundary layer flow of Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Malik, M.Y.; Khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Eyring-Powell nanofluid over a streching sheet: A numerical study. AIP Adv. 2015, 5, 117–118. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. Unsteady Casson nano over a rotating cone in a rotating frame filled with ferrous nanoparticles: A numerical study. J. Magn. Magn. Mater. 2017, 421, 216–224. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. Analytical study of third grade fluid over a rotating vertical cone in thepresence of nanoparticles. Int. J. Heat Mass Transf. 2015, 85, 1041–1048. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Malvandi, A. Free convective heat and mass transfer of MHD Non-Newtonian nanofluids over a cone in the presence of non-uniform heat soure/sink. J. Mol. Liq. 2016, 221, 108–115. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. Unsteady mixed convection flow of nanofluid on a rotating cone with magnetic field. Appl. Nanosci. 2014, 4, 405–414. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liq. 2016, 221, 567–573. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.; Khan, Z.H. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl. Nanosci. 2014, 4, 625–631. [Google Scholar] [CrossRef]
- Hsiao, K.L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Hsiao, K.L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, L.; Zhang, X.; Chen, G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Appl. Math. Model. 2015, 39, 161–184. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Rahman, M.M.; Roşca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 77, 1133–1143. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Rashidi, M.M. Numerical simulation of Fluid flow over a shrinking porous sheet by Successive linearization method. Alexandria Eng. J. 2016, 55, 51–56. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Hsiao, K.L. Numerical solution for Ohmic Soret-Dufour heat and mass mixed convection of viscoelastic fluid over a stretching sheet with multimedia physical features. J. Aerosp. Eng. 2016, 30, 04016082. [Google Scholar] [CrossRef]
- Shahid, A.; Bhatti, M.M.; Bég, O.A.; Kadir, A. Numerical study of radiative Maxwell viscoelastic magnetized flow from a stretching permeable sheet with the Cattaneo–Christov heat flux model. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Mishra, S.R.; Bhatti, M.M. Simultaneous effects of Chemical reaction and Ohmic heating with heat and mass transfer over a stretching surface: A numerical study. Chin. J. Chem. Eng. 2017. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2006, 18, 123. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M.; Pop, I. Entropy Generation with nonlinear heat and Mass transfer on MHD Boundary Layer over a Moving Surface using SLM. Nonlinear Eng. 2017, 6, 43–52. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.S. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bagheri, S.; Momoniat, E.; Freidoonimehr, N. Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretching sheet. Ain Shams Eng. J. 2015. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Entropy generation as a practical tool of optimisation for non-Newtonian nanofluid flow through a permeable stretching surface using SLM. J. Comput. Des. Eng. 2017, 4, 21–28. [Google Scholar] [CrossRef]
- Lee, S.; Choi, S.U.-S.; Li, S.; Eastman, J.A. Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf. 1999, 121, 280–289. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.-S. Thermal conductivity of nanoparticles-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer behaviors of nanofluids in a uniformly heated tube. Superlattices Microstruct. 2004, 35, 543–557. [Google Scholar] [CrossRef]
- Pop, C.V.; Fohanno, S.; Polidori, G.; Nguyen, C.T. Analysis of laminar-to-turbulent threshold with water c Al2O3 and ethylene glycol-c Al2O3 nanofluids in free convection. In Proceedings of the 5th IASME/WSEAS International Conference on Heat Transfer, Thermal Engineering and Environment, Athens, Greece, 25–27 August 2017; p. 188. [Google Scholar]
- Bhatti, M.M.; Rashidi, M.M. Entropy generation with nonlinear thermal radiation in MHD boundary layer flow over a permeable shrinking/stretching sheet: Numerical solution. J. Nanofluids 2016, 5, 543–548. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Numerical Study of Entropy Generation with Nonlinear Thermal Radiation on Magnetohydrodynamics non-Newtonian Nanofluid Through a Porous Shrinking Sheet. J. Magn. 2016, 21, 468–475. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Numerical simulation of entropy generation on MHD nanofluid towards a stagnation point flow over a stretching surface. Int. J. Appl. Comput. Math. 2017, 3, 2275–2289. [Google Scholar] [CrossRef]
- Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Ali, M.E. Heat transfer characteristics of a continuous stretching surface. Heat Mass Transf. 1994, 429, 227–234. [Google Scholar] [CrossRef]
- Grubka, L.J.; Bobba, K.M. Heat transfer characteristics of a continuous, stretching surface with variable temperature. ASME J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 2009, 44, 369–375. [Google Scholar] [CrossRef]

| (J/kg·K) | (K−1) | (kg/m3) | (W/m·K) | |
|---|---|---|---|---|
| Water (H2O) | 4182 | 20.06 | 998.3 | 0.60 |
| Ethylene glycol (C2H6O2) | 2382 | 65 | 1116.6 | 0.249 |
| Alumina (Al2O3) | 765 | 0.85 | 3970 | 40 |
| λ | Pr | Ali [34] | Grubka and Bobba [35] | Ishak et al. [36] | Present Results |
|---|---|---|---|---|---|
| 0 | 0.72 | 0.8058 | 0.8086 | 0.8086 | 0.80883 |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.00001 | |
| 3 | 1.9237 | 1.9144 | 1.9237 | 1.92368 | |
| 7 | 3.0723 | 3.07225 | |||
| 10 | 3.7006 | 3.7207 | 3.7207 | 3.72067 | |
| 100 | 12.2940 | 12.2941 | 12.29408 | ||
| 1 | 1 | 1.0873 | 1.08728 | ||
| 2 | 1.1423 | 1.14234 | |||
| 3 | 1.1853 | 1.18528 |
| For γAl2O3-H2O | For Al2O3-C2H6O2 | |||||||
|---|---|---|---|---|---|---|---|---|
| With Effective Prandtl Parameter | Without Effective Prandtl Parameter | With Effective Prandtl Parameter | Without Effective Prandtl Parameter | With Effective Prandtl Parameter | Without Effective Prandtl Parameter | With Effective Prandtl Paramet | Without Effective Prandtl Paramet | |
| 1 | 1.29991 | 1.28495 | 1.25372 | 0.78594 | 1.43666 | 1.39986 | 27.6293 | 14.0726 |
| 3 | 1.31432 | 1.30461 | 2.30596 | 1.49072 | 1.45995 | 1.43458 | 50.1784 | 26.4527 |
| 6.96 | 1.32164 | 1.31481 | 3.60726 | 2.36655 | 1.4718 | 1.45394 | 78.076 | 41.9535 |
| 10 | 1.32407 | 1.31821 | 4.35964 | 2.87282 | 1.47573 | 1.46041 | 94.2088 | 50.9162 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashidi, M.M.; Abbas, M.A. Effect of Slip Conditions and Entropy Generation Analysis with an Effective Prandtl Number Model on a Nanofluid Flow through a Stretching Sheet. Entropy 2017, 19, 414. https://doi.org/10.3390/e19080414
Rashidi MM, Abbas MA. Effect of Slip Conditions and Entropy Generation Analysis with an Effective Prandtl Number Model on a Nanofluid Flow through a Stretching Sheet. Entropy. 2017; 19(8):414. https://doi.org/10.3390/e19080414
Chicago/Turabian StyleRashidi, Mohammad Mehdi, and Munawwar Ali Abbas. 2017. "Effect of Slip Conditions and Entropy Generation Analysis with an Effective Prandtl Number Model on a Nanofluid Flow through a Stretching Sheet" Entropy 19, no. 8: 414. https://doi.org/10.3390/e19080414




