Power-Law Distributions from Sigma-Pi Structure of Sums of Random Multiplicative Processes
Abstract
:1. Introduction
2. Model Description and Formal Solution
2.1. Model Definition
2.2. Dependence Structure of the Growth Factors
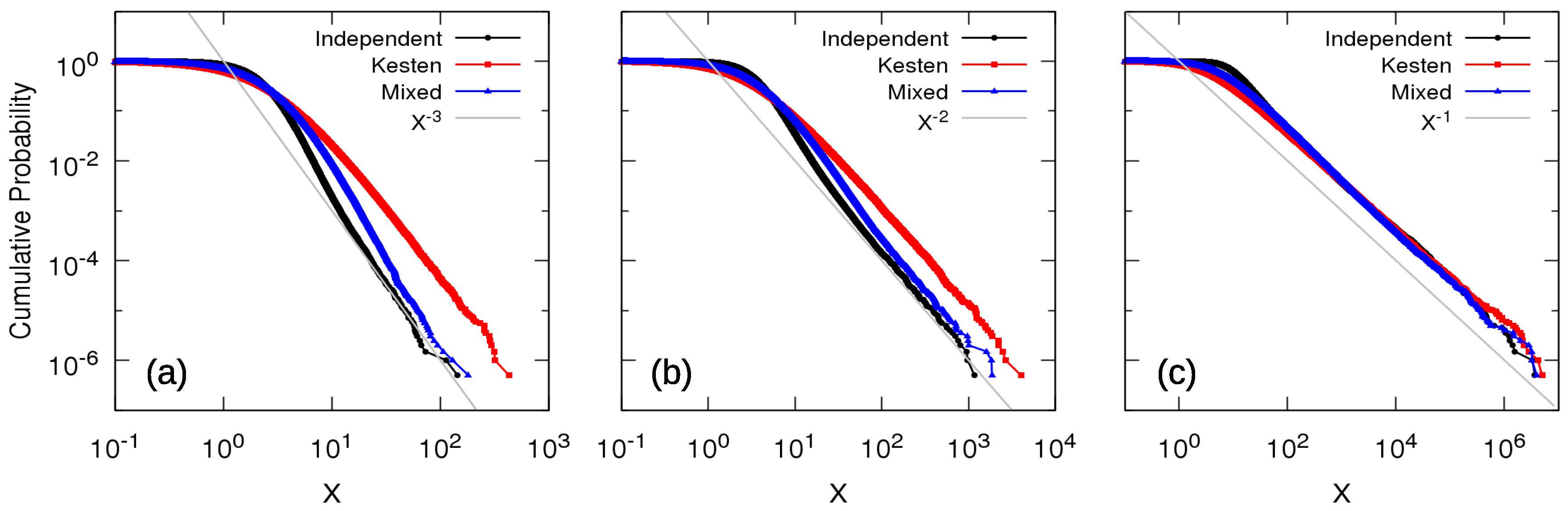
- Independence: all entities are growing independently:Observe that the notation does not mean that these variables cannot have by chance the same value. This notation just expresses that they are independent random variables.
- Kesten dependence: external influences determine the same growth factor for all existing entities at each given time, but the growth factor is a random variable as a function of time. This case reproduces the solution of the Kesten process (3) and constitutes a novel interpretation of the said process, originally representing a single entity evolving in the presence of an additive term:
- Mixed dependence: alternation between independence and Kesten dependence, say independence for odd t and Kesten dependence for even t, representing a time-changing dependence. Note that this is only one of the many possibilities for the combination of independence and Kesten dependence.
2.3. Asymptotic Power-Law Tails
2.4. Generalization
3. Numerical Simulations and Discussion
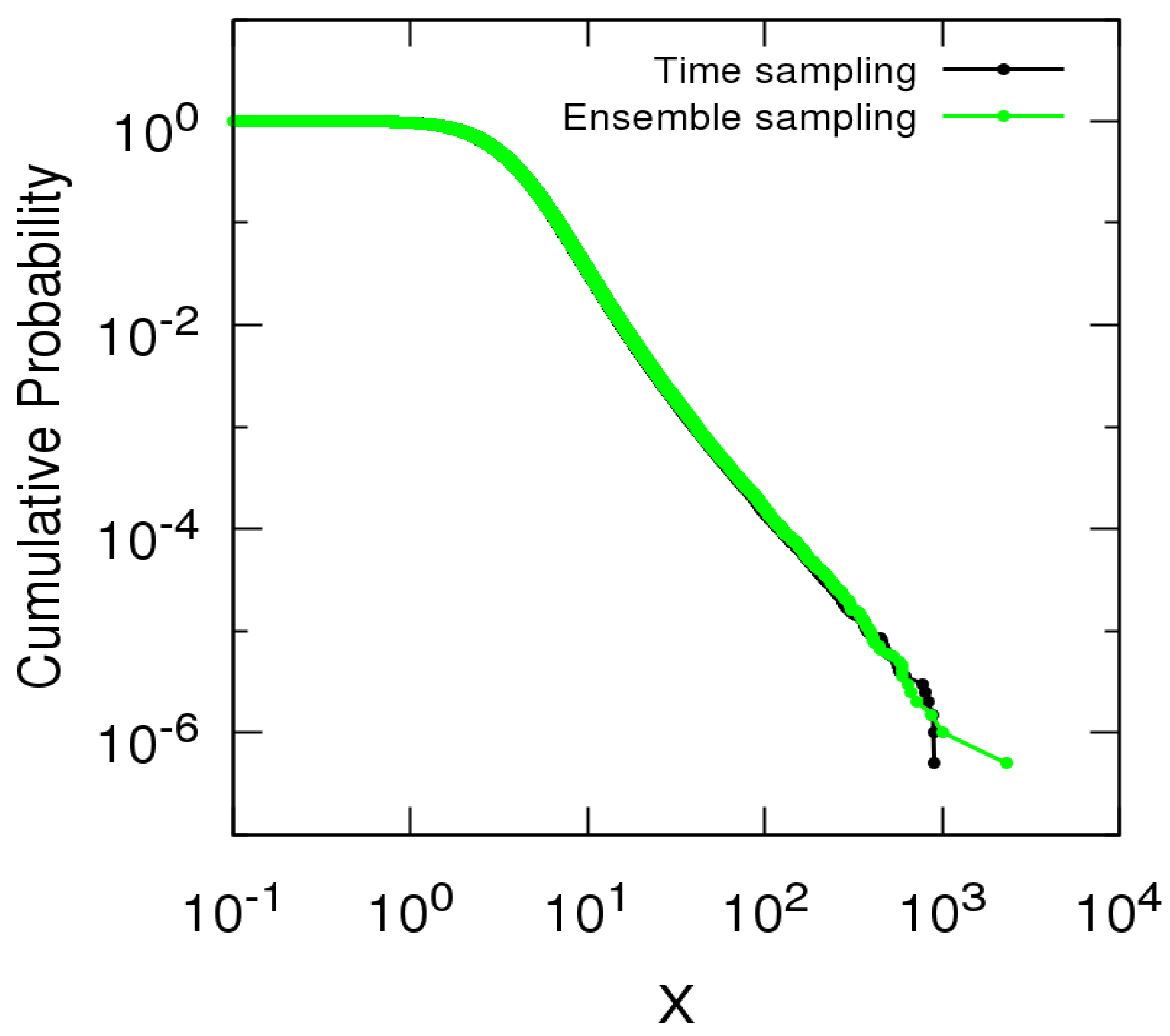
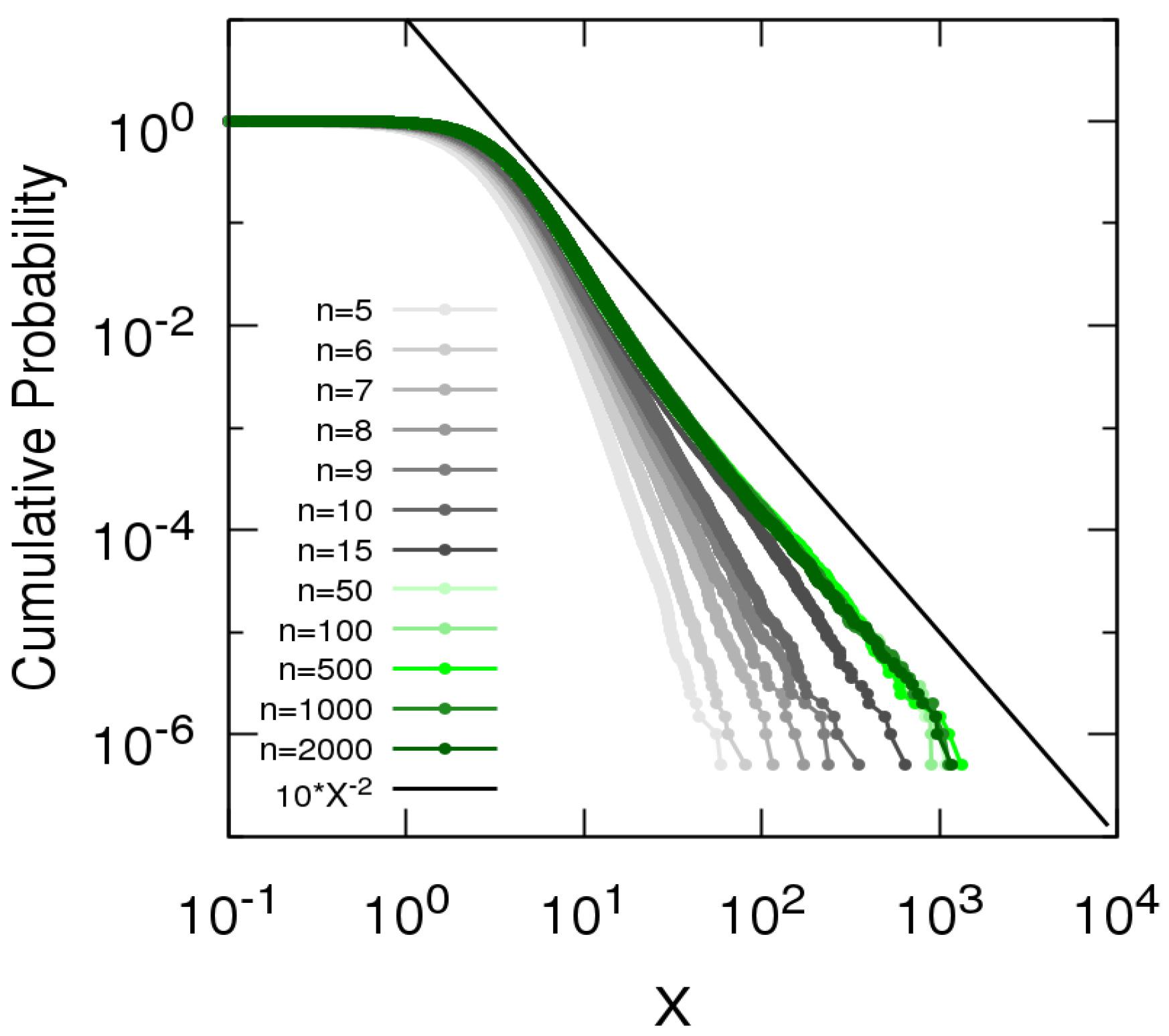
3.1. Numerical Construction of the Complementary Cumulative Distribution Function of Sum of Sizes
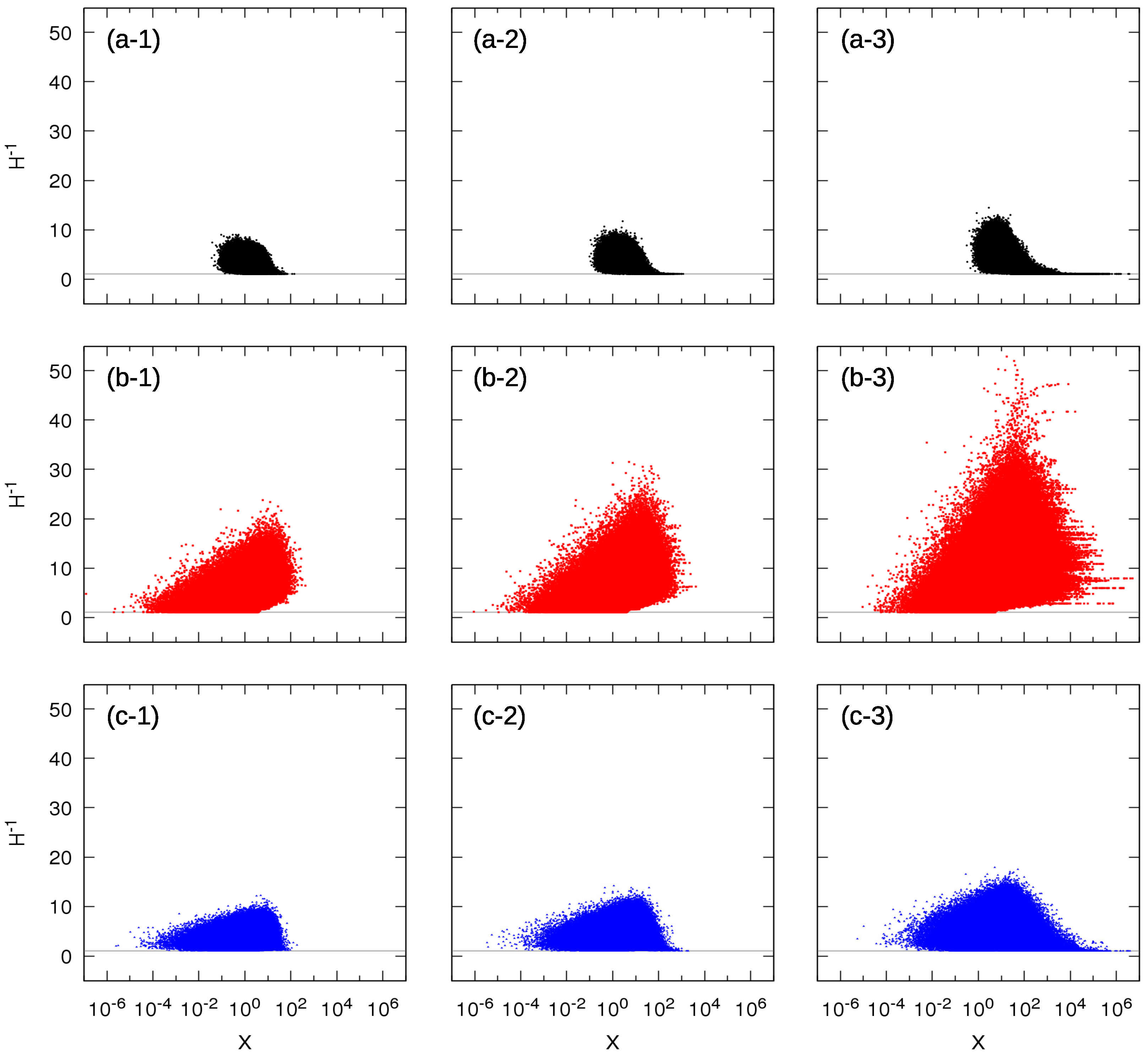
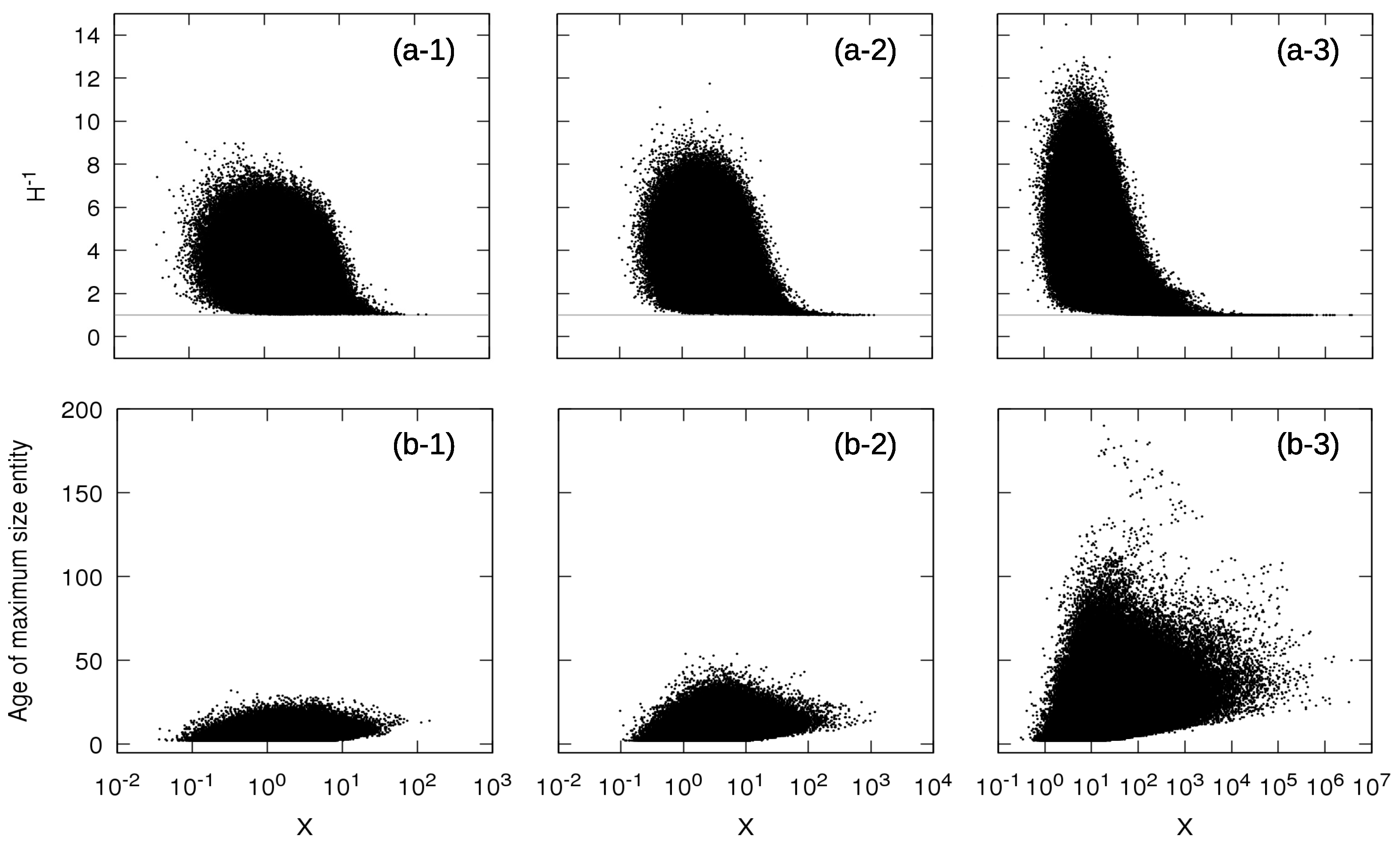
3.2. Study of the Entities Contributing to the Sum of Sizes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Newman, M.E. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Foss, S.; Korshunov, D.; Zachary, S. An Introduction to Heavy-Tailed and Subexponential Distributions; Springer: New York, NY, USA, 2011; Volume 6. [Google Scholar]
- Mitzenmacher, M. A brief history of generative models for power law and lognormal distributions. Internet Math. 2004, 1, 226–251. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yule, G.U. A mathematical theory of evolution, based on the conclusions of Dr. JC Willis, FRS. Philos. Trans. R. Soc. Lond. Ser. B Contain. Pap. Biol. Character 1925, 213, 21–87. [Google Scholar] [CrossRef]
- Simon, H.A. On a class of skew distribution functions. Biometrika 1955, 42, 425–440. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R.; Jeong, H. Mean-field theory for scale-free random networks. Phys. A Stat. Mech. Appl. 1999, 272, 173–187. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef] [PubMed]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Copernicus Press: New York, NY, USA, 1996. [Google Scholar]
- Taguchi, Y.H.; Takayasu, H. Power law velocity fluctuations due to inelastic collisions in numerically simulated vibrated bed of powder. Europhys. Lett. 1995, 30, 499. [Google Scholar] [CrossRef]
- Frisch, U.; Sornette, D. Extreme deviations and applications. J. Phys. I 1997, 7, 1155–1171. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A Stat. Mech. Appl. 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Beck, C. Superstatistics: Theoretical concepts and physical applications. arXiv, 2007; arXiv:0705.3832. [Google Scholar]
- Hanel, R.; Thurner, S.; Gell-Mann, M. Generalized entropies and the transformation group of superstatistics. Proc. Natl. Acad. Sci. USA 2011, 108, 6390–6394. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Buldyrev, S.V.; Havlin, S.; Salinger, M.A.; Stanley, H.E. Power law scaling for a system of interacting units with complex internal structure. Phys. Rev. Lett. 1998, 80, 1385. [Google Scholar] [CrossRef]
- Huynen, M.A.; van Nimwegen, E. The frequency distribution of gene family sizes in complete genomes. Mol. Biol. Evol. 1998, 15, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Blank, A.; Solomon, S. Power laws in cities population, financial markets and internet sites (scaling in systems with a variable number of components). Phys. A Stat. Mech. Appl. 2000, 287, 279–288. [Google Scholar] [CrossRef]
- Keitt, T.H.; Amaral, L.A.; Buldyrev, S.V.; Stanley, H.E. Scaling in the growth of geographically subdivided populations: Invariant patterns from a continent-wide biological survey. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002, 357, 627–633. [Google Scholar] [CrossRef] [PubMed]
- Picoli, S., Jr.; Mendes, R.S. Universal features in the growth dynamics of religious activities. Phys. Rev. E 2008, 77, 036105. [Google Scholar] [CrossRef] [PubMed]
- Saichev, A.I.; Malevergne, Y.; Sornette, D. Theory of Zipf’s Law and Beyond; Springer: Berlin/Heidelberg, Germany, 2009; Volume 632. [Google Scholar]
- Alves, L.G.; Ribeiro, H.V.; Mendes, R.S. Scaling laws in the dynamics of crime growth rate. Phys. A Stat. Mech. Appl. 2013, 392, 2672–2679. [Google Scholar] [CrossRef]
- Takayasu, M.; Watanabe, H.; Takayasu, H. Generalised central limit theorems for growth rate distribution of complex systems. J. Stat. Phys. 2014, 155, 47–71. [Google Scholar] [CrossRef]
- Sutton, J. Gibrat’s legacy. J. Econ. Lit. 1997, 35, 40–59. [Google Scholar]
- Kesten, H. Random difference equations and renewal theory for products of random matrices. Acta Math. 1973, 131, 207–248. [Google Scholar] [CrossRef]
- Goldie, C.M. Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Probab. 1991, 126–166. [Google Scholar] [CrossRef]
- Takayasu, H.; Sato, A.H.; Takayasu, M. Stable infinite variance fluctuations in randomly amplified Langevin systems. Phys. Rev. Lett. 1997, 79, 966. [Google Scholar] [CrossRef]
- Sornette, D. Multiplicative processes and power laws. Phys. Rev. E 1998, 57, 4811. [Google Scholar] [CrossRef]
- Buraczewski, D.; Damek, E.; Mikosch, T. Stochastic Models with Power-Law Tails; Springer: New York, NY, USA, 2016. [Google Scholar]
- Sornette, D.; Cont, R. Convergent multiplicative processes repelled from zero: Power laws and truncated power laws. J. Phys. I 1997, 7, 431–444. [Google Scholar] [CrossRef]
- Hisano, R.; Sornette, D.; Mizuno, T. Predicted and verified deviations from Zipf’s law in ecology of competing products. Phys. Rev. E 2011, 84, 026117. [Google Scholar] [CrossRef] [PubMed]
- Malevergne, Y.; Saichev, A.; Sornette, D. Zipf’s law and maximum sustainable growth. J. Econ. Dyn. Control 2013, 37, 1195–1212. [Google Scholar] [CrossRef]
- Weisstein, E.W. Half-Normal Distribution. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/Half-NormalDistribution.html (accessed on 16 August 2017).
- Mikosch, T.; Rezapour, M.; Wintenberger, O. Heavy tails for an alternative stochastic perpetuity model. arXiv, 2017; arXiv:1703.07272. [Google Scholar]
- Herfindahl-Hirschman Index—HHI. Available online: http://investopedia.com/terms/h/hhi.asp (accessed on 20 July 2017).
- Mézard, M.; Parisi, G.; Virasoro, M.A. Random free energies in spin glasses. J. Phys. Lett. 1985, 46, 217–222. [Google Scholar] [CrossRef]
- Sornette, D. Dragon-kings, black swans and the prediction of crises. Int. J. Terrasp. Sci. Eng. 2009, 2, 1–18. [Google Scholar] [CrossRef]
- Sornette, D.; Ouillon, G. Dragon-kings: Mechanisms, statistical methods and empirical evidence. Eur. Phys. J. Spec. Top. 2012, 205, 1–26. [Google Scholar] [CrossRef]
- Huberman, B.A.; Adamic, L.A. Internet: Growth dynamics of the world-wide web. Nature 1999, 401, 131. [Google Scholar]
- Reed, W.J. The Pareto law of incomes—An explanation and an extension. Phys. A Stat. Mech. Appl. 2003, 319, 469–486. [Google Scholar] [CrossRef]
- Weisstein, E.W. Multinomial Series. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/MultinomialSeries.html (accessed on 16 August 2017).
- Flajolet, P.; Gourdon, X.; Dumas, P. Mellin transforms and asymptotics: Harmonic sums. Theor. Comput. Sci. 1995, 144, 3–58. [Google Scholar] [CrossRef]
- Weisstein, E.W. Mellin Transform. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/MellinTransform.html (accessed on 16 August 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, A.M.Y.R.d.; Takayasu, H.; Sornette, D.; Takayasu, M. Power-Law Distributions from Sigma-Pi Structure of Sums of Random Multiplicative Processes. Entropy 2017, 19, 417. https://doi.org/10.3390/e19080417
Sousa AMYRd, Takayasu H, Sornette D, Takayasu M. Power-Law Distributions from Sigma-Pi Structure of Sums of Random Multiplicative Processes. Entropy. 2017; 19(8):417. https://doi.org/10.3390/e19080417
Chicago/Turabian StyleSousa, Arthur Matsuo Yamashita Rios de, Hideki Takayasu, Didier Sornette, and Misako Takayasu. 2017. "Power-Law Distributions from Sigma-Pi Structure of Sums of Random Multiplicative Processes" Entropy 19, no. 8: 417. https://doi.org/10.3390/e19080417



