Rate-Distortion Theory for Clustering in the Perceptual Space
Abstract
:1. Introduction
2. Related Work
2.1. Information Visualization and Information Theory
2.2. Information Visualization and Clustering
3. Theoretical Background
3.1. Information-Theoretic Measures
3.2. Rate-Distortion Theory
3.2.1. Blahut–Arimoto Algorithm
3.2.2. Rate-Distortion Theory and Clustering
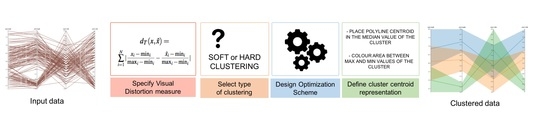
4. Method
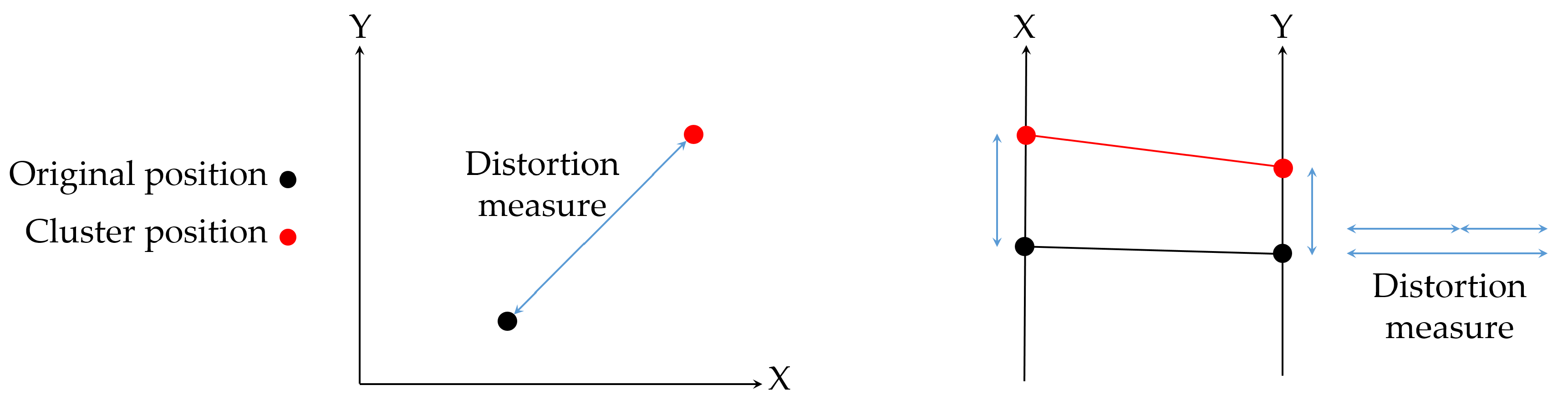
4.1. Perceptual Distortion
4.1.1. Single-Channel Distortion
- Position Channel. This channel can be restricted to a given direction (for instance, the horizontal and vertical directions) or in the 2D plane. In both cases, the most natural measure of distortion is the Euclidean distance between the actual position and the position of the cluster that represents the data. More formally, for the 1D case (limited to one direction), the distortion is given bywhere the subindex i indicates the position along the axis, and, for the 2D case, bywhere the subindexes i and j indicate the position coordinates in the 2D plane. Special attention requires the 3D case, since although humans live in a 3D space, our perceptual system does not really work in 3D. Most of the visual information that we have is about the projected 2D image plane while the depth has a minor perceptual weight [35,36]. This fact can be considered in the definition of the perceptual distortion measure and, hence, a possible measure of distortion iswhere the subindexes and indicate the projection of the 3D position in the image plane, the subindex d stands for the depth of the 3D position, and the parameter weights the contribution of the depth in the distortion measure. Perceptual studies could be performed to determine how to adjust the value of for a specific application.
- Color Channel. Two main uses are given to the color channel. First, a scalar value can be encoded, typically, through the luminance or the saturation color channels. In this case, the difference between the values in the original data and the cluster center would be the most natural distortion measure. Second, a categorical value can be encoded, typically, through the hue color channel. In this case, the most natural measure is the Hamming distortion, which is defined asIn general, if a more complex color encoding scheme is used, the distortion measure could be defined in the CIELab color space [37], since distances in this color space are perceptually uniform.
- Shape Channel. This channel refers to the different shapes that visual marks can take. Usually, it is used to encode categorical values, assigning a different shape (for instance, a circle, a square, a cross, or a triangle) to each category. In this case, the most appropriate measure would be the Hamming distortion (see Equation (17)). Other perceptual measures can also be defined. For instance, Demiralp et al. [38] analyzed the perceptual similarity of different shapes (as well as other channels such as color and size). From similar experiments, a similarity value between any pair of shapes can be computed and used for the clustering process.Other examples involving shape are to represent numerical data, such as the use of ellipsoids to represent the eigenvectors and eigenvalues of a tensor. In this case, the distortion measure can be related to the differences between the ellipsoid surfaces of the original data and the clustered one.
- Tilt Channel. This channel, also called angle, encodes a numerical value as an angular representation. A typical example is its use in a pie chart. In this case, the most natural measure of distortion would be the angular distance (equivalently to Equation (14)).
- Size Channel. This channel encodes a number as length when the mark is 1D, as area when it is 2D, and as volume when it is 3D. Here again, the most natural measure is the absolute difference between both values (see Equation (14)), although other measures arise due to the perceptual differences between the different number of dimensions of the mark. For instance, according to the Stevens’ psychophysical law [39], visual areas have a coefficient . Thus, in this case, an alternative distortion measure would bewith equals to 0.7.
4.1.2. Multi-Channel Distortion
4.2. Perceptual Clustering
- Specify the perceptual distortion measure. Following the guidelines presented in the previous section and according to the selected visual channel, we have to define the distortion measure between original data representation and the cluster centroid one.
- Select the type of clustering. We can select between hard or soft clustering. For applications where each data element has to be identified in a single cluster, a hard clustering technique is more appropriate, while, in the other applications, the recommended strategy is soft clustering.
- Design the optimization scheme. The optimization strategy depends on the selected clustering. As we have shown in Section 3.2.1, for a soft clustering strategy, the Blahut–Arimoto algorithm is the most common algorithm. In this case, the parameter has to be chosen to tune the trade-off between compression and accuracy. With the given distortion measure, the function that fulfills the centroid condition must also be found. For a hard clustering, a great variety of optimization techniques can be applied [40].
- Design the cluster centroid representation. Finally, the centroid values have to be shown in an appropriate way to the final user. In addition to the value itself, other information such as cluster probability could also be introduced in the final visualization.
5. Application Examples
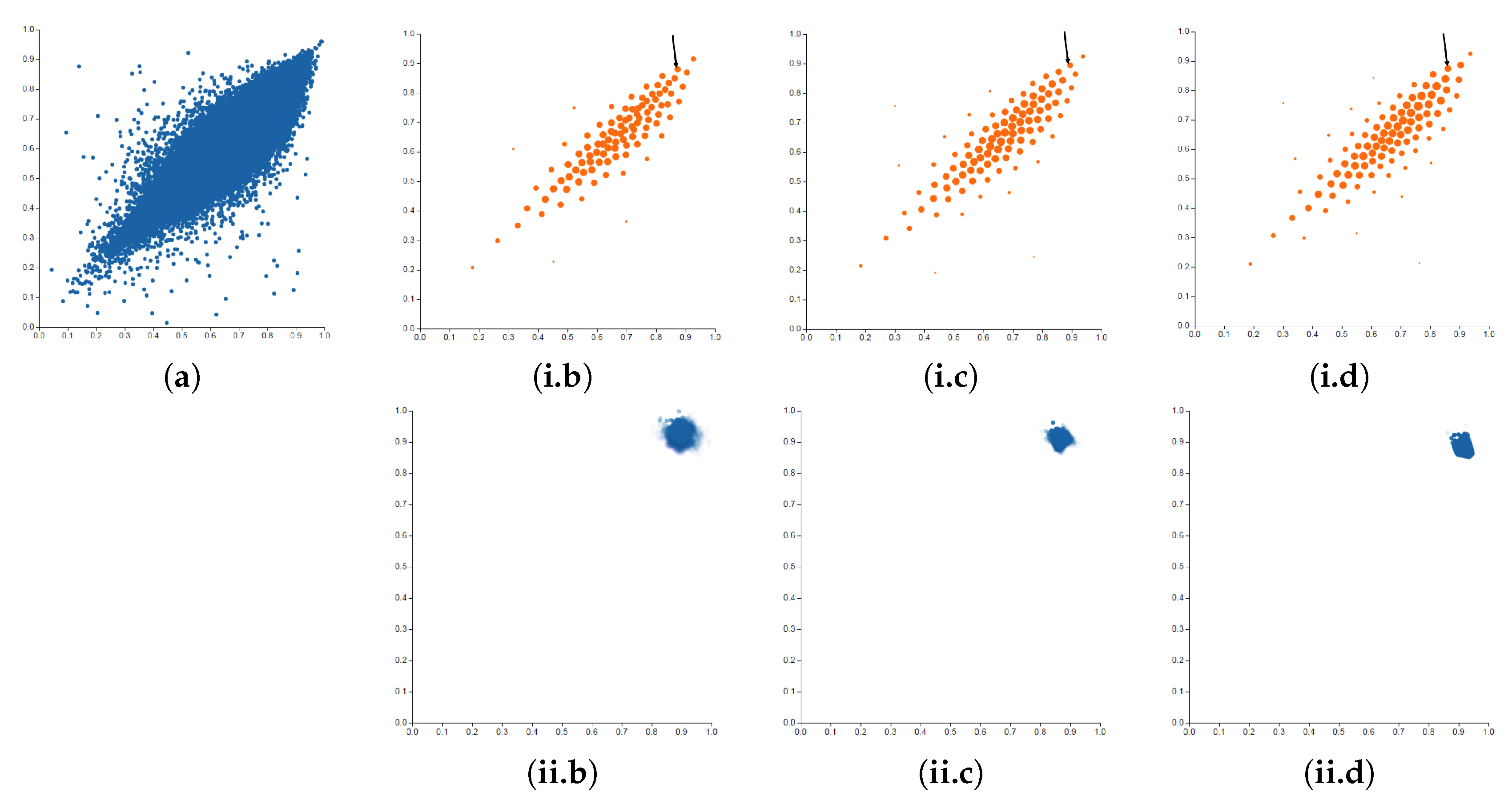
5.1. Example 1: Scatterplot
- The second step refers to the definition of the type of clustering. In this case, we are not specially constrained to the fact that each data element corresponds to a single cluster and, thus, the most appropriate selection would be soft clustering.
- In the third step, we have to decide the optimization scheme. In this case, we can use the Blahut–Arimoto algorithm, and it can be proved that the function that fulfills the centroid condition is the expected mean value of the centroid. Note that we have not discovered a new clustering strategy. This method is known in the literature as the soft k-means [42]. In this study, we will let the user modify the value of the parameter in order to illustrate its performance.
- Finally, the fourth step determines the cluster centroids representation. In our case, we assign the two values of the centroid to the 2D position (in the same way than the original data) and we encode the probability of the cluster (i.e., how many data are represented by the cluster) to the area.
5.2. Example 2: Parallel Coordinates
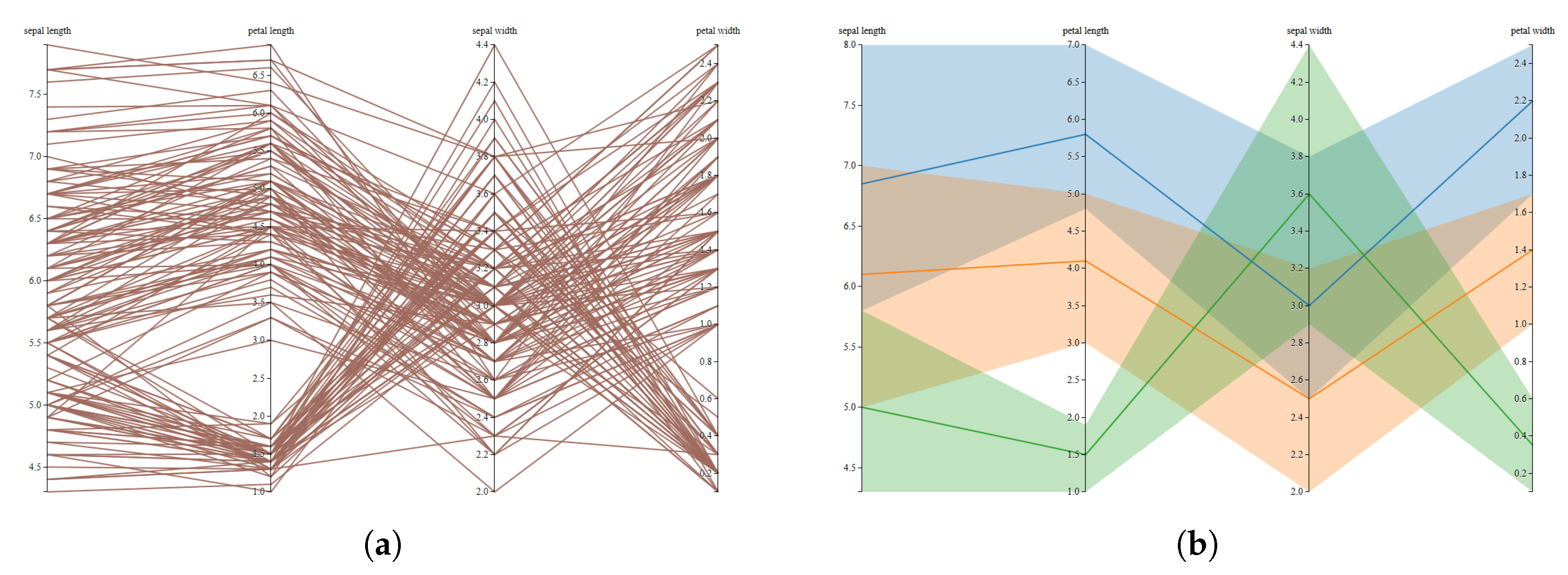
- The visual encoding for parallel coordinates converts each data value into a polygonal line whose m vertices are at on the axes for ( are the axes of the parallel coordinates system for the Euclidean m-dimensional space ). In this scenario, the well-known root mean square distance is not the most appropriate, since it lacks of geometrical meaning in the visual space of the parallel coordinates visualization. Instead of this, a more suitable choice would be the following distortion measure:where and represent the maximum and the minimum values of the ith variable. Note that this distortion measure can be seen as the generalization of Equation (14) to several variables. This measure is also known as -distance or Manhattan distance. The lack of geometrical significance of the Euclidean distance and the suitability of the Manhattan distance for the parallel coordinates visualization is presented in Figure 5.
- Once the distortion measure has been defined, the second step requires selecting the type of clustering. In this example, in order to have a different scenario than the previous one, we have considered hard clustering. Thus, every data element will belong to a single cluster.
- In the third step, we have to decide the optimization scheme. In order to minimize the distortion measure of Equation (22), the centroid of the cluster has to be placed in the median point of the data. This clustering process has been previously introduced with the name of k-medians [45]. This method is an expectation-maximization algorithm that iteratively converges to the final clustering. Note that the fact of representing the data with parallel coordinates has lead us to considering the k-medians method as the most suitable clustering algorithm to perform this task.
- The last step defines the visualization strategy. As shown in Figure 6b, each polyline centroid has been placed in the median value of the cluster and a different color has been assigned to the area contained between maximum and minimum values of the cluster.
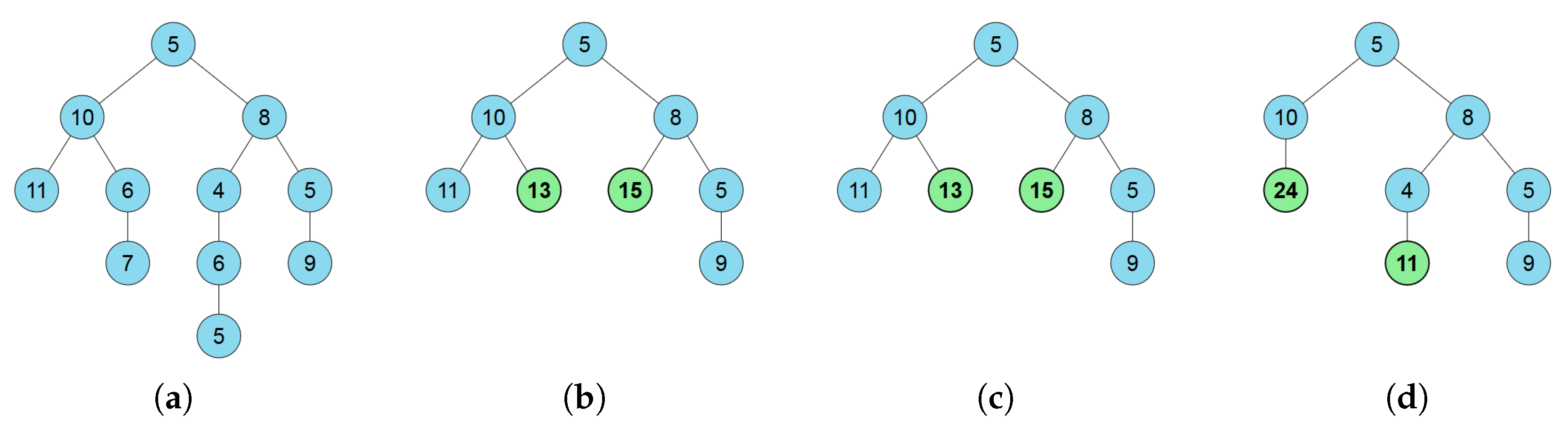
5.3. Example 3: Summary Trees
- In the presented theoretical framework, we propose minimizing the functional (see Equation (9)). In this example context, the first term of the functional, the mutual information between the original data and the clustered one, issince there is not uncertainty on the cluster when the original node is known and, thus, .Note that corresponds to the same measure proposed in [49], but, while in our approach the measure has to be minimized, in [49], it has to be maximized. This is due to the fact that the maximum entropy approach tends to maximize the information, leading to as much as possible equal-sized nodes, while, in our approach, this term is used together with a second term, , that measures the expected distortion and, therefore, is a trade-off between two components.The second term of the functional is the expected distortion. In our context, a basic measure to quantify the distortion is the Hamming distortion:Observe that this measure does not take into account how different the original node is from the clustered one, but only if it is contracted or not. Note that more complex measures that quantify in some aspect the distance between the original node and the cluster one can also be used. For instance,where the function is the depth level on the tree of the node, being 0 for the root node. With this second measure, depending on the level of distance from the original node to the contracted one, the distortion will vary. Note that this measure allows introducing new considerations that were not taken into account in the first approach or in the maximum entropy one. Therefore, the proposed method gives more flexibility to the visualization designers, allowing, for instance, to give importance on the subtree depth on the clustering criterion.
- Once the distortion rate function has been defined, we select the type of clustering. As it was previously described, from the summary tree definition, we consider a hard clustering, since each original node is only represented by a single cluster.
- The optimization scheme is a force-brute algorithm, since in the used example there are only a small number of possible solutions. To summarize a real-world tree with a large number of nodes, other strategies such as simulated annealing or genetic algorithms could be used in this application. Note that the Blahut–Arimoto algorithm could not be used due to the discrete nature of the problem.
- Finally, we determine the visualization strategy. As shown in Figure 7c,d, contracted nodes are represented in bold and green backgrounds in contrast to original nodes that are represented with regular font and blue background.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ko, S.; Maciejewski, R.; Jang, Y.; Ebert, D.S. MarketAnalyzer: An Interactive Visual Analytics System for Analyzing Competitive Advantage Using Point of Sale Data. Comput. Graph. Forum 2012, 31, 1245–1254. [Google Scholar] [CrossRef]
- ElHakim, R.; ElHelw, M. Interactive 3d visualization for wireless sensor networks. Vis. Comput. 2010, 26, 1071–1077. [Google Scholar] [CrossRef]
- Chen, T.; Lu, A.; Hu, S. Visual storylines: Semantic visualization of movie sequence. Comput. Graph. 2012, 36, 241–249. [Google Scholar] [CrossRef]
- Fayyad, U.; Grinstein, G.G.; Wierse, A. (Eds.) Information Visualization in Data Mining and Knowledge Discovery; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2002. [Google Scholar]
- Liu, S.; Cui, W.; Wu, Y.; Liu, M. A Survey on Information Visualization: Recent Advances and Challenges. Vis. Comput. 2014, 30, 1373–1393. [Google Scholar] [CrossRef]
- Everitt, B.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Hartigan, J. Clustering Algorithms; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of Clustering Algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Kindlmann, G.; Scheidegger, C. An Algebraic Process for Visualization Design. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2181–2190. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Feixas, M.; Viola, I.; Bardera, A.; Shen, H.W.; Sbert, M. Information Theory Tools for Visualization; AK Peters: Natick, MA, USA; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chen, M.; Jänicke, H. An Information-theoretic Framework for Visualization. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1206–1215. [Google Scholar] [CrossRef] [PubMed]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, September 1999; pp. 368–377. [Google Scholar]
- Bramon, R.; Ruiz, M.; Bardera, A.; Boada, I.; Feixas, M.; Sbert, M. An Information-Theoretic Observation Channel for Volume Visualization. Comput. Graph. Forum 2013, 32, 411–420. [Google Scholar] [CrossRef]
- Demiralp, Ç.; Scheiddegger, C.E.; Kindlmann, G.L.; Laidlaw, D.H.; Heer, J. Visual Embedding: A Model for Visualization. IEEE Comput. Graph. Appl. 2014, 34, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Berkhin, P. A Survey of Clustering Data Mining Techniques. In Grouping Multidimensional Data-Recent Advances in Clustering; Springer: Berlin/Heidelberg, Germany, 2006; pp. 25–71. [Google Scholar]
- Daxin, J.; Chun, T.; Aidong, Z. Cluster Analysis for Gene Expression Data: A Survey. IEEE Trans. Knowl. Data Eng. 2004, 16, 1370–1386. [Google Scholar] [CrossRef]
- Feixas, M.; Bardera, A.; Rigau, J.; Xu, Q.; Sbert, M. Information Theory Tools for Image Processing; Synthesis Lectures on Computer Graphics and Animation; Morgan & Claypool Publishers: San Rafael, CA, USA, 2014. [Google Scholar]
- Kriegel, H.P.; Krüger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Technique, 3th ed.; The Morgan Kaufmann Series in Data Management Systems; Morgan Kaufmann Publishers: Burlington, MA, USA, 2011. [Google Scholar]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A Survey of Clustering Algorithms for Big Data: Taxonomy and Empirical Analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Seo, J.; Shneiderman, B. Interactively Exploring Hierarchical Clustering Results. Computer 2002, 35, 80–86. [Google Scholar]
- Lex, A.; Streit, M.; Partl, C.; Schmalstieg, D. Comparative Analysis of Multidimensional, Quantitative Data. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1027–1035. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, P.; Pinheiro, P.; Broeksema, B.; Otjacques, B. Cluster Sculptor, an interactive visual clustering system. Neurocomputing 2015, 150, 627–644. [Google Scholar] [CrossRef]
- Schreck, T.; Bernard, J.; Von Landesberger, T.; Kohlhammer, J. Visual Cluster Analysis of Trajectory Data with Interactive Kohonen Maps. Inf. Vis. 2009, 8, 14–29. [Google Scholar] [CrossRef]
- Yi, S.L.; Ko, B.; Shin, D.; Cho, Y.; Lee, J.; Kim, B.; Seo, J. XCluSim: A visual analytics tool for interactively comparing multiple clustering results of bioinformatics data. BMC Bioinf. 2015, 16, 1–15. [Google Scholar]
- Demiralp, Ç. Clustrophile: A Tool for Visual Clustering Analysis. In Proceedings of the Workshop on Interactive Data Exploration and Analytics, San Francisco, CA, USA, 14 August 2016; pp. 1–9. [Google Scholar]
- Etemadpour, R.; Linsen, L.; Crick, C.; Forbes, A. A user-centric taxonomy for multidimensional data projection tasks. In Proceedings of the IVAPP 2015—6th International Conference on Information Visualization Theory and Applications, Berlin, Germany, 11–14 March 2015; pp. 51–62. [Google Scholar]
- Etemadpour, R.; Forbes, A.G. Density-based motion. Inf. Vis. 2017, 16, 3–20. [Google Scholar] [CrossRef]
- Sedlmair, M.; Tatu, A.; Munzner, T.; Tory, M. A Taxonomy of Visual Cluster Separation Factors. Comput. Graph. Forum 2012, 31, 1335–1344. [Google Scholar] [CrossRef]
- Etemadpour, R.; Motta, R.; de Souza Paiva, J.G.; Minghim, R.; Ferreira de Oliveira, M.C.; Linsen, L. Perception-Based Evaluation of Projection Methods for Multidimensional Data Visualization. IEEE Trans. Vis. Comput. Graph. 2015, 21, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley Series in Telecommunications; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Blahut, R.E. Computation of channel capacity and rate distortion functions. IEEE Trans. Inf. Theory 1972, 18, 460–473. [Google Scholar] [CrossRef]
- Arimoto, S. An algorithm for computing the capacity of arbitrary memoryless channels. IEEE Trans. Inf. Theory 1972, 18, 14–20. [Google Scholar] [CrossRef]
- Rose, K. Deterministic annealing for clustering, compression, classification, regression, and related optimization problems. Proc. IEEE 1998, 86, 2210–2239. [Google Scholar] [CrossRef]
- Munzner, T. Visualization Analysis and Design; AK Peters: Natick, MA, USA; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ware, C. Visual Thinking for Design; Morgan Kaufmann: Burlington, MA, USA, 2008. [Google Scholar]
- International Commission on Illumination. Colorimetry L*a*b* Colour Space. 1976. Available online: http://cie.co.at/index.php?i_ca_id=485 (accessed on 22 August 2017).
- Demiralp, Ç.; Bernstein, M.S.; Heer, J. Learning Perceptual Kernels for Visualization Design. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1933–1942. [Google Scholar] [CrossRef] [PubMed]
- Stevens, S.S. On the psychophysical law. Psychol. Rev. 1957, 64, 153–181. [Google Scholar] [CrossRef] [PubMed]
- Jensi, R.; Jiji, D.G.W. A Survey on Optimization Approaches to Text Document Clustering. Int. J. Comput. Sci. Appl. 2013, 3. [Google Scholar] [CrossRef]
- Newman, D.; Hettich, S.; Blake, C.; Merz, C. UCI Repository of Machine Learning Databases. 1998. Available online: http://archive.ics.uci.edu/ml/index.php (accessed on 22 August 2017).
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Kluwer Academic Publishers: Norwell, MA, USA, 1981. [Google Scholar]
- Inselberg, A. The plane with parallel coordinates. Vis. Comput. 1985, 1, 69–97. [Google Scholar] [CrossRef]
- Inselberg, A.; Dimsdale, B. Parallel Coordinates: A Tool for Visualizing Multi-dimensional Geometry. In Proceedings of the 1st Conference on Visualization, San Francisco, CA, USA, 23–26 October 1990; IEEE Computer Society Press: Washington, DC, USA, 1990; pp. 361–378. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall: Upper Saddle River, NJ, USA, 1981. [Google Scholar]
- Lima, M. The Book of Trees: Visualizing Branches of Knowledge; Princeton Architectural Press: New York, NY, USA, 2014. [Google Scholar]
- Reingold, E.M.; Tilford, J.S. Tidier drawing of trees. IEEE Trans. Softw. Eng. 1981, 7, 223–228. [Google Scholar] [CrossRef]
- Graham, M.; Kennedy, J. A Survey of Multiple Tree Visualisation. Inf. Vis. 2010, 9, 235–252. [Google Scholar] [CrossRef]
- Karloff, H.; Shirley, K.E. Maximum Entropy Summary Trees. Comput. Graph. Forum 2013, 32, 71–80. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bardera, A.; Bramon, R.; Ruiz, M.; Boada, I. Rate-Distortion Theory for Clustering in the Perceptual Space. Entropy 2017, 19, 438. https://doi.org/10.3390/e19090438
Bardera A, Bramon R, Ruiz M, Boada I. Rate-Distortion Theory for Clustering in the Perceptual Space. Entropy. 2017; 19(9):438. https://doi.org/10.3390/e19090438
Chicago/Turabian StyleBardera, Anton, Roger Bramon, Marc Ruiz, and Imma Boada. 2017. "Rate-Distortion Theory for Clustering in the Perceptual Space" Entropy 19, no. 9: 438. https://doi.org/10.3390/e19090438