Entropy Analysis on Electro-Kinetically Modulated Peristaltic Propulsion of Magnetized Nanofluid Flow through a Microchannel
Abstract
:1. Introduction
2. Mathematical Formulation
3. Entropy Generation Analysis
4. Solution of the Problem
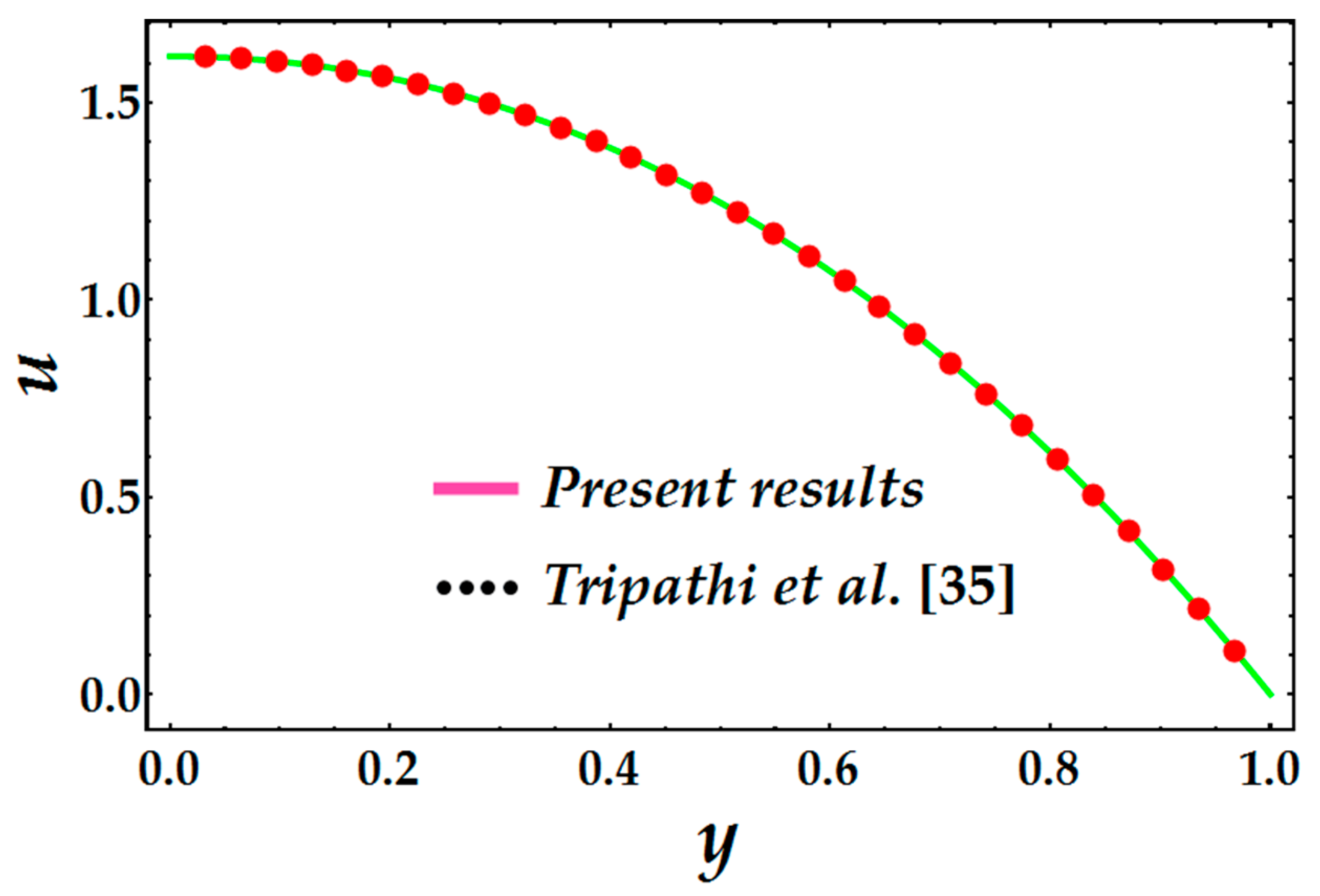
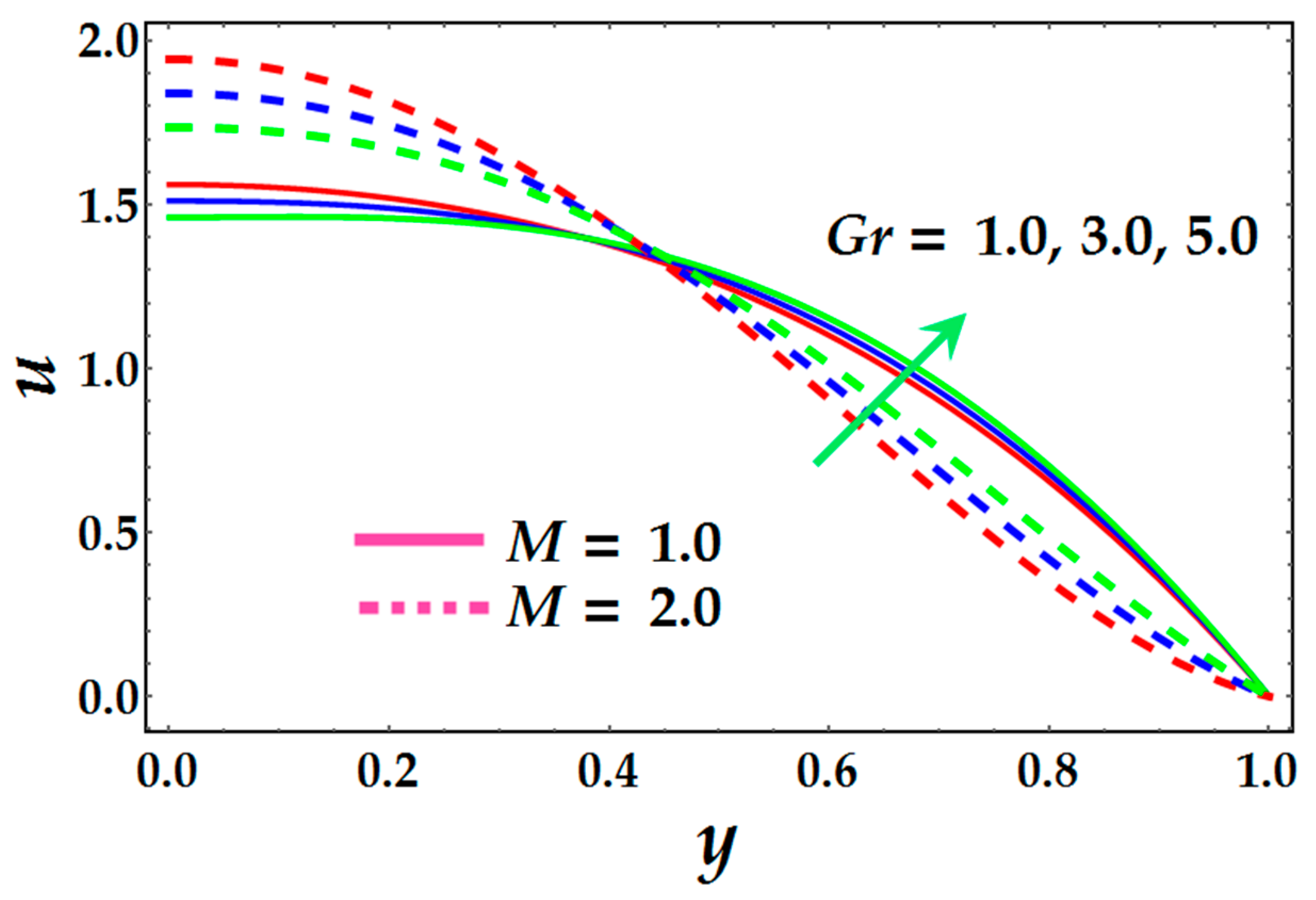
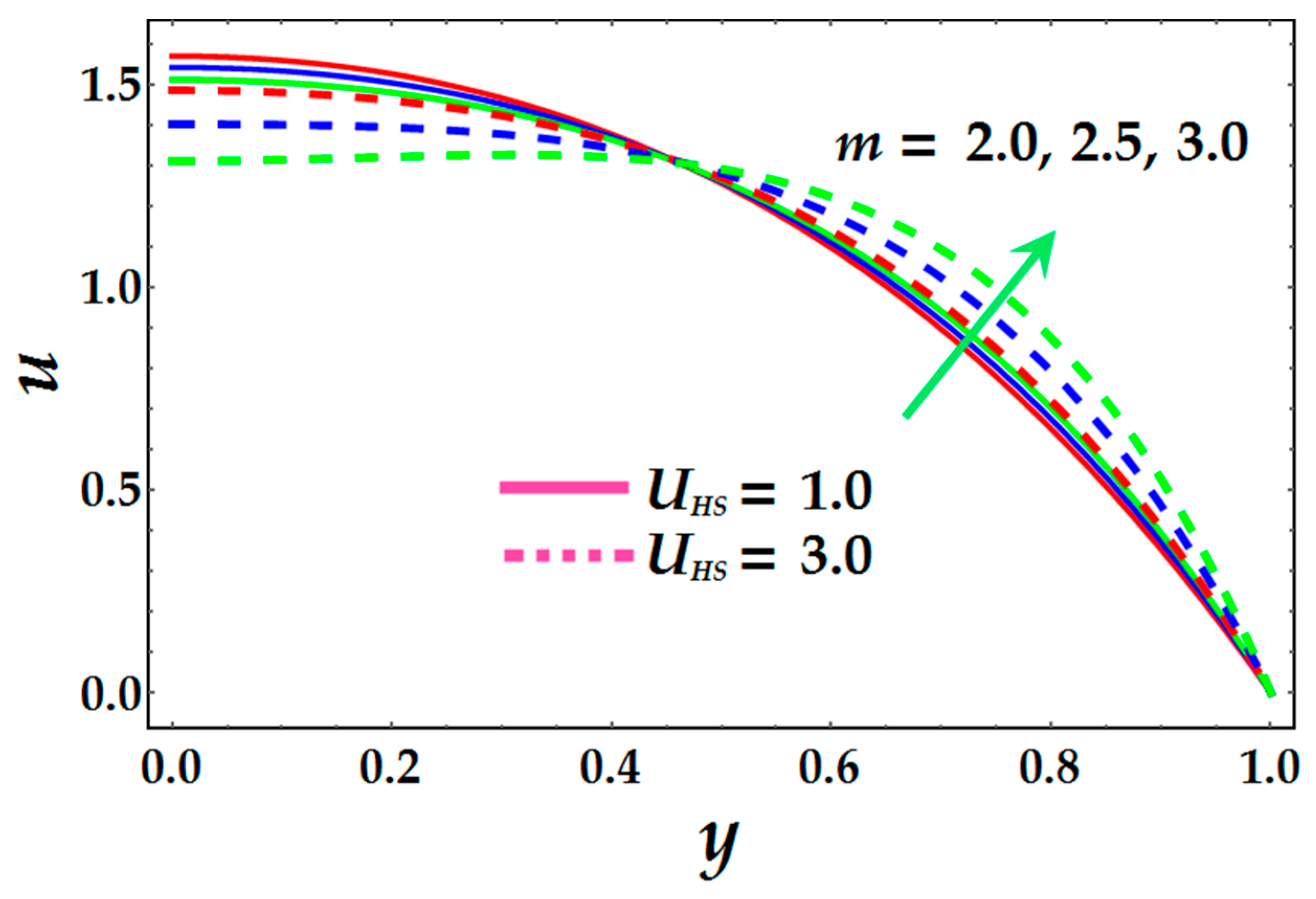
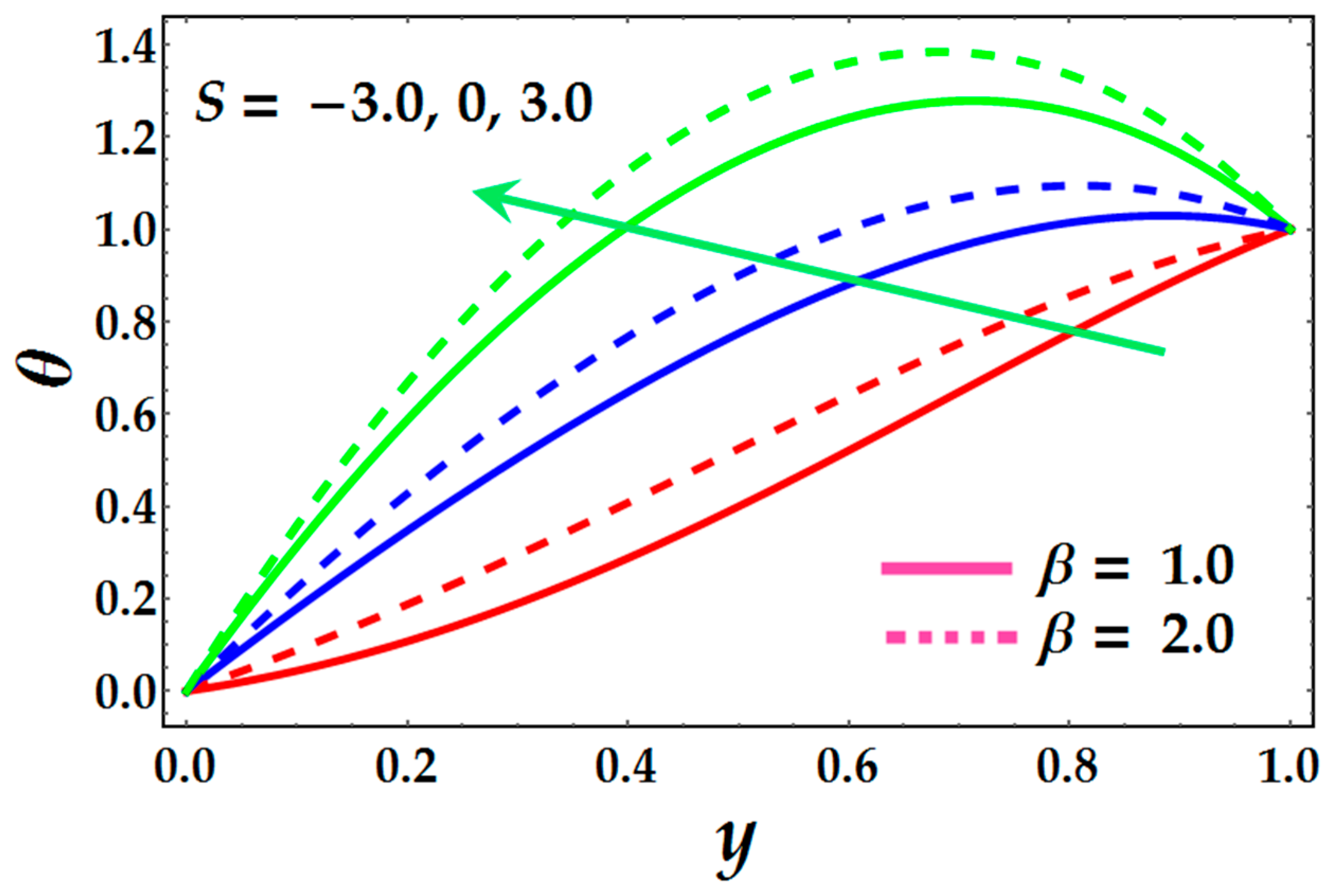
5. Results and Discussion
6. Conclusions
- The velocity of the fluid behaves in a similar manner due to the increment in thermal Grashof number and magnetic field.
- The velocity profile increases when for higher values of electro-osmotic parameter and Helmholtz–Smoluchowski velocity (or “maximum electro-osmotic velocity”).
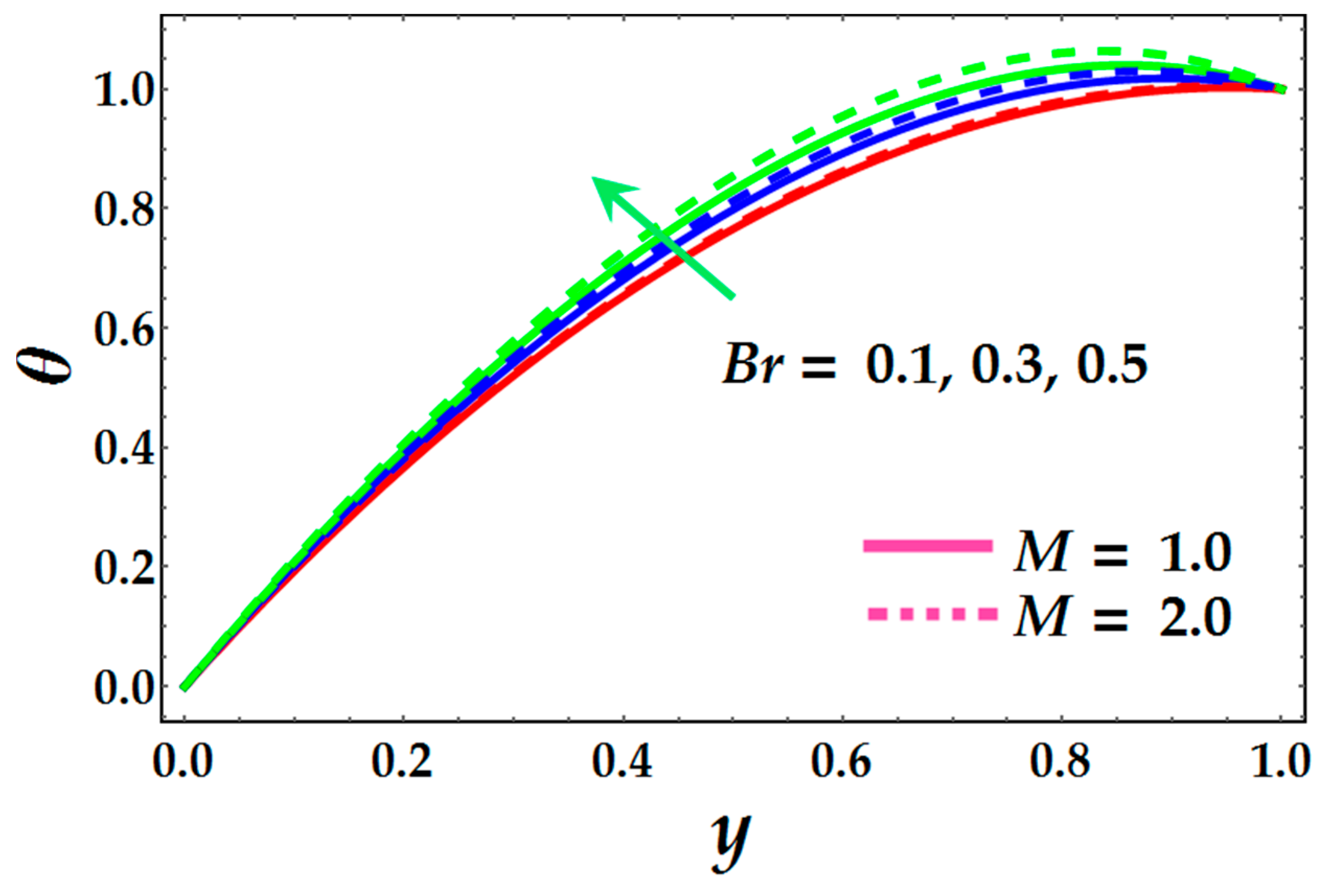
- The temperature profile reveals a significant increment due to the higher presence of Brinkmann number and magnetic field.
- An increment in the Joule heating parameter and heat source/sink significantly accelerates the temperature profile.
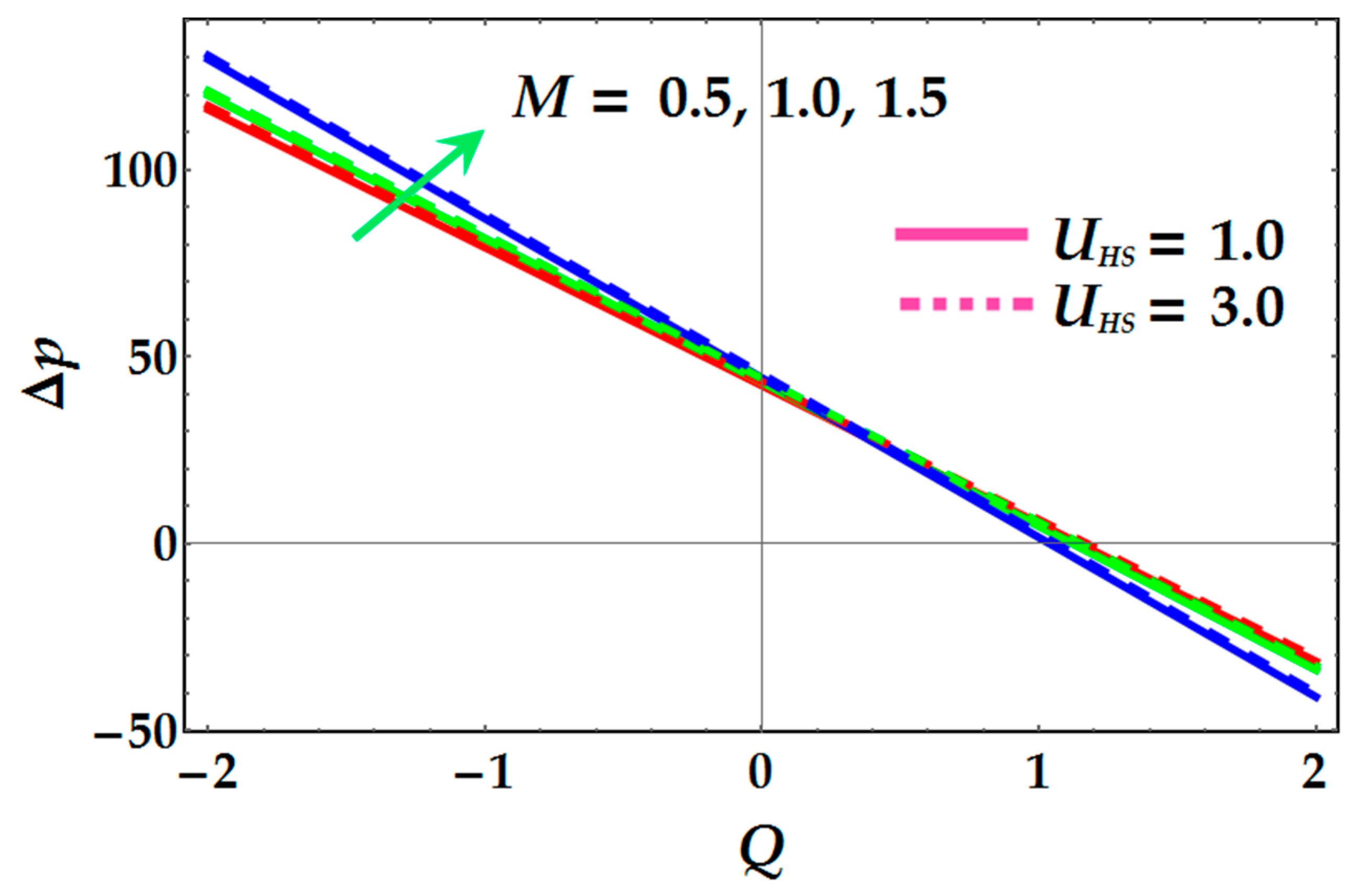
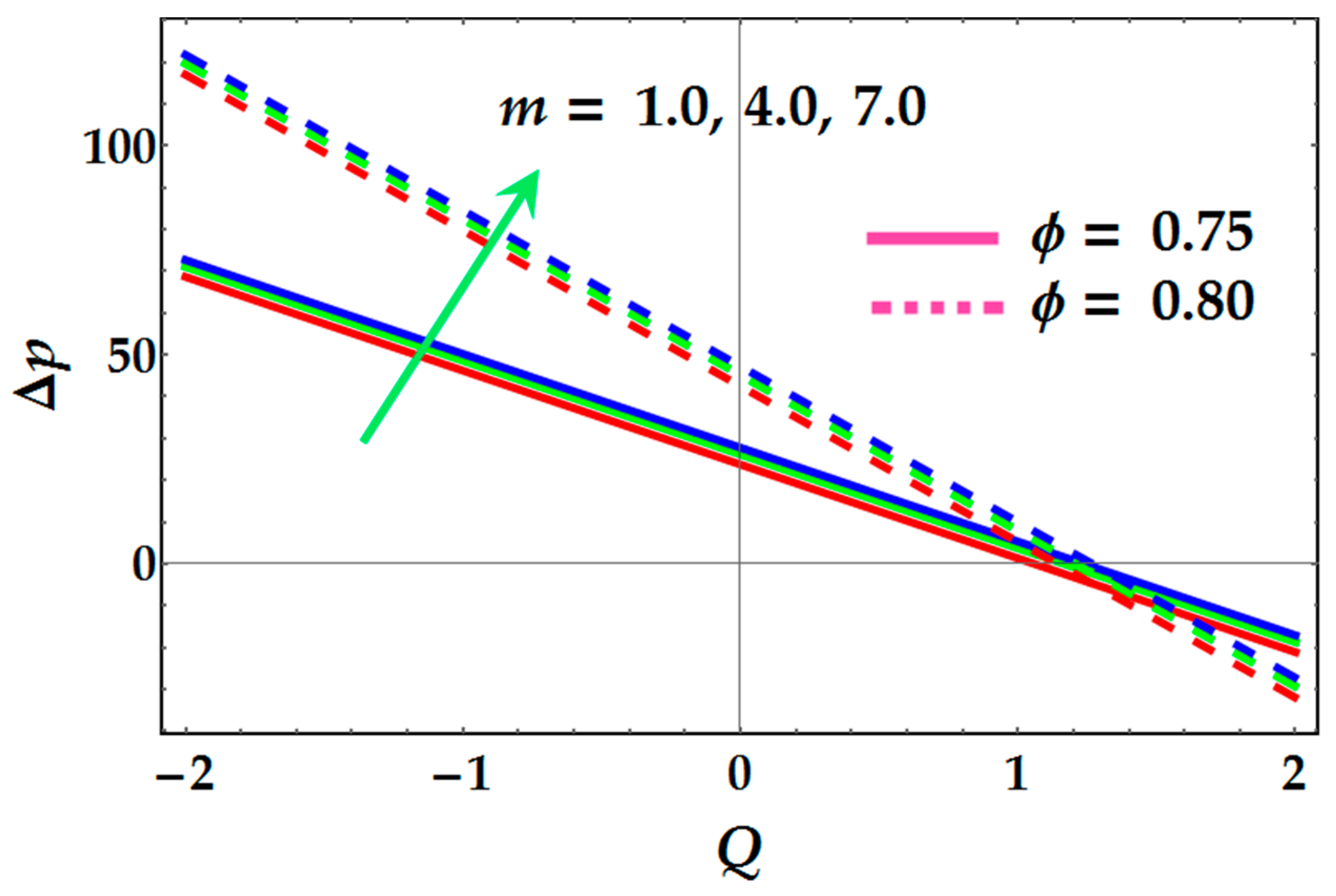
- Pressure rise exhibits similar behavior to higher values of an electro-osmotic parameter, magnetic field, and Helmholtz–Smoluchowski velocity (or “maximum electro-osmotic velocity”).
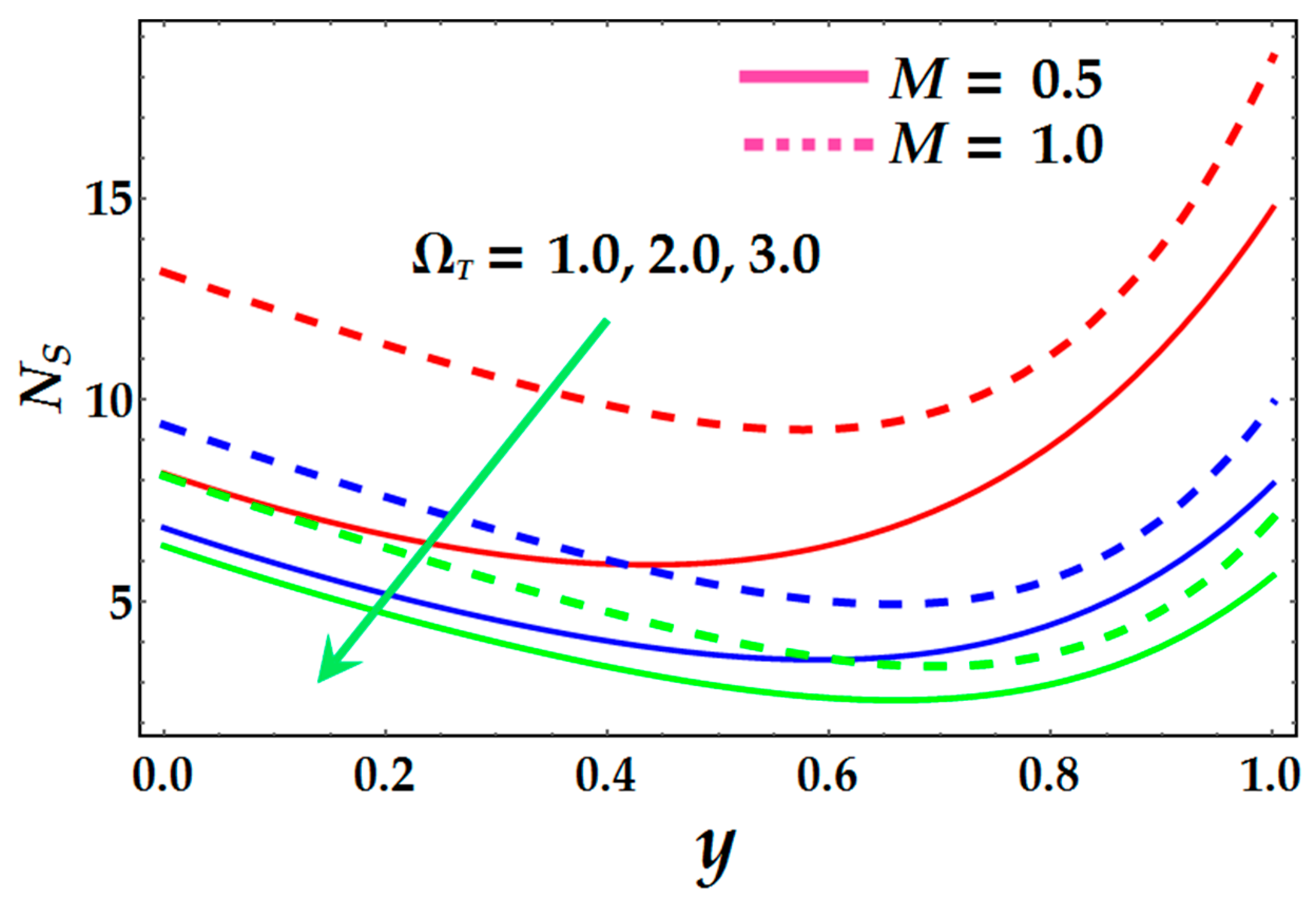
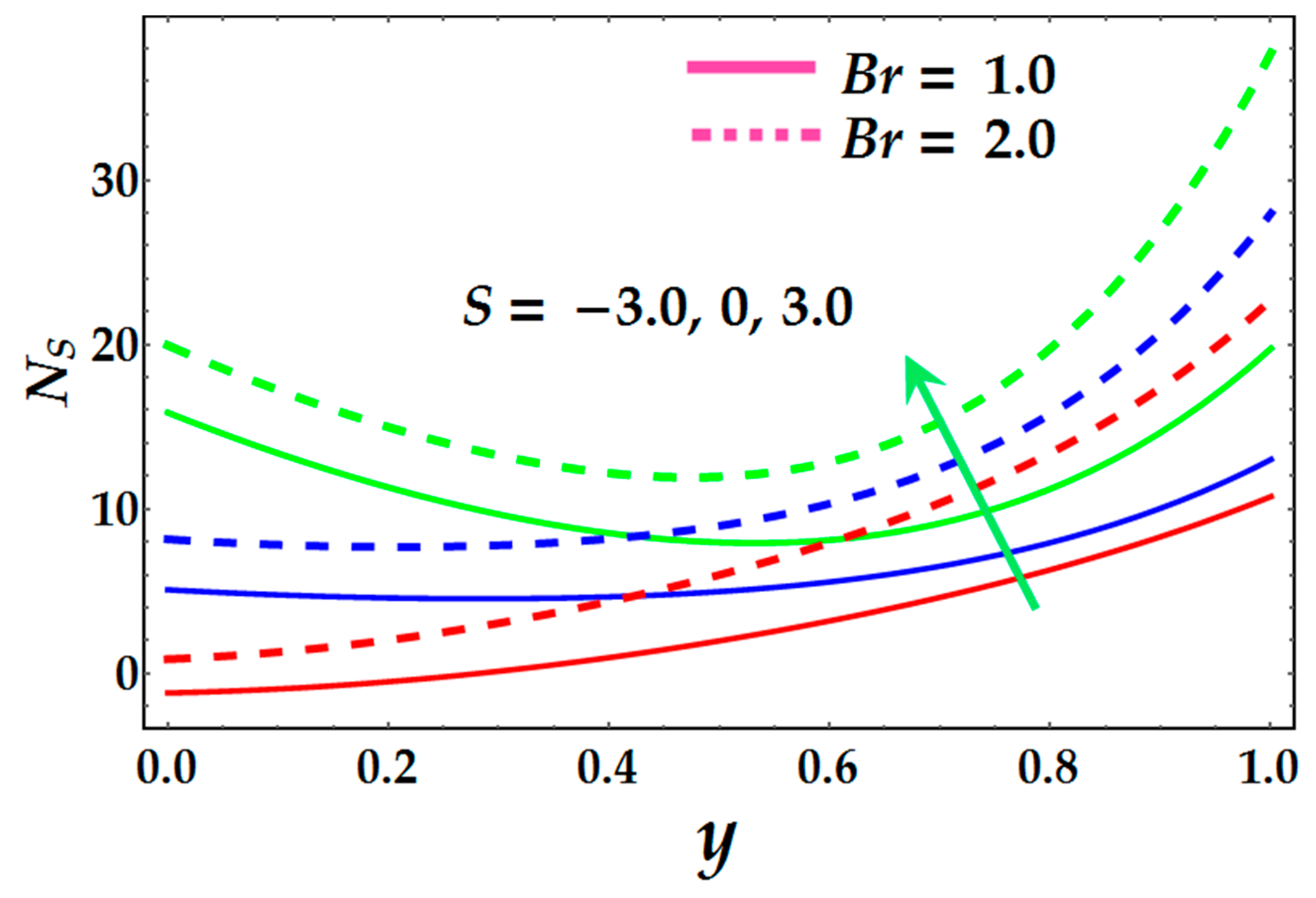
- The entropy profile also shows a positive response due to the greater impact of Brinkmann number, magnetic field, and the Joule heating parameter.
Author Contributions
Conflicts of Interest
Nomenclature
| Transverse vibration of the wall | |
| Half width of the channel | |
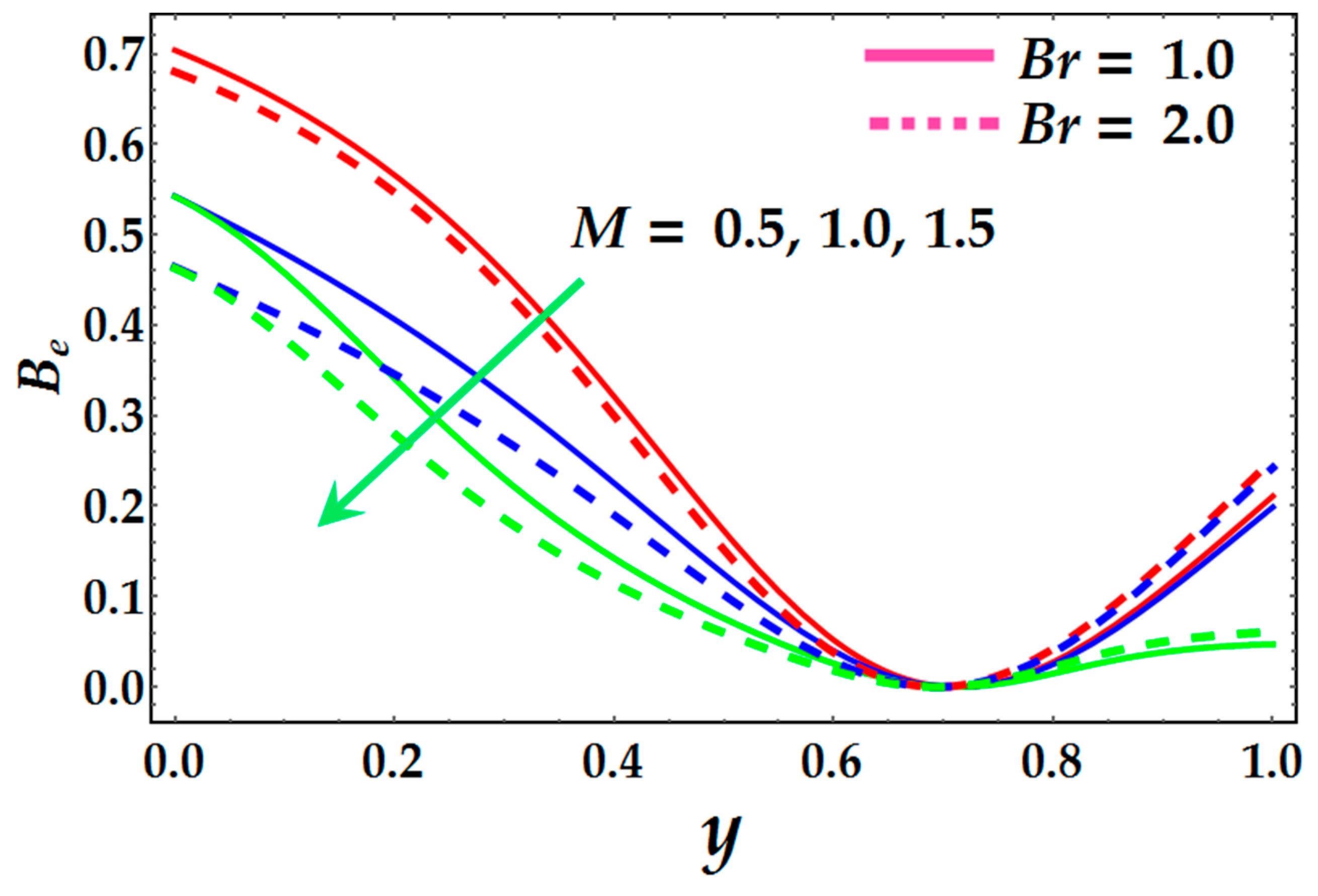
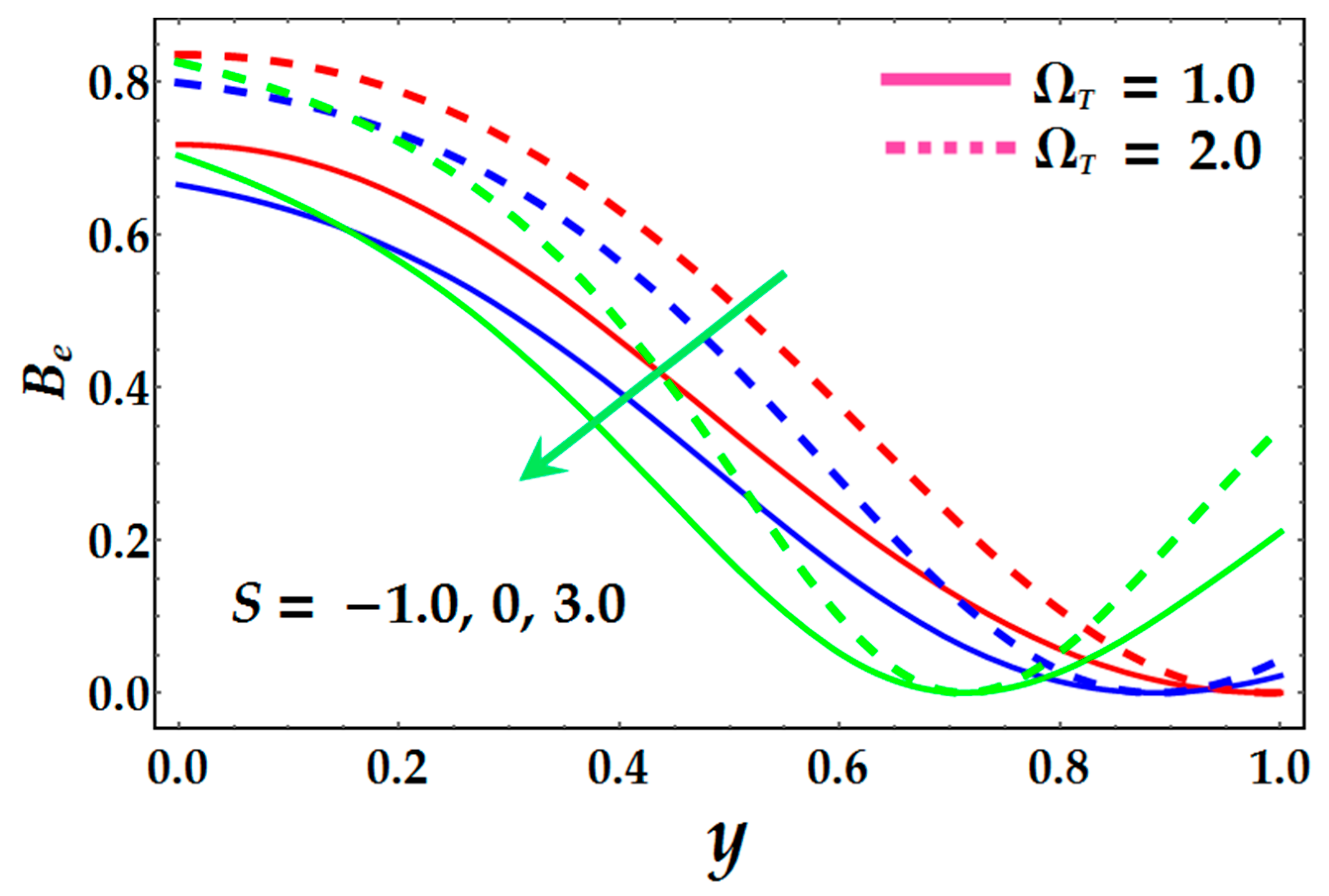
| Local Bejan number | |
| Average Bejan number | |
| Pressure | |
| Velocity of the wave | |
| Reynolds number | |
| Dimensionless entropy number | |
| Time | |
| Velocity field | |
| Electrokinetic body force | |
| Thermal conductivity | |
| Cartesian coordinate axis | |
| Diffusivity of an ionic species | |
| Boltzmann constant | |
| Electroosmosis parameter | |
| Joule heating parameter | |
| Helmholtz–Smoluchowski velocity | |
| Brinkman number | |
| Grashof number | |
| Average volume flow rate | |
| Hartman number | |
| Magnetic field | |
| Volume flow rate | |
| Temperature | |
| Acceleration due to gravity | |
| Bulk concentration (number density) | |
| Elementary charge |
Greek Symbol
| Density of the fluid | |
| Coefficient of linear thermal expansion of fluid | |
| Heat absorption coefficient | |
| Viscosity of the fluid | |
| Permittivity | |
| Debye length | |
| Wave length | |
| Electrical charge density | |
| Amplitude of the wave | |
| Temperature profile | |
| Embedding parameter | |
| Electrical conductivity | |
| Dimensionless temperature difference | |
| Dimensionless heat source/sink | |
| Wave number |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fed 1995, 231, 99–106. [Google Scholar]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I. Natural convection in a wavy porous cavity with sinusoidal temperature distributions on both side walls filled with a nanofluid: Buongiorno’s mathematical model. J. Heat Transf. 2015, 137, 072601. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, Y.; Chen, L. Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry. Powder Technol. 2013, 239, 409–414. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Bachok, N. Effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid: Tiwari and Das’ nanofluid model. Int. J. Heat Mass Transf. 2016, 92, 1053–1060. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Fan, J.; Chen, H.; Hu, X.; Zhao, D.; Zhang, X.; Ren, W. Optimization of the fractal-like architecture of porous fibrous materials related to permeability, diffusivity and thermal conductivity. Fractals 2017, 25, 1750030. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetic field influence on CuO–H2O nanofluid convective flow in a permeable cavity considering various shapes for nanoparticles. Int. J. Hydrog. Energy 2017, 42, 19611–19621. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M.M. Active method for nanofluid heat transfer enhancement by means of EHD. Int. J. Heat Mass Transf. 2017, 109, 115–122. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M.M. Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int. J. Heat Mass Transf. 2017, 111, 1039–1049. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Lattice Boltzmann Method simulation of MHD non-Darcy nanofluid free convection. Phys. B Cendens. Matter 2017, 516, 55–71. [Google Scholar] [CrossRef]
- Ellahi, R.; Mubashir Bhatti, M.; Riaz, A.; Sheikholeslami, M. Effects of magnetohydrodynamics on peristaltic flow of Jeffrey fluid in a rectangular duct through a porous medium. J. Porous Media 2014, 17, 143–157. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Endoscope analysis on peristaltic blood flow of Sisko fluid with Titanium magneto-nanoparticles. Comput. Biol. Med. 2016, 78, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, D.; Bég, O.A. A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Peristaltic flow of a Phan-Thien-Tanner nanofluid in a diverging tube. Heat Transf. Asian Res. 2012, 41, 10–22. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R.; Ijaz, N. Heat and mass transfer of two-phase flow with Electric double layer effects induced due to peristaltic propulsion in the presence of transverse magnetic field. J. Mol. Liq. 2017, 230, 237–246. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. Int. J. Heat Mass Transf. 2017, 115, 1203–1233. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Copper oxide nanoparticles analysis with water as base fluid for peristaltic flow in permeable tube with heat transfer. Comput. Methods Progr. Biomed. 2016, 130, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, F.M.; Hayat, T.; Ahmad, B. Peristaltic transport of copper–water nanofluid saturating porous medium. Phys. E 2015, 67, 47–53. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Trans. 1982, 15, 1–58. [Google Scholar]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.S. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2015, 18, 9. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Trans. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Ranjit, N.K.; Shit, G.C. Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 2017, 128, 649–660. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Peristaltic flow with thermal conductivity of H2O+ Cu nanofluid and entropy generation. Results Phys. 2015, 5, 115–124. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Physica A 2015, 417, 273–286. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Tripathi, D.; Bhushan, S.; Bég, O.A. Transverse magnetic field driven modification in unsteady peristaltic transport with electrical double layer effects. Colloids Surf. A 2016, 506, 32–39. [Google Scholar] [CrossRef]
- Sokalski, T.; Lingenfelter, P.; Lewenstam, A. Numerical solution of the coupled Nernst–Planck and Poisson equations for liquid junction and ion selective membrane potentials. J. Phys. Chem. B 2003, 107, 2443–2452. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A.; Tiwari, A. Electrothermal Transport in Biological Systems: An Analytical Approach for Electrokinetically Modulated Peristaltic Flow. J. Therm. Sci. Eng. Appl. 2017, 9, 041010. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, M.M.; Sheikholeslami, M.; Zeeshan, A. Entropy Analysis on Electro-Kinetically Modulated Peristaltic Propulsion of Magnetized Nanofluid Flow through a Microchannel. Entropy 2017, 19, 481. https://doi.org/10.3390/e19090481
Bhatti MM, Sheikholeslami M, Zeeshan A. Entropy Analysis on Electro-Kinetically Modulated Peristaltic Propulsion of Magnetized Nanofluid Flow through a Microchannel. Entropy. 2017; 19(9):481. https://doi.org/10.3390/e19090481
Chicago/Turabian StyleBhatti, Muhammad Mubashir, Mohsen Sheikholeslami, and Ahmed Zeeshan. 2017. "Entropy Analysis on Electro-Kinetically Modulated Peristaltic Propulsion of Magnetized Nanofluid Flow through a Microchannel" Entropy 19, no. 9: 481. https://doi.org/10.3390/e19090481




