On Generalized Stam Inequalities and Fisher–Rényi Complexity Measures
Abstract
:1. Introduction
2. -Fisher–Rényi Complexity and the Extended Stam Inequality
2.1. Rényi Entropy, Extended Fisher Information and Rényi–Fisher Complexity
2.2. Shift and Scale Invariance, Bounding from Below and Minimizing Distributions
2.3. Some Explicitly Known Minimizing Distributions
2.3.1. The Case
2.3.2. Stretched Deformed Gaussian: The Symmetric Case
2.3.3. Dealing with the Usual Fisher Information
2.3.4. The Symmetrical of the Usual Fisher Information
3. Extended Optimal Stam Inequality: A Step Further
3.1. Differential-Escort Distribution: A Brief Overview
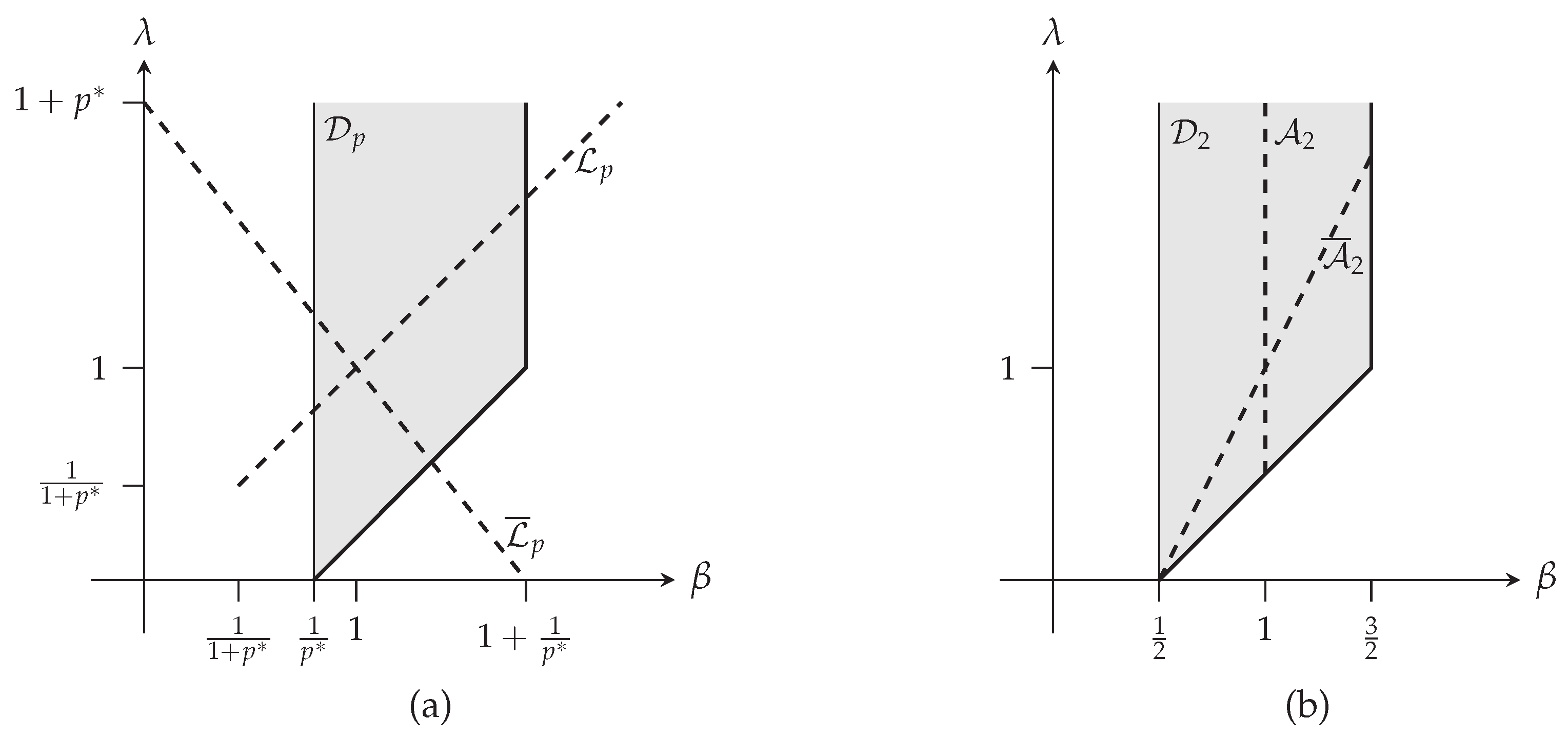
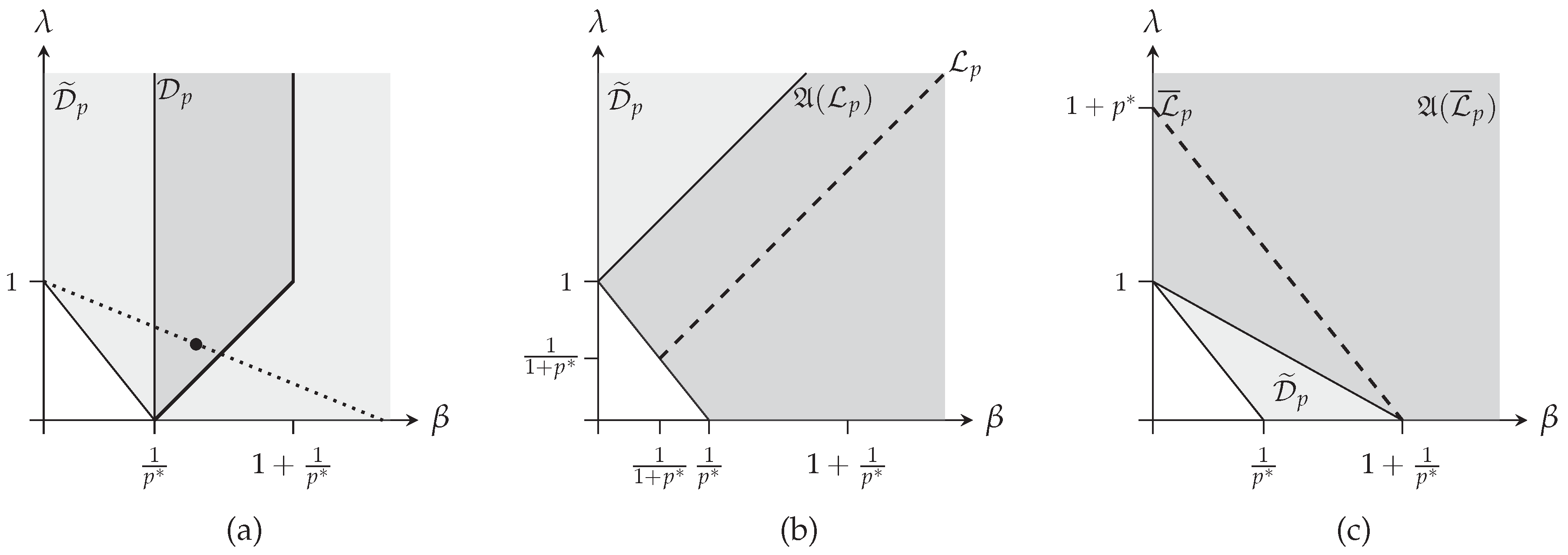
3.2. Enlarging the Validity Domain of the Extended Stam Inequality
- Consider a point and find an index such that , which is a point of the intersection between and the line joining and .
- Apply Proposition 2 for the point , leading to the minimizing distribution and its corresponding bound.
- Then, remarking that , the minimizer of the extended complexity writes and the corresponding bound can be computed from this minimizer or noting that .
4. Applications to Quantum Physics
4.1. Brief Review on the Quantum Systems with Radial Potential
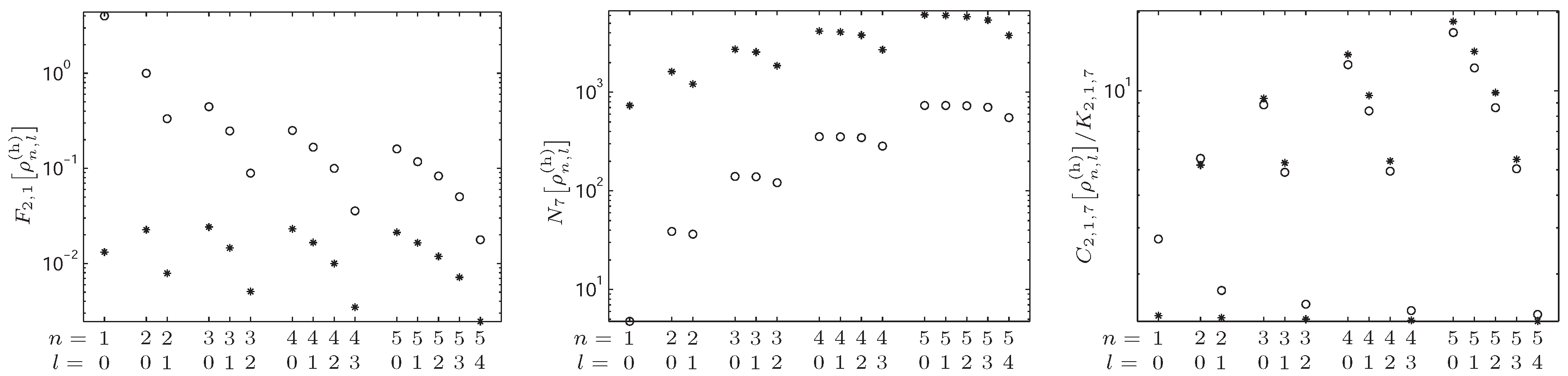
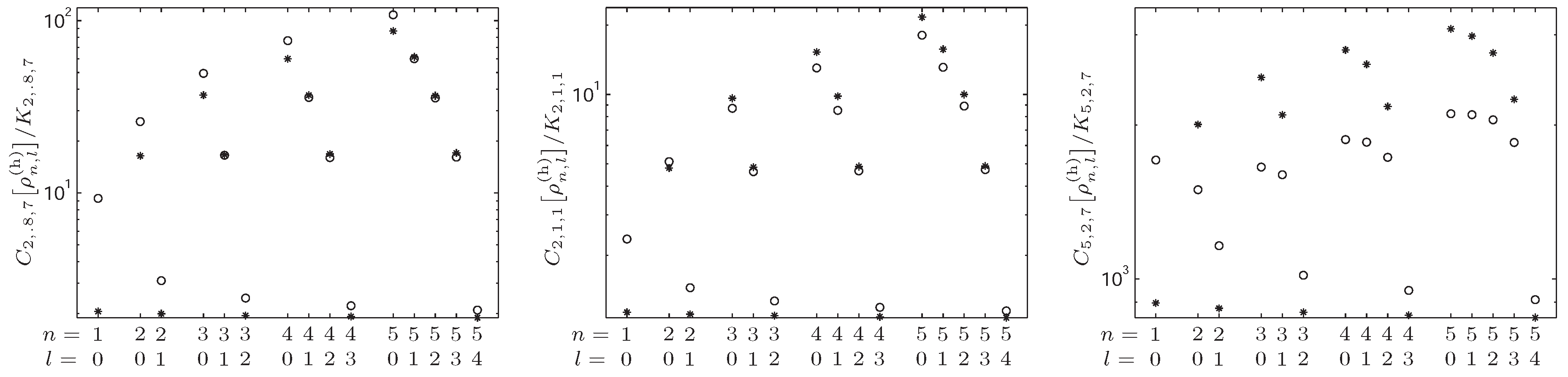
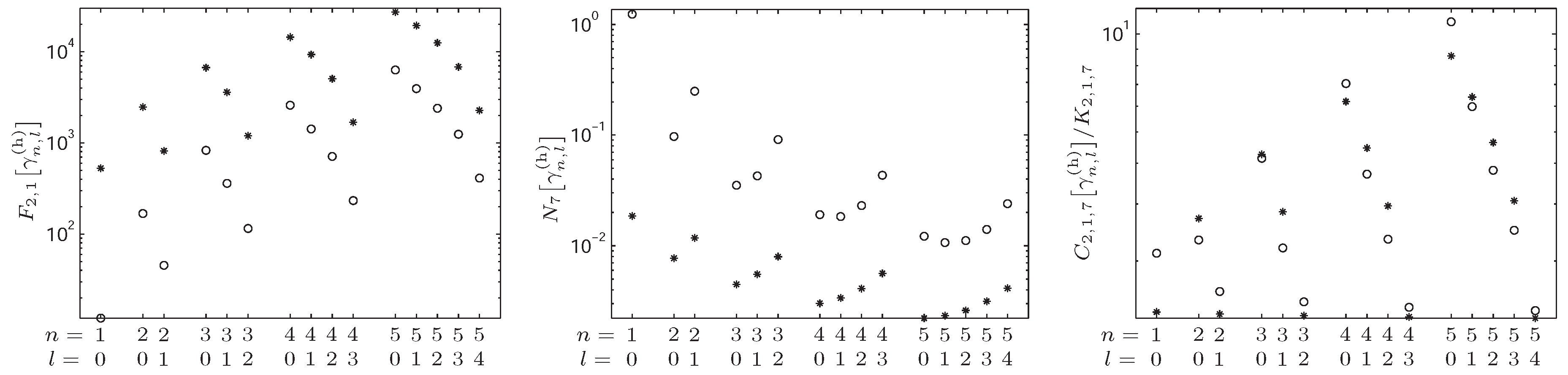
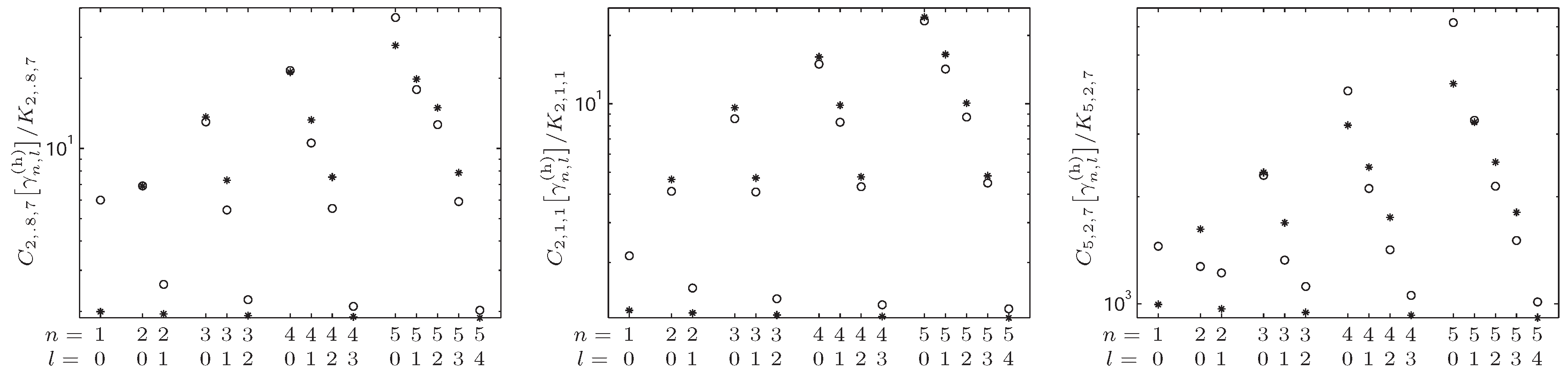
4.2. -Fisher–Rényi Complexity and the Hydrogenic System
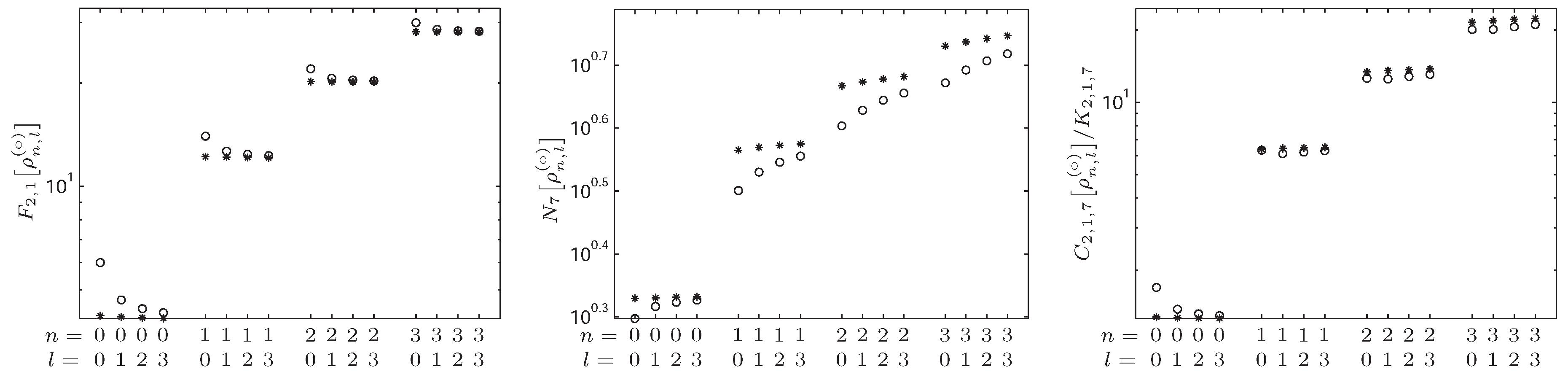
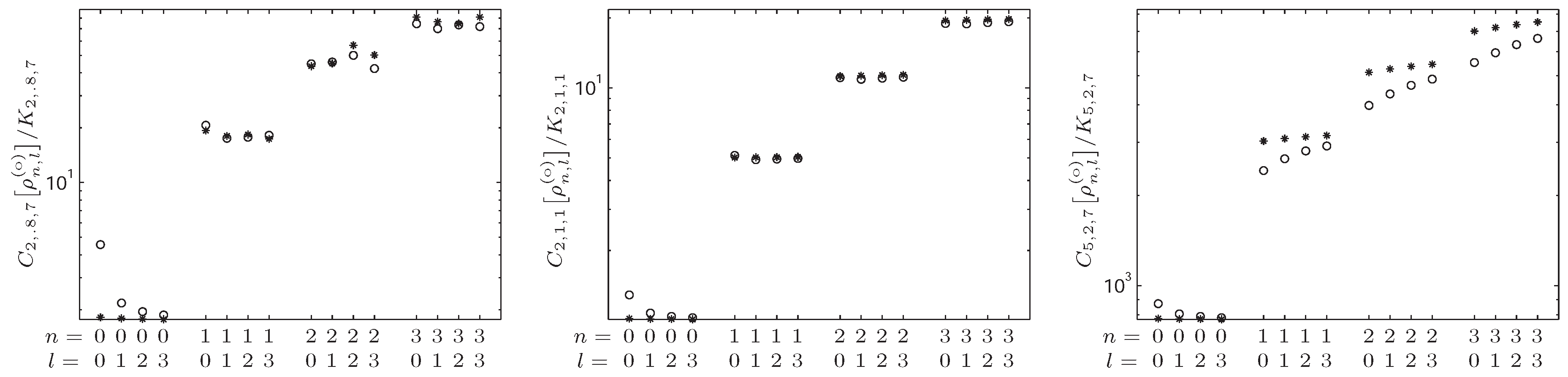
4.3. -Fisher–Rényi Complexity and the Harmonic System
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Proposition 2
Appendix A.1. The Case λ ≠ 1
Appendix A.1.1. The Sub-Case λ < 1
Appendix A.1.2. The Sub-Case λ > 1
Appendix A.2. The Case λ = 1
Appendix B. Proof of Proposition 3
Appendix C. Proof of Proposition 5
Appendix C.1. The (p,β,λ)-Fisher–Rényi Complexity is Lowerbounded over
Appendix C.2. Explicit Expression for the Minimizers.
Appendix C.2.1. The Case 1 − p*β < λ < 1
Appendix C.2.2. The Case λ > 1
Appendix C.2.3. The Case λ = 1
Appendix C.3. Symmetry through the Involution .
Appendix C.4. Explicit Expression of the Lower Bound.
References
- Sen, K.D. Statistical Complexity. Application in Electronic Structure; Springer: New York, NY, USA, 2011. [Google Scholar]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- López-Ruiz, R. Shannon information, LMC complexity and Rényi entropies: A straightforward approach. Biophys. Chem. 2005, 115, 215–218. [Google Scholar] [CrossRef] [PubMed]
- Chatzisavvas, K.C.; Moustakidis, C.C.; Panos, C.P. Information entropy, information distances, and complexity in atoms. J. Chem. Phys. 2005, 123, 174111. [Google Scholar] [CrossRef] [PubMed]
- Sen, K.D.; Panos, C.P.; Chatzisavvas, K.C.; Moustakidis, C.C. Net Fisher information measure versus ionization potential and dipole polarizability in atoms. Phys. Lett. A 2007, 364, 286–290. [Google Scholar] [CrossRef] [Green Version]
- Bialynicki-Birula, I.; Rudnicki, Ł. Entropic uncertainty relations in quantum physics. In Statistical Complexity. Application in Electronic Structure; Sen, K.D., Ed.; Springer: Berlin, Germay, 2010. [Google Scholar]
- Dehesa, J.S.; López-Rosa, S.; Manzano, D. Entropy and complexity analyses of D-dimensional quantum systems. In Statistical Complexities: Application to Electronic Structure; Sen, K.D., Ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Huang, Y. Entanglement detection: Complexity and Shannon entropic criteria. IEEE Trans. Inf. Theor. 2013, 59, 6774–6778. [Google Scholar] [CrossRef]
- Ebeling, W.; Molgedey, L.; Kurths, J.; Schwarz, U. Entropy, complexity, predictability and data analysis of time series and letter sequences. In Theory of Disaster; Springer: Berlin, Germany, 2000. [Google Scholar]
- Angulo, J.C.; Antolín, J. Atomic complexity measures in position and momentum spaces. J. Chem. Phys. 2008, 128, 164109. [Google Scholar] [CrossRef] [PubMed]
- Rosso, O.A.; Ospina, R.; Frery, A.C. Classification and verification of handwritten signatures with time causal information theory quantifiers. PLoS ONE 2016, 11, e0166868. [Google Scholar] [CrossRef] [PubMed]
- Toranzo, I.V.; Sánchez-Moreno, P.; Rudnicki, Ł.; Dehesa, J.S. One-parameter Fisher-Rényi complexity: Notion and hydrogenic applications. Entropy 2017, 19, 16. [Google Scholar] [CrossRef]
- Angulo, J.C.; Romera, E.; Dehesa, J.S. Inverse atomic densities and inequalities among density functionals. J. Math. Phys. 2000, 41, 7906–7917. [Google Scholar] [CrossRef]
- Dehesa, J.S.; López-Rosa, S.; Martínez-Finkelshtein, A.; Yáñez, R.J. Information theory of D-dimensional hydrogenic systems: Application to circular and Rydberg states. Int. J. Quantum Chem. 2010, 110, 1529–1548. [Google Scholar] [CrossRef]
- López-Rosa, S.; Esquievel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; Flores-Gallegos, N. Fisher information study in position and momentum spaces for elementary chemical reactions. J. Chem. Theor. Comput. 2010, 6, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Romera, E.; Sánchez-Moreno, P.; Dehesa, J.S. Uncertainty relation for Fisher information of D-dimensional single-particle systems with central potentials. J. Math. Phys. 2006, 47, 103504. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Zozor, S.; Dehesa, J.S. Upper bounds on Shannon and Rényi entropies for central potential. J. Math. Phys. 2011, 52, 022105. [Google Scholar] [CrossRef]
- Zozor, S.; Portesi, M.; Sánchez-Moreno, P.; Dehesa, J.S. Position-momentum uncertainty relation based on moments of arbitrary order. Phys. Rev. A 2011, 83, 052107. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.R.; Plastino, A. Tsallis-like information measures and the analysis of complex signals. Phys. A Stat. Mech. Appl. 2000, 275, 262–271. [Google Scholar] [CrossRef]
- Portesi, M.; Plastino, A. Generalized entropy as measure of quantum uncertainty. Phys. A Stat. Mech. Appl. 1996, 225, 412–430. [Google Scholar] [CrossRef]
- Massen, S.E.; Panos, C.P. Universal property of the information entropy in atoms, nuclei and atomic clusters. Phys. Lett. A 1998, 246, 530–533. [Google Scholar] [CrossRef]
- Guerrero, A.; Sanchez-Moreno, P.; Dehesa, J.S. Upper bounds on quantum uncertainty products and complexity measures. Phys. Rev. A 2011, 84, 042105. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Sánchez-Moreno, P.; Yáñez, R.J. Crámer-Rao information plane of orthogonal hypergeometric polynomials. J. Comput. Appl. Math. 2006, 186, 523–541. [Google Scholar] [CrossRef]
- Antolín, J.; Angulo, J.C. Complexity analysis of ionization processes and isoelectronic series. Int. J. Quantum Chem. 2009, 109, 586–593. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolín, J.; Sen, K.D. Fisher-Shannon plane and statistical complexity of atoms. Phys. Lett. A 2008, 372, 670–674. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher-Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Puertas-Centeno, D.; Toranzo, I.V.; Dehesa, J.S. The biparametric Fisher-Rényi complexity measure and its application to the multidimensional blackbody radiation. J. Stat. Mech. Theor. Exp. 2017, 2017, 043408. [Google Scholar] [CrossRef]
- Sobrino-Coll, N.; Puertas-Centeno, D.; Toranzo, I.V.; Dehesa, J.S. Complexity measures and uncertainty relations of the high-dimensional harmonic and hydrogenic systems. J. Stat. Mech. Theor. Exp. 2017, 2017, 083102. [Google Scholar] [CrossRef]
- Puertas-Centeno, D.; Toranzo, I.V.; Dehesa, J.S. Biparametric complexities and the generalized Planck radiation law. arXiv, 2017; arXiv:1704.08452v. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. A 1922, 222, 309–368. [Google Scholar]
- Rudnicki, Ł.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa., J.S. Monotone measures of statistical complexity. Phys. Lett. A 2016, 380, 377–380. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561. [Google Scholar]
- Lutwak, E.; Yang, D.; Zhang, G. Cramér-Rao and moment-entropy inequalities for Rényi entropy and generalized Fisher information. IEEE Trans. Inf. Theor. 2005, 51, 473–478. [Google Scholar] [CrossRef]
- Bercher, J.F. On a (β,q)-generalized Fisher information and inequalities invoving q-Gaussian distributions. J. Math. Phys. 2012, 53, 063303. [Google Scholar] [CrossRef] [Green Version]
- Lutwak, E.; Lv, S.; Yang, D.; Zhang, G. Extension of Fisher information and Stam’s inequality. IEEE Trans. Inf. Theor. 2012, 58, 1319–1327. [Google Scholar] [CrossRef]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kay, S.M. Fundamentals for Statistical Signal Processing: Estimation Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Bourret, R. A note on an information theoretic form of the uncertainty principle. Inf. Control 1958, 1, 398–401. [Google Scholar] [CrossRef]
- Leipnik, R. Entropy and the uncertainty principle. Inf. Control 1959, 2, 64–79. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.F. Analysis of signals in the Fisher-Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Sañudo, J.; López-Ruiz, R. Statistical complexity and Fisher-Shannon information in the H-atom. Phys. Lett. A 2008, 372, 5283–5286. [Google Scholar]
- Dehesa, J.S.; López-Rosa, S.; Manzano, D. Configuration complexities of hydrogenic atoms. Eur. Phys. J. D 2009, 55, 539–548. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Sañudo, J.; Romera, E.; Calbet, X. Statistical complexity and Fisher-Shannon information: Application. In Statistical Complexity. Application in Electronic Structure; Springer: New York, NY, USA, 2012. [Google Scholar]
- Manzano, D. Statistical measures of complexity for quantum systems with continuous variables. Phys. A Stat. Mech. Appl. 2012, 391, 6238–6244. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. (Eds.) Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Puertas-Centeno, D.; Rudnicki, L.; Dehesa, J.S. LMC-Rényi complexity monotones, heavy tailed distributions and stretched-escort deformation. 2017; in preparation. [Google Scholar]
- Agueh, M. Sharp Gagliardo-Nirenberg inequalities and mass transport theory. J. Dyn. Differ. Equ. 2006, 18, 1069–1093. [Google Scholar] [CrossRef]
- Agueh, M. Sharp Gagliardo-Nirenberg inequalities via p-Laplacian type equations. Nonlinear Differ. Equ. Appl. 2008, 15, 457–472. [Google Scholar]
- Costa, J.A.; Hero, A.O., III; Vignat, C. On solutions to multivariate maximum α-entropy problems. In Proceedings of the 4th International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, Lisbon, Portugal, 7–9 July 2003; pp. 211–226. [Google Scholar]
- Johnson, O.; Vignat, C. Some results concerning maximum Rényi entropy distributions. Ann. Inst. Henri Poincare B Probab. Stat. 2007, 43, 339–351. [Google Scholar] [CrossRef]
- Nanda, A.K.; Maiti, S.S. Rényi information measure for a used item. Inf. Sci. 2007, 177, 4161–4175. [Google Scholar] [CrossRef]
- Panter, P.F.; Dite, W. Quantization distortion in pulse-count modulation with nonuniform spacing of levels. Proc. IRE 1951, 39, 44–48. [Google Scholar] [CrossRef]
- Loyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theor. 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Kluwer: Boston, MA, USA, 1992. [Google Scholar]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Humblet, P.A. Generalization of the Huffman coding to minimize the probability of buffer overflow. IEEE Trans. Inf. Theor. 1981, 27, 230–232. [Google Scholar] [CrossRef]
- Baer, M.B. Source coding for quasiarithmetic penalties. IEEE Trans. Inf. Theor. 2006, 52, 4380–4393. [Google Scholar] [CrossRef]
- Bercher, J.F. Source coding with escort distributions and Rényi entropy bounds. Phys. Lett. A 2009, 373, 3235–3238. [Google Scholar] [CrossRef] [Green Version]
- Bobkov, S.G.; Chistyakov, G.P. Entropy Power Inequality for the Rényi Entropy. IEEE Trans. Inf. Theor. 2015, 61, 708–714. [Google Scholar] [CrossRef]
- Pardo, L. Statistical Inference Based on Divergence Measures; Chapman & Hall: Boca Raton, FL, USA, 2006. [Google Scholar]
- Harte, D. Multifractals: Theory and Applications, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Beck, C.; Schögl, F. Thermodynamics of Chaotic Systems: An Introduction; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Bialynicki-Birula, I. Formulation of the uncertainty relations in terms of the Rényi entropies. Phys. Rev. A 2006, 74, 052101. [Google Scholar] [CrossRef]
- Zozor, S.; Vignat, C. On classes of non-Gaussian asymptotic minimizers in entropic uncertainty principles. Phys. A Stat. Mech. Appl. 2007, 375, 499–517. [Google Scholar] [CrossRef]
- Zozor, S.; Vignat, C. Forme entropique du principe d’incertitude et cas d’égalité asymptotique. In Proceedings of the Colloque GRETSI, Troyes, France, 11–14 Septembre 2007. (In French). [Google Scholar]
- Zozor, S.; Portesi, M.; Vignat, C. Some extensions to the uncertainty principle. Phys. A Stat. Mech. Appl. 2008, 387, 4800–4808. [Google Scholar] [CrossRef]
- Zozor, S.; Bosyk, G.M.; Portesi, M. General entropy-like uncertainty relations in finite dimensions. J. Phys. A 2014, 47, 495302. [Google Scholar] [CrossRef]
- Jizba, P.; Dunningham, J.A.; Joo, J. Role of information theoretic uncertainty relations in quantum theory. Ann. Phys. 2015, 355, 87–115. [Google Scholar] [CrossRef]
- Jizba, P.; Ma, Y.; Hayes, A.; Dunningham, J.A. One-parameter class of uncertainty relations based on entropy power. Phys. Rev. E 2016, 93, 060104. [Google Scholar] [CrossRef] [PubMed]
- Hammad, P. Mesure d’ordre α de l’information au sens de Fisher. Rev. Stat. Appl. 1978, 26, 73–84. (In French) [Google Scholar]
- Pennini, F.; Plastino, A.R.; Plastino, A. Rényi entropies and Fisher information as measures of nonextensivity in a Tsallis setting. Phys. A Stat. Mech. Appl. 1998, 258, 446–457. [Google Scholar] [CrossRef]
- Chimento, L.P.; Pennini, F.; Plastino, A. Naudts-like duality and the extreme Fisher information principle. Phys. Rev. E 2000, 62, 7462–7465. [Google Scholar] [CrossRef]
- Casas, M.; Chimento, L.; Pennini, F.; Plastino, A.; Plastino, A.R. Fisher information in a Tsallis non-extensive environment. Chaos Solitons Fractals 2002, 13, 451–459. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A.; Ferri, G.L. Semiclassical information from deformed and escort information measures. Phys. A Stat. Mech. Appl. 2007, 383, 782–796. [Google Scholar] [CrossRef]
- Bercher, J.F. On generalized Cramér-Rao inequalities, generalized Fisher information and characterizations of generalized q-Gaussian distributions. J. Phys. A 2012, 45, 255303. [Google Scholar] [CrossRef] [Green Version]
- Bercher, J.F. Some properties of generalized Fisher information in the context of nonextensive thermostatistics. Phys. A Stat. Mech. Appl. 2013, 392, 3140–3154. [Google Scholar] [CrossRef] [Green Version]
- Bercher, J.F. On escort distributions, q-gaussians and Fisher information. In Proceedings of the 30th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Chamonix, France, 4–9 July 2010; pp. 208–215. [Google Scholar]
- Devroye, L. Non-Uniform Random Variate Generation; Springer: New York, NY, USA, 1986. [Google Scholar]
- Korbel, J. Rescaling the nonadditivity parameter in Tsallis thermostatistics. Phys. Lett. A 2017, 381, 2588–2592. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1970. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 3: More Special Functions; Gordon and Breach: New York, NY, USA, 1990. [Google Scholar]
- Nieto, M.M. Hydrogen atom and relativistic pi-mesic atom in N-space dimensions. Am. J. Phys. 1979, 47, 1067–1072. [Google Scholar] [CrossRef]
- Yáñez, R.J.; van Assche, W.; Dehesa, J.S. Position and momentum information entropies of the D-dimensional harmonic oscillator and hydrogen atoms. Phys. Rev. A 1994, 50, 3065–3079. [Google Scholar] [CrossRef] [PubMed]
- Avery, J.S. Hyperspherical Harmonics and Generalized Sturmians; Kluwer Academic: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Yáñez, R.J.; van Assche, W.; González-Férez, R.; Sánchez-Dehesa, J. Entropic integrals of hyperspherical harmonics and spatial entropy of D-dimensional central potential. J. Math. Phys. 1999, 40, 5675–5686. [Google Scholar] [CrossRef]
- Louck, J.D.; Shaffer, W.H. Generalized orbital angular momentum of the n-fold degenerate quantum-mechanical oscillator. Part I. The twofold degenerate oscillator. J. Mol. Spectrosc. 1960, 4, 285–297. [Google Scholar]
- Louck, J.D.; Shaffer, W.H. Generalized orbital angular momentum of the n-fold degenerate quantum-mechanical oscillator. Part II. The n-fold degenerate oscillator. J. Mol. Spectrosc. 1960, 4, 298–333. [Google Scholar]
- Nirenberg, L. On elliptical partial differential equations. Annali della Scuola Normale Superiore di Pisa 1959, 13, 115–169. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Prentice Hall: Englewood Cliff, NJ, USA, 1963. [Google Scholar]
- Van Brunt, B. The Calculus of Variations; Springer: New York, NY, USA, 2004. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zozor, S.; Puertas-Centeno, D.; Dehesa, J.S. On Generalized Stam Inequalities and Fisher–Rényi Complexity Measures. Entropy 2017, 19, 493. https://doi.org/10.3390/e19090493
Zozor S, Puertas-Centeno D, Dehesa JS. On Generalized Stam Inequalities and Fisher–Rényi Complexity Measures. Entropy. 2017; 19(9):493. https://doi.org/10.3390/e19090493
Chicago/Turabian StyleZozor, Steeve, David Puertas-Centeno, and Jesús S. Dehesa. 2017. "On Generalized Stam Inequalities and Fisher–Rényi Complexity Measures" Entropy 19, no. 9: 493. https://doi.org/10.3390/e19090493




