State Estimation for General Complex Dynamical Networks with Incompletely Measured Information
Abstract
:1. Introduction
2. Network Models and Preliminaries
3. Main Results
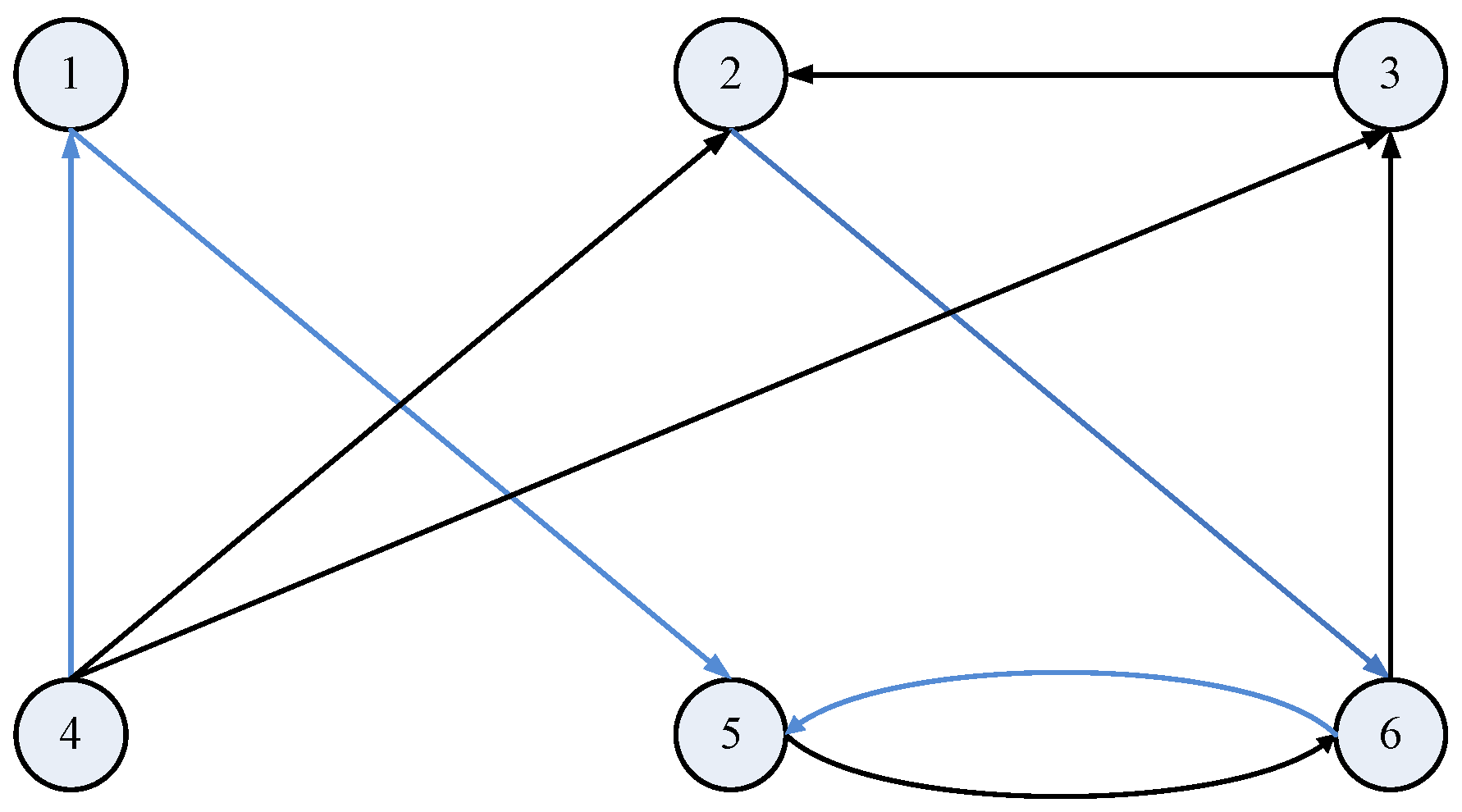
4. Numerical Simulations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Hooper, P.L.; DeDeo, S.; Caldwell Hooper, A.E.; Gurven, M.; Kaplan, H.S. Dynamical structure of a traditional Amazonian social network. Entropy 2013, 15, 4932–4955. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, F.; Zseby, T. Entropy-based characterization of Internet background radiation. Entropy 2014, 17, 74–101. [Google Scholar] [CrossRef] [Green Version]
- Nandi, A.; Kafashan, M.M.; Ching, S.N. Control analysis and design for statistical models of spiking networks. IEEE Trans. Control Netw. Syst. 2017. [Google Scholar] [CrossRef]
- Kaluza, P.; Kölzsch, A.; Gastner, M.T.; Blasius, B. The complex network of global cargo ship movements. J. R. Soc. Interface 2010, 7, 1093–1103. [Google Scholar] [CrossRef] [PubMed]
- Rosas-Casals, M.; Solé, R. Analysis of major failures in Europe’s power grid. Int. J. Electr. Power 2011, 33, 805–808. [Google Scholar] [CrossRef] [Green Version]
- Kurzynski, M.; Chelminiak, P. Stochastic dynamics of proteins and the action of biological molecular machines. Entropy 2014, 16, 1969–1982. [Google Scholar] [CrossRef]
- Singh, S.; Samal, A.; Giri, V.; Krishna, S.; Raghuram, N.; Jain, S. Flux-based classification of reactions reveals a functional bow-tie organization of complex metabolic networks. Phys. Rev. E 2013, 87, 052708. [Google Scholar] [CrossRef] [PubMed]
- Kakar, J.; Sezgin, A. A Survey on Robust Interference Management in Wireless Networks. Entropy 2017, 19, 362. [Google Scholar] [CrossRef]
- Summers, T.H.; Cortesi, F.L.; Lygeros, J. On submodularity and controllability in complex dynamical networks. IEEE Trans. Control Netw. Syst. 2016, 3, 91–101. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L. Exponential outer synchronization between two uncertain time-varying complex networks with nonlinear coupling. Entropy 2015, 17, 3097–3109. [Google Scholar] [CrossRef]
- Jalili, M. Enhancing synchronizability of diffusively coupled dynamical networks: A survey. IEEE Trans. Neural Netw. Learn. 2013, 24, 1009–1022. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wei, G.; Shu, H. State estimation for complex networks with randomly occurring coupling delays. Neurocomputing 2013, 122, 513–520. [Google Scholar] [CrossRef]
- Tong, D.; Zhou, W.; Wang, H. Exponential state estimation for stochastic complex dynamical networks with multi-delayed base on adaptive control. Int. J. Control Autom. 2014, 12, 963–968. [Google Scholar] [CrossRef]
- Gelb, A.; Kasper, J.F.; Nash, R.A.; Price, C.F.; Sutherland, A.A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- NøRgaard, M.; Poulsen, N.K.; Ravn, O. New developments in state estimation for nonlinear systems. Automatica 2000, 36, 1627–1638. [Google Scholar] [CrossRef]
- Balasubramaniam, P.; Lakshmanan, S.; Theesar, S.J.S. State estimation for Markovian jumping recurrent neural networks with interval time-varying delays. Nonlinear Dyn. 2010, 60, 661–675. [Google Scholar] [CrossRef]
- Shen, B.; Wang, Z.; Liu, X. Bounded H∞ Synchronization and state estimation for discrete time-varying stochastic complex networks over a finite horizon. IEEE Trans. Neural Netw. 2011, 22, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Wang, Z.; Gao, H.; Liu, X. State estimation for discrete-time dynamical networks with time-varying delays and stochastic disturbances under the Round-Robin protocol. IEEE Trans. Neural Netw. Learn. 2016, 28, 1139–1151. [Google Scholar] [CrossRef] [PubMed]
- Sakthivel, R.; Sathishkumar, M.; Kaviarasan, B.; Anthoni, S.M. Synchronization and state estimation for stochastic complex networks with uncertain inner coupling. Neurocomputing 2017, 238, 44–55. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Ding, D.; Song, Y. Finite-horizon bounded H∞ synchronisation and state estimation for discrete-time complex networks: Local performance analysis. IET Control Theory Appl. 2017, 11, 827–837. [Google Scholar] [CrossRef]
- Shen, B.; Wang, Z.; Ding, D.; Shu, H. H∞ state estimation for complex networks with uncertain inner coupling and incomplete measurement. IEEE Trans. Neural Netw. Learn. 2013, 40, 2027–2037. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Chen, H. H∞ state estimation for discrete-time delayed systems of the neural network type with multiple missing measurements. IEEE Trans. Neural Netw. Learn. 2015, 26, 2987–2998. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Luan, X.; Liu, F. H∞ filtering for discrete-time systems with stochastic incomplete measurement and mixed delays. IEEE Trans. Ind. Electron. 2012, 59, 2732–2739. [Google Scholar] [CrossRef]
- Du, D.; Fei, M.; Jia, T. Modelling and stability analysis of MIMO networked control systems withmulti-channel random packet losses. Trans. Inst. Meas. Control 2013, 35, 66–74. [Google Scholar] [CrossRef]
- Li, J.N.; Bao, W.D.; Li, S.B.; Wen, C.L.; Li, L.S. Exponential synchronization of discrete-time mixed delay neural networks with actuator constraints and stochastic missing data. Neurocomputing 2016, 207, 700–707. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Li, D.; Lu, J.A.; Wu, X.; Chen, G. Estimating the ultimate bound and positively invariant set for the Lorenz system and a unified chaotic system. J. Math. Anal. Appl. 2006, 323, 844–853. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, X.; Lu, J.A.; Feng, H.; Lü, J. Recovering Structures of Complex Dynamical Networks Based on Generalized Outer Synchronization. IEEE Trans. Circuits Syst. I 2014, 61, 3216–3224. [Google Scholar] [CrossRef]

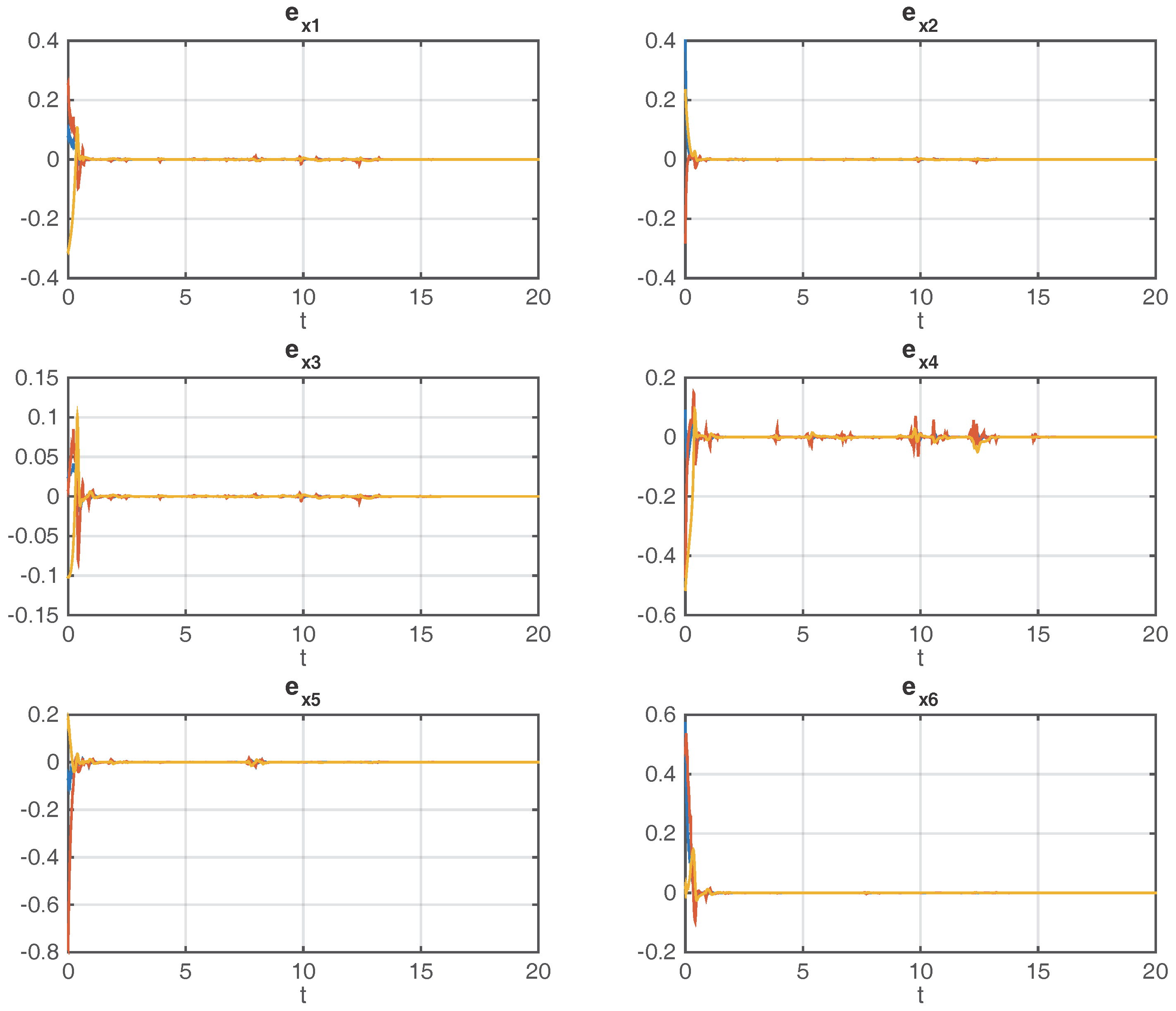
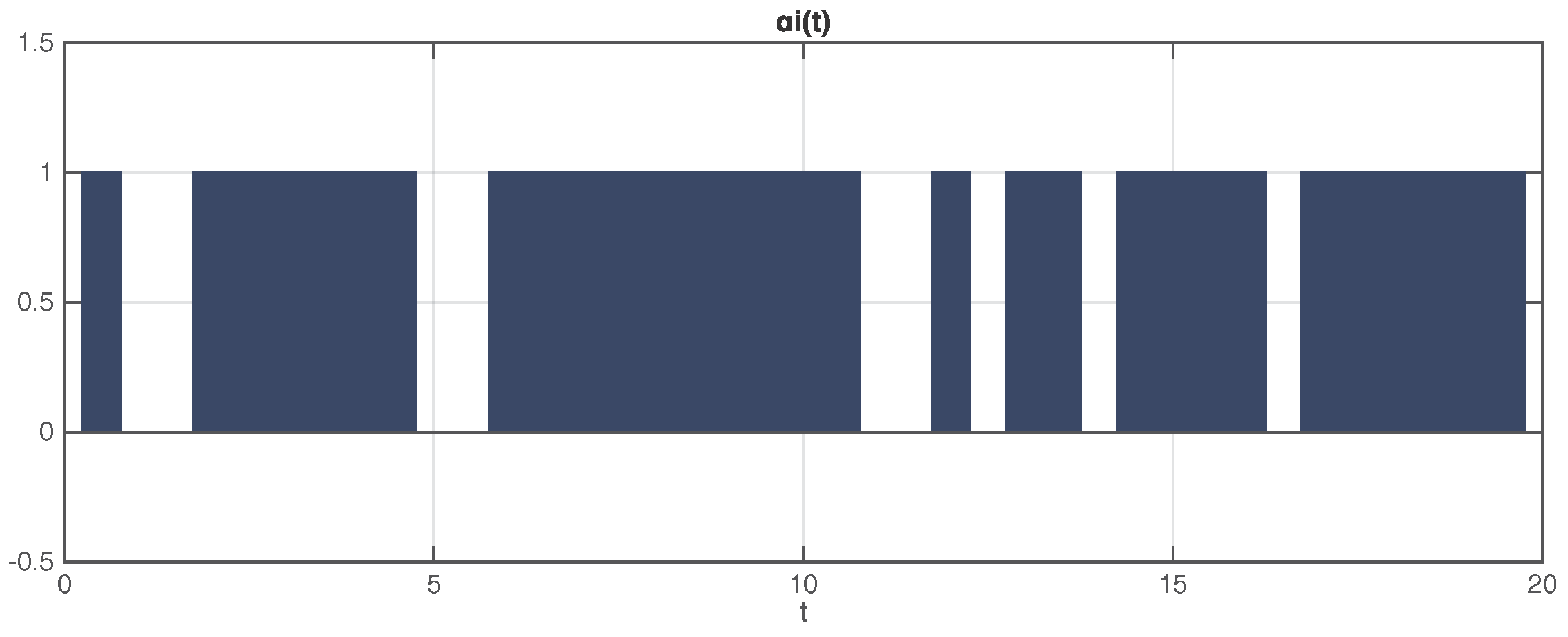
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jiang, G.-P.; Wu, X. State Estimation for General Complex Dynamical Networks with Incompletely Measured Information. Entropy 2018, 20, 5. https://doi.org/10.3390/e20010005
Wang X, Jiang G-P, Wu X. State Estimation for General Complex Dynamical Networks with Incompletely Measured Information. Entropy. 2018; 20(1):5. https://doi.org/10.3390/e20010005
Chicago/Turabian StyleWang, Xinwei, Guo-Ping Jiang, and Xu Wu. 2018. "State Estimation for General Complex Dynamical Networks with Incompletely Measured Information" Entropy 20, no. 1: 5. https://doi.org/10.3390/e20010005




