Robustification of a One-Dimensional Generic Sigmoidal Chaotic Map with Application of True Random Bit Generation
Abstract
:1. Introduction
2. Generic One-Dimensional Sigmoidal Chaotic Maps
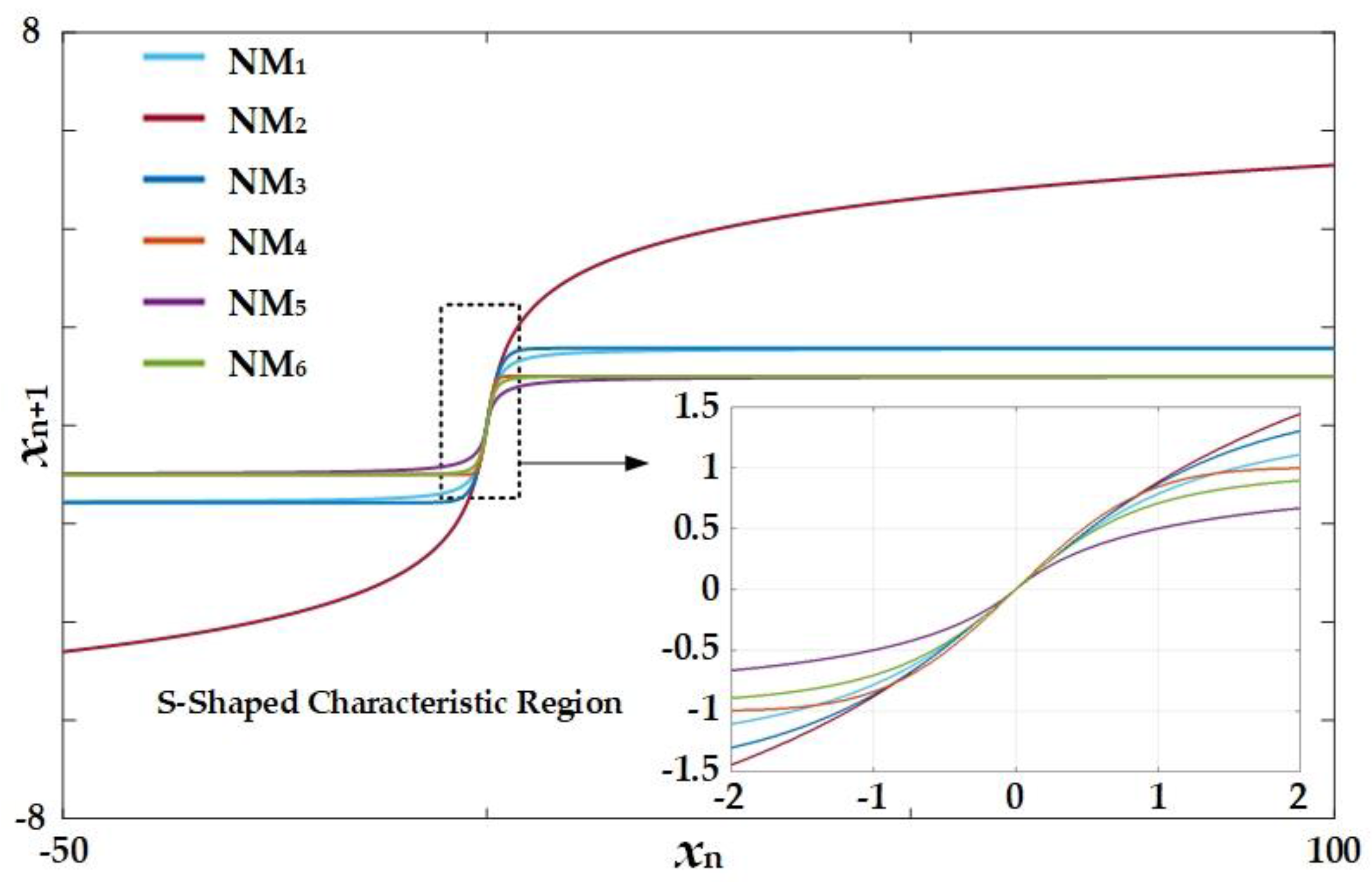
2.1. Unification of Generic Sigmoidal Chaotic Map
2.2. Simplification of Generic Sigmoidal Chaotic Map
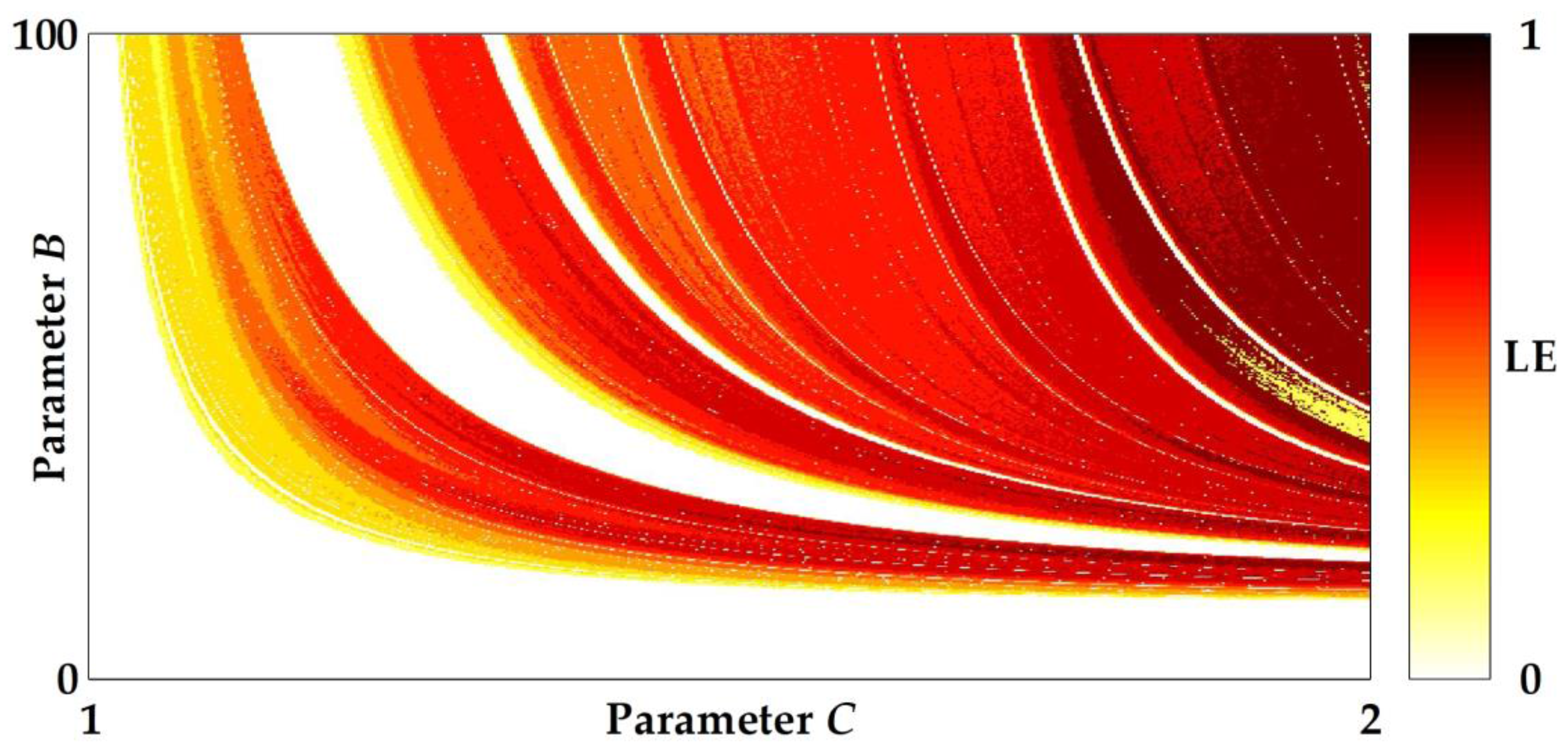
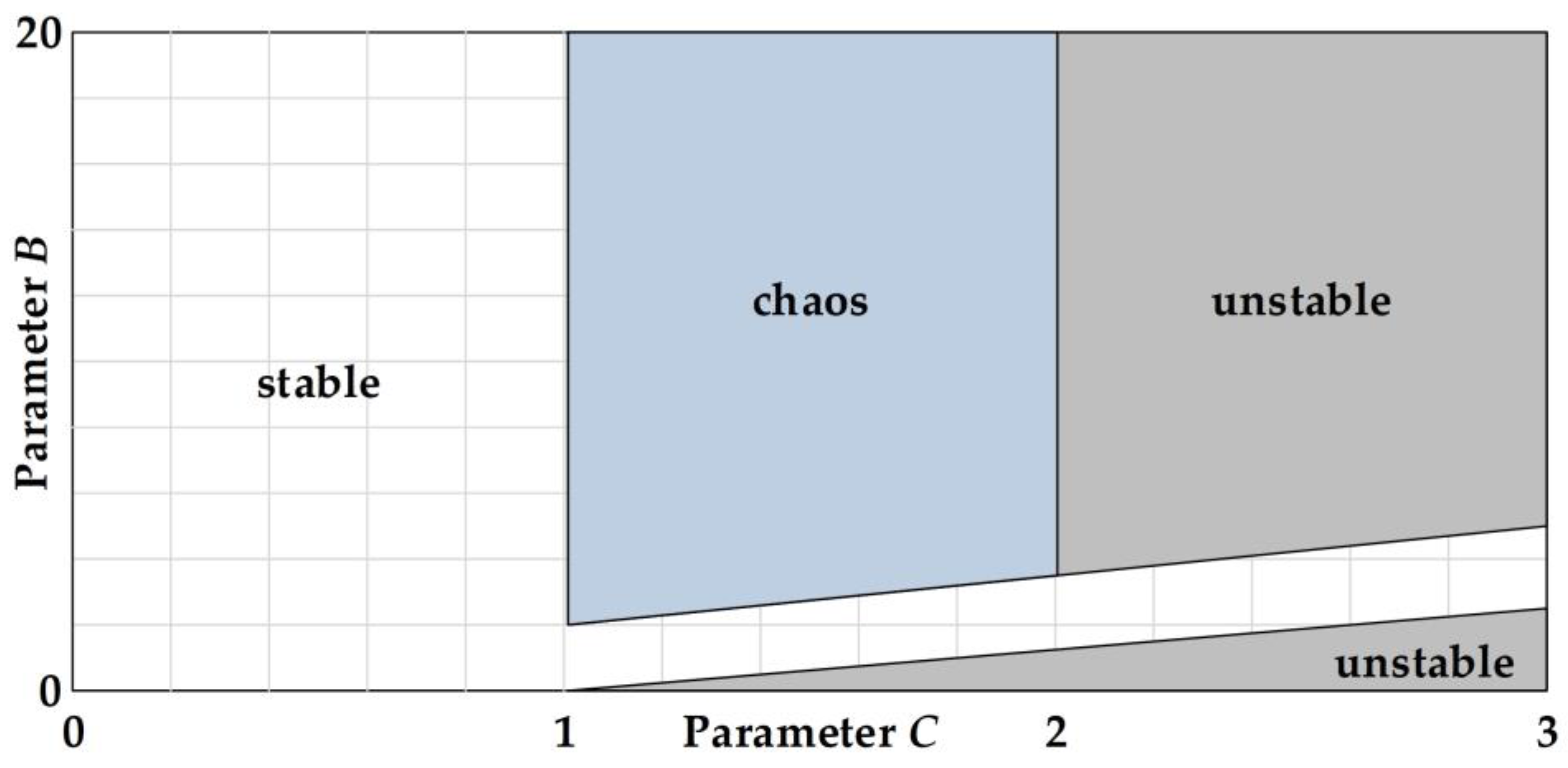
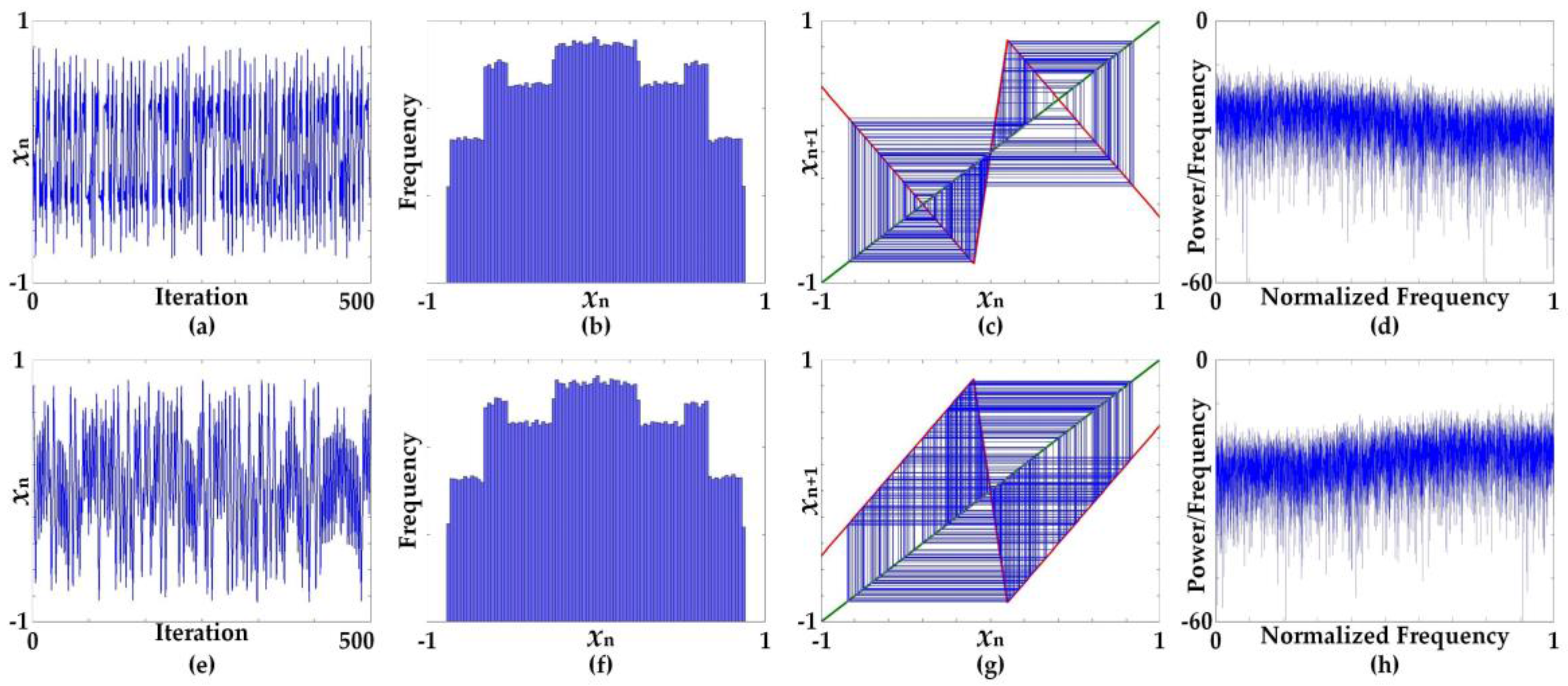
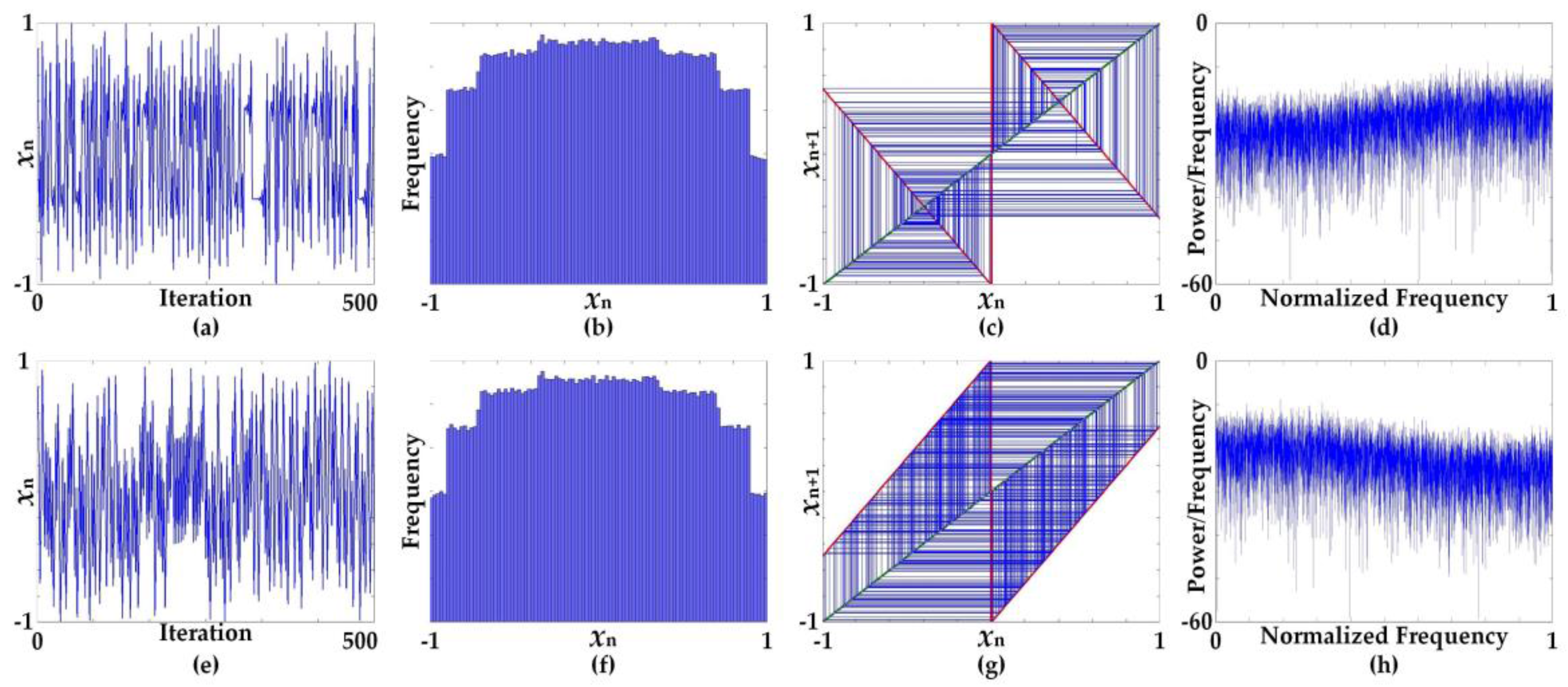
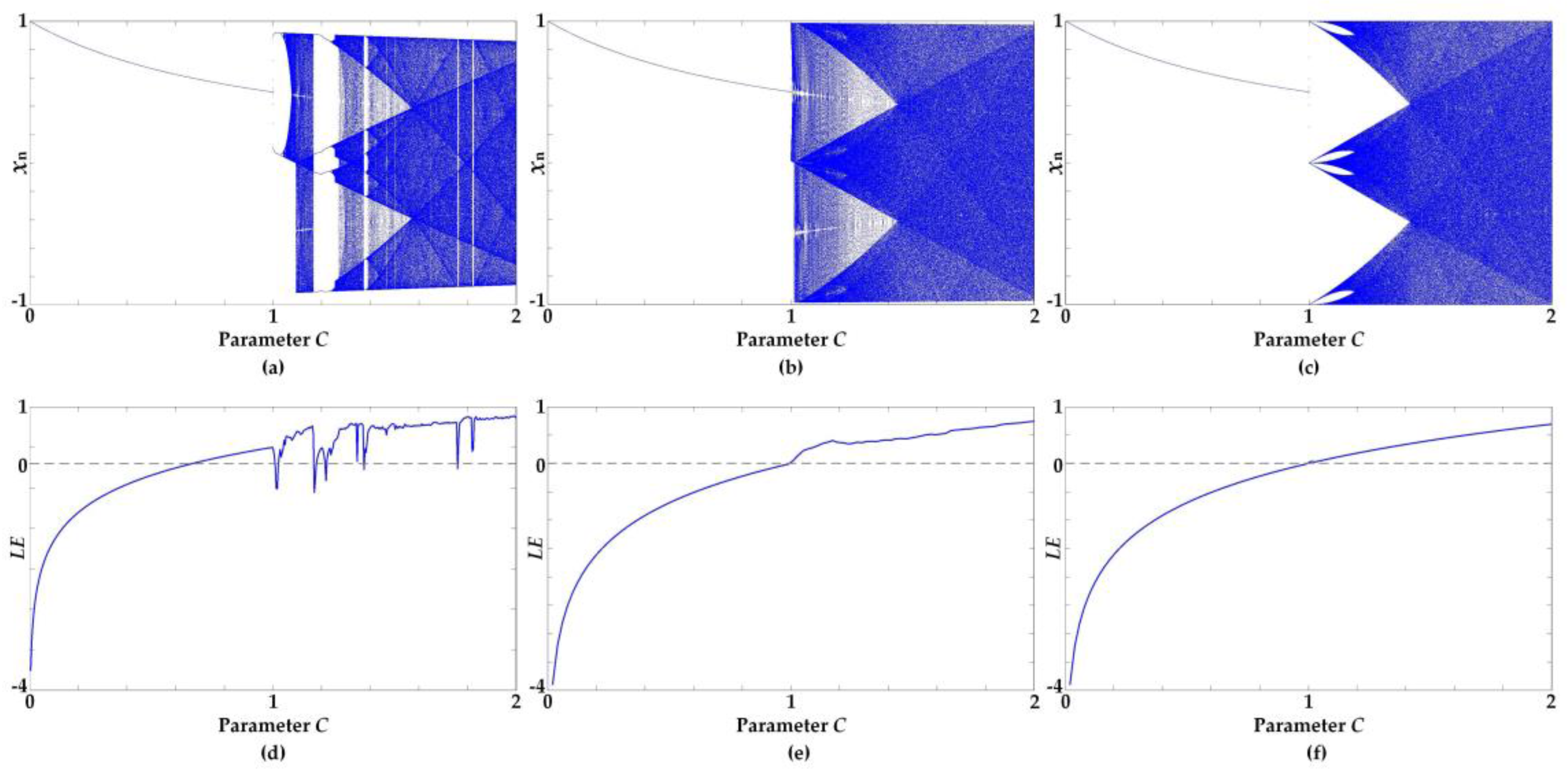
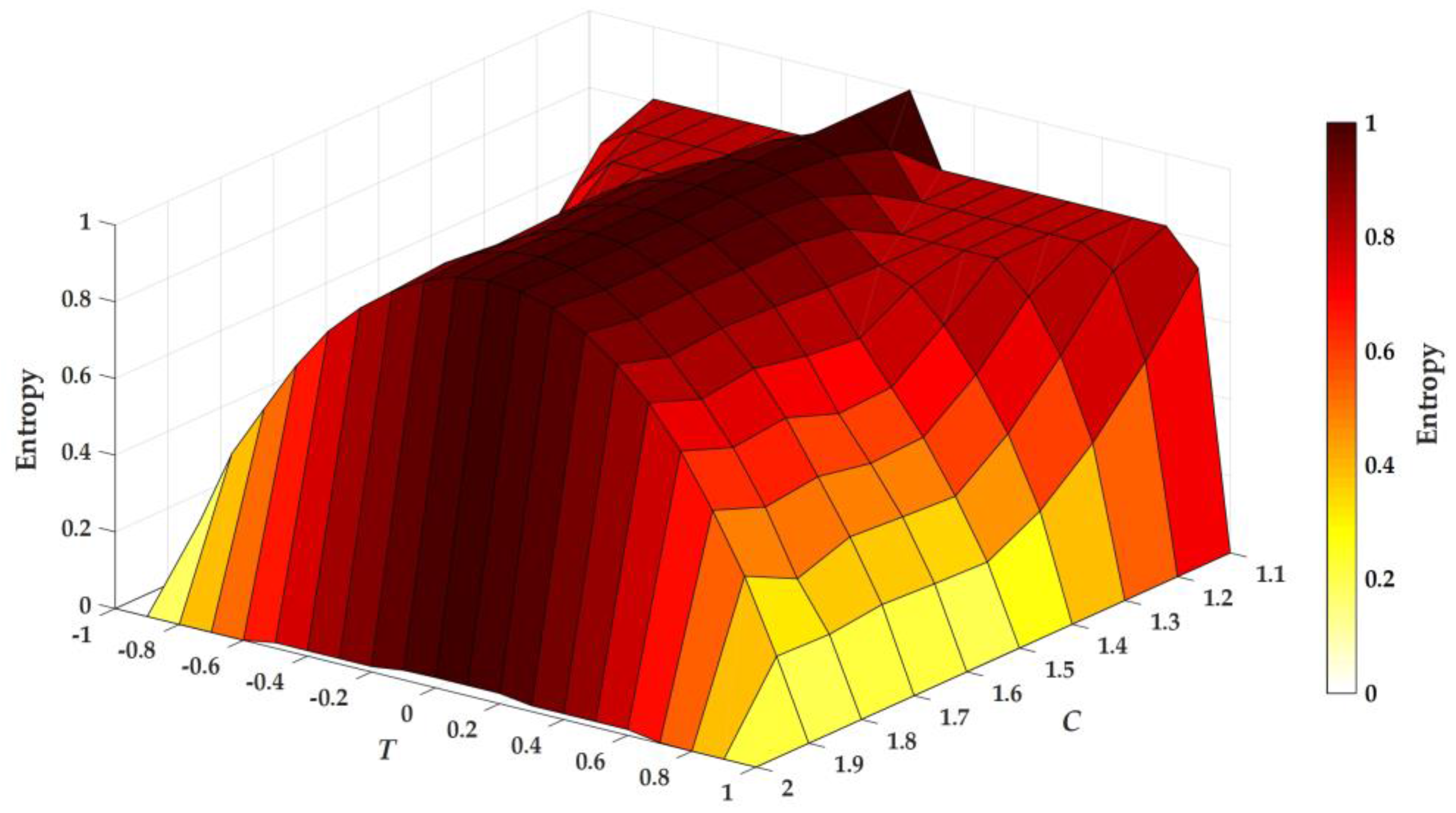
3. Linearization of Simplified Sigmoidal Chaotic Map for Robust Chaos
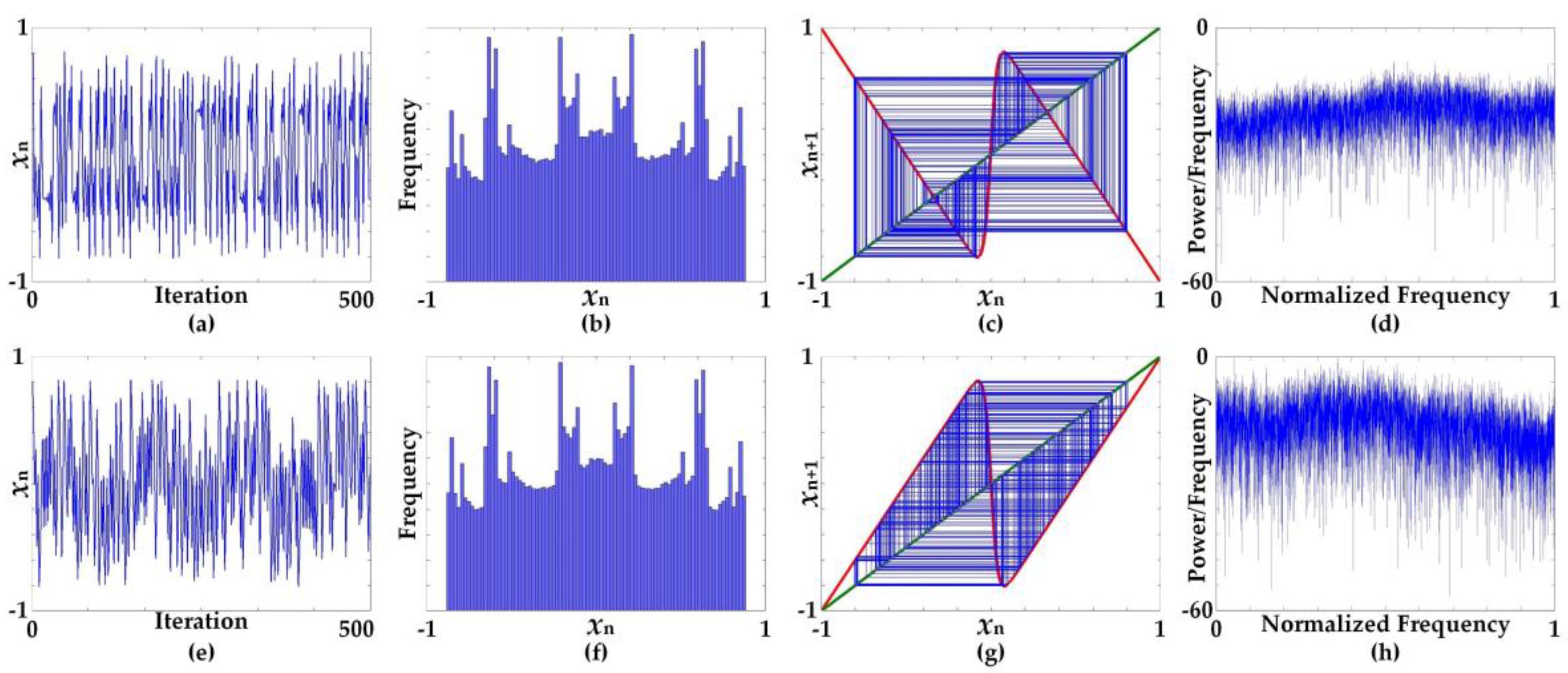
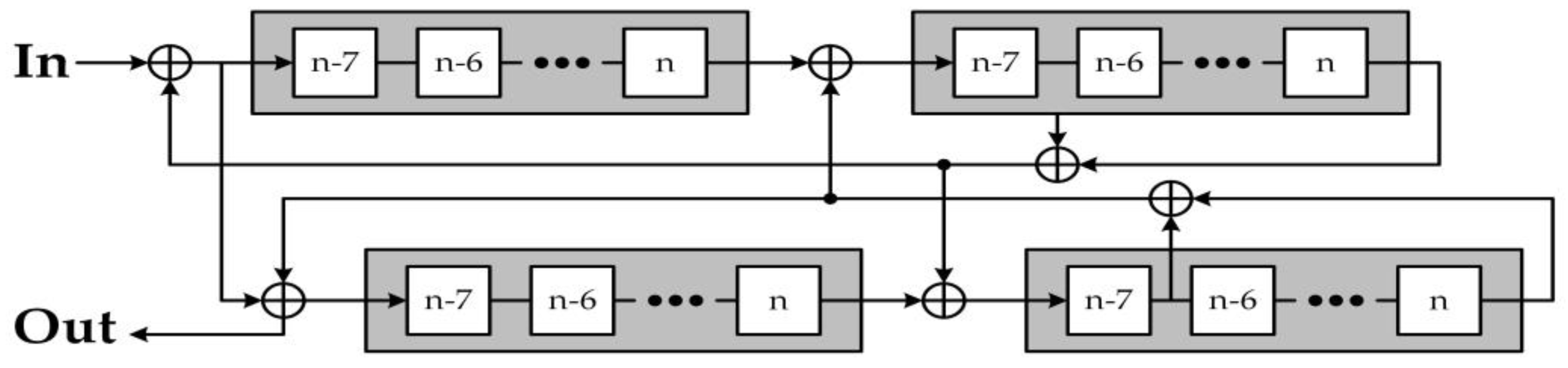
4. True Random Bit Generation Based on the Proposed Linearized Sigmoidal Chaotic Map
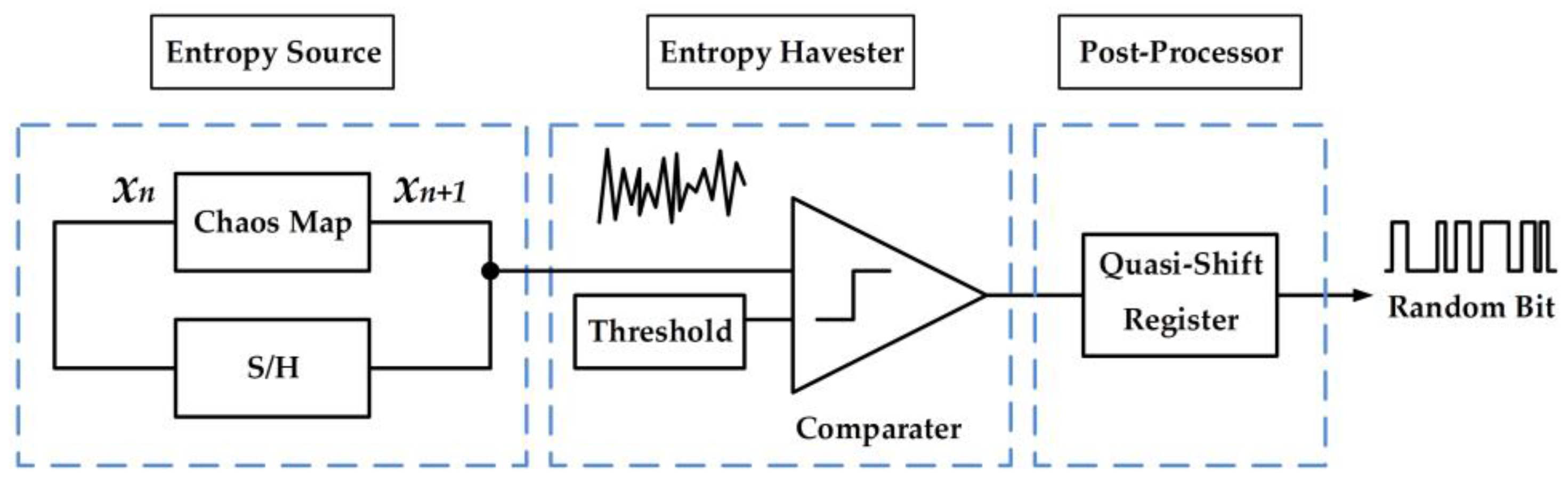
4.1. Random Bit Generator
4.1.1. Entropy Source
4.1.2. Entropy Harvester
4.1.3. Post-Processor
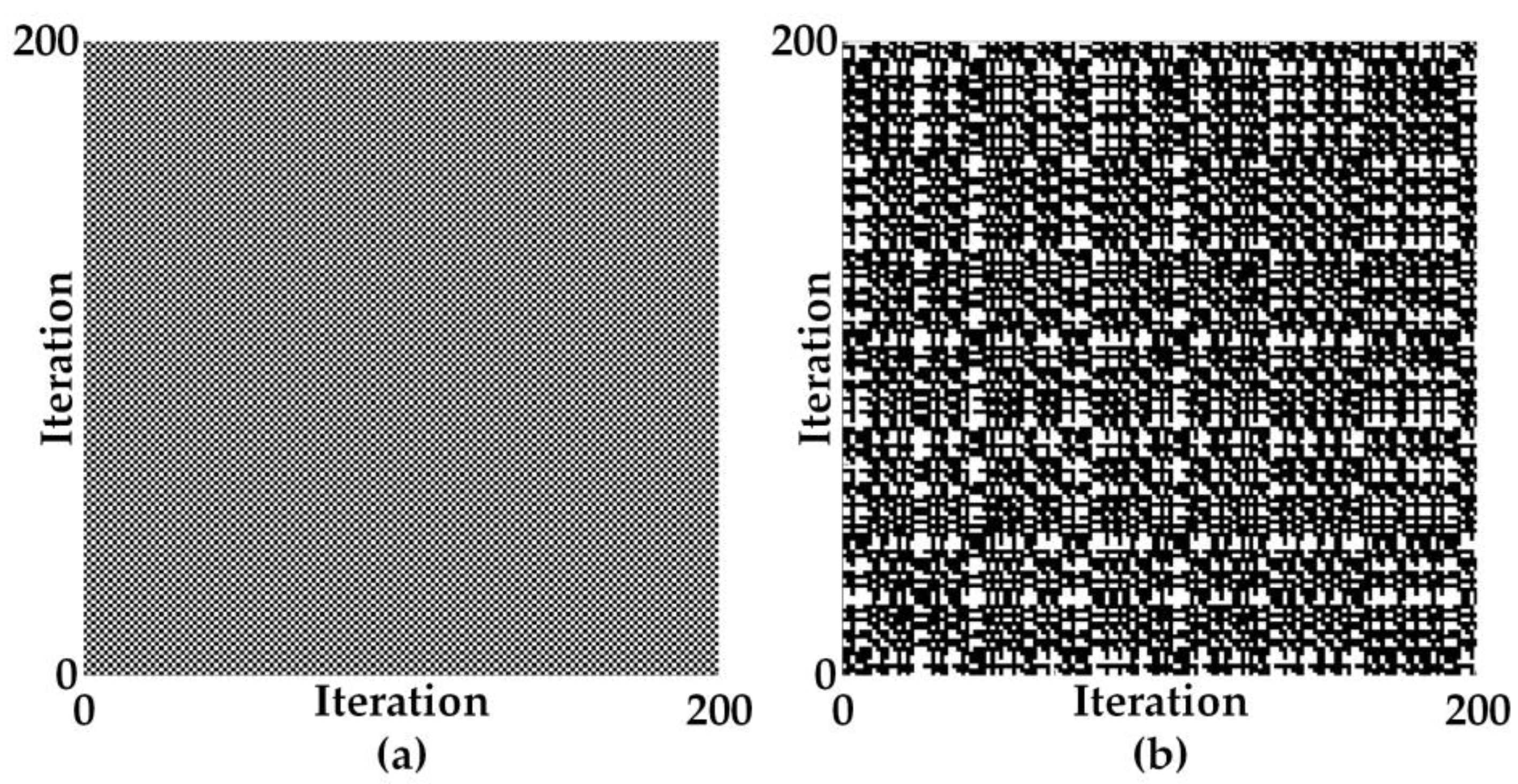
4.2. Randomness Performance Evaluation
4.2.1. NIST SP800-22 Test Suite
4.2.2. TestU01
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Majumdar, M.; Mitra, T. Robust ergodic chaos in discounted dynamic optimization models. Econ. Theory 1994, 4, 677–688. [Google Scholar] [CrossRef]
- Dogaru, R.; Murgan, A.T.; Ortmann, S.; Glesner, M. Searching for robust chaos in discrete time neural networks using weight space exploration. Int. Conf. Neural Netw. 1996, 2, 688–693. [Google Scholar]
- Banerjee, S.; Yorke, J.A.; Grebogi, C. Robust chaos. Phys. Rev. Lett. 1998, 80, 3049–3052. [Google Scholar] [CrossRef]
- Shukla, P.K.; Khare, A.; Rizvi, M.A.; Stalin, S.; Kumar, S. Applied cryptography using chaos function for fast digital logic-based systems in ubiquitous computing. Entropy 2015, 17, 1387–1410. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A colour image encryption scheme using permutation-substitution based on chaos. Entropy 2015, 17, 3877–3897. [Google Scholar] [CrossRef]
- Fallahi, K.; Leung, H. A chaos secure communication scheme based on multiplication modulation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 368–383. [Google Scholar] [CrossRef]
- Miliou, A.N.; Antoniades, I.P.; Stavrinides, S.G.; Anagnostopoulos, A.N. Secure communication by chaotic synchronization: Robustness under noisy conditions. Nonlinear Anal. Real World Appl. 2007, 8, 1003–1012. [Google Scholar] [CrossRef]
- Xu, G.; Shekofteh, Y.; Akgül, A.; Li, C.; Panahi, S. A New Chaotic System with a Self-Excited Attractor: Entropy Measurement, Signal Encryption, and Parameter Estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- San-Um, W.; Srichavengsup, W. A robust hash function using cross-coupled chaotic maps with absolute-valued sinusoidal nonlinearity. Int. J. Adv. Comput. Sci. Appl. 2016. [Google Scholar] [CrossRef]
- Andrecut, M.; Ali, M. On the occurrence of robust chaos in a smooth system. Mod. Phys. Lett. 2001, 15, 391–395. [Google Scholar] [CrossRef]
- Andrecut, M.; Ali, M. Robust chaos in a smooth system. Int. J. Mod. Phys. 2001, 15, 177–189. [Google Scholar] [CrossRef]
- Pérez, G. Robust chaos in polynomial unimodal maps. Int. J. Bifurc. Chaos 2004, 14, 2431–2437. [Google Scholar] [CrossRef]
- Alvarez-Llamoza, O.; Cosenza, M.G.; Ponce, G.A. Critical behavior of the Lyapunov exponent in type-III intermittency. Chaos Solitons Fractals 2008, 36, 150–156. [Google Scholar] [CrossRef]
- Aguirregabiria, J.M. Robust chaos with prescribed natural invariant measure and Lyapunov exponent. arXiv, 2009; arXiv:0907.3790. [Google Scholar]
- Hrusak, J.; Mayer, D.; Stork, M. Structural synthesis of state space energy based adaptive controller for robust chaos-generating systems of arbitrary finite order. In Proceedings of the 2012 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 5–7 September 2012; pp. 107–110. [Google Scholar]
- Nikulchev, E. Robust chaos generation on the basis of symmetry violations in attractors. In Proceedings of the 2nd International Conference on Emission Electronics (ICEE), St. Petersburg, Russia, 30 June–4 July 2014; pp. 1–3. [Google Scholar]
- Nikulchev, E.V. Generation of robust chaos in the invariant centre manifold. In Proceedings of the 2015 International Conference "Stability and Control Processes" in Memory of V.I. Zubov (SCP), St. Petersburg, Russia, 5–9 October 2015; 2015; pp. 290–291. [Google Scholar]
- Elhadj, Z.; Sprott, J.C. Is A Unifying Chaotic Dynamical System Possible? Int. J. Open Probl. Comput. Sci. Math. 2012, 5, 75–78. [Google Scholar] [CrossRef]
- Elhadj, Z.; Sprott, J.C. The unified chaotic system describing the Lorenz and Chua systems. Facta Univ. Series Electron. Energ. 2010, 23, 345–355. [Google Scholar] [CrossRef]
- Elhadj, Z.; Sprott, J.C. A unified piecewise smooth chaotic mapping that contains the Hénon and the Lozi systems. Annu. Rev. Chaos Theory Bifurc. Dyn. Syst. 2011, 1, 50–60. [Google Scholar]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Nejati, H.; Beirami, A.; Ali, W.H. Discrete-time chaotic-map truly random number generators: Design, implementation, and variability analysis of the zigzag map. Analog. Integr. Circuits Signal Process. 2012, 73, 363–374. [Google Scholar] [CrossRef]
- Callegari, S.; Rovatti, R.; Setti, G. Embeddable ADC-based true random number generator for cryptographic applications exploiting nonlinear signal processing and chaos. IEEE Trans. Signal Process. 2005, 53, 793–805. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Hu, H.; Deng, Y. Pseudorandom bit generator based on non-stationary logistic maps. IET Inf. Secur. 2016, 10, 87–94. [Google Scholar] [CrossRef]
- Elhadj, Z.; Sprott, J.C. On the robustness of chaos in dynamical systems: Theories and applications. Front. Phys. China 2008, 3, 195–204. [Google Scholar] [CrossRef]
- Pareschi, F.; Rovatti, R.; Setti, G. Simple and effective post-processing stage for random stream generated by a chaos-based RNG. In Proceedings of the 2006 International Symposium on Nonlinear Theory and its Applications (NOLTA2006), Bologna, Italy, 11–14 September 2006. [Google Scholar]
- Rukin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001.
- L'Ecuyer, P.; Simard, R. TestU01: AC library for empirical testing of random number generators. ACM Trans. Math. Softw 2007, 33, 22. [Google Scholar] [CrossRef]



| Cases | Descriptions | fNL(x) with No Parameters | Chaotic Maps |
|---|---|---|---|
| NM1 | Inverse Tangent Function | ||
| NM2 | Inverse Hyperbolic Sine Function | ||
| NM3 | Gudermannian Function | ||
| NM4 | Error Function | ||
| NM5 | Soft Signum Function | ||
| NM6 | Specific Algebraic Function |
| Chaotic Map Equations | x* = f(x*) | Fixed Points x* |
|---|---|---|
| (10) | and | |
| (11) | and | |
| (12) | and | |
| (13) | and |
| Test Methods | P-Value | Proportion | Result |
|---|---|---|---|
| Frequency (monobit) | 0.7981 | 0.99 | Pass |
| Block Frequency | 0.5544 | 0.99 | Pass |
| Runs | 0.6163 | 1.00 | Pass |
| Longest Run | 0.7399 | 1.00 | Pass |
| Binary Matrix Rank | 0.2133 | 1.00 | Pass |
| Discrete Fourier Transform | 0.7791 | 1.00 | Pass |
| Non-overlapping Template Matching | 0.4980 | 0.99 | Pass |
| Overlapping Template Matching | 0.9114 | 0.98 | Pass |
| Universal Statistical | 0.7597 | 0.99 | Pass |
| Linear Complexity | 0.6579 | 0.99 | Pass |
| Serial | 0.4983 | 0.98 | Pass |
| Approximate Entropy | 0.3669 | 1.00 | Pass |
| Cumulative Sums | 0.5139 | 0.99 | Pass |
| Random Excursions | 0.3322 | 0.98 | Pass |
| Random Excursions Variant | 0.3384 | 0.99 | Pass |
| Random Bit Generator | Test Batteries | ||
|---|---|---|---|
| Rabbit | Alphabit | BlockAlphabit | |
| 220 bits | |||
| Proposed TRBG | 38/38 | 17/17 | 102/102 |
| 225 bits | |||
| Proposed TRBG | 39/39 | 17/17 | 102/102 |
| 230 bits | |||
| Proposed TRBG | 40/40 | 17/17 | 102/102 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiteurtragool, N.; Masayoshi, T.; San-Um, W. Robustification of a One-Dimensional Generic Sigmoidal Chaotic Map with Application of True Random Bit Generation. Entropy 2018, 20, 136. https://doi.org/10.3390/e20020136
Jiteurtragool N, Masayoshi T, San-Um W. Robustification of a One-Dimensional Generic Sigmoidal Chaotic Map with Application of True Random Bit Generation. Entropy. 2018; 20(2):136. https://doi.org/10.3390/e20020136
Chicago/Turabian StyleJiteurtragool, Nattagit, Tachibana Masayoshi, and Wimol San-Um. 2018. "Robustification of a One-Dimensional Generic Sigmoidal Chaotic Map with Application of True Random Bit Generation" Entropy 20, no. 2: 136. https://doi.org/10.3390/e20020136





