The Identity of Information: How Deterministic Dependencies Constrain Information Synergy and Redundancy
Abstract
:1. Introduction
2. A Review of the PID Framework
- Symmetry: is invariant to the order of the sources in the collection.
- Self-redundancy: The redundancy of a collection formed by a single source is equal to the mutual information of that source.
- Monotonicity: Adding sources to a collection can only decrease the redundancy of the resulting collection, and redundancy is kept constant when adding a superset of any of the existing sources.
- Identity axiom: For two sources and , is equal to .
- Independent identity property: For two sources and , .
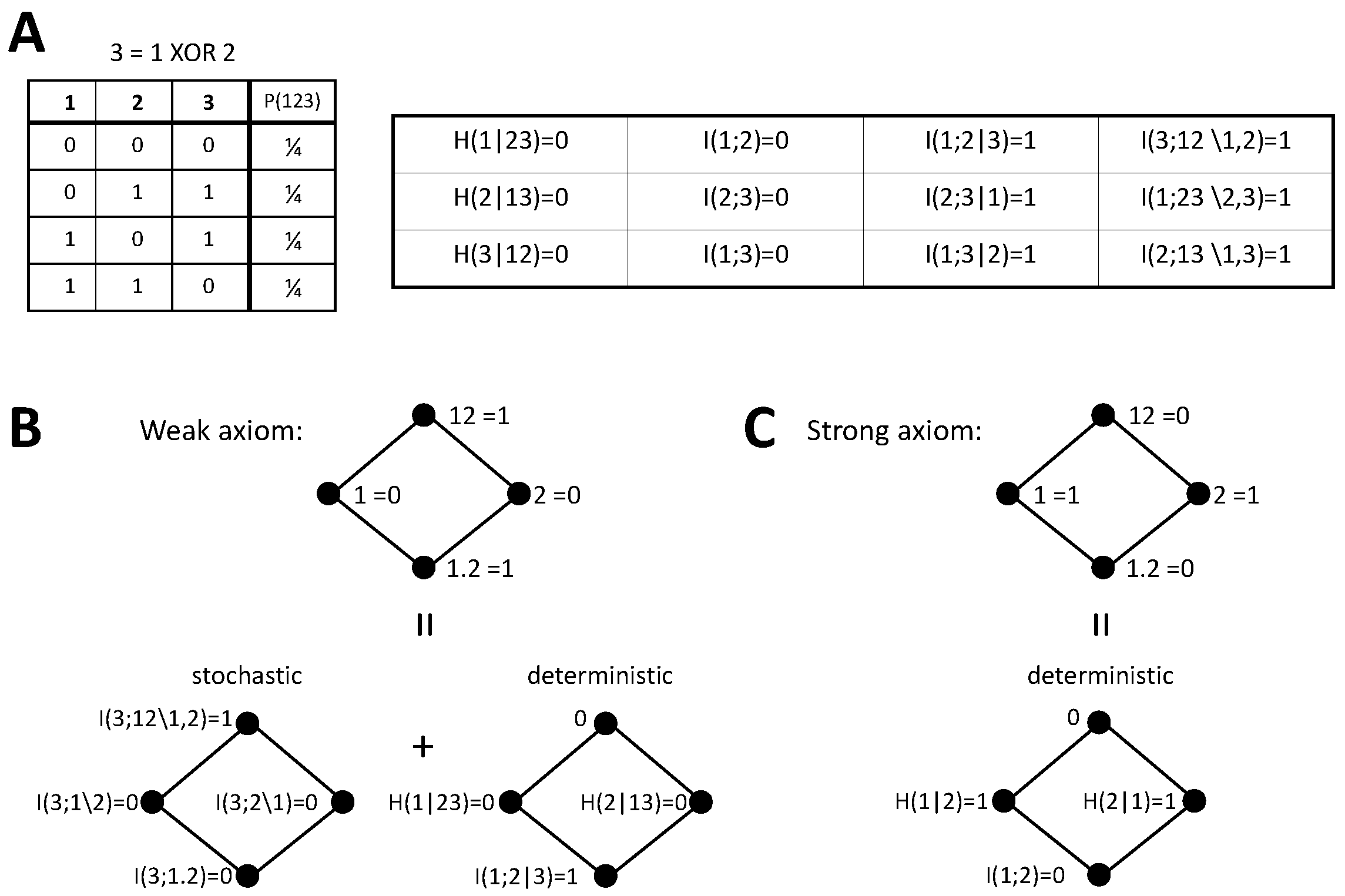
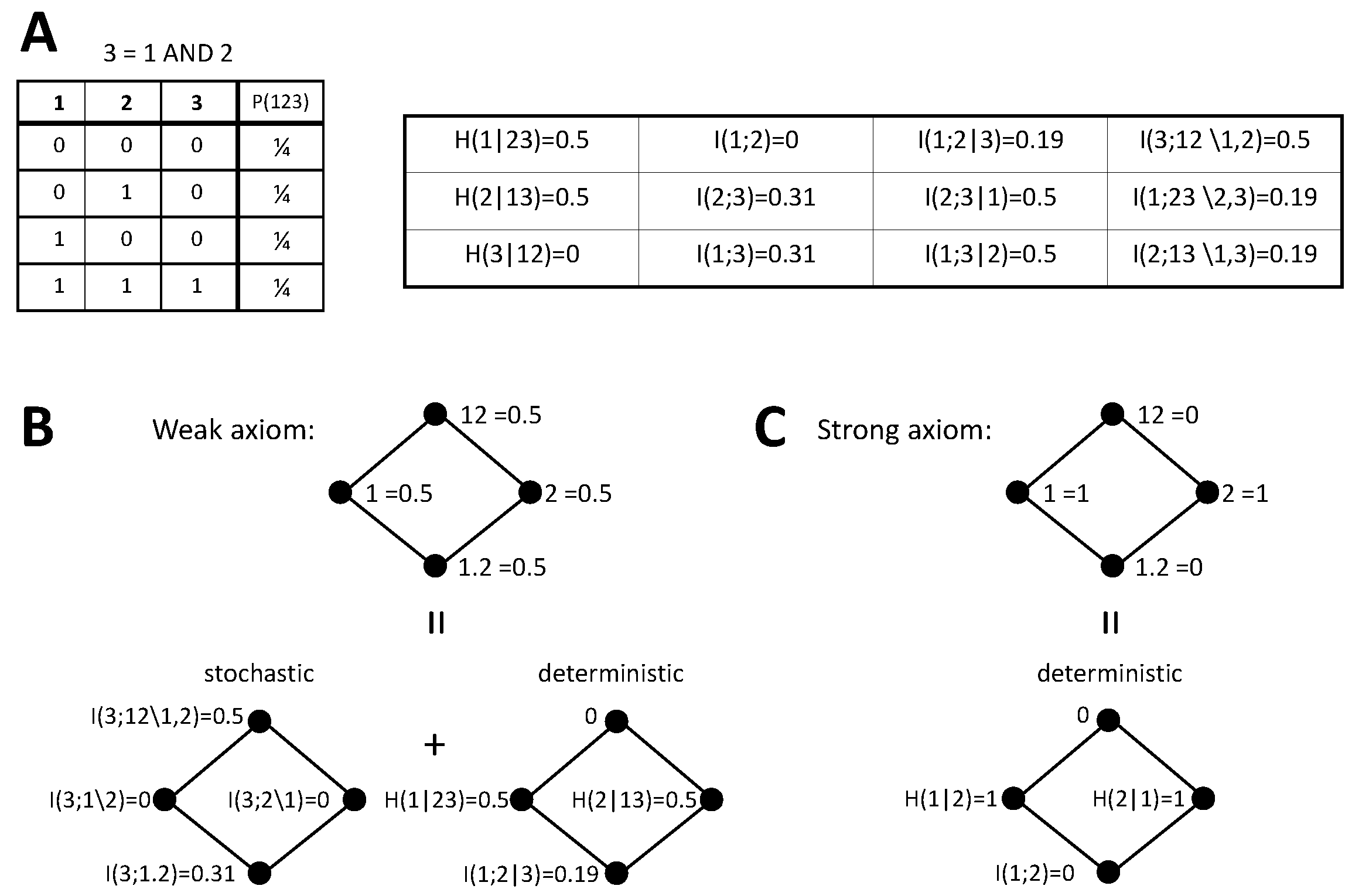
3. Stochasticity Axioms for Synergistic Information
3.1. Constraints on Synergistic PID Terms That Formalize the Weak Axiom
3.2. Constraints on Synergistic PID Terms that Formalize the Strong Axiom
3.3. Using the Stochasticity Axioms to Examine the Role of Information Identity Criteria in the Mutual Information Decomposition
4. Bivariate Decompositions with Deterministic Target-Source Dependencies
4.1. General Formulation
4.1.1. PIDs with the Weak Axiom
4.1.2. PIDs with the Strong Axiom
4.2. The Relation between the Stochasticity Axioms and the Identity Axiom
4.3. How Different PID Measures Comply with the Stochasticity Axioms
4.4. Illustrative Systems
4.4.1. XOR
4.4.2. AND
4.5. Implications of Target-Source Identity Associations for the Quantification of Redundant, Unique, and Synergistic Information
4.6. The Notion of Redundancy and the Identity of Target Variables
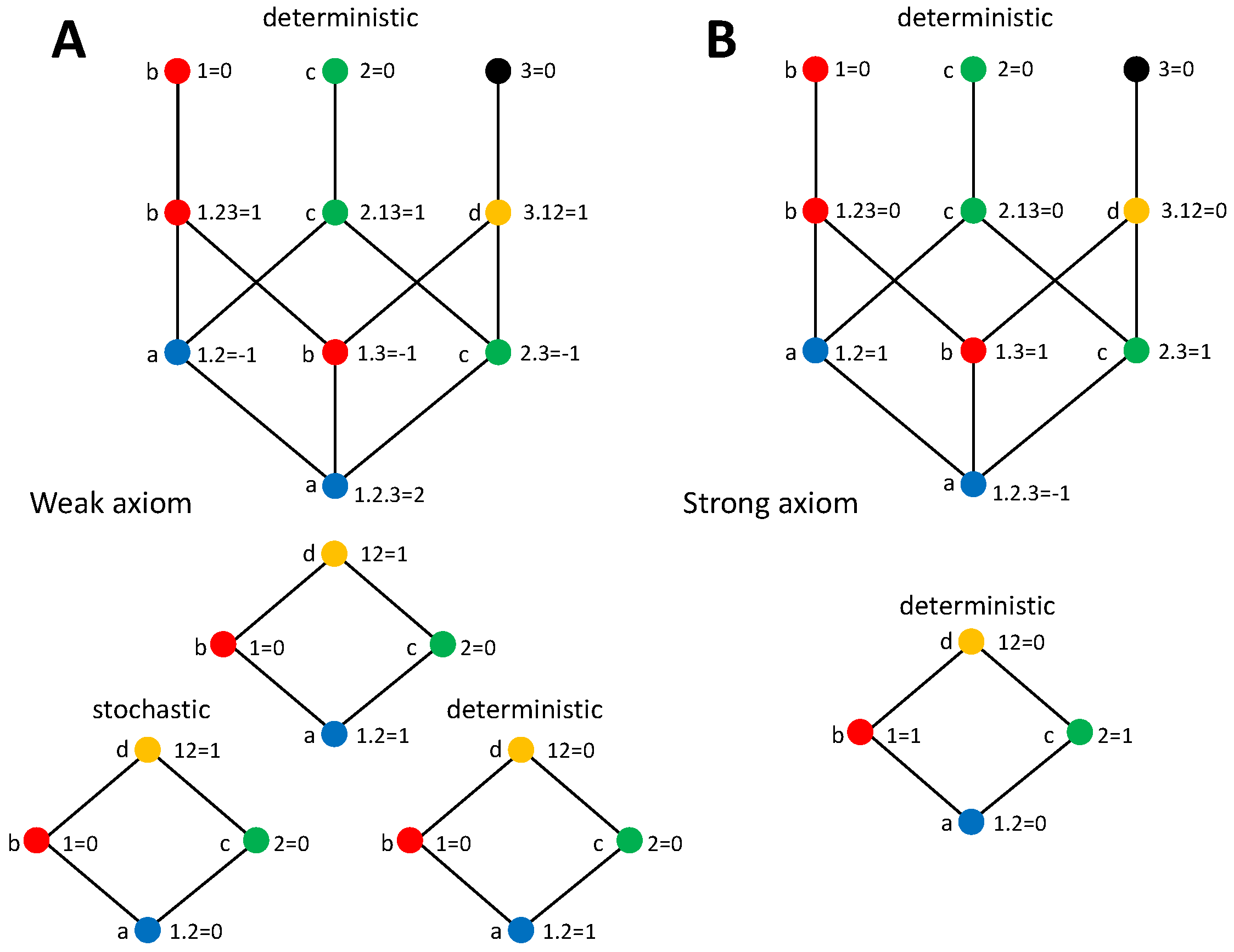
5. Trivariate Decompositions with Deterministic Target-Source Dependencies
5.1. General Formulation
5.1.1. PIDs with the Weak Axiom
5.1.2. PIDs with the Strong Axiom
5.2. Illustrative Systems
5.2.1. XOR
5.2.2. AND
5.3. PID Terms’ Nonnegativity and Information Identity
6. Discussion
6.1. Implications for the Theoretical Definition of Redundant, Synergistic and Unique Information
6.2. Implications for Studying Neural Codes
6.3. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The Relations between the Constraints to Synergy Resulting from the Strong Axiom for the General Case of Functional Dependencies and for the Case of Sources Being Part of the Target
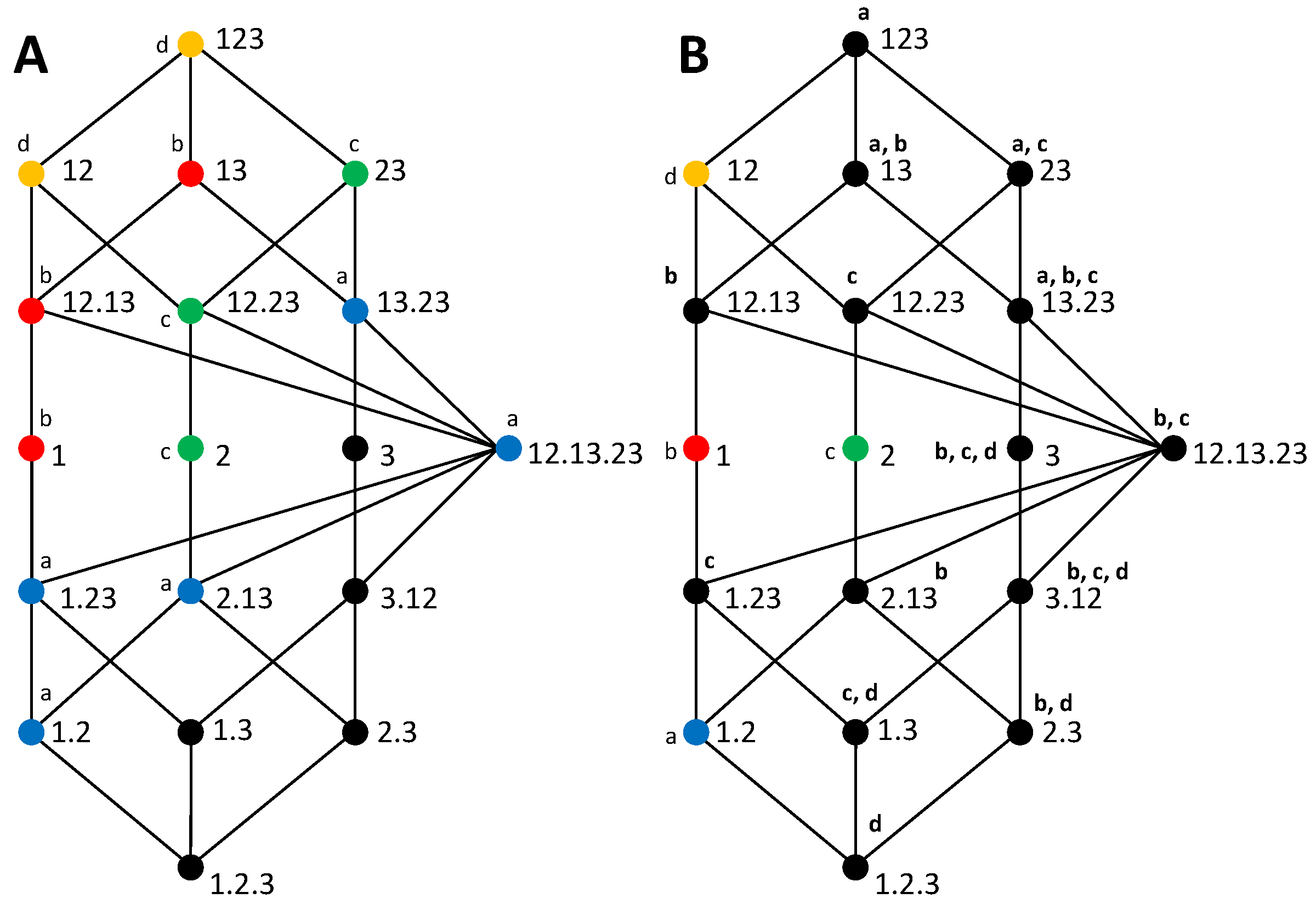
Appendix B. Alternative Partitioning Orders for the Bivariate Decomposition with Target-Source Overlap
Appendix C. The Fulfillment of the Strong Axiom by the Measures SI, and Ired
Appendix D. The Relation between the Constraints of Equations (11) and (12) for SI, Idep, and Ired
Appendix E. Derivations of the Trivariate Decomposition with Target-Source Overlap
Appendix F. The Counterexample of Nonnegativity of Bertschinger et al. (2012), Rauh et al. (2014), and Rauh (2017)
References
- Amari, S. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Ince, R.A.A.; Senatore, R.; Arabzadeh, E.; Montani, F.; Diamond, M.E.; Panzeri, S. Information-theoretic methods for studying population codes. Neural Netw. 2010, 23, 713–727. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Schultz, S.; Treves, A.; Rolls, E.T. Correlations and the encoding of information in the nervous system. Proc. R. Soc. Lond. B Biol. Sci. 1999, 266, 1001–1012. [Google Scholar] [CrossRef] [PubMed]
- Chicharro, D. A Causal Perspective on the Analysis of Signal and Noise Correlations and Their Role in Population Coding. Neural Comput. 2014, 26, 999–1054. [Google Scholar] [CrossRef] [PubMed]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Watkinson, J.; Liang, K.C.; Wang, X.; Zheng, T.; Anastassiou, D. Inference of regulatory gene interactions from expression data using three-way mutual information. Ann. N. Y. Acad. Sci. 2009, 1158, 302–313. [Google Scholar] [CrossRef] [PubMed]
- Erwin, D.H.; Davidson, E.H. The evolution of hierarchical gene regulatory networks. Nat. Rev. Genet. 2009, 10, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, P.; Pal, N.R. Construction of synergy networks from gene expression data related to disease. Gene 2016, 590, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Magri, C.; Logothetis, N.K. On the use of information theory for the analysis of the relationship between neural and imaging signals. Magn. Reson. Imaging 2008, 26, 1015–1025. [Google Scholar] [CrossRef] [PubMed]
- Marre, O.; El Boustani, S.; Fregnac, Y.; Destexhe, A. Prediction of Spatiotemporal Patterns of Neural Activity from Pairwise Correlations. Phys. Rev. Lett. 2009, 102, 138101. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Marinazzo, D.; Nollo, G.; Porta, A. An Information-Theoretic Framework to Map the Spatiotemporal Dynamics of the Scalp Electroencephalogram. IEEE Trans. Biomed. Eng. 2016, 63, 2488–2496. [Google Scholar] [CrossRef] [PubMed]
- Katz, Y.; Tunstrøm, K.; Ioannou, C.C.; Huepe, C.; Couzin, I.D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. USA 2011, 108, 18720–18725. [Google Scholar] [CrossRef] [PubMed]
- Flack, J.C. Multiple time-scales and the developmental dynamics of social systems. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 1802–1810. [Google Scholar] [CrossRef] [PubMed]
- Ay, N.; Der, R.; Prokopenko, M. Information-driven self-organization: The dynamical system approach to autonomous robot behavior. Theory Biosci. 2012, 131, 125–127. [Google Scholar] [CrossRef] [PubMed]
- Latham, P.E.; Nirenberg, S. Synergy, Redundancy, and Independence in Population Codes, Revisited. J. Neurosci. 2005, 25, 5195–5206. [Google Scholar] [CrossRef] [PubMed]
- Rauh, J.; Ay, N. Robustness, canalyzing functions and systems design. Theory Biosci. 2014, 133, 63–78. [Google Scholar] [CrossRef] [PubMed]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Averbeck, B.B.; Latham, P.E.; Pouget, A. Neural correlations, population coding and computation. Nat. Rev. Neurosci. 2006, 7, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Harvey, C.D.; Piasini, E.; Latham, P.E.; Fellin, T. Cracking the neural code for sensory perception by combining statistics, intervention and behavior. Neuron 2017, 93, 491–507. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Timme, N.M.; Ito, S.; Myroshnychenko, M.; Nigam, S.; Shimono, M.; Yeh, F.C.; Hottowy, P.; Litke, A.M.; Beggs, J.M. High-Degree Neurons Feed Cortical Computations. PLoS Comput. Biol. 2016, 12, e1004858. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Brunel, N.; Logothetis, N.K.; Kayser, C. Sensory neural codes using multiplexed temporal scales. Trends Neurosci. 2010, 33, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Macke, J.H.; Gross, J.; Kayser, C. Neural population coding: Combining insights from microscopic and mass signals. Trends Cogn. Sci. 2015, 19, 162–172. [Google Scholar] [CrossRef] [PubMed]
- Valdes-Sosa, P.A.; Roebroeck, A.; Daunizeau, J.; Friston, K. Effective connectivity: Influence, causality and biophysical modeling. Neuroimage 2011, 58, 339–361. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy: A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Ince, R.A.A.; van Rijsbergen, N.J.; Thut, G.; Rousselet, G.A.; Gross, J.; Panzeri, S.; Schyns, P.G. Tracing the Flow of Perceptual Features in an Algorithmic Brain Network. Sci. Rep. 2015, 5, 17681. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Tononi, G.; Boly, M.; Kringelbach, M.L. Rethinking segregation and integration: Contributions of whole-brain modelling. Nat. Rev. Neurosci. 2015, 16, 430–439. [Google Scholar] [CrossRef] [PubMed]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Bell, A.J. The co-information lattice. In Proceedings of the 4th International Symposium Independent Component Analysis and Blind Source Separation, Nara, Japan, 1–4 April 2003; pp. 921–926. [Google Scholar]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information decomposition and synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Perrone, P.; Ay, N. Hierarchical quantification of synergy in channels. Front. Robot. AI 2016, 2, 35. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Williams, P.L. Information Dynamics: Its Theory and Application to Embodied Cognitive Systems. PhD. Thesis, Indiana University, Bloomington, IN, USA, 2011. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. arXiv, 2013; arXiv:1205.4265v6. [Google Scholar]
- Ince, R.A.A. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Rauh, J.; Banerjee, P.K.; Olbrich, E.; Jost, J.; Bertschinger, N. On Extractable Shared Information. Entropy 2017, 19, 328. [Google Scholar] [CrossRef]
- Chicharro, D. Quantifying multivariate redundancy with maximum entropy decompositions of mutual information. arXiv, 2017; arXiv:1708.03845v1. [Google Scholar]
- Rauh, J. Secret Sharing and shared information. Entropy 2017, 19, 601. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer: Cham, Switzerland, 2012; pp. 251–269. [Google Scholar]
- James, R.G.; Emenheiser, J.; Crutchfield, J.P. Unique Information via Dependency Constraints. arXiv, 2017; arXiv:1709.06653v1. [Google Scholar]
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. In Proceedings of the 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2232–2236. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2006. [Google Scholar]
- Chicharro, D.; Panzeri, S. Synergy and Redundancy in Dual Decompositions of Mutual Information Gain and Information Loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef]
- Pica, G.; Piasini, E.; Chicharro, D.; Panzeri, S. Invariant components of synergy, redundancy, and unique information among three variables. Entropy 2017, 19, 451. [Google Scholar] [CrossRef]
- Griffith, V.; Chong, E.K.P.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection Information based on Common Randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Banerjee, P.K.; Griffith, V. Synergy, redundancy, and common information. arXiv, 2015; arXiv:1509.03706v1. [Google Scholar]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- James, R.G.; Crutchfield, J.P. Multivariate Dependence Beyond Shannon Information. Entropy 2017, 19, 531. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell. Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover: Mineola, NY, USA, 1959. [Google Scholar]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from brains for biologically inspired computing. Front. Robot. AI 2015, 2, 5. [Google Scholar] [CrossRef]
- Thomson, E.E.; Kristan, W.B. Quantifying Stimulus Discriminability: A Comparison of Information Theory and Ideal Observer Analysis. Neural Comput. 2005, 17, 741–778. [Google Scholar] [CrossRef] [PubMed]
- Pica, G.; Piasini, E.; Safaai, H.; Runyan, C.A.; Diamond, M.E.; Fellin, T.; Kayser, C.; Harvey, C.D.; Panzeri, S. Quantifying how much sensory information in a neural code is relevant for behavior. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017. [Google Scholar]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Stramaglia, S.; Angelini, L.; Wu, G.; Cortes, J.M.; Faes, L.; Marinazzo, D. Synergetic and redundant information flow detected by unnormalized Granger causality: Application to resting state fMRI. IEEE Trans. Biomed. Eng. 2016, 63, 2518–2524. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Generalized Measures of Information Transfer. arXiv, 2011; arXiv:1102.1507v1. [Google Scholar]
- Marko, H. Bidirectional communication theory—Generalization of information-theory. IEEE Trans. Commun. 1973, 12, 1345–1351. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D.; Williams, P.L. Information Processing and Dynamics in Minimally Cognitive Agents. Cogn. Sci. 2015, 39, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Chicharro, D.; Panzeri, S. Algorithms of causal inference for the analysis of effective connectivity among brain regions. Front. Neuroinform. 2014, 8, 64. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, D.H.; Hires, S.A.; Guo, Z.V.; Li, N.; Yu, J.; Sun, Q.Q.; Huber, D.; Svoboda, K. Neural coding during active somatosensation revealed using illusory touch. Nat. Neurosci. 2013, 16, 958–965. [Google Scholar] [CrossRef] [PubMed]
- Otchy, T.M.; Wolff, S.B.E.; Rhee, J.Y.; Pehlevan, C.; Kawai, R.; Kempf, A.; Gobes, S.M.H.; Olveczky, B.P. Acute off-target effects of neural circuit manipulations. Nature 2015, 528, 358–363. [Google Scholar] [CrossRef] [PubMed]

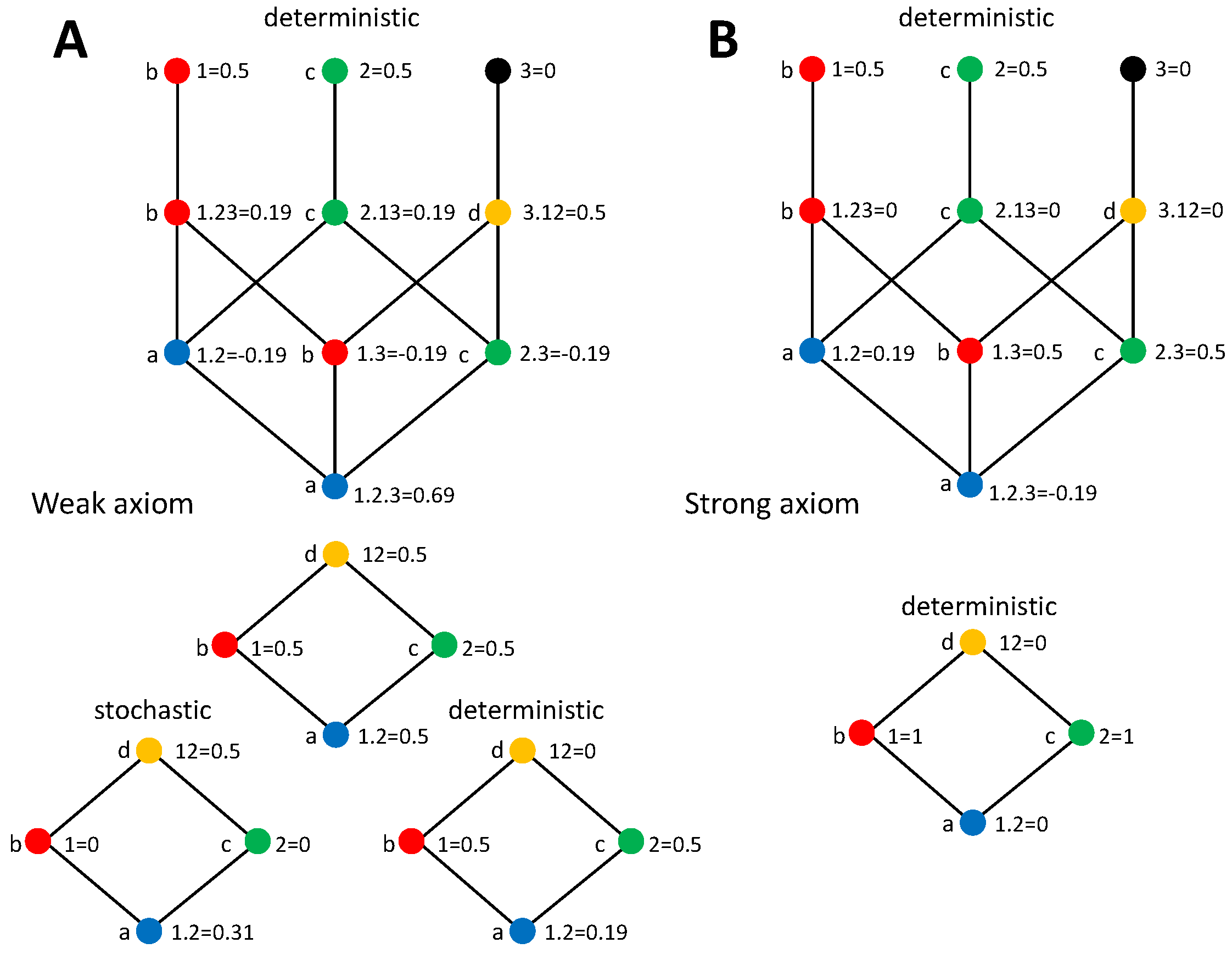
| Term | Decomposition |
|---|---|
| Term | Measure |
| 0 | |
| Term | Decomposition |
|---|---|
| 0 | |
| Term | Measure |
| 0 | |
| Term | Measure |
|---|---|
| Term | Measure |
|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chicharro, D.; Pica, G.; Panzeri, S. The Identity of Information: How Deterministic Dependencies Constrain Information Synergy and Redundancy. Entropy 2018, 20, 169. https://doi.org/10.3390/e20030169
Chicharro D, Pica G, Panzeri S. The Identity of Information: How Deterministic Dependencies Constrain Information Synergy and Redundancy. Entropy. 2018; 20(3):169. https://doi.org/10.3390/e20030169
Chicago/Turabian StyleChicharro, Daniel, Giuseppe Pica, and Stefano Panzeri. 2018. "The Identity of Information: How Deterministic Dependencies Constrain Information Synergy and Redundancy" Entropy 20, no. 3: 169. https://doi.org/10.3390/e20030169





