1. History
In correspondence with Peter Guthrie Tait in 1867 Maxwell [
10] introduced what William Thompson [
11] later called “Maxwell’s intelligent demon”. Maxwell envisioned a microscopic being who controlled a ‘massless’ sliding door between two very large collections of gas molecules each of identical average molecular kinetic energy. By measuring a gas molecule approaching the sliding door, the demon could allow only higher energy molecules to pass in one direction and lower energy molecules to pass in the other. Without requiring any work, this would eventually produce a temperature imbalance between the two collections of gas, in contradiction of the Second Law of Thermodynamics.
Leo Szilard described his demon-operated heat engine in 1929 [
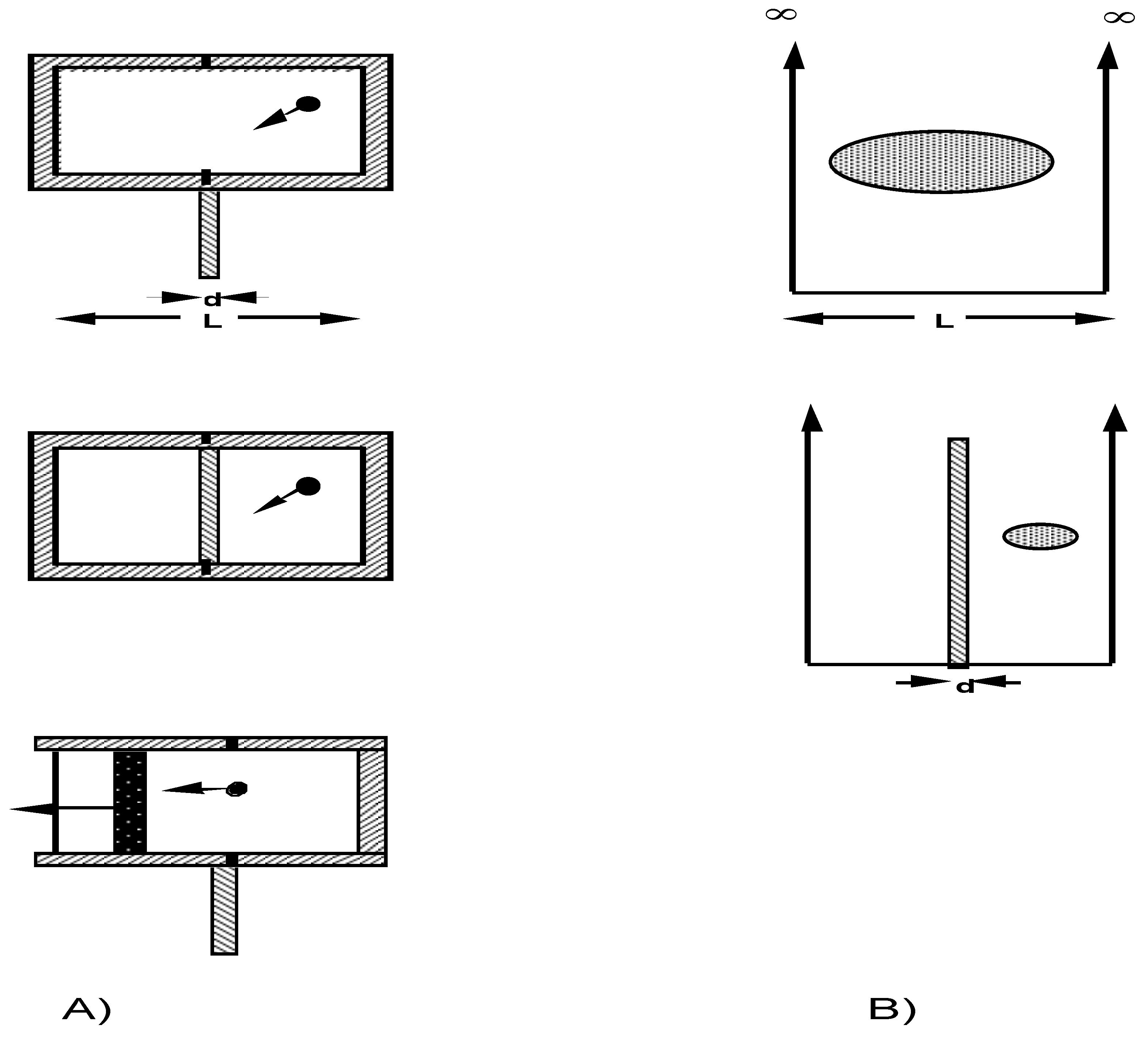
2]. A cylinder of length L, shown in
Figure 1 A), contains a working fluid of a single ideal gas molecule. The cylinder can be divided in half by a thin partition of thickness d << L, analogous to the sliding door of Maxwell’s model. The demon would then measure which half of the original cylinder now confines the molecule. Using this information, the partition is replaced by an appropriate piston, aligned toward one or the other end of the cylinder, and coupled to a load upon which work may be done by the gas. The cylinder can be surrounded by a reservoir which would transfer heat to the gas during a quasistatic, reversible expansion. The engine is thereby returned to its original state, seemingly without any work required of the demon, and creating a perpetuum mobile, in violation of the Second Law. Szilard believed the Second Law was saved by “the measurement procedure (which) is fundamentally associated with a certain definite average entropy production...” [
12]. The calculations below show that it is operation of the partition which must entail entropy production in order to preserve the Second Law.
Today, the most widely accepted defense of the Second Law from the threat of Maxwell’s demon rests on Landauer’s idea that information written to some memory register by a computer program must be discarded to the environment in order to reset the register and complete the cyclic process. Bennett [
13] argues that such information (represented, say, by 10110010010....) increases the entropy of the register relative to its initial configuration ( 11111111111....). Others have disagreed [
14]. Bennett believes the demon in Szilard's engine must discard its measurement-generated information, increase environment entropy and thus save the Second Law.
Zurek examined Bennett’s idea via a quantum mechanical treatment of Szilard's engine
(7). Zurek finds that the simplest measuring apparatus, a two-state quantum system, is sufficient to record the effect of inserting a partition in the engine’s cylinder. Initially, the apparatus is in the ‘ready to measure’ superposition state,
, and measurement produces the mixture,
. According to Zurek, this change causes an entropy increase of kln(2), just compensating the gas entropy loss predicted by classical thermodynamics at partition. Unfortunately, Zurek’s paper and its conclusions have been widely accepted without a careful, critical reading. The paper has several fatal errors [
15]. For an excellent review of the demon, Szilard's engine, and measurement, the reader is referred to the compilation by Harvey S. Leff and Andrew F. Rex [
16].
2. Szilard’s Engine with Isolated Measurements
We will reexamine the treatment of Szilard's engine, and slightly modify the engine cycle by isolating the cylinder and its gas molecule during the measurement. We also require a very thin layer of thermal insulation through the metal cylinder, dividing it in half at the location of the movable partition.
Measurement is the transfer of information between an examined physical object and an apparatus, Any energy transfer between objects will carry information about the shift in energy state of those objects. So, every energy transfer between two separate physical objects is a measurement. And a collision between a gas molecule and its confining cylinder which results in energy exchange is thus a measurement [
17]. Information about the change in energy state of the gas molecule is recorded in the ‘memory’ (total energy state) of each cylinder. The insulation layer permits an energy transfer determination of either right or left molecular confinement, the operative measurement, no extrinsic apparatus is necessary . We will isolate engine cylinders (the apparatus) in order to calculate any entropy change.
Following Zurek’s lead, we now conceive a thermodynamic system from Szilard’s single-cylinder engine by replacing it with an engine of many identical cylinders. Entropy, as Maxwell emphasized [
18], is statistical in origin, so we choose to examine the macroscopic system consisting of a great number of gas molecules (the measured object) and the system designated as all the cylinders enclosing those molecules (the apparatus). Equally informative would be the examination of a single cylinder engine over very many cycles. Quantum mechanically, we model each cylinder by an infinite square well of width L,
Figure 1 B), with, of course, discrete energy levels for the enclosed molecule. The well may be divided in its middle by a barrier (the thin partition) of potential height U and thickness d.
Initially, we take every unpartitioned cylinder in the engine to be at the same temperature, T
0, approximately 300° K. (No heat reservoir surrounding the cylinders is implied at this point, but the entire cylinder is at temperature T
0.) The enclosed molecule has allowed energies of
with m the mass of the molecule (roughly 10
-27 Kg), L of about 0.1m , and n = 1, 2, 3,.... If the cylinder were divided by the partition, eigenfunctions for the molecule would be either symmetric or antisymmetric. And the corresponding eigenvalues are
, and
, with
and
. The potential height of the partition, U, is such that U >> E
n for all those values of E
n which make a significant contribution to the entropy calculations. So, following partition, collision of the molecule with its cylinder confines it (as
U → ∞) to one side or the other, with discrete energies,
In general, the occupation probability of level E
n by a gas molecule in a cylinder at temperature T is just
, with Z the partition function. To calculate entropy we use the von Neumann formula,
for the quantum system. We may then determine the entropy of the system of gas molecules and any change resulting from partition. We start with the probability of a given configuration of N molecules:
, so that,
If the cylinders are initially unpartitioned and at temperature T
0, the gas system entropy becomes [
19],
Where
. To calculate the partition function we approximate the sum with an integral, introducing a negligible maximum error of about
.
in agreement with the well-known Boltzmann partition function for an ideal gas. We may thus treat our gas system as ideal, even though each molecule is separately confined to its own cylinder.
We make a similar (excellent) integral approximation for the gas entropy before partition,
Now, if the partitions are inserted, measurement of the molecule’s position by the cylinder, at the first collision between the two, reduces the allowed gas energy levels to 4
n2ε′. We choose d << L such that ε´ may be replaced by ε. So,
Thus, the entropy change of the gas, due to partition, is
in agreement with the standard thermodynamic result.
We may now show that our apparatus (the cylinders) actually loses entropy, and gains information at measurement [
20]. An isolated, unpartitioned cylinder, initially at temperature T
0, may gain or lose energy when struck by the gas molecule [
21]. It may be helpful to think of each cylinder as a massive particle, albeit a very heavy one, which collides with another particle, the single gas molecule. It follows that the allowed total energy states for a cylinder after a single collision will be
, where c is the specific heat of the cylinder of mass M (approximately 0.5 Kg), and δE
if ≡ E
f - E
i . Given enough cylinders, equilibrium will be reached after a single collision, while mean cylinder temperatures remain T
0. (With the collection of individually-confined molecules initially at temperature T
0, and each cylinder exactly at that same temperature, a single collision in each cylinder results in no net heat exchange between all the cylinders and all the molecules; if the number of cylinders is sufficiently large.)
As with the gas, the cylinders now completely fill energy phase space, specifying an entropy for the collection of cylinders. Initially, every cylinder had total energy McT0, but now there is a distribution of energy values among the set of cylinders, like there is, say, for the collection of molecules of an ideal gas. And the cylinders are in thermal equilibrium with the gas. I acknowledge this as a novel idea for objects as large as engine cylinders, but, considering each cylinder as isolated from everything except its own contained molecule, the analogy with ideal gas molecules, for example, is exact, and the associated entropy is just as real. We may ignore the entropy associated with the internal structure of the cylinders (as we do with an ideal gas molecule) because, in this case, there is no net heat transfer after one collision in each cylinder.
Cylinder energy probability at equilibrium, attained after a single collision in each cylinder, is uniquely determined by the gas molecule probabilities. The probability that energy δE
if is transferred to a cylinder by collision with its enclosed molecule is, obviously, the product of the probability of the molecule’s energy before collision times the molecule’s energy probability after the collision. And every cylinder has an identical energy before collision so this probable energy transfer
is the cylinder energy probability at equilibrium:
Now, it is the probability of an energy configuration of the N cylinders that is of interest,
. So, the entropy is,
Since
depends on both the initial and final molecule energy probabilities (Eq. (9)), we have the double sum,
. And the entropy of the energy distribution of the unpartitioned cylinders is thus,
Next, the partition is inserted in each isolated cylinder [
22]. Again, a single collision is sufficient to establish equilibrium. The gas temperature, and thus the mean temperature of the cylinders, remains T
0 by energy conservation. As an ideal gas, the total energy of the collection of gas molecules is proportional to its temperature. If partition resulted in re-establishment of equilibrium at a lower (higher) temperature then both the gas and cylinders would lose (gain) energy, impossible for an isolated system.
The first gas-cylinder collision following partition of the cylinder will, of course, result in a jump of cylinder energy. The probability of that jump,
, is the product of the probable molecular energy before collision times the molecule’s probable energy immediately after the collision [
23],
. And the probability of a given cylinder energy state just before partition is given by equation (9),
. The product of these two is the probable energy of a cylinder just after the partition occurs. But, the gas energy state E
j = εj
2 must be the state E
f = εf
2 since the molecule’s energy state just after a collision must be its energy state just before the next collision. As usual, we sum over this intermediate molecular state to determine the total probability that the cylinder will end up in energy state
,
The entropy of the system of N partitioned cylinders is thus,
So, partitioning results in entropy loss to the system of cylinders (information gain) of
[
24]. The entropy change of the total gas-cylinders system, ΔS = ΔS
g + ΔS
C = -2Nkln(2), is obviously disconcerting. We have attempted to isolate this system by isolating each individual cylinder, and so any entropy decrease would violate the Second Law. I believe, however, that careful consideration shows this system is not really isolated. Some agent must move each cylinder partition. While no minimum amount of work is necessary if the frictionless partition is arbitrarily light, it must, however, receive at least one quantum of energy to achieve the kinetic energy which slides the partition shut. And this same energy must be extracted from the partition to finally stop its motion, lest an inelastic collision with the cylinder should perturb the energy state, and thus disorder the acquired information. We could characterize these actions of the partition’s agent as two measurements.
As conceived by Maxwell, his demon both measured the properties of a single molecule and moved the sliding door. We may preserve the Second Law if we accept an entropy increase of at least 2Nkln(2) by the agent of partition, our demon.
It is usual to attribute no entropy change to partition activation in Szilard’s engine. Thus, salvation of the Second law might require an entropy increase by the measurement apparatus. That was Szilard’s conjecture, what Bennett claimed, and also what Zurek, Lubkin, Fahn and Leff and Rex found. But I’ve been able to actually calculate the entropy change for this apparatus; it loses entropy and gains, rather than loses, information at measurement.
We’d now like to return the engine to its original state, prepared for another measurement, and complete the thermodynamic cycle. To do this we surround the cylinders with a semi-infinite heat reservoir at temperature T
0. A piston bearing a load is inserted into the appropriate side of each cylinder based on the information acquired by measurement. It replaces the partition. Entropy of the system of cylinders, each now at energy
, is reduced to zero, with a concomitant increase of reservoir entropy. The gas molecules are allowed to push each piston out, doing work and extracting an equal quantity of heat from the reservoir during the reversible process. Expansion increases the entropy of the enclosed gas,
and decreases the reservoir entropy by the same amount .
Lastly, the reservoir is withdrawn, once again isolating the engine. In what is analogous to the free expansion of an ideal gas, the cylinders’ entropy will increase to
when they are struck by the enclosed molecules. One could view this as a form of the ‘energy mixing’ with which Leff explicates system entropy changes [
25]. The gas and cylinders remain in equilibrium at temperature T
0. At the cost of entropy increase, the cylinders have now been prepared for another measurement. And this entropy increase seems to indicate an irreversible cycle for the modified engine. Magnasco, too, finds that the engine cycle is irreversible [
26].
3. A Simplified Measurement
A molecule-cylinder collision, with attendant energy exchange, determines the location of the molecule in every cylinder. The cylinders, however, are a more complex measuring apparatus than one could wish; they also determine the energy transferred by every collision. In order to help clarify the process we may examine a much-simplified model of the measurement that records only the necessary operative information, the right or left side capture of the molecule.
Suppose that a molecule which strikes the right side of a cylinder transfers energy which is registered as cylinder state R; on the left side as state L [
27]. A subsequent collision overwrites the previous result. Initially, the unpartitioned cylinders, at temperature T
0, are isolated. Equilibrium is established between the cylinders and their colliding molecules. We describe the cylinder system in thermodynamic terms, with either state, R or L, equally likely in a particular cylinder. The entropy of the system of N cylinders is thus
. Gas entropy is
.
The partitions are inserted. As before, we will find that the cylinders’ entropy decreases and information increases. The entropy of the set of cylinders is now zero since every cylinder is in a determined state, either R or L, and the state of the thermodynamic system is, for example, (R, R, L, R, L, L, …). The cylinders entropy change, carrying information that the molecule is confined to half its original volume, is now ΔSC = 0 - Nkln(2) = -Nkln(2). And the partitioned gas entropy is . So, the total system entropy change is . And preservation of the Second Law does still entail a minimum entropy gain of 2Nkln(2) by our demon.
Now, return the system to its original state, once again by a quasistatic, reversible expansion, replacing the partition with a piston and surrounding the cylinders with a heat reservoir at T0. Every cylinder is now in the state , and stays there. A collision effects no change in the cylinder state and the cylinders’ entropy remains zero. Each gas molecule pushes its piston out to the initial volume. Heat supplied by the reservoir allows work by the engine and gas entropy increases by Nkln(2) at the expense of an equal amount of reservoir entropy.
To permit another measurement each cylinder must be isolated, so the reservoir is removed. Via a ‘free expansion’ the cylinder states, R and L, resume equilibrium with the gas, increasing to Nkln(2) the cylinders’ entropy. The entropy balance for the complete cycle of this engine is thus positive, ΔS ≥ Nkln(2), indicative of an irreversible engine cycle. We might denominate isolation of the cylinders as the necessary preparation or ‘premeasurement’ by the apparatus, increasing its entropy just enough to allow sufficient information transfer at partition to specify either right or left capture of the gas molecule.