Entropy Analysis for Non-Newtonian Fluid Flow in Annular Pipe: Constant Viscosity Case

Abstract

In the present study, non-Newtonian flow in annular pipe is considered. The analytical solution for velocity and temperature fields is presented while entropy generation due to fluid friction and heat transfer is formulated. The third grade fluid with constant properties is accommodated in the analysis. It is found that reducing non-Newtonian parameter increases maximum velocity magnitude and maximum temperature in the annular pipe. Total entropy generation number attains high values in the region close to the inner wall of the annular pipe, which becomes significant for low non-Newtonian parameters. Increasing Brinkman number enhances entropy generation number, particularly in the region close to the annular pipe inner wall. 

Introduction

Annular flow in concentric pipes finds wide application in industry, particularly in heating and cooling applications. The flowing fluid can be a mixture of two non-condensable fluids. To simulate such flow situations, the governing equations of flow need to be accommodated for each fluid and coupled equations for the fluids should also be introduced. This leads extensive computational effort and results are only valid for the flow parameters used in the simulations; consequently, generalized solution is difficult to achieve. However, the fluid can be considered as homogenous medium with the assumption that the flow behavior is non-Newtonian. In this case, the error associated with the analysis could be acceptably small [1]. Moreover, the analytical solution to the problem becomes possible, which in turn gives general solution to flow and temperature fields. In modeling the non-Newtonian flow situations, such as coal-based slurries as retrofit fuels, the power-law model was used widely to characterize the rheological properties of the fluid [2]. Although the power-law model adequately fit the shear stress and shear rate measurements for many non-Newtonian fluids, it could not always be used to predict accurately the pressure loss data measured during the transport of a coal-liquid mixture in a fuel delivery system [3]. Moreover, the power-law model could not predict correctly the normal stress effects that lead to phenomena like road climbing, in which case the stresses are developed orthogonal to planes of shear [4]. Consequently, a third grade fluid model is fruitful for non-Newtonian flow in pipe situations.

Considerable research studies were carried out to examine the non-Newtonian flow through pipes. Szeri and Rajagopal [5] studied the flow of non-Newtonian fluid between two heated horizontal parallel plates. They employed the third grade fluid model and introduced temperature dependent viscosity. The flow of a non-Newtonian fluid in a pipe was studied by Massoudi and Christie [6]. They accommodated a third grade fluid model and variable viscosity in the analysis. They showed numerically that increasing non-Newtonian parameter lowered the temperature and velocity of the fluid in the pipe. Yurusoy and Pakdemirli [7] presented an approximate analytical solution to the same problem using perturbations. They showed that within the range of validity of the expansion, the numerical solution and the perturbation solution were in good agreement. Yurusoy [8] extended the approximate analysis to the case of annular flow. The boundary layer equations of third grade fluids were derived by Pakdemirli [9]. He showed that the boundary layer equations did not have similarity solutions. Pinarbasi and Ozalp [10] investigated the effect of viscosity models on the stability of a non-Newtonian fluid flow in an externally heated channel. They indicated that fluids obeying the Arrhenius law were more stable than those of Nahme law if both models were used for the same viscosity and temperature. Non-Newtonian pipe flow with heat transfer was examined by Hecht [11]. They derived the expression for Stanton number as a function of Reynolds, Prandtl and Shmidt numbers. The downward liquid-gas flows in inclined eccentric annular pipes were studied by Baca et al. [12]. They developed a flow map in terms of liquid and gas superficial velocities, which showed the transitions between countercurrent and cocurrent gas flows. The unsteady axial laminar Couette flow of power-law fluids in a concentric annulus was investigated by Wang et al. [13]. The solutions of the resulting pressure gradient equations were presented in both dimensionless and graphical forms for different pipe/borehole diameter ratios and power-law index values.

In the flow systems, thermodynamic irreversibility can be quantified through entropy analysis. Considerable research studies were carried out to examine entropy generation in the flow systems. Entropy generation and minimization in thermal systems was investigated by Bejan [14]. He showed that entropy minimization improved system efficiency. The modeling of non-isothermal viscoelastic flows was considered by Peters and Baajens [15]. They formulated the partitioning between dissipated and elastically stored energy and showed the difference between entropy and energy elasticity. Demirel and Kahraman [16] carried out the second law analysis for convective heat transfer in annular packed bed. They indicated that the volumetric entropy generation map showed the regions with excessive entropy generation due to operating conditions or design parameters for a required task and lead to enhance the understanding of the behavior of the system. Carey [17] examined the advantages of using two-phase flow and phase change processes in thermal systems to improve the second law efficiency. He suggested that ongoing efforts to develop condenser passage design, which enhanced annular flow heat transfer and provided large surface area, helped to improve the thermal efficiency of the system and component performance. The irreversibility analysis of concentrically rotating annuli was carried out by Mahmud and Fraser [18]. They presented the distributions of volumetric average entropy generation rate for both isothermal and isoflux conditions.

To investigate the thermodynamic irreversibility in non-Newtonian annular flow, the present study is carried out. The flow and temperature fields are presented analytically after considering a third grade fluid model. The closed form solutions for entropy generation due to fluid friction and heat transfer are obtained and entropy number is computed for various non-Newtonian parameters. By incorporating the entropy analysis, the work presented here further contributes to the fluid flow solutions presented in [8].

Velocity and Temperature Profiles

The non-dimensional steady state, fully developed, variable viscosity form of the equations of motion of a third grade fluid in a pipe with heat transfer was derived by Massoudi and Christie [6]:

$$\frac{\mathrm{d}\mathsf{\mu }}{\mathrm{d}\mathrm{r}}\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}+\frac{\mathsf{\mu }}{\mathrm{r}}\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}+\mathrm{r}\frac{{\mathrm{d}}^2\mathrm{v}}{\mathrm{d}{\mathrm{r}}^2}\right)+\frac{\mathrm{\Lambda }}{\mathrm{r}}{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}+3\mathrm{r}\frac{{\mathrm{d}}^2\mathrm{v}}{\mathrm{d}{\mathrm{r}}^2}\right)=\mathrm{C}$$

(1)

$$\frac{{\mathrm{d}}^2\mathsf{\theta }}{\mathrm{d}{\mathrm{r}}^2}+\frac{1}{\mathrm{r}}\frac{\mathrm{d}\mathsf{\theta }}{\mathrm{d}\mathrm{r}}+\mathrm{\Gamma }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\left[\mathsf{\mu }+\mathrm{\Lambda }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\right]=0$$

(2)

v(r_i ) = v(r_o ) = θ(r_i ) = θ(r_o) = 0

(3)

where r is the dimensionless radius (r_i < r < r_o), r_i is dimensionless radius of inner cylinder, r_o is dimensionless radius of outer cylinder, v is the dimensionless velocity, θ is the dimensionless temperature and µ is the dimensionless viscosity. The terms are related to the dimensional ones (with over bars) through the following relations

$$\begin{array}{c}{\mathrm{R}}^{*}={\overline{\mathrm{r}}}_{\mathrm{o}}-{\overline{\mathrm{r}}}_{\mathrm{i}},\mathrm{R}=\frac{{\overline{\mathrm{r}}}_{\mathrm{i}}}{{\overline{\mathrm{r}}}_{\mathrm{o}}},{\mathrm{r}}_{\mathrm{i}}=\frac{3\mathrm{R}}{1-\mathrm{R}},{\mathrm{r}}_{\mathrm{o}}=\frac{3}{1-\mathrm{R}}\\ \mathrm{r}=\frac{\overline{\mathrm{r}}}{{\mathrm{R}}^{*}},\mathrm{v}=\frac{\overline{\mathrm{v}}}{{\mathrm{V}}_0},\mathsf{\theta }=\frac{\overline{\mathsf{\theta }}-{\mathsf{\theta }}_{\mathrm{w}}}{{\overline{\mathsf{\theta }}}_{\mathrm{m}}-{\mathsf{\theta }}_{\mathrm{w}}},\mathsf{\mu }=\frac{\overline{\mathsf{\mu }}}{{\mathsf{\mu }}_{*}}\end{array}$$

(4)

where R is the ratio of inner to outer radius, V₀ is a reference velocity, µ_* is a reference viscosity, ${\overline{\mathsf{\theta }}}_{\mathrm{m}}$ and θ_w are the bulk mean fluid temperature and wall temperature respectively.

The dimensionless parameters involved in equations (1) and (2) are

$$\mathrm{C}=\frac{{\mathrm{C}}_1{\mathrm{R}}^{*2}}{{\mathsf{\mu }}_{*}{\mathrm{V}}_0}{\mathrm{C}}_1=\frac{\partial \mathrm{p}}{\partial \mathrm{z}}\mathrm{\Gamma }=\frac{{\mathsf{\mu }}_{*}{\mathrm{V}}_0^2}{\mathrm{k}({\overline{\mathsf{\theta }}}_{\mathrm{m}}-{\mathsf{\theta }}_{\mathrm{w}})}\mathrm{\Lambda }=\frac{2{\mathsf{\beta }}_3{\mathrm{V}}_0^2}{{\mathsf{\mu }}_{*}{\mathrm{R}}^{*2}}$$

(5)

where C₁ is the pressure drop in the axial direction, Γ is the Brinkman number, Λ is the dimensionless non-Newtonian viscosity, β₃ is the dimensional material constant for the third grade fluid and k is the thermal conductivity.

Approximate solutions for velocity and temperature profiles using perturbation methods were presented for the above equations due to non-Newtonian fluid flow in annular pipe (Figure (1)) [8]

$$\mathrm{v}=\frac{\mathrm{C}{\mathrm{r}}^2}{4}+{\mathrm{c}}_1\ln \left(\mathrm{r}\right)+{\mathrm{c}}_2+\in \left(\frac{{\mathrm{t}}_0}{{\mathrm{r}}^2}+{\mathrm{t}}_1{\mathrm{r}}^2-{\mathrm{t}}_2{\mathrm{r}}^4+{\mathrm{h}}_1\ln \left(\mathrm{r}\right)+{\mathrm{h}}_2\right)$$

(6)

$$\begin{array}{l}\mathsf{\theta }=-\mathrm{\Gamma }\left(\frac{{\mathrm{C}}^2{\mathrm{r}}^4}{64}+\frac{\mathrm{C}{\mathrm{c}}_1{\mathrm{r}}^2}{4}+\frac{{\mathrm{c}}_1^2\ln {\left(\mathrm{r}\right)}^2}{2}\right)+{\mathrm{d}}_1\ln \left(\mathrm{r}\right)+{\mathrm{d}}_2+\in ({\mathrm{k}}_1{\mathrm{r}}^6\\ +{\mathrm{k}}_2{\mathrm{r}}^4+{\mathrm{r}}^2\left({\mathrm{k}}_3\ln {\left(\mathrm{r}\right)}^2+{\mathrm{k}}_4\right)\\ +{\mathrm{k}}_5\ln \left({\mathrm{r}}^2\right)+\frac{{\mathrm{k}}_6}{{\mathrm{r}}^2}+{\mathrm{m}}_1\ln \left(\mathrm{r}\right)+{\mathrm{m}}_2)\end{array}$$

(7)

where c₁,c₂,d₁,d₂, t_0,1,2, h₁,h₂, k_1,2…,6, m₁ and m₂ are given as follows

$${\mathrm{c}}_1=\frac{\mathrm{C}\left({\mathrm{r}}_{\mathrm{i}}^2-{\mathrm{r}}_0^2\right)}{4\ln \left({\mathrm{r}}_0/{\mathrm{r}}_{\mathrm{i}}\right)},{\mathrm{c}}_2=-\frac{\mathrm{C}}{4}{\mathrm{r}}_{\mathrm{i}}^2-{\mathrm{c}}_1\ln \left({\mathrm{r}}_{\mathrm{i}}\right)$$

(8)

$${\mathrm{d}}_1=-\frac{\mathrm{\Gamma }}{\ln \left({\mathrm{r}}_0/{\mathrm{r}}_{\mathrm{i}}\right)}\left(\frac{{\mathrm{C}}^2\left({\mathrm{r}}_{\mathrm{i}}^4-{\mathrm{r}}_0^4\right)}{64}+\frac{\mathrm{C}{\mathrm{c}}_1\left({\mathrm{r}}_{\mathrm{i}}^2-{\mathrm{r}}_{\mathrm{o}}^2\right)}{4}+\frac{{\mathrm{c}}_1^2}{2}\left(\ln {\left({\mathrm{r}}_{\mathrm{i}}\right)}^2-\ln {\left({\mathrm{r}}_0\right)}^2\right)\right)$$

(9)

$${\mathrm{d}}_2=\mathrm{\Gamma }\left(\frac{{\mathrm{C}}^2}{64}{\mathrm{r}}_{\mathrm{i}}^4+\frac{\mathrm{C}{\mathrm{c}}_1}{4}{\mathrm{r}}_{\mathrm{i}}^2+\frac{{\mathrm{c}}_1^2}{2}\ln {\left({\mathrm{r}}_{\mathrm{i}}\right)}^2\right)-{\mathrm{d}}_1\ln \left({\mathrm{r}}_{\mathrm{i}}\right)$$

(10)

$${\mathrm{t}}_0=\frac{{\mathrm{c}}_1^3\mathsf{\lambda }}{2}$$

(11)

$${\mathrm{t}}_1=-\frac{3{\mathrm{C}}^2{\mathrm{c}}_1\mathsf{\lambda }}{8}$$

(12)

$${\mathrm{t}}_2=\frac{{\mathrm{C}}^3\mathsf{\lambda }}{32}$$

(13)

$${\mathrm{h}}_1=\frac{1}{\ln \left({\mathrm{r}}_0/{\mathrm{r}}_{\mathrm{i}}\right)}\left[{\mathrm{t}}_0\left(\frac{1}{{\mathrm{r}}_{\mathrm{i}}^2}-\frac{1}{{\mathrm{r}}_{\mathrm{o}}^2}\right)+{\mathrm{t}}_1\left({\mathrm{r}}_{\mathrm{i}}^2-{\mathrm{r}}_{\mathrm{o}}^2\right)-{\mathrm{t}}_2\left({\mathrm{r}}_{\mathrm{i}}^4-{\mathrm{r}}_{\mathrm{o}}^4\right)\right]$$

(14)

$${\mathrm{h}}_2=-\frac{{\mathrm{t}}_{\mathrm{o}}}{{\mathrm{r}}_{\mathrm{i}}^2}-{\mathrm{t}}_1{\mathrm{r}}_{\mathrm{i}}^2+{\mathrm{t}}_2{\mathrm{r}}_{\mathrm{i}}^4-{\mathrm{h}}_1\ln \left({\mathrm{r}}_{\mathrm{i}}\right)$$

(15)

$${\mathrm{k}}_1=-\frac{\mathsf{\lambda }\mathrm{\Gamma }{\mathrm{C}}^4}{576}+\frac{\mathrm{\Gamma }\mathrm{C}{\mathrm{t}}_2}{9}$$

(16)

$${\mathrm{k}}_2=-\frac{\mathsf{\lambda }\mathrm{\Gamma }{\mathrm{C}}^3{\mathrm{c}}_1}{32}-\frac{\mathrm{\Gamma }\mathrm{C}{\mathrm{t}}_1}{8}+\frac{\mathrm{\Gamma }{\mathrm{c}}_1{\mathrm{t}}_2}{2}$$

(17)

$${\mathrm{k}}_3=-\frac{3\mathrm{\Gamma }\mathrm{C}{\mathrm{t}}_2}{4}$$

(18)

$${\mathrm{k}}_4=-\mathrm{\Gamma }{\mathrm{c}}_1{\mathrm{t}}_1-\frac{3\mathsf{\lambda }\mathrm{\Gamma }{\mathrm{c}}_1^2{\mathrm{C}}^2}{8}$$

(19)

$${\mathrm{k}}_5=\mathrm{\Gamma }\mathrm{C}{\mathrm{t}}_0-\mathsf{\lambda }\mathrm{\Gamma }{\mathrm{c}}_1^3\mathrm{C}$$

(20)

$${\mathrm{k}}_6=\frac{-\mathsf{\lambda }\mathrm{\Gamma }{\mathrm{c}}_1^4+4\mathrm{\Gamma }{\mathrm{c}}_1{\mathrm{t}}_0}{4}$$

(21)

$$\begin{array}{l}{\mathrm{m}}_1=\frac{1}{\ln ({\mathrm{r}}_{\mathrm{o}}/{\mathrm{r}}_{\mathrm{i}})}[{\mathrm{k}}_1({\mathrm{r}}_{\mathrm{i}}^6-{\mathrm{r}}_{\mathrm{o}}^6)\\ +({\mathrm{r}}_{\mathrm{i}}^4-{\mathrm{r}}_{\mathrm{o}}^4){\mathrm{k}}_2+({\mathrm{r}}_{\mathrm{i}}^2-{\mathrm{r}}_{\mathrm{o}}^2)({\mathrm{k}}_3(\ln {({\mathrm{r}}_{\mathrm{i}})}^2-\ln {({\mathrm{r}}_{\mathrm{o}})}^2))+{\mathrm{k}}_4)\\ +{\mathrm{k}}_5(\ln {({\mathrm{r}}_{\mathrm{i}})}^2-\ln {({\mathrm{r}}_{\mathrm{o}})}^2)+{\mathrm{k}}_6\left(\frac{1}{{\mathrm{r}}_{\mathrm{i}}^2}-\frac{1}{{\mathrm{r}}_{\mathrm{o}}^2}\right)]\end{array}$$

(22)

$$\begin{array}{l}{\mathrm{m}}_2=-[{\mathrm{k}}_1{\mathrm{r}}_{\mathrm{i}}^6+{\mathrm{r}}_{\mathrm{i}}^4{\mathrm{k}}_2+{\mathrm{r}}_{\mathrm{i}}^2({\mathrm{k}}_3\ln {({\mathrm{r}}_{\mathrm{i}})}^2+{\mathrm{k}}_4)\\ +{\mathrm{k}}_5\ln {({\mathrm{r}}_{\mathrm{i}})}^2+{\mathrm{k}}_6/{\mathrm{r}}_{\mathrm{i}}^2]-{\mathrm{m}}_1\ln ({\mathrm{r}}_{\mathrm{i}})\end{array}$$

(23)

The perturbation solution is valid if the correction terms are much smaller than the leading terms. Since, there are many physical parameters involved, analytical criteria formulas for validity cannot be accomplished. For a simpler case of normal pipe flow, criteria of validity have already been presented in Ref [7]. In our case, as well as in the simpler case of [7], validity does not depend on one parameter, but a combination of parameters. In all numerical computations, validity is ensured by checking the numerical values of correction terms to be much smaller than the leading terms.

Viscous Dissipation and Entropy Generation

The dimensional viscous dissipation term ($\overline{\mathsf{\varphi }}$) can be obtained from equations of motion, i.e.:

$$\overline{\mathsf{\varphi }}=\overline{\mathsf{\mu }}{\left(\frac{\mathrm{d}\overline{\mathrm{v}}}{\mathrm{d}\overline{\mathrm{r}}}\right)}^2+2{\mathsf{\beta }}_3{\left(\frac{\mathrm{d}\overline{\mathrm{v}}}{\mathrm{d}\overline{\mathrm{r}}}\right)}^4$$

(24)

or inserting the dimensionless quantities yields

$$\overline{\mathsf{\varphi }}=\frac{{\mathsf{\mu }}_{*}{\mathrm{V}}_0^2}{{\mathrm{R}}^{{*}^2}}{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\left[\mathsf{\mu }+\mathrm{\Lambda }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\right]$$

(25)

The dimensional volumetric entropy generation is defined as [14],

$${\mathrm{S}}_{\mathrm{g}\mathrm{e}\mathrm{n}}^{‴}=\frac{\mathrm{k}}{{\overline{\mathsf{\theta }}}_0^2}{\left(\frac{\mathrm{d}\overline{\mathsf{\theta }}}{\mathrm{d}\overline{\mathrm{r}}}\right)}^2+\frac{\overline{\mathsf{\varphi }}}{{\overline{\mathsf{\theta }}}_0}$$

(26)

where ${\overline{\mathsf{\theta }}}_0$ is the reference temperature. The first term in equation (25) is the volumetric entropy generation due to heat transfer and the second term is the entropy generation due to viscous dissipation. Substituting equation (25) into (26), expressing the terms in dimensionless forms, one finally obtains:

$$\mathrm{N}\mathrm{s}={\left(\frac{\mathrm{d}\mathsf{\theta }}{\mathrm{d}\mathrm{r}}\right)}^2+{\mathsf{\theta }}_0\mathrm{\Gamma }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\left[\mathsf{\mu }+\mathrm{\Lambda }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\right]$$

(27)

where Ns is the entropy generation number. It is defined by dividing the dimensional volumetric entropy generation to a reference volumetric entropy generation ${\mathrm{S}}_{\mathrm{G}}^{‴}$. The relevant definitions are:

$$\mathrm{N}\mathrm{s}=\frac{{\mathrm{S}}_{\mathrm{g}\mathrm{e}\mathrm{n}}^{‴}}{{\mathrm{S}}_{\mathrm{G}}^{‴}},{\mathrm{S}}_{\mathrm{G}}^{‴}=\frac{\mathrm{k}{\left({\mathsf{\theta }}_{\mathrm{m}}-{\mathsf{\theta }}_{\mathrm{w}}\right)}^2}{{\overline{\mathsf{\theta }}}_0^2{\mathrm{R}}^{{*}^2}}{\mathsf{\theta }}_0=\frac{{\overline{\mathsf{\theta }}}_0}{{\mathsf{\theta }}_{\mathrm{m}}-{\mathsf{\theta }}_{\mathrm{w}}}$$

(28)

In equation (27), the first term due to heat generation can be assigned as Ns₁ and the second term due to viscous dissipation as Ns₂, i.e.:

$$\mathrm{N}{\mathrm{s}}_1={\left(\frac{\mathrm{d}\mathsf{\theta }}{\mathrm{d}\mathrm{r}}\right)}^2,\mathrm{N}{\mathrm{s}}_2={\mathsf{\theta }}_0\mathrm{\Gamma }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\left[\mathsf{\mu }+\mathrm{\Lambda }{\left(\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{r}}\right)}^2\right]$$

(29)

Results and Discussions

Non-Newtonian fluid flow through annular pipe and entropy generation are considered. The velocity and temperature fields are formulated and entropy generation rates due to fluid friction and heat transfer are obtained.

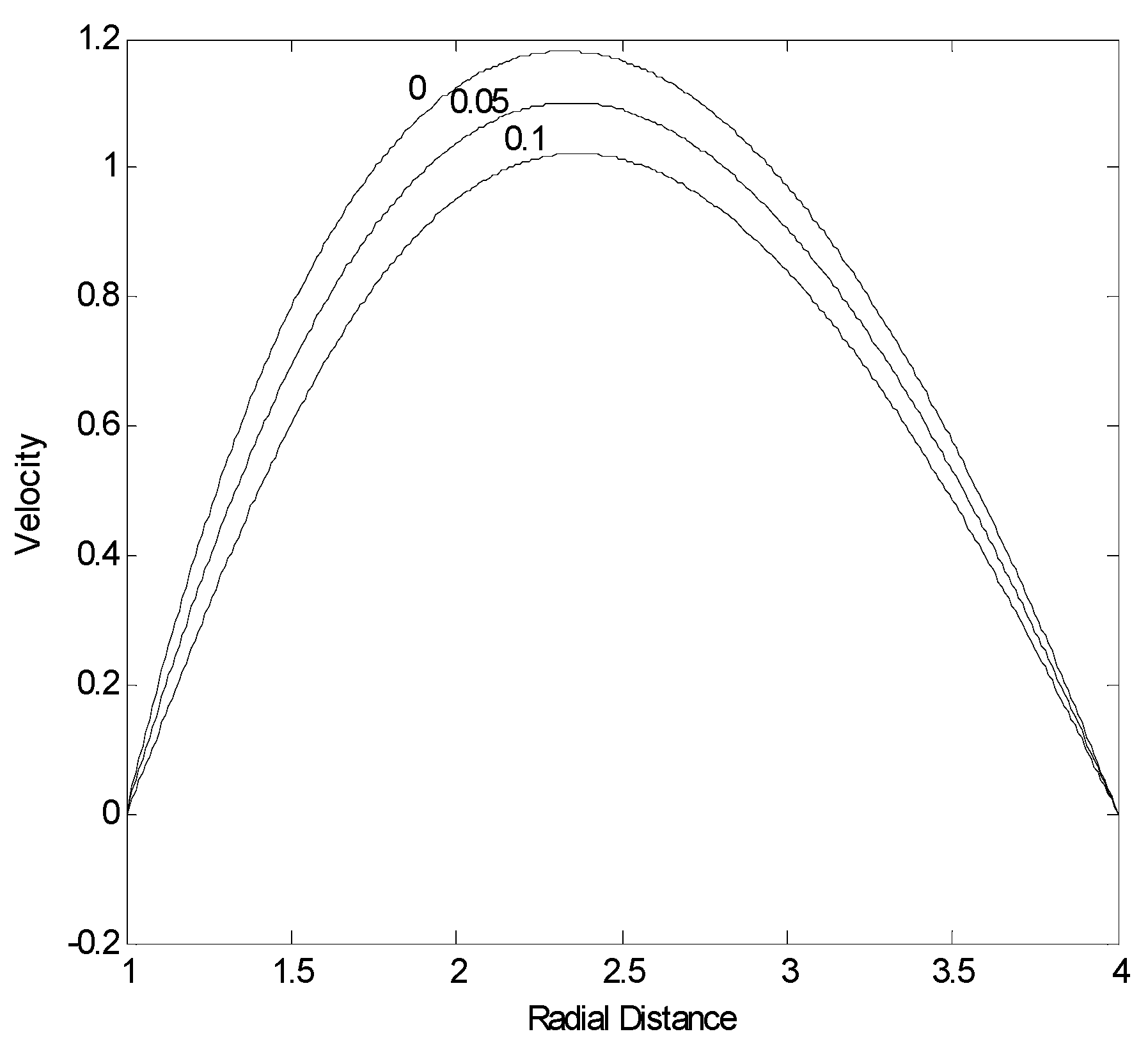
Figure (2) shows velocity profiles in the annular pipe for different values of non-Newtonian parameter. The maximum velocity moves towards the inner pipe wall due to the convective acceleration (annular effect). As the non-Newtonian parameter reduces, the velocity magnitude increases, in which case the rate of fluid strain increases in the region of the pipe wall. Moreover, the location of maximum velocity magnitude moves towards the inner pipe wall as the non-Newtonian parameter reduces. This indicates that convective acceleration of the fluid enhances with reducing non-Newtonian parameter, i.e. the maximum velocity magnitude and its location in the annular pipe changes.

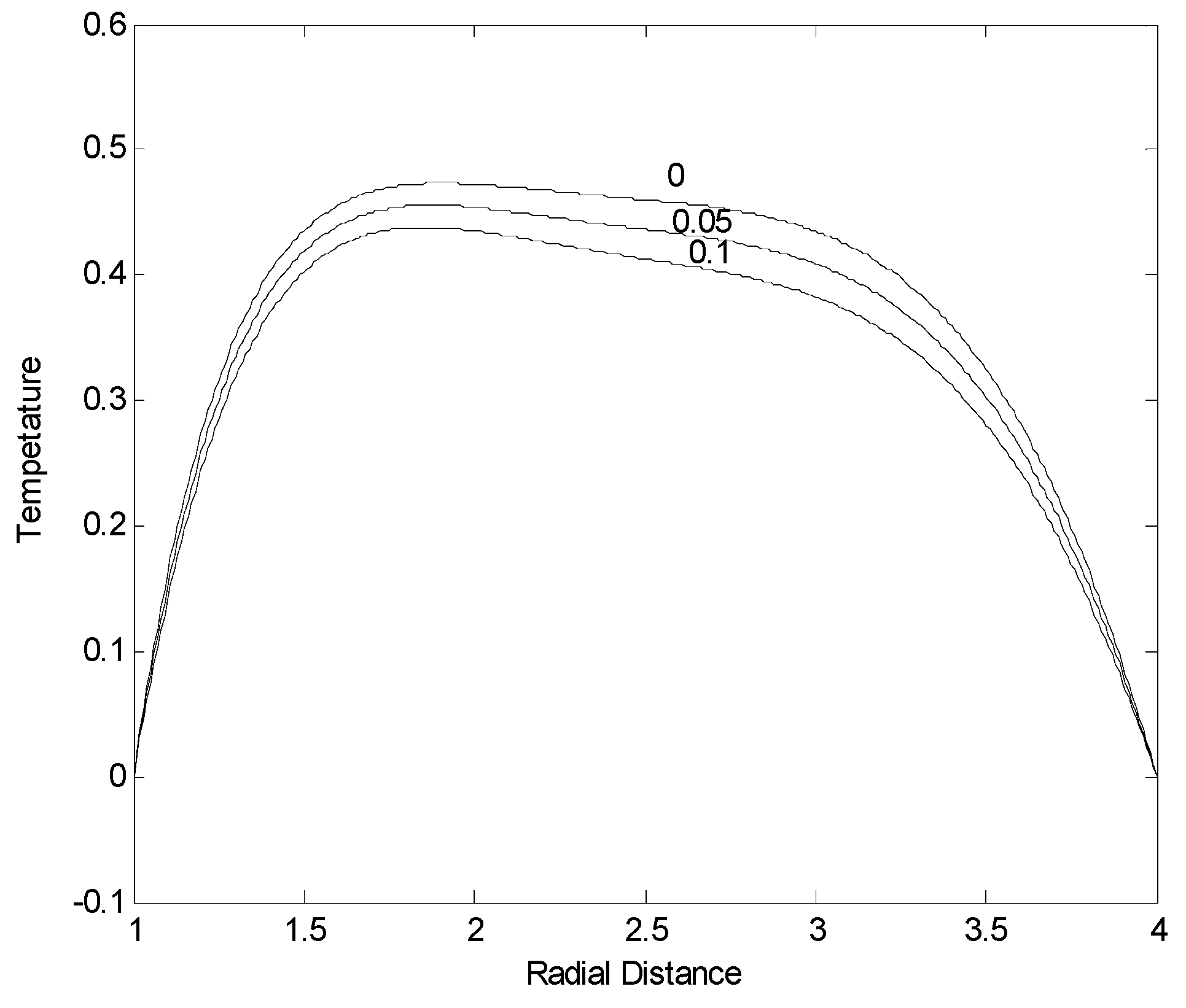
Figure (3) shows temperature profiles in the annular pipe for different values of non-Newtonian parameter. Temperature profiles do not follow velocity profiles. In this case, convective heat transfer from fluid to the pipe wall influences significantly the temperature profiles. Moreover, due to the diffusional heat transfer in the central region of the annular pipe, temperature gradient gradually decays in this region, i.e. temperature gradient is less than the velocity gradient in this region. Moreover, reducing non-Newtonian parameter enhances the temperature rise in the annular pipe, i.e. the magnitude of temperature attains high values in this region. Consequently, reducing non-Newtonian parameter enhances the velocity magnitude and temperature in the central region of the annular pipe.

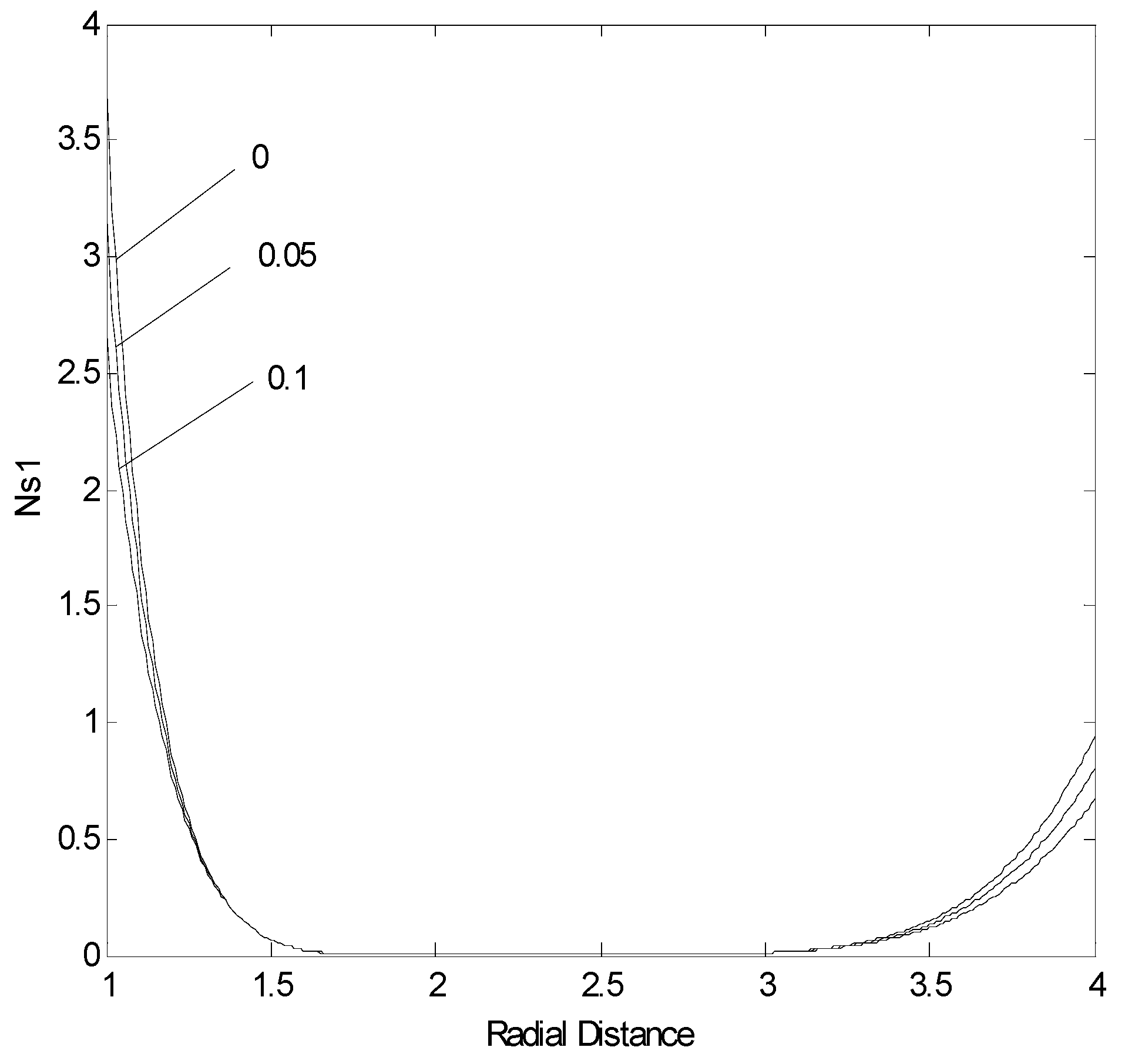
Figure (4) shows entropy generation number due to heat transfer in the annular pipe for different values of non-Newtonian parameter. Entropy generation number in the central region of the annular pipe is low due to gradually varying and small temperature gradient in this region. Moreover, entropy generation number attains high values in the region close to the annular pipe walls, which is more pronounced towards the inner wall. This is because of the high temperature gradient attainment in this region. Entropy generation number decays sharply in the vicinity of the annular pipe wall due to the high rate of convective heat transfer taking place in this region. As the non-Newtonian parameter decreases, entropy generation number increases. In this case, reducing non-Newtonian parameter increases maximum velocity magnitude and temperature in the pipe. This, then, enhances convective and diffusive heat transfer in the region close to the annular pipe wall.

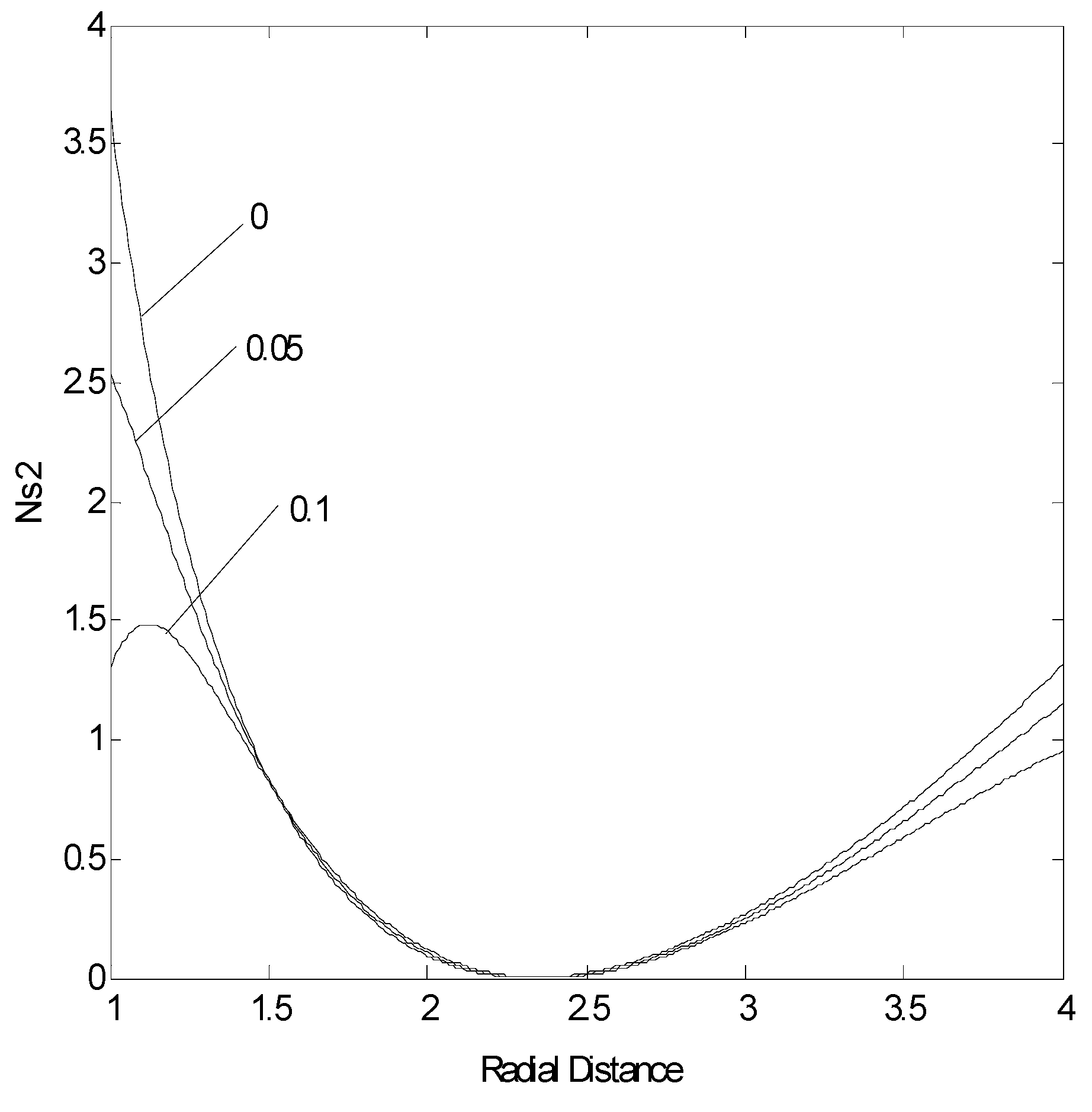
Figure (5) shows entropy generation number due to fluid friction in the annular pipe for different non-Newtonian parameter. Entropy generation number reduces to minimum in the central region of the annular pipe where the velocity magnitude is maximum. Due to high rate of fluid strain in the region close to the annular pipe wall, entropy generation number due to fluid friction attains high values in this region. This is more pronounced in the region close to the inner pipe wall due to enhanced fluid convective deceleration in this region. Increasing non-Newtonian parameter lowers the entropy generation number, particularly in the pipe wall region. Moreover, a local peak in entropy generation number is observed near the pipe wall region for non-Newtonian parameter of 0.1. This indicates that, the rate of fluid strain in this region is higher than that corresponding to the next to the pipe wall region.

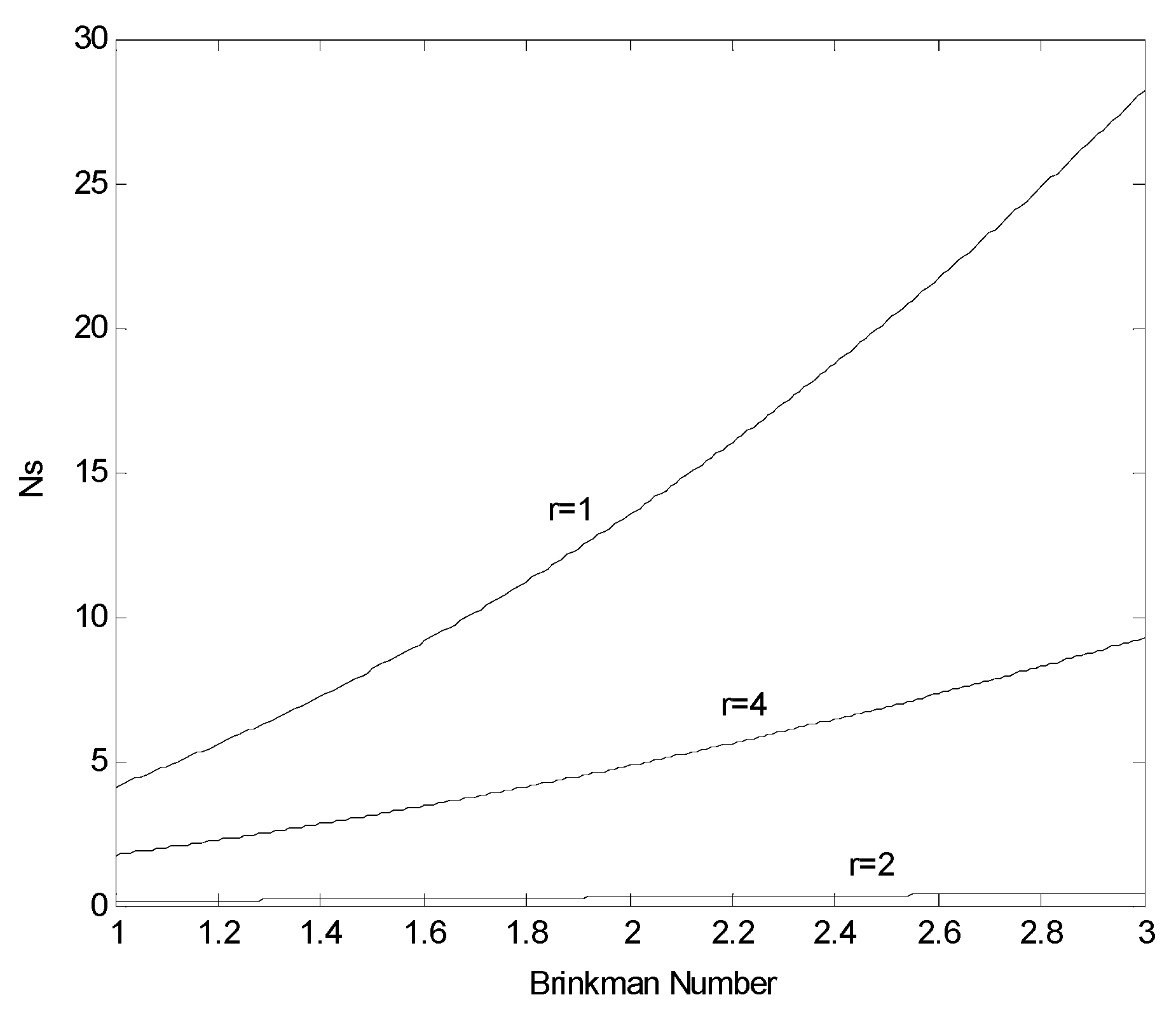
Figure (6) shows the variation of total entropy generation number with Brinkman number for different locations in the annular pipe. Location 1 is in the region close to the inner pipe while location 4 corresponds to outer wall and location 2 is in the region close to the center of the annular pipe. Total entropy generation number increases with increasing Brinkman number, which is more pronounced in the region of inner wall of the annular pipe. The increase in Brinkman number results in enhanced convective transport in the pipe. Consequently, increasing kinetic energy of the fluid in the annular pipe results in increasing entropy generation particularly in the region close to the inner wall of the annular pipe. This is because of both enhanced heat transfer rates and fluid friction in this region. Lowering the Brinkman number results in less entropy production in the annular pipe. This is because of the reduced convection transport which is the result of low Brinkman number. Moreover, the entropy minimization can be delivered by reducing the Brinkman number in the annular pipe.

Figure (7) shows the variation of total entropy generation number with non-Newtonian parameter for different locations in the annular pipe. Entropy generation number reduces with increasing non-Newtonian parameter. This becomes significant in the region close to the inner wall of the annular pipe. However, the variation of the total entropy generation number with non-Newtonian parameter is minimal for locations in the regions of center and close to the outer wall of the annular pipe. This indicated that once the fluid kinetic energy increases, which is high in the inner region due to convective acceleration, the influence of non-Newtonian parameter on the total entropy generation number signifies. In this case, convective heat transfer and viscous dissipation enhance with decreasing non-Newtonian parameter.

The rate of entropy generation can be reduced by reducing both non-Newtonian parameter and Brinkman number; in this case, the entropy generation number reduces significantly, particularly in the region close to the inner wall of the annular pipe.

Conclusions

Non-Newtonian flow in annular pipe is examined and analytical solutions for velocity and temperature fields are presented by considering third-grade fluid with constant viscosity case. The entropy generation in the annular pipe due to heat transfer and fluid friction is formulated. It is found that velocity and temperature gradients in the region close to inner wall of the annular pipe is high due to convective acceleration as similar to the Newtonian fluid. Moreover, reducing non-Newtonian parameter enhances the maximum velocity magnitude and maximum temperature in the annular pipe. Entropy generation due to fluid friction and heat transfer is high in the region close to the inner wall of the annular pipe due to enhancement of convective heat transfer and increased fluid friction due to high shear strain in this region. Increasing non-Newtonian parameter reduces the entropy generation number in this region. Total entropy generation number increases with increasing Brinkman number, which is more pronounced in the region of the inner wall of the annular pipe. Consequently, enhancement of fluid kinetic energy improves the heat transfer rates and increases the fluid friction in this region. Total entropy generation number decreases with increasing non-Newtonian parameter. This becomes significant in the inner wall region of the annular pipe. This indicates that influence of non-Newtonian parameter on the entropy generation rate becomes significant once the kinetic energy of the fluid increases in the annular pipe.