Energetics of Glucose Metabolism: A Phenomenological Approach to Metabolic Network Modeling
Abstract
:1. Introduction
2. Results and Discussion
2.1. Pathway Fluxes and Phenomenology
2.1.1. Flux Equations
2.1.2. Constant versus Variable Conductances
2.1.3. Phenomenological Relations
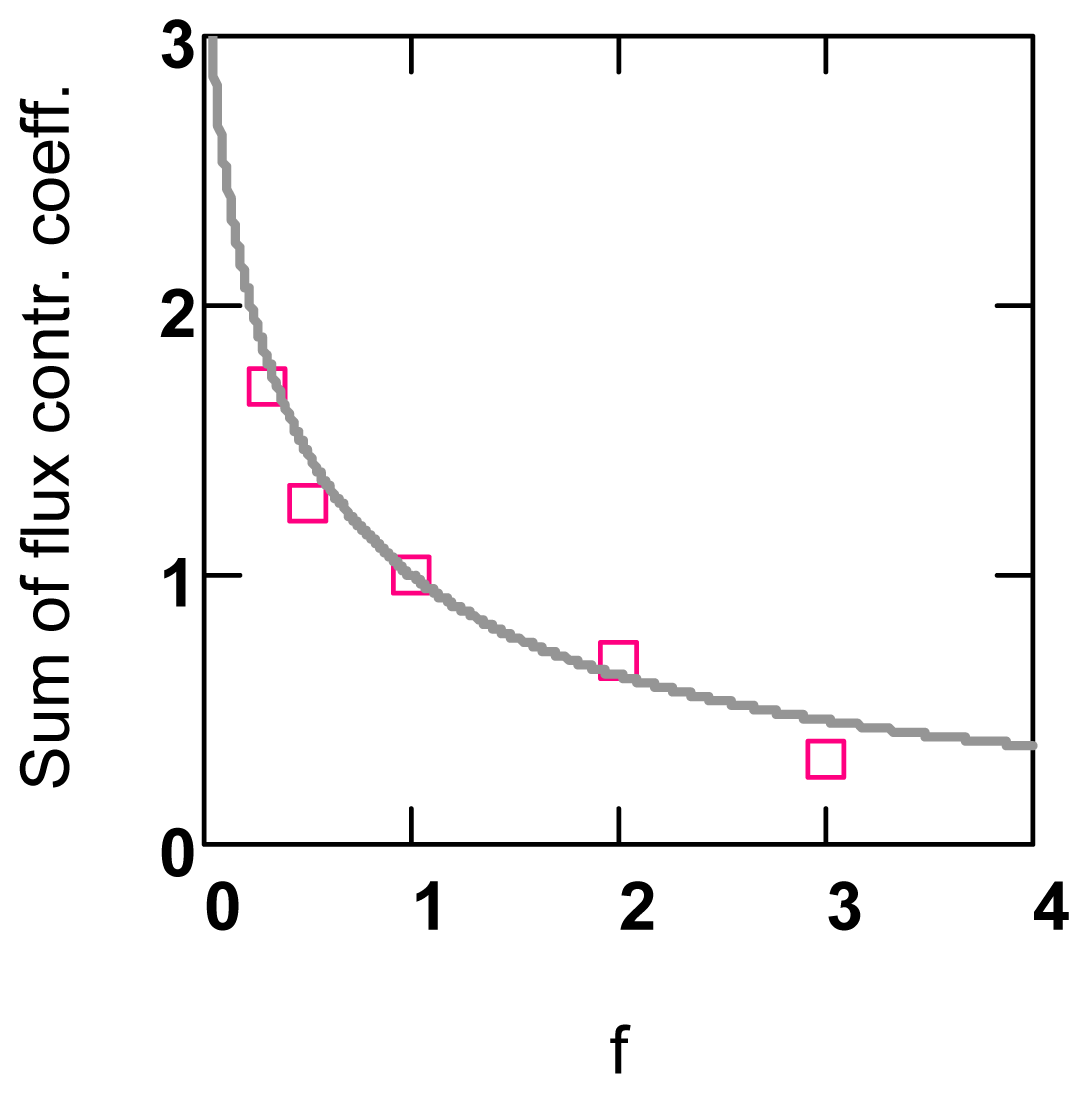
2.1.4. Flux Control Coefficients
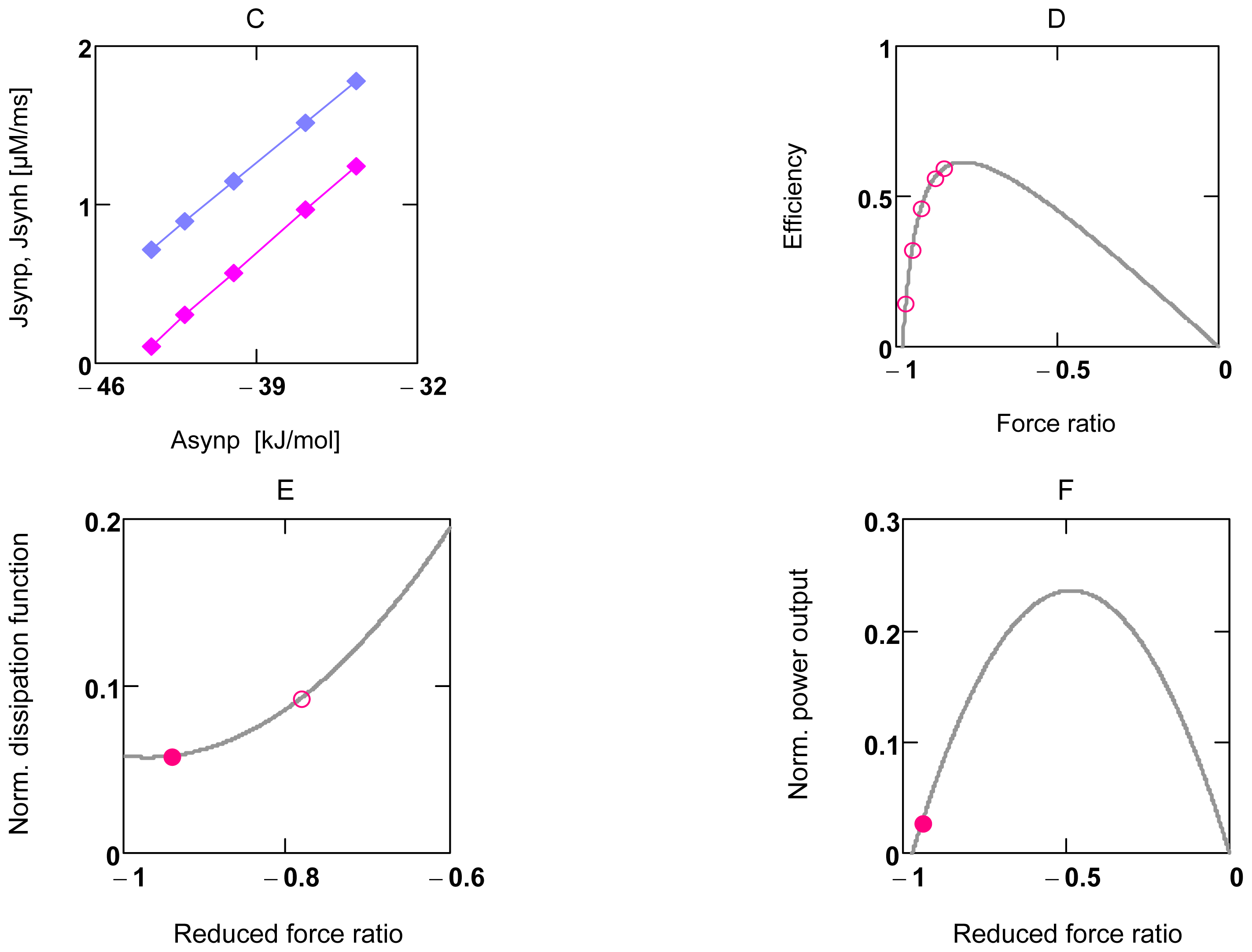
2.2. Energetic Coupling in Metabolism
2.2.1. Coupling in Oxidative Phosphorylation
2.2.2. Indirect Uncoupling
2.2.3. Stucki’s Conductance Matching
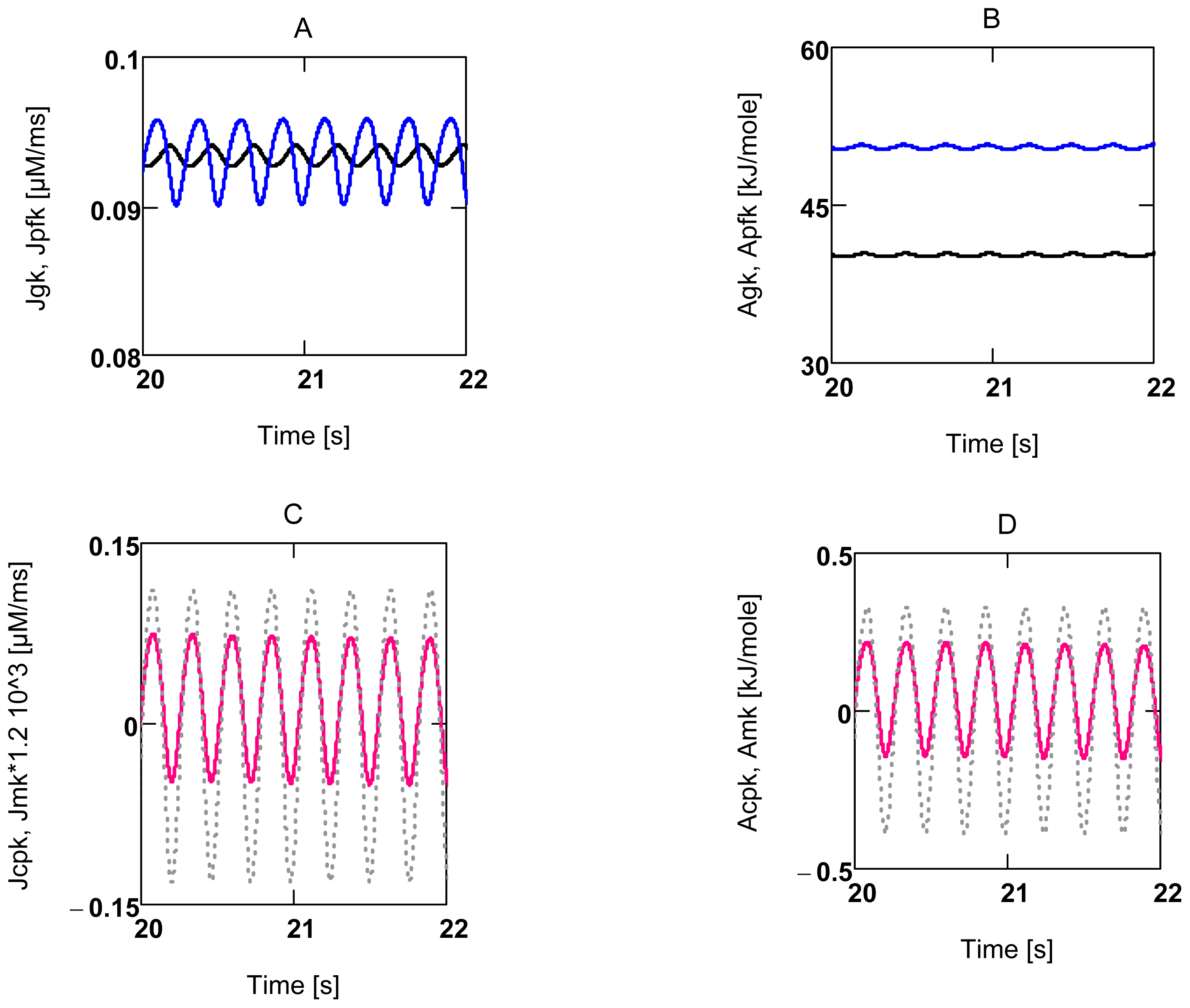
2.3. Activation of Power Output in Glucose Metabolism
2.3.1. Ventricular Myocytes
2.3.2. Forced Oscillations
2.3.3. Conductance Matching for Glucose Oxidation and Power Output
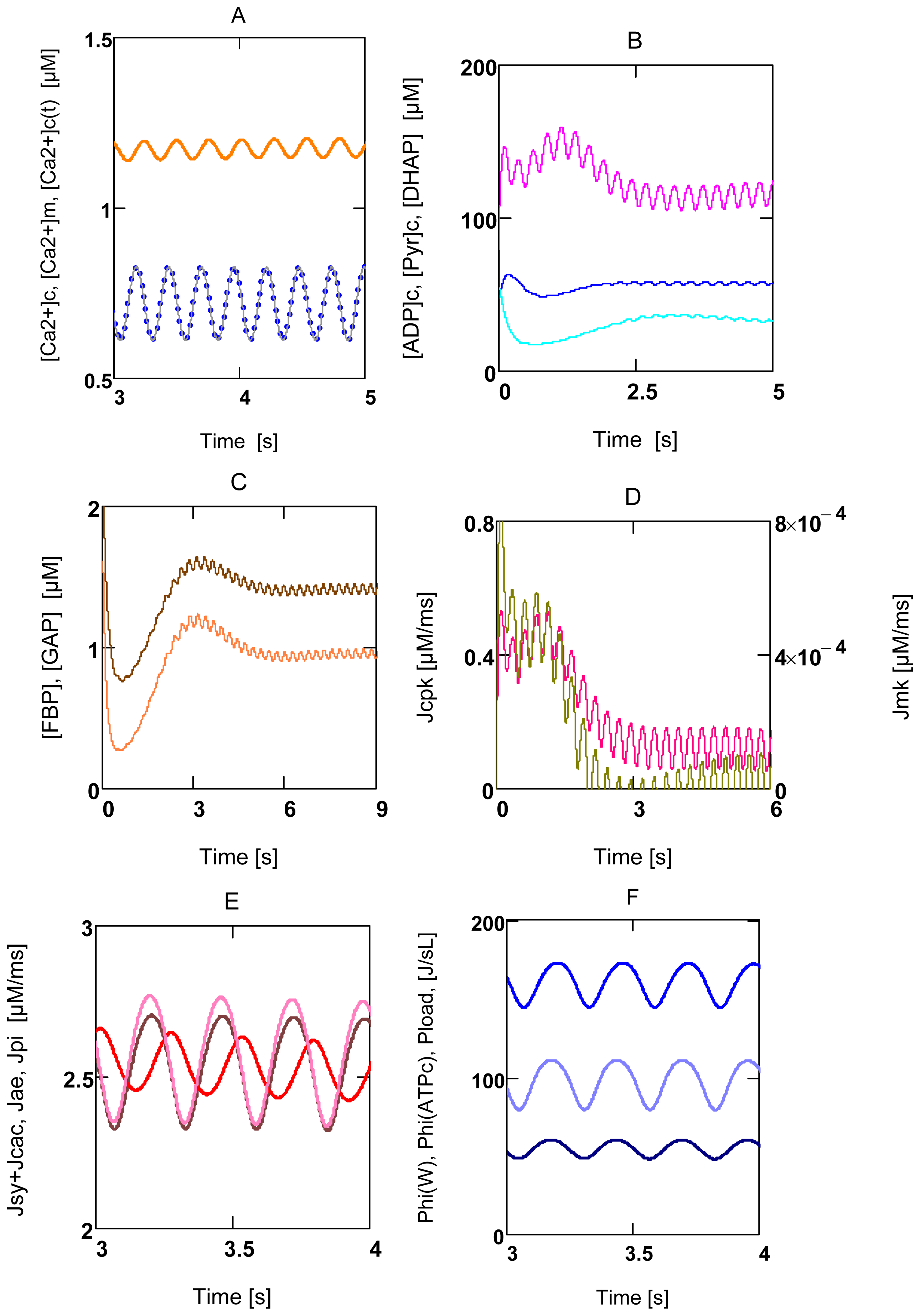
2.4. Replenishment of [ATP]c
2.5. Pancreatic β-Cells
3. Methods
4. Conclusions
Appendix
1. Ventricular Muscle Cells
2. Oxidative Phosphorylation
3. Simulations
4. Forced Oscillations
5. Maximal Conductances for VMs
6. OP as a Two-Flux-System
References
- Wegschneider, R. Über simultane Gleichgewichte und die Beziehungen zwischen Thermodynamik und Reaktionskinetik homogener Systeme. Z. Phys. Chem 1902, 39, 257–303. [Google Scholar]
- Qian, H; Beard, DA; Liang, S. Stoichiometric network theory for nonequilibrium biochemical systems. Eur. J. Biochem 2003, 270, 415–421. [Google Scholar]
- Qian, H; Beard, DA. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem 2005, 114, 213–220. [Google Scholar]
- Beard, DA; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE 2007, 2, e144. [Google Scholar]
- Heinrich, R; Schuster, S. The Regulation of Cellular Systems; Chapman & Hall: New York, NY, USA, 1996. [Google Scholar]
- Diederichs, F. Mathematical simulation of membrane processes and metabolic fluxes of the pancreatic beta-cell. Bull. Math. Biol 2006, 68, 1779–1818. [Google Scholar]
- Liebermeister, W; Klipp, E. Bringing metabolic networks to life: Convenience rate law and thermodynamic constraints. Theor. Biol. Med. Model 2006, 3, 41. [Google Scholar] [CrossRef]
- Ederer, M; Gilles, ED. Thermodynamically feasible kinetic models of reaction networks. Biophys. J 2007, 92, 1846–1857. [Google Scholar]
- Ederer, M; Gilles, ED. Thermodynamic constraints in kinetic modeling: Thermodynamic-kinetic modeling in comparison to other approaches. Eng. Life Sci 2008, 8, 467–476. [Google Scholar]
- Diederichs, F. Ion homeostasis and the functional roles of SERCA reactions in stimulus-secretion coupling of the pancreatic β-cell A mathematical simulation. Biophys. Chem 2008, 134, 119–143. [Google Scholar]
- Segel, IH. Enzyme Kinetics; John Wiley & sons: New York, NY, USA, 1975. [Google Scholar]
- Katchalsky, A; Curran, PF. Nonequilibrium Thermodynamics in Biophysics; Harvard University Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Caplan, SR; Essig, A. Bioenergetics and Linear Nonequilibrium Thermodynamics; Harvard University Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Pietrobon, D; Caplan, SR. Use of nonequilibrium thermodynamics in the analysis of transport: general flow-force relationships and the linear domain. Methods Enzymol 1989, 171, 397–444. [Google Scholar]
- Demirel, Y; Sandler, SI. Thermodynamics and bioenergetics. Biophys. Chem 2002, 97, 87–111. [Google Scholar]
- Kondepudi, D; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Korzeniewski, B; Zoladz, JA. A model of oxidative phosphorylation in mammalian skeletal muscle. Biophys. Chem 2001, 92, 17–34. [Google Scholar]
- Nicholls, DG; Ferguson, SJ. Bioenergetics 3; Academic press: London, UK, 2002. [Google Scholar]
- Beard, DA. A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PloS Comput. Biol 2005, 1, e36. [Google Scholar]
- Lebon, G; Jou, D; Casas-Vázquez, J. Understanding Non-equilibrium Thermodynamics; Springer-Verlag: Heidelberg, Berlin, Germany, 2008. [Google Scholar]
- Neely, JR; Liebermeister, H; Battersby, EJ; Morgan, HE. Effect of pressure development on oxygen consumption by isolated rat heart. Am. J. Physiol 1967, 212, 804–814. [Google Scholar]
- Neely, JR; Denton, RM; England, PJ; Randle, PJ. The effects of increased heart work on the tricarboxylate cycle and its interactions with glycolysis in the perfused rat heart. Biochem. J 1972, 128, 147–159. [Google Scholar]
- Katz, LA; Swain, JA; Portman, MA; Balaban, RS. Relation between phosphate metabolites and oxygen consumption of heart in vivo. Am. J. Physiol 1989, 256, H265–H274. [Google Scholar]
- Balaban, RS. Domestication of the cardiac mitochondrion for energy conversion. J. Mol. Cell. Cardiol 2009, 46, 832–841. [Google Scholar]
- Saks, VA; Kuznetsov, AV; Vendelin, M; Guerrero, K; Kay, L; Seppet, EK. Functional coupling as a basic mechanism of feedback regulation of cardiac energy metabolism. Mol. Cell. Biochem 2004, 256–257, 185–99. [Google Scholar]
- Saks, V; Favier, R; Guzun, R; Schlattner, U; Wallimann, T. Molecular system bioenergetics: regulation of substrate supply in response to heart energy demands. J. Physiol 2006, 577, 769–777. [Google Scholar]
- Saks, V; Beraud, N; Wallimann, T. Metabolic compartmentation: A system level property of muscle cells. Int. J. Mol. Sci 2008, 9, 751–767. [Google Scholar]
- Guzun, R; Saks, V. Application of the principle of systems biology and Wiener’s cybernetics for analysis of regulation of energy fluxes in muscle cells in vivo. Int. J. Mol. Sci 2010, 11, 982–1019. [Google Scholar]
- Ashcroft, FM; Harris, DE; Ashcroft, SJH. Glucose induces closure of single potassium channels in isolated rat pancreatic β-cells. Nature 1984, 312, 446–448. [Google Scholar]
- Beauvois, MC; Merezak, C; Jonas, JC; Ravier, MA; Henquin, JC; Gilon, P. Glucose-induced mixed [Ca2+]c oscillations in mouse β-cells are controlled by the membrane potential and the SERCA3 Ca2+-ATPase of the endoplasmic reticulum. Am. J. Physiol.: Cell Physiol 2006, 290, C1503–C1511. [Google Scholar]
- Hill, AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol 1910, 40, IV–VII. [Google Scholar]
- Huang, X; Holden, HM; Rauschel, FM. Channeling of substrates and intermediates in enzyme-catalyzed reactions. Annu. Rev. Biochem 2001, 70, 149–180. [Google Scholar]
- Bauler, P; Huber, G; Leyh, T; McCammon, JA. Channeling by proximity: The catalytic advantages of active site colocalisation using Brownian dynamics. J. Phys. Chem. Lett 2010, 1, 1332–1335. [Google Scholar]
- Fell, D. Understanding the Control of Metabolism; Portland Press: London, UK, 1997. [Google Scholar]
- Vogel, F; Bornhövd, C; Neupert, W; Reichert, AS. Dynamic subcompartmentalization of the mitochondrial inner membrane. J. Cell Biol 2006, 175, 237–247. [Google Scholar]
- Strauss, M; Hofhaus, G; Schröder, RR; Kühlbrandt, W. Dimer ribbons of ATP synthase shape the inner mitochondrial membrane. EMBO J 2008, 27, 1154–1160. [Google Scholar]
- Zick, M; Rabl, R; Reichert, AS. Cristae formation-linking ultrastructure and function of mitochondria. Biochim. Biophys. Acta 2009, 1793, 5–19. [Google Scholar]
- Vonck, J; Schäfer, E. Supramolecular organisation of protein complexes in the mitochondrial inner membrane. Biochem. Biophys. Acta 2009, 1793, 117–124. [Google Scholar]
- Weiss, TF. Cellular Biophysics, Volume 1: Transport; MIT Press: Cambridge, UK, 1996. [Google Scholar]
- Stucki, JW. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem 1980, 109, 269–283. [Google Scholar]
- McCormack, JG; Halestrap, AP; Denton, RM. Role of calcium ions in regulation of mammalian intramitochondrial metabolism. Phys. Rev 1990, 70, 391–425. [Google Scholar]
- Brandes, R; Bers, DM. Simultaneous measurement of mitochondrial NADH and Ca2+ during increased work in intact rat heart trabeculae. Biophys. J 2002, 83, 587–604. [Google Scholar]
- Rizzuto, R; Marchi, S; Bonora, M; Aguiari, P; Bononi, A; De Stefani, D; Giorgi, C; Leo, S; Rimessi, A; Siviero, R; Zecchini, E; Pinton, P. Ca2+ transfer from the ER to mitochondria: When, how and why. Biochim. Biophys. Acta 2009, 1787, 1342–1351. [Google Scholar]
- Baniene, R; Naucienne, Z; Maslauskaite, S; Baliutyte, G; Mildaziene, V. Contribution of ATP synthase to stimulation of respiration by Ca2+ in heart mitochondria. Syst. Biol. (Stevenage) 2006, 153, 350–353. [Google Scholar]
- Brdizka, D. Saks, VA, Ed.; Mitochondrial VDAC and its complexes. In Molecular Systems Bioenergetics Energy for Life; Wiley-VCH: Weinheim, Germany, 2007; pp. 165–194. [Google Scholar]
- Bose, S; French, S; Evans, FJ; Joubert, F; Balaban, RS. Metabolic network control of oxidative phosphorylation: Multiple roles of inorganic phosphate. J. Biol. Chem 2003, 278, 39155–39165. [Google Scholar]
- Scheibye-Knudsen, M; Quistorff, B. regulation of mitochondrial respiration by inorganic phosphate; comparing permeabilized muscle fibers with isolated mitochondria prepared from typ-1 and type-2 rat skeletal muscles. Eur. J. Appl. Physiol 2009, 105, 279–287. [Google Scholar]
- Wallimann, T; Wyss, M; Brdizka, D; Nicolay, K; Eppenberger, HM. Intracellular compartmentation, structure and function of creatine kinase isoenzymes in tissues with high and fluctuating energy demands: The ‘phosphocreatine circuit’ for cellular energy homeostasis. Biochem. J 1992, 281, 21–40. [Google Scholar]
- Vendelin, M; Eimre, M; Seppet, E; Peet, N; Andrienko, T; Lemba, M; Engelbrecht, J; Seppet, EK; Saks, VA. Intracellular diffusion of adenosine phosphates is locally restricted in cardiac muscle. Mol. Cell. Biochem 2004, 256/257, 229–241. [Google Scholar]
- Honda, H; Tanaka, K; Akita, N; Haneda, T. Cyclical changes in high-energy phosphates during the cardiac cycle by pacing-gated 31P nuclear magnetic resonance. Circ. Res 2002, 66, 80–86. [Google Scholar]
- Drews, G; Krippeit-Drews, P; Düfer, M. Electrophysiology of islet cells. Adv. Exp. Med. Biol 2010, 654, 115–163. [Google Scholar]
- Aliev, MK; Dos Santos, P; Hoerter, JA; Soboll, S; Tikhonov, AN; Saks, VA. Water content and its intracellular distribution in intact and saline perfused rat hearts revisited. Cardiovasc. Res 2002, 53, 48–58. [Google Scholar]
- Satoh, H; Delbridge, LM; Blatter, LA; Bers, DM. Surface: volume relationship in cardiac myocytes studied with confocal microscopy and membrane capacitance measurements: Species-dependence and developmental effects. Biophys. J 1996, 70, 1494–1504. [Google Scholar]
- Golding, EM; Teague, WE, Jr; Dobson, GP. Adjustment of K’ to varying pH and pMg for the creatine kinase, adenylate kinase and ATP hydrolysis equilibria permitting quantitative bioenergetic assessment. J. Exp. Biol 1995, 198, 81775–81782. [Google Scholar]







© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Diederichs, F. Energetics of Glucose Metabolism: A Phenomenological Approach to Metabolic Network Modeling. Int. J. Mol. Sci. 2010, 11, 2921-2961. https://doi.org/10.3390/ijms11082921
Diederichs F. Energetics of Glucose Metabolism: A Phenomenological Approach to Metabolic Network Modeling. International Journal of Molecular Sciences. 2010; 11(8):2921-2961. https://doi.org/10.3390/ijms11082921
Chicago/Turabian StyleDiederichs, Frank. 2010. "Energetics of Glucose Metabolism: A Phenomenological Approach to Metabolic Network Modeling" International Journal of Molecular Sciences 11, no. 8: 2921-2961. https://doi.org/10.3390/ijms11082921



