Qualitative Analysis of the Helical Electronic Energy of Inherently Chiral Calix[4]arenes: An Approach to Effectively Assign Their Absolute Configuration
1. Introduction
2. Results and Discussion
| Dihedral Angle (°) | ||
| ϕC1−Cf−Ca−Br = 4.2828 | ϕBr−Ca−Cb−N = 2.8760 | ϕN−Cb−Cc−N = −0.1161 |
| ϕN−Cc−Cd−C4 = −6.3989 | ϕC4−Cd−Ce−O = 6.7100 | ϕO−Ce−Cf−C1 = −7.0711 |
| Exterior Angle (°) | ||
| ∠BrCaCb = 118.450 | ∠NCbCa = 122.317 | ∠HCcCb = 119.125 |
| ∠BrCaCf = 119.182 | ∠NCbCc = 119.757 | ∠HCcCd = 119.096 |
| ∠C4CdCc = 121.734 | ∠OCeCd = 118.688 | ∠C1CfCe = 118.703 |
| ∠C4CdCe = 120.026 | ∠OCeCf = 118.095 | ∠C1CfCa = 124.316 |
| Distance (Å) | |||||
| dC1D1 = 2.9240 | dC4D1 = 2.9161 | dC1D2 = 2.9212 | dC4D4 = 2.9209 | ||
| dC2D2 = 2.9308 | dC3D4 = 2.9385 | dC2D3 = 2.9094 | dC3D3 = 2.9144 | ||
| Angle (°) | |||||
| ∠D1C1D2 = 104.257 | ∠C1D2C2 = 121.606 | ∠D2C2D3 = 102.747 | |||
| ∠D1C4D4 = 108.995 | ∠C4D4C3 = 121.172 | ∠D4C3D3 = 102.767 | |||
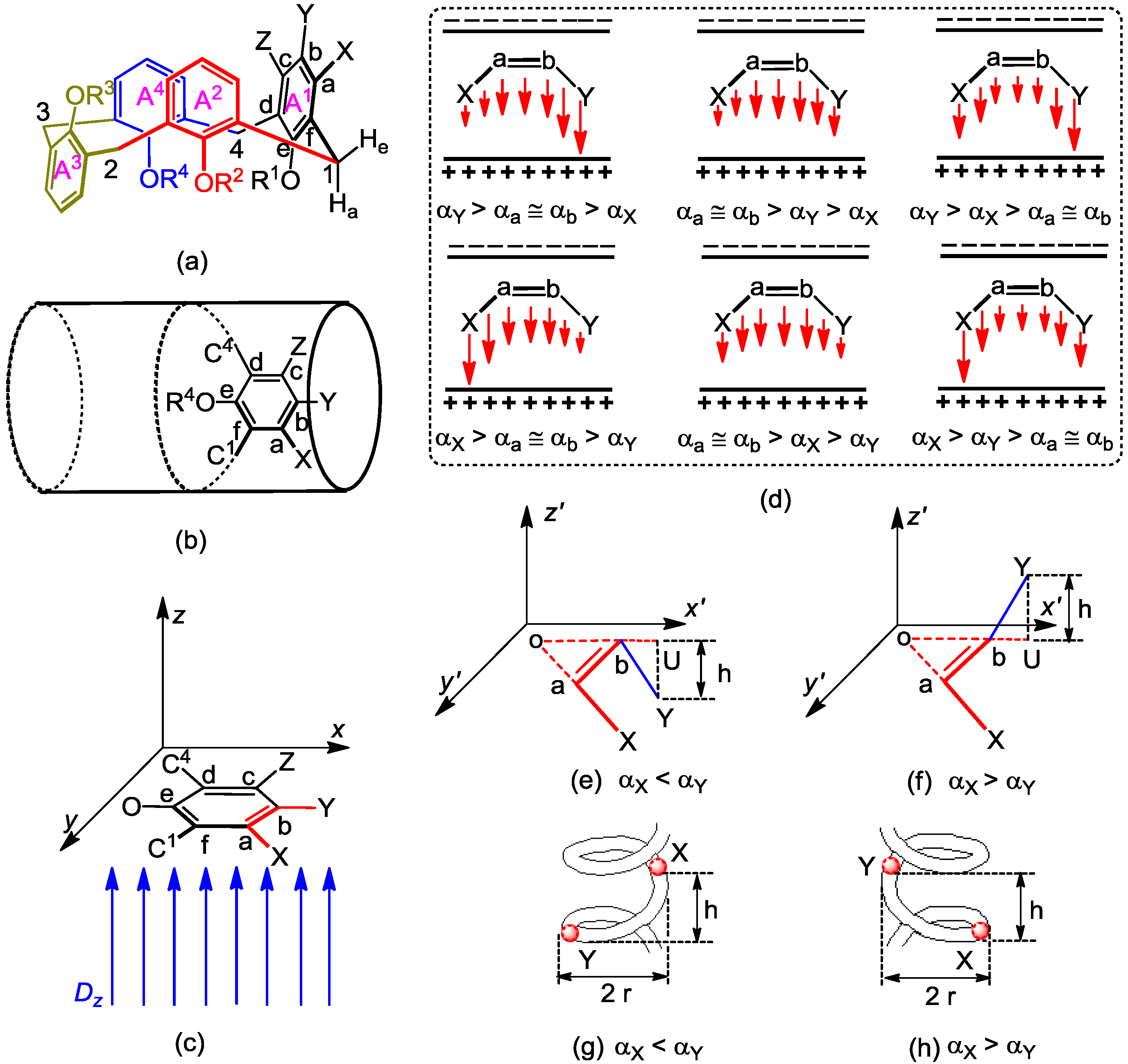
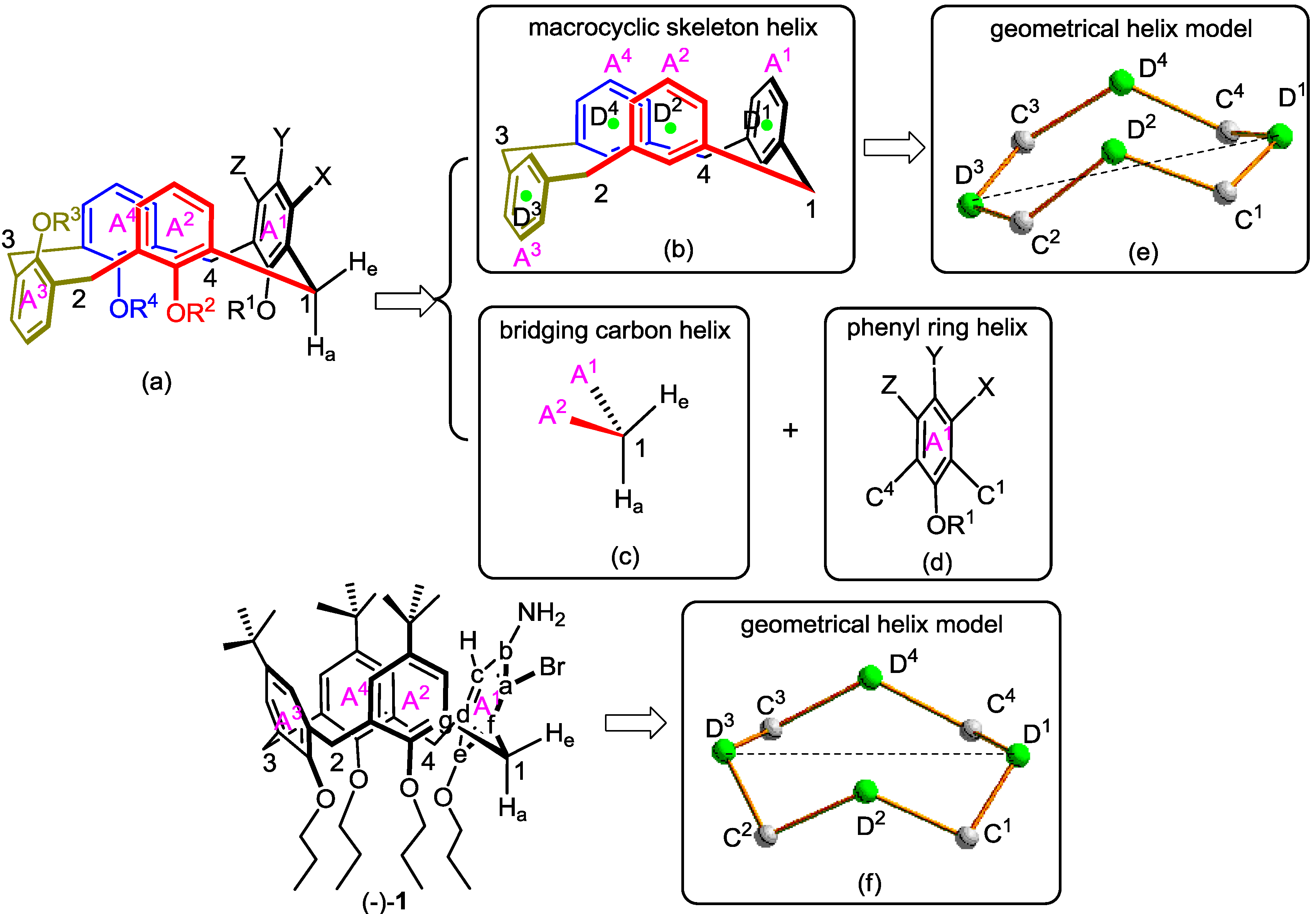
2.1. Microhelical Model
2.2. Microhelical Radius
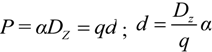
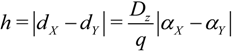
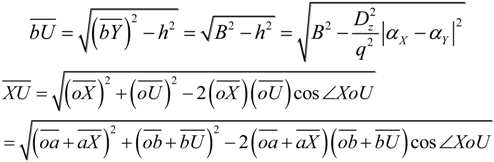
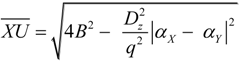
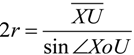
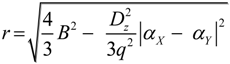
2.3. Microhelical Electronic Energy
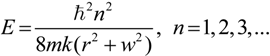
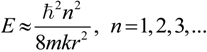
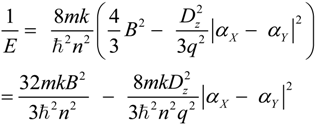
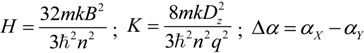
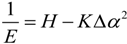
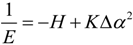
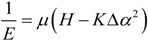
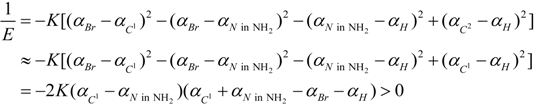
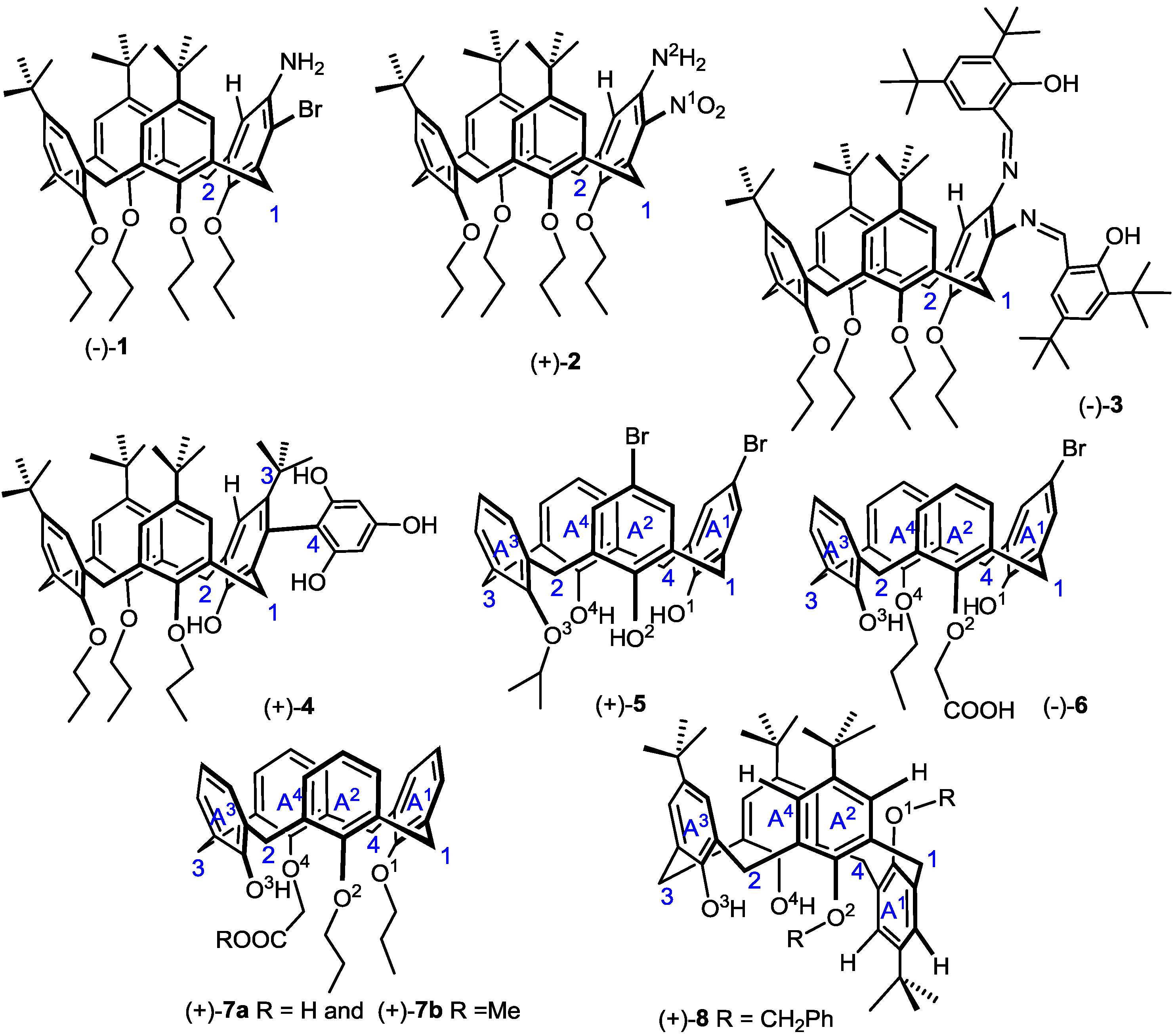
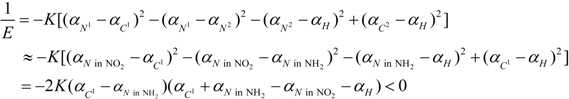
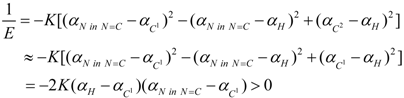
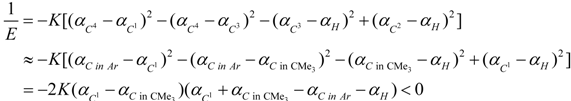
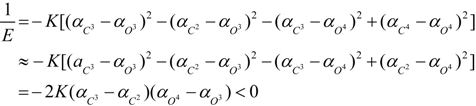
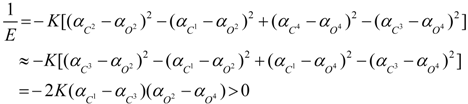
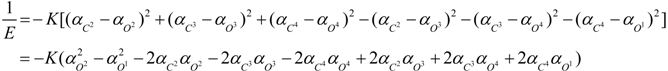
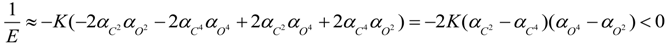
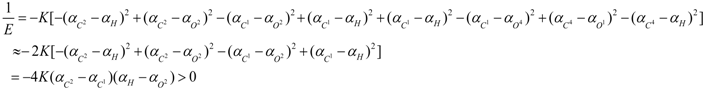
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, S.Y.; Xu, Y.W.; Liu, J.M.; Su, C.Y. Inherently chiral calixarenes: Synthesis, optical resolution, chiral recognition and asymmetric catalysis. Int. J. Mol. Sci. 2011, 12, 429–455. [Google Scholar]
- Luo, J.; Zheng, Q.; Chen, C.; Huang, Z. Progress in inherently chiral calixarenes. Prog. Chem. 2006, 18, 897–906. [Google Scholar]
- Böhmer, V.; Kraft, D.; Tabatabai, M. Inherently chiral calixarenes. J. Incl. Phenom. Mol. Recognit. Chem. 1994, 19, 17–39. [Google Scholar]
- Szumna, A. Inherently chiral concave molecules—Rrom synthesis to applications. Chem. Soc. Rev. 2010, 39, 4274–4285. [Google Scholar]
- Cort, A.D.; Mandolini, L.; Pasquini, C.; Schiaffino, L. “Inherent chirality” and curvature. New J. Chem. 2004, 28, 1198–1199. [Google Scholar]
- Zheng, Y.S.; Luo, J. Inherently chiral calixarenes: A decade’s review. J. Incl. Phenom. Macrocycl. Chem. 2011, 71, 35–56. [Google Scholar]
- No, K.H.; Gutsche, C.D. Calixarenes 8: Short, stepwise synthesis of p-phenylcalix[4]arene, p-phenyl-p-tert-butylcalix[4]arene, and derived products. J. Org. Chem. 1982, 47, 2713–2719. [Google Scholar]
- Jin, T.; Monde, K. Synthesis and optical resolution of a fluorescent chiral calix[4]arene with two pyrene moieties forming an intramolecular excimer. Chem. Commun. 1998, 1357–1358. [Google Scholar]
- Luo, J.; Zheng, Q.Y.; Chen, C.F.; Huang, Z.T. Facile synthesis and optical resolution of inherently chiral fluorescent calix[4]crowns: Enantioselective recognition towards chiral leucinol. Tetrahedron 2005, 61, 8517–8528. [Google Scholar]
- Shirakawa, S.; Moriyama, A.; Shimizu, S. Design of a novel inherently chiral calix[4]arene for chiral molecular recognition. Org. Lett. 2007, 9, 3117–3119. [Google Scholar]
- Shirakawa, S.; Moriyama, A.; Shimizu, S. Synthesis, optical resolution and enantiomeric recognition ability of novel, inherently chiral calix[4]arenes: Trial application to asymmetric reactions as organocatalysts. Eur. J. Org. Chem. 2008, 5957–5964. [Google Scholar]
- Kliachyna, M.A.; Yesypenko, O.A.; Pirozhenko, V.V.; Shishkina, S.V.; Shishkin, O.V.; Boyko, V.I.; Kalchenko, V.I. Synthesis, optical resolution and absolute configuration of inherently chiral calixarene carboxylic acids. Tetrahedron 2009, 65, 7085–7091. [Google Scholar]
- Xia, Y.X.; Zhou, H.H.; Shi, J.; Li, S.Z.; Zhang, M.; Luo, J.; Xiang, G.Y. An inherently chiral calix[4]crown carboxylic acid in the 1,2-alternate conformation. J. Incl. Phenom. Macrocycl. Chem. 2012, 74, 277–284. [Google Scholar]
- Shi, J.; Li, S.Z.; Xia, Y.X.; Wang, X.G.; Luo, J.; Wan, Q. An inherently chiral calix[4]crown carboxylic acid in the partial cone conformation. J. Incl. Phenom. Macrocycl. Chem. 2013, 77, 327–335. [Google Scholar]
- Dieleman, C.; Steyer, S.; Jeunesse, C.; Matt, D. Diphosphines based on an inherently chiral calix[4]arene scaffold: Synthesis and use in enantioselective catalysis. J. Chem. Soc. Dalton Trans. 2001, 17, 2508–2517. [Google Scholar]
- Xu, Z.X.; Li, G.K.; Chen, C.F.; Huang, Z.T. Inherently chiral calix[4]arene-based bifunctional organocatalysts for enantioselective aldol reactions. Tetrahedron 2008, 64, 8668–8675. [Google Scholar]
- Miao, R.; Xu, Z.X.; Huang, Z.T.; Chen, C.F. Enantiopure inherently chiral calix[4]arene derivatives containing quinolin-2-yl-methanol moiety: Synthesis and application in the catalytic asymmetric addition of diethylzinc to benzaldehyde. Sci. China B Chem. 2009, 52, 505–512. [Google Scholar]
- Shirakawa, S.; Kimura, T.; Murata, S.; Shimizu, S. Synthesis and resolution of a multifunctional inherently chiral calix[4]arene with an ABCD substitution pattern at the wide rim: The effect of a multifunctional structure in the organocatalyst on enantioselectivity in asymmetric reactions. J. Org. Chem. 2009, 74, 1288–1296. [Google Scholar]
- Shirakawa, S.; Shimizu, S. Synthesis of an inherently chiral calix[4]arene amino acid and its derivatives: Their application to asymmetric reactions as organocatalysts. Eur. J. Org. Chem. 2009, 1916–1924. [Google Scholar]
- Shirakawa, S.; Shimizu, S. Improved design of inherently chiral calix[4]arenes as organocatalysts. New J. Chem. 2010, 34, 1217–1222. [Google Scholar]
- Xu, Z.X.; Zhang, C.; Zheng, Q.Y.; Chen, C.F.; Huang, Z.T. A new approach to enantiopure inherently chiral calix[4]arenes: Determination of their absolute configurations. Org. Lett. 2007, 9, 4447–4450. [Google Scholar]
- Xu, Z.X.; Huang, Z.T.; Chen, C.F. Synthesis and structures of novel enantiopure inherently chiral calix[4]arene-derived salphen ligands and their transition-metal complexes. Tetrahedron Lett. 2009, 50, 5430–5433. [Google Scholar]
- Yakovenko, A.V.; Boyko, V.I.; Danylyuk, O.; Suwinska, K.; Lipkowski, J.; Kalchenko, V.I. Diastereoselective lower rim (1S)-camphorsulfonylation as the shortest way to the inherently chiral calix[4]arene. Org. Lett. 2007, 9, 1183–1185. [Google Scholar]
- Karpus, A.O.; Yesypenko, O.A.; Andronov, L.P.; Boyko, V.I.; Garasevich, S.G.; Voitenko, Z.V.; Chernega, A.N.; Kalchenko, V.I. Stereoselective synthesis of enantiomerically pure inherently chiral p-tert-butylcalix[4]arene carboxylic acids. Tetrahedron Asymmetry 2012, 23, 1243–1250. [Google Scholar]
- Narumi, F.; Hattori, T.; Yamabuki, W.; Kabutoc, C.; Kameyama, H. Resolution of inherently chiral anti-O,O'-dialkylated calix[4]arenes and determination of their absolute stereochemistries by CD and X-ray methods. Tetrahedron Asymmetry 2005, 16, 793–800. [Google Scholar]
- Talotta, C.; Gaeta, C.; Troisi, F.; Monaco, G.; Zanasi, R.; Mazzeo, G.; Rosini, C.; Neri, P. Absolute configuration assignment of inherently chiral calix[4]arenes using DFT calculations of chiroptical properties. Org. Lett. 2010, 12, 2912–2915. [Google Scholar]
- Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds; Wiley: New York, NY, USA, 1994; pp. 126–144. [Google Scholar]
- Wang, D.Z. A helix theory for molecular chirality and chiral interaction. Mendeleev Commun. 2004, 14, 244–247. [Google Scholar]
- Wang, D.Z. Conservation of helical asymmetry in chiral interactions. Tetrahedron 2005, 61, 7125–7133. [Google Scholar]
- Wang, D.Z. Catalyst-substrate helical character matching determines enantiomeric excess. Tetrahedron 2005, 61, 7134–7143. [Google Scholar]
- Wang, D.Z. Conservation of helicity and helical character matching in chiral interactions. Chirality 2005, 17, S177–S182. [Google Scholar]
- Stone, A.J. The Theory of Intermolecular Forces; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Yin, Y. Helix structure and opticity activity. Hua Xue Tong Bao 1993, 10, 1–9. [Google Scholar]
- Tinoco, I., Jr.; Woody, R.W. Optical rotation of oriented helices IV: A free electron on a helix. J. Chem. Phys. 1964, 40, 160–165. [Google Scholar]
- Brewster, J.H. Helix models for optical activity. Top. Steroechem. 1967, 2, 1–72. [Google Scholar]
- Caldwell, D.J.; Eyring, H. The Theory of Optical Activity; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Miller, K.J. Additivity methods in molecular polarizability. J. Am. Chem. Soc. 1990, 112, 8533–8542. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zheng, S.; Chang, M.-L.; Zhou, J.; Fu, J.-W.; Zhang, Q.-W.; Li, S.-Y.; Qiao, W.; Liu, J.-M. Qualitative Analysis of the Helical Electronic Energy of Inherently Chiral Calix[4]arenes: An Approach to Effectively Assign Their Absolute Configuration. Int. J. Mol. Sci. 2014, 15, 9844-9858. https://doi.org/10.3390/ijms15069844
Zheng S, Chang M-L, Zhou J, Fu J-W, Zhang Q-W, Li S-Y, Qiao W, Liu J-M. Qualitative Analysis of the Helical Electronic Energy of Inherently Chiral Calix[4]arenes: An Approach to Effectively Assign Their Absolute Configuration. International Journal of Molecular Sciences. 2014; 15(6):9844-9858. https://doi.org/10.3390/ijms15069844
Chicago/Turabian StyleZheng, Shuang, Ming-Liang Chang, Jing Zhou, Jing-Wei Fu, Qing-Wei Zhang, Shao-Yong Li, Wei Qiao, and Jun-Min Liu. 2014. "Qualitative Analysis of the Helical Electronic Energy of Inherently Chiral Calix[4]arenes: An Approach to Effectively Assign Their Absolute Configuration" International Journal of Molecular Sciences 15, no. 6: 9844-9858. https://doi.org/10.3390/ijms15069844




