Solvent and rovibrational effects
It is well known that spin-spin coupling constants measured in NMR spectra are solvent-dependent. The dependence can be negligibly small for some chemical compounds but it is always present in every measurement performed for a macroscopic sample. Molecular interactions are responsible for the modification of coupling constants and this effect is certainly smaller for gases than for liquids. Early measurements in the gas phase have been described by Laszlo [
4]. More results have been shown in a review of solvent effects on nuclear spin-spin coupling constant provided by Barfield et al. [
5]. These data are sometimes used for the verification of
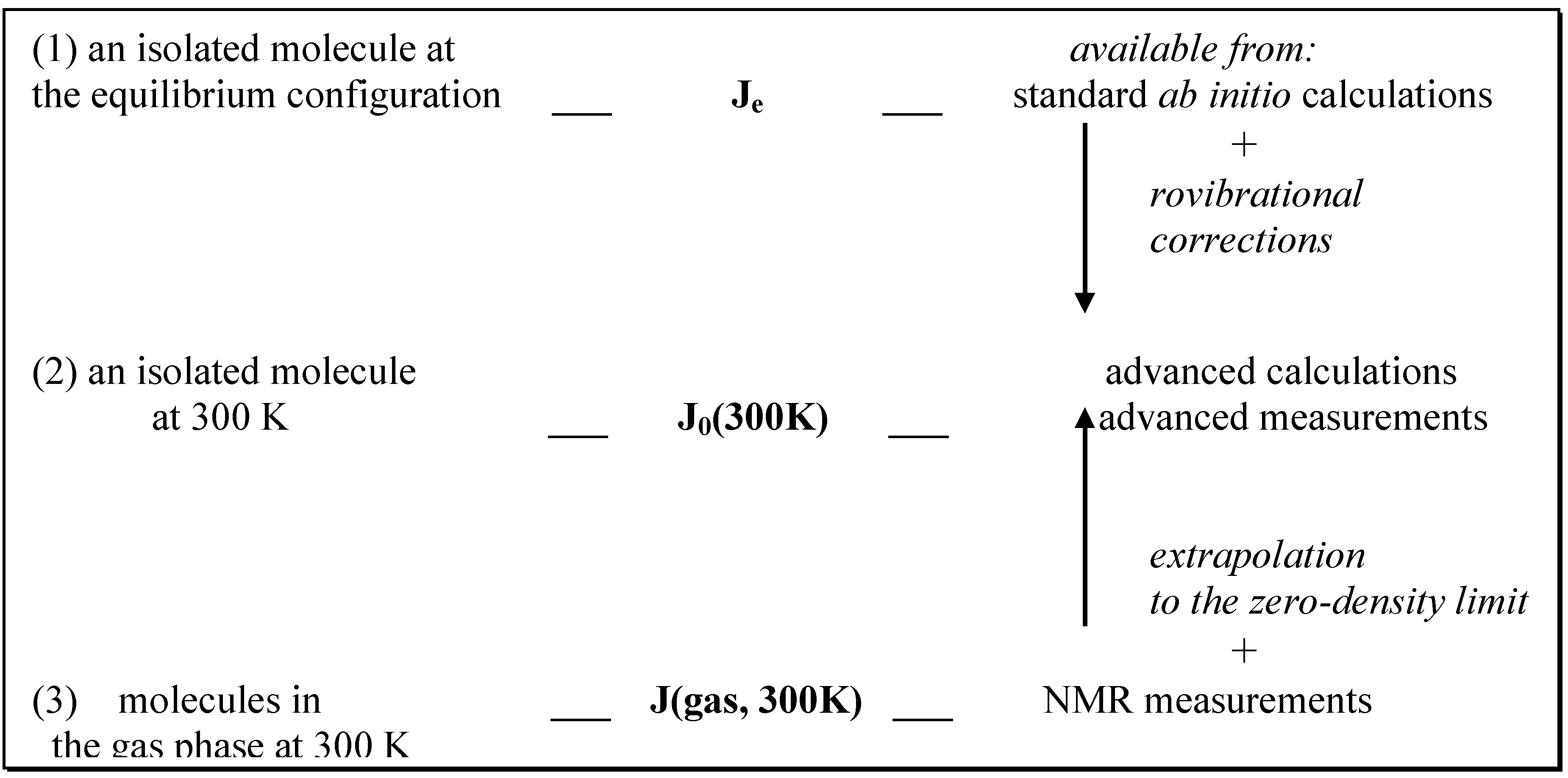
ab initio calculations performed for isolated molecules. Measurements in the gas phase certainly give better approximation than any other experiments made for liquids. However, intermolecular interactions and intramolecular nuclear motions are obviously present in the gas phase and they influence experimental results. Fig. 1 gives a qualitative description of this problem. As seen, the intermolecular effects can be eliminated from the experimental coupling constants if NMR measurements are performed in the gas phase and extrapolated to the zero-density limit.
Figure 1.
Modifications of spin-spin coupling constants due to internal rovibrational motion of a molecule (1) → (2) and molecular interactions (2) → (3).
Figure 1.
Modifications of spin-spin coupling constants due to internal rovibrational motion of a molecule (1) → (2) and molecular interactions (2) → (3).
This can be done at room temperature or even better at 300 K. The small increase of temperature is really useful because it allows the stabilization of temperature without any cooling system. The next step belongs to theoretical studies. Spin-spin coupling constants calculated for the equilibrium geometry of a molecule require rovibrational corrections and this has already been done for some molecules, i.e. hydrogen [
6], acetylene [
7,
8], water [
9], methane [
10] and silane [
11]. As an example,
Table 1 shows the magnitude of solvent effects and rovibrational corrections for the spin-spin coupling constants of 1,2-
13C-acetylene [
12]. As shown, these contributions are significant, especially for the one-bond
1J(
13C-
13C) coupling constants, and cannot be ignored when theoretical and experimental coupling constants are compared.
Table 1.
Experimental spin-spin coupling constants for 1,2-
13C-acetylene in Hz [
12].
Table 1.
Experimental spin-spin coupling constants for 1,2-13C-acetylene in Hz [12].
| J | Je a | J0(300K)b | Jsoln.(300K)c |
|---|
| 1J(13C-13C) | 185.04 | 174.78 | 165.8 |
| 1J(13C-1H) | 242.69 | 247.56 | 248.3 |
| 2J(13C-1H) | 53.84 | 50.14 | 49.9 |
| 3J(1H-1H) | 10.89 | 9.62 | 9.6 |
Density dependence of coupling constants
In a gas of low density, the nuclear spin-spin coupling (J) can be written as an expansion in powers of density (ρ):
where J
0(T) is the spin-spin coupling constant for an isolated molecule, T is temperature and J
1(T) is a measure of the effects on spin-spin coupling due to binary collisions. The higher order terms, starting from J
2(T), are negligible for low-density samples. Then the density dependence is linear and the two spin-spin coupling parameters (J
0(T) and J
1(T)) are easily available from eq.(1). This approach has first been applied by Jameson and Reger [
13] when the one-bond
29Si -
19F coupling was studied for pure SiF
4 and its gaseous solutions in CH
4, HCl and CO
2. The authors obtained the
1J
o(
29Si-
19F) and
1J
1(
29Si-
19F) values for pure SiF
4 and the appropriate
1J
1AB(
29Si-
19F) values for the gaseous solutions (the
1J
1AB parameter is defined by eq.(2) later in this text). It seems that the precision of these early measurements was considerably overestimated [
13], especially for the
1J
1(
29Si-
19F) and
1J
1AB(
29Si-
19F) parameters but the original results have been cited in
Table 2 of this review. Within the experimental error no density dependence was observed for the one-bond coupling constants in CH
4, SiH
4 and PF
3 [
13]. Jameson et al. [
14] have analyzed the broad 1:3:3:1 multiplet in the
11B NMR spectrum of gaseous BF
3. The dependence on density and temperature has been found for the
19F -
11B spin-spin coupling constant. The
1J
o(
19F-
11B) and
1J
1(
19F-
11B) parameters at 300 K are shown in
Table 2. Recently, the large density dependence has been measured for the
19F -
13C spin-spin coupling in pure CD
3F [
15]. Its second virial coefficient of eq. (1) is equal to -1008(72) (Hz ml mol
-1) and it is almost an order of magnitude larger than the previously known values of J
1, cf.
Table 2. This example is pronounced and clearly shows that the extrapolation to the zero-density limit is absolutely necessary if we need to obtain the J
o coupling constant. It is interesting that the other coupling constants of CD
3F (
1J(
13C-
2H) and
2J(
19F-
2H)) have no distinct dependence on density.
Table 2.
Spin-spin coupling constants at the zero-density limit (nJo) and their dependence on density in pure gaseous compounds (nJ1) and in binary mixtures (nJ1AB).
Table 2.
Spin-spin coupling constants at the zero-density limit (nJo) and their dependence on density in pure gaseous compounds (nJ1) and in binary mixtures (nJ1AB).
| Coupling constant | Molecule | Gas solvent | Jo [Hz] | J1 or J1AB
[Hz ml mol-1] | Method, temperature | Reference |
|---|
| 1J(29Si-19F) | SiF4 | SiF4
CH4
HCl
CO2 | -169.0(1)a | -158(22)a
-239(25)a
-172(5)a
-123(15)a | 19F | [13] |
| 1J(19F-11B) | BF3 | BF3 | 17.77 | 154 | 11B, 300 K | [14] |
| 1J(13C-13C) | 13C2H2 | Xe
CO2 | 174.77(2)174.78(2) | -30(20)
-301(20) | 1H and 13C, 300 K | [12] |
| 1J(19F-13C) | CD3F | CD3F | 160.72(5) | -1008(72) | 13C, 300 K | [15] |
| 1J(13C-2H) | CD3F | CD3F | 22.45(5) | 43(46) | 13C, 300 K | [15] |
| 2J(19F-2H) | CD3F | CD3F | 7.20(5) | 0 | 19F, 300 K | [15] |
| 1J(15N-13C) | CH313C15N | SF6
CO2 | -16.20(1)
-16.23(2) | -62(14)
-191(44) | 15N and 13C, 300 K | [16] |
| 2J(13C-1H) | CH313C15N | SF6
CO2 | -10.18(2)
-10.19(2) | -13(37)
6(46) | 1H and 13C, 300 K | [16] |
| 3J(15N-1H) | CH313C15N | SF6
CO2 | -1.34(2)
-1.43(9) | -325(77)
-134(171) | 15N and 1H, 300 K | [16] |
| 1J(13C-1H) | 13CH313CN | SF6
CO2 | 134.03(1)
134.05(1) | 95(24)
148(23) | 1H and 13C, 300 K | [17] |
| 1J(13C-13C) | 13CH313CN | SF6
CO2 | 60.12(5)
60.12(3) | -86(87)
-151(56) | 13C, 300 K | [17] |
Many results shown in
Table 2 have been obtained for gaseous binary mixture where the solute gas (A) was observed at constant pressure and the density dependence was due to the solvent gas (B). Generally, nuclear spin-spin coupling is modified by interactions of pairs of molecules in the binary mixtures of gases (A and B) as follows:
where J
o(XY) is the spin-spin coupling between X and Y nuclei at the zero-density limit and J
1AA(XY), J
1AB(XY) are solely due to intermolecular effects in the binary collisions of A-A and A-B molecules, respectively. Usually, the density of A is kept sufficiently low for eq. (2) to simplify it to
This experimental method is especially attractive when the solute can produce a strong NMR spectrum, then the approximation described by eq. (3) can easily be achieved and the small quantity of solute permits the exact measurements of spin-spin coupling constants.
Table 2 contains the
1J
o(
13C-
13C) and
1J
1AB(
13C-
13C) parameters for the one-bond coupling in 1,2-
13C-enriched acetylene [
12]. As seen, the same coupling constant has different density dependence in the investigated solvents (cf.
1J
1AB for Xe and CO
2) and the constant for an isolated molecule (
1J
o) remains the same confirming the accuracy of the measurement. Similar results have been obtained for the 2 isotopomers of acetonitrile: CH
313C
15N [
16] and
13CH
313CN [
17]. For the first time all the J
o coupling constants except one (
2J
o(
15N-
13C)) have been established for the chemical compound which exhibits strong molecular interactions in the liquid state. The results for acetonitrile are shown in
Table 2. As seen, the dependence on density for the
2J(
13C-
1H) coupling constant is within the experimental error. It certainly means that every value of
2J(
13C-
1H) measured in the gas phase is very close to the accurate result for an isolated molecule,
2J
o(
13C-
1H). The other coupling constants of acetonitrile are dependent on the density of gas solvent.
Table 3 gives more experimental coupling constants determined in the gas phase. Some of them were carefully verified over the range of density and found to be independent of density. Such coupling constants can safely be used as the experimental standards (J
o). However, it does not mean that the spin-spin coupling constants presented in
Table 3 always remain unchanged in the gas phase. Their values are still dependent on temperature and the sort of gaseous solvent. One can certainly find that every coupling constant from
Table 3 is density dependent if the gaseous solvent is changed. In such a case the extrapolated value to the zero-density limit (J
o) will remain the same. For this reason, only the J
o measurements can be recommended as the experimental standards for any comparison with the results of theoretical studies.
Finally, let us demonstrate the benefits of accurate experimental J
o values for quantum-chemistry calculations. As shown in
Table 1, the spin-spin coupling constants for 1,2-
13C-acetylene are solvent dependent. 1,2-
13C-acetylene gives an AA´XX´ NMR spectrum of which the AA´ and XX´ parts have separately been monitored in the gas phase by the
1H and
13C NMR methods [
12]. Xenon (Xe) and carbon dioxide (CO
2) have been used as gaseous solvents. It enabled us to observe the
1H and
13C NMR spectra of
13C
2H
2 as a function of Xe (or CO
2) density and after extrapolation to zero density it was possible to determine the four spin-spin coupling constants independent of molecular interactions (J
o).
Table 4 shows the experimental results together with the theoretical coupling constants for acetylene calculated during last few years.
Table 3.
Representative one-bond spin-spin coupling constants measured in the gas phase.
Table 3.
Representative one-bond spin-spin coupling constants measured in the gas phase.
| Compound | Spin-spin coupling | 1J(NN′) [Hz] | Method, temperature | Reference |
|---|
| HD | 2H - 1H | 43.130(15) | 1H, 294 K | cited in ref. [6] |
| CH4 | 13C - 1H | 125.308(20)a | 1H, 300 K | [18] |
| CH4 | 13C - 1H | 125.304(10)a | 13C, 300 K | [18] |
| CH3D | 13C - 1H | 124.953a | 1H, 300 K | [18] |
| CH3D | 13C - 1H | 124.948a | 13C, 300 K | [18] |
| CH3D | 13C - 2H | 19.224a | 13C, 300 K | [18] |
| CHD3 | 13C - 1H | 124.259a | 1H, 300 K | [18] |
| CHD3 | 13C - 1H | 124.262a | 13C, 300 K | [18] |
| CHD3 | 13C - 2H | 19.113a | 13C, 300 K | [18] |
| CD4 | 13C - 2H | 19.056a | 13C, 300 K | [18] |
| CH3Cl | 13C - 1H | 147.5(3) | 1H | [19] |
| (CH3)3N | 13C - 1H | 131.5(2) | 1H | [19] |
| CH3F | 19F - 13C | 160.2(1) | 13C, 298 K | [20] |
| CH2F2 | 19F - 13C | 232.7(1) | 13C, 298 K | [20] |
| CHF3 | 19F - 13C | 272.4(1) | 13C, 298 K | [20] |
| CF4 | 19F - 13C | 259.4(1) | 13C, 298 K | [20] |
| PF3 | 31P - 19F | 1402(1)a | 19F, 298 K | [13] |
| SiH4 | 29Si - 1H | -201.9(1)a | 1H, 298 K | [13] |
| SiH4 | 29Si - 1H | -201.3(4)a | 1H, 298 K | [11] |
| SiHD3 | 29Si - 1H | -199.9(4)a | 1H, 298 K | [11] |
| SF6 | 33S - 19F | 250.1(4)a | 33S, 298 K | [21] |
Table 4.
Comparison of calculated and observed spin-spin coupling constants [Hz] for 1,2-13C-acetylene at 300 K.
Table 4.
Comparison of calculated and observed spin-spin coupling constants [Hz] for 1,2-13C-acetylene at 300 K.
| J0(300K) | Calculated | Observed |
|---|
| Ref. [22]a | Ref. [7,8]a | Ref. [23]a | Ref.[12] |
|---|
| 1J0(13C-13C) | 170.9 | 179.74 | 174.42 | 174.78 |
| 1J0(13C-1H) | 237.0 | 259.81 | 249.27 | 247.56 |
| 2J0(13C-1H) | 46.4 | 48.02 | 49.38 | 50.14 |
| 3J0(1H-1H) | 9.5 | 10.04 | 9.53 | 9.62 |
The first column of results was obtained by Kaski et al. [
22] in 1998, the second set comes the elaborate study performed by Wigglesworth et al. [
7,
8] in 2000 and the third column presents the calculations done by Jaszuński and Ruud [
23] in 2001. An improvement in the accuracy of
ab initio calculations of spin-spin coupling is well seen in
Table 4 due to the presence of the experimental J
o values for acetylene. It is also true that this comparison is possible because the rovibrational corrections have carefully been calculated by Wigglesworth et al. [
7,
8]. It is worth noting that the step (1) - (2) in Fig. 1 can be completed only by advanced calculations. NMR measurements of J
o constant as a function of temperature can partially verify the latter calculations but molecules at the equilibrium geometry will never be available for experimental investigations. As seen, experimental and theoretical studies are complementary in the investigations of spin-spin coupling constants for molecules.