Customized Multiwavelets for Planetary Gearbox Fault Detection Based on Vibration Sensor Signals
Abstract
:1. Introduction
2. The Theory of Multiwavelets and the Symmetric Lifting Schemes
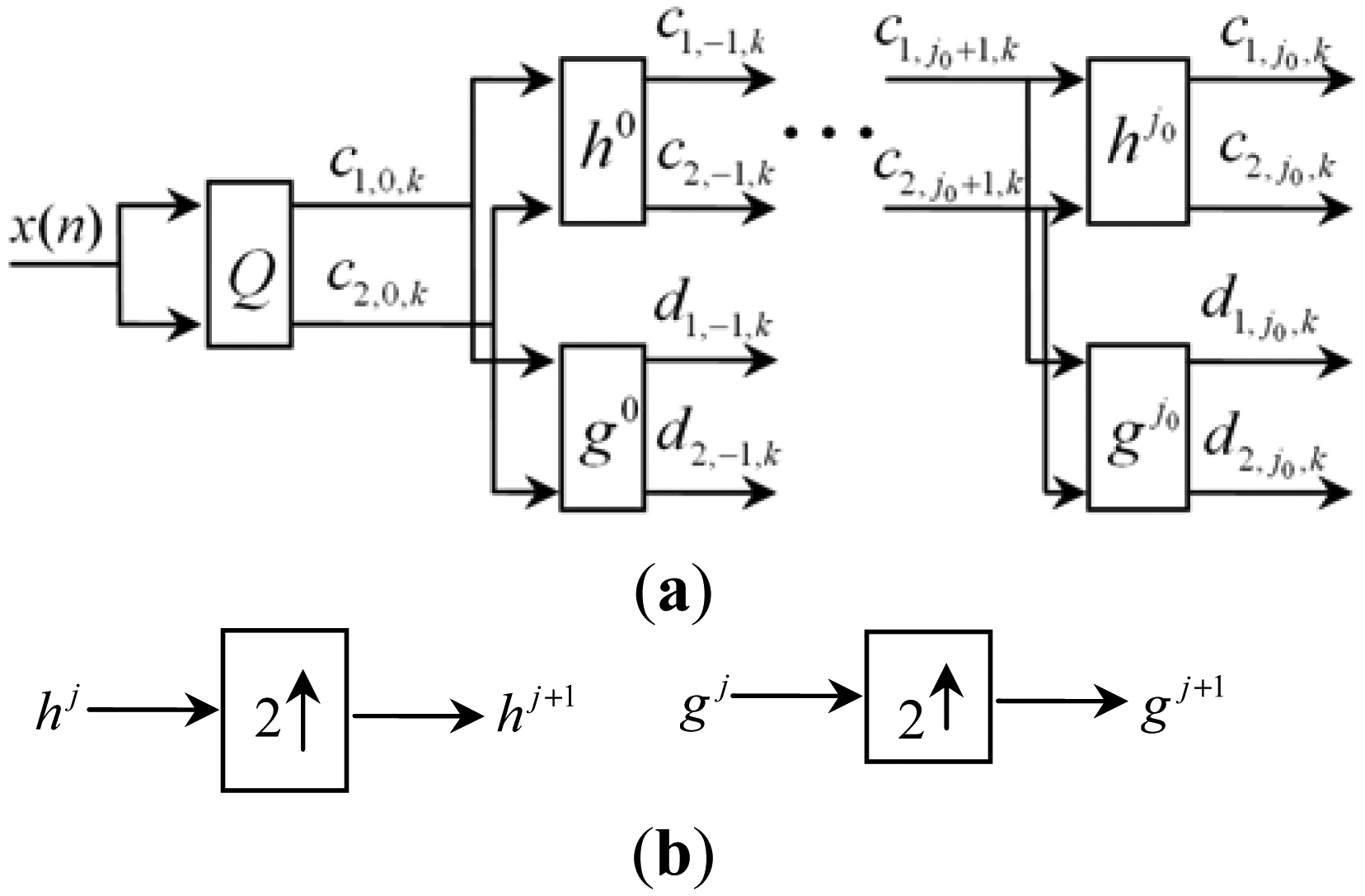
2.1. Multiwavelet Transform
2.2. Multiwavelet Lifting Scheme
Theorem 2.1
Definition 2.2
2.3. The Symmetric Lifting Scheme
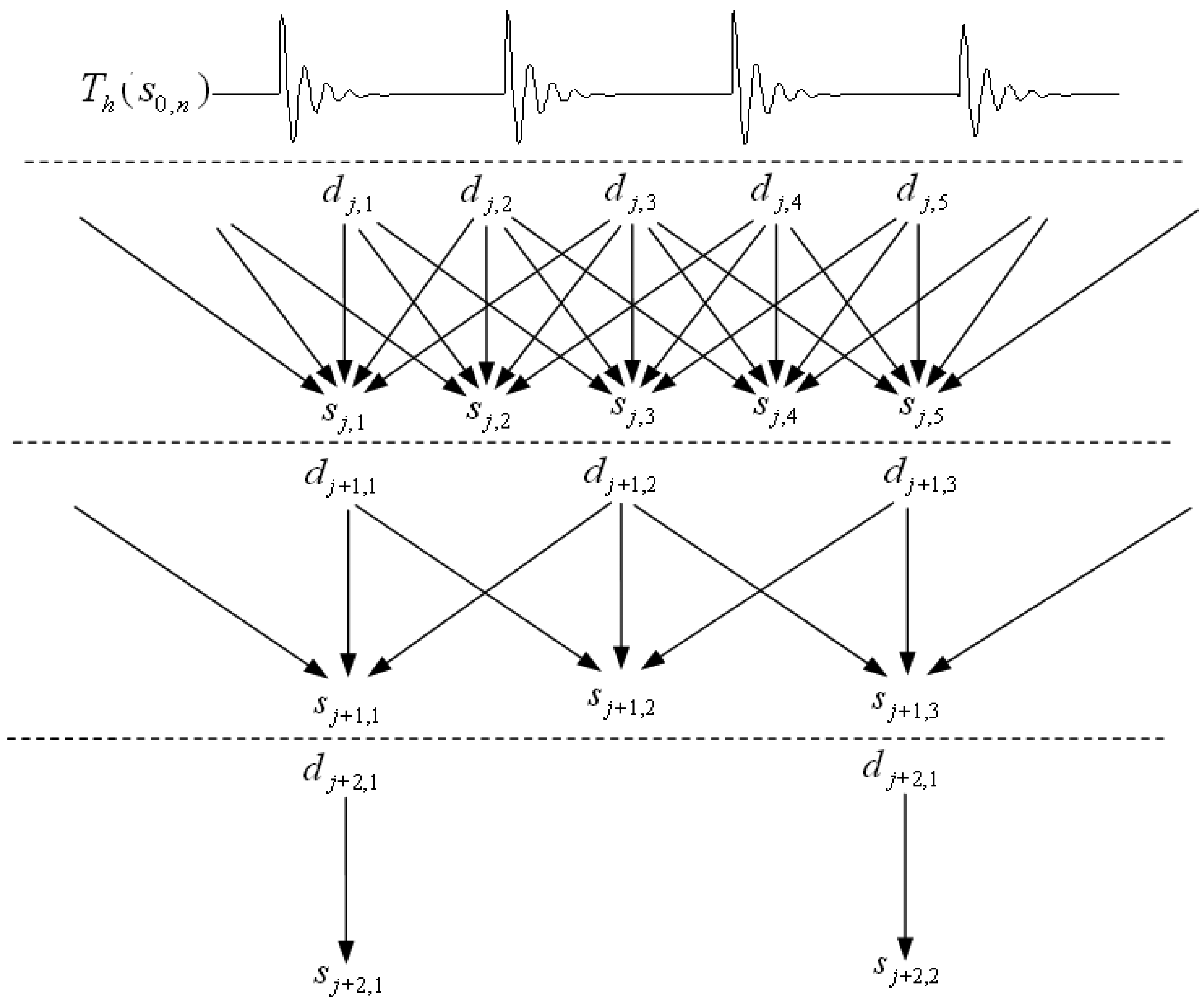
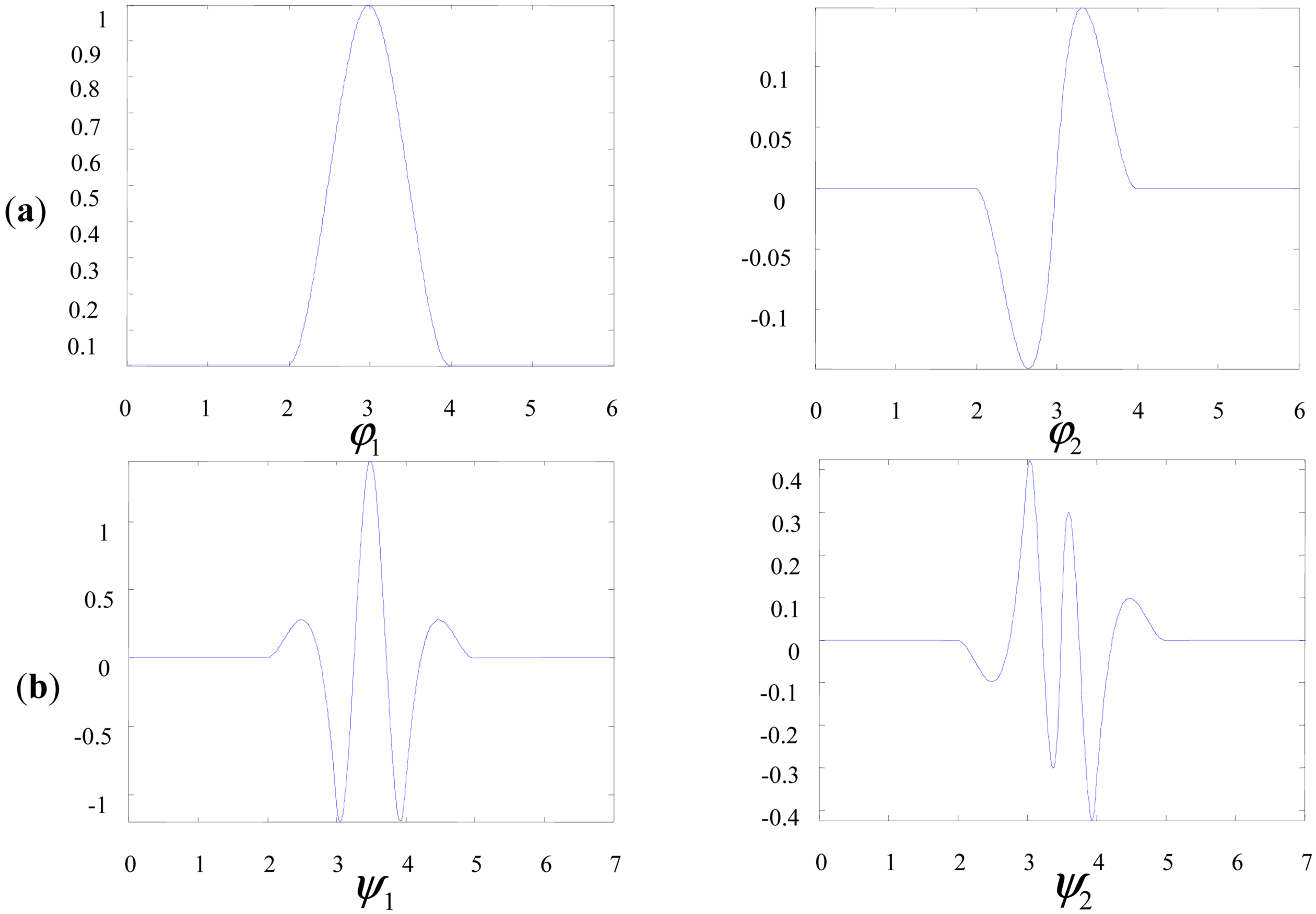
2.4. Redundant Multiwavelet Transform
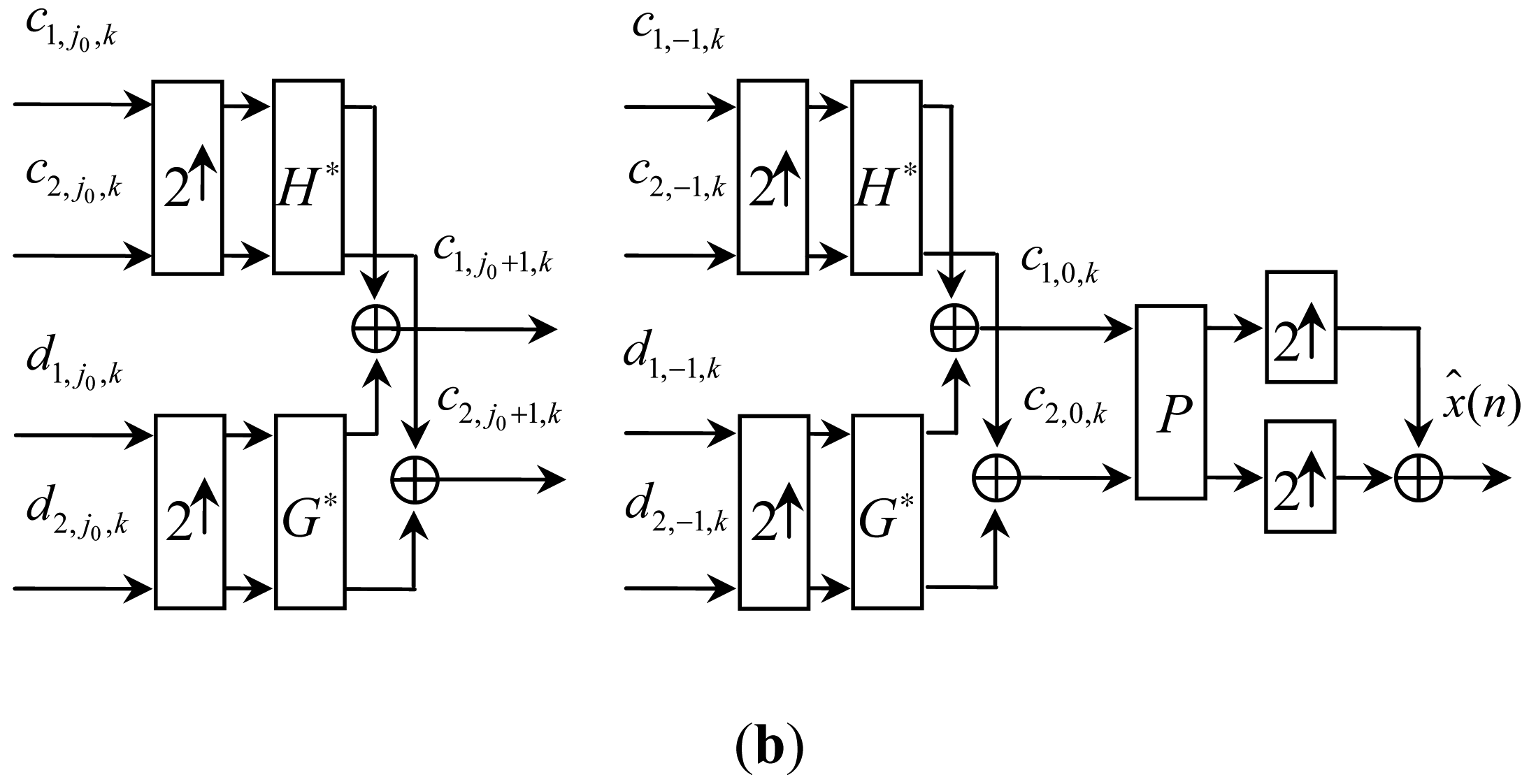
3. Redundant Symmetric Lifting Schemes and the Improved Neighboring Coefficients
3.1. Improved Neighboring Coefficients Denoising
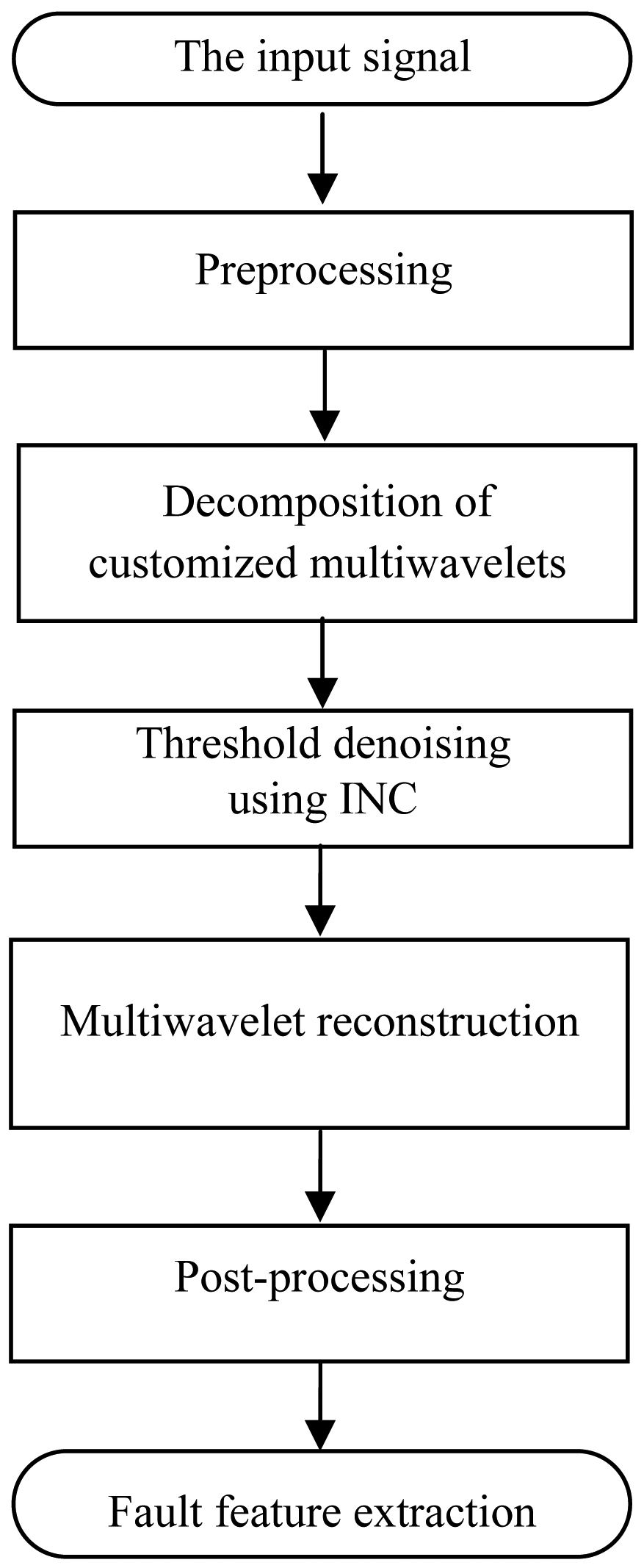
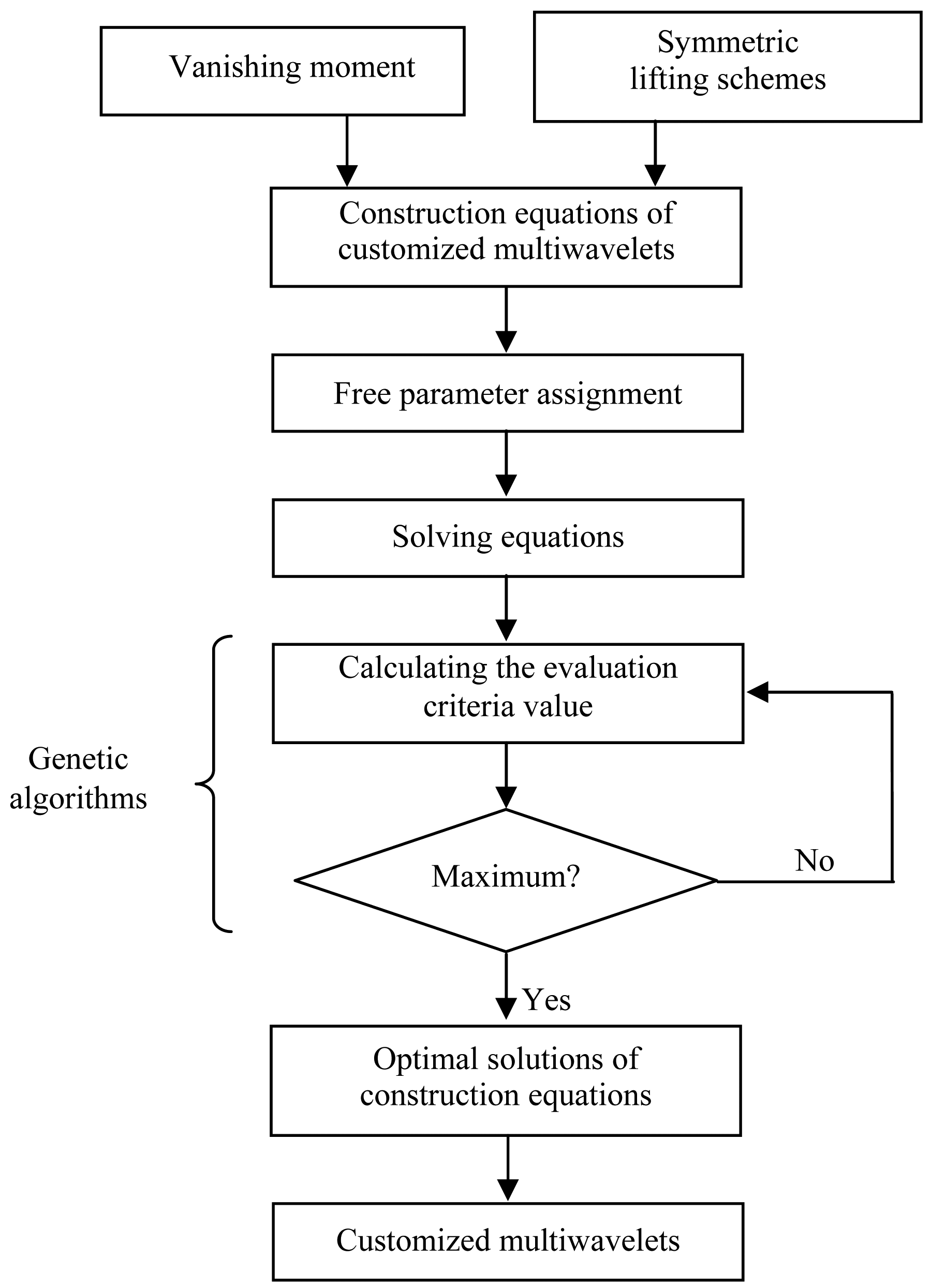
3.2. The Proposed Method Using Customized Multiwavelets and the Improved Neighboring Coefficients
- Preprocessing method is performed to translate the one-stream input signal into multiple streams.
- The multiple streams are decomposed by using the customized multiwavelets.
- Apply INC to shrink the multiwavelet coefficients.
- The thresholded multiwavelet coefficients are reconstructed.
- Post-processing method is performed to translate the multiple streams into one-stream. The denoising result is obtained to detect the fault features.
- Initialize the free parameters {f1,f2,…fNf}.
- Substitute {f1,f2,…fNf} into matrix MB and make the matrix satisfy Rank(MB) = p′−p.
- Compute the lifting coefficients and get T(z) and S(z).
- Decompose the signal with new multiwavelet.
- Compute KE of the detail coefficients and compare it with the maximum value.
- Generate the more optimal values of the free parameters and return to step 2), otherwise finish the computation.
4. Experimental Results
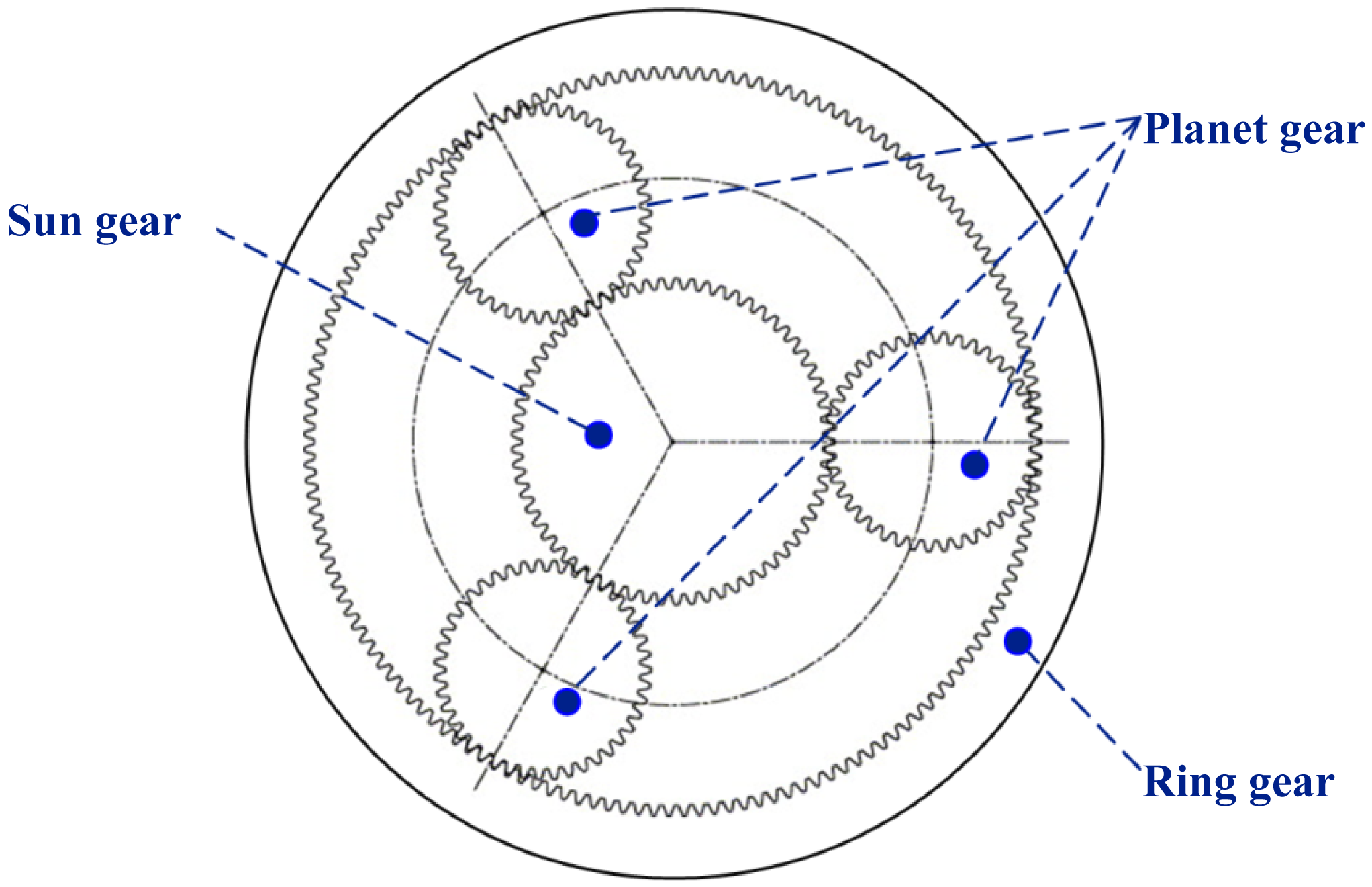
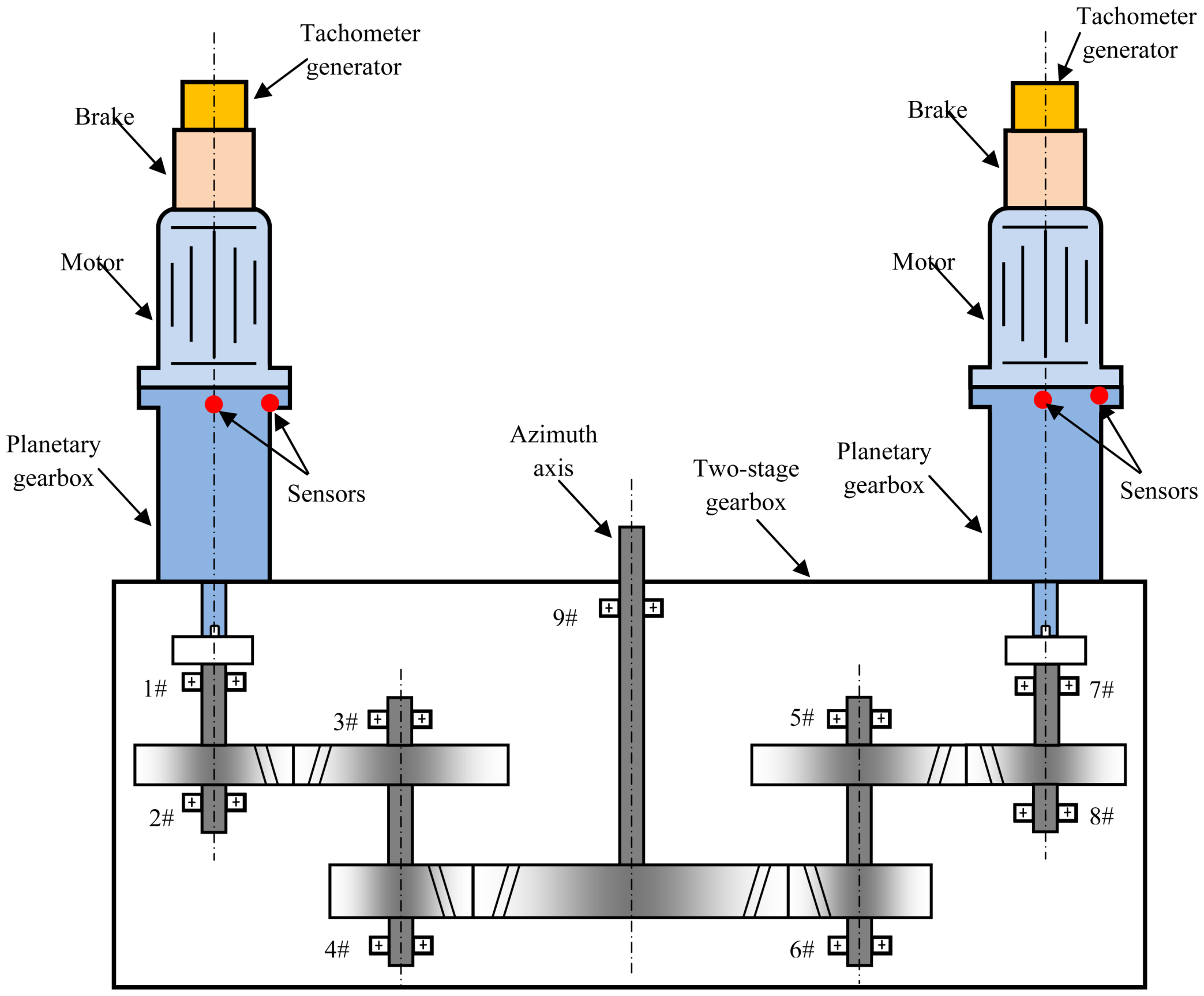
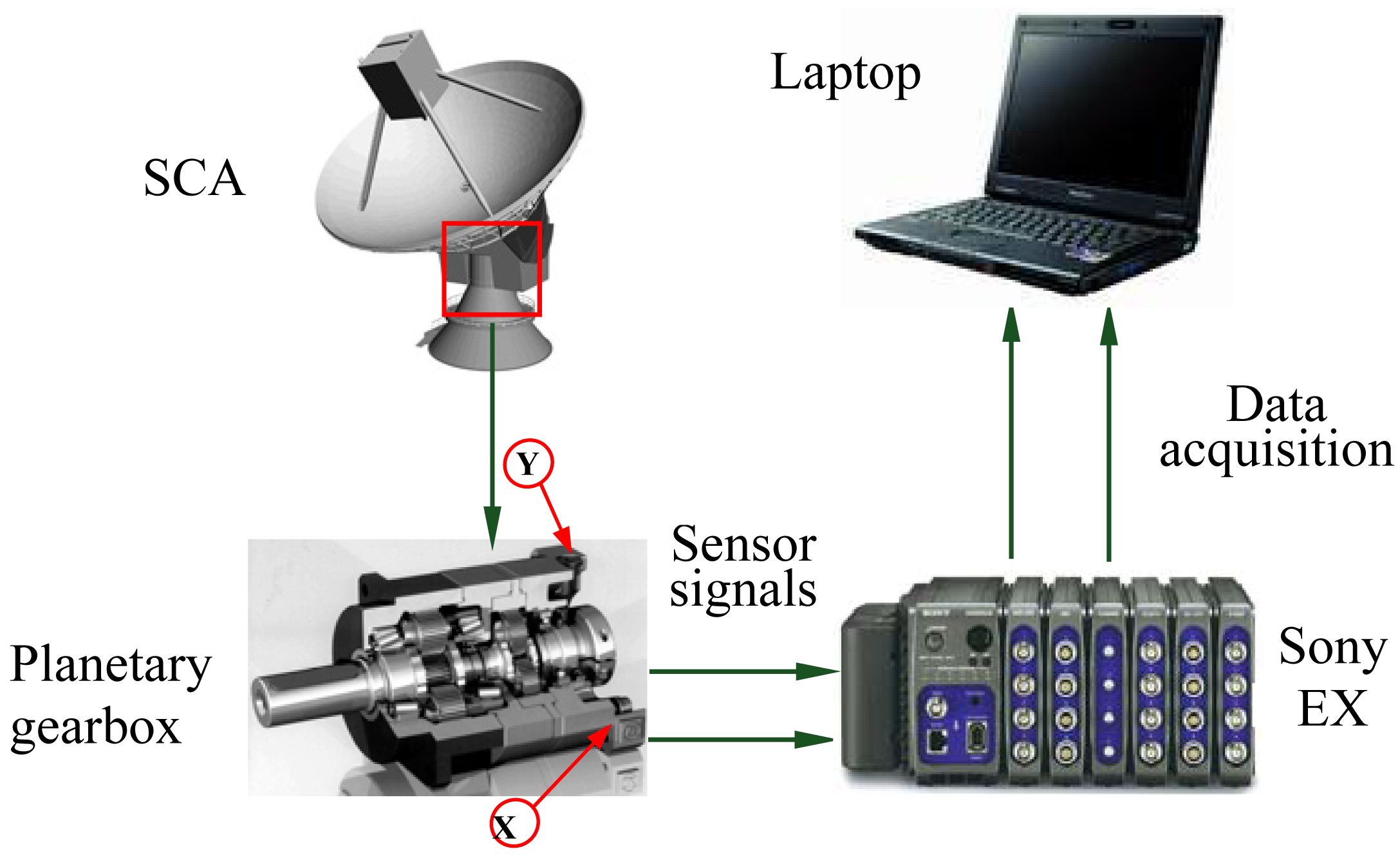
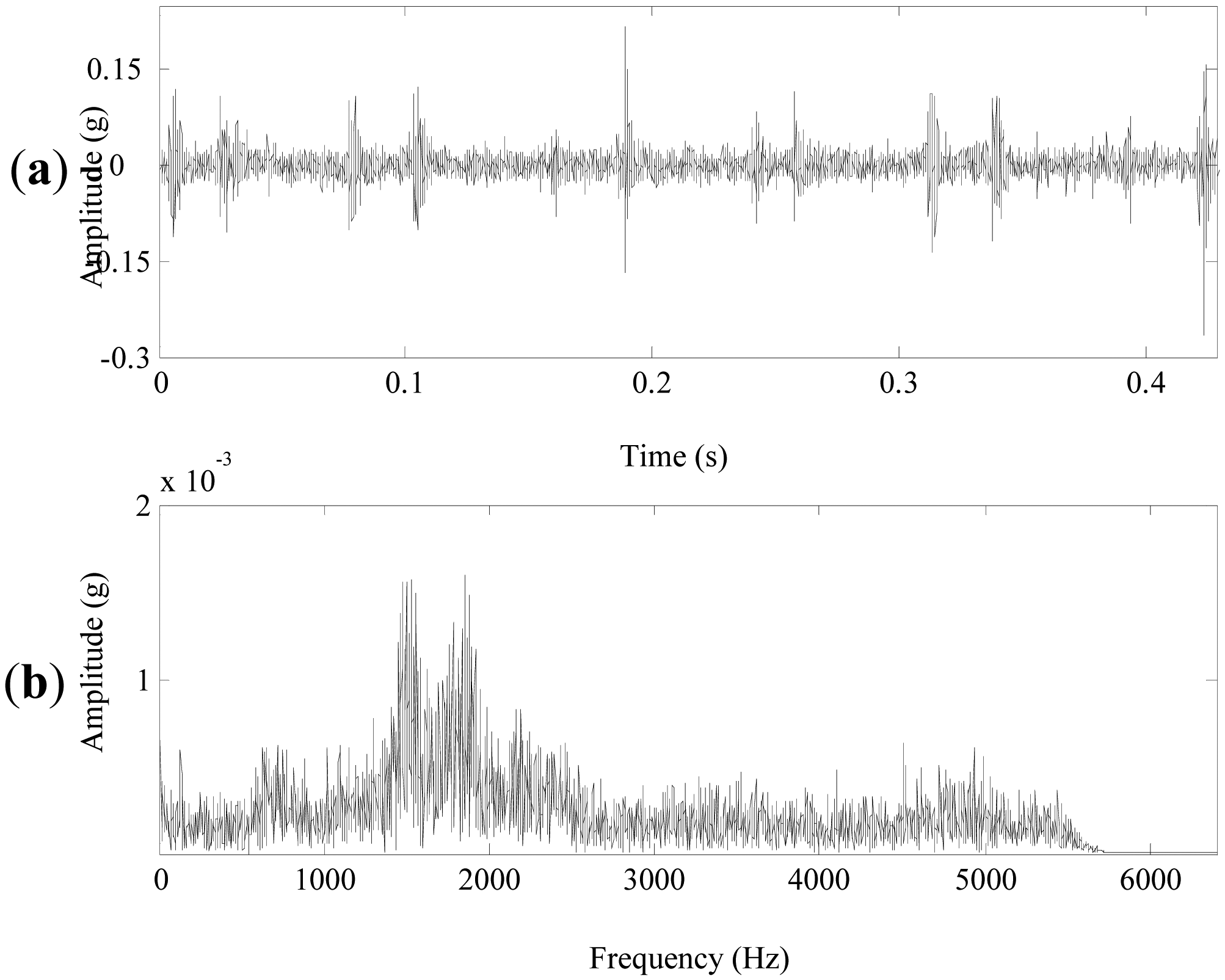
4.1. Experimental Setup and Data Acquisition
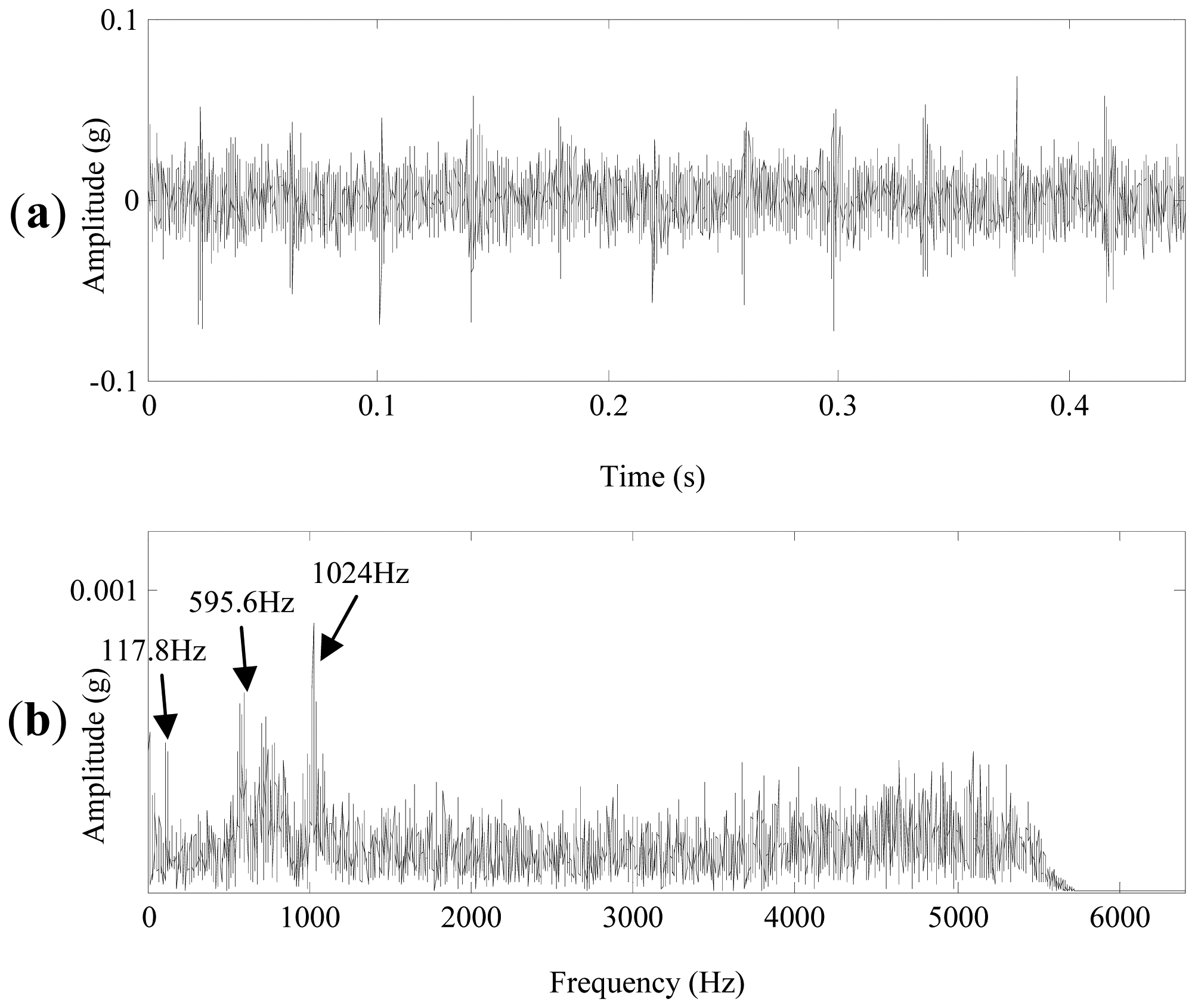
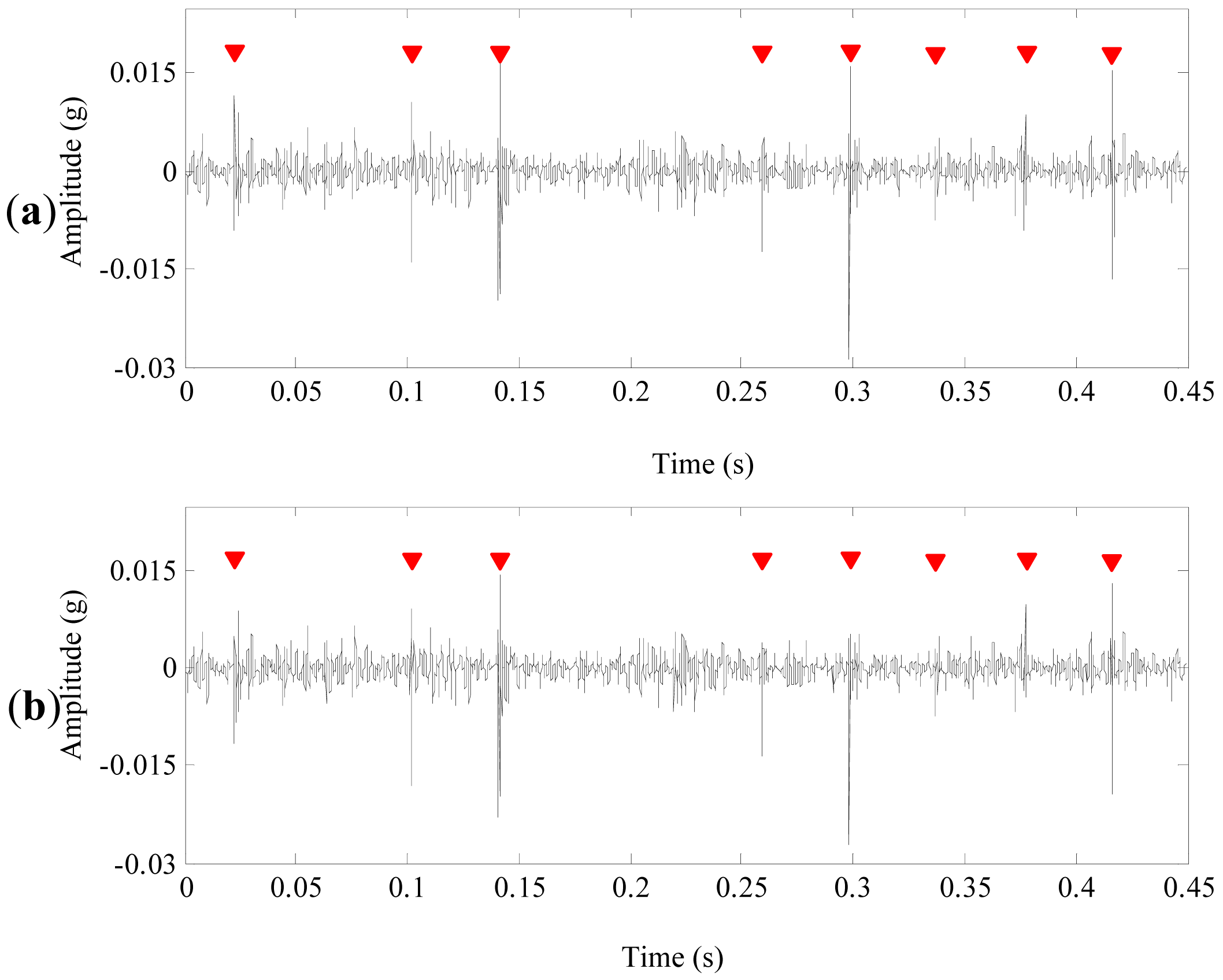
4.2. The Experimental Results of the Normal Planetary Gearbox
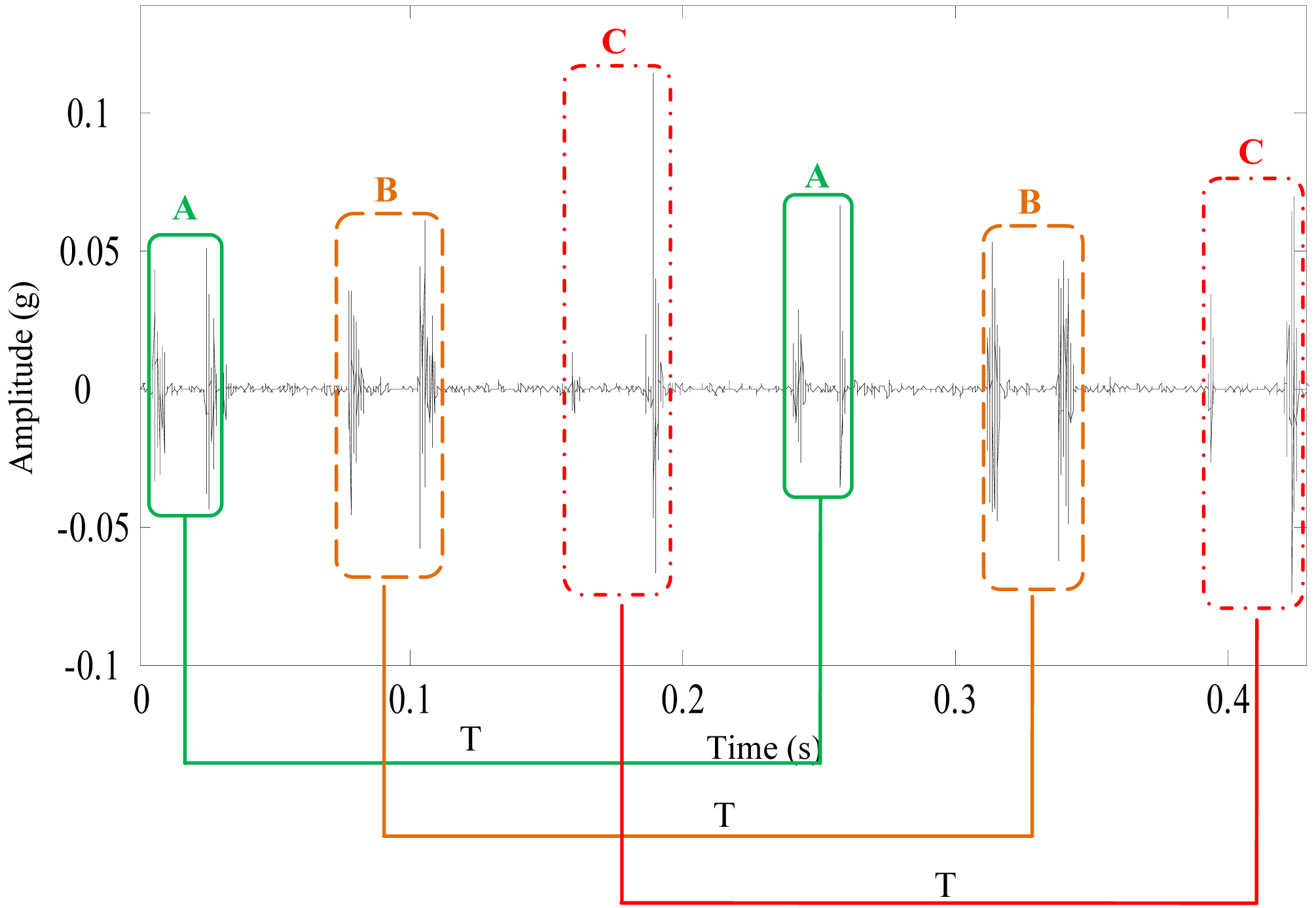
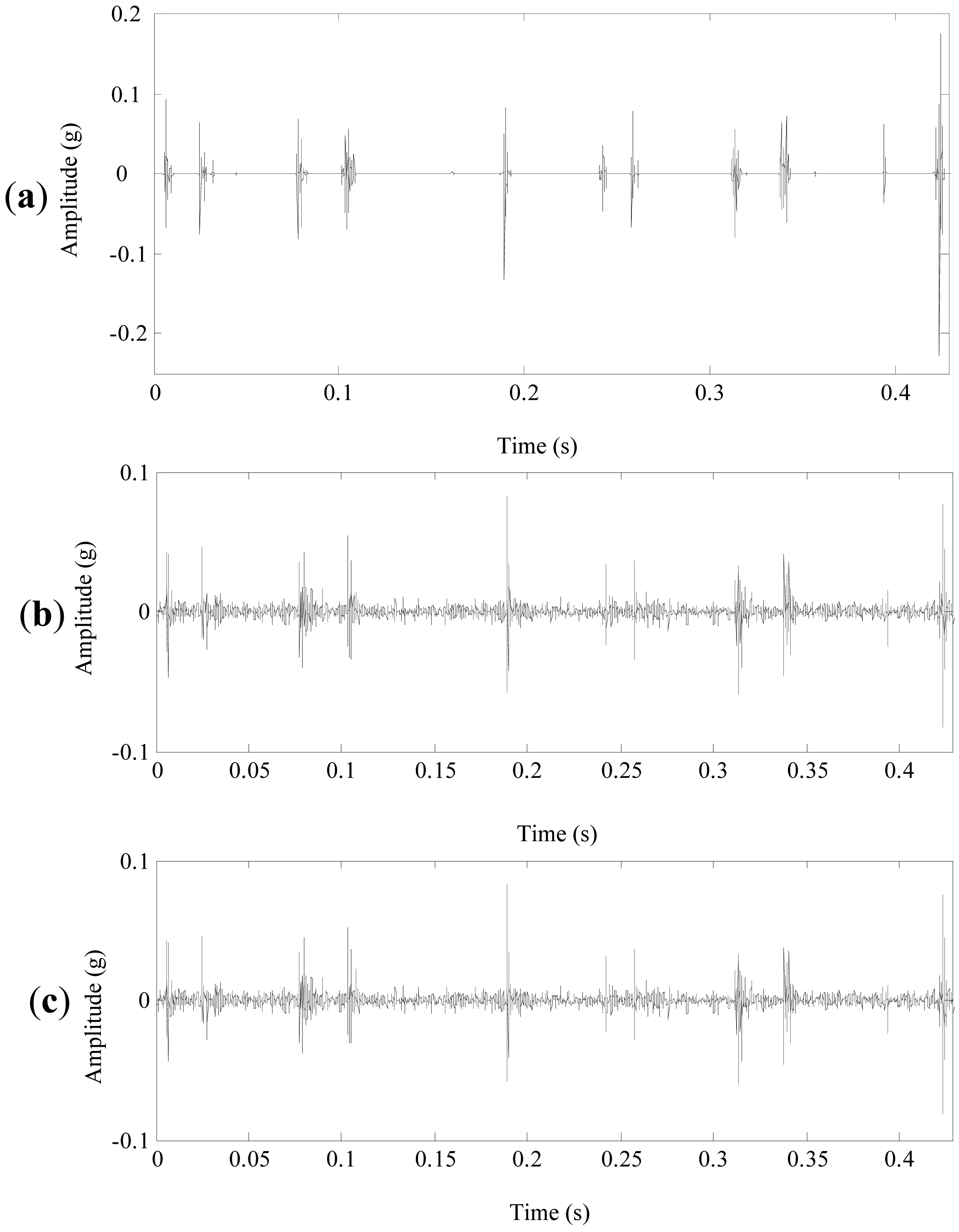
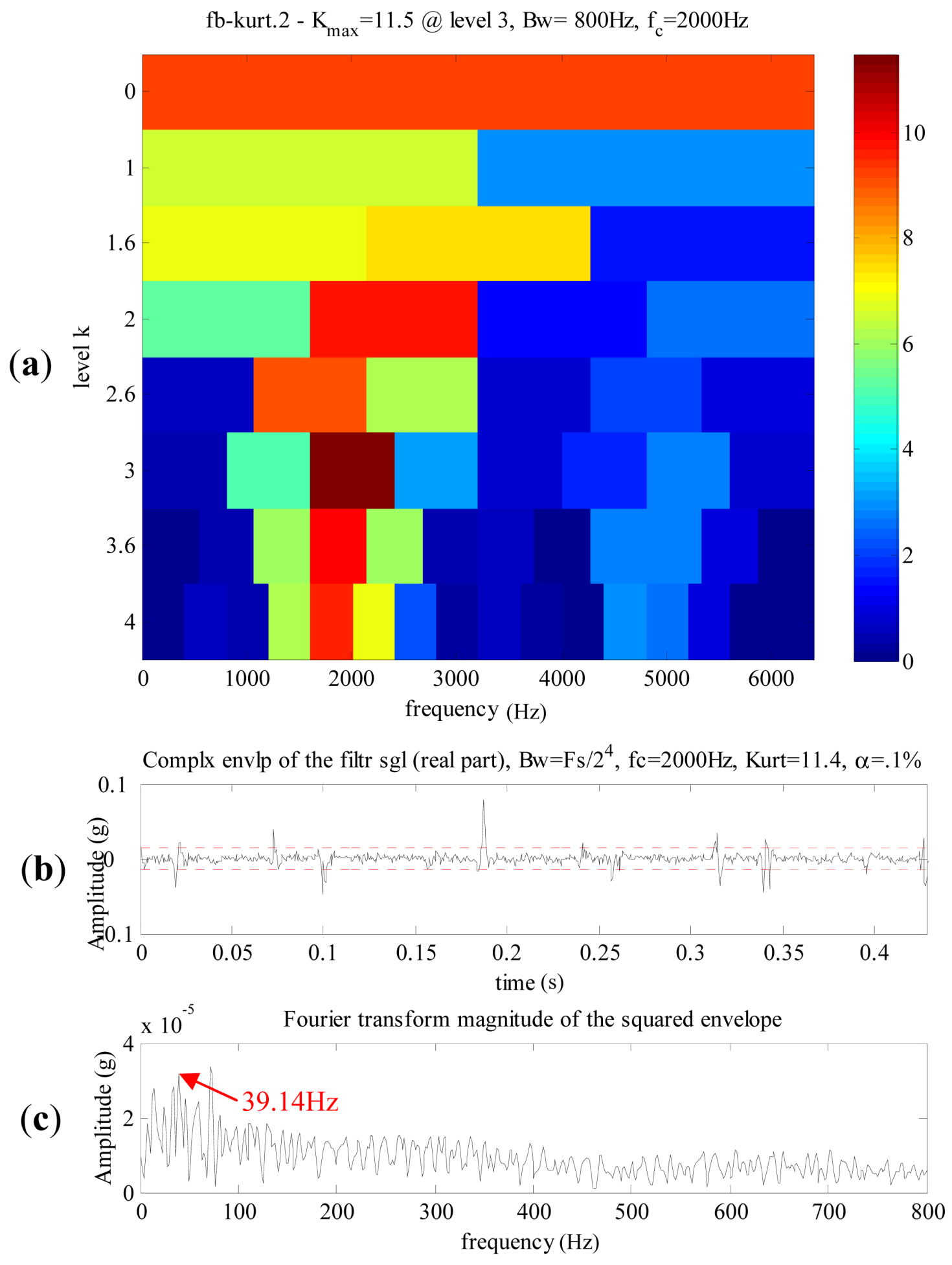
4.3. The Analysis Results of the Defective Planetary Gearbox
4.4. Results and Discussion
- From the planetary gearbox fault detections, it can be seen that multiwavelet denoising methods can effectively eliminate noise and improve the signal-to-noise ratio so as to outstand the fault features. Besides, the denoising methods using customized multiwavelets [shown in Figures 11(b) and 16(a) ] have a better result than the denoising methods using GHM multiwavelet. However, only the proposed method using the customized multiwavelets and the improved neighboring coefficients [shown in Figures 11(a) and 15] could effectively enhance the fault features. Thus, the appropriate multiwavelet functions for feature separation and the optimal threshold and length of neighbors for denoising are both important, neither of them could be dispensed with in planetary gearbox fault detections.
- The computing times of these methods in planetary gearbox fault detections are listed in Table 3. All the tests of time consumption are carried out and recorded in Matlab software with the same computer platform of Intel Pentium Dual CPU E5200 @2.5 GHz and DDR2 memory 2 G. As it is known that every coin has two sides, the optimization of the customized multiwavelets has to take some time for the effective planetary gearbox fault detections. For example, a signal of length 4096 has to take about 2 minutes using the proposed method. In practice, the customized multiwavelets are suitable for a certain kind of fault. For example, the customized multiwavelets proposed in this paper are effective for detecting the pitting faults of other gears in planetary gearboxes, without constructing customized multiwavelets again. Therefore, the calculation efficiency of the proposed method is similar to other denoising methods using standard multiwavelets after the customized multiwavelets have been constructed.
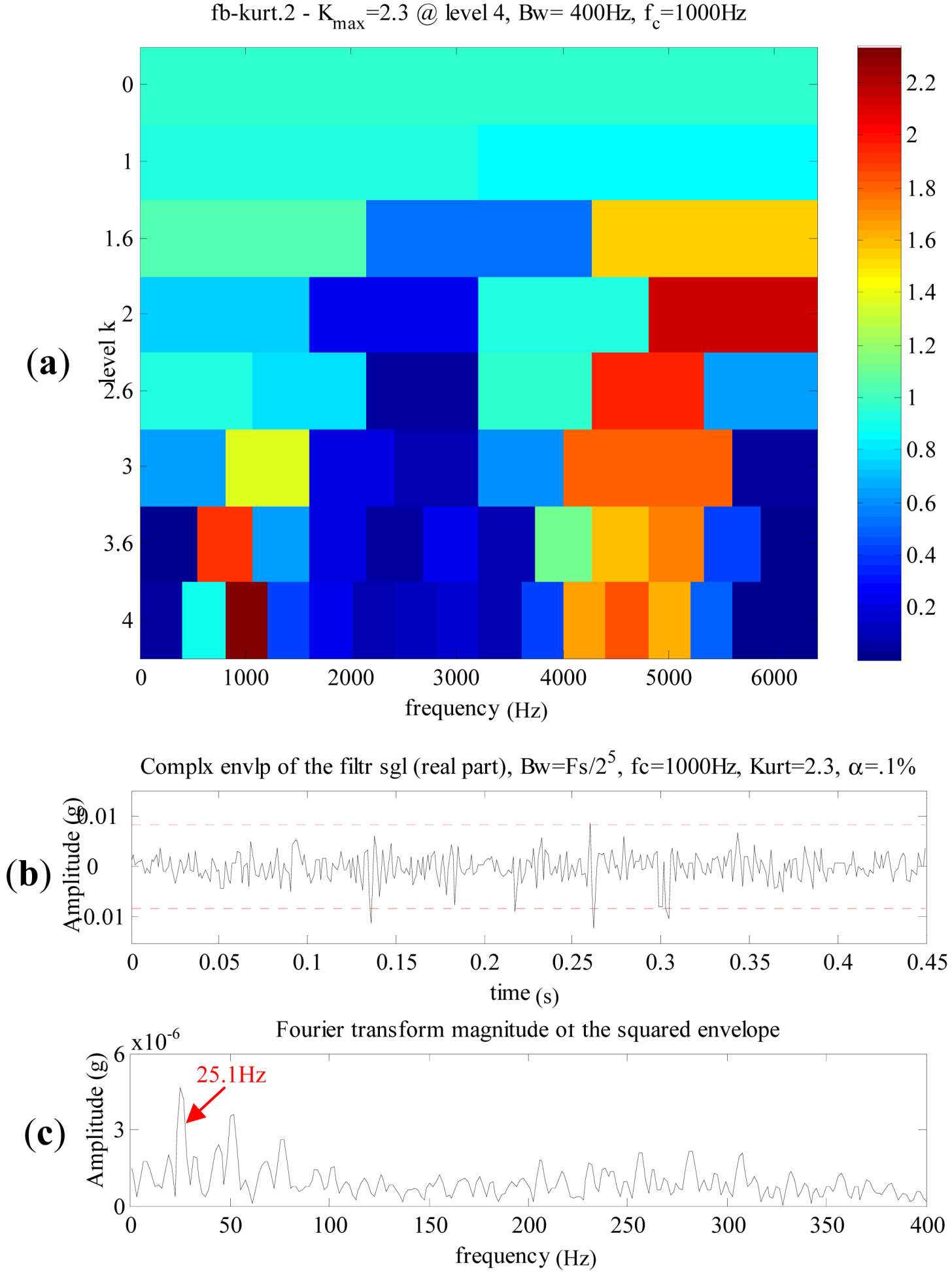
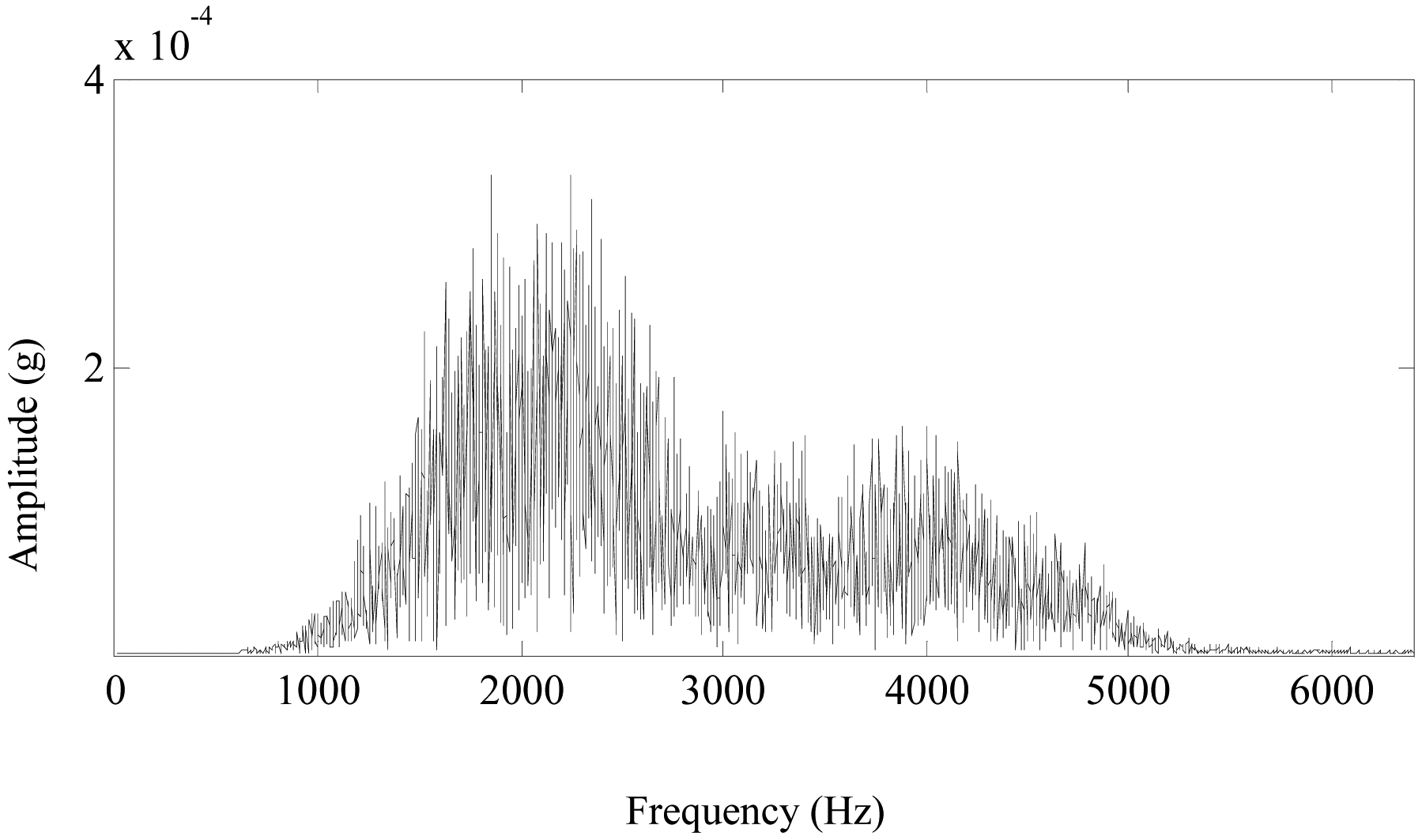
- As shown in Figure 14, the denoising result in time domain could accurately represent the shock impulses caused by the pittings of the sun gear. Its Fourier spectrum is shown in Figure 19, the frequency components mainly distribute at 1,000–3,000 Hz. The rotating frequency or the meshing frequency and their harmonics of the planetary gearbox cannot be detected in the spectrum. The spectrum is not so distinct as the denoising result in the time domain of Figure 14. Besides, the spectrums of denoising results using other methods are similar to the spectrum in Figure 19. Therefore, FFT is not effective to detect the pittings of the sun gear in the planetary gearbox.
5. Conclusions
Acknowledgments
References
- Yan, R.Q.; Gao, R.X. Rotary machine health diagnosis based on empirical mode decompositon. J. Vib. Acoust. 2008, 130, 1–12. [Google Scholar]
- James, M. Fourier series analysis of epicyclic gearbox vibration. J. Vib. Acoust. 2002, 124, 150–152. [Google Scholar]
- Vecchiato, D. Tooth contact analysis of a misaligned isostatic planetary gear train. Mech. Mach. Theory 2006, 41, 617–631. [Google Scholar]
- Lei, Y.G.; Kong, D.T.; Lin, J.; Zuo, M.J. Fault detection of planetary gearboxes using new diagnostic parameters. Meas. Sci. Technol. 2012. [Google Scholar] [CrossRef]
- Blunt, D.M.; Keller, J.A. Detection of a fatigue crack ina UH-60A planet gear carrier using vibration analysis. Mech. Syst. Signal Process. 2006, 20, 2095–2111. [Google Scholar]
- Mosher, M. Understanding Vibration Spectra of Planetary Gear Systems for Fault Detection. Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003.
- Hines, J.A.; Muench, D.S.; Keller, J.A.; Garga, A.K. Effects of Time-Synchronous Averaging Implementations on HUMS Features for UH-60A Planetary Carrier Cracking. Proceedings of the American Helicopter Society 61st Annual Forum, Grapevine, TX, USA, 1–3 June 2005.
- Inalpolat, M.; Kahraman, A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets. J. Sound Vib. 2009, 323, 677–696. [Google Scholar]
- Barszcz, T.; Randall, R.B. Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine. Mech. Syst. Signal Process. 2009, 23, 1352–1365. [Google Scholar]
- Bartelmus, W.; Zimroz, R. A new feature for monitoring the condition of gearboxes in non-stationary operating conditions. Mech. Syst. Signal Process. 2009, 23, 1528–1534. [Google Scholar]
- Bartelmus, W.; Zimroz, R. Vibration condition monitoring of planetary gearbox under varying external load. Mech. Syst. Signal Process. 2009, 23, 246–257. [Google Scholar]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar]
- Lei, Y.G.; Lin, J.; He, Z.J; Kong, D.T. A method based on multi-sensor data fusion for fault detection of planetary gearboxes. Sensors 2012, 12, 2005–2017. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Keinert, F. Wavelets and Multiwavelets; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Geronimo, J.S.; Hardin, D.P.; Massopust, P.R. Fractal functions and wavelet expansions based on several scaling functions. J. Approx. Theory 1994, 78, 373–401. [Google Scholar]
- Geronimo, J.S.; Hardin, D.P.; Massopust, P.R. Construction of orthogonal wavelets using fractal interpolation functions. SIAM J. Math. Anal. 1996, 27, 1158–1192. [Google Scholar]
- Chui, C.K.; Lian, J.A. A study of orthonormal multiwavelets. Appl. Numer. Math. 1996, 20, 273–298. [Google Scholar]
- Strela, V.; Strang, G. Finite Element Multiwavelets. In Approximation Theory, Wavelets and Applications; Kluwer: Boston, MA, USA, 1995; pp. 485–496. [Google Scholar]
- Khadem, S.E.; Rezaee, M. Development of vibration signature analysis using multiwavelet systems. J. Sound Vib. 2003, 261, 613–633. [Google Scholar]
- Yuan, J.; He, Z.J.; Zi, Y.Y.; Liu, H. Gearbox fault diagnosis of rolling mills using multiwavelet sliding window neighbouring coefficient denoising and optimal blind deconvolution. Sci. China Ser. E Technol. Sci. 2009, 52, 2801–2809. [Google Scholar]
- Li, Z.; He, Z.J.; Zi, Y.Y.; Jiang, H.K. Rotating machinery fault diagnosis using signal-adapted lifting scheme. Mech. Syst. Signal Process. 2008, 22, 542–556. [Google Scholar]
- Sweldens, W. The lifting scheme: A custom-design construction of biorthogonal wavelets. Appl. Comput. Harmonic Anal. 1996, 3, 186–200. [Google Scholar]
- Sweldens, W. The lifting scheme: A construction of second generation wavelet. SIAM J. Math. Anal. 1998, 29, 511–546. [Google Scholar]
- Wang, X.D.; Zi, Y.Y.; He, Z.J. Multiwavelet construction via an adaptive symmetric lifting scheme and its applications for rotating machinery fault diagnosis. Meas. Sci. Technol. 2009. [Google Scholar] [CrossRef]
- Yuan, J.; He, Z.J.; Zi, Y.Y. Gear fault detection using customized multiwavelet lifting schemes. Mech. Syst. Signal Process. 2010, 24, 1509–1528. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; China Machine Press: Beijing, China, 2003. [Google Scholar]
- Wang, X.D.; Zi, Y.Y.; He, Z.J. Multiwavelet denoising with improved neighboring coefficients for application on rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 285–304. [Google Scholar]
- Xia, X.G.; Geronimo, J.S.; Hardin, D.P.; Suter, B.W. Design of prefilters for discrete multiwavelet transform. IEEE Trans. Signal Process. 1996, 44, 25–35. [Google Scholar]
- Strela, V.; Heller, P.N.; Strang, G.; Topiwala, P.; Heil, C. The application of multiwavelet filter banks to signal and image processing. IEEE Trans. Image Process. 1996, 8, 548–563. [Google Scholar]
- Bradley, A.P. Shift-Invariance in the Discrete Wavelet Transform. Proceedings of the 7th Digital Image Computing: Techniques and Applications, Sydney, Australia, 10–12 December 2003.
- Bulat, J. Image Compression Using Lifted Wavelet Packets. Proceedings of the International Conference on Signals and Electronic Systems, Ustron, Poland, 17–20 October 2000; pp. 137–142.
- Cai, T.T.; Silverman, B.W. Incorporating information on neighboring coefficients into wavelet estimation. Sankhya 2001, 63, 127–148. [Google Scholar]
- Chen, G.Y.; Bui, T.D. Multiwavelets denoising using neighboring coefficients. IEEE Signal Process. Lett. 2003, 10, 211–214. [Google Scholar]
- Lin, J.; Qu, L.S. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar]
- PACS Classification: 89.20.Kk; 89.20.Bb; 07.50.Qx



| Model | Sensitivity (±10%) | Measurement Range | Frequency Range (±10%) | Non-Linerity | Sensing Element |
|---|---|---|---|---|---|
| 333B32 | 100 mv/g | ±50,g pk | 0.5–3,000 Hz | ≤1% | Caremic |
| Type | The first stage | Sun gear tooth number | 12 |
| Planet gear tooth number | 36 | ||
| Ring gear tooth number | 84 | ||
| PLS142-32 | The second stage | Sun gear tooth number | 28 |
| Planet gear tooth number | 28 | ||
| Ring gear tooth number | 84 |
| Method | Time in healthy planetary gearbox (s) (Signal length 5760) | Time in defective planetary gearbox (s) (Signal length 5760) |
|---|---|---|
| Customized multiwavelets with INC | 156.05 (150.81) | 156.05 (150.81) |
| Customized multiwavelet with NC | 155.18 (150.81) | 155.18 (150.81) |
| GHM multiwavelet with INC | 3.79 | 3.79 |
| GHM multiwavelet with NC | 3.71 | 3.71 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sun, H.; Zi, Y.; He, Z.; Yuan, J.; Wang, X.; Chen, L. Customized Multiwavelets for Planetary Gearbox Fault Detection Based on Vibration Sensor Signals. Sensors 2013, 13, 1183-1209. https://doi.org/10.3390/s130101183
Sun H, Zi Y, He Z, Yuan J, Wang X, Chen L. Customized Multiwavelets for Planetary Gearbox Fault Detection Based on Vibration Sensor Signals. Sensors. 2013; 13(1):1183-1209. https://doi.org/10.3390/s130101183
Chicago/Turabian StyleSun, Hailiang, Yanyang Zi, Zhengjia He, Jing Yuan, Xiaodong Wang, and Lue Chen. 2013. "Customized Multiwavelets for Planetary Gearbox Fault Detection Based on Vibration Sensor Signals" Sensors 13, no. 1: 1183-1209. https://doi.org/10.3390/s130101183





