Adaptive PIF Control for Permanent Magnet Synchronous Motors Based on GPC
Abstract
:1. Introduction
2. System Model of PMSM
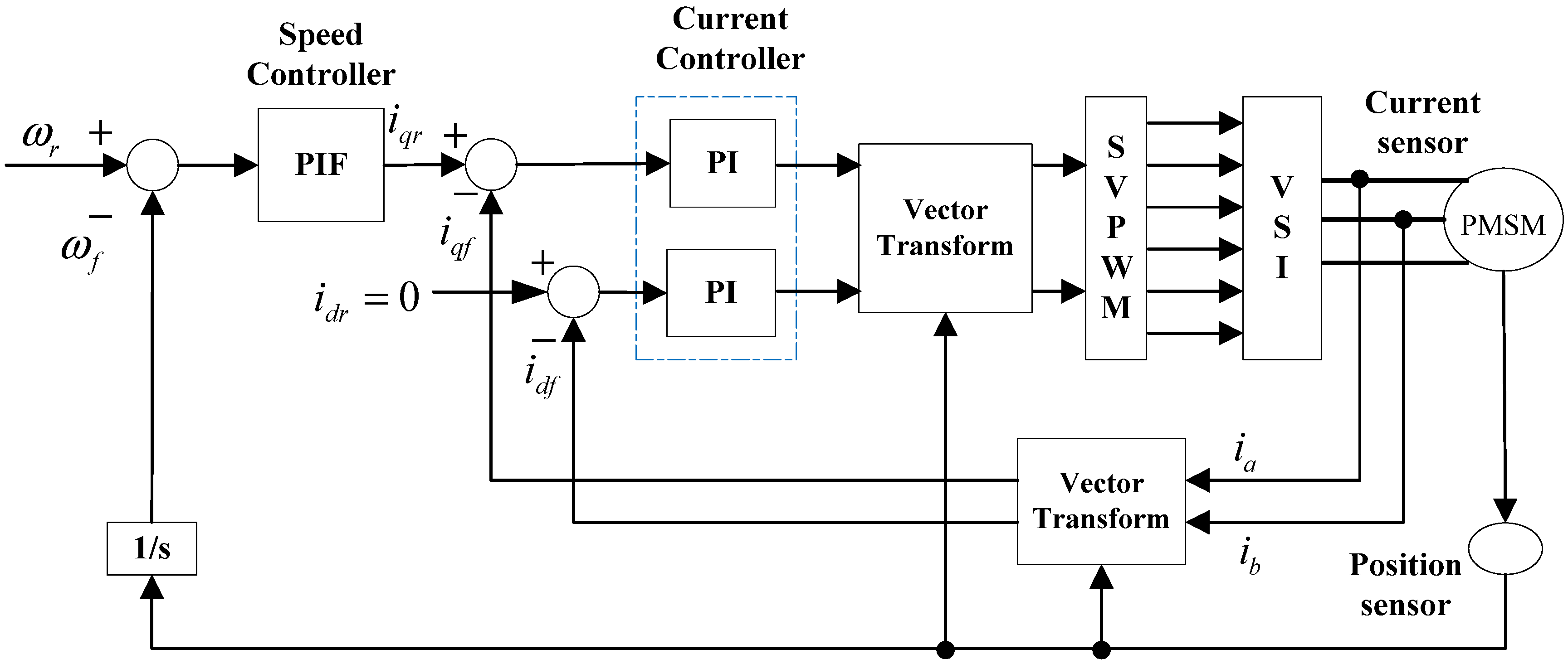
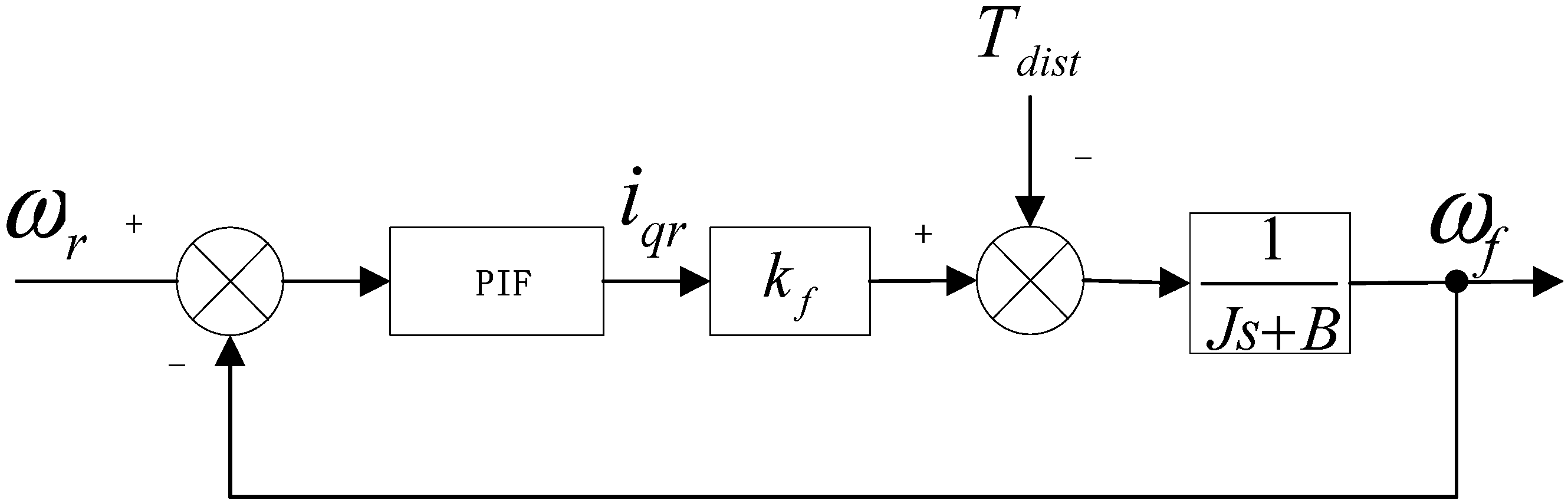
2.1. Speed Control System of PMSM
2.2. Discrete-Time Model and Controller
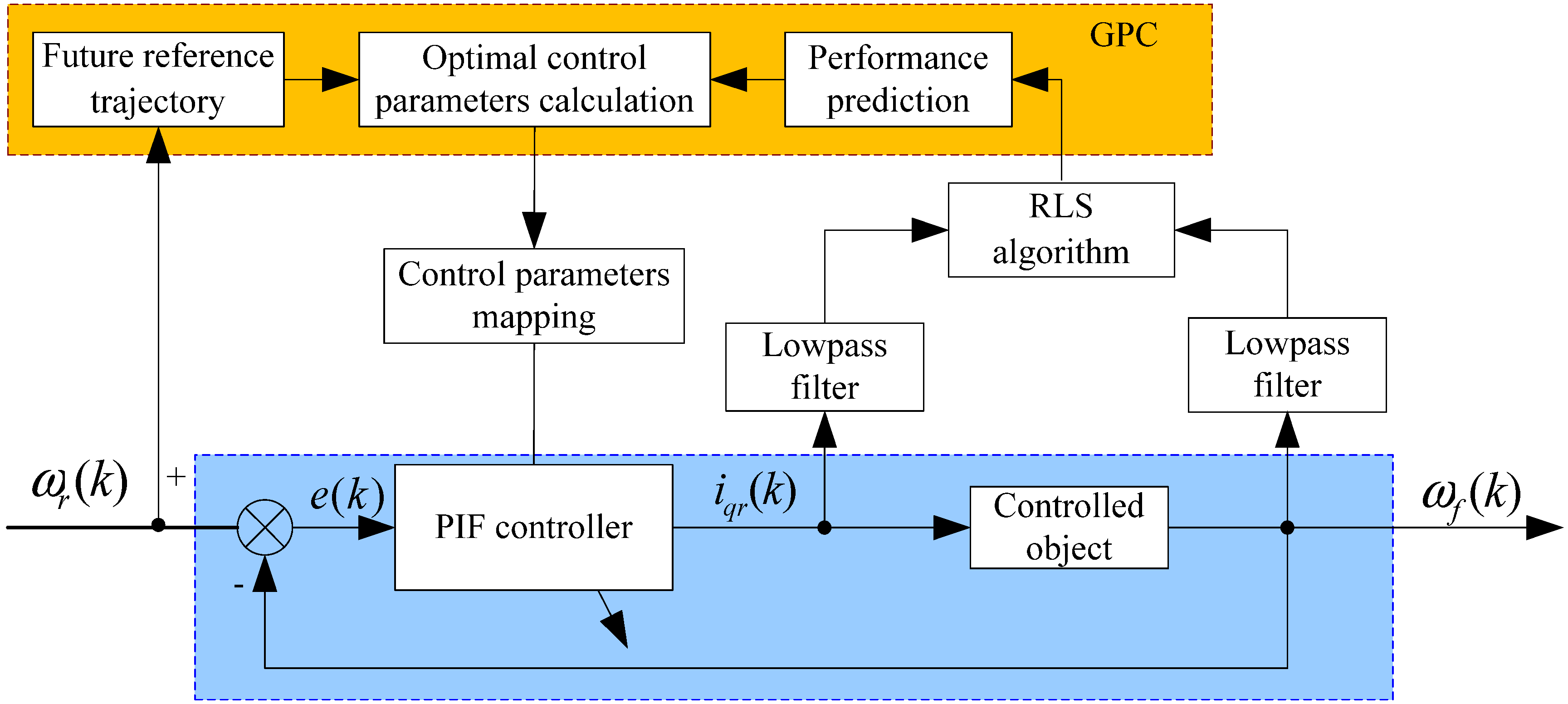
3. The design of Adaptive PIF Controller
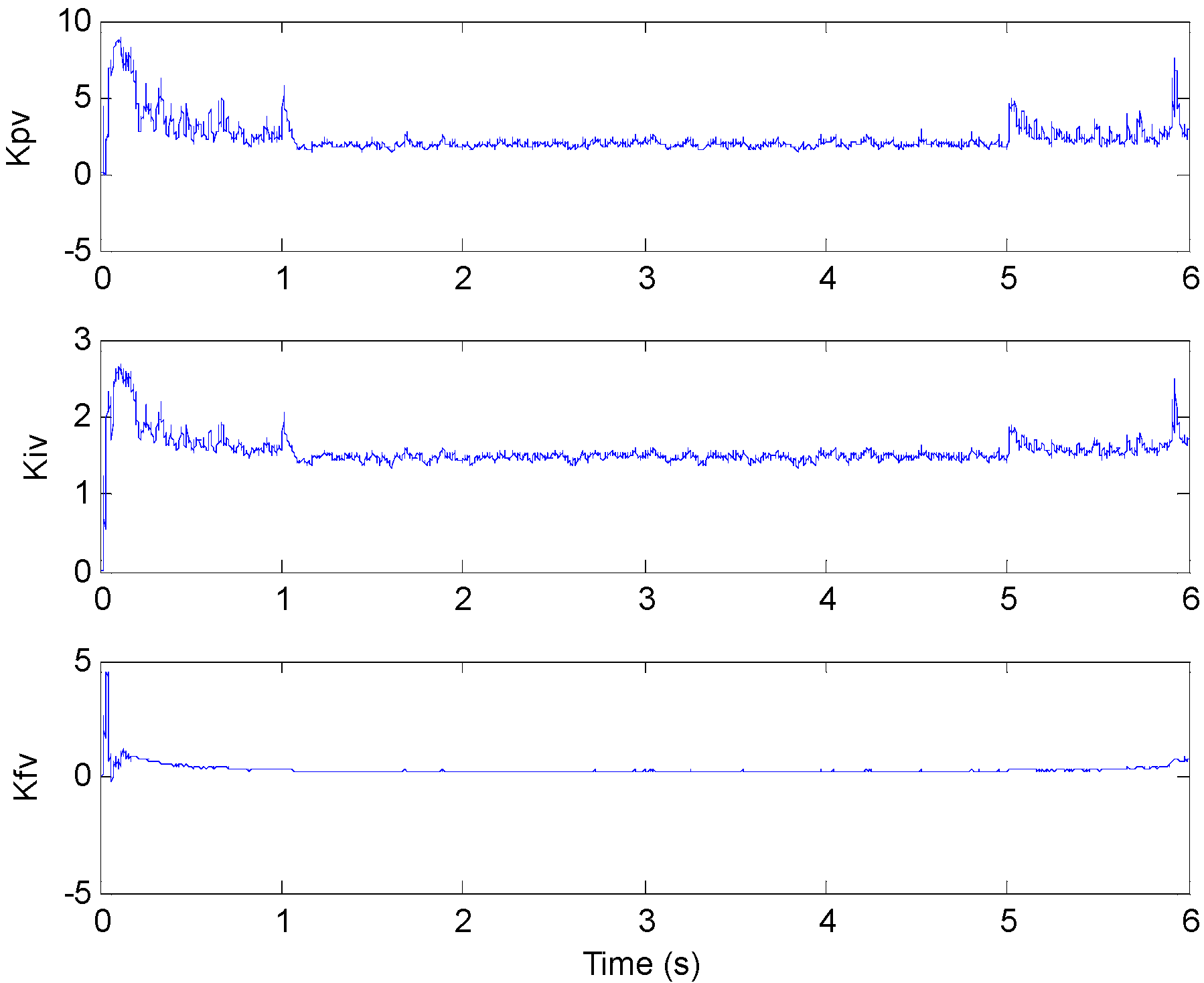
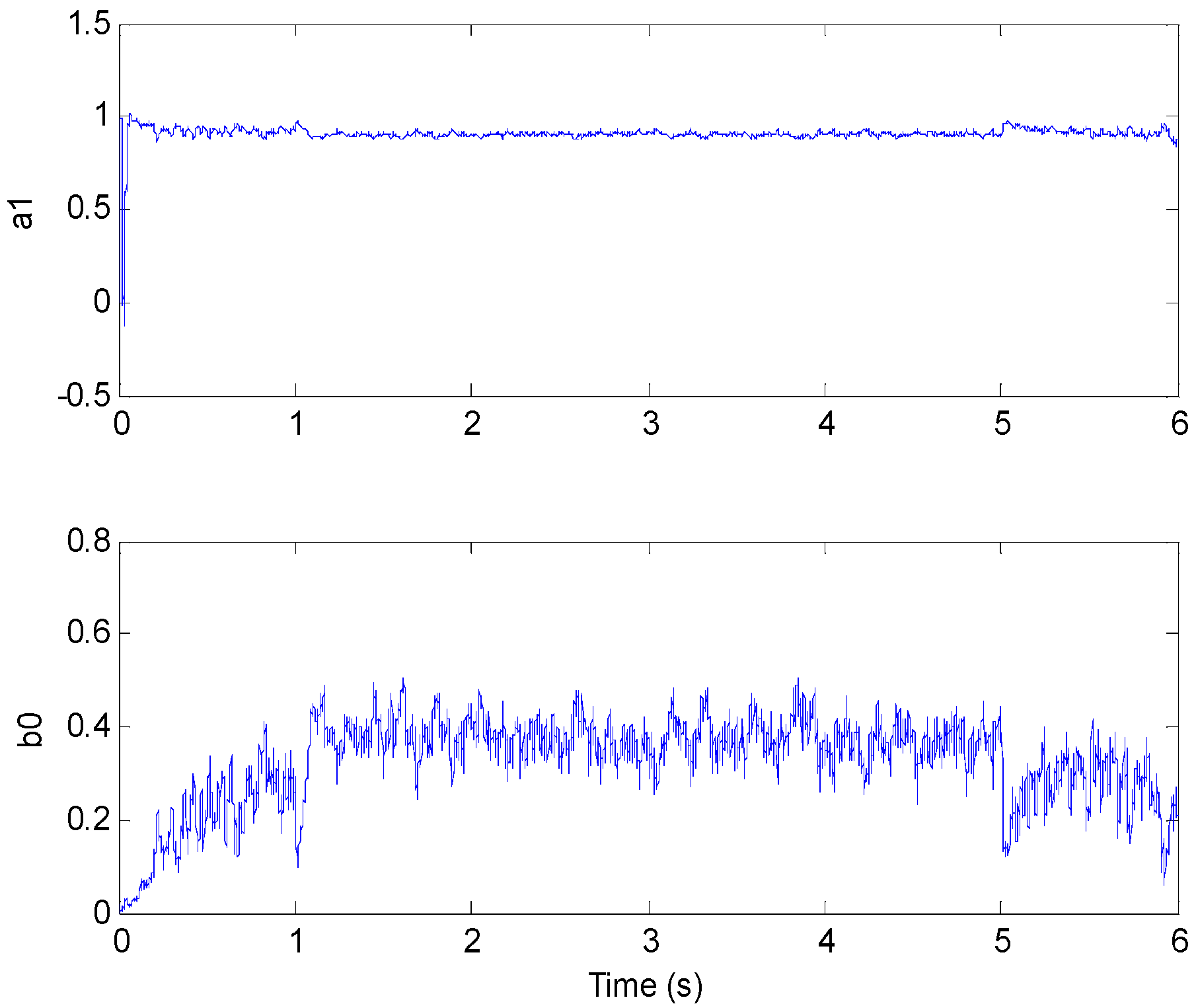
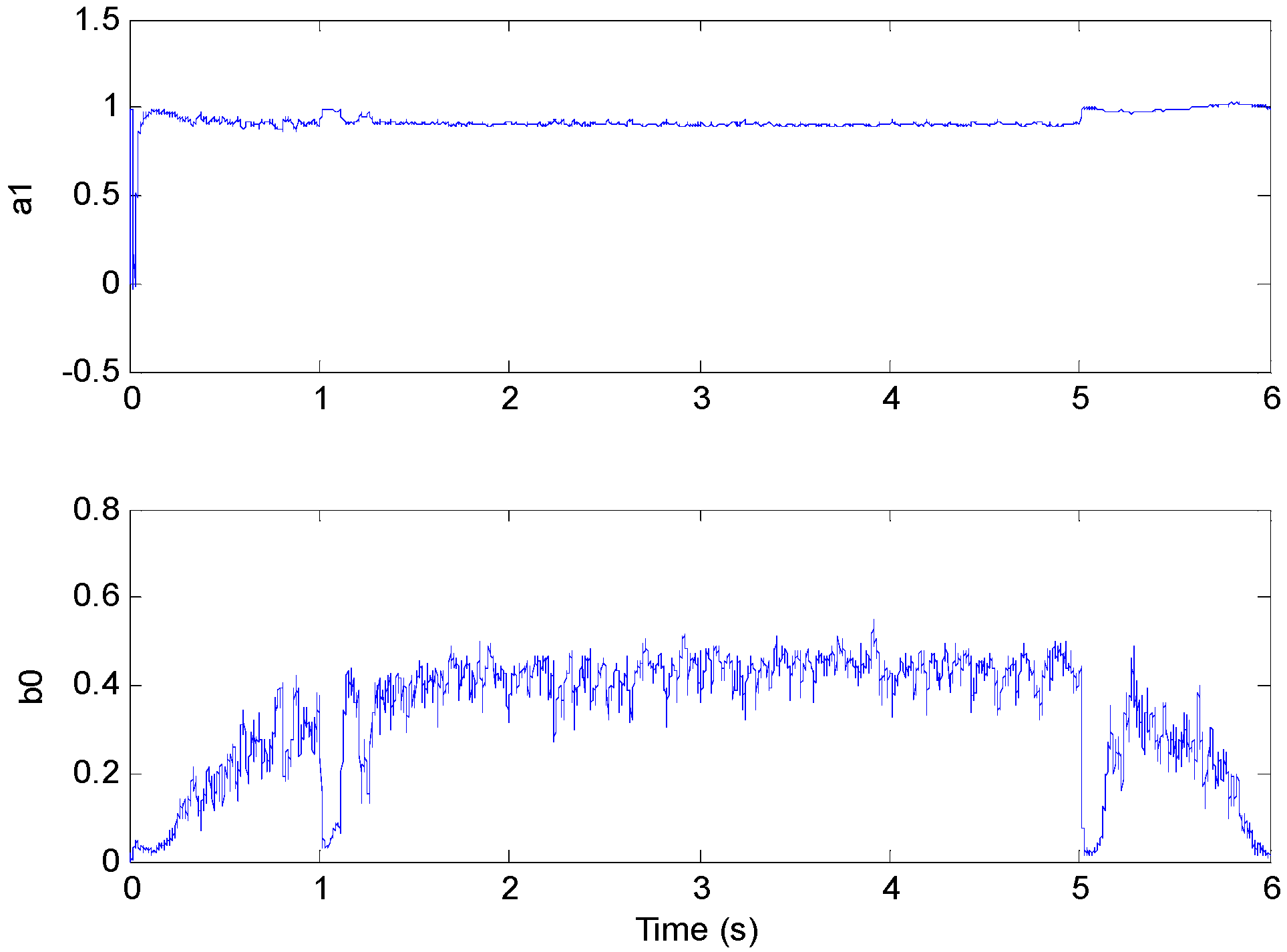
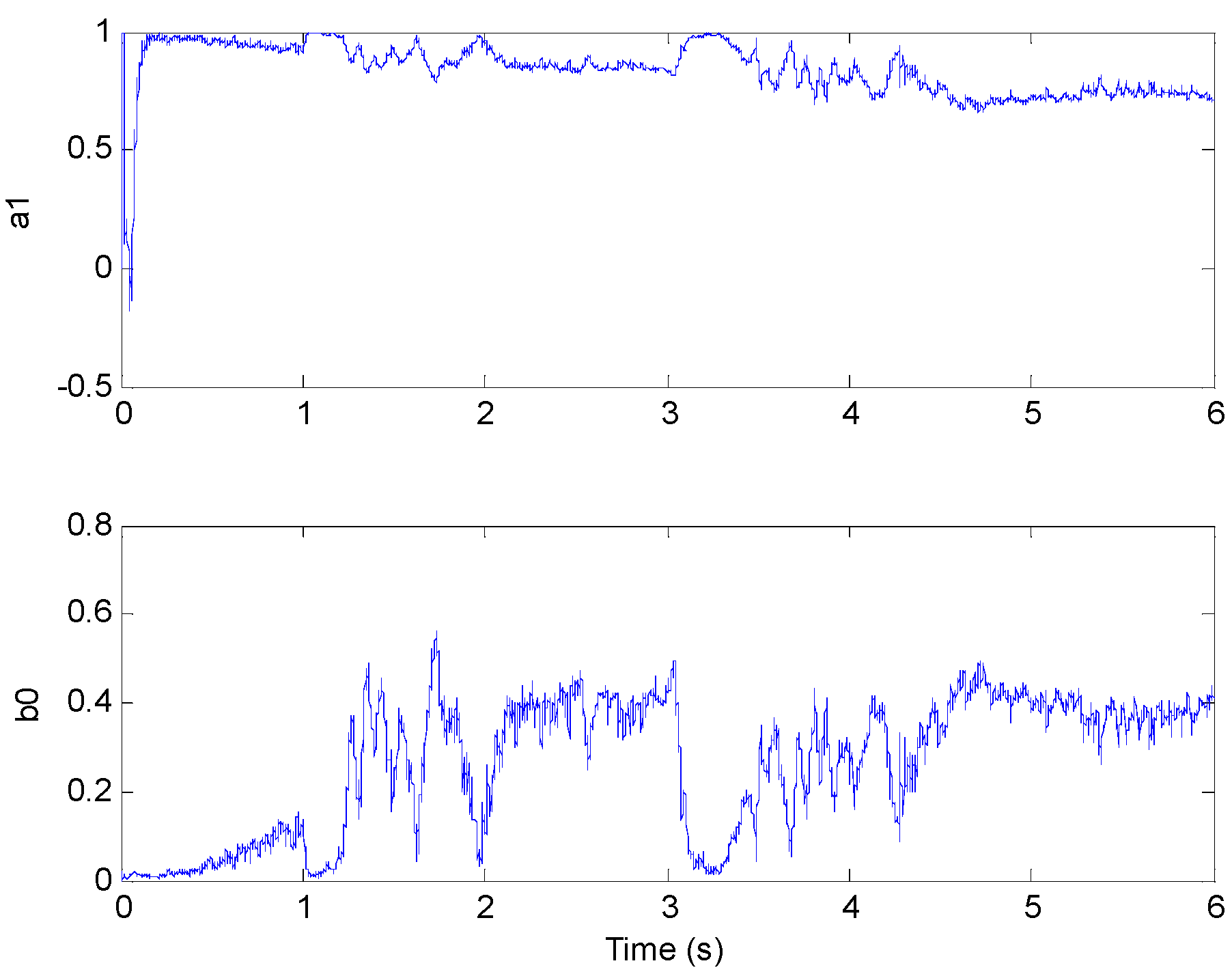
3.1. The Identification of Model Parameters
3.2. Performance Prediction
3.3. Future Reference Trajectory
Remark 1
Remark 2
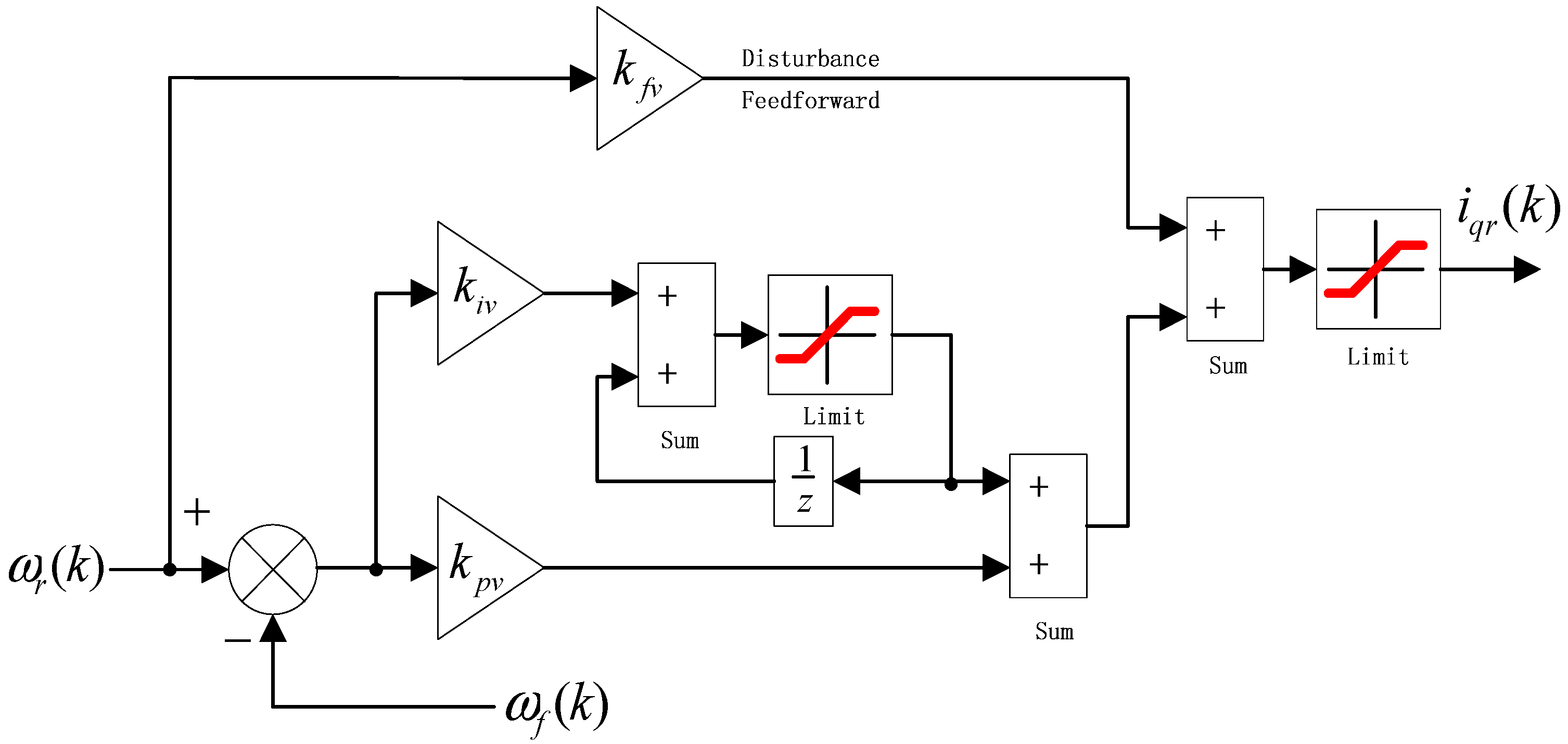
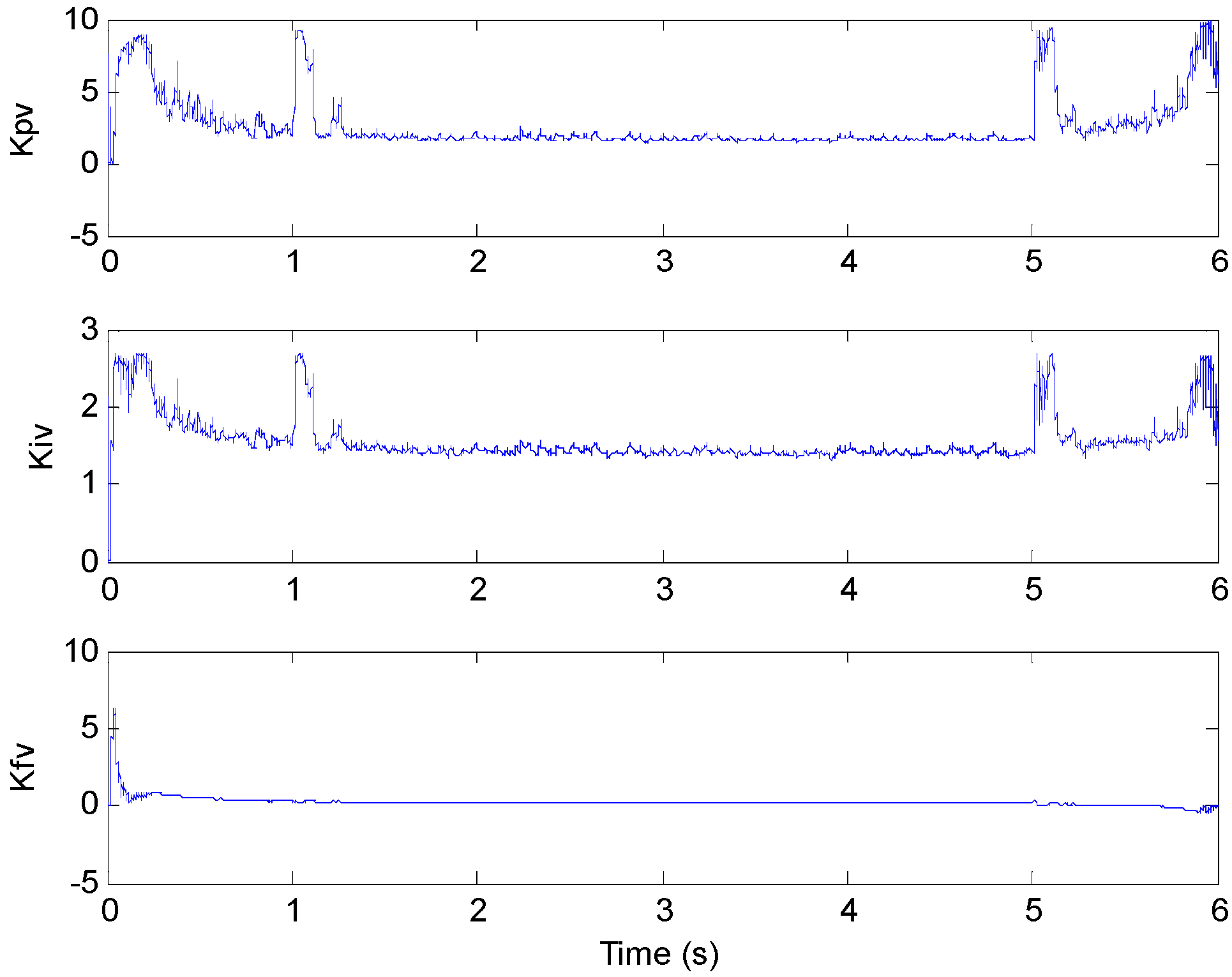
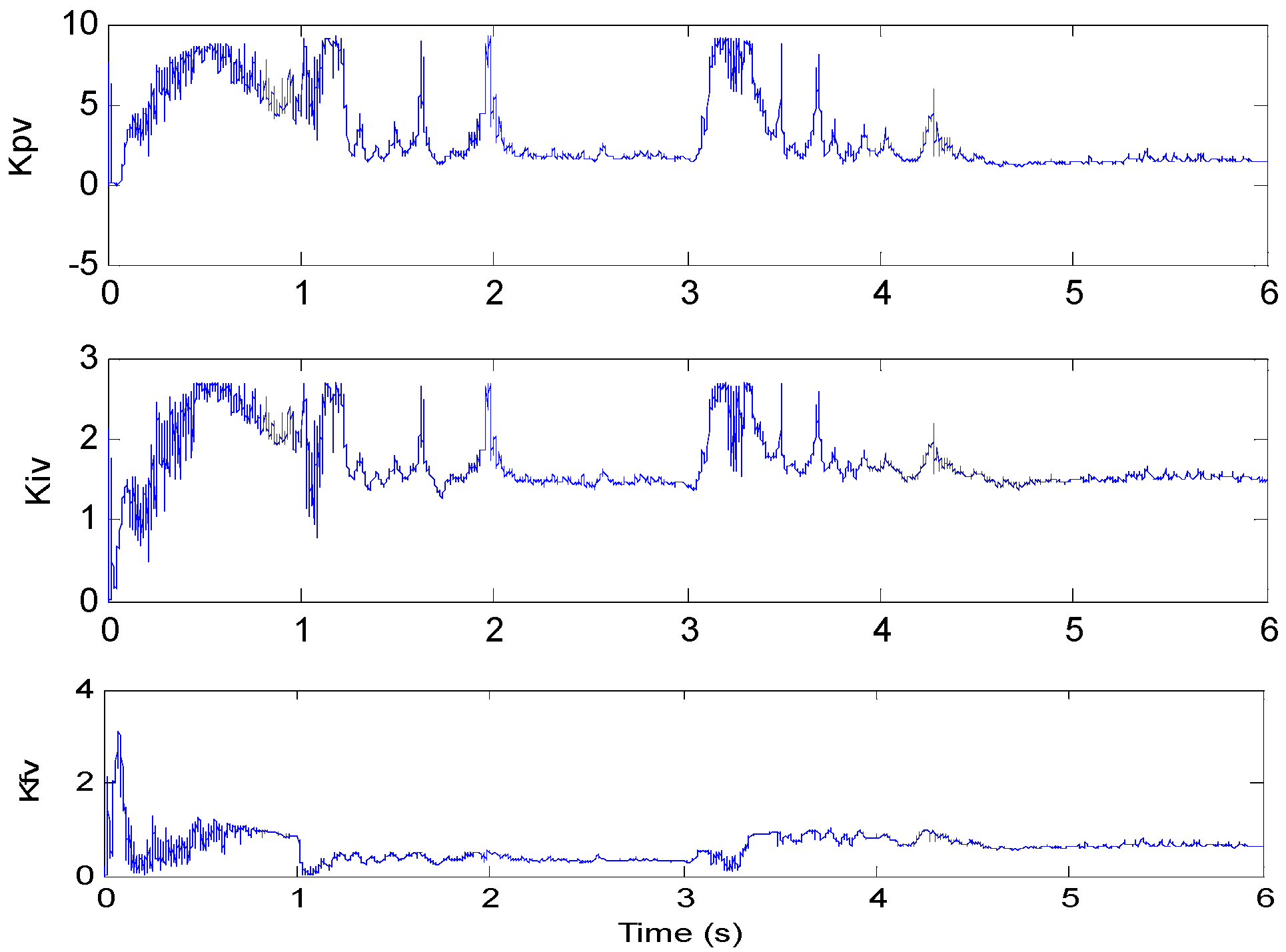
3.4. Optimal Control Parameters Calculating
- Step 1: Given the related parameters for an RLS law and a GPC algorithm.
- Step 2: The controlled model parameters a1 and b0 are updated online by the RLS law.
- Step 3: Based on the controlled model, Diophantine Equations (11) and (12) are solved to obtain ωf (k + j) and Δiqr(k) is obtained by Equation (25).
- Step 4: Speed command can be expressed as Equation (28), then, the PIF controller gain parameters can be tuned by Equation (32).
- Step 5: Set k = k + 1 and go to step 2.
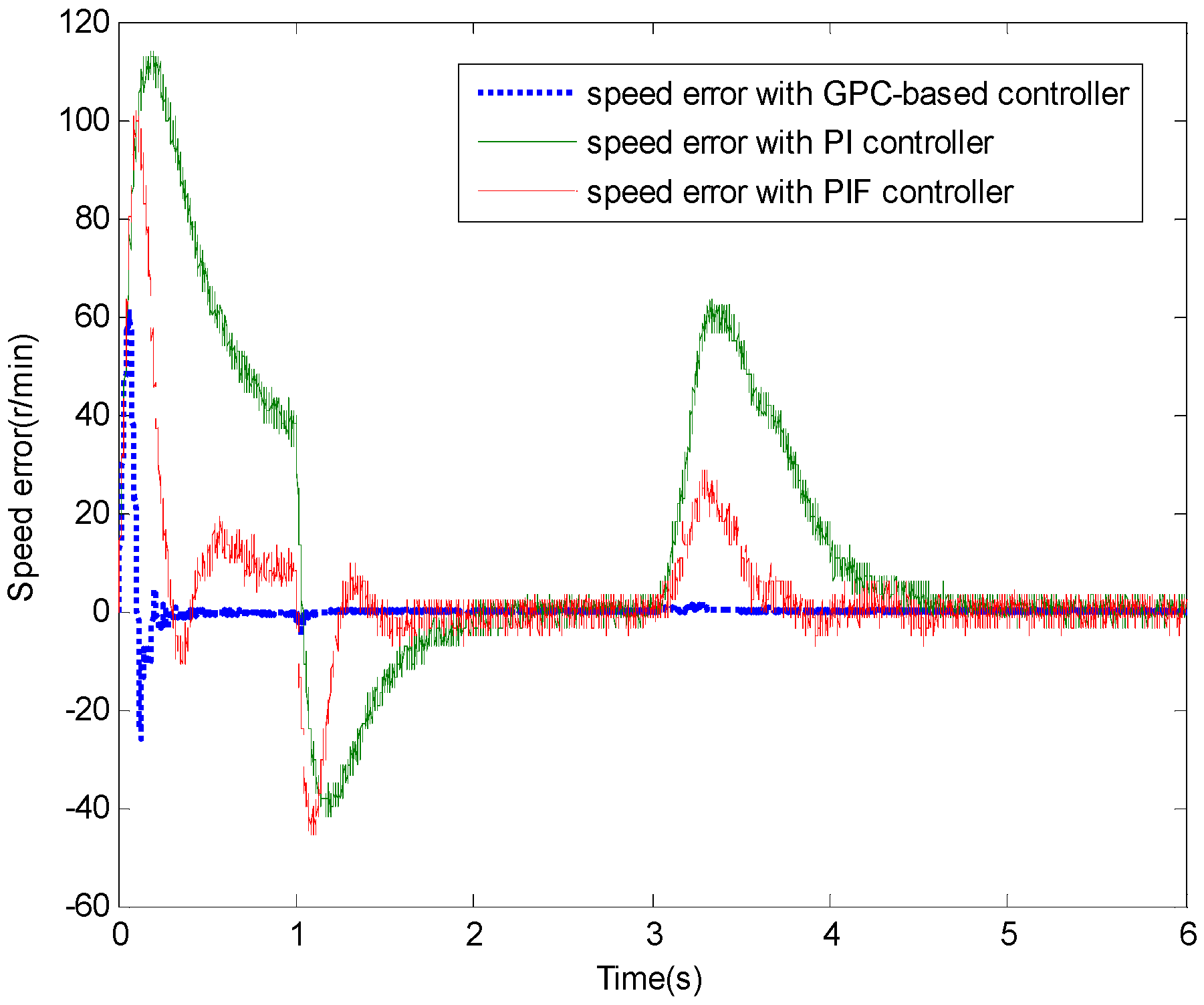
4. Experiment
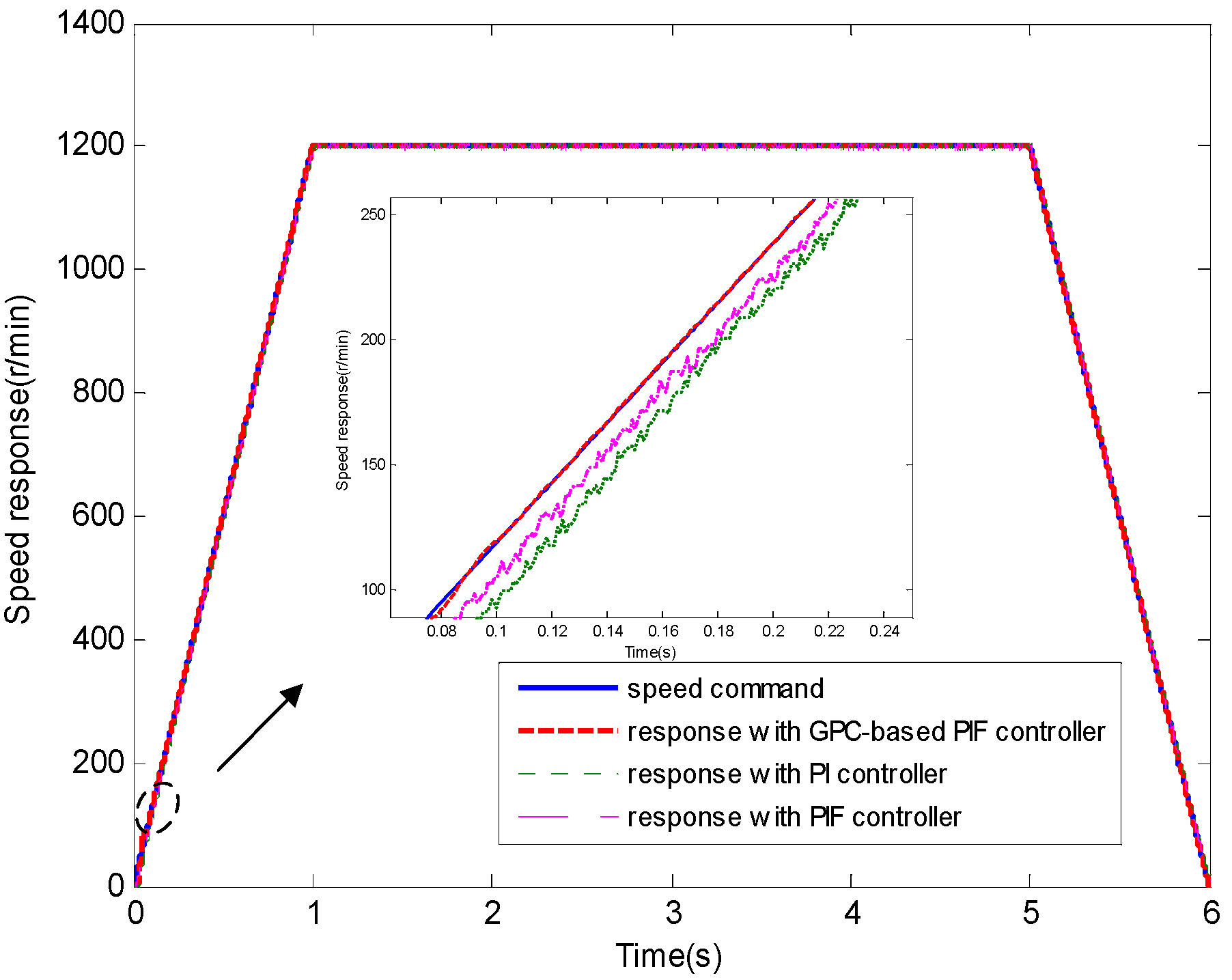
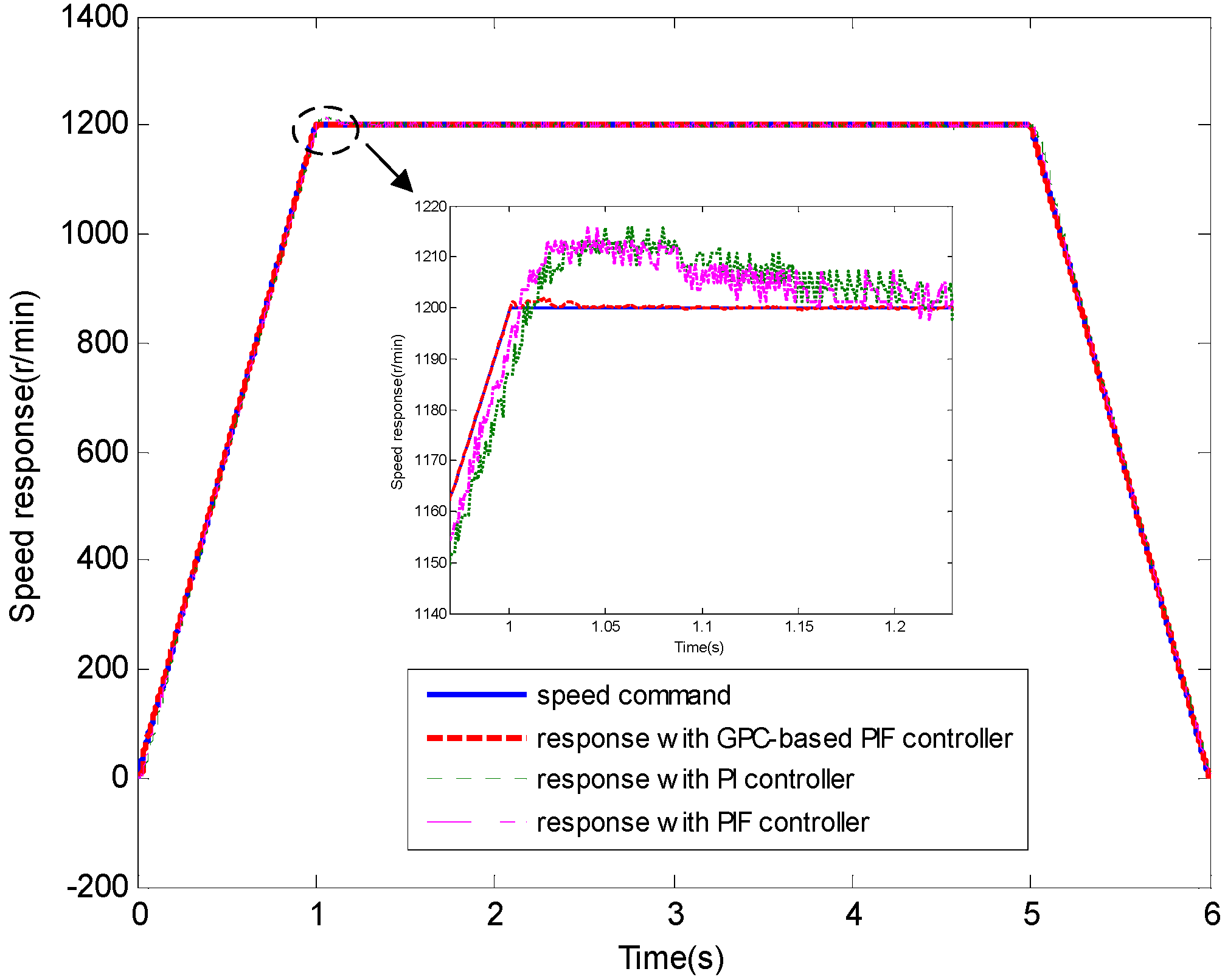
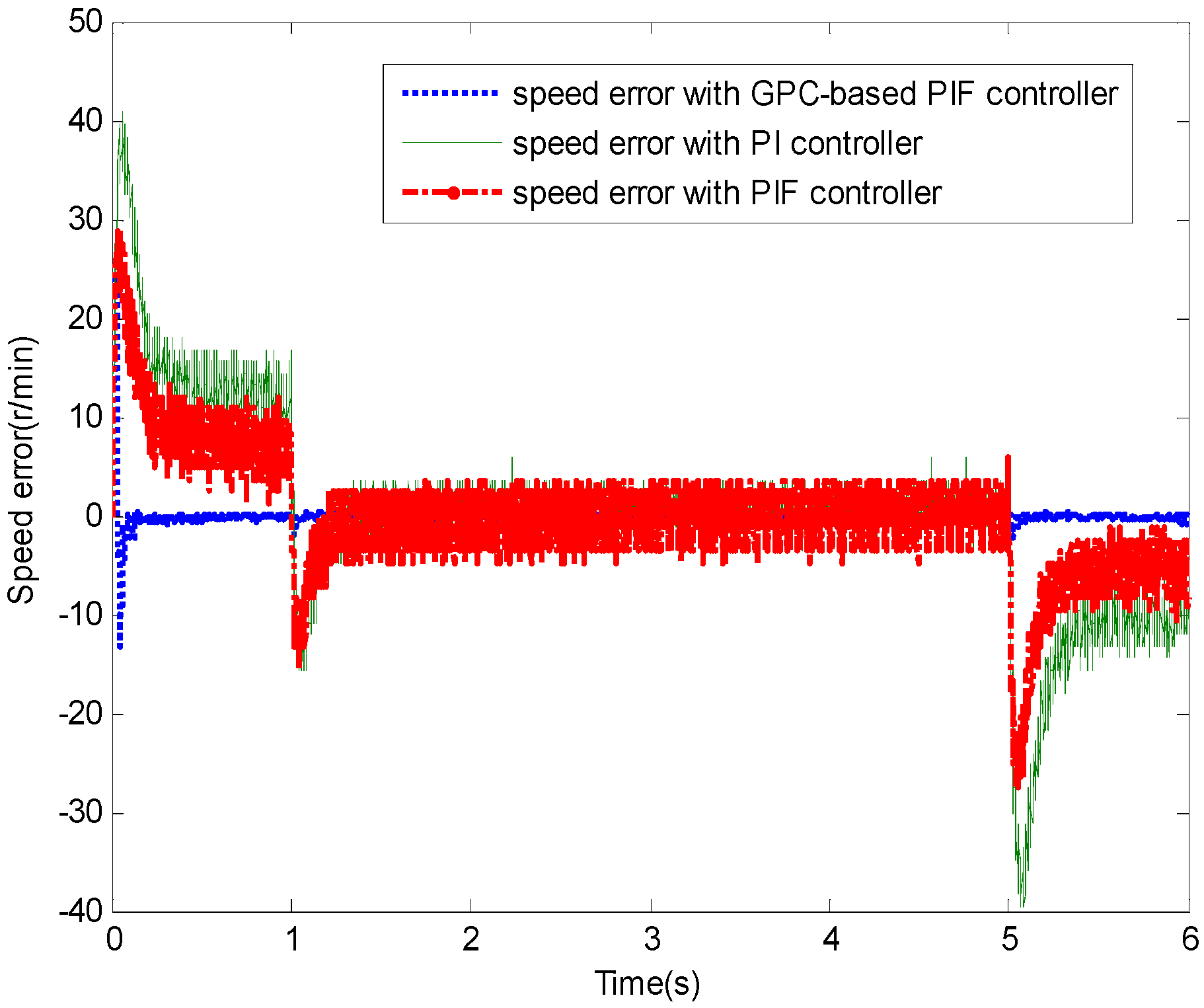
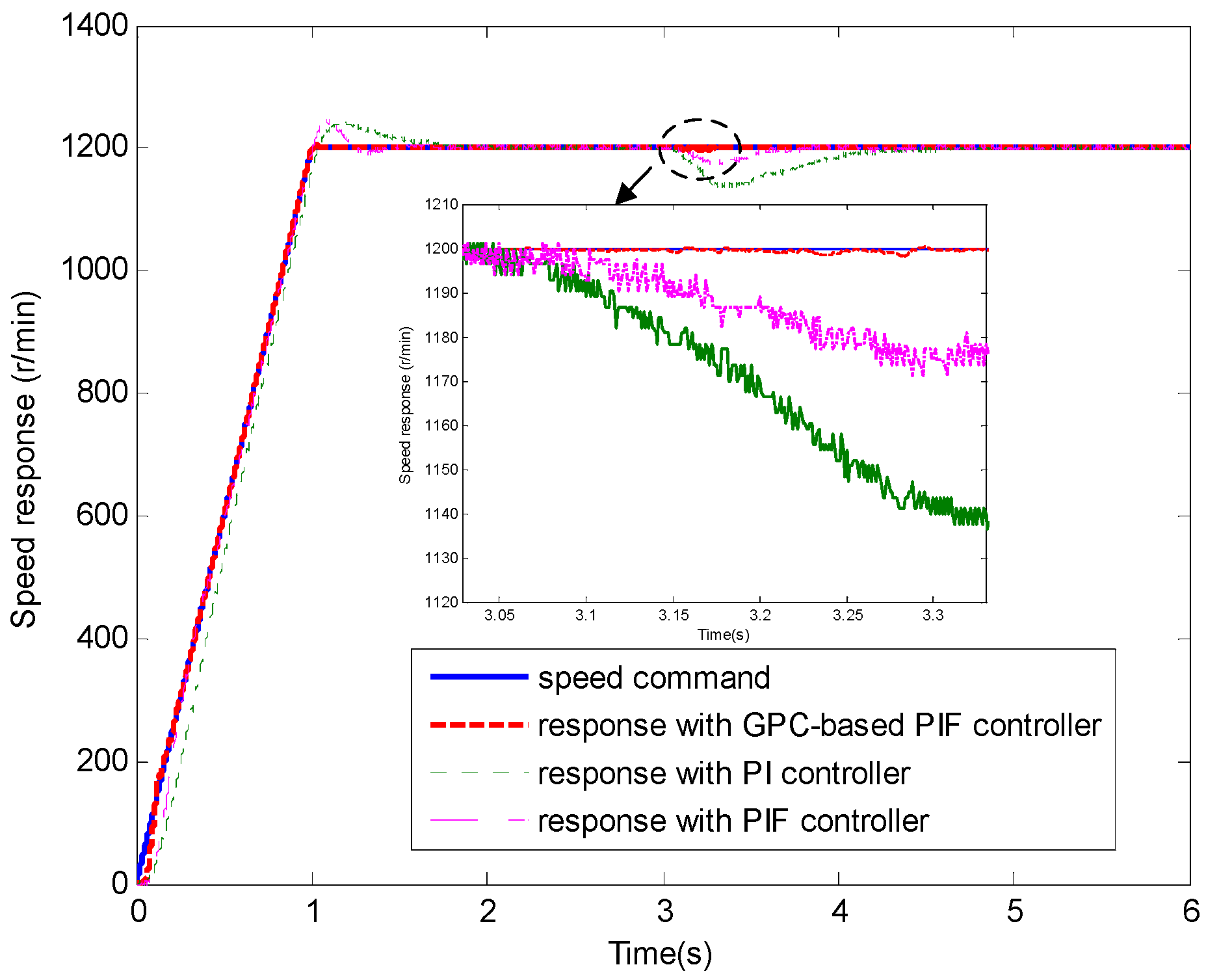
4.1. Test 1 without Applied Load
4.2. Test 2 with Applied Load Inertia
4.3. Test 3 with Applied Load Torque
5. Conclusions
Acknowledgments
Appendix A
References
- Cheng, S.; Li, C.-W. Fuzzy PDFF-IIR controller for PMSM drive systems. Cont. Eng. Pract. 2011, 19, 828–835. [Google Scholar]
- Errouissi, R.; Ouhrouche, M.; Chen, W.H.; Trzynadlowski, A.M. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost function. IEEE Trans. Indust. Electron. 2012, 59, 2849–2858. [Google Scholar]
- Choi, H.H.; Vu, N.T.-T.; Jung, J.-W. Digital implementation of an adaptive speed regulator for a PMSM. IEEE Trans. Power Electron. 2011, 26, 3–8. [Google Scholar]
- Claveau, F.; Chevrel, P.; Knittel, K. A 2DOF gain-scheduled controller design methodology for a multi-motor web transport system. Contr. Eng. Pract. 2008, 16, 609–622. [Google Scholar]
- Sanchez, J.; Visioli, A.; Dormido, S. A two-degree-of-freedom PI controller based on events. J. Process Contr. 2011, 21, 639–651. [Google Scholar]
- Krebs, G.; Tounzi, A.; Pauwels, B.; Willemot, D. Modeling and control of a 2Dof PM synchronous actuator using Hall effect sensors. Mechatronics 2010, 20, 153–161. [Google Scholar]
- Alfaro, V.M.; Vilanova, R. Model-reference robust tuning of 2Dof PI controllers for first- and second-order plus dead-time controlled processes. J. Process Contr. 2012, 22, 359–374. [Google Scholar]
- Pan, I.; Das, S.; Gupta, A. Tuning of an optimal fuzzy PID controller with stochastic algorithms for networked control systems with random time delay. ISA Trans. 2011, 50, 28–36. [Google Scholar]
- Mohan, B.M.; Sinha, A. Mathematical models of the simplest fuzzy PI/PD controllers with skewed input and output fuzzy sets. ISA Trans. 2008, 47, 300–310. [Google Scholar]
- Zeng, S.W.; Hu, H.G.; Xu, L.H.; Li, G.H. Nonlinear adaptive PID control for greenhouse environment based on RBF network. Sensors 2012, 16, 365–375. [Google Scholar]
- Yamamoto, T.; Takao, K.; Yamada, T. Design of a data-driven PID controller. IEEE Tran. Contr. Syst. Technol. 2009, 17, 29–39. [Google Scholar]
- Asano, M.; Yamamoto, T.; Oki, T.; Kaneda, M. A Design of neural-net based predictive PID controllers. Proc. IEEE Conf. Syst. Man Cyber. 1999, 4, 1113–1118. [Google Scholar]
- Miller, R.M.; Shah, S.L.; Wood, R.K.; Kwok, E.K. Predictive PID. ISA Trans. 1999, 38, 11–23. [Google Scholar]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive control in power electronics and drives. IEEE Trans. Indust. Electron. 2008, 55, 4312–4324. [Google Scholar]
- Beerten, J.; Vervekken, J.; Driesen, J. Predictive direct torque control for flux and torque ripple reduction. IEEE Trans. Indust. Electron. 2010, 57, 404–412. [Google Scholar]
- Nemec, M.; Nedeljkovic, D.; Ambrozic, V. Predictive torque control of induction machines using immediate flux control. IEEE Trans. Indust. Electron. 2007, 54, 2009–2017. [Google Scholar]
- Miranda, H.; Cortes, P.; Yuz, J.I.; Rodriguez, J. Predictive torque control of induction machines based on state-space models. IEEE Trans. Indust. Electron. 2009, 56, 1916–1924. [Google Scholar]
- Sato, T. Design of a GPC-based PID controller for controlling a weigh feeder. Control Eng. Pract. 2010, 18, 105–113. [Google Scholar]
- Papafotiou, G.; Kley, J.; Papadopoulos, K.G.; Bohren, P.; Morari, M. Model predictive direct torque control-part II: Implementation and experimental evaluation. IEEE Trans. Indust. Electron. 2009, 56, 1906–1915. [Google Scholar]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and implementation of model predictive control for electrical motor drives. IEEE Trans. Indust. Electron. 2009, 56, 1925–1936. [Google Scholar]
- Liu, H.; Li, S. Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans. Indust. Electron. 2012, 59, 1171–1183. [Google Scholar]
- Sato, T.; Inoue, A.; Yamamoto, T. Improvement of tracking performance in designing a GPC-based PID controller using a time-varying proportional gain. Int. J. Innov. Comput. Inform. Contr. 2006, 2, 491–503. [Google Scholar]
- Errouissi, R.; Ouhrouche, M.; Chen, W.H.; Trzynadlowski, A.M. Robust cascaded nonlinear predictive control of a permanent magnet synchronous motor with an antiwindup compensator. IEEE Trans. Indust. Electron. 2012, 59, 3078–3088. [Google Scholar]
- Gamazo-Real, J.C.; Vazquez-Sanchez, E.; Gomez-Gil, J. Position and speed control of brushless DC motors using sensorless techniques and application trends. Sensors 2010, 10, 6901–6947. [Google Scholar]
- Gaeid, K.S.; Ping, H.W.; Khalid, M. Sensor and sensorless fault tolerant control for induction motors using a wavelet index. Sensors 2012, 12, 4031–4050. [Google Scholar]
- Yasser, A.-R.; Mohamed, I. Adaptive self-tuning speed control for permanent-magnet synchronous motor drive with dead time. IEEE Trans. Energy Convers. 2006, 21, 855–862. [Google Scholar]
- Kuo, C.-F.J.; Hsu, C.-H. Precise speed control of a permanent magnet synchronous motor. Int. J. Adv. Manufact. Technol. 2006, 28, 942–949. [Google Scholar]
- Correa, P.; Pacas, M.; Rodriguez, J. Predictive torque control for inverter fed induction machines. IEEE Trans. Indust. Electron. 2007, 54, 1073–1079. [Google Scholar]
- Morel, F.; Lin-Shi, X.F.; Retif, J.M.; Allard, B.; Buttay, C. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive. IEEE Trans. Indust. Electron. 2009, 56, 2715–2728. [Google Scholar]
- Wang, D.Q.; Ding, F. Input-output data filtering based recursive least squares identification for CARARMA systems. Digit. Signal Process. 2010, 20, 991–999. [Google Scholar]


| Name | Values |
|---|---|
| Phase current | 3.7 A |
| The number of poles | 3 |
| Rated torque | 4.5 Nm |
| Rotor inertia | 0.00067 kgm2 |
| Rated speed | 1,200 r/min |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lu, S.; Tang, X.; Song, B. Adaptive PIF Control for Permanent Magnet Synchronous Motors Based on GPC. Sensors 2013, 13, 175-192. https://doi.org/10.3390/s130100175
Lu S, Tang X, Song B. Adaptive PIF Control for Permanent Magnet Synchronous Motors Based on GPC. Sensors. 2013; 13(1):175-192. https://doi.org/10.3390/s130100175
Chicago/Turabian StyleLu, Shaowu, Xiaoqi Tang, and Bao Song. 2013. "Adaptive PIF Control for Permanent Magnet Synchronous Motors Based on GPC" Sensors 13, no. 1: 175-192. https://doi.org/10.3390/s130100175




