1. Introduction
The artificial olfactory system, also referred to as the electronic nose (E-nose) system, has been used in numerous applications. These include air quality monitoring, food quality control [
1], hazardous gas detection, medical treatment and health care [
2], and diagnostics [
3]. An E-nose system comprises a sensor array, a signal processing unit, and a pattern recognition system. During recent decades a substantial amount of research and development has been reported on E-nose systems. Because of the complex classification algorithms embedded in the pattern recognition system, a central processing unit (CPU) is usually required [
1,
2]. Consequently, the majority of E-nose systems is large and consumes considerable power. However, heavy and power-hungry equipment is inconvenient to use, and designing a low-power small device would be preferable. Some researchers and companies [
4–
6] have used microprocessors or field-programmable gate arrays (FPGAs) as a computational cell to develop portable E-noses, but these systems are still too power-intensive and large. To further reduce the power consumption and device area, analog VLSI implementation of the learning algorithm for E-nose application has been proposed [
7–
14].
The multilayer perceptron neural network (MLPNN) is an algorithm that has been continuously developed for many years. Consequently, when VLSI implementation of a learning algorithm is necessary, MLPNN is a common choice. In 1986, Hopfield and Tank proposed the first analog MLPNN circuit [
10]. Since then, several analog VLSI implementations of MLPNN have been proposed [
11–
14]. Some have focused on the improvement of the multiplier [
14–
18] and some have attempted to design a nonlinear synapse to remove the analog multiplier [
19,
20]. However, the power consumption for most of the MLPNN circuits range from a few milliwatts to a few hundred milliwatts [
11–
14]. This power consumption is still too high for portable applications. Consequently, an MLPNN circuit with considerably lower power consumption (lower than 1 mW) is required when an MLPNN is being implemented in a portable E-nose.
This study implemented a low power MLPNN by analog VLSI circuit to serve as a classification unit in an E-nose. Neural networks is one of the most popular algorithms used in an E-nose system [
2,
5], because it can recognize and identify odor signal patterns. A typical MLPNN contains one input layer; one or more hidden layer(s), depending on the application; and an output layer. Apart from the input layer, both the hidden and output layers contain several neurons with nonlinear activation functions, which constitute the signal processing unit. Synapses connect the neurons of different layers, and a weight unit is included in each synapse. The weight units and the outputs of neurons determine the input of neurons in subsequent layers. An analog circuit realizes a nonlinear function with a simple structure [
15]. Thus, implementing an analog MLPNN circuit reduces the need for power and the size of the pattern recognition unit required to build an E-nose.
The weight adaptation algorithm used in this study was the back propagation (BP) learning algorithm [
21]. This algorithm allows the weights to be adjusted so that the MLP network can learn the target function; that is, pattern recognition. The details of the MLPNN and BP algorithms are provided below.
The input of a neuron can be represented as:
where
ajH is the input of the
jth hidden neuron;
WjiH represents the weight of the synapse that connects the
jth hidden neuron and the
ith input neuron;
XiI represents the output of the
ith input neuron; and
nI is the number of input neurons. Neuron output is determined by its input and activation function. The hyper tangent function is one of the most commonly used activation functions. This function can be easily implemented by analog VLSI with small chip area and power consumption. Consequently, the hyper tangent activation was chosen for this work. By choosing hyper tangent activation function, the neuron output is:
where
XjH is the output of the
jth hidden neuron, and
bj represents the bias value.
Similar to the hidden neuron, the input of the
kth output neuron is:
The output of the
kth output neuron
XkO is:
where
ck represents the bias value.
After calculating the output XkO of the output neuron, we derived the adapting value by comparing the circuit output XkO with target output Xt.
According to the BP algorithm, the general weight update value
ΔW is derived by:
where
a represents the neuron input;
η is the learning rate, and
Ep is the error term derived from the comparison between circuit output
XkO and target
Xt. In the following content, we used the mean square error and assumed that there was a single output neuron. Consequently,
XkO was simplified to
XO.
The order of weight adaptation proceeds from the output layer to the input layer. When deriving
ΔW in each layer, repeatedly differentiating the error by weight is unnecessary because certain computations have already been performed in later layers (for the hidden layer, the later layer is the output layer). The later layer propagates the computation to the previous layer; this propagating value is called the “back propagation error.” For the output layer, the BP error
δO is:
where
DO represents the differentiation of the output neuron's activation function. For the hidden layer, the BP error of the
jth hidden neuron
is:
The MLPNN was trained by adapting the weights according to
Equation (10). During the training phase, the new weight
Wnew in a synapse was acquired from the previous weight
Wold in the same synapse plus the weight update value
ΔW:
The rest of this paper is organized as follows: Section 2 describes the system architecture, Section 3 presents the measurement results, and Section 4 presents the conclusion.
2. Architecture and Implementation
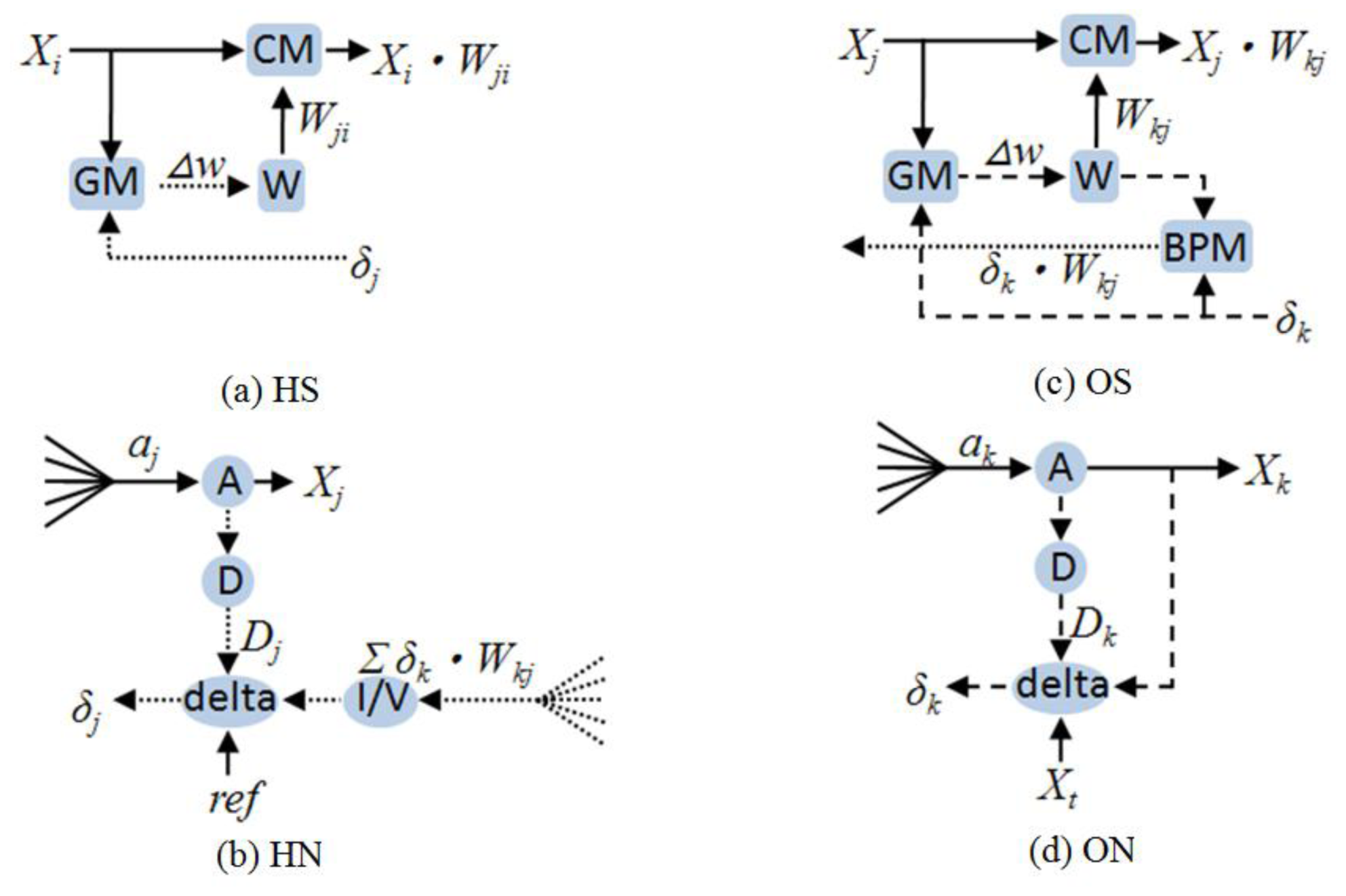
This paper proposes a 4-4-1 MLPNN. The 4-4-1 notation represents four input neurons, four hidden neurons, and one output neuron. This structure was proven by Matlab to be able to learn the odor data we used before really doing chip design. The block diagram is shown in
Figure 1. The symbols
X1–
X4 refer to four signal inputs;
Xbi is the bias in the input layer;
HSs are the synapses between the input and hidden layers;
HNs are the hidden neurons;
Xbj is the bias in the hidden layer;
OSs are the synapses between the hidden and output layers; and
ON is the output neuron.
Based on
Equations (1) to
(10), the detailed block diagram of
HS,
HN,
OS, and
ON was obtained, as shown in
Figure 2. The
CM, BPM and
GM are multipliers;
W is weight;
A is the activation function;
D is the differentiation of activation function;
delta is the BP error generator; and
I/V is the current-to-voltage converter.
Because several multiplication results are summed in
Equations (1) and
(3), the output signals of all multipliers are designed as current signals. Using Kirchhoff's current laws (KCL), the current is summed if the outputs of the synapses are connected. Thus, the area and power of the system are reduced because no extra analog adder is necessary. For signals that require transmission to several nodes (e.g., X
1 to X
4), a voltage signal is preferred. Further description of the subblocks shown in
Figure 2 and the relations between the equations and sub-blocks are provided below. When approximating the equations by analog circuit, second-order effects, such as the body or Early effect, are neglected; thus, particular errors may be introduced. These errors may result in nonlinearity. However, by carefully designing the bias, size, and dynamic range of the circuit, the nonlinearity has little effect on the learning performance of the application in this study.
2.1. Synapses
The synapses at the hidden layer and the output layer comprise two multipliers (
CM and
GM) and a weight unit
W; the output layer synapse needs one more multiplier (
BPM) to generate the term
δOkkWjO. The terms
BPM and
CM are both Chible's multipliers [
16,
17]. The
BPM multiplies the weight by BP error, whereas
CM is used to multiply the input by weight. The results represent the current. This study used the Chible's multiplier because of its wide operation range [
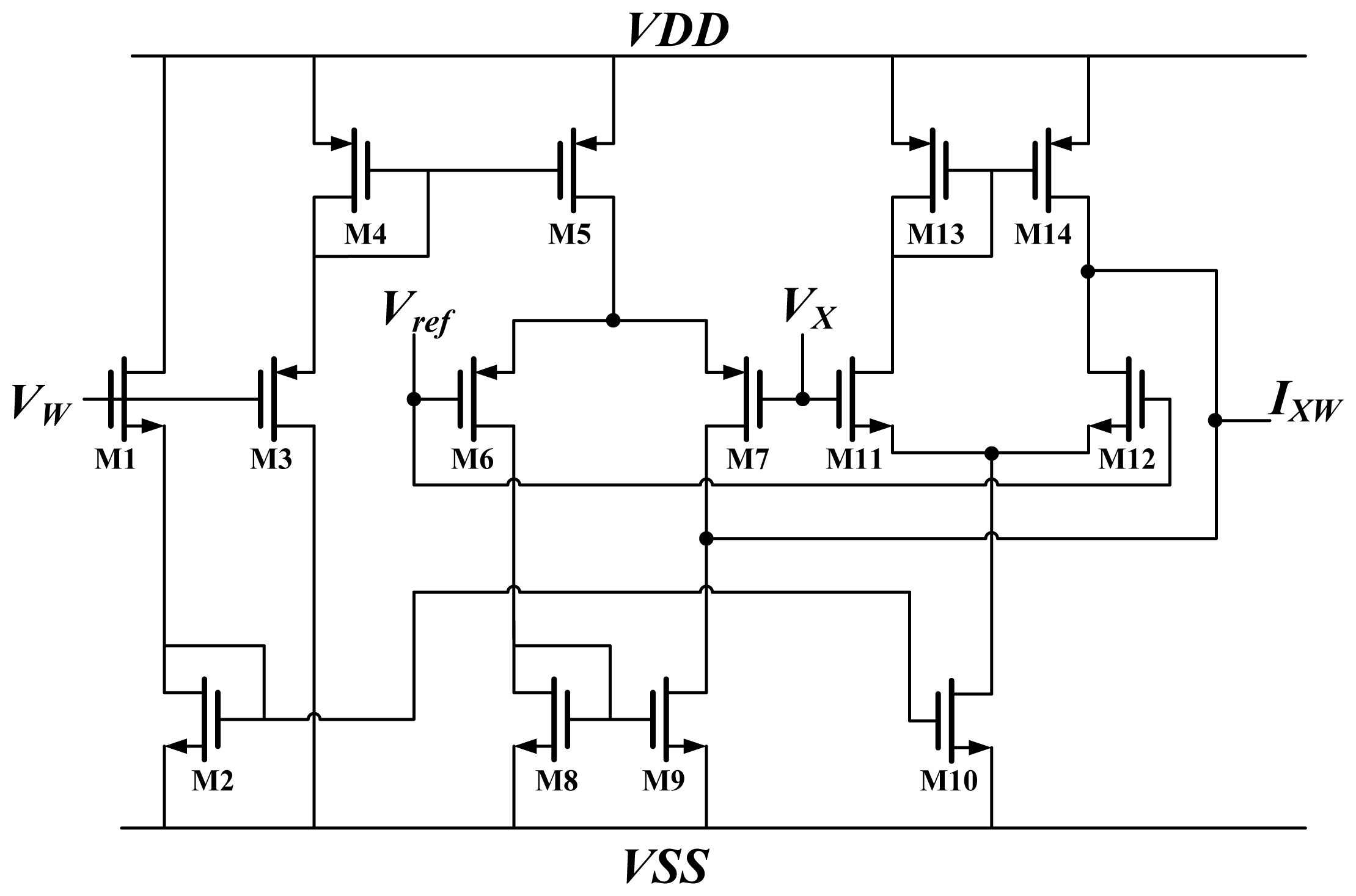
16]. A schematic diagram of Chible's multiplier is shown in
Figure 3.
The weight and input are voltages, denoted by
VW and
VX, respectively. The output of the multiplier is
IXW. M1, M3 operate in strong inversion regions, whereas M6, M7, M11, and M12 operate in weak inversion regions. According to the equation of MOSFET in strong and weak inversion, the output current is:
where
Vref is a reference voltage;
UT is thermal voltage; and
Iwp and
Iwn represent the bias current for M6 and M7 and for M11 and M12, respectively. Both
Iwp and
Iwn are related to weight
VW. Assuming that the parameters for NMOS and PMOS are equal and
Vx-ref is sufficiently small,
IWX is equal to
VW_offset multiplied by
VX_offset. Furthermore,
VW_offset and
VX_offset represent
VW and
VX plus an offset, respectively.
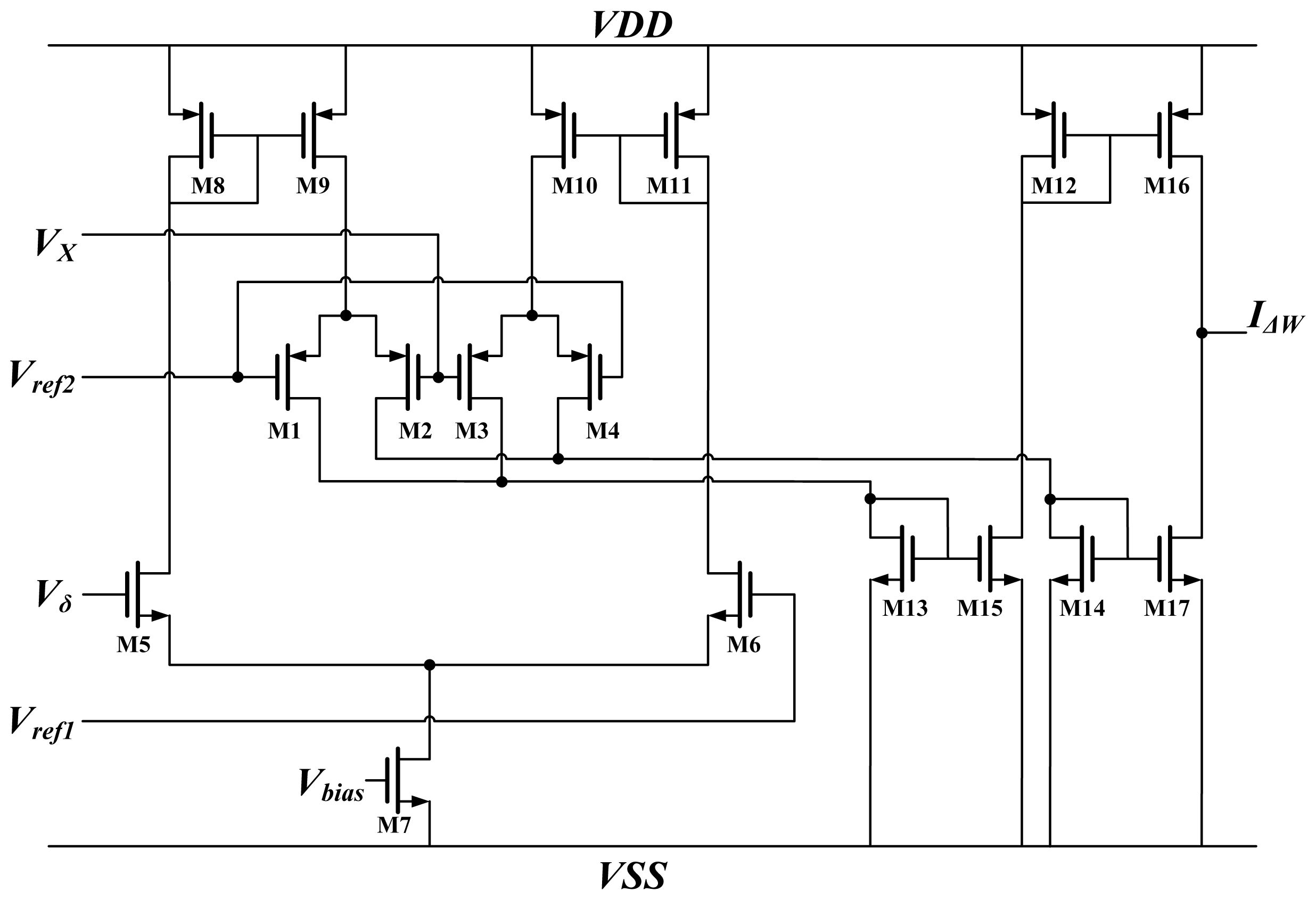
The
GM term represents the Gilbert multiplier [
22,
23]. This type of multiplier provides good linearity but a small dynamic range. Thus, this block multiplies the neuron output
X and error term
δ in
Equations (8) and
(9). The schematic is shown in
Figure 4. The output
X and BP error
δ are voltages, denoted by
VX and
Vδ, respectively. The output of the multiplier is
IΔW, whereas
Vref1 and
Vref2 are reference voltages. All of the MOSFETs operate in subthreshold regions. According to the voltage and current relationship of MOSFETs in subthreshold regions, the output current is represented as:
when the difference of
VX and
Vδ to the reference voltage are sufficiently small,
IΔW can be simplified to:
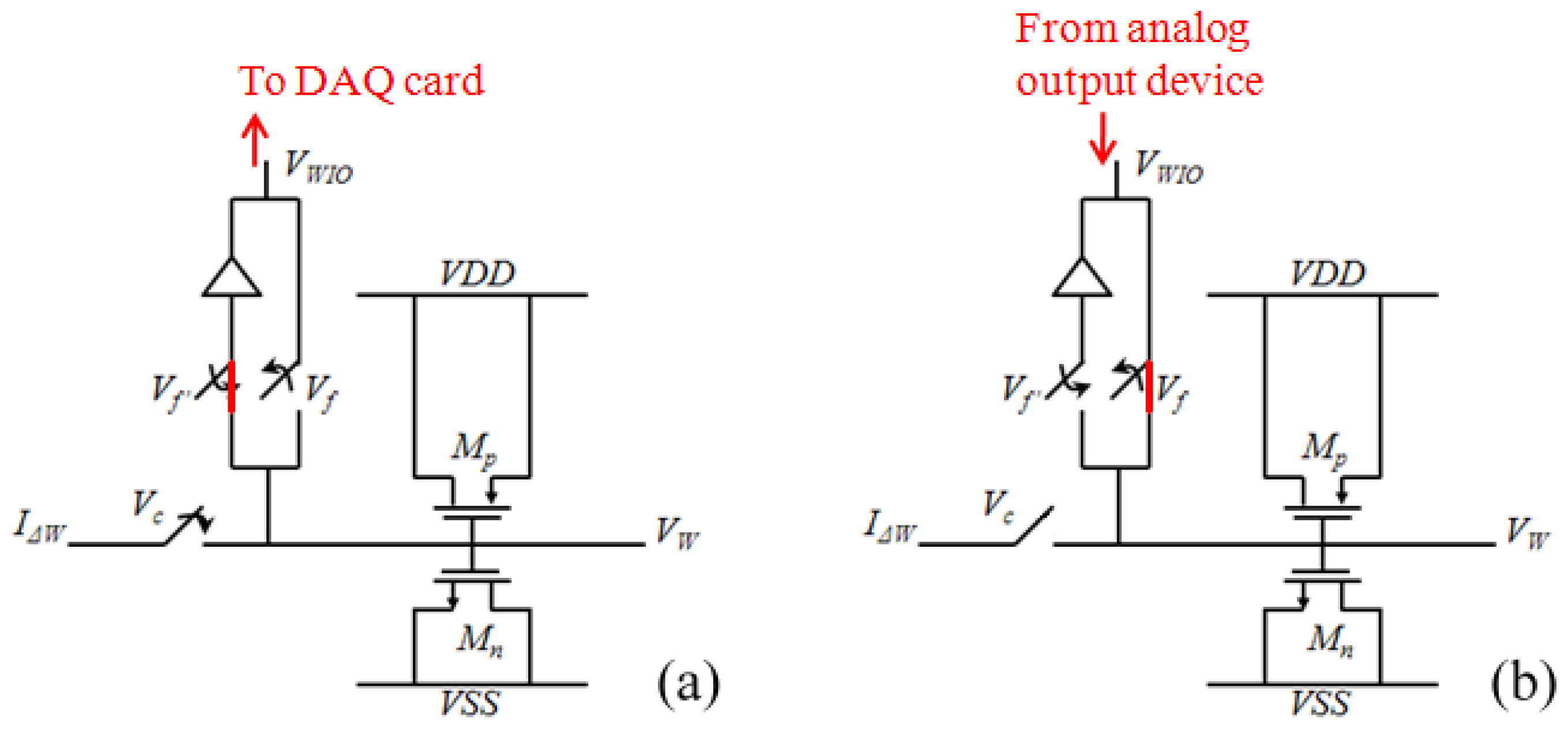
The weight unit
W is a temporal signal storage device showing the characteristic of
Equation (10). The circuit implementation of the weight unit is shown
Figure 5. The weight is represented by a voltage that is stored on a capacitor. This study used metal-oxide semiconductors to form a MOSCap. Compared to other types of capacitors, the MOSCap has a larger capacitance per unit area. Thus, the chip area is reduced by using a MOSCap. In the training phase, the weight adaptation is performed using a weight-updating current
IΔW from the
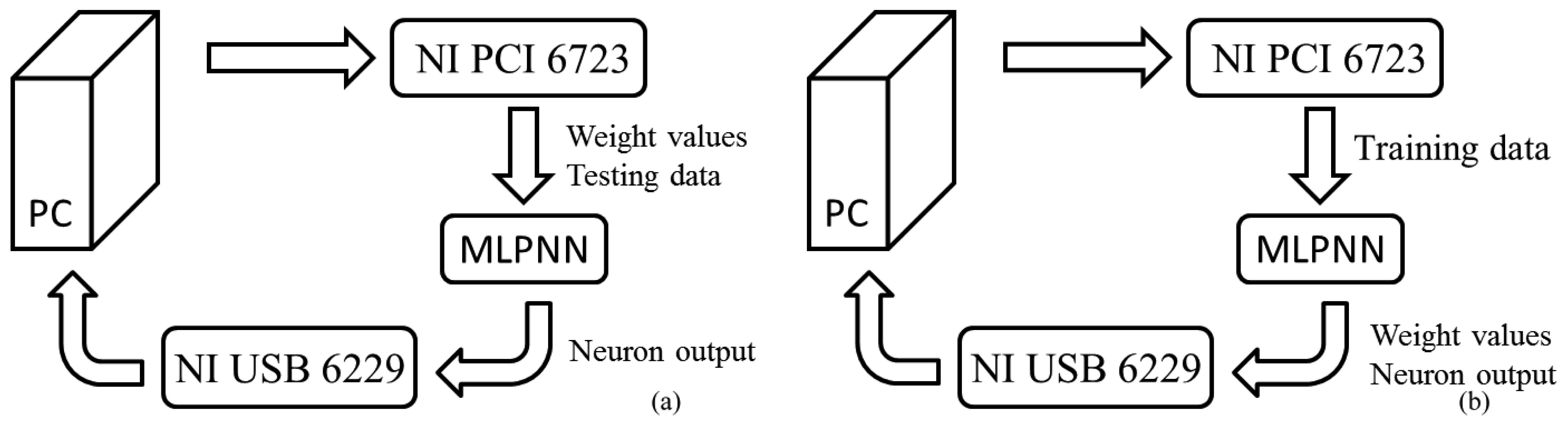
GM to charge or discharge the storage capacitor. The control voltage Vc determined the period for the current to charge or discharge the capacitor; in other words, this control voltage determines the learning rate of the network. The weight value is collected simultaneously by a data acquisition device (NI 6229). These weight values are stored in a computer. In the classifying phase,
IΔW no longer updates the weight values; rather, the computer sets the weights on the MLPNN chip using pre-stored weight values through a data application device (NI PCI 6723).
2.2. Neurons
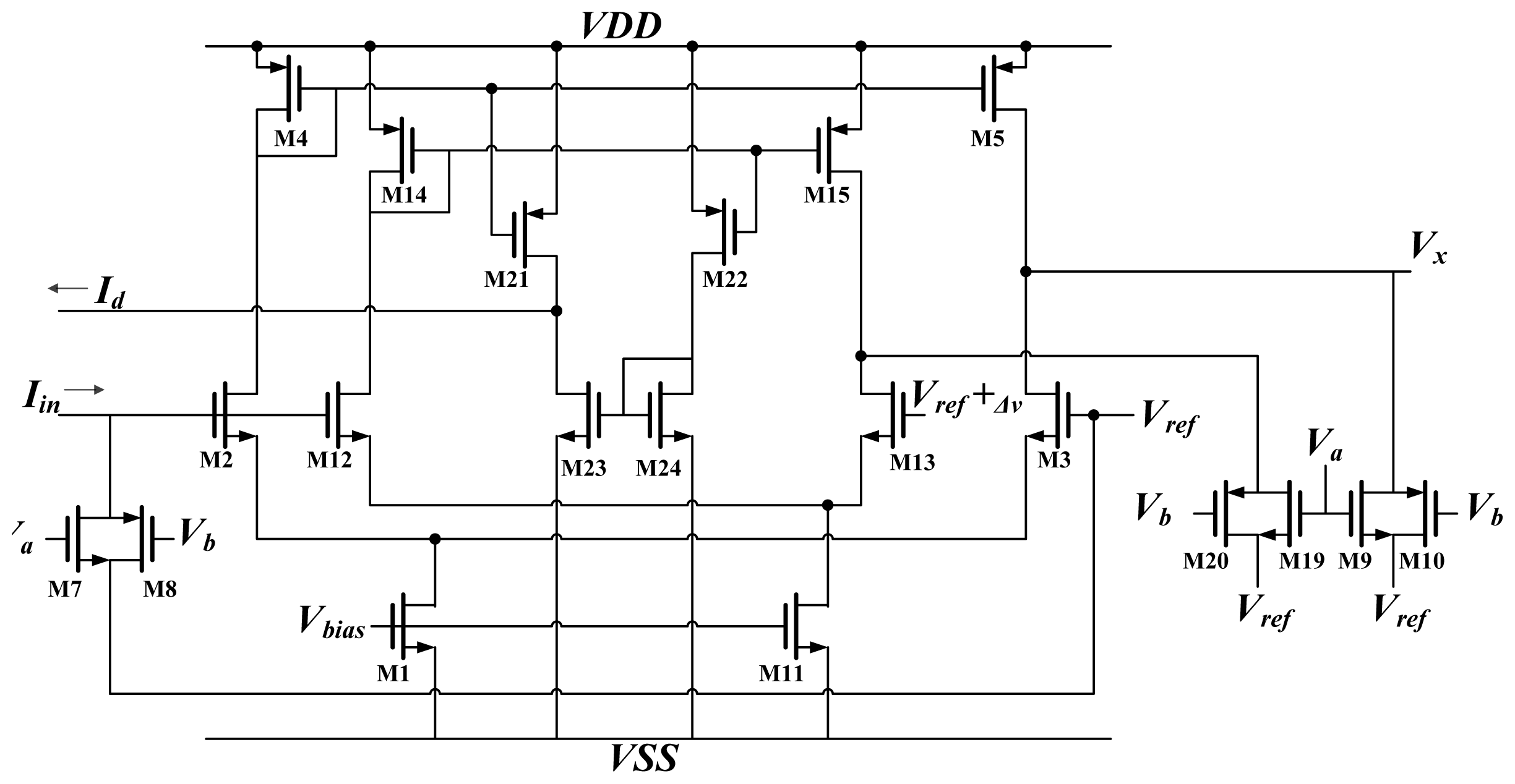
A schematic diagram of the activation function circuit
A and differential approximation circuit
D are shown in
Figure 6. The activation function was hyper tangent in this work. An analog circuit can easily implement the hyper tangent function using a differential pair [
15]. As shown in
Figure 6, the input current
Iin is delivered through the synapse circuit and converted to voltage by M7 and M8. This voltage is compared with the reference voltage
Vref, and an output current is produced. Because M2 and M3 operate in the subthreshold region, the output current is:
The output current Ix is then converted to voltage Vx by M9 and M10. This voltage Vx constitutes the output of the neuron.
According to the definition of differentiation:
This study used the function
fD(x) to approximate the actual differentiation
f'(x) [
12]. Consequently, this involved duplicating the activation function circuit (M12 and M13). The reference voltage for this replica differed from
Vref by a small amount. The output current of this replica became:
The difference between
Ix and
Ix_r is the differential approximation of the activation function:
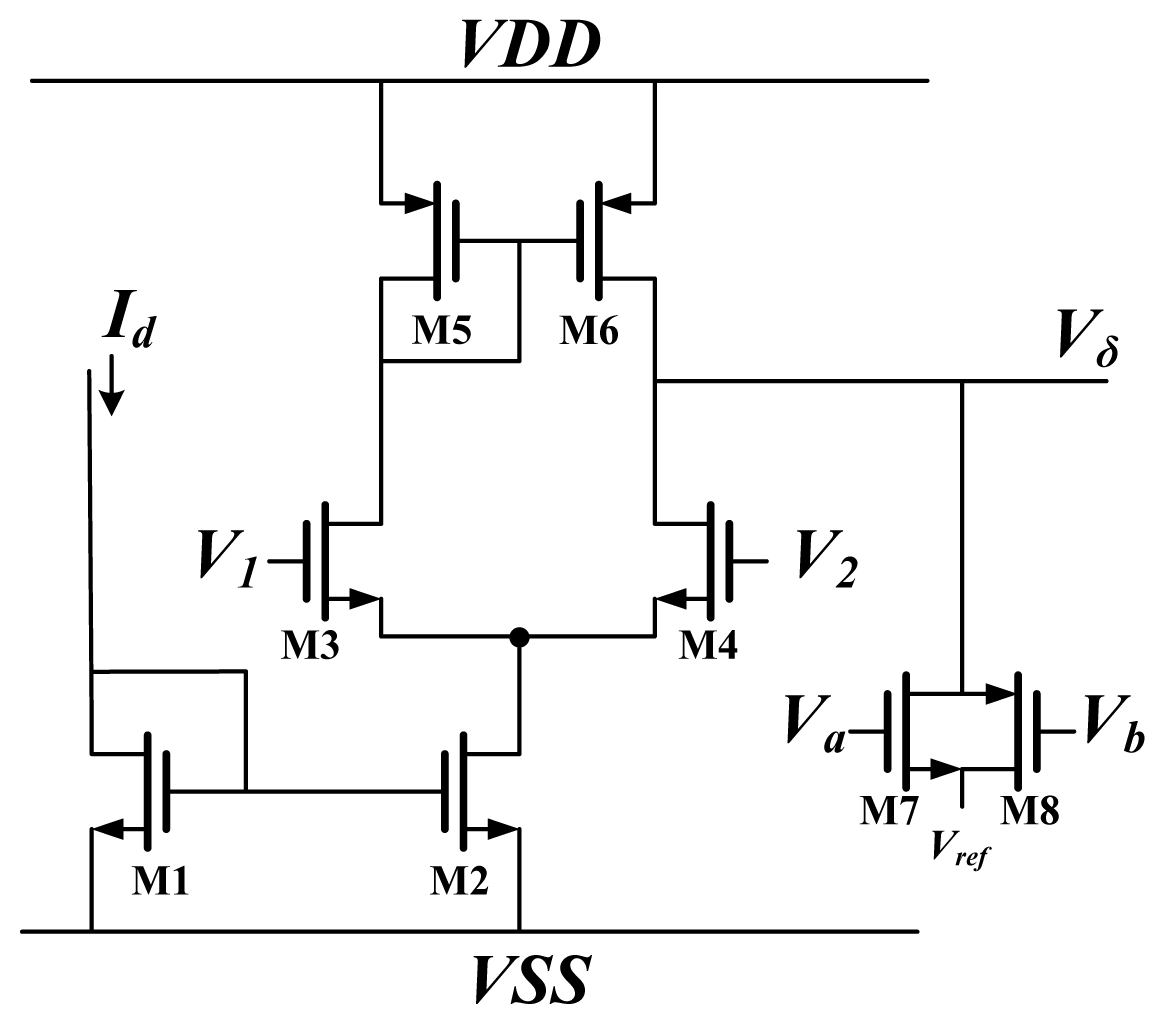
The schematic diagram of a Delta block is shown in
Figure 7. It is used to times the back propagate error by the differentiation of activation function. The block is used to multiply the BP error by the differentiation of activation function. The differential approximation of the activation function is represented by current
Id, and the BP error is represented by voltage. This circuit used differential pairs operated in the subthreshold region; thus, the circuit output was the same as
Equation (5). For
ON,
V1 and
V2 in
Figure 7 are replaced by
XO and
Xt respectively. For
HN,
V1 and
V2 were replaced by
Vδ× W and
Vref, respectively.