Pull-In Effect of Suspended Microchannel Resonator Sensor Subjected to Electrostatic Actuation
Abstract
:1. Introduction
2. Model Development
3. Results and Discussions
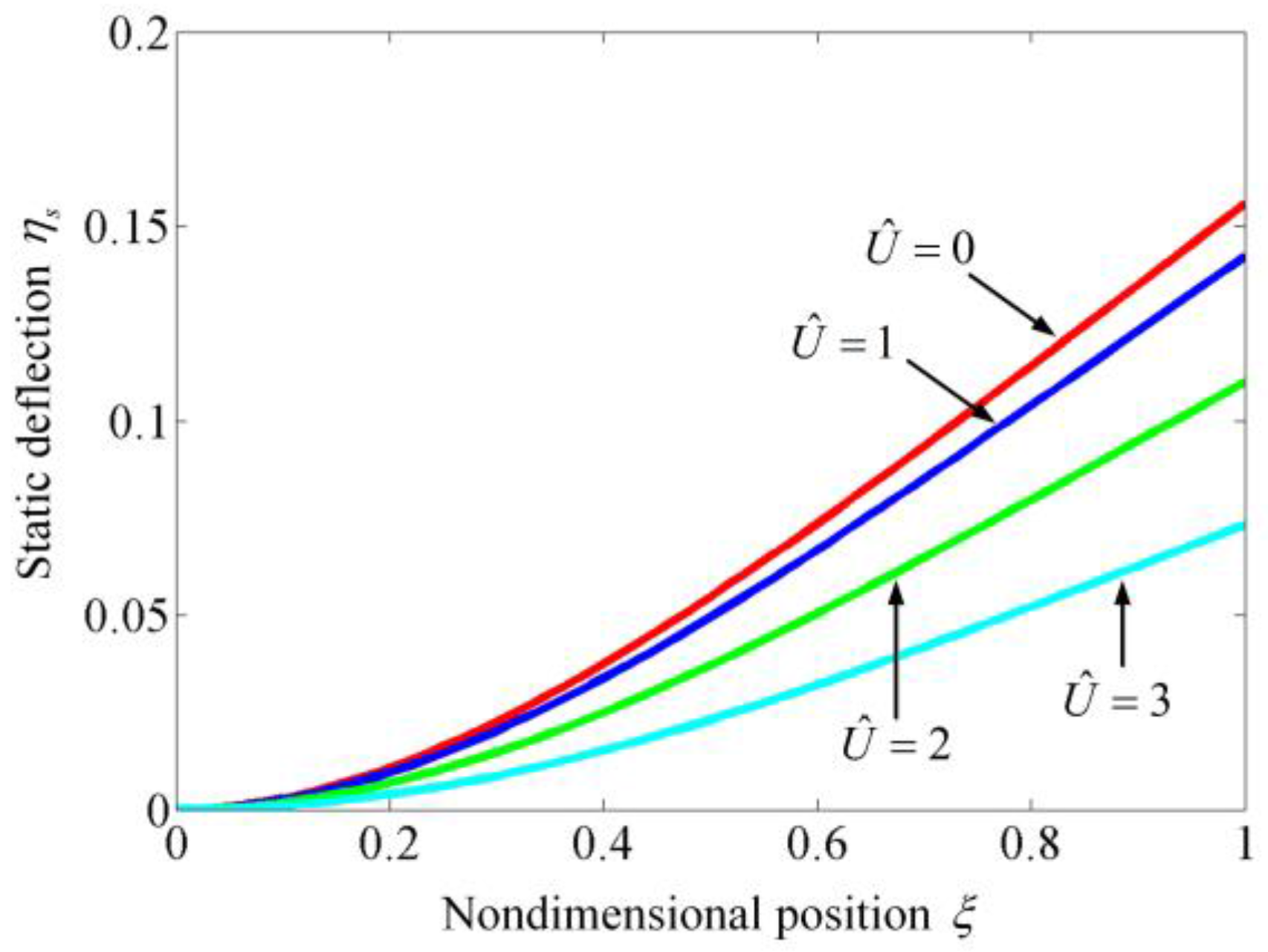
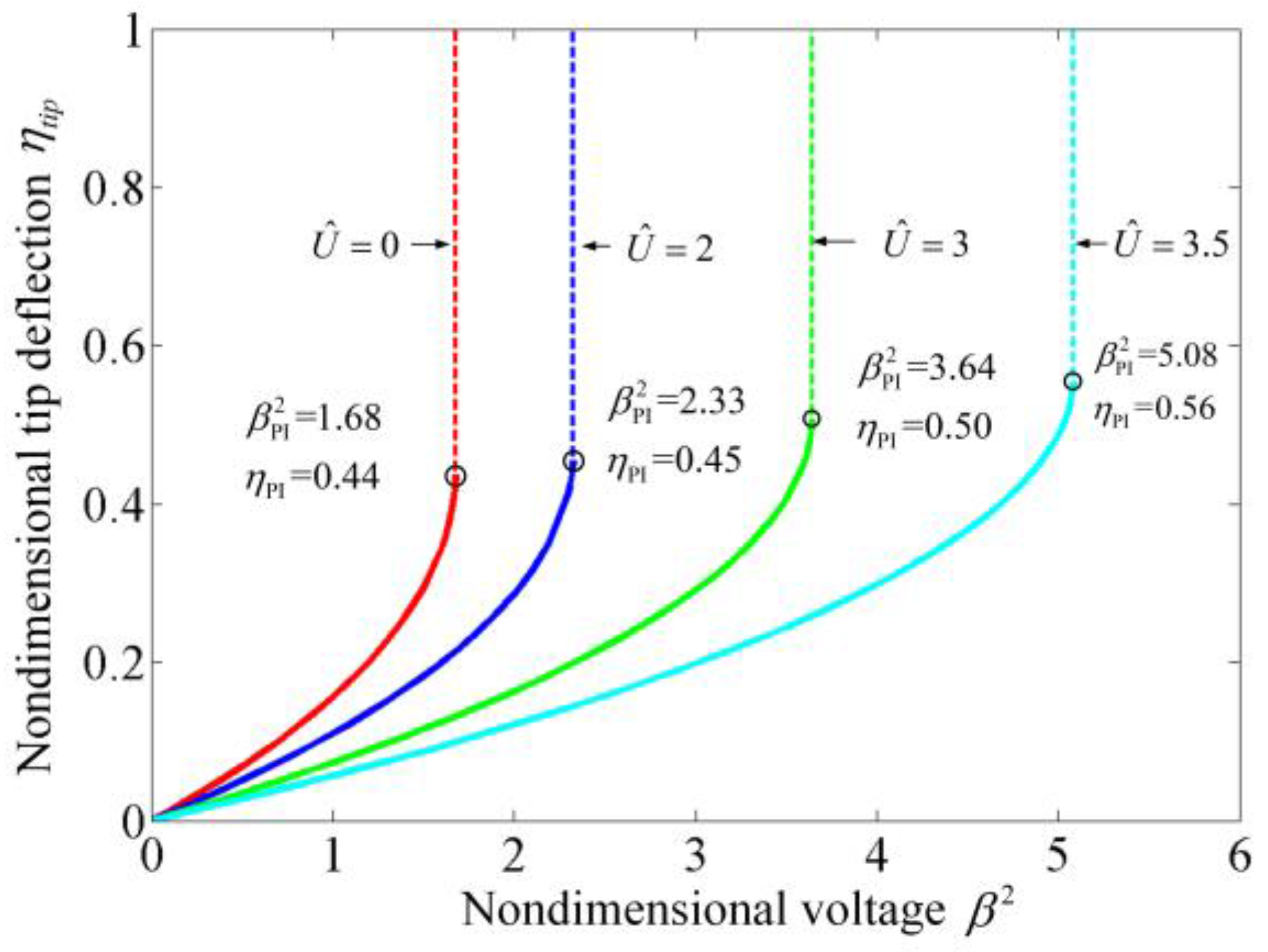
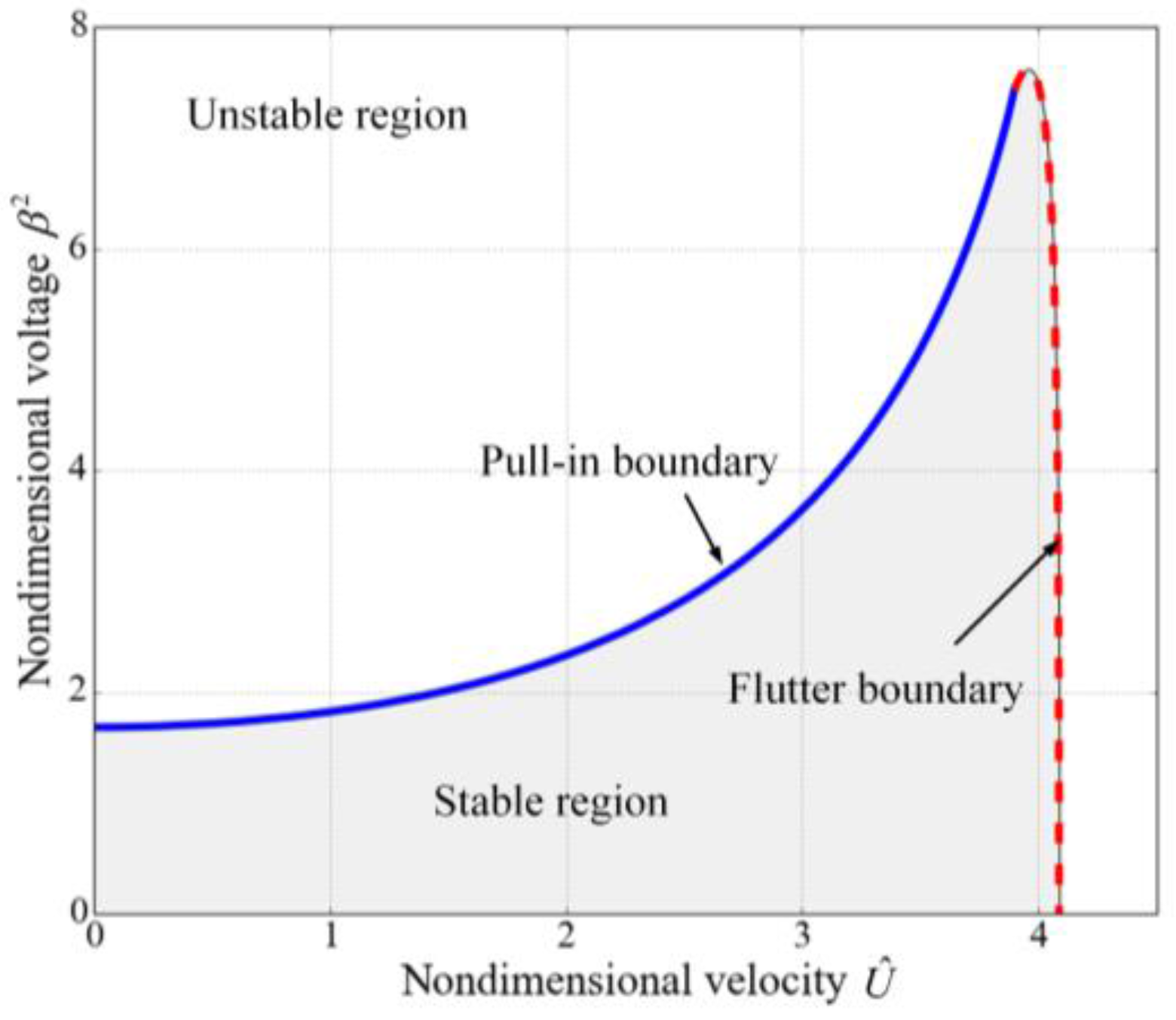
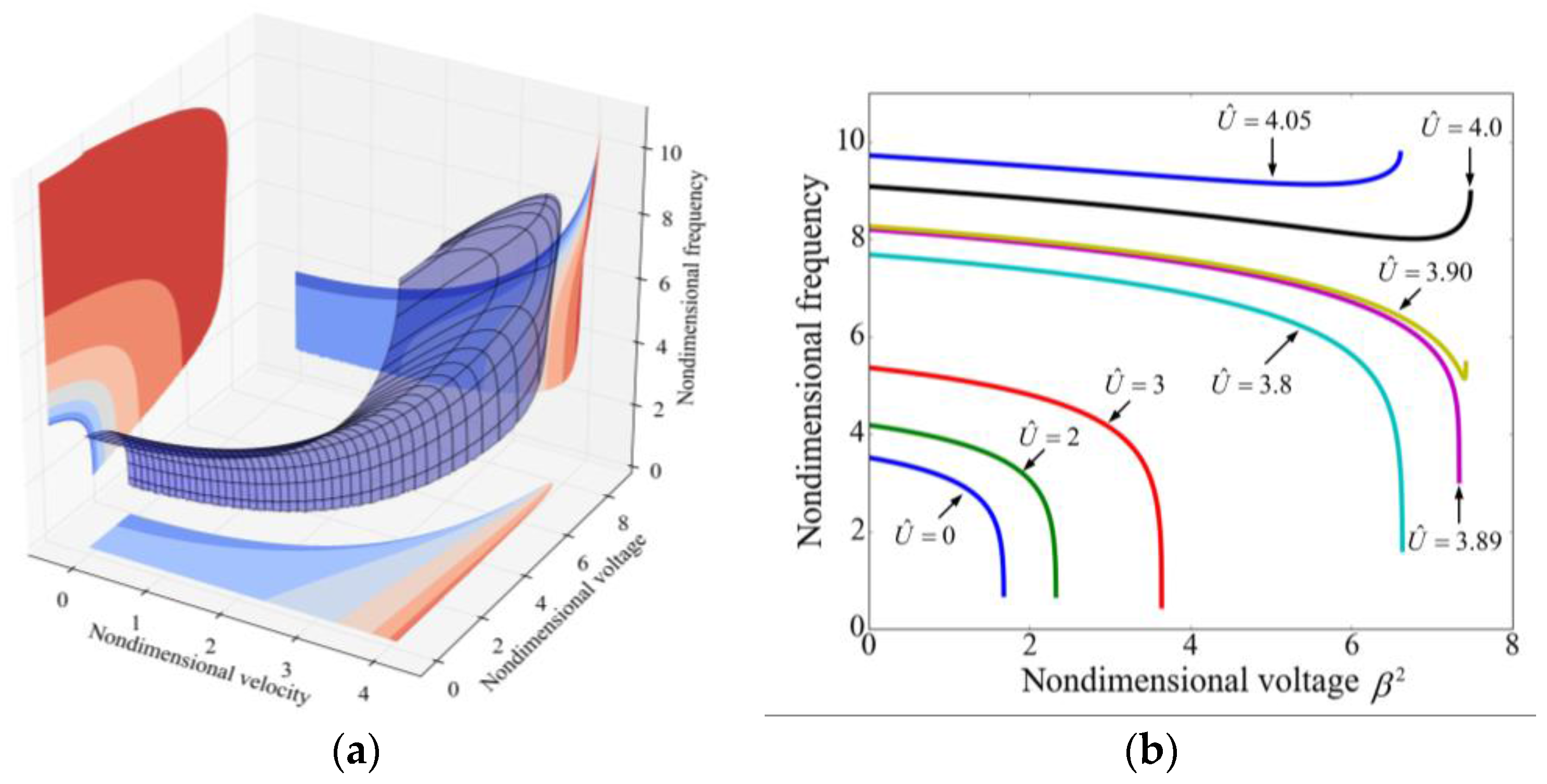
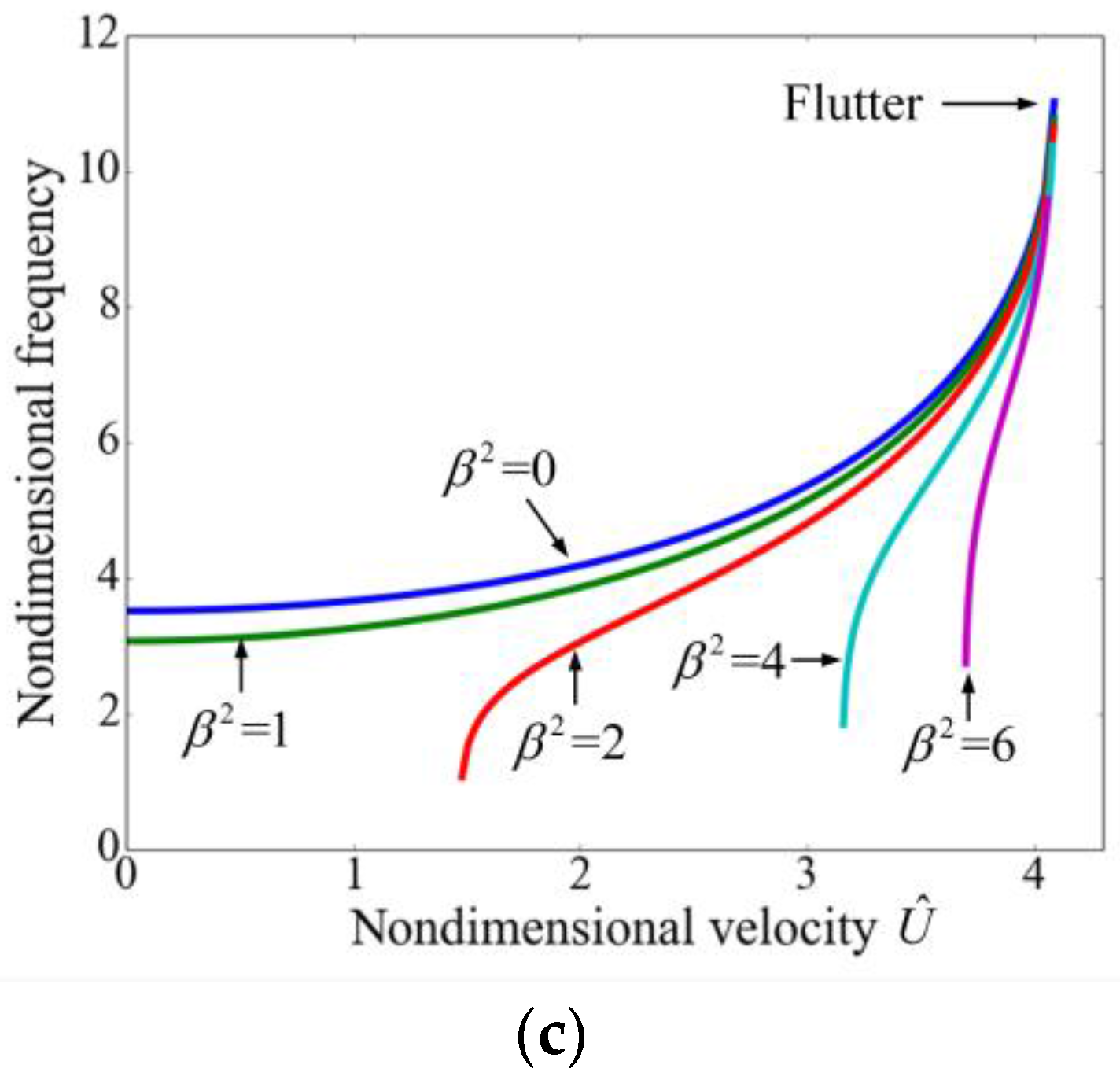
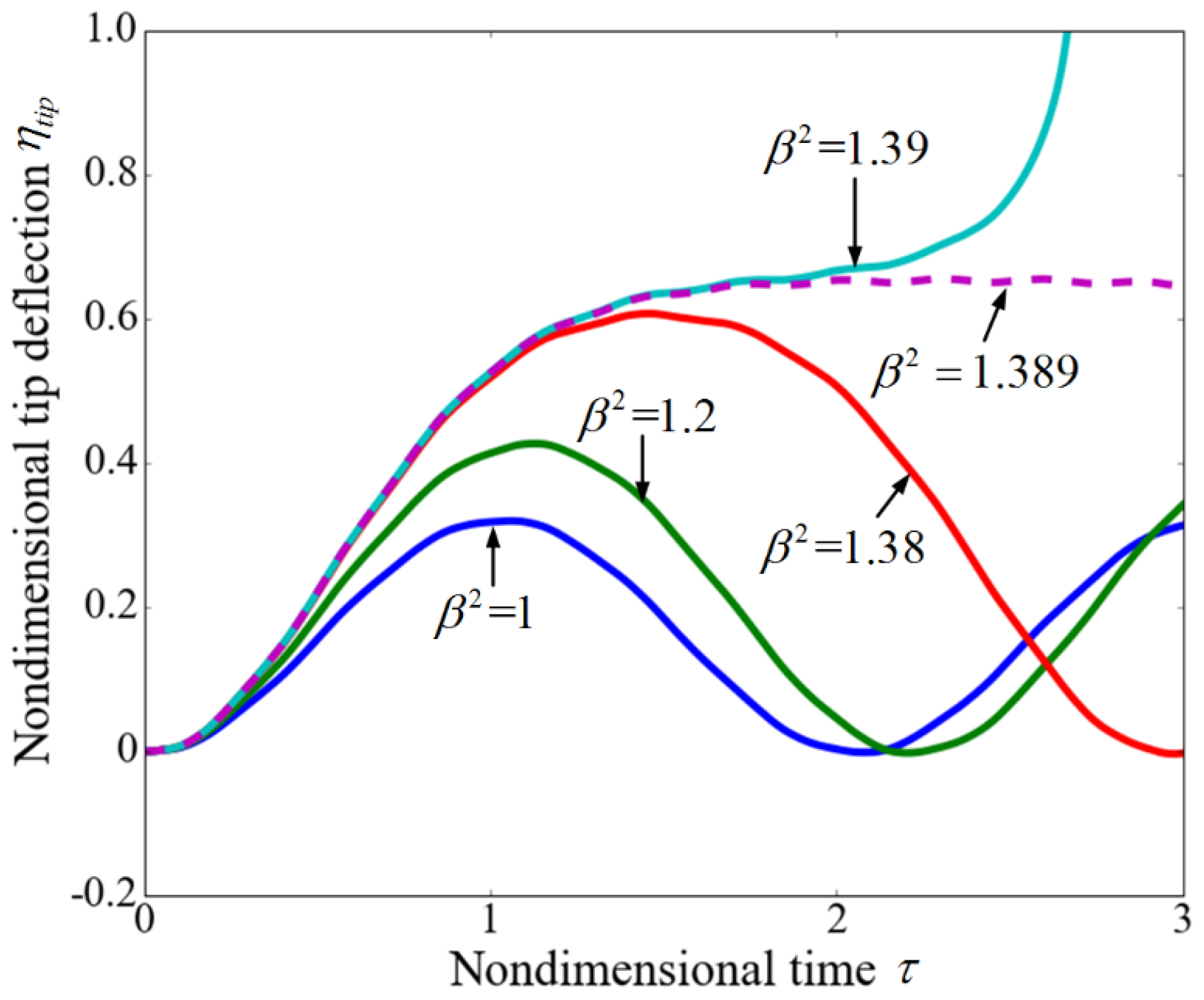
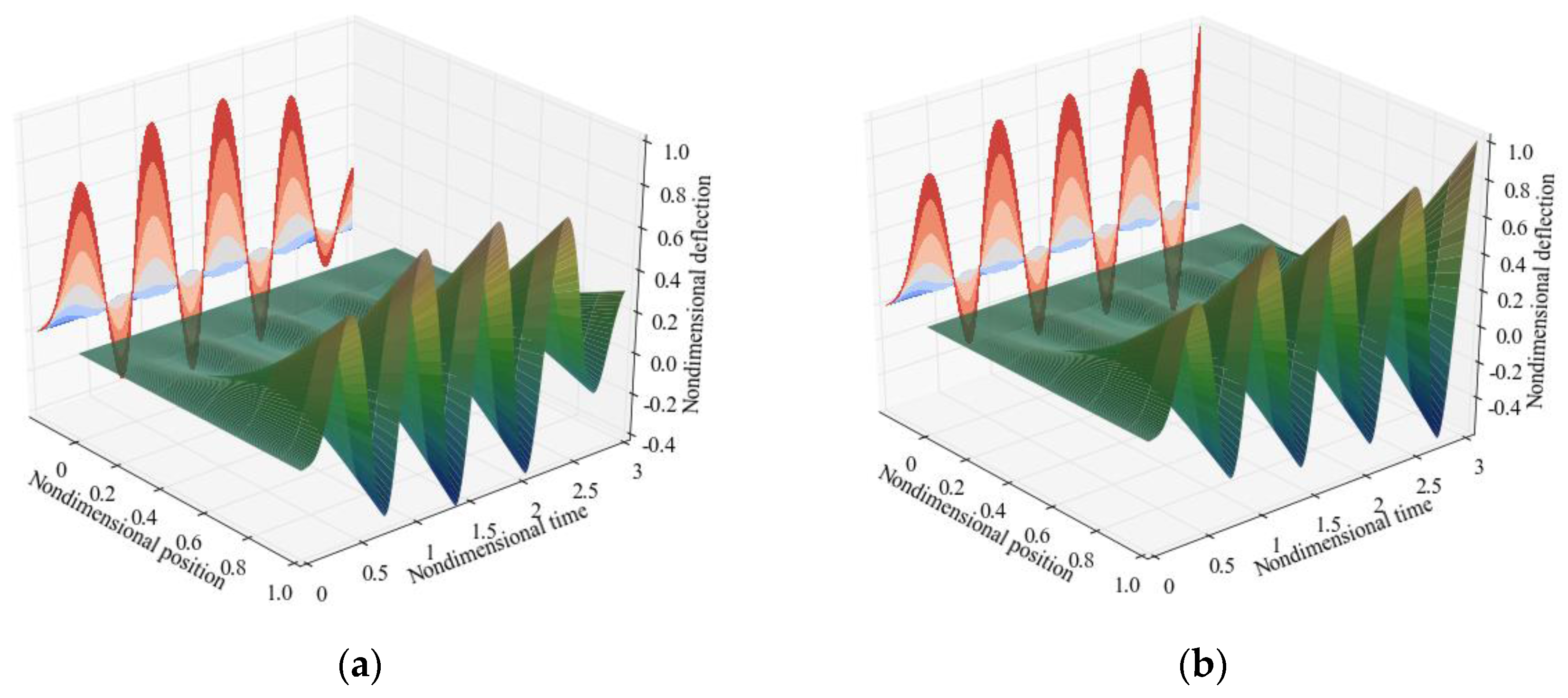
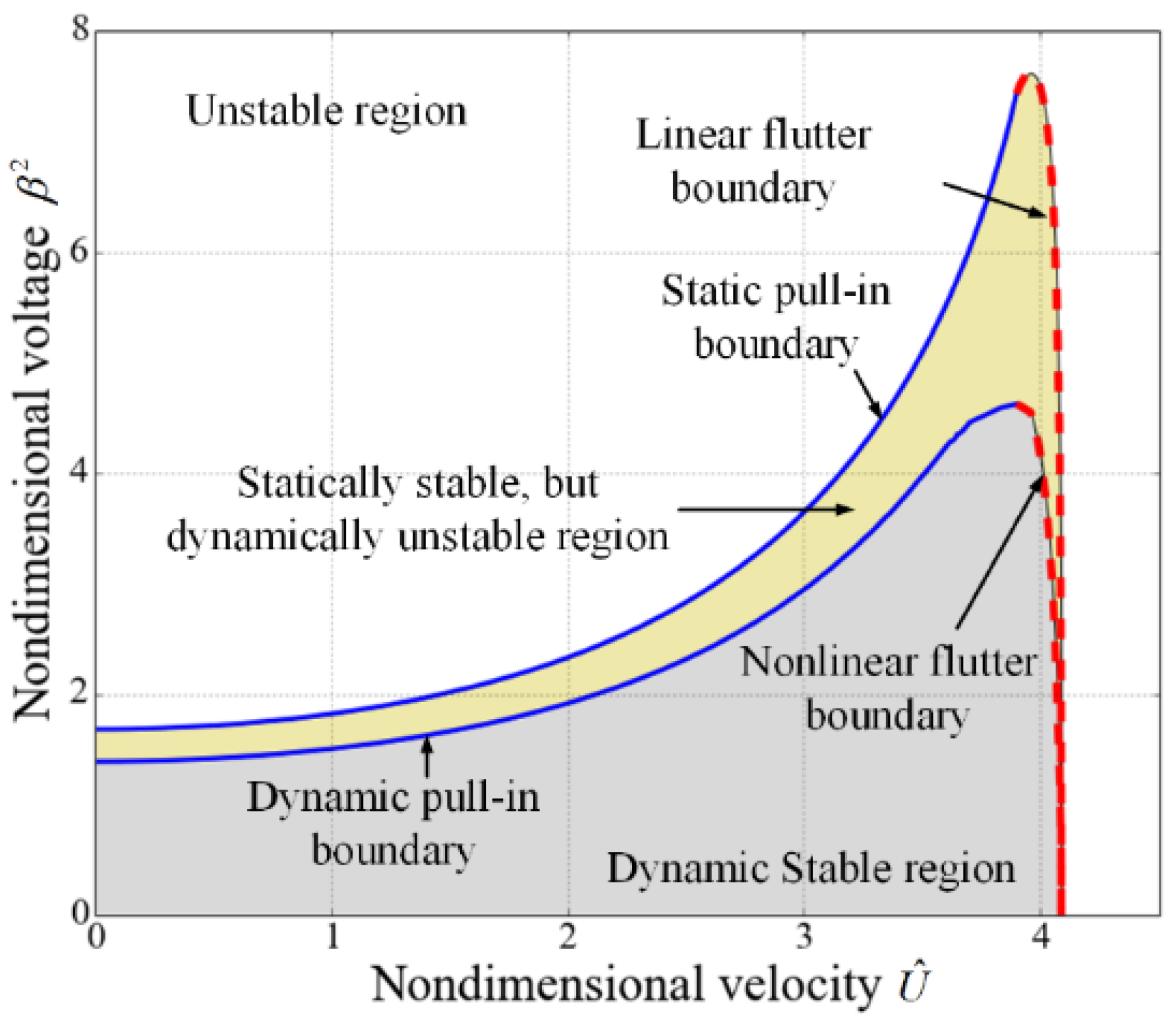
3.1. Instability Analysis
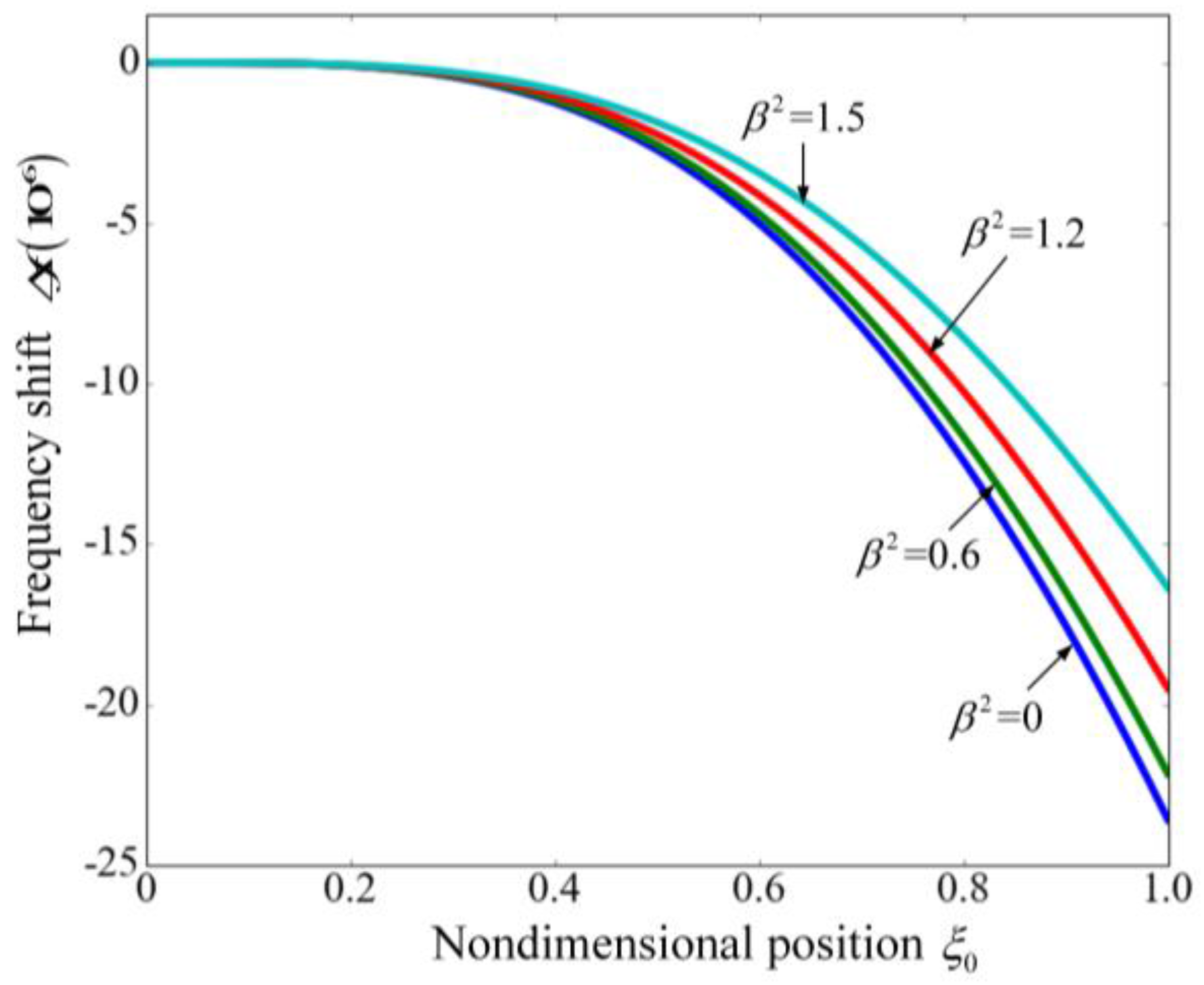
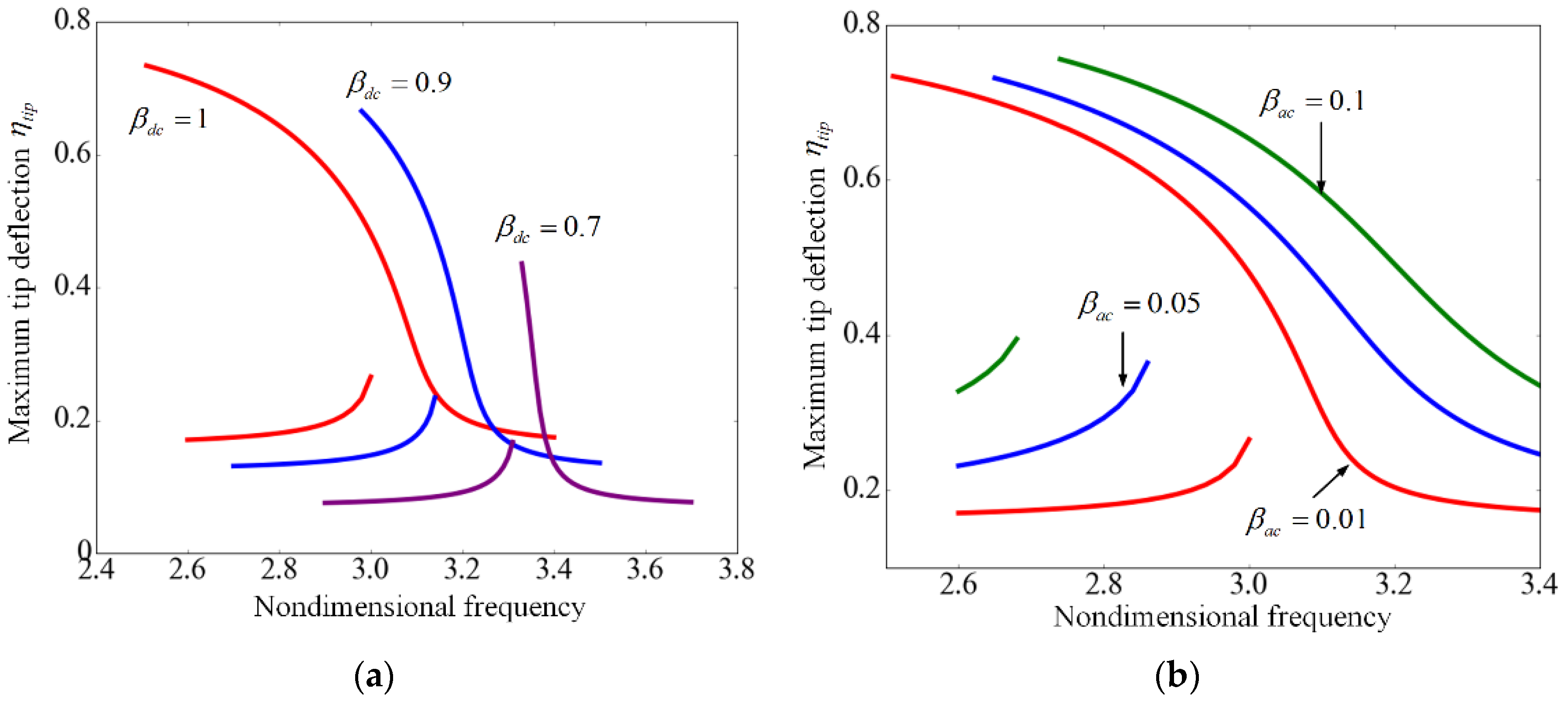
3.2. Frequency Shift
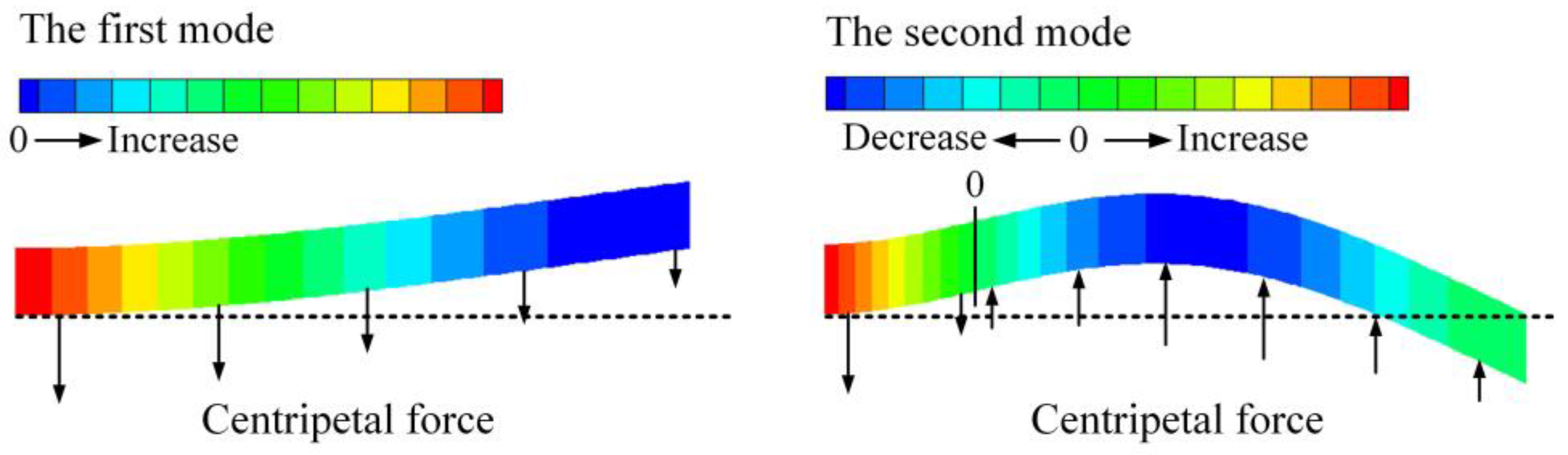
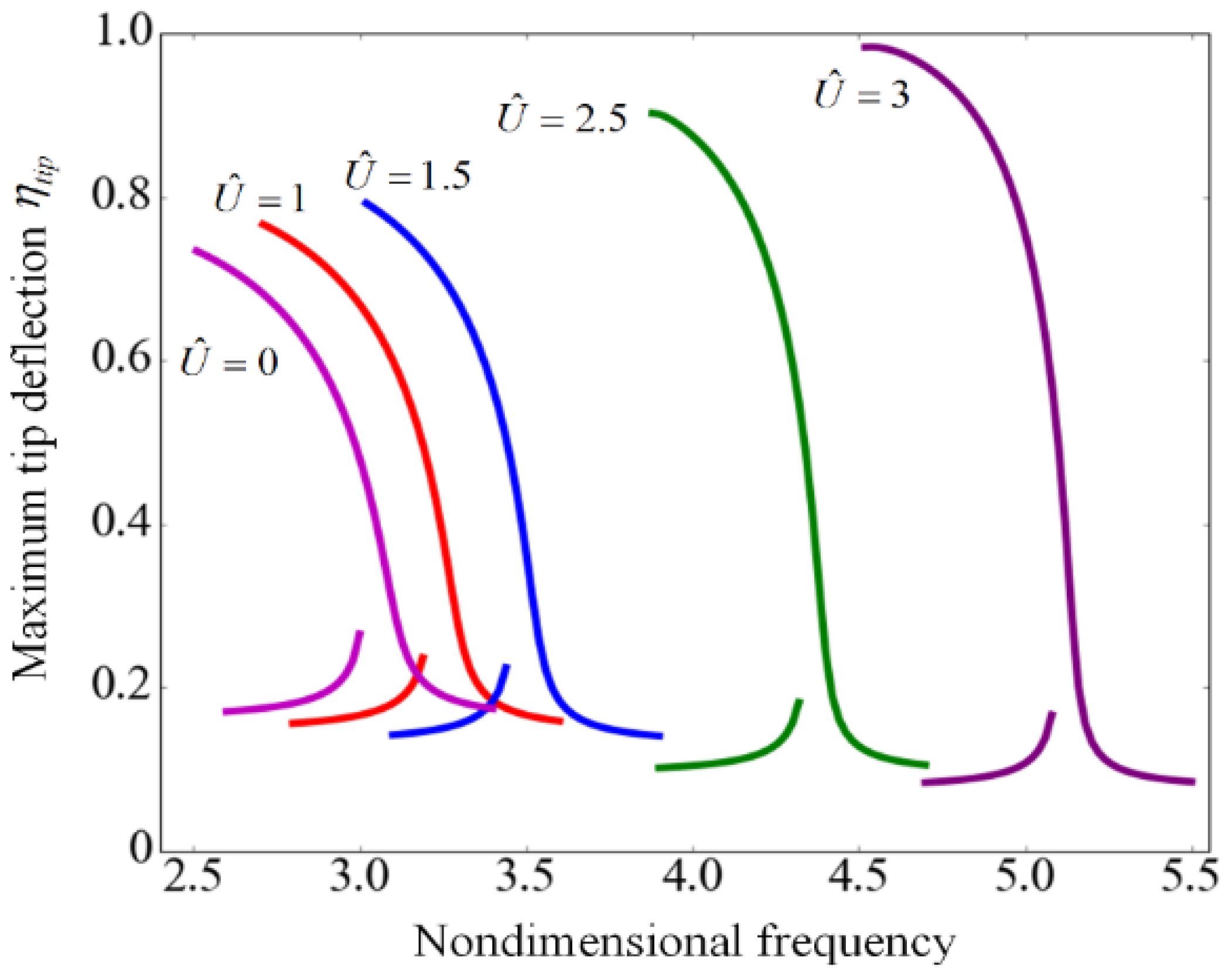
3.3. Dynamic Characteristics
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yin, L.; Qian, Q.; Wang, L. Size effect on the static behavior of electrostatically actuated microbeams. Acta Mech. Sin. 2011, 27, 445–451. [Google Scholar] [CrossRef]
- Faegh, S.; Jalili, N.; Sridhar, S. A self-sensing piezoelectric microcantilever biosensor for detection of ultrasmall adsorbed masses: Theory and experiments. Sensors 2013, 13, 6089–6108. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
- Sader, J.E.; Burg, T.P.; Manalis, S.R. Energy dissipation in microfluidic beam resonators. J. Fluid Mech. 2010, 650, 215–250. [Google Scholar] [CrossRef]
- Wang, Y.; Modena, M.M.; Platen, M.; Schaap, I.A.T.; Burg, T.P. Label-Free Measurement of Amyloid Elongation by Suspended Microchannel Resonators. Anal. Chem. 2015, 87, 1821–1828. [Google Scholar] [CrossRef] [PubMed]
- Folzer, E.; Khan, T.A.; Schmidt, R.; Finkler, C.; Huwyler, J.; Mahler, H.; Koulov, A.V. Determination of the Density of Protein Particles Using a Suspended Microchannel Resonator. J. Pharm. Sci. 2015, 104, 4034–4040. [Google Scholar] [CrossRef] [PubMed]
- Accoto, C.; Qualtieri, A.; Pisanello, F.; Ricciardi, C. Two-Photon Polymerization Lithography and Laser Doppler Vibrometry of a SU-8-Based Suspended Microchannel Resonator. J. Microelectromech. Syst. 2015, 24, 1038–1042. [Google Scholar] [CrossRef]
- Minhyuk, Y.; Il, L.; Sangmin, J.; Jungchul, L. Facile Phase Transition Measurements for Nanogram Level Liquid Samples Using Suspended Microchannel Resonators. IEEE Sens. J. 2014, 14, 781–785. [Google Scholar]
- Lee, I.; Park, K.; Lee, J. Note: precision viscosity measurement using suspended microchannel resonators. Rev. Sci. Instrum. 2012, 83, 116106. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.F.; Schmid, S.; Larsen, P.E.; Davis, Z.J.; Yan, W.; Stenby, E.H.; Boisen, A. Online measurement of mass density and viscosity of pL fluid samples with suspended microchannel resonator. Sens. Actuators B Chem. 2013, 185, 456–461. [Google Scholar] [CrossRef]
- Malvar, O.; Ramos, D.; Martinez, C.; Kosaka, P.; Tamayo, J.; Calleja, M. Highly Sensitive Measurement of Liquid Density in Air Using Suspended Microcapillary Resonators. Sensors 2015, 15, 7650–7657. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 2003, 83, 2698–2700. [Google Scholar] [CrossRef]
- Lee, J.; Bryan, A.K.; Manalis, S.R. High precision particle mass sensing using microchannel resonators in the second vibration mode. Rev. Sci. Instrum. 2011, 82, 023704. [Google Scholar] [CrossRef] [PubMed]
- Olcum, S.; Cermak, N.; Wasserman, S.C.; Manalis, S.R. High-speed multiple-mode mass-sensing resolves dynamic nanoscale mass distributions. Nat. Commun. 2015, 6, 7070. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Sader, J.E.; Manalis, S.R. Nonmonotonic Energy Dissipation in Microfluidic Resonators. Phys. Rev. Lett. 2009, 102, 228103. [Google Scholar] [CrossRef] [PubMed]
- Sader, J.E.; Lee, J.; Manalis, S.R. Energy dissipation in microfluidic beam resonators: Dependence on mode number. J. Appl. Phys. 2010, 108, 114507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sader, J.E.; Burg, T.P.; Lee, J.; Manalis, S.R. Energy dissipation in microfluidic beam resonators: Effect of Poisson’s ratio. Phys. Rev. E 2011, 84, 026304. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.M.; Yan, H.; Jiang, H.M.; Hu, K.M.; Peng, Z.K.; Meng, G. Dynamics of suspended microchannel resonators conveying opposite internal fluid flow: Stability, frequency shift and energy dissipation. J. Sound Vib. 2016, 368, 103–120. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L. The nonlinear response of resonant microbeam systems with purely-parametric electrostatic actuation. J. Micromech. Microeng. 2006, 16, 890–899. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Jalili, N. Coupled flexural-torsional nonlinear vibrations of piezoelectrically actuated microcantilevers with application to friction force microscopy. J. Vib. Acoust. 2008, 130. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Kumar, V.; Shaw, S.W.; Turner, K.L. The non-linear dynamics of electromagnetically actuated microbeam resonators with purely parametric excitations. Int. J. Nonlinear Mech. 2013, 55, 79–89. [Google Scholar] [CrossRef]
- Burg, T.P.; Mirza, A.R.; Milovic, N.; Tsau, C.H. Vacuum-Packaged Suspended Microchannel Resonant Mass Sensor for Biomolecular Detection. J. Microelectromech. Syst. 2006, 15, 1466–1476. [Google Scholar] [CrossRef]
- Zhang, W.M.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuator A Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Younis, M.I.; Abdel-Rahman, E.M. Dynamic pull-in phenomenon in MEMS resonators. Nonlinear Dyn. 2007, 48, 153–163. [Google Scholar] [CrossRef]
- Mobki, H.; Rezazadeh, G.; Sadeghi, M.; Vakili-Tahami, F.; Seyyed-Fakhrabadi, M. A comprehensive study of stability in an electro-statically actuated micro-beam. Int. J. Nonlinear Mech. 2013, 48, 78–85. [Google Scholar] [CrossRef]
- Chaterjee, S.; Pohit, G. A large deflection model for the pull-in analysis of electrostatically actuated microcantilever beams. J. Sound Vib. 2009, 322, 969–986. [Google Scholar] [CrossRef]
- Jabbari, G.; Shabani, R.; Rezazadeh, G. Frequency response of an electrostatically actuated micro resonator in contact with incompressible fluid. Microsyst. Technol. 2016. [Google Scholar] [CrossRef]
- Hosseini, I.I.; Zand, M.M.; Lotfi, M. Dynamic pull-in and snap-through behavior in micro/nano mechanical memories considering squeeze film damping. Microsyst. Technol. 2016. [Google Scholar] [CrossRef]
- De Sudipto, K.; Aluru, N. A hybrid full-Lagrangian technique for the static and dynamic analysis of magnetostatic MEMS. J. Micromech. Microeng. 2006, 16, 2646–2658. [Google Scholar]
- De, S.K.; Aluru, N.R. Full-Lagrangian schemes for dynamic analysis of electrostatic MEMS. J. Microelectromech. Syst. 2004, 13, 737–758. [Google Scholar] [CrossRef]
- Mojahedi, M.; Zand, M.M.; Ahmadian, M.T. Static pull-in analysis of electrostatically actuated microbeams using homotopy perturbation method. Appl. Math. Model. 2010, 34, 1032–1041. [Google Scholar] [CrossRef]
- Rinaldi, S.; Prabhakar, S.; Vengallatore, S.; Paidoussis, M.P. Dynamics of microscale pipes containing internal fluid flow: Damping, frequency shift, and stability. J. Sound Vib. 2010, 329, 1081–1088. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.T.; Ni, Q.; Wu, Y. Flexural vibrations of microscale pipes conveying fluid by considering the size effects of micro-flow and micro-structure. Int. J. Eng. Sci. 2013, 71, 92–101. [Google Scholar] [CrossRef]
- Wang, Y.; Masoumi, M.; Gaucher-Petitdemange, M. Damping analysis of a flexible cantilever beam containing an internal fluid channel: Experiment, modeling and analysis. J. Sound Vib. 2015, 340, 331–342. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Norouzzadeh, A.; Sahmani, S. Size-dependent vibration and instability of fluid-conveying functionally graded microshells based on the modified couple stress theory. Microfluid. Nanofluid. 2015, 19, 509–522. [Google Scholar] [CrossRef]
- Abbasnejad, B.; Shabani, R.; Rezazadeh, G. Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid. Microfluid. Nanofluid. 2015, 19, 577–584. [Google Scholar] [CrossRef]
- Kutin, J.; Bajsic, I. Fluid-dynamic loading of pipes conveying fluid with a laminar mean-flow velocity profile. J. Fluid Struct. 2014, 50, 171–183. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Zhao, H.; Liu, Y.; Wen, X. Flexural vibration band gap in a periodic fluid-conveying pipe system based on the Timoshenko beam theory. J. Vib. Acoust. 2011, 133, 73–74. [Google Scholar] [CrossRef]
- Dai, H.L.; Wang, L.; Ni, Q. Dynamics and pull-in instability of electrostatically actuated microbeams conveying fluid. Microfluid. Nanofluid. 2015, 18, 49–55. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Yan, H.; Zhang, W.M.; Jiang, H.M.; Hu, K.M.; Peng, Z.K.; Meng, G. Dynamical characteristics of fluid-conveying microbeams actuated by electrostatic force. Microfluid. Nanofluid. 2016, 20, 137. [Google Scholar] [CrossRef]
- Huang, K.R.; Chang, J.S.; Chao, S.D.; Wu, K.C. Beam model and three dimensional numerical simulations on suspended microchannel resonators. AIP Adv. 2012, 2, 149–158. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Younis, M.I.; Abdel-Rahman, E.M. Reduced-order models for MEMS applications. Nonlinear Dyn. 2005, 41, 211–236. [Google Scholar] [CrossRef]
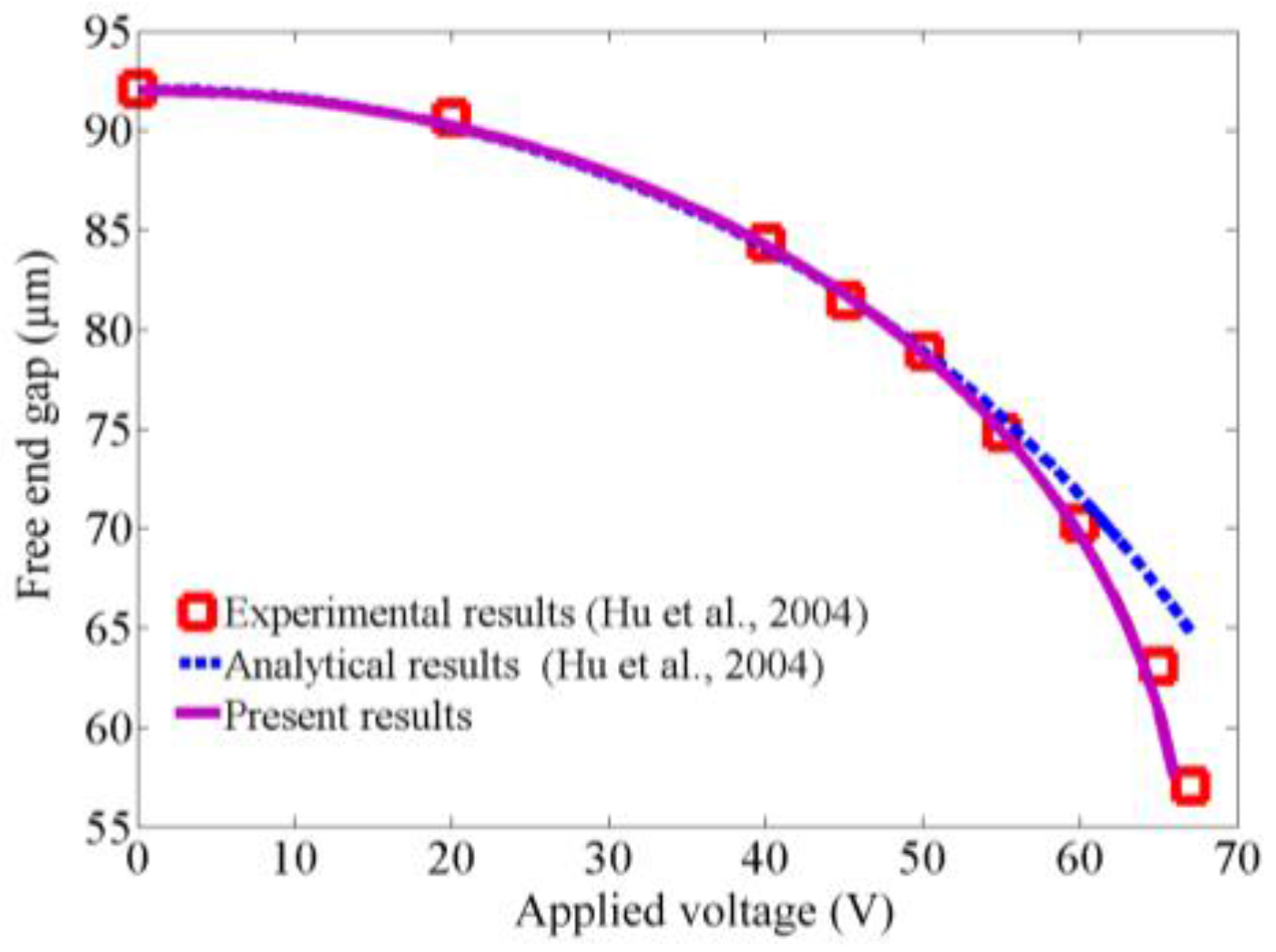
- Hu, Y.C.; Chang, C.; Huang, S. Some design considerations on the electrostatically actuated microstructures. Sens. Actuator A Phys. 2004, 112, 155–161. [Google Scholar] [CrossRef]
- Dohn, S.; Svendsen, W.; Boisen, A.; Hansen, O. Mass and position determination of attached particles on cantilever based mass sensors. Rev. Sci. Instrum. 2007, 78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdel-Rahman, E.M.; Younis, M.I.; Nayfeh, A.H. Characterization of the mechanical behavior of an electrically actuated microbeam. J. Micromech. Microeng. 2002, 12, 759. [Google Scholar] [CrossRef]
- Das, K.; Batra, R.C. Pull-in and snap-through instabilities in transient deformations of microelectromechanical systems. J. Micromech. Microeng. 2009, 19, 605–627. [Google Scholar] [CrossRef]




| n | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| i | ||||||
| 1 | 0 | 0 | 0 | 0 | ||
| 2 | 0 | 0 | 0 | 0 | ||
| 3 | 0 | 0 | 0 | 0 | ||
| 4 | 0 | 0 | 0 | 0 | ||
| 5 | 0 | 0 | 0 | 0 | ||
| The Employed Modes in the Calculation | Nondimensional Pull-In Voltage | Nondimensional Pull-In Displacement |
|---|---|---|
| One mode | 4.66 | 0.67 |
| Two modes | 5.21 | 0.54 |
| Three modes | 5.04 | 0.56 |
| Four modes | 5.11 | 0.56 |
| Five modes | 5.08 | 0.56 |
| () | (p.p.m) | |||
|---|---|---|---|---|
| The First Mode | The Second Mode | The First Mode | The Second Mode | |
| 0 | −23.58 | −1.477 | −6.705 | −6.705 |
| 0.6 | −22.15 | −1.475 | −6.708 | −6.704 |
| 1.2 | −19.49 | −1.470 | −6.720 | −6.693 |
| 1.5 | −16.36 | −1.463 | −6.742 | −6.675 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Zhang, W.-M.; Jiang, H.-M.; Hu, K.-M. Pull-In Effect of Suspended Microchannel Resonator Sensor Subjected to Electrostatic Actuation. Sensors 2017, 17, 114. https://doi.org/10.3390/s17010114
Yan H, Zhang W-M, Jiang H-M, Hu K-M. Pull-In Effect of Suspended Microchannel Resonator Sensor Subjected to Electrostatic Actuation. Sensors. 2017; 17(1):114. https://doi.org/10.3390/s17010114
Chicago/Turabian StyleYan, Han, Wen-Ming Zhang, Hui-Ming Jiang, and Kai-Ming Hu. 2017. "Pull-In Effect of Suspended Microchannel Resonator Sensor Subjected to Electrostatic Actuation" Sensors 17, no. 1: 114. https://doi.org/10.3390/s17010114





