Finite Element Analysis of Single Cell Stiffness Measurements Using PZT-Integrated Buckling Nanoneedles
Abstract
:1. Introduction
2. Finite Element Modelling of the PZT-Integrated Buckling Nanoneedle
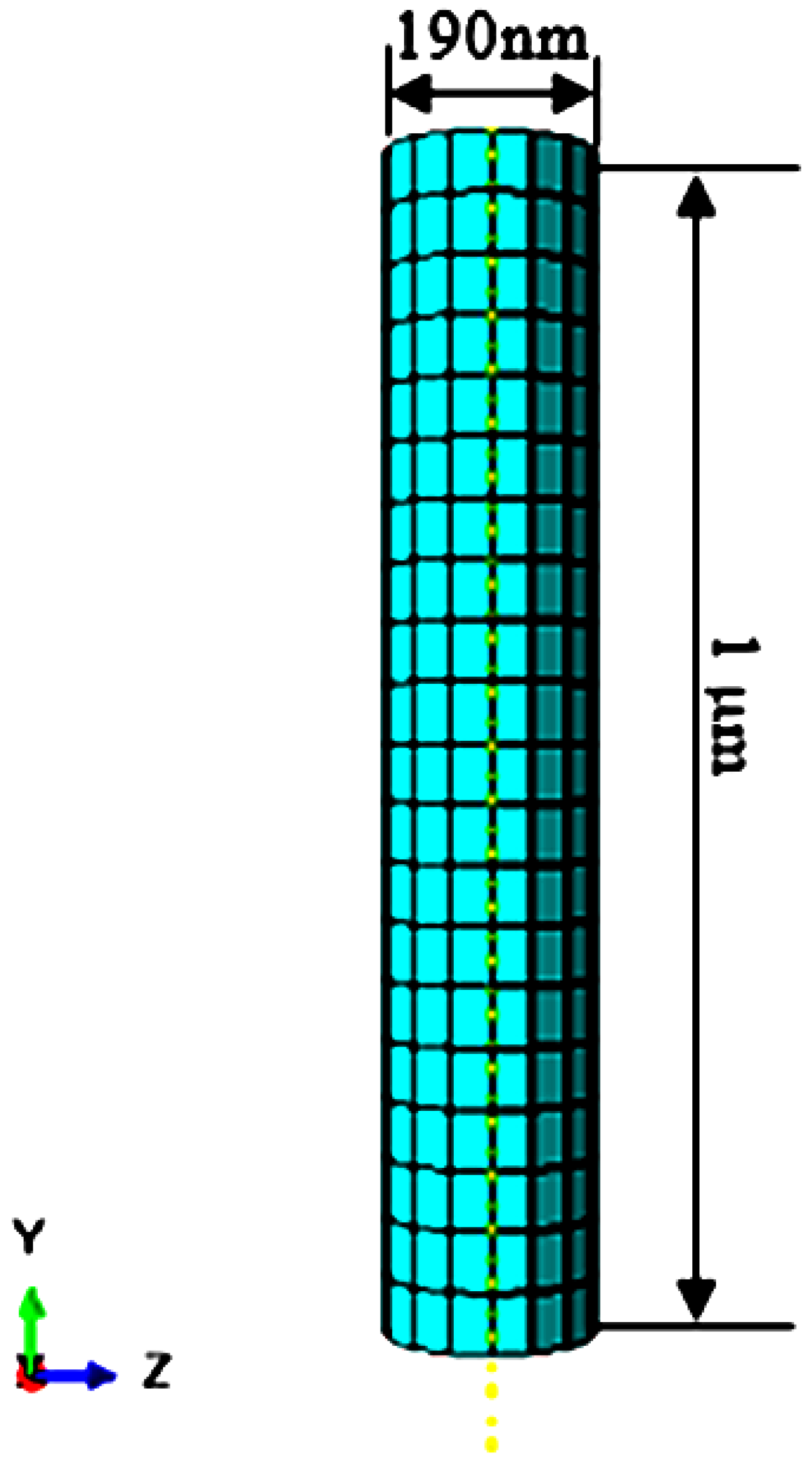
2.1. Finite Element Modelling of the PZT Sensor
- Axial sensors, where the force or stress is applied along the polarization axis, called 33-mode.
- Bending sensors, where the force or stress is applied at right angle to the polarization axis, called 31-mode.
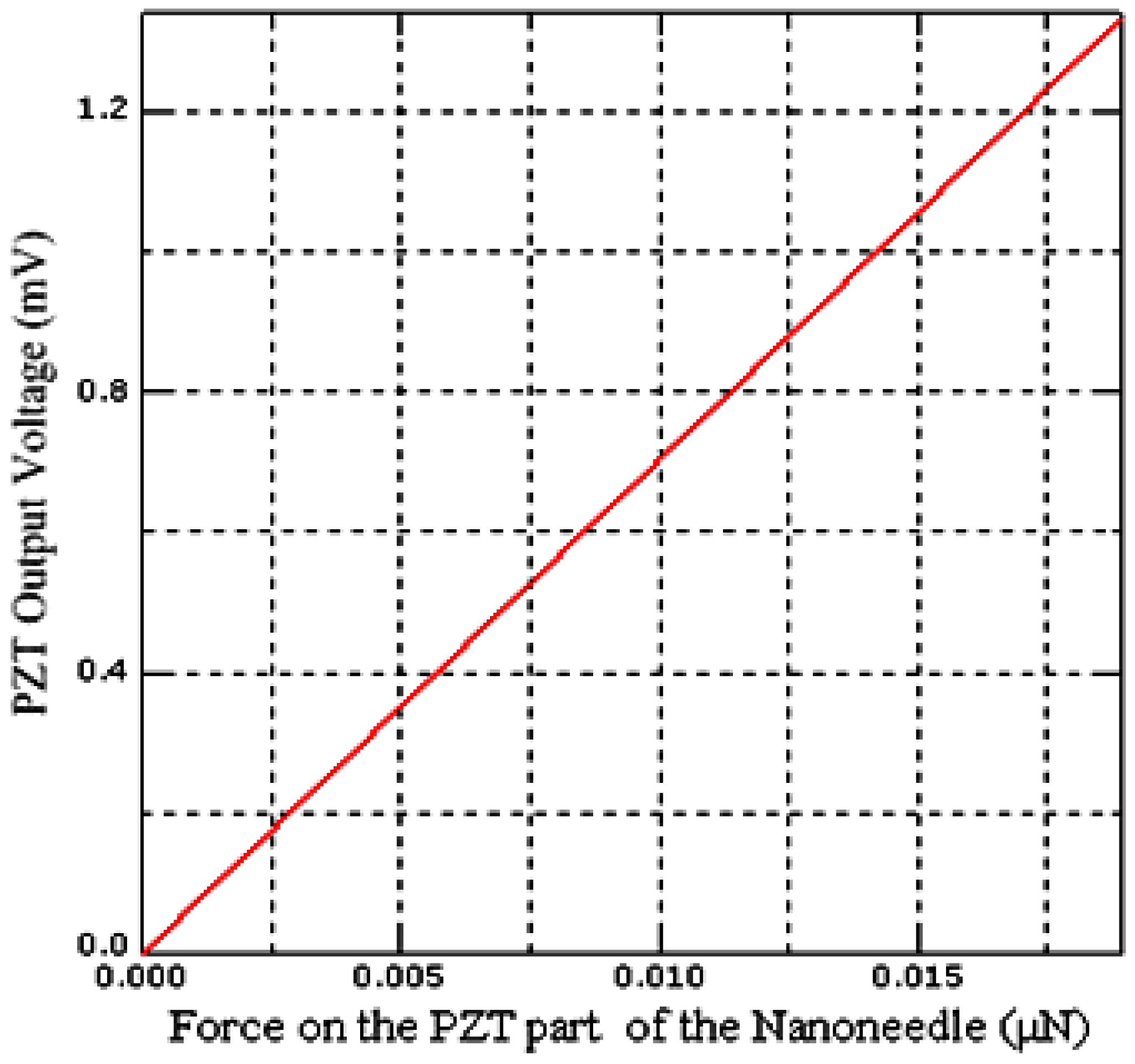
2.2. Electric Potential Analysis of the PZT Sensor
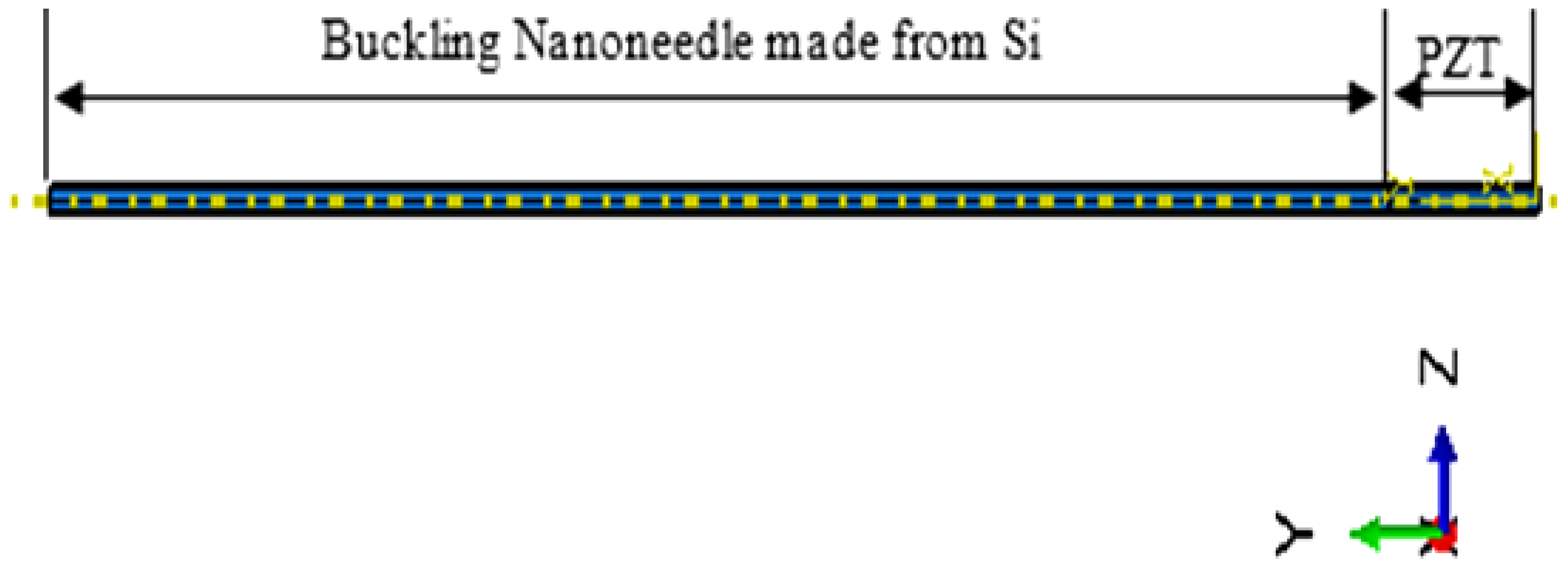
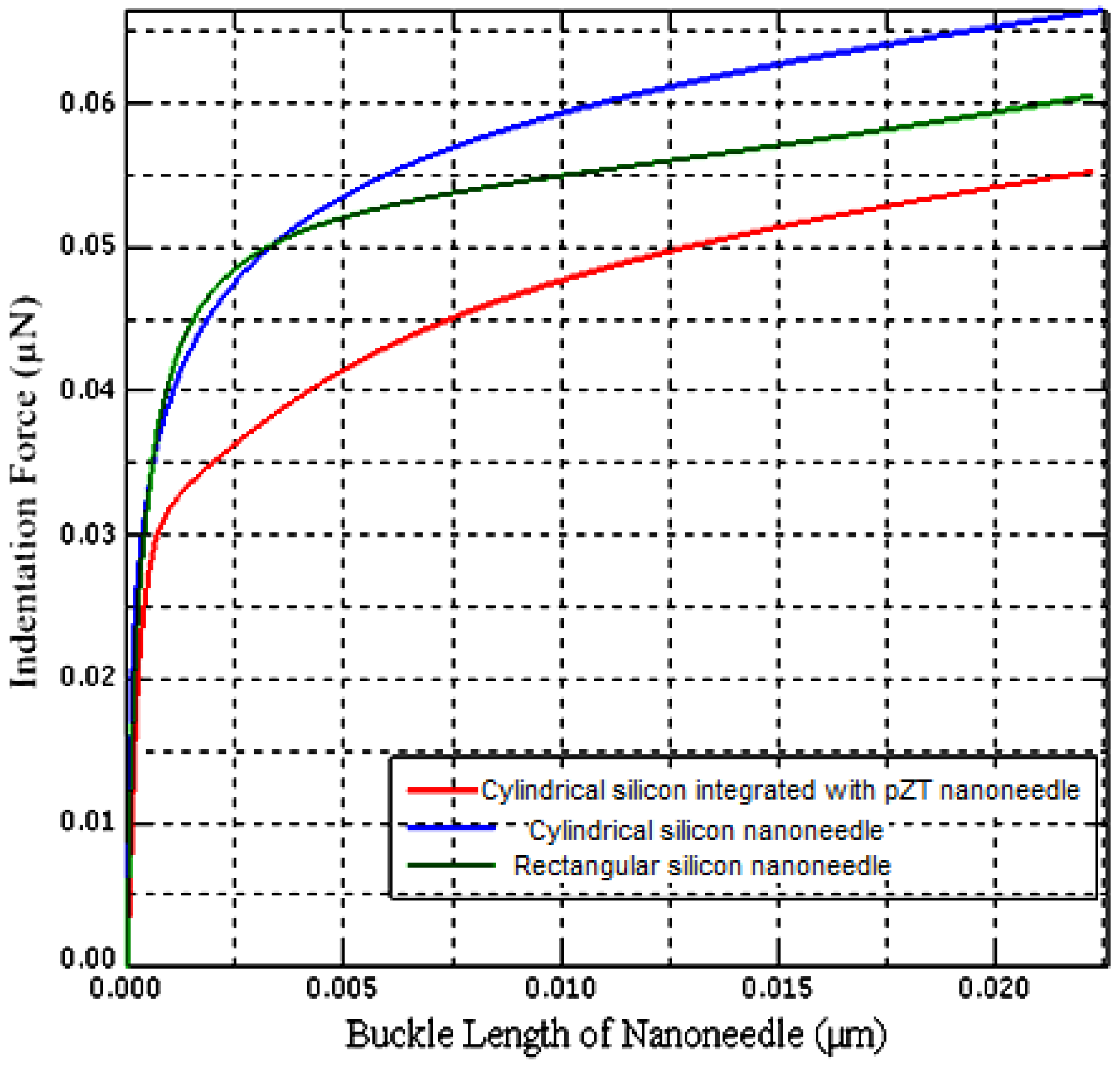
2.3. Finite Element Modelling of the Buckling Part of the Nanoneedle
2.4. Integrating the PZT Sensor with the Buckling Part of the Nanoneedle
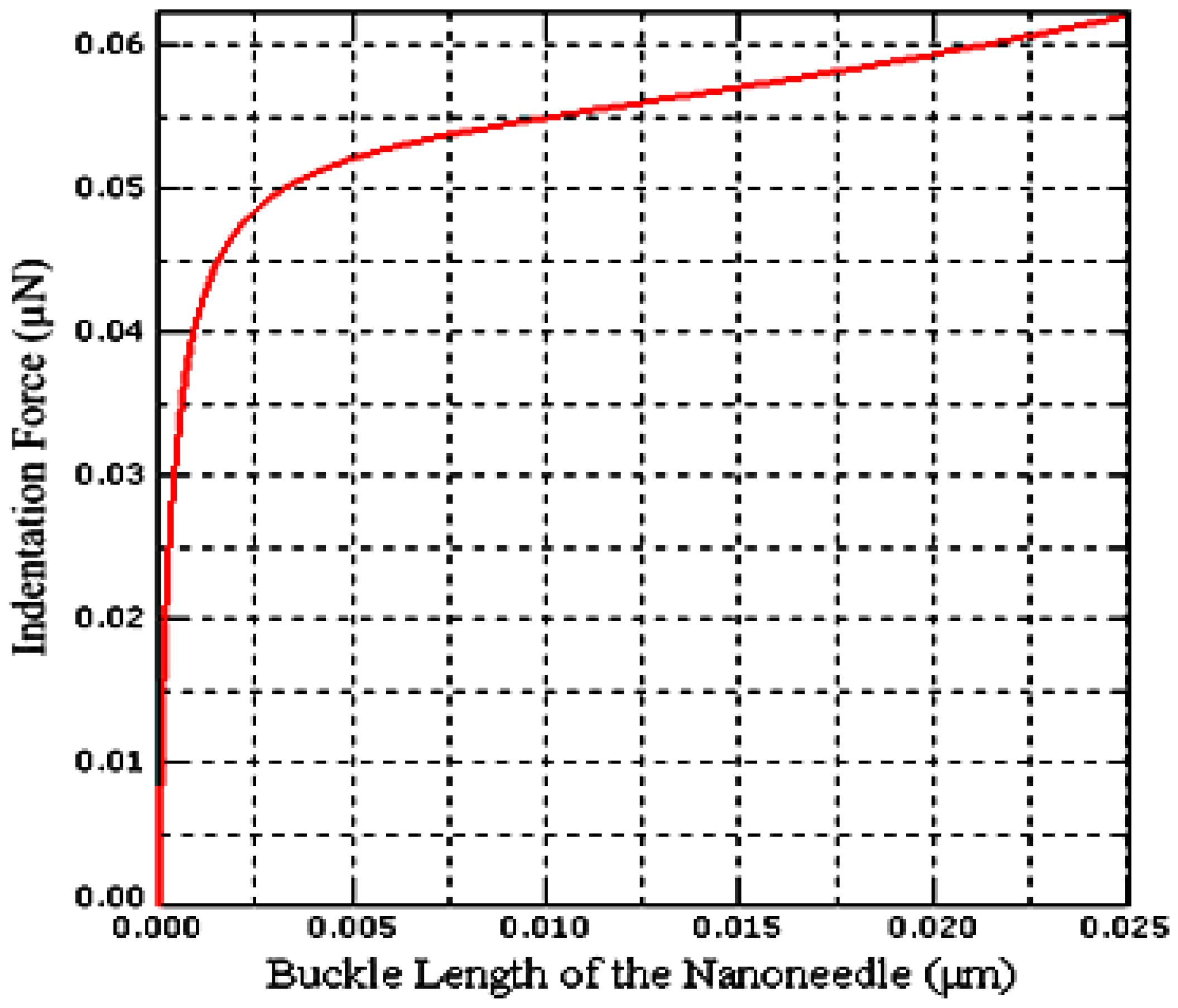
2.5. Buckling Analysis of the PZT-Integrated Buckling Nanoneedle
3. Calibration of PZT-Integrated Buckling Nanoneedle
3.1. Experimental Method Using Nano Manipulation
3.2. Calibration by the Finite Element Method
- *NODE FILE
- U
- *IMPERFECTION, FILE = Pre-buckling_analysis, STEP = 1
- 1, 0.01
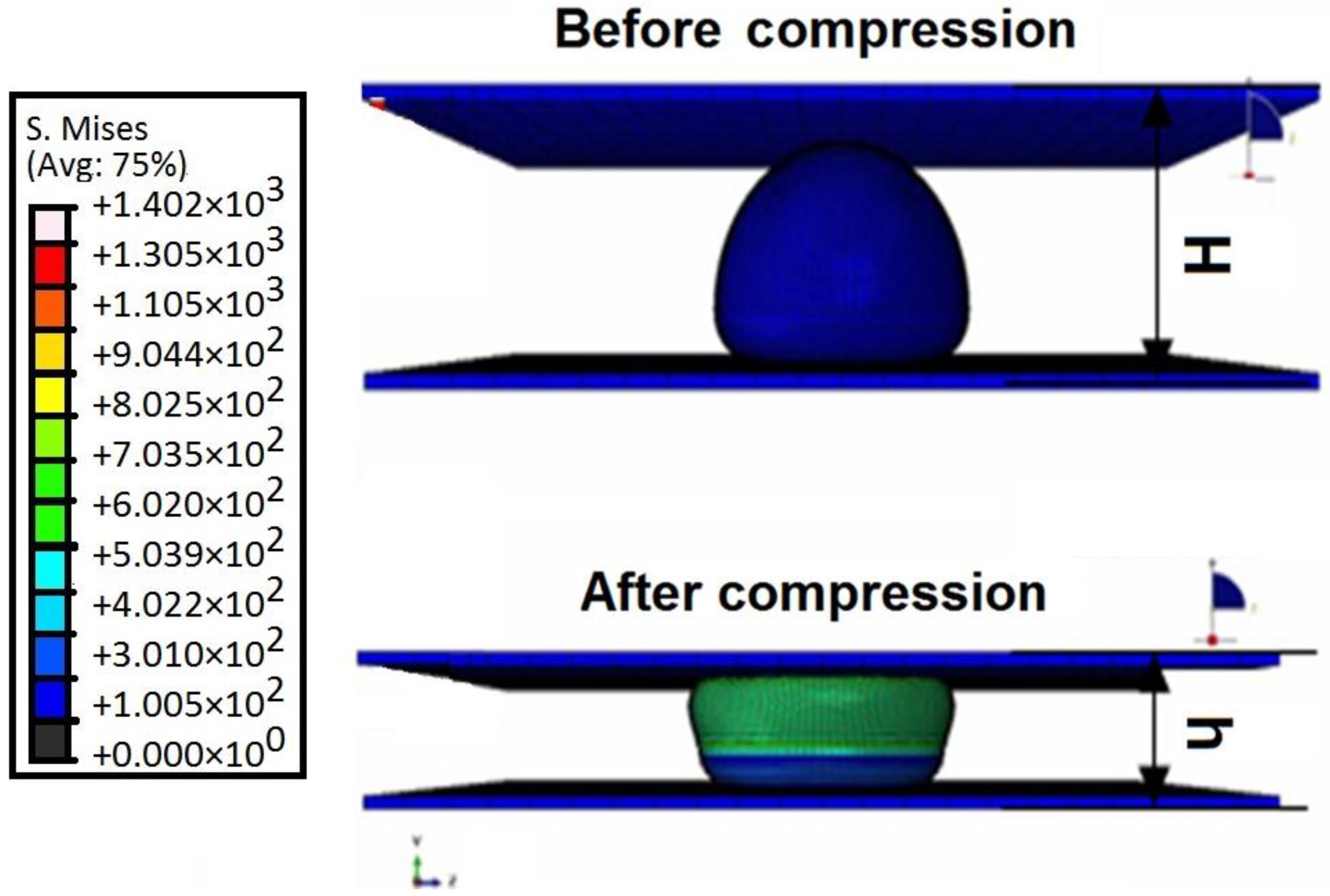
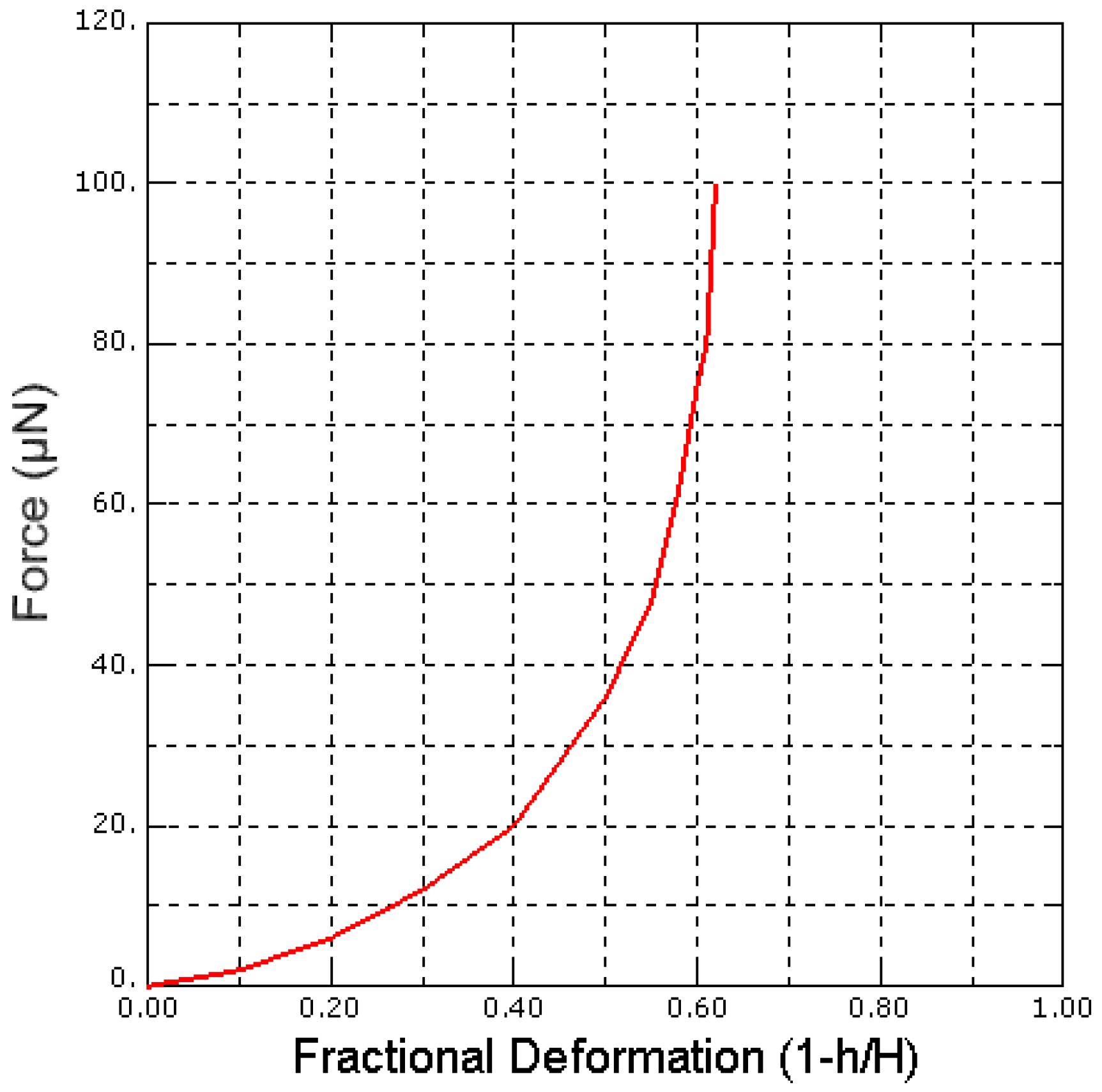
4. Finite Element Modelling and Validation for Saccharomyces cerevisiae Yeast Cells
5. Finite Element Analysis of Saccharomyces cerevisiae Stiffness Measurement Using the PZT-Integrated Buckling Nanoneedle
5.1. Effect of Pressure on Local Stiffness Measurements of a Single Saccharomyces cerevisiae Cell
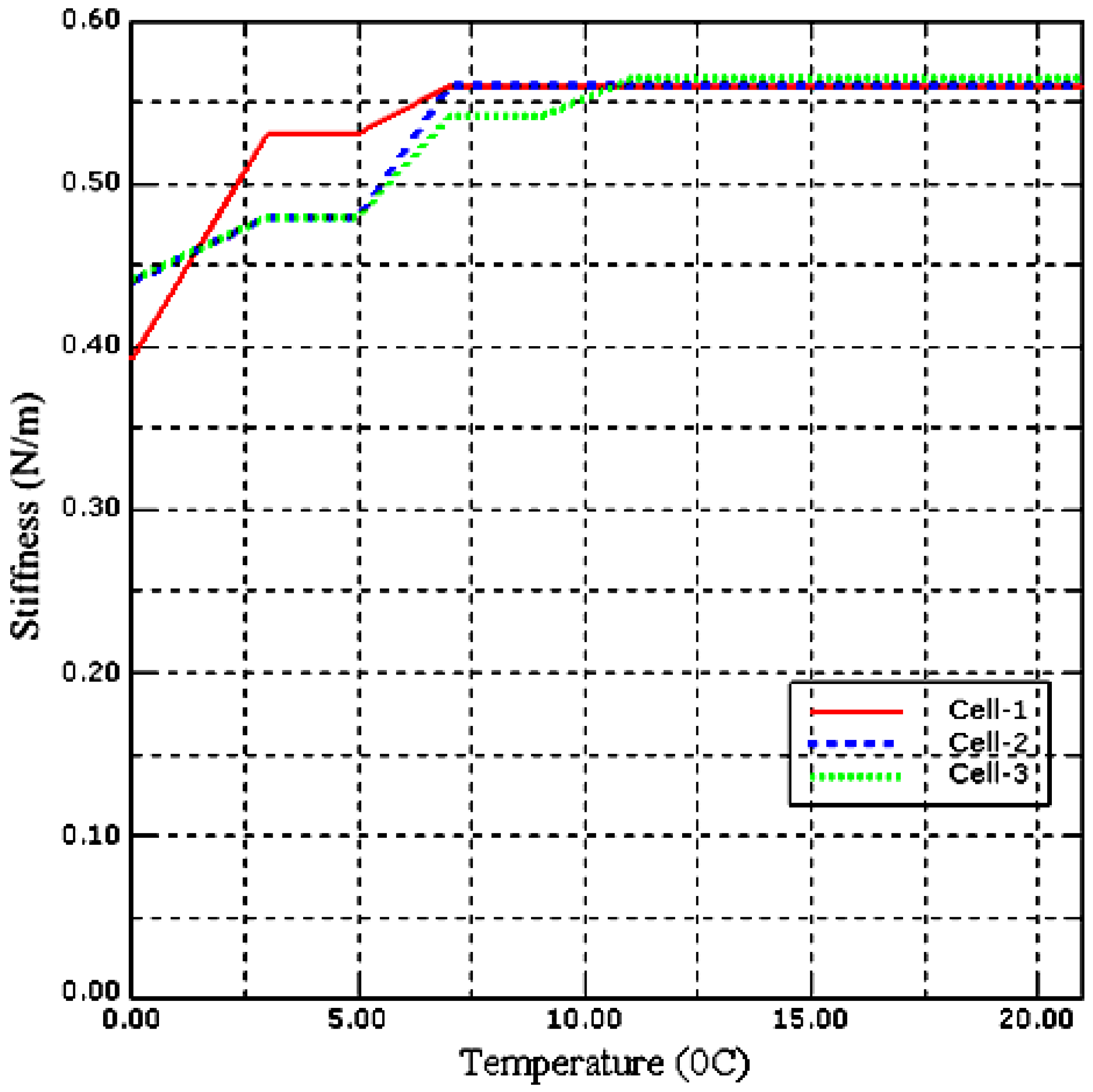
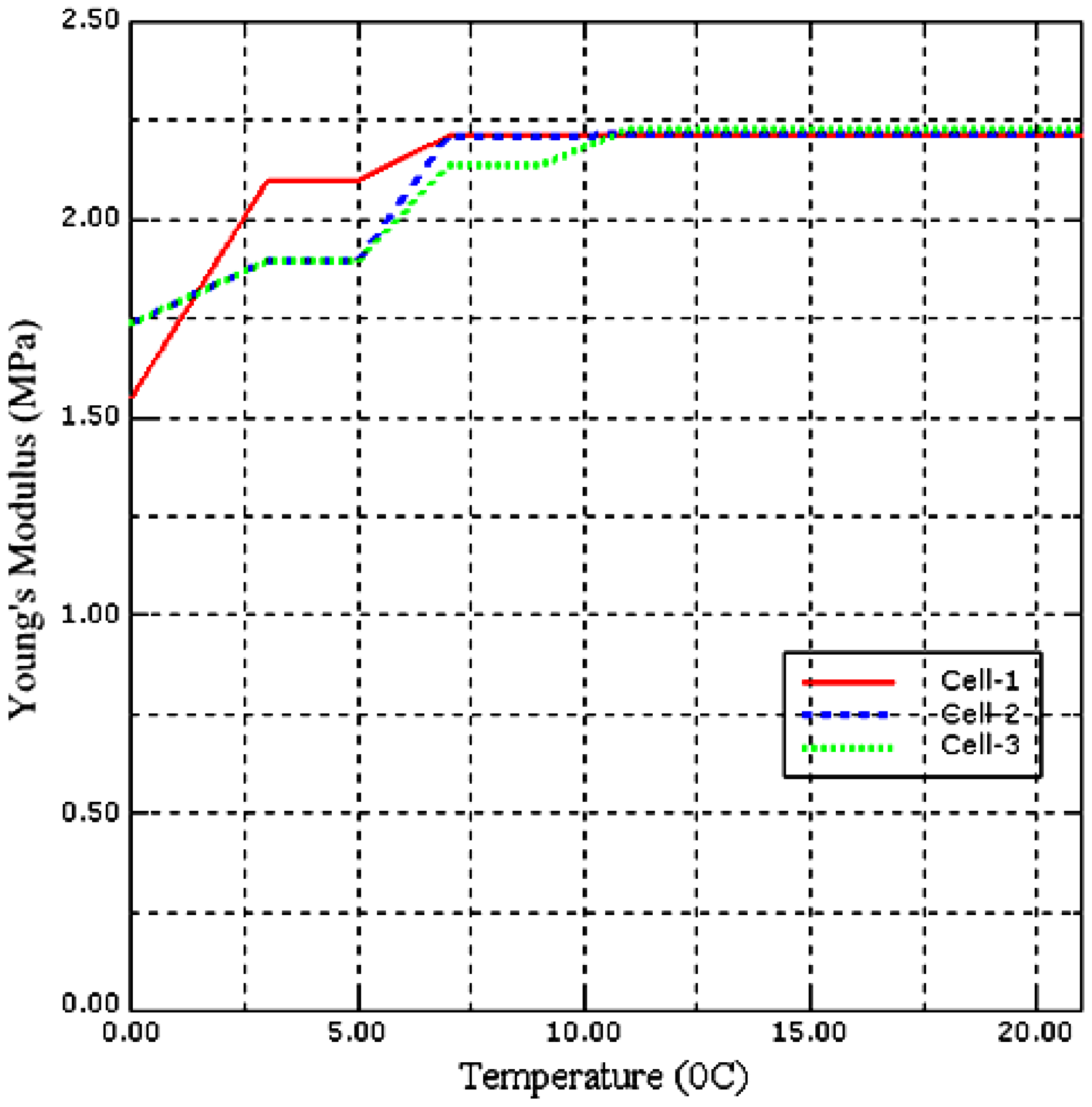
5.2. Effect of Temperature on Local Stiffness Measurement of a Single Saccharomyces cerevisiae Cell
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shibata, T.; Kato, N.; Horiike, S.; Kawashima, T.; Nagai, M.; Mineta, T.; Makino, E. Fabrication of bioprobe integrated with hollow nanoneedle for cellular function analysis. In Proceedings of the IEEE 24th International Conference on Micro Electro Mechanical Systems (MEMS), Cancun, Mexico, 23–27 January 2011; pp. 861–864.
- Hensel, M.; Egerer, G.; Schneeweiss, A.; Goldschmidt, H.; Ho, A.D. Quality of life and rehabilitation in social and professional life after autologous stem cell transplantation. Ann. Oncol. 2002, 13, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, L.; Xi, N.; Wang, Y.; Xiao, X.; Zhang, W. Effects of temperature and cellular interactions on the mechanics and morphology of human cancer cells investigated by atomic force microscopy. Sci. China Life Sci. 2015, 58, 889–901. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.R.; Nakajima, M.; Kojima, S.; Homma, M.; Fukuda, T. Buckling nanoneedle for characterizing single cells mechanics inside environmental SEM. IEEE Trans. Nanotechnol. 2011, 10, 226–236. [Google Scholar] [CrossRef]
- Shen, Y.; Nakajima, M.; Homma, M.; Fukuda, T. Auto nanomanipulation system for single cell mechanical property characterization inside an environmental sem. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 646–651.
- Ahmad, M.R.; Nakajima, M.; Kojima, S.; Homma, M.; Fukuda, T. In situ single cell mechanics characterization of yeast cells using nanoneedles inside environmental sem. IEEE Trans. Nanotechnol. 2008, 7, 607–616. [Google Scholar] [CrossRef]
- Zdunek, A.; Kurenda, A. Determination of the elastic properties of tomato fruit cells with an atomic force microscope. Sensors 2013, 13, 12175–12191. [Google Scholar] [CrossRef] [PubMed]
- Binslem, S.A.; Ahmad, M.R. Thermistor based nano-needle for single cell thermal characterization. In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 29 November–1 December 2013; pp. 590–595.
- Ahmad, M.R.; Nakajima, M.; Kojima, S.; Homma, M.; Fukuda, T. Various local stiffness characterizations of single cells using buckling nanoneedles. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Bangkok, Thailand, 22–25 February 2009; pp. 55–60.
- Shulev, A.; Roussev, I.; Kostadinov, K. Force sensor for cell injection and characterization. In Proceedings of the International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Xi’an, China, 29 August–1 September 2012; pp. 335–338.
- Rahman, M.H.; Sulaiman, A.H.M.; Ahmad, M.R.; Fukuda, T. Finite element analysis of single cell wall cutting by piezoelectric-actuated vibrating rigid nanoneedle. IEEE Trans. Nanotechnol. 2013, 12, 1158–1165. [Google Scholar] [CrossRef]
- Rahman, M.H.; Ahmad, M.R. Finite element analysis of single cell surgery using rigid nanoneedle. In Proceedings of the 2012 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Langkawi, Malaysia, 17–19 December 2012; pp. 167–170.
- Shen, Y.; Nakajima, M.; Yang, Z.; Homma, M.; Fukuda, T. Nano needle with buffering beam for single cell stiffness measurement by nanorobotic manipulators inside ESEM. In Proceedings of the 2012 12th IEEE Conference on Nanotechnology (IEEE-NANO), Birmingham, UK, 20–23 August 2012; pp. 1–4.
- Lekka, M.; Laidler, P.; Gil, D.; Lekki, J.; Stachura, Z.; Hrynkiewicz, Z.A. Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur. Biophys. J. 1999, 28, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.R.; Nakajima, M.; Kojima, S.; Homma, M.; Fukuda, T. Nanoindentation methods to measure viscoelastic properties of single cells using sharp, flat, and buckling tips inside esem. IEEE Trans. NanoBiosci. 2010, 9, 12–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Park, G.; Sohn, H.; Farar, C.R.; Inman, J. Overview of piezoelectric impedance-based health monitoring and path forward. J. Shork Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef]
- Janshoff, A.; Galla, H.-J.; Steinem, C. Piezoelectric mass-sensing devices as biosensors—An alternative to optical biosensors? Angew. Chemie Int. Ed. 2000, 39, 4004–4032. [Google Scholar] [CrossRef]
- Park, S.; Anton, S.R.; Kim, J.-K.; Inman, D.J.; Ha, D.S. Instantaneous baseline structural damage detection using a miniaturized piezoelectric guided waves system. KSCE J. Civ. Eng. 2010, 14, 889–895. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Yang, B.D.; Su, Y.; Tran, P.L.; Joe, P.; Anderson, E.; Xia, J.; Doraiswamy, V.; Dehdashti, B.; Feng, X.; et al. Conformal piezoelectric energy harvesting and storage from motions of the heart, lung, and diaphragm. Proc. Natl. Acad. Sci. USA 2014, 111, 1927–1932. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N.; Dagdeviren, C.; Rogers, J.A.; Ferreira, P.M. Active polymeric composite membranes for localized actuation and sensing in microtransfer printing. J. Microelectromech. Syst. 2015, 24, 1016–1028. [Google Scholar] [CrossRef]
- Feng, X.; Yang, B.D.; Liu, Y.; Wang, Y.; Dagdeviren, C.; Liu, Z.; Carlson, A.; Li, J.; Huang, Y.; Rogers, J.A. Stretchable ferroelectric nanoribbons with wavy configurations on elastomeric substrates. ACS Nano 2011, 5, 3326–3332. [Google Scholar] [CrossRef] [PubMed]
- Dagdeviren, C.; Su, Y.; Joe, P.; Yona, R.; Liu, Y.; Kim, Y.-S.; Huang, Y.; Damadoran, A.R.; Xia, J.; Martin, L.W.; et al. Conformable amplified lead zirconate titanate sensors with enhanced piezoelectric response for cutaneous pressure monitoring. Nat. Commun. 2014, 5, 4496. [Google Scholar] [CrossRef] [PubMed]
- IEEE Standard on Piezoelectricity. ANSI/IEEE Std 176-1987 1988, 0_1. Available online: http://ieeexplore.ieee.org/document/26560/ (accessed on 26 October 2016).
- Wang, Q.-M.; Cross, L.E. Constitutive equations of symmetrical triple layer piezoelectric benders. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1343–1351. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shi, Y. PZT nano active fiber composites-based acoustic emission sensor. In Selected Topics in Micro/Nano-Robotics for Biomedical Applications; Guo, Y., Ed.; Springer: New York, NY, USA, 2013; pp. 9–22. [Google Scholar]
- Chen, X.; Gold, R.; Shi, Y. A self powered PZT nanofiber composite sensor for structural health monitoring. In Proceedings of the 6th International Workshop on Advanced Smart Materials and Smart Structures Technology (ANCRiSST 2011), Dalian, China, 25–26 July 2011.
- Tseng, H.-J.; Tian, W.-C.; Wu, W.-J. Flexible PZT thin film tactile sensor for biomedical monitoring. Sensors 2013, 13, 5478–5492. [Google Scholar] [CrossRef] [PubMed]
- Zamarrena, C.R.; Arregui, F.J.; Garcia, Y.R.; Vazquez, R.; Liobet, E.; Lakhmi, R.; Clement, P.; Debeda, H. Electrospun nanofiber fabrication on screen-printed PZT cantilevers for room temperature vocs detection. In Proceedings of the 14th International Meeting on Chemical Sensors (IMCS 2012), Nuremberg, Germany, 20–23 May 2012.
- Chen, X.; Xu, S.; Yao, N.; Shi, Y. 1.6 V nanogenerator for mechanical energy harvesting using PZT nanofibers. Nano Lett. 2010, 10, 2133–2137. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.E.; Zhang, Z.; Thomas, C.R. Wall material properties of yeast cells: Part 1. Cell measurements and compression experiments. Chem. Eng. Sci. 2000, 55, 2031–2041. [Google Scholar] [CrossRef]
- Smith, A.E.; Moxham, K.E.; Middelberg, A.P.J. Wall material properties of yeast cells. Part II. Analysis. Chem. Eng. Sci. 2000, 55, 2043–2053. [Google Scholar] [CrossRef]
- Smith, A.E.; Moxham, K.E.; Middelberg, A.P.J. On uniquely determining cell–wall material properties with the compression experiment. Chem. Eng. Sci. 1998, 53, 3913–3922. [Google Scholar] [CrossRef]
- Stenson, J.D.; Thomas, C.R.; Hartley, P. Modelling the mechanical properties of yeast cells. Chem. Eng. Sci. 2009, 64, 1892–1903. [Google Scholar] [CrossRef]
- Overbeck, A.; Kampen, I.; Kwade, A. Mechanical characterization of yeast cells: Effects of growth conditions. Lett. Appl. Microbiol. 2015, 61, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Mashmoushy, H.; Zhang, Z.; Thomas, C.R. Micromanipulation measurement of the mechanical properties of baker's yeast cells. Biotechnol. Tech. 1998, 12, 925–929. [Google Scholar] [CrossRef]
- Smith, A.E.; Zhang, Z.; Thomas, C.R.; Moxham, K.E.; Middelberg, A.P.J. The mechanical properties of saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2000, 97, 9871–9874. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.R.; Nakajima, M.; Kojima, S.; Homma, M.; Fukuda, T. The effects of cell sizes, environmental conditions, and growth phases on the strength of individual W303 yeast cells inside ESEM. IEEE Trans. NanoBiosci. 2008, 7, 185–193. [Google Scholar] [CrossRef] [PubMed]

| Category | Matrix of Parameters for Polarization Along y-Axis | Units |
|---|---|---|
| Compliance | µN/µm2 | |
| Stress coefficient | C/µm2 | |
| Dielectric constants |
| Nanoneedle Geometry | Stiffness (N/m) | Young’s Modulus (GPa) | Poisson’s Ratio | PZT Sensitivity (V·m·N−1) |
|---|---|---|---|---|
| Rectangular | 0.5000 | 104.0000 | 0.2200 | No PZT |
| Cylindrical | 0.4300 | 106.6900 | 0.2200 | No PZT |
| Cylindrical integrated with PZT | 0. 7100 | 123.4700 | 0.3000 | 0.0693 |
| Sample | Stiffness (N/m) | Young’s Modulus (MPa) | Fcell (nN) | Voltage (nVolt) |
|---|---|---|---|---|
| Cell-1 | 0.3925 | 1.5493 | 77.7890 | 5.3931 |
| Cell-2 | 0.4400 | 1.7370 | 80.1190 | 5.5546 |
| Cell-3 | 0.4410 | 1.7369 | 73.6050 | 5.1030 |
| Sample | Stiffness (N/m) | Young’s Modulus (MPa) | Fcell (µN) | Voltage (nVolt) |
|---|---|---|---|---|
| Cell-1 | 4.1877 | 16.5301 | 0.8103 | 57.5406 |
| Cell-2 | 4.2404 | 16.7402 | 0.7851 | 54.1712 |
| Cell-3 | 4.3257 | 17.0371 | 0.9034 | 56.0545 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rad, M.A.; Tijjani, A.S.; Ahmad, M.R.; Auwal, S.M. Finite Element Analysis of Single Cell Stiffness Measurements Using PZT-Integrated Buckling Nanoneedles. Sensors 2017, 17, 14. https://doi.org/10.3390/s17010014
Rad MA, Tijjani AS, Ahmad MR, Auwal SM. Finite Element Analysis of Single Cell Stiffness Measurements Using PZT-Integrated Buckling Nanoneedles. Sensors. 2017; 17(1):14. https://doi.org/10.3390/s17010014
Chicago/Turabian StyleRad, Maryam Alsadat, Auwal Shehu Tijjani, Mohd Ridzuan Ahmad, and Shehu Muhammad Auwal. 2017. "Finite Element Analysis of Single Cell Stiffness Measurements Using PZT-Integrated Buckling Nanoneedles" Sensors 17, no. 1: 14. https://doi.org/10.3390/s17010014






