A Weighted Measurement Fusion Particle Filter for Nonlinear Multisensory Systems Based on Gauss–Hermite Approximation
Abstract
:1. Introduction
2. Problem Formulation
3. Gauss–Hermite Approximation
4. Universal WMF Based on Gauss–Hermite Approximation
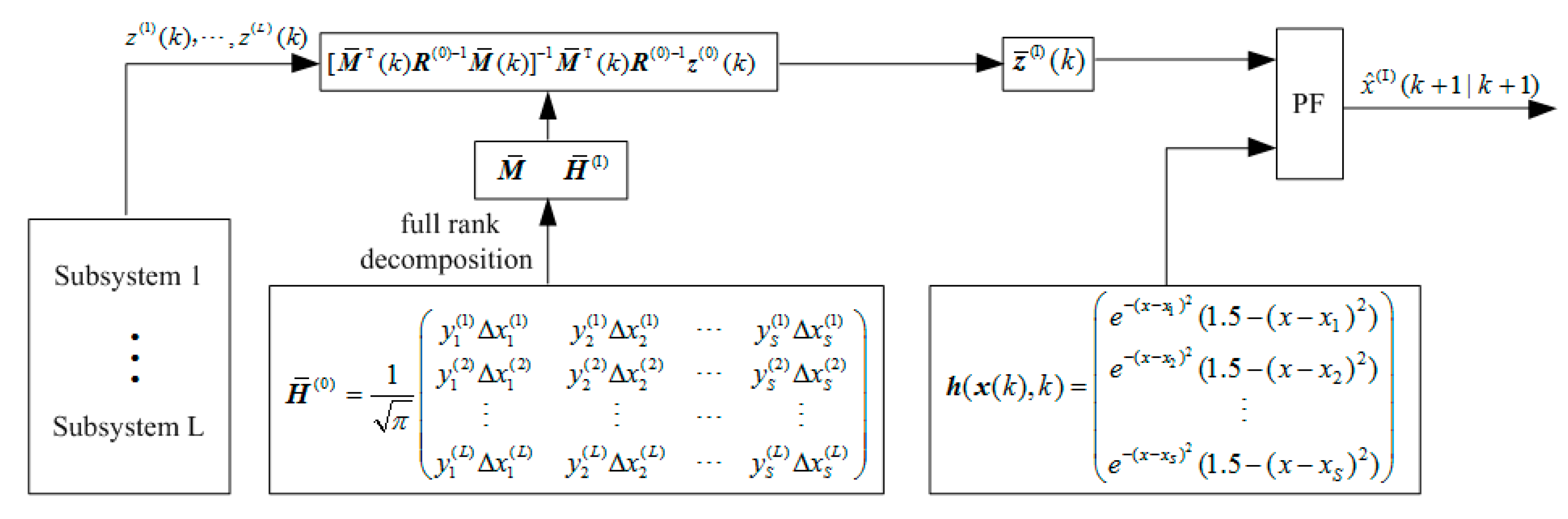
5. WMF-PF Based on Gauss–Hermite Approximation
5.1. WMF-PF Algorithm
5.2. Time Complexity Analysis
6. Simulation Examples
6.1. Model Description
6.2. Gauss–Hermite Approximation
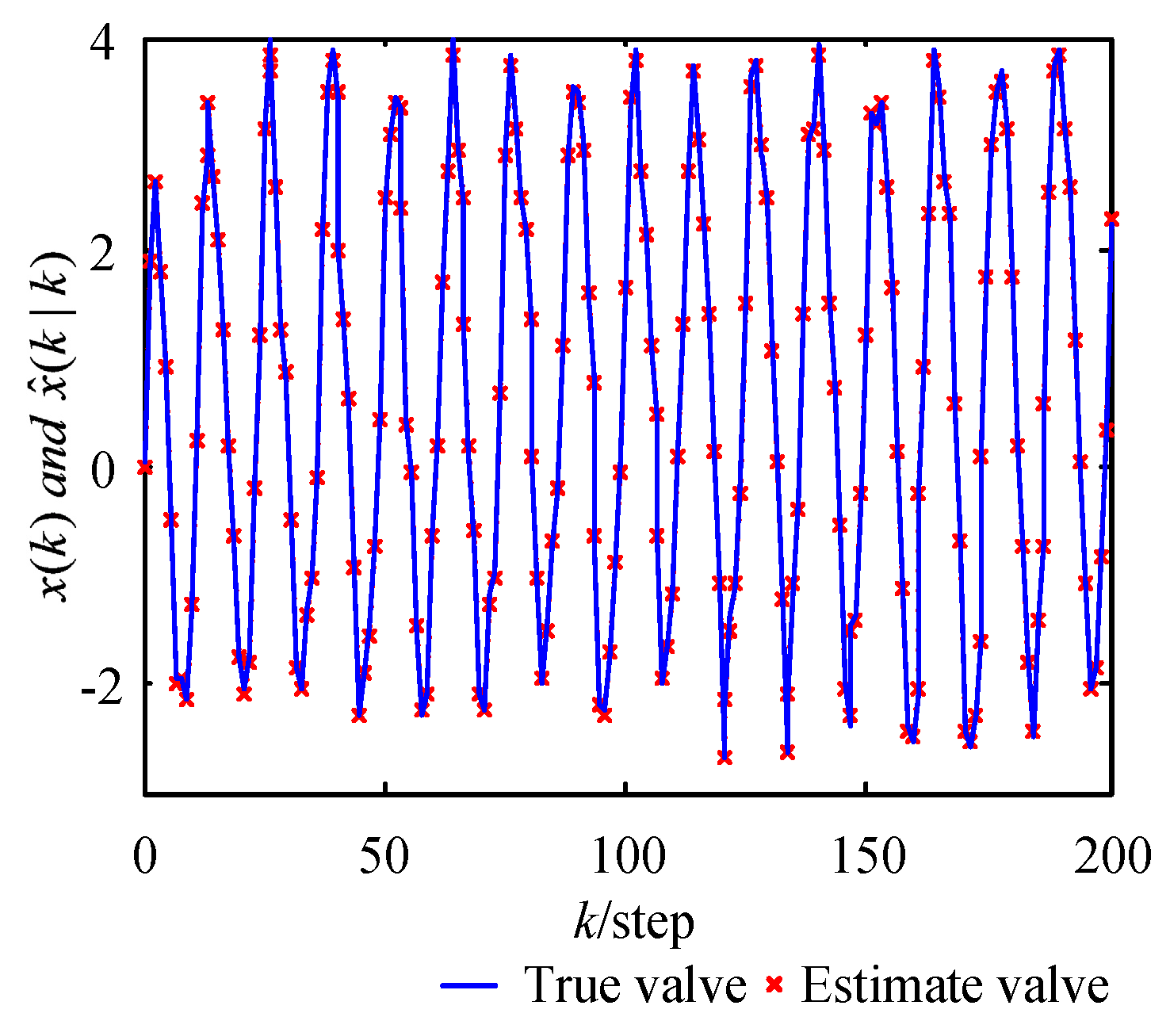
6.3. Estimation Using WMF-PF
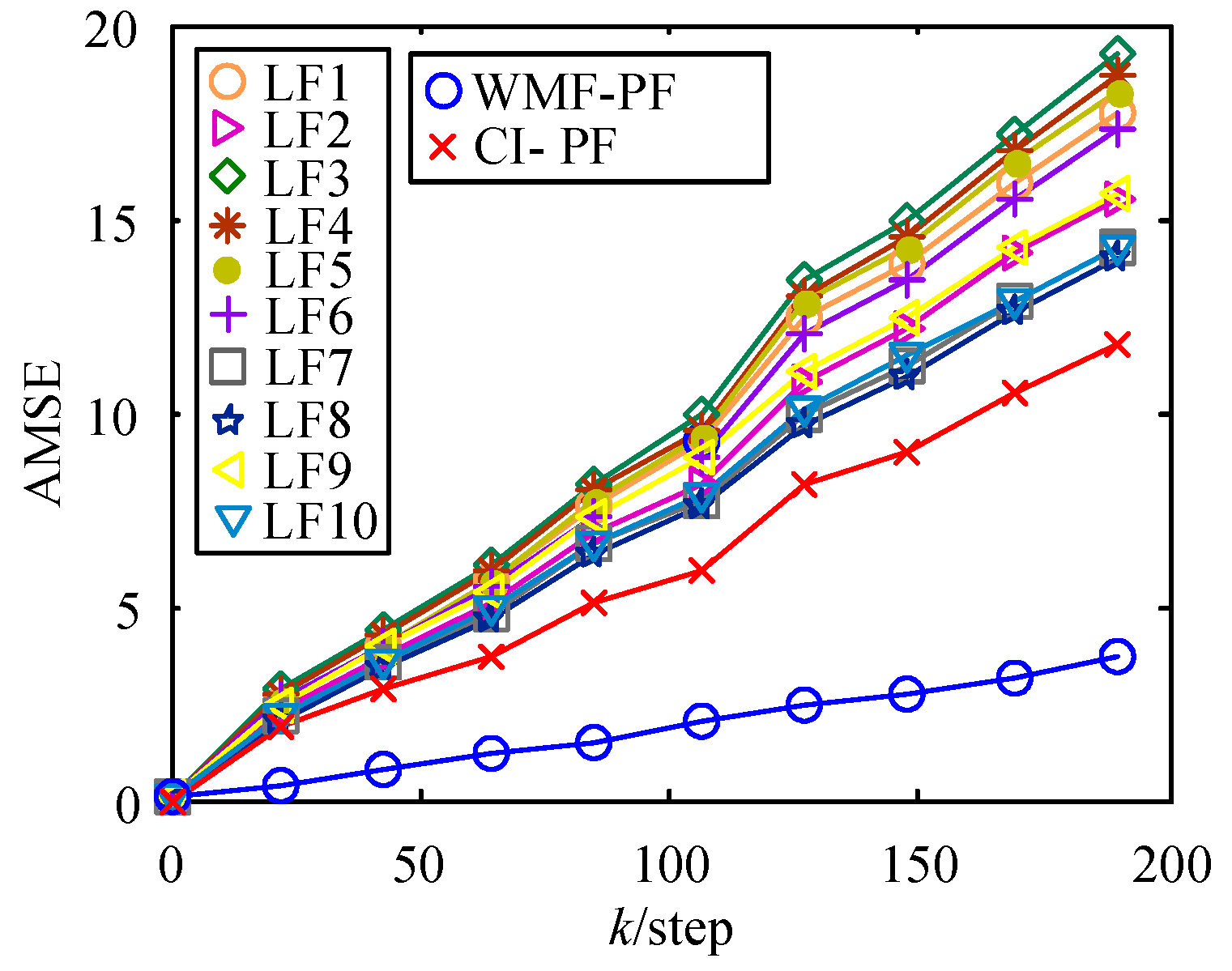
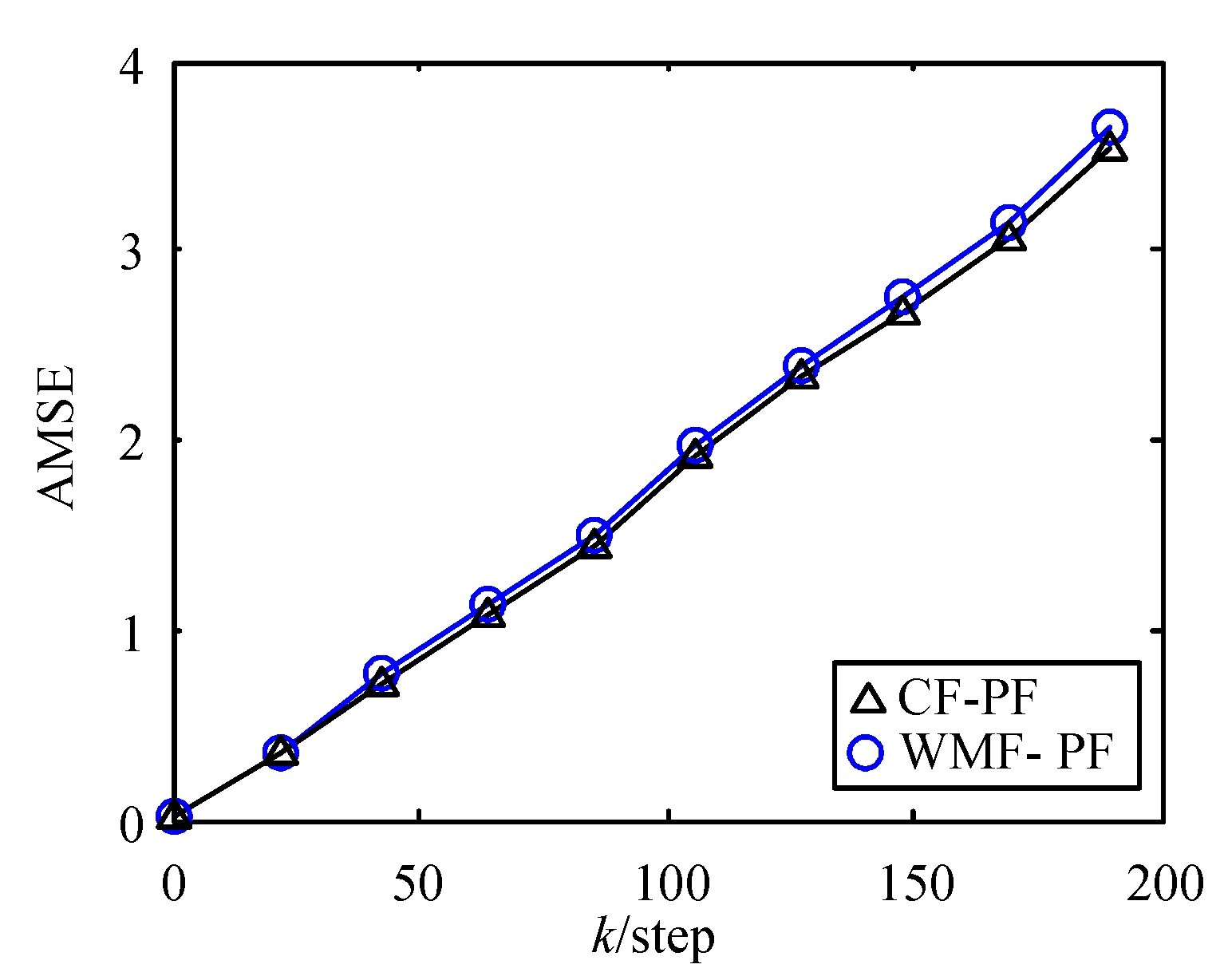
6.4. Analysis
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gispan, L.; Leshem, A.; Be’ery, Y. Decentralized estimation of regression coefficients in sensor networks. Digit. Signal Proc. 2017, 68, 16–23. [Google Scholar] [CrossRef]
- Song, E.B.; Zhu, Y.M.; Zhou, J. Sensors’ optimal dimensionality compression matrix in estimation fusion. Automatica 2005, 41, 2131–2139. [Google Scholar] [CrossRef]
- Sun, S.; Lin, H.; Ma, J.; Li, X. Multi-sensor distributed fusion estimation with applications in networked systems: A review paper. Inf. Fusion 2017, 38, 122–134. [Google Scholar] [CrossRef]
- Sun, S.L.; Deng, Z.L. Multi-sensor optimal information fusion Kalman filter. Automatica 2004, 40, 1017–1023. [Google Scholar] [CrossRef]
- Ma, J.; Sun, S.L. Information fusion estimators for systems with multiple sensors of different packet dropout rates. Inf. Fusion 2011, 12, 213–222. [Google Scholar] [CrossRef]
- Tian, T.; Sun, S.L.; Li, N. Multi-sensor information fusion estimators for stochastic uncertain systems with correlated noises. Inf. Fusion 2016, 27, 126–137. [Google Scholar] [CrossRef]
- Ge, Q.B.; Shao, T.; Duan, Z.S.; Wen, C.L. Performance Analysis of the Kalman Filter with Mismatched Measurement Noise Covariance. IEEE Trans. Autom. Control 2016, 61, 4014–4019. [Google Scholar] [CrossRef]
- Carlson, N. Federated square root filter for decentralized parallel processes. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 517–525. [Google Scholar] [CrossRef]
- Kim, K. Development of track to track fusion algorithm. In Proceedings of the American Control Conference, Baltimore, MD, USA, 29 June–1 July 1994. [Google Scholar]
- Julier, S.; Uhlmann, J. A non-divergent estimation algorithm in the presence of unknown correlation. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 6 June 1997; pp. 2369–2373. [Google Scholar]
- Qiang, G.; Harris, C.J. Comparison of two measurement fusion methods for Kalman-filter-based multisensor data fusion. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 273–280. [Google Scholar] [CrossRef]
- Oussalah, M.; Messaoudi, Z.; Ouldali, A. Track-to-Track Measurement Fusion Architectures and Correlation Analysis. J. Univers. Comput. Sci. 2010, 16, 37–61. [Google Scholar]
- Ran, C.J.; Deng, Z.L. Self-tuning weighted measurement fusion Kalman filtering algorithm. Comput. Stat. Data Anal. 2012, 56, 2112–2128. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. A Survey of Maneuvering Target Tracking: Approximation Techniques for Nonlinear Filtering. Proc. SPIE 2004, 5428, 537–550. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R. Multitarget-Multisensor Tracking: Principles and Techniques; YBS Publishing: Storrs, CT, USA, 1995. [Google Scholar]
- Assa, A.; Janabi-Sharifi, F. A Kalman Filter-Based Framework for Enhanced Sensor Fusion. IEEE Sens. J. 2015, 15, 3281–3292. [Google Scholar] [CrossRef]
- Straka, O.; Duník, J.; Šimandl, M. Truncation nonlinear filters for state estimation with nonlinear inequality constraints. Automatica 2012, 48, 273–286. [Google Scholar] [CrossRef]
- Hlinka, O.; Slučiak, O.; Hlawatsch, F.; Djuric, P.M.; Rupp, M. Likelihood consensus and its application to distributed particle filtering. IEEE Trans. Signal Proc. 2012, 60, 4334–4349. [Google Scholar] [CrossRef]
- Ge, Q.B.; Xu, D.X.; Wen, C.L. Cubature information filters with correlated noises and their applications in decentralized fusion. Signal Proc. 2014, 94, 434–444. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A new extension of the Kalman filter to nonlinear systems. In Proceedings of the International Symposium on Aerospace/Defense Sensing, Simulation and Controls, Orlando, FL, USA, 28 July 1997. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Arulampalam, S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Proc. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Chatzi, E.N.; Smyth, A.W. The unscented Kalman filter and particle filter methods for nonlinear structural system identification with non-collocated heterogeneous sensing. Struct. Control Health Monit. 2009, 16, 99–123. [Google Scholar] [CrossRef]
- Azam, E.S. Online damage detection in structural systems: Applications of proper orthogonal decomposition, and Kalman and particle filters. Springerbriefs Appl. Sci. Technol. 2014, 1–45. [Google Scholar] [CrossRef]
- Mirzazadeh, R.; Azam, E.S.; Mariani, S. Micromechanical characterization of polysilicon films through on-chip tests. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Cacace, F.; Germanib, A.; Palumboc, P. The observer follower filter: A new approach to nonlinear suboptimal filtering. Automatica 2013, 49, 548–553. [Google Scholar] [CrossRef]
- Hao, G.; Sun, S.L.; Li, Y. Nonlinear weighted measurement fusion Unscented Kalman Filter with asymptotic optimality. Inf. Sci. 2015, 299, 85–98. [Google Scholar] [CrossRef]
- Pomorski, K. Gauss-Hermite approximation formula. Comput. Phys. Commun. 2006, 174, 181–186. [Google Scholar] [CrossRef]
- Santhanam, B.; Santhanam, T.S. On discrete Gauss-Hermite functions and eigenvectors of the discrete Fourier transform. Signal Proc. 2008, 88, 2738–2746. [Google Scholar] [CrossRef]
- Strutinsky, V.M. Shells in deformed nuclei. Nucl. Phys. A 1968, 122, 1–33. [Google Scholar] [CrossRef]
- Strutinsky, V.M. Shell effects in nuclear masses and deformation energies. Nucl. Phys. A 1967, 95, 420–442. [Google Scholar] [CrossRef]
- Ge, Q.; Shao, T.; Chen, S.D.; Wen, C.L. Carrier Tracking Estimation Analysis by Using the Extended Strong Tracking Filtering. IEEE Trans. Ind. Electron. 2017, 64, 1415–1424. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 237–246. [Google Scholar] [CrossRef]
- Yuen, K.V.; Hoi, K.I.; Mok, K.M. Selection of noise parameters for Kalman filter. Earthq. Eng. Eng. Vib. 2007, 6, 49–56. [Google Scholar] [CrossRef]
- Kontoroupi, T.; Smyth, A.W. Online Noise Identification for Joint State and Parameter Estimation of Nonlinear Systems; ASCE: Reston, VA, USA, 2015. [Google Scholar]
- Kitagawa, G. Non-Gaussian state space modeling of time series. In Proceedings of the 26th Conference on Decision and Control, Los Angeles, CA, USA, 9–11 December 1987; pp. 1700–1705. [Google Scholar]
- Cong, J.; Li, Y.; Qi, G.; Sheng, A. An order insensitive sequential fast covariance intersection fusion algorithm. Inf. Sci. 2016, 367–368, 28–40. [Google Scholar] [CrossRef]
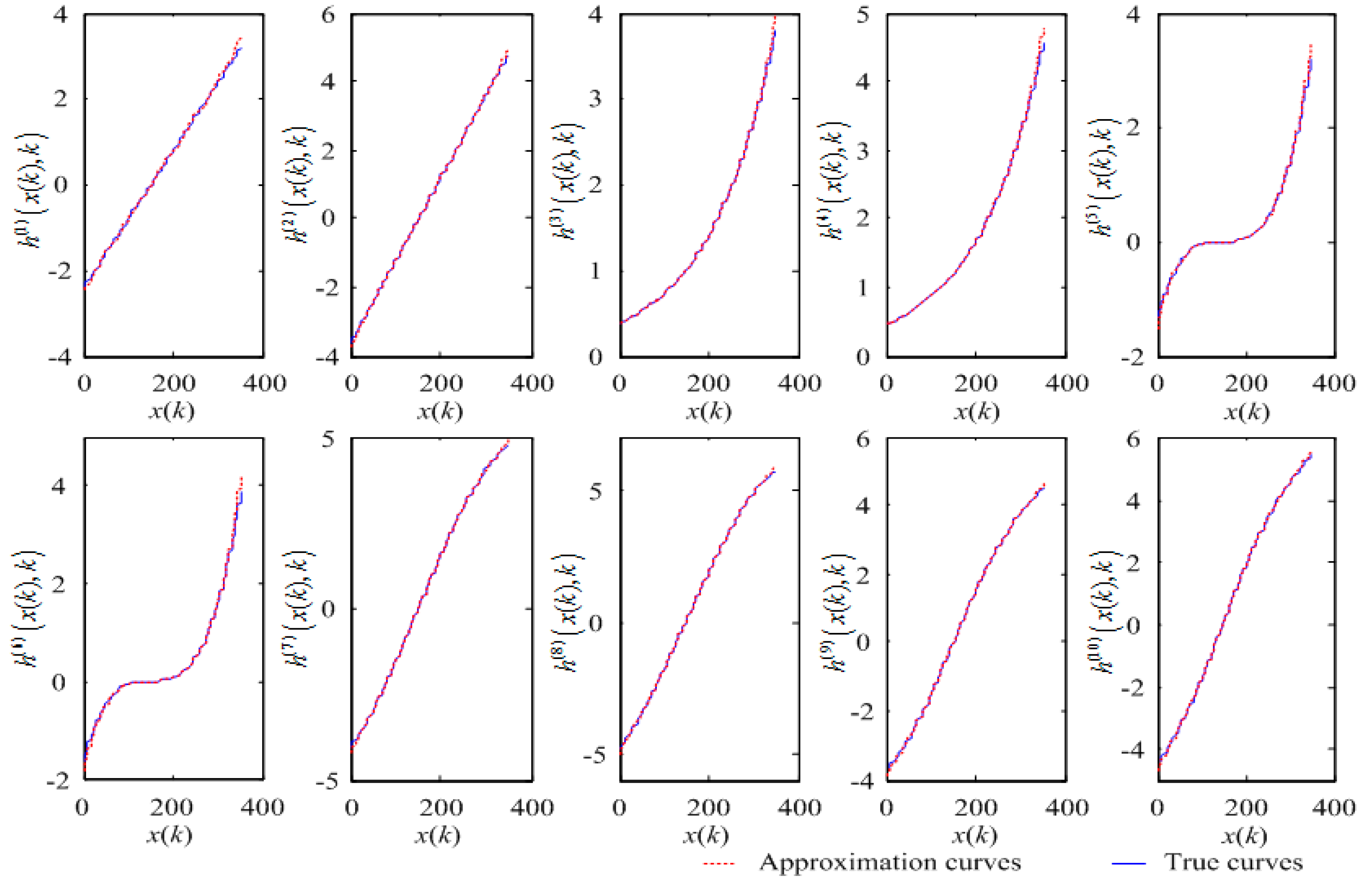

| Sensor Functions | ||||||||||
| MSEs using Gauss–Hermite | 0.0032 | 0.0017 | 0.0010 | 0.0014 | 0.0029 | 0.0042 | 0.0009 | 0.0013 | 0.0010 | 0.0015 |
| MSEs using McLaughlin series | 0 | 0 | 0.0258 | 0.0371 | 0.9621 | 1.3854 | 0.2286 | 0.3292 | 0.3963 | 0.5707 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, S.L.; Hao, G. A Weighted Measurement Fusion Particle Filter for Nonlinear Multisensory Systems Based on Gauss–Hermite Approximation. Sensors 2017, 17, 2222. https://doi.org/10.3390/s17102222
Li Y, Sun SL, Hao G. A Weighted Measurement Fusion Particle Filter for Nonlinear Multisensory Systems Based on Gauss–Hermite Approximation. Sensors. 2017; 17(10):2222. https://doi.org/10.3390/s17102222
Chicago/Turabian StyleLi, Yun, Shu Li Sun, and Gang Hao. 2017. "A Weighted Measurement Fusion Particle Filter for Nonlinear Multisensory Systems Based on Gauss–Hermite Approximation" Sensors 17, no. 10: 2222. https://doi.org/10.3390/s17102222





