ESPRIT-Like Two-Dimensional DOA Estimation for Monostatic MIMO Radar with Electromagnetic Vector Received Sensors under the Condition of Gain and Phase Uncertainties and Mutual Coupling
Abstract
:1. Introduction
2. Signal Model
3. ESPRIT-Like 2D-DOA Estimation Algorithm
3.1. Centralized Electromagnetic Vector Receiver
3.1.1. New Rotational Invariance Property of the SPD with Gain and Phase Error
3.1.2. Closed form Solution of RIFs
3.1.3. Estimation of 2D-DOA and PSA
- Step 1.
- Perform matched filtering and vectorization to the received data by (5) and (6);
- Step 2.
- Calculate the covariance matrix of virtual array by (17). And perform the eigen-decomposition to it to get the signal subspace by (18);
- Step 3.
- Compute the estimation of the relative GPU of the transmit and receive sensors by (28). Substituting the result into (24), get the estimation of , then compute the eigenvalues of to obtain the RIFs estimations ;
- Step 4.
- Pairing the estimation of RIFs for the same target by the connection between eigenvalues and corresponding eigenvectors;
- Step 5.
- Implementing the vector cross product by (33) based on to the paired estimations RIFs . And get the estimation of direction cosines by normalization processing;
- Step 6.
- Last, we can get the 2D-DOA estimations by (34). And the auxiliary polarization angle and polarization phase difference can be obtained by (36).
- Anti gain and phase error unknown;
- Suitable for any configuration;
- Similarly to the ESPRIT method, the calculation is small without angle searching;
- The angle of the whole airspace can be estimated;
- It is applicable to multiple EMVSs at the receiver;
- MN targets can be estimated at most.
3.2. Separated Electromagnetic Vector Receiver
4. Comparison of Advantages and Disadvantages of Each Method
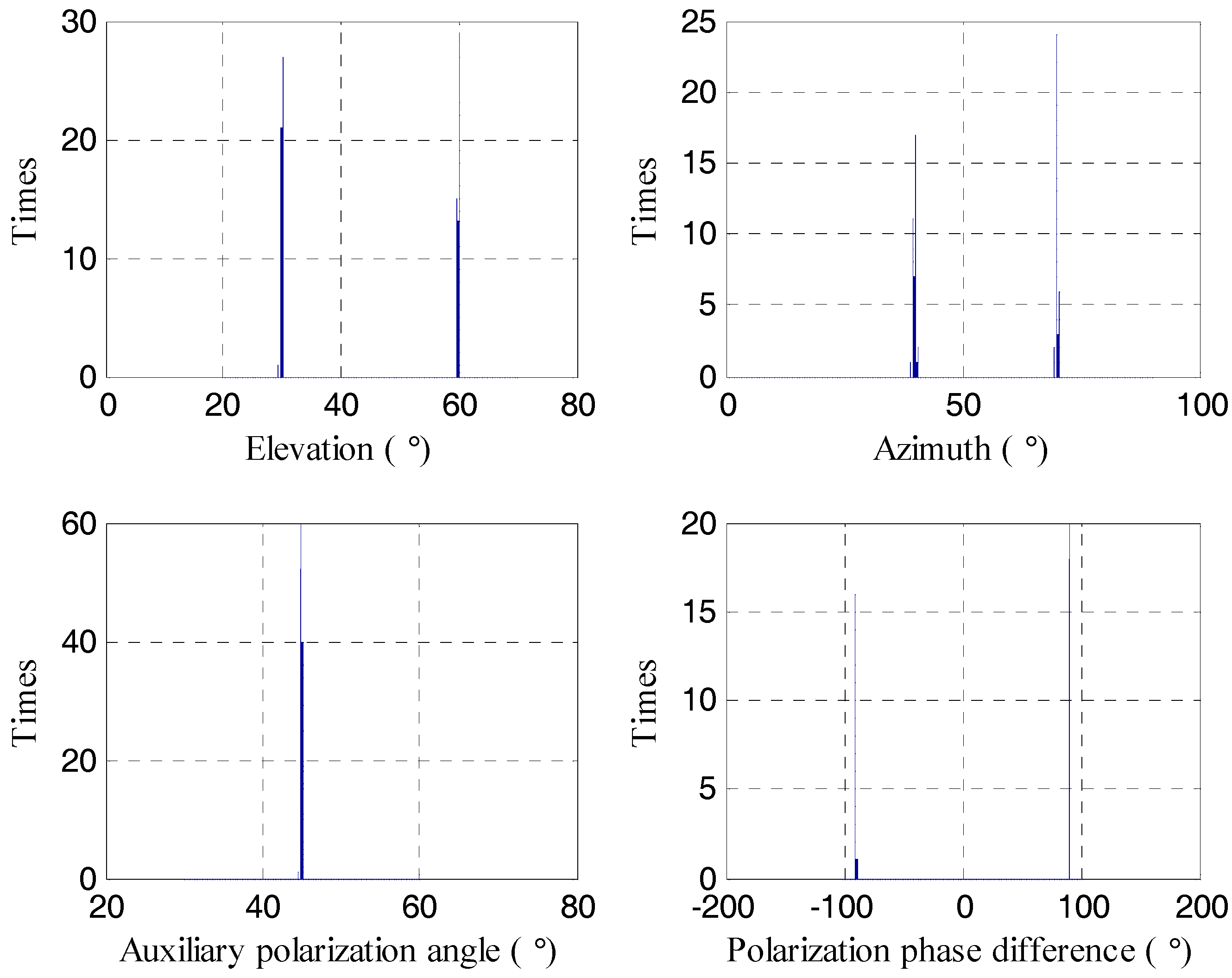
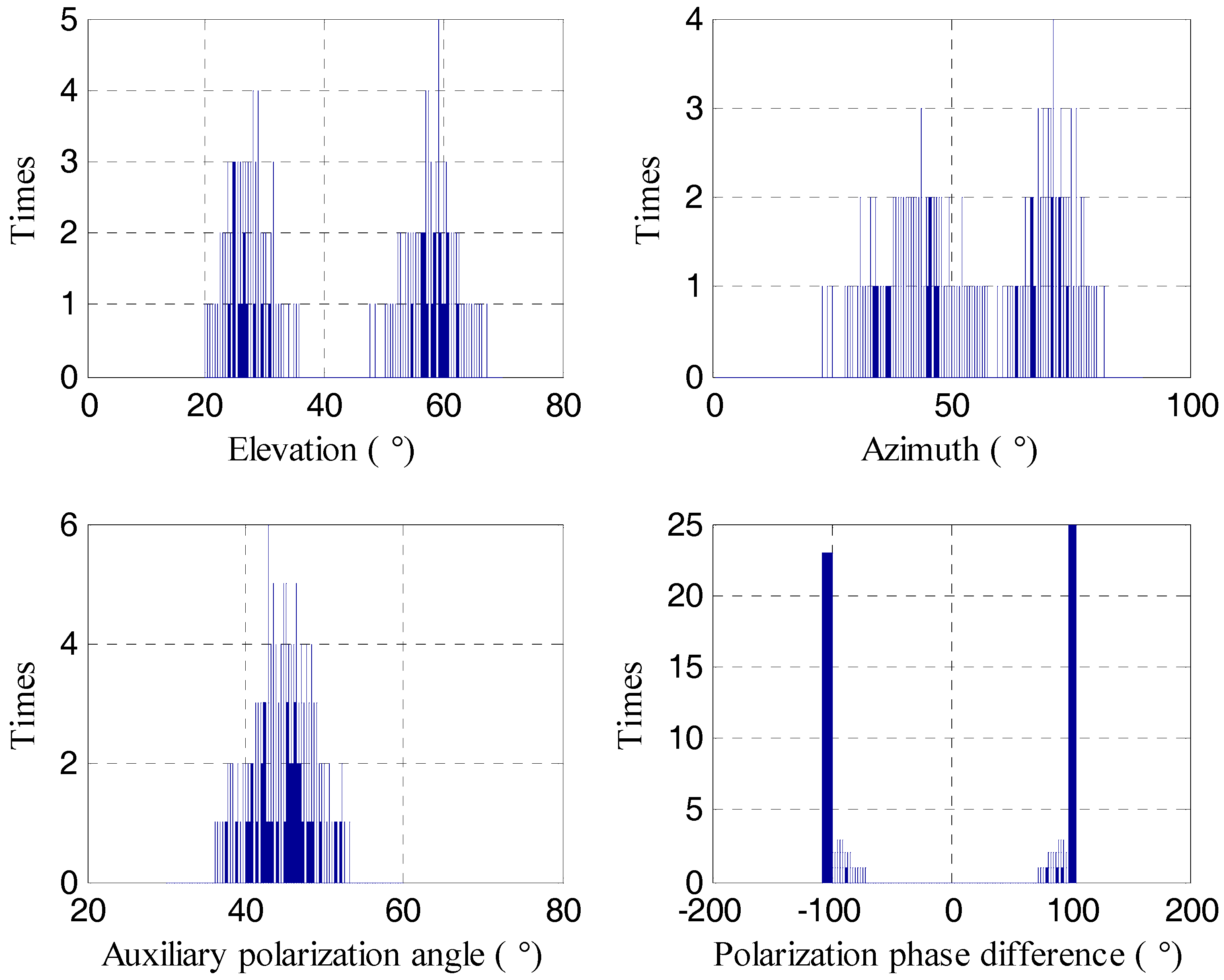
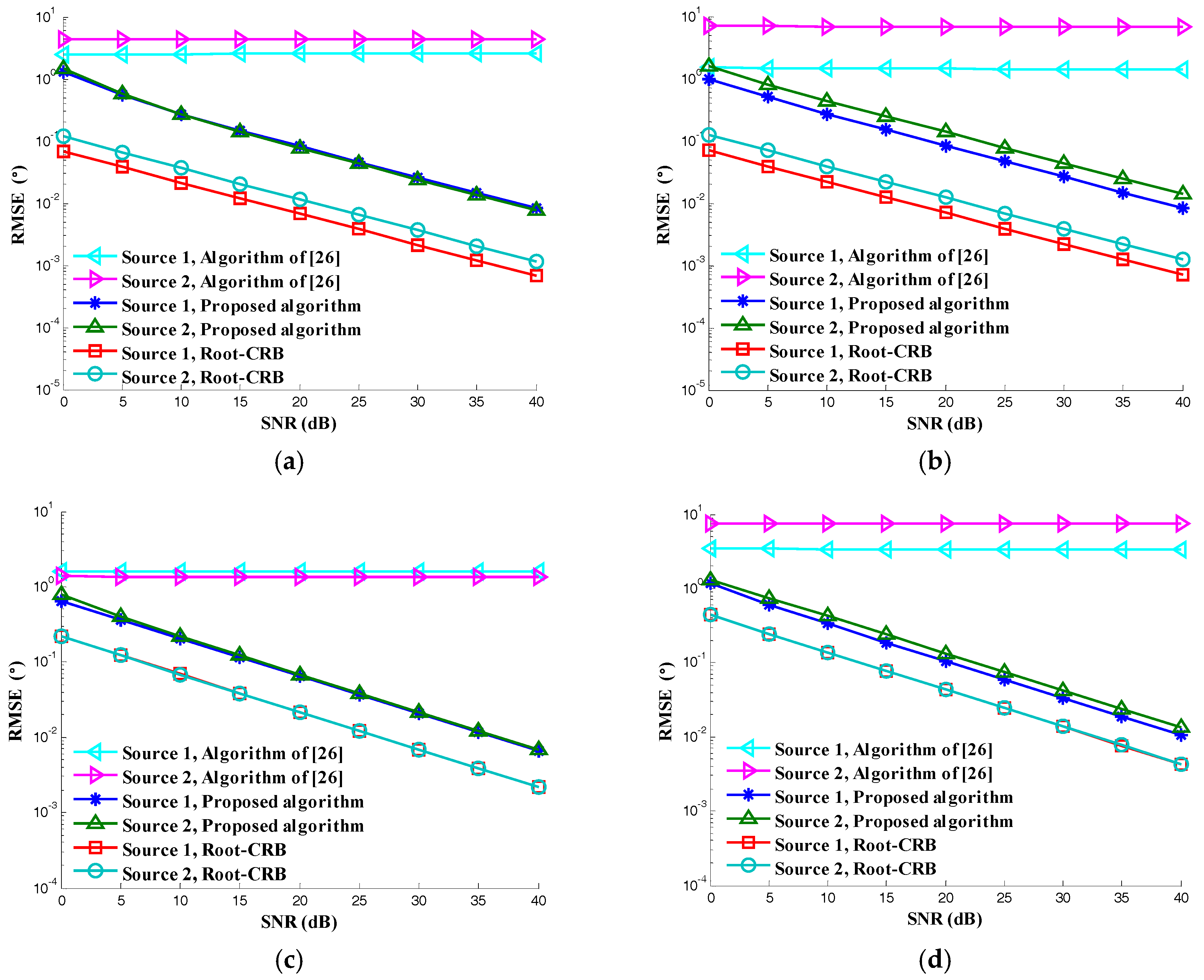
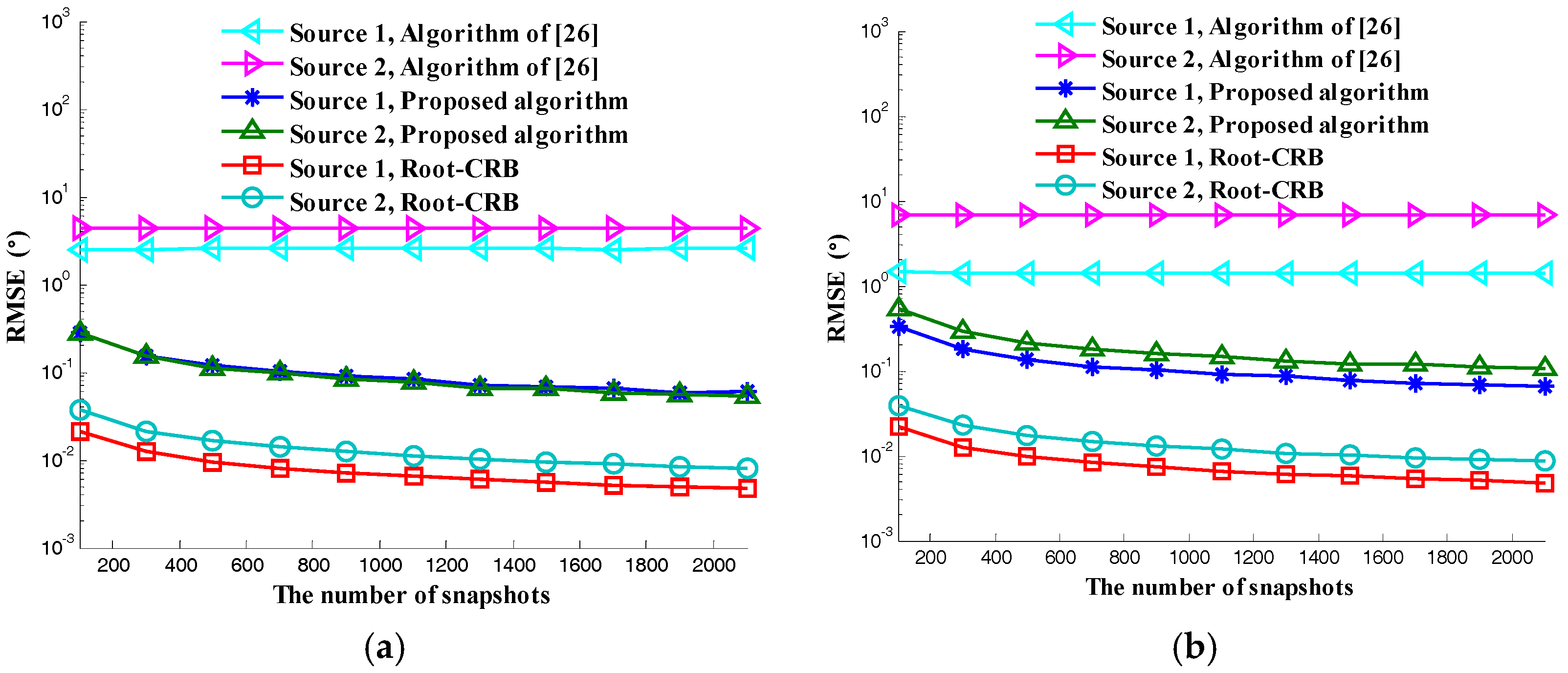
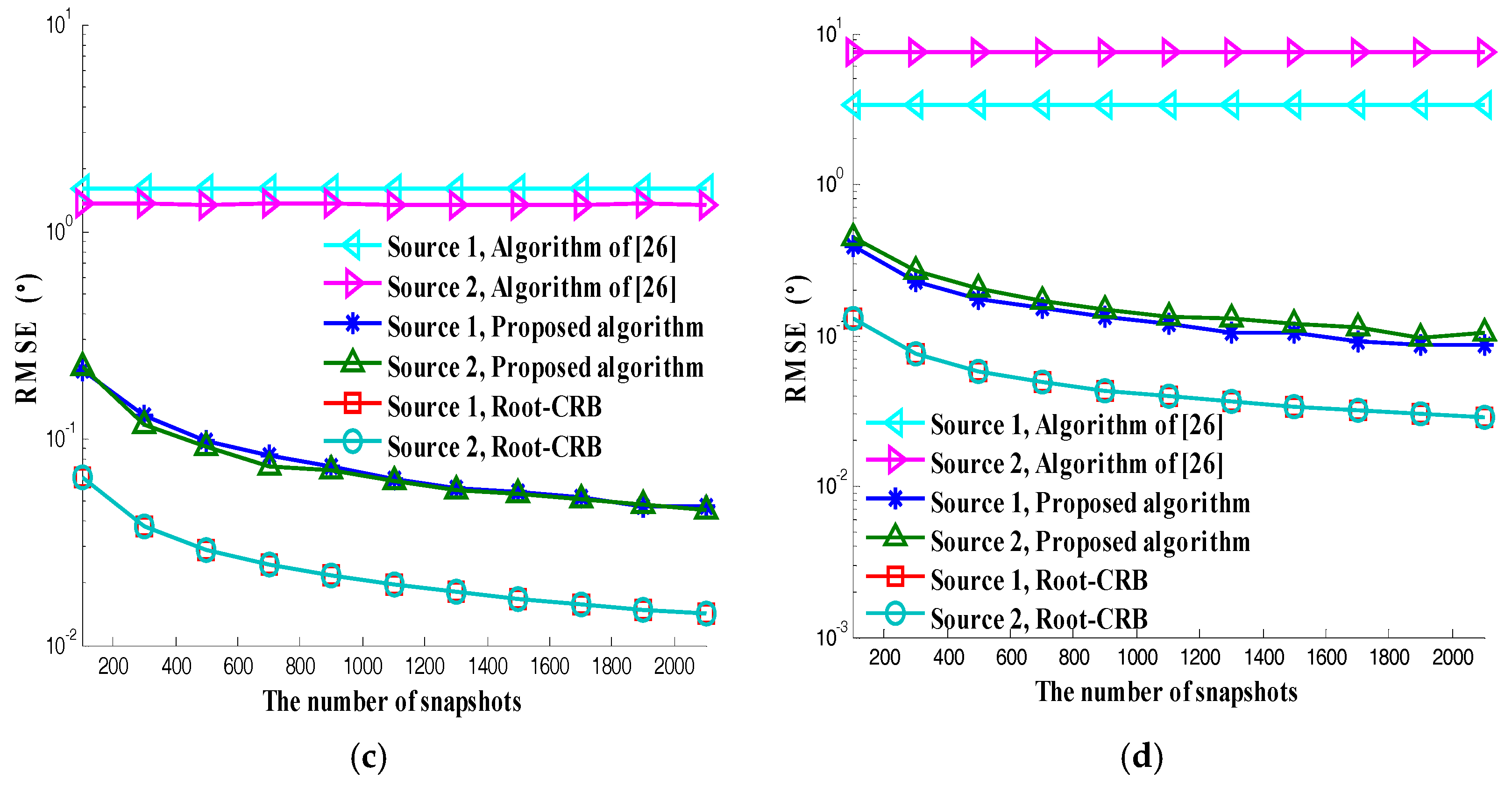
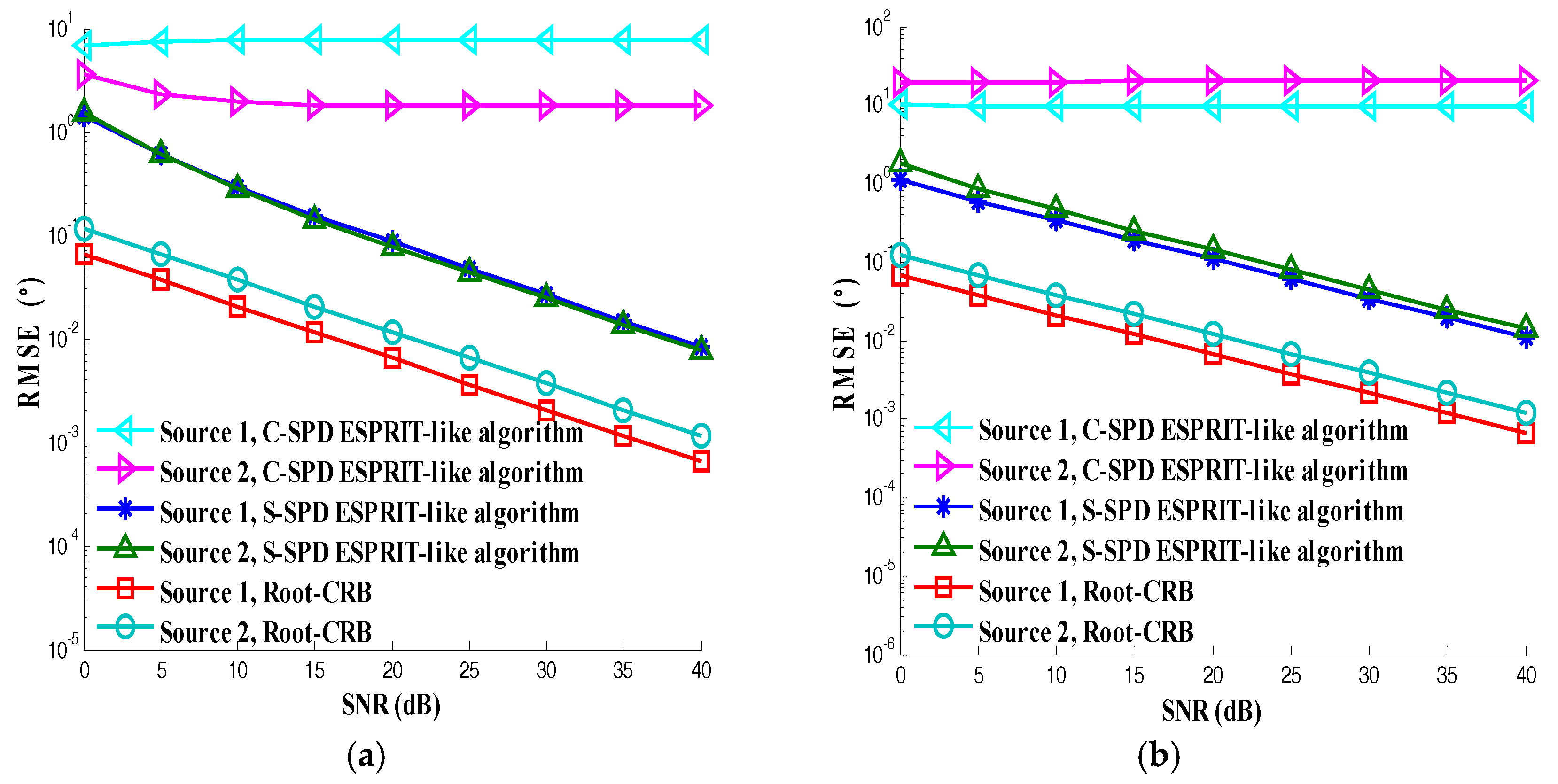
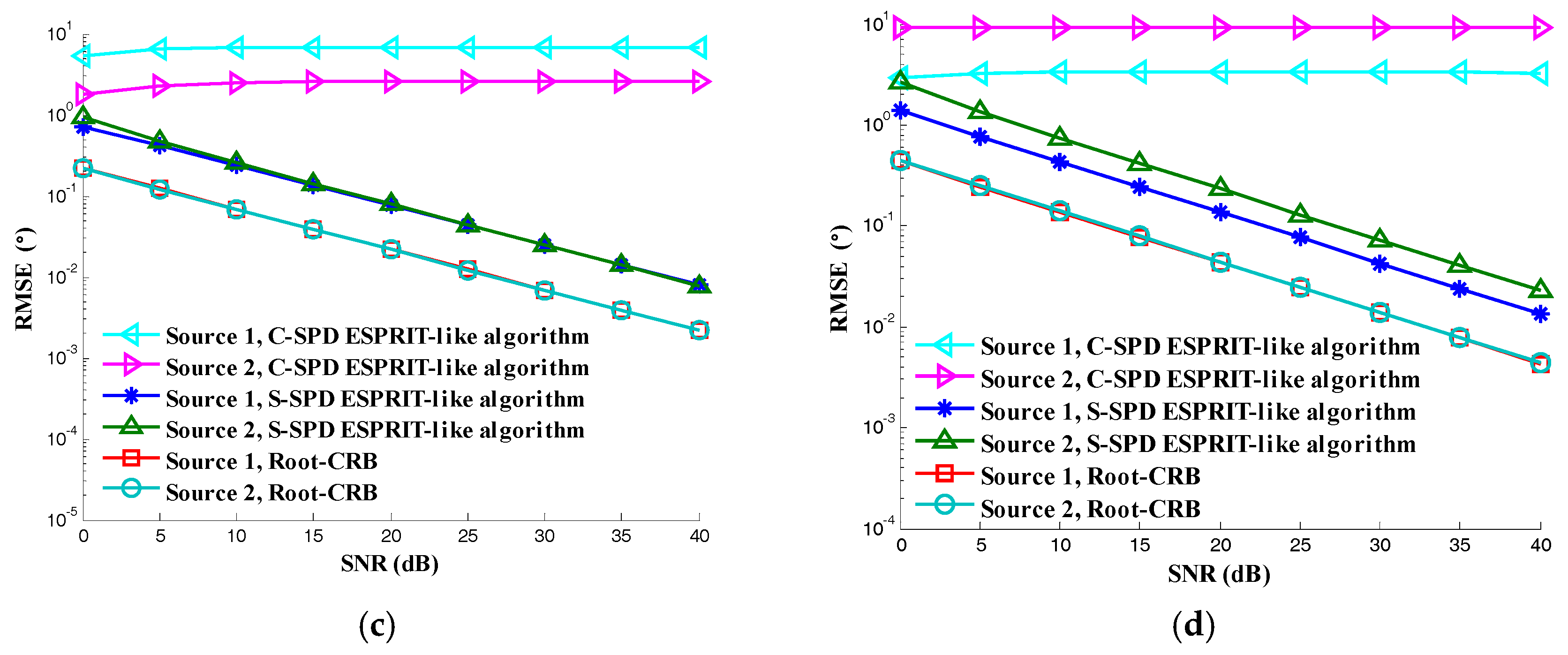
5. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Bliss, D.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the Thirty Seventh Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 1, pp. 54–59. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 26–29 April 2004; pp. 71–78. [Google Scholar]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Fisher, E.; Hairmovich, A.; Blum, R.; Cimini, L.; Chizhik, D.; Cimini, L.; Valenzuela, R. Spatial diversity in radars-models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Tang, B.; Tang, J.; Peng, Y.N. MIMO Radar waveform design in colored noise based on information theory. IEEE Trans. Signal Process. 2010, 58, 4684–4697. [Google Scholar] [CrossRef]
- Marzetta, T. A new interpretation of Capon’s maximum likelihood method of frequency-wavenumber spectral estimation. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 445–449. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z.S. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Aubry, A.; Carotenuto, V.; Maio, A.D. A new optimality property of the Capon estimator. IEEE Signal Process. Lett. 2017, 24, 1706–1708. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with colocated antenas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Ahmed, S.; Alouini, M.S. MIMO Radar transmit beampattern design without synthesising the covariance matrix. IEEE Trans. Signal Process. 2014, 62, 2278–2289. [Google Scholar] [CrossRef]
- Aubry, A.; Maio, A.D.; Huang, Y.W. MIMO Radar beampattern design via PSL/ISL optimization. IEEE Trans. Signal Process. 2016, 64, 3955–3967. [Google Scholar] [CrossRef]
- Liu, H.W.; Zhou, S.H.; Su, H.T.; Yu, Y. Detection performance of spatial-frequency diversity MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3137–3155. [Google Scholar]
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO Radar with widely separated antennas. IEEE Signal Process. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.S.; Hu, X.W.; Zheng, G.M.; Tang, J.; Feng, C.Q. Fast OMP algorithm for 3D parameters super-resolution estimation in bistatic MIMO radar. Electron. Lett. 2016, 52, 1164–1166. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Xu, L.; Roberts, W. On parameter identifiability of MIMO radar. IEEE Signal Process. Lett. 2007, 14, 968–971. [Google Scholar]
- Hassanien, A.; Vorobyov, S.A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas. IEEE Trans. Signal Process. 2011, 59, 2669–2682. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Stoica, P. Target detection and parameter estimation for MIMO radar systems. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 927–939. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. In Proceedings of the RADC Spectrum Estimation Workshop, Griffiths AFB, Rome, NY, USA, 3–5 October 1979; pp. 243–258. [Google Scholar]
- Roy, R.; Kailath, T. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Malioutov, D.; Çetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization withsensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Yan, H.; Li, J.; Liao, G. Multitarget identification and localization using bistatic MIMO radar system. EURASIP J. Adv. Signal Process. 2007, 2008, 1–8. [Google Scholar]
- Gao, X.; Zhang, X.; Feng, G.; Wang, Z.; Xu, D. On the MUSIC-derived approaches of angle estimation for bistatic MIMO radar. In Proceedings of the 2009 International Conference on Wireless Networks and Information Systems, Shanghai, China, 28–29 December 2009; pp. 343–346. [Google Scholar]
- Chen, D.F.; Chen, B.X.; Qin, G.D. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 770–771. [Google Scholar]
- Compton, R.T. The tripole antenna: An adaptive array with full polarization flexibility. IEEE Trans. Antennas Propag. 1981, 29, 944–952. [Google Scholar] [CrossRef]
- Zheng, G.M.; Tang, J. Two-dimensional DOA estimation for monostatic MIMO radar with electromagnetic vector received sensors. Int. J. Antennas Propag. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Li, J.; Cui, H.A. PARAFAC-based algorithm for multidimensional parameter estimation in polarimetric bistatic MIMO radar. EURASIP J. Adv. Signal Process. 2013, 2013, 133–146. [Google Scholar]
- Li, J.; Compton, R.T. Angle and polarization estimation using ESPRIT with a polarization sensitive array. IEEE Trans. Antennas Propag. 1991, 39, 1376–1383. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zheng, D. Efficient direction and polarization estimation with a COLD array. IEEE Trans. Antennas Propag. 1996, 44, 539–547. [Google Scholar]
- Gu, C.; He, J.; Li, H.T.; Zhu, X.H. Target localization using MIMO electromagnetic vector array systems. Signal Process. 2013, 93, 2103–2107. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, D.F.; Liu, C. Joint parameter estimation of DOD/DOA/polarization for bistatic MIMO radar. J. China Univ. Posts Telecommun. 2010, 17, 32–37. [Google Scholar] [CrossRef]
- Wang, W.J.; Ren, S.W.; Ding, Y.T.; Wang, H.Y. An efficient algorithm for direction finding against unknown mutual coupling. Sensors 2014, 14, 20064–20077. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wang, W.; Gu, Y.J.; Lei, S.J. Underdetermined DOA estimation of quasi-stationary signals using a partly-calibrated array. Sensors 2017, 17, 702. [Google Scholar] [CrossRef] [PubMed]
- Si, W.J.; Wu, D.; Liu, L.T.; Qu, X.G. Direction finding with gain/phase errors and mutual coupling errors in the presence of auxiliary sensors. Math. Probl. Eng. 2014, 2014, 429426. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations. IEEE Trans. Antennas Propag. 2000, 48, 671–681. [Google Scholar] [CrossRef]
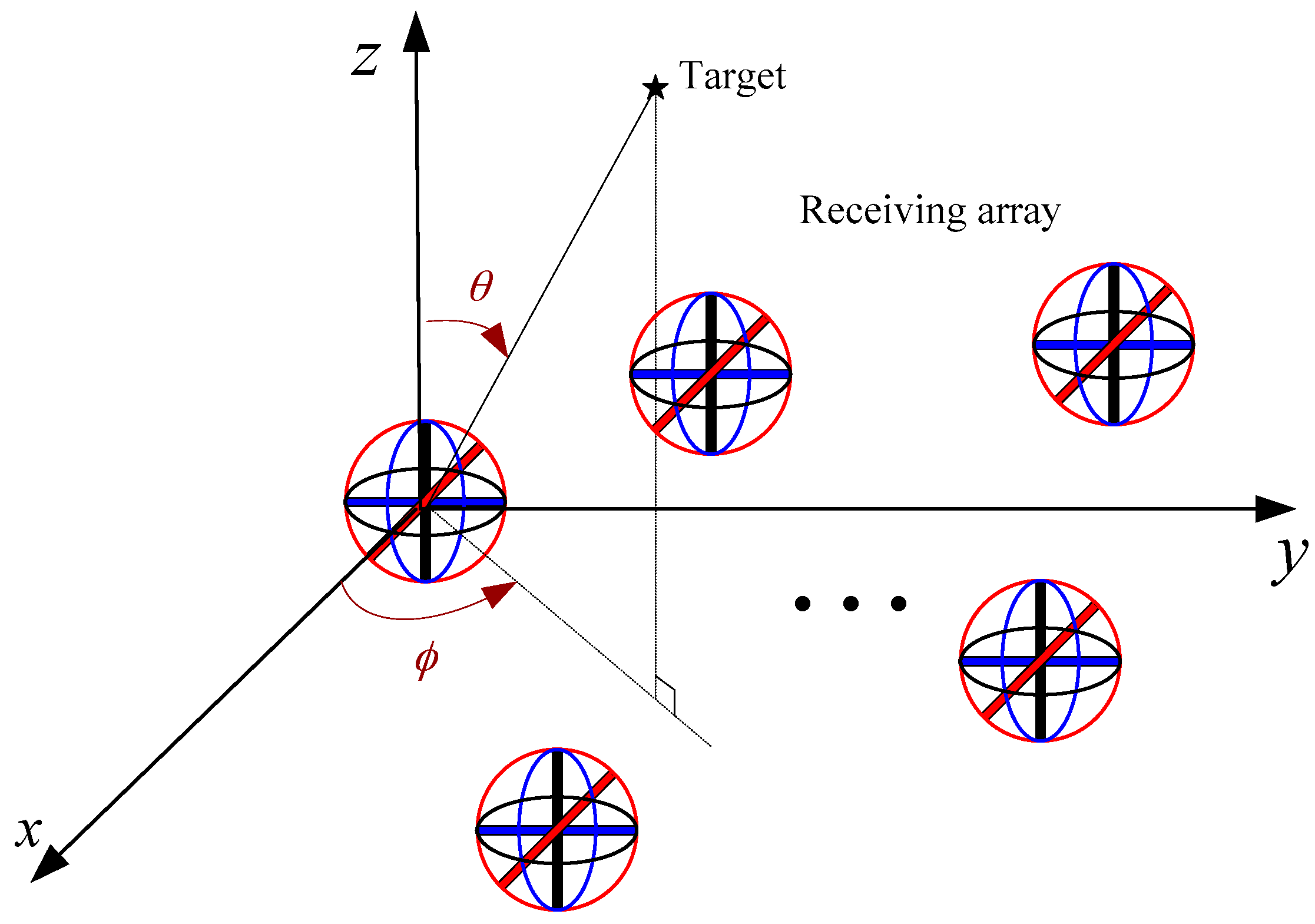
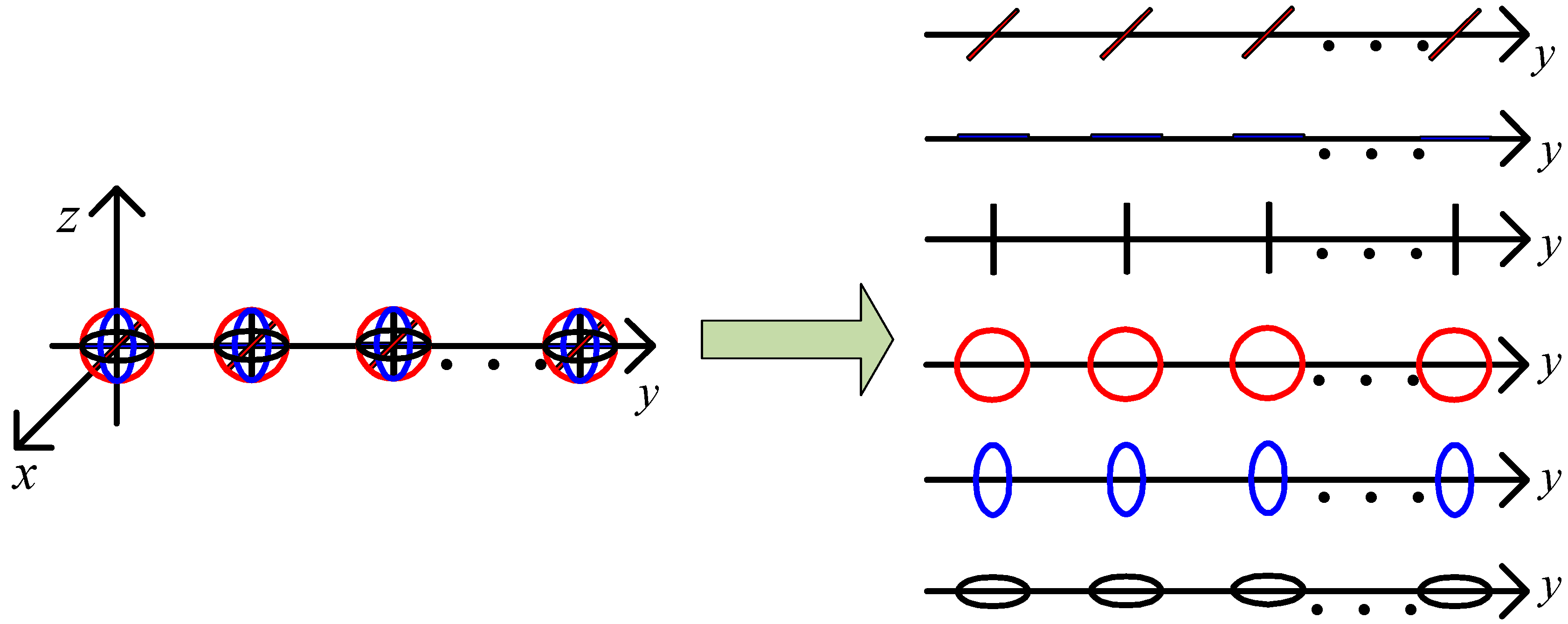

| Single Component Antenna Name | Antenna Position | Spatial Phase Shift Factor |
|---|---|---|
| Algorithm of Ref. [26] | C-SPD ESPRIT-Like | S-SPD ESPRIT-Like | |
|---|---|---|---|
| Anti gain phase uncertainty | N | Y | Y |
| Anti mutual coupling | N | N | Y |
| Structure of EMVS | C | C | S |
| Arbitrary array configuration | Y | Y | Y |
| Require prior information of target | N | N | Y |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhang, Y.; Zheng, G.; Feng, C.; Tang, J. ESPRIT-Like Two-Dimensional DOA Estimation for Monostatic MIMO Radar with Electromagnetic Vector Received Sensors under the Condition of Gain and Phase Uncertainties and Mutual Coupling. Sensors 2017, 17, 2457. https://doi.org/10.3390/s17112457
Zhang D, Zhang Y, Zheng G, Feng C, Tang J. ESPRIT-Like Two-Dimensional DOA Estimation for Monostatic MIMO Radar with Electromagnetic Vector Received Sensors under the Condition of Gain and Phase Uncertainties and Mutual Coupling. Sensors. 2017; 17(11):2457. https://doi.org/10.3390/s17112457
Chicago/Turabian StyleZhang, Dong, Yongshun Zhang, Guimei Zheng, Cunqian Feng, and Jun Tang. 2017. "ESPRIT-Like Two-Dimensional DOA Estimation for Monostatic MIMO Radar with Electromagnetic Vector Received Sensors under the Condition of Gain and Phase Uncertainties and Mutual Coupling" Sensors 17, no. 11: 2457. https://doi.org/10.3390/s17112457





