Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method
Abstract
:1. Introduction
2. The Enhanced iFEM-RZT Formulation
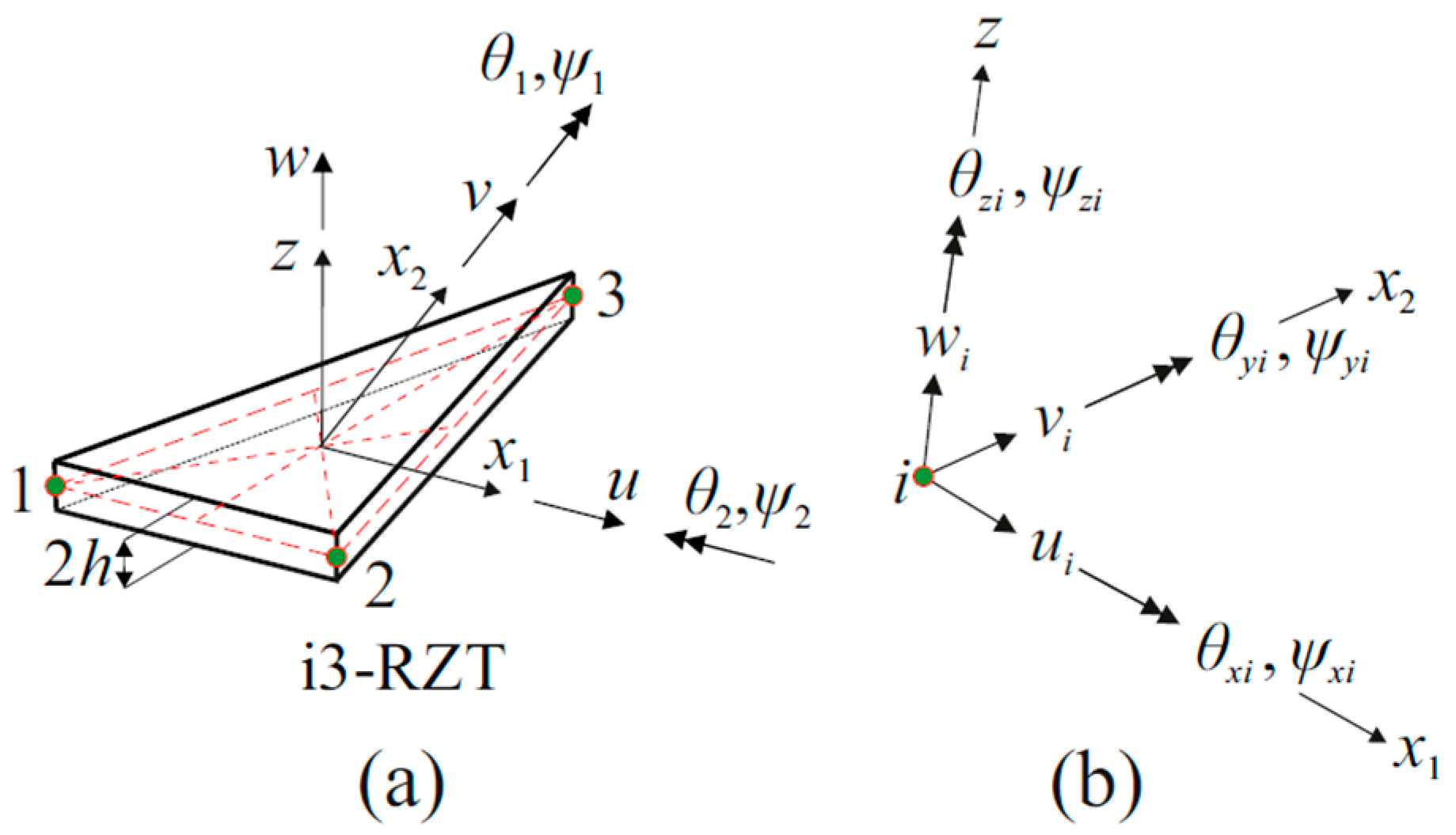
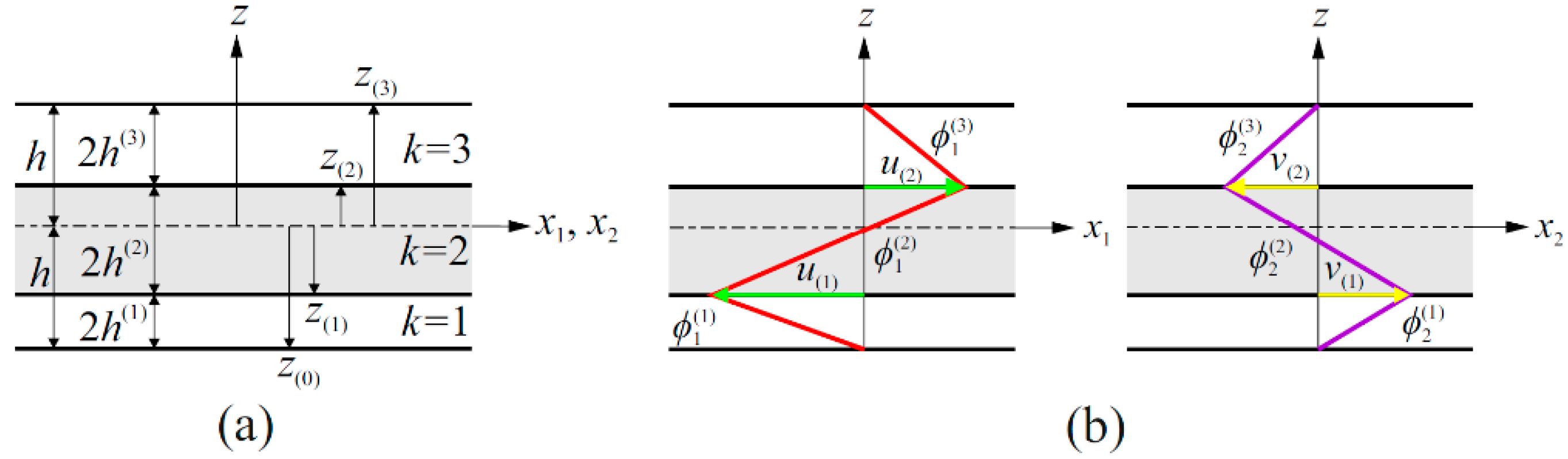
2.1. The i3-RZT Inverse-Shell Element
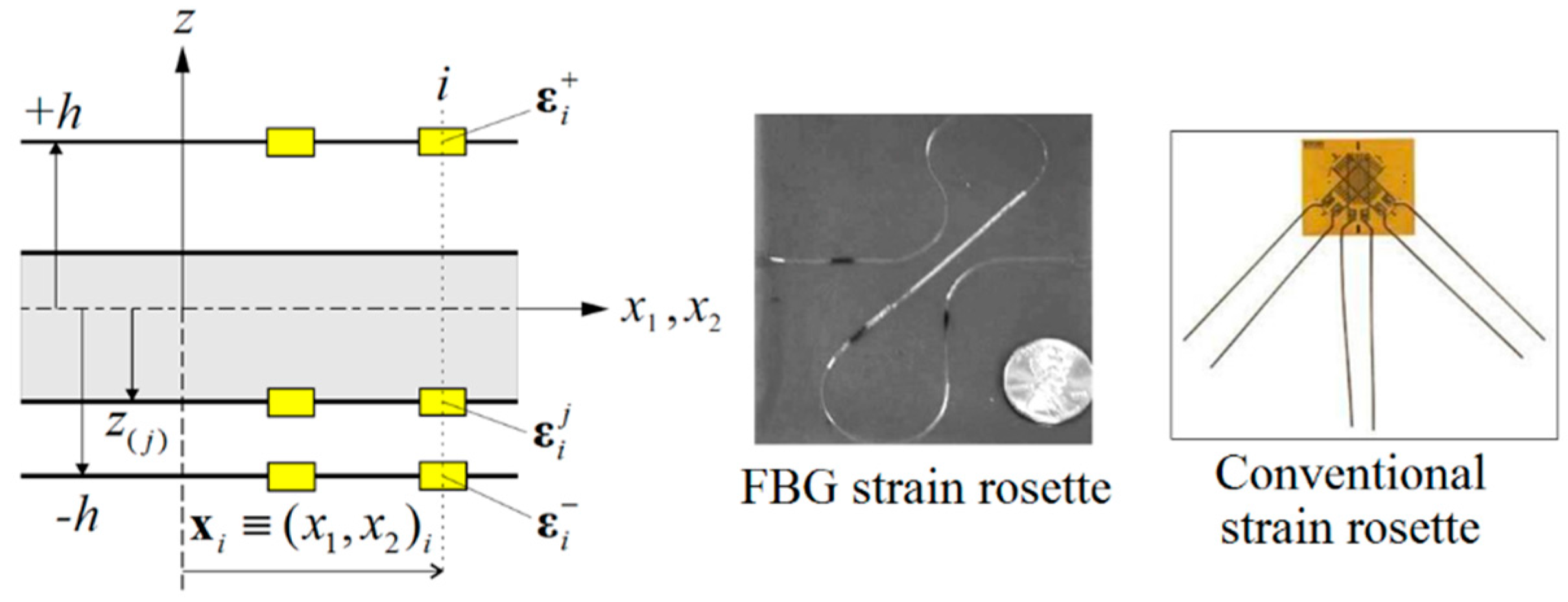
2.2. In Situ Section Strains
2.3. The Weighted-Least-Squares Functional
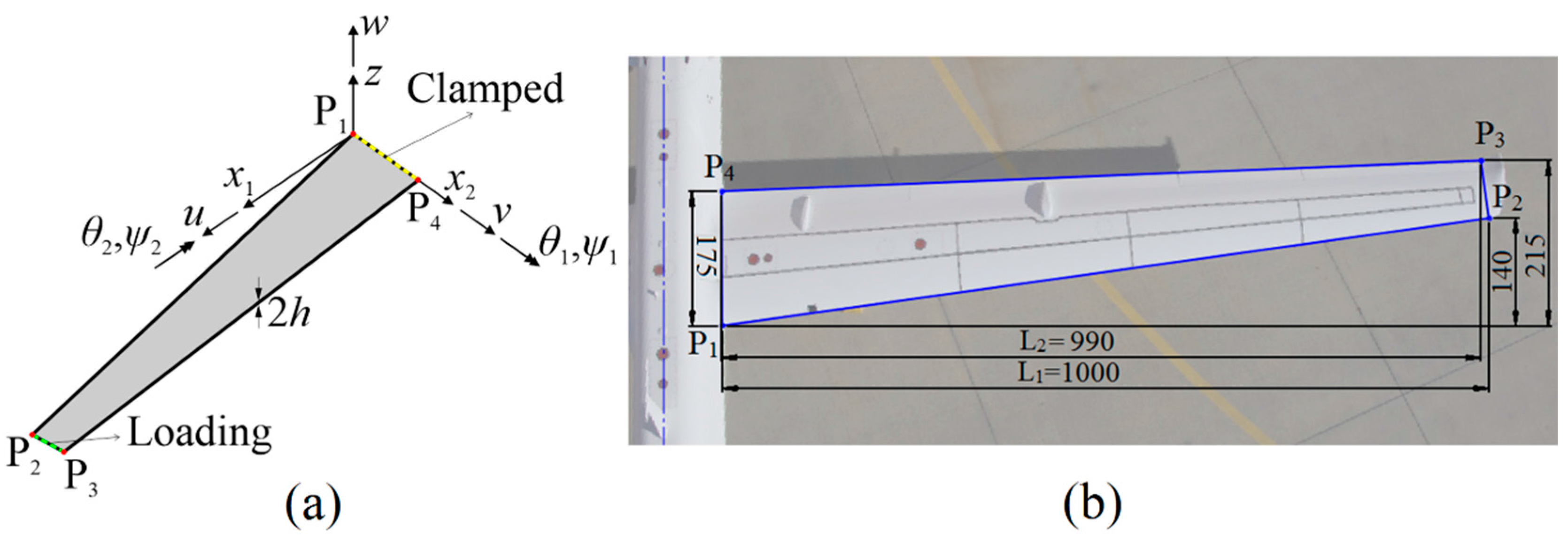
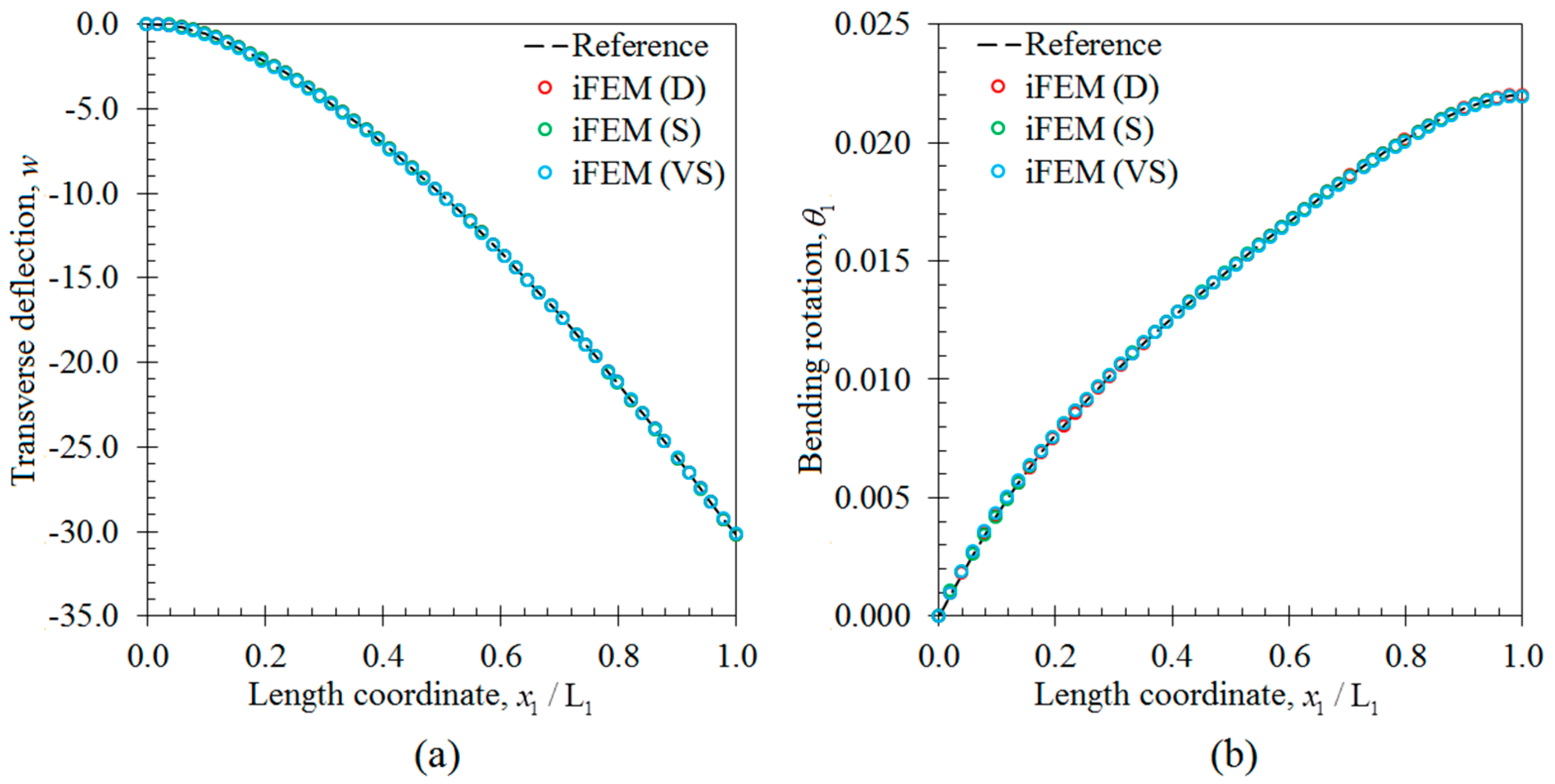
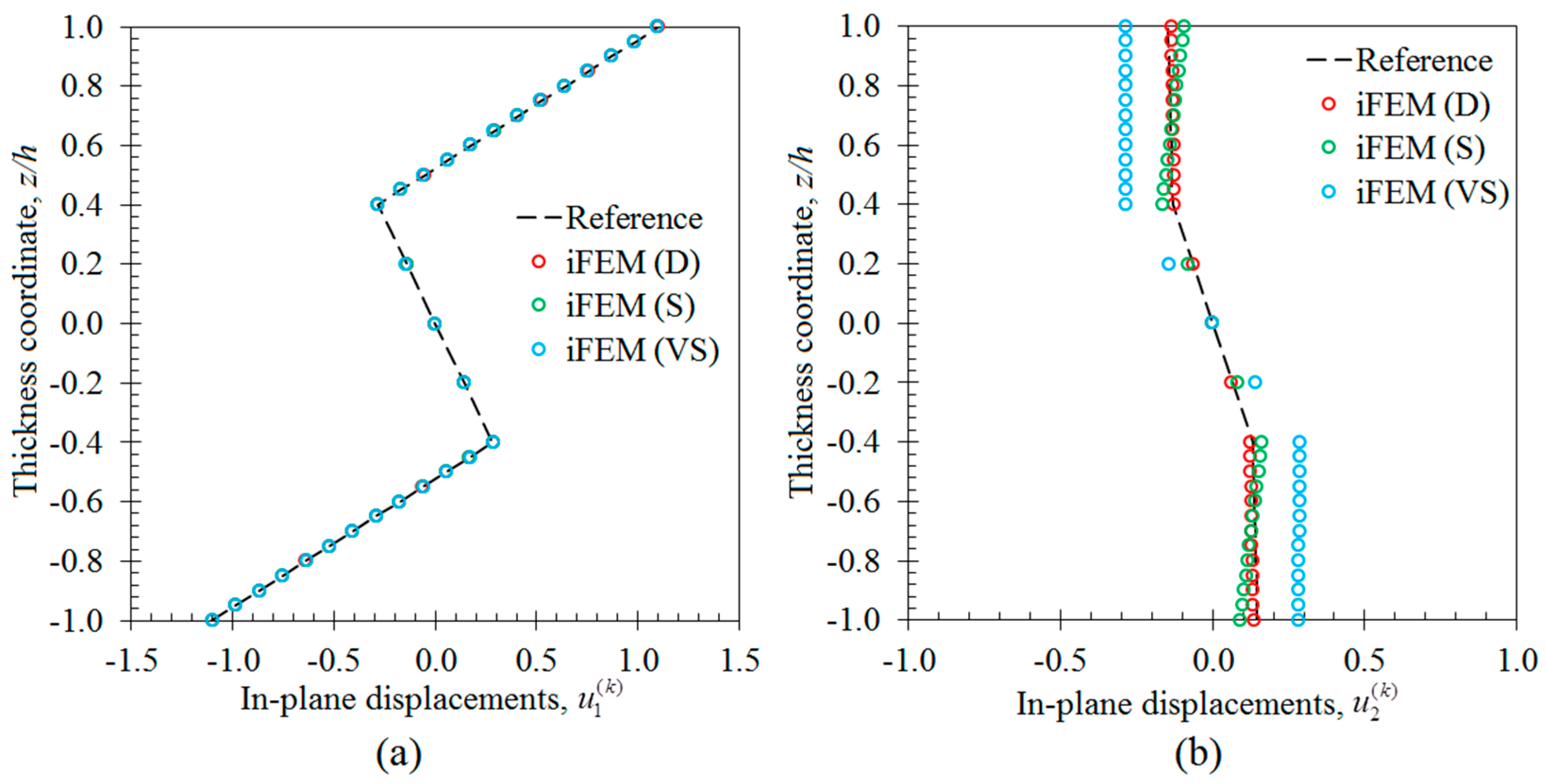
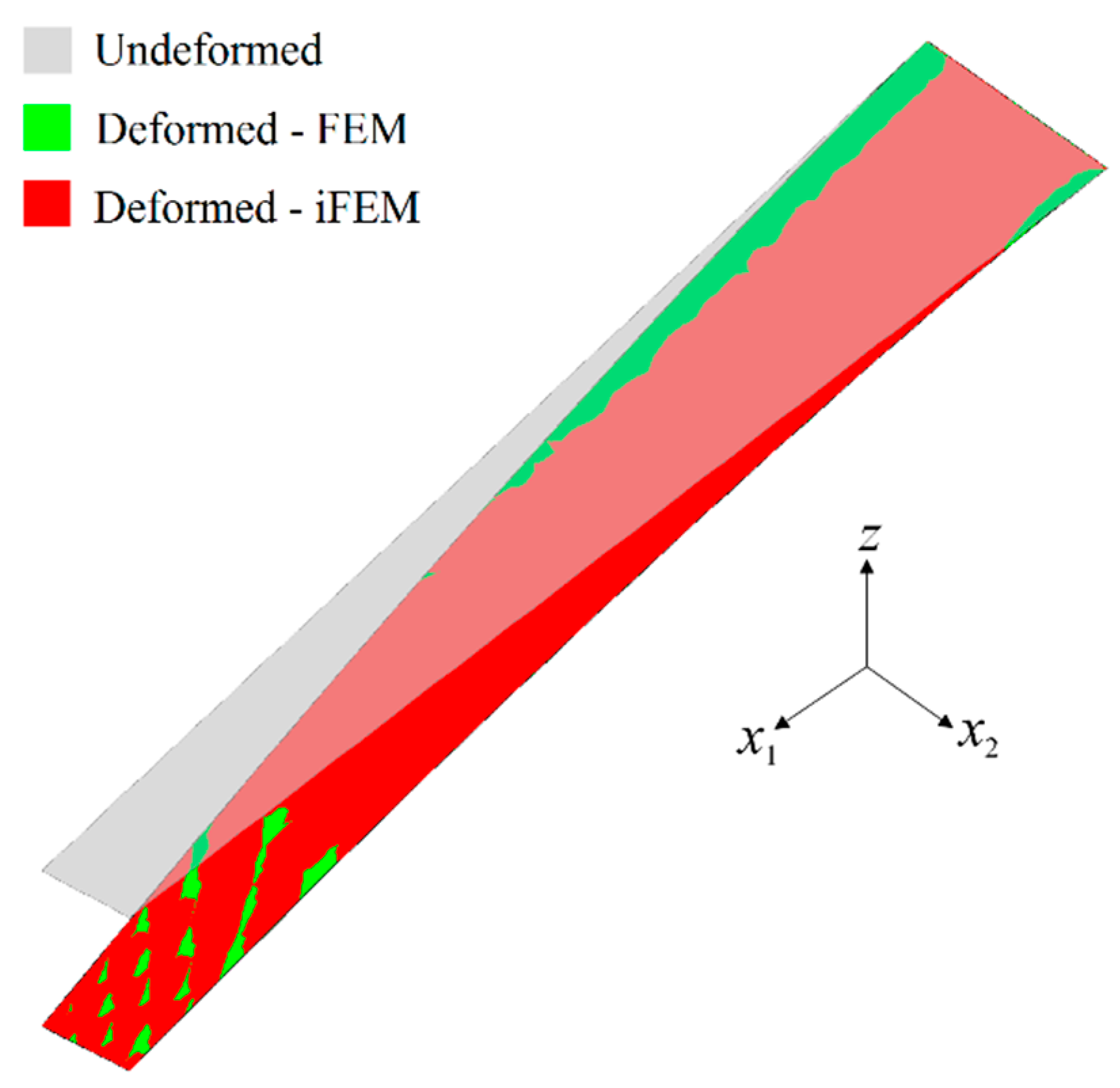
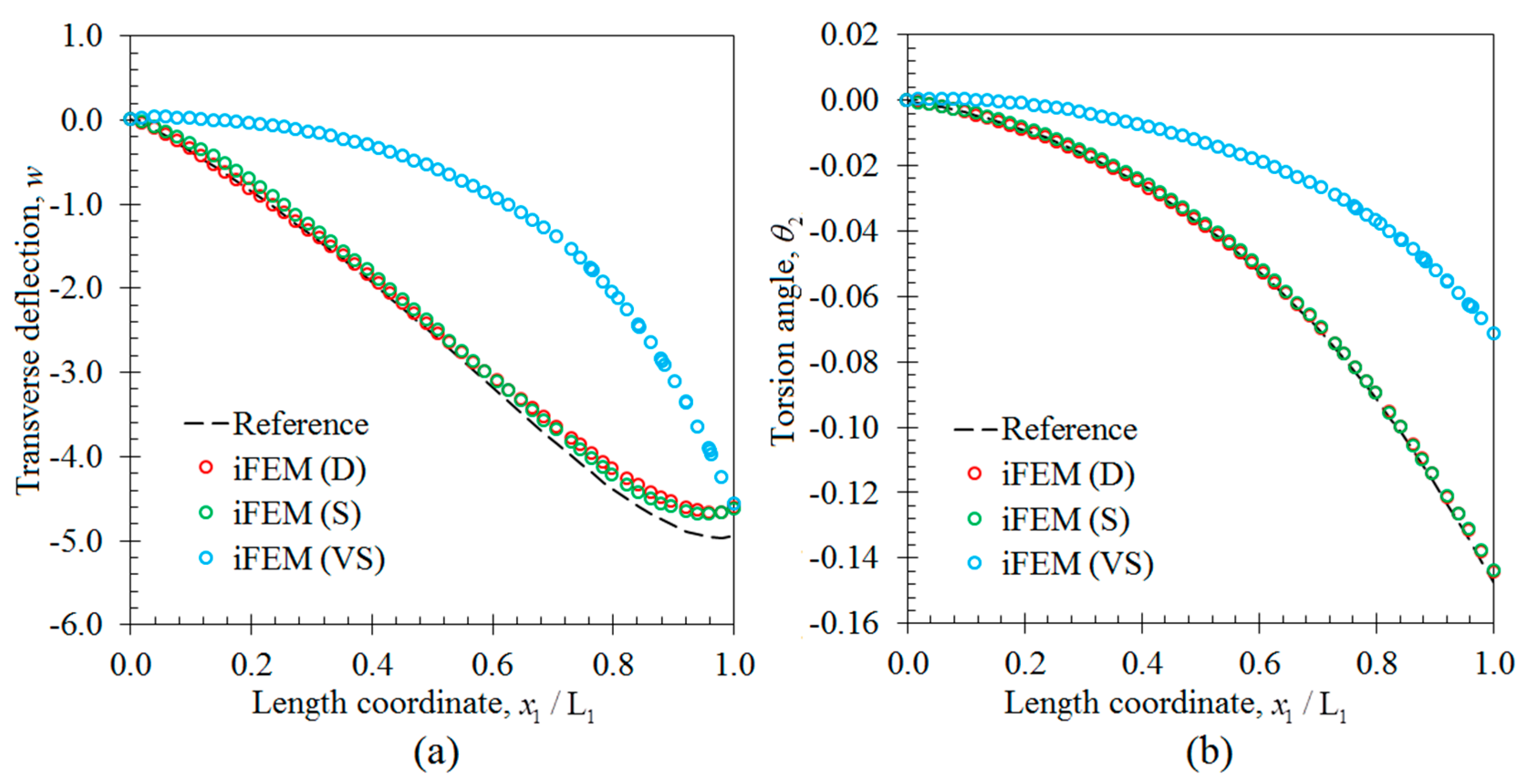
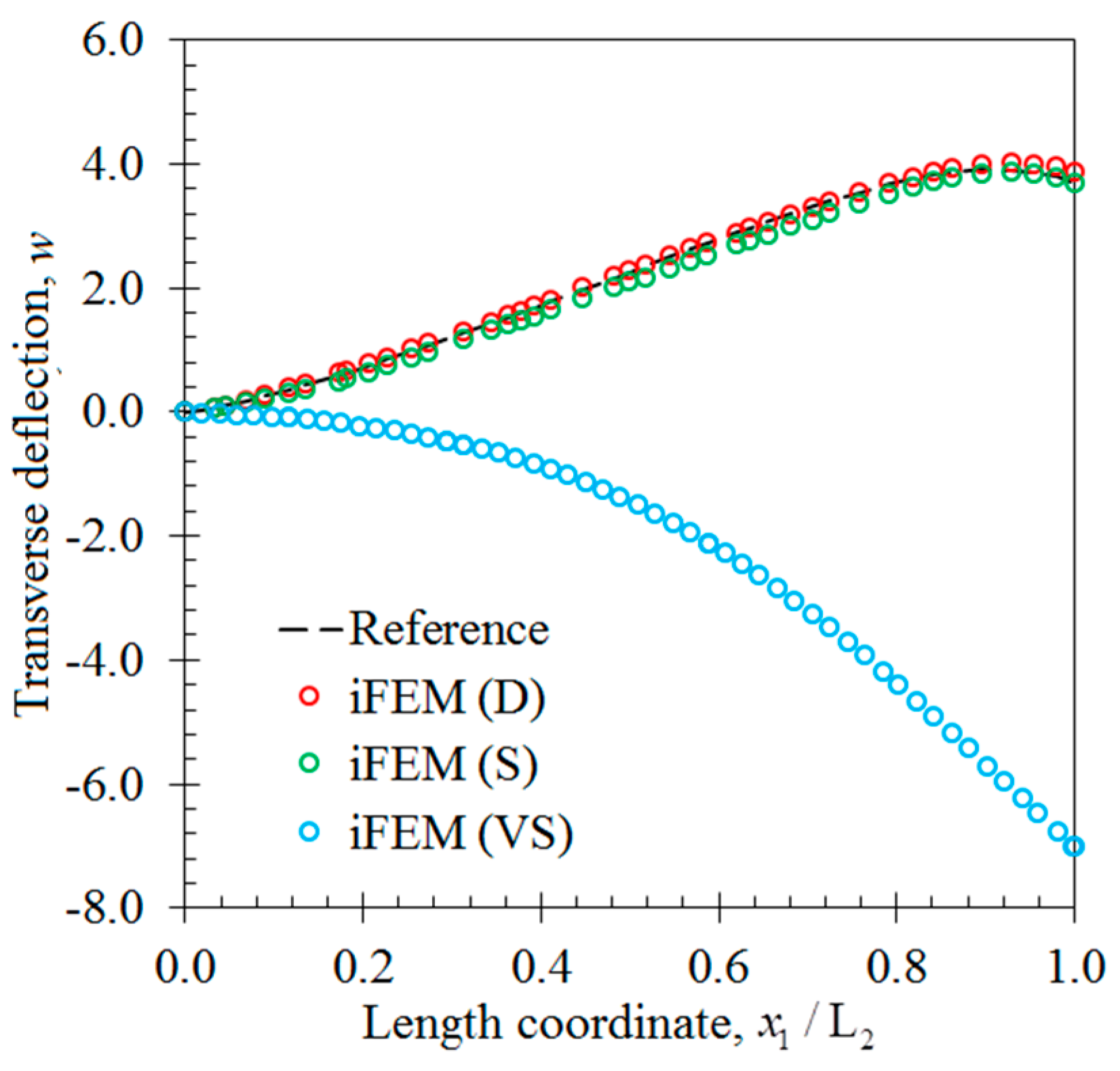
3. Numerical Examples
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Herrmann, A.S.; Zahlen, P.C.; Zuardy, I. Sandwich structures technology in commercial aviation. In Sandwich Structures 7: Advancing with Sandwich Structures and Materials; Thomsen, O.T., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 13–26. [Google Scholar]
- Lolive, E.; Casari, P.; Davies, P. Loading rate effects on foam cores for marine sandwich structures. In Sandwich Structures 7: Advancing with Sandwich Structures and Materials; Thomsen, O.T., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 895–903. [Google Scholar]
- Berggreen, C.; Branner, K.; Jensen, J.F.; Schultz, J.P. Application and analysis of sandwich elements in the primary structure of large wind turbine blades. J. Sandw. Struct. Mater. 2007, 9, 525–552. [Google Scholar] [CrossRef]
- Zou, Y.; Tong, L.P.S.G.; Steven, G.P. Vibration-based model-dependent damage (delamination) identification and health monitoring for composite structures—A review. J. Sound Vib. 2000, 230, 357–378. [Google Scholar] [CrossRef]
- Vadakke, V.; Carlsson, L.A. Experimental investigation of compression failure of sandwich specimens with face/core debond. Compos. Part B Eng. 2004, 35, 583–590. [Google Scholar] [CrossRef]
- Keulen, C.J.; Akay, E.; Melemez, F.F.; Kocaman, E.S.; Deniz, A.; Yilmaz, C.; Boz, T.; Yildiz, M.; Turkmen, H.S.; Suleman, A. Prediction of fatigue response of composite structures by monitoring the strain energy release rate with embedded fiber Bragg gratings. J. Intell. Mater. Syst. Struct. 2016, 27, 17–27. [Google Scholar] [CrossRef]
- Kocaman, E.S.; Yilmaz, C.; Deniz, A.; Yildiz, M. The performance of embedded fiber Bragg grating sensors for monitoring failure modes of foam cored sandwich structures under flexural loads. J. Sandw. Struct. Mater. 2016. [Google Scholar] [CrossRef]
- Yin, W.; Fu, T.; Liu, J.; Leng, J. Structural shape sensing for variable camber wing using FBG sensors. Proc. Int. Soc. Opt. Eng. 2009, 7292, 72921H. [Google Scholar]
- Tian, S.; Yang, Z.; Chen, X.; Xie, Y. Damage detection based on static strain responses using FBG in a wind turbine blade. Sensors 2015, 15, 19992–20005. [Google Scholar] [CrossRef] [PubMed]
- Dawood, T.A.; Shenoi, R.A.; Sahin, M. A procedure to embed fibre Bragg grating strain sensors into GFRP sandwich structures. Compos. Part A Appl. Sci. Manuf. 2007, 38, 217–226. [Google Scholar] [CrossRef]
- Pisoni, A.C.; Santolini, C.; Hauf, D.E.; Dubowsky, S. Displacements in a vibrating body by strain gauge measurements. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; pp. 119–125. [Google Scholar]
- Foss, G.C.; Haugse, E.D. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; pp. 112–118. [Google Scholar]
- Bogert, P.B.; Haugse, E.D.; Gehrki, R.E. Structural shape identification from experimental strains using a modal transformation technique. In Proceedings of the 44th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Todd, M.D.; Vohra, S.T. Shear deformation correction to transverse shape reconstruction from distributed strain measurements. J. Sound Vib. 1999, 225, 581–594. [Google Scholar] [CrossRef]
- Davis, M.A.; Kersey, A.D.; Sirkis, J.; Friebele, E.J. Shape and vibration mode sensing using a fiber optic Bragg grating array. Smart Mater. Struct. 1996, 5, 759–765. [Google Scholar] [CrossRef]
- Kim, N.S.; Cho, N.S. Estimating deflection of a simple beam model using fiber optic Bragg-grating sensors. Exp. Mech. 2004, 44, 433–439. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; Fleischer, V.T. Applications of Ko displacement theory to the deformed shape predictions of the doubly-tapered Ikhana Wing. In NASA/TP-2009-214652; NASA Dryden Flight Research Center: Edwards, CA, USA, 2009. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Winston and Sons: Washington, DC, USA, 1977. [Google Scholar]
- Maniatty, A.M.; Zabaras, N.J.; Stelson, K. Finite element analysis of some inverse elasticity problems. J. Eng. Mech. 1989, 115, 1303–1317. [Google Scholar] [CrossRef]
- Schnur, D.S.; Zabaras, N. Finite element solution of two-dimensional inverse elastic problems using spatial smoothing. Int. J. Numer. Methods Eng. 1990, 30, 57–75. [Google Scholar] [CrossRef]
- Maniatty, A.M.; Zabaras, N.J. Investigation of regularization parameters and error estimating in inverse elasticity problems. Int. J. Numer. Methods Eng. 1994, 37, 1039–1052. [Google Scholar] [CrossRef]
- Jones, R.T.; Bellemore, D.G.; Berkoff, T.A.; Sirkis, J.S.; Davis, M.A.; Putnam, M.A.; Kersey, A.D. Determination of cantilever plate shapes using wavelength division multiplexed fiber Bragg grating sensors and a least-squares strain-fitting algorithm. Smart Mater. Struct. 1998, 7, 178–188. [Google Scholar] [CrossRef]
- Shkarayev, S.; Krashantisa, R.; Tessler, A. An inverse interpolation method utilizing in-flight strain measurements for determining loads and structural response of aerospace vehicles. In Proceedings of the 3rd International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2001. [Google Scholar]
- Nishio, M.; Mizutani, T.; Takeda, N. Structural shape reconstruction with consideration of the reliability of distributed strain data from a Brillouin-scattering-based optical fiber sensor. Smart Mater. Struct. 2010, 19, 035011. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Variational Principal for Reconstruction of Elastic Deformation of Shear Deformable Plates and Shells; NASA TM-2003-212445; NASA Langley Research Center: Hampton, VA, USA, 2003. [Google Scholar]
- Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. Inverse FEM for full-field reconstruction of elastic deformations in shear deformable plates and shells. In Proceedings of the 2nd European Workshop on Structural Health Monitoring, Munich, Germany, 7–9 July 2004. [Google Scholar]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef] [Green Version]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse finite element method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. An inverse finite element method for beam shape sensing: Theoretical framework and experimental validation. Smart Mater. Struct. 2014, 23, 045027. [Google Scholar] [CrossRef]
- Tessler, A. Structural analysis methods for structural health management of future aerospace vehicles. Key Eng. Mater. 2007, 347, 57–66. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Tessler, A. Real-time displacement monitoring of a composite stiffened panel subjected to mechanical and thermal loads. Meccanica 2015, 50, 2487–2496. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Shape sensing of aerospace structures by coupling of isogeometric analysis and inverse finite element method. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Kefal, A.; Oterkus, E. Structural health monitoring of marine structures by using inverse finite element method. In Analysis and Design of Marine Structures V; Guedes Soares, C., Shenoi, R.A., Eds.; Taylor and Francis Group: London, UK, 2015; pp. 341–349. [Google Scholar]
- Kefal, A.; Hizir, O.; Oterkus, E. A smart system to determine sensor locations for structural health monitoring of ship structures. In Proceedings of the 9th International Workshop on Ship and Marine Hydrodynamics, Glasgow, UK, 26–28 August 2015. [Google Scholar]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Kefal, A.; Mayang, J.B.; Oterkus, E.; Yildiz, M. Three dimensional shape and stress monitoring of bulk carriers based on iFEM methodology. Ocean Eng. 2018, 147, 256–267. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Shape and stress sensing of offshore structures by using inverse finite element method. In Progress in the Analysis and Design of Marine Structures; Guedes Soares, C., Garbatov, Y., Eds.; Taylor and Francis Group: London, UK, 2017; pp. 141–148. [Google Scholar]
- Stoesz, C.W. Method for Analyzing Strain Data. U.S. Patent 8,515,675 B2, 20 August 2013. [Google Scholar]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. A novel approach for displacement and stress monitoring of sandwich structures based on the inverse finite element method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A consistent refinement of first-order shear deformation theory for laminated composite and sandwich plates using improved zigzag kinematics. J. Mech. Mater. Struct. 2010, 5, 341–367. [Google Scholar] [CrossRef]
- Kefal, A.; Tessler, A.; Oterkus, E. An enhanced inverse finite element method for displacement and stress monitoring of multilayered composite and sandwich structures. Compos. Struct. 2017, 179, 514–540. [Google Scholar] [CrossRef]
- Tessler, A.; Dong, S.B. On a hierarchy of conforming Timoshenko beam elements. Comput. Struct. 1981, 14, 335–344. [Google Scholar] [CrossRef]
- Tessler, A. Comparison of interdependent interpolations for membrane and bending kinematics in shear-deformable shell elements. In Proceedings of the 8th International Conference on Computational Engineering and Sciences, Los Angeles, CA, USA, 18–24 August 2000. [Google Scholar]
- Tessler, A.; Hughes, T.J.R. A three-node Mindlin plate element with improved transverse shear. Comput. Methods Appl. Mech. Eng. 1985, 50, 71–101. [Google Scholar] [CrossRef]
- Tessler, A.; Riggs, H.R.; Freese, C.E.; Cook, G.M. An improved variational method for finite element stress recovery and a posteriori error estimation. Comput. Methods Appl. Mech. Eng. 1998, 155, 15–30. [Google Scholar] [CrossRef]
- Tessler, A.; Riggs, H.R.; Dambach, M. A novel four-node quadrilateral smoothing element for stress enhancement and error estimation. Int. J. Numer. Methods Eng. 1999, 44, 1527–1541. [Google Scholar] [CrossRef]
- Cobleigh, B.R. Ikhana: A NASA UAS Supporting Long Duration Earth Science Missions; NASA TM-2007-214614; NASA Dryden Flight Research Center: Edwards, CA, USA, 2007. [Google Scholar]
- Versino, D.; Gherlone, M.; Mattone, M.; Di Sciuva, M.; Tessler, A. C0 triangular elements based on the Refined Zigzag Theory for multilayer composite and sandwich plates. Compos. Part B Eng. 2013, 44, 218–230. [Google Scholar] [CrossRef]






| Lamina Material | Young’s Modulus [GPa] | Poisson’s Ratio | Shear Modulus [GPa] | |
|---|---|---|---|---|
| C | Carbon-epoxy unidirectional composite | |||
| P | PVC core | |||
| Laminate | Normalized Lamina Thickness, | Lamina Materials | Lamina Orientation [] |
|---|---|---|---|
| Quasi-isotropic sandwich | (0.1/0.1/0.1/0.4/0.1/0.1/0.1) | (C/C/C/P/C/C/C) | (60/0/−60/0/−60/0/60) |
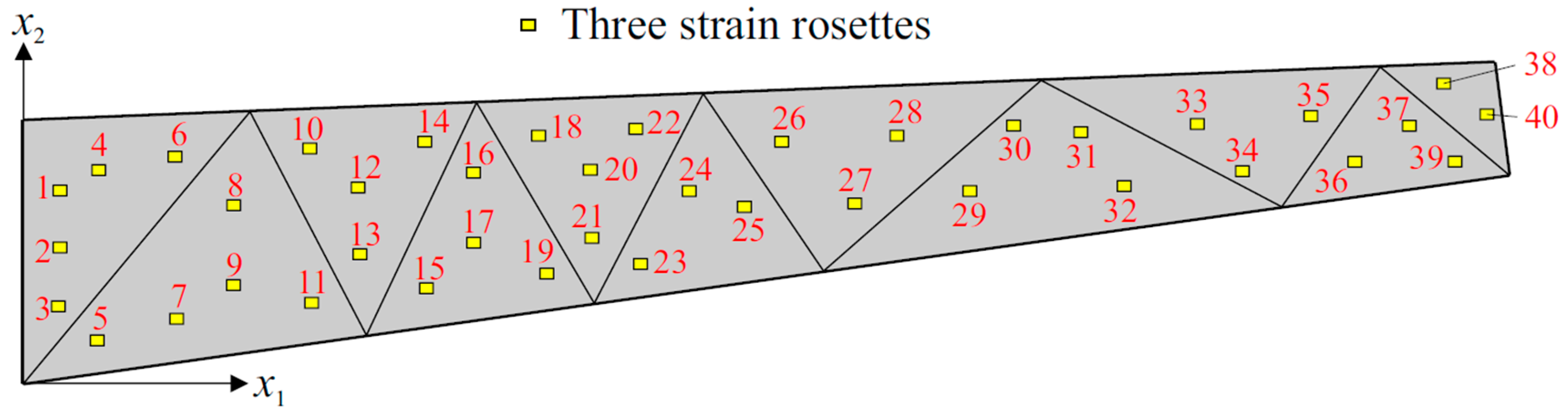
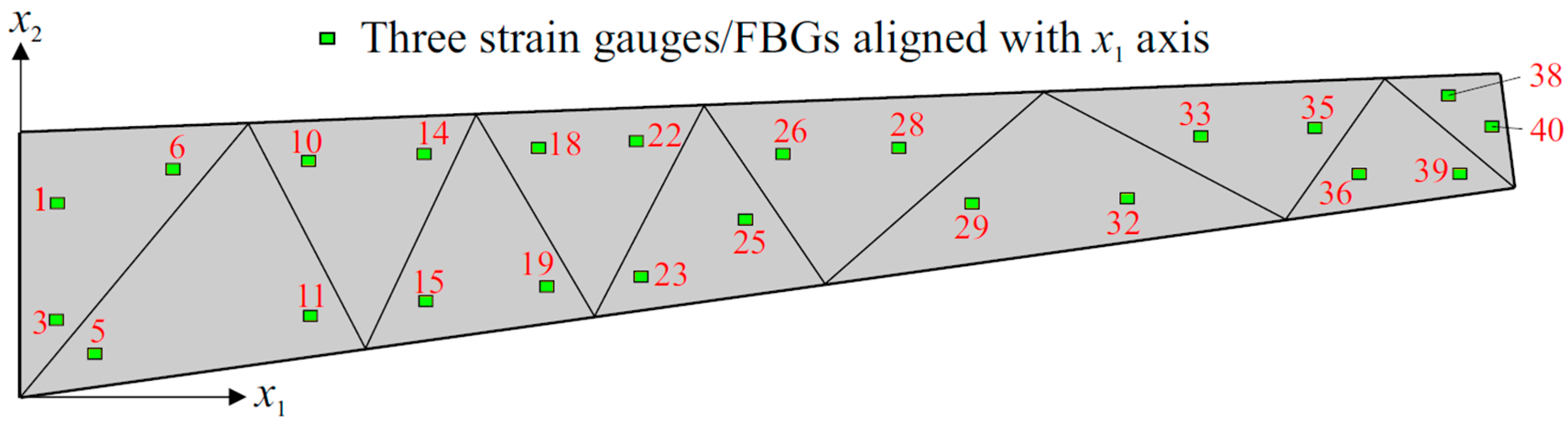
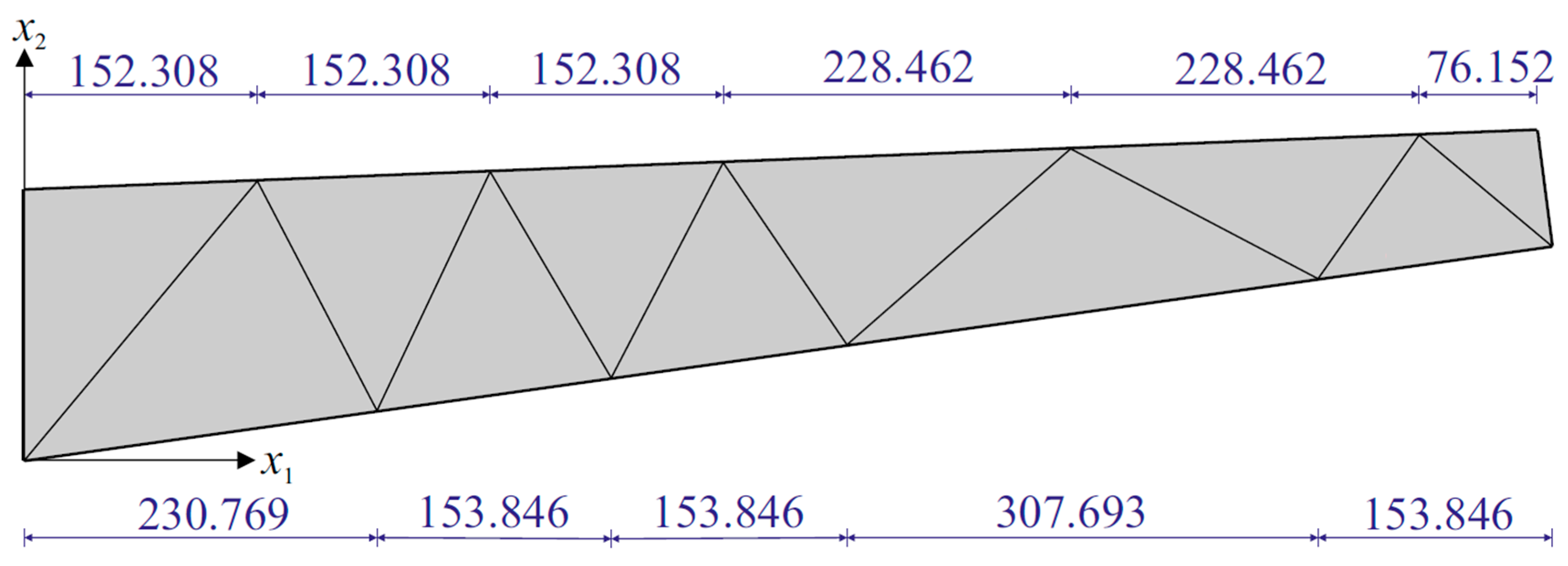
| Sensors | x1 [mm] | x2 [mm] | Sensors | x1 [mm] | x2 [mm] |
|---|---|---|---|---|---|
| 1 | 22.71 | 127.94 | 21 | 381.15 | 96.59 |
| 2 | 22.76 | 89.56 | 22 | 411.57 | 169.35 |
| 3 | 22.81 | 51.18 | 23 | 414.34 | 80.35 |
| 4 | 48.63 | 142.31 | 24 | 445.47 | 127.79 |
| 5 | 48.96 | 28.91 | 25 | 485.03 | 117.29 |
| 6 | 100.46 | 151.57 | 26 | 509.37 | 161.16 |
| 7 | 101.14 | 41.66 | 27 | 556.86 | 120.15 |
| 8 | 139.66 | 118.03 | 28 | 587.23 | 166.48 |
| 9 | 140.13 | 64.38 | 29 | 635.01 | 128.37 |
| 10 | 191.20 | 156.76 | 30 | 665.10 | 171.80 |
| 11 | 192.49 | 52.95 | 31 | 711.05 | 167.24 |
| 12 | 224.03 | 130.38 | 32 | 739.77 | 131.86 |
| 13 | 224.70 | 85.21 | 33 | 788.97 | 173.13 |
| 14 | 268.98 | 161.20 | 34 | 817.98 | 140.66 |
| 15 | 270.79 | 62.62 | 35 | 866.89 | 179.03 |
| 16 | 301.84 | 141.63 | 36 | 896.20 | 149.46 |
| 17 | 302.85 | 93.43 | 37 | 933.22 | 171.91 |
| 18 | 346.76 | 165.65 | 38 | 956.02 | 200.46 |
| 19 | 349.09 | 72.29 | 39 | 962.45 | 148.07 |
| 20 | 379.88 | 142.17 | 40 | 984.88 | 179.43 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kefal, A.; Yildiz, M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors 2017, 17, 2775. https://doi.org/10.3390/s17122775
Kefal A, Yildiz M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors. 2017; 17(12):2775. https://doi.org/10.3390/s17122775
Chicago/Turabian StyleKefal, Adnan, and Mehmet Yildiz. 2017. "Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method" Sensors 17, no. 12: 2775. https://doi.org/10.3390/s17122775





