Inspection and Reconstruction of Metal-Roof Deformation under Wind Pressure Based on Bend Sensors
Abstract
:1. Introduction
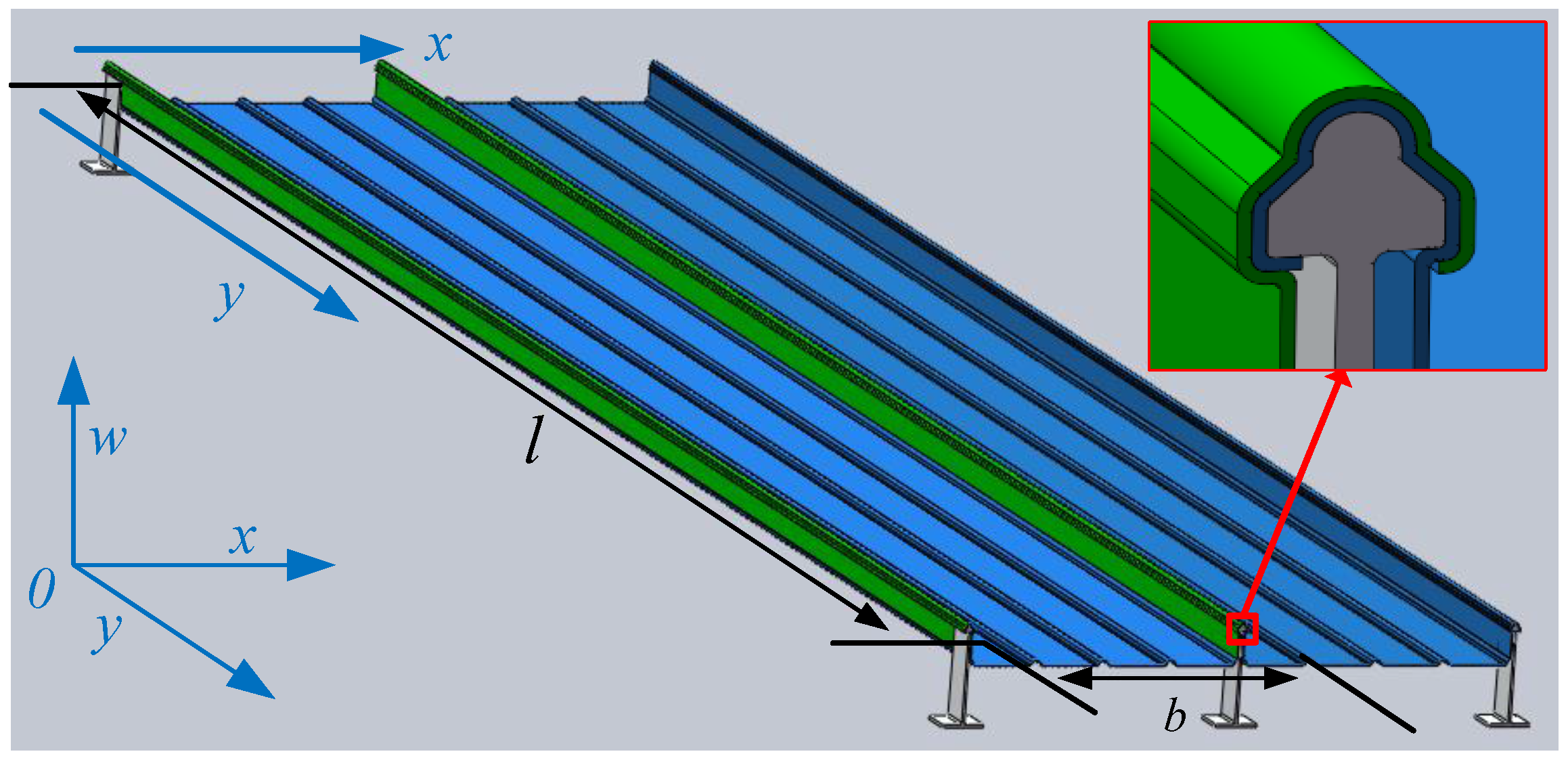
2. Fast Reconstruction Model for Deflection Distribution of Metal Roof
2.1. A Fast Reconstruction Model for the Deflection Distribution of Metal Roof
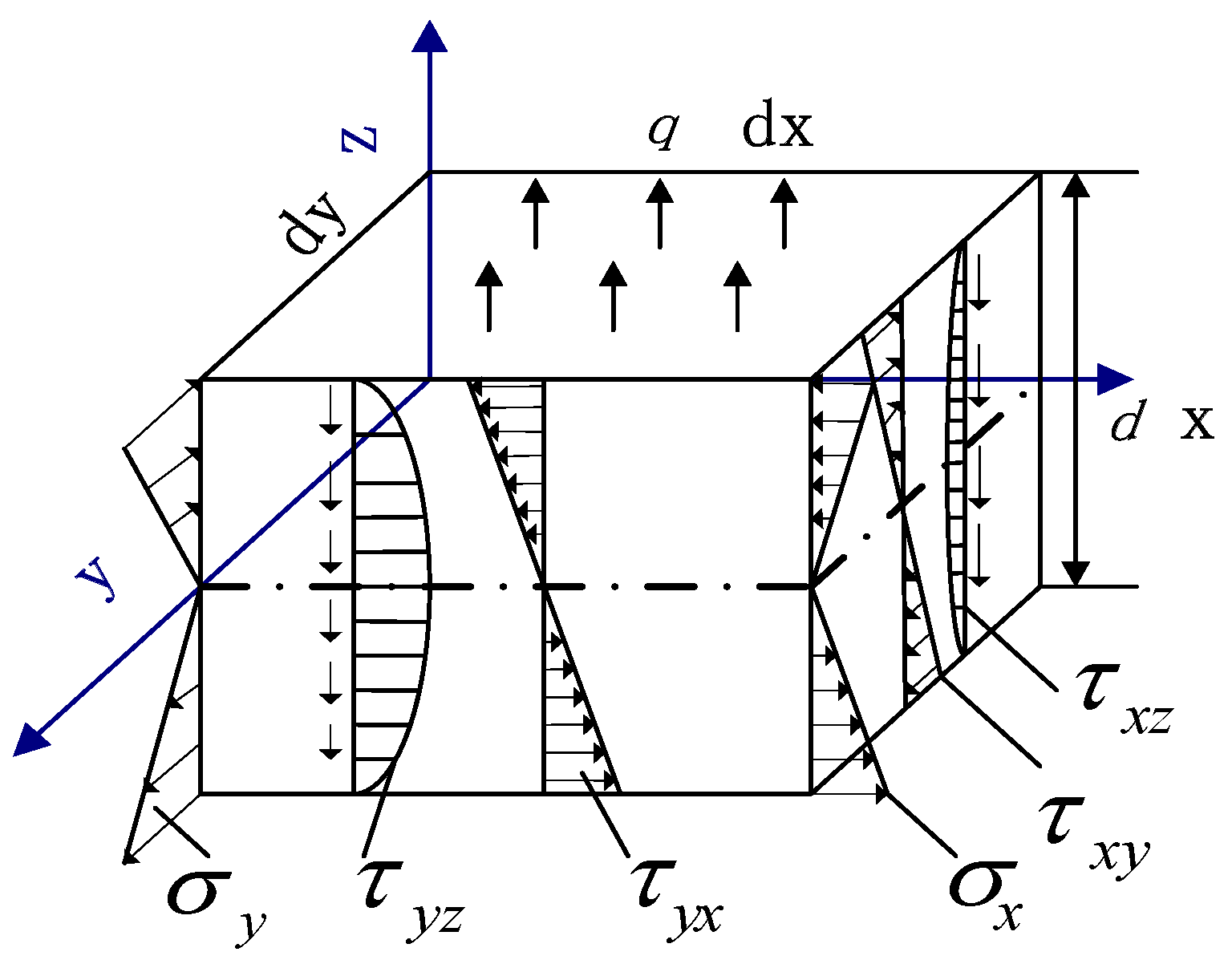
2.1.1. Governing Equations for Deflection Deformation of Thin Plate
- I
- Free edges (y = 0, y = l): the bending moment and shear force are zero, and formulated as:
- II
- Supported Edges (x = 0, x = b): the deflection and bending moment are zero:
- (a)
- A thin rectangular plate with four sides simply supported, and subjected to uniform load q.
- (b)
- A rectangular plate with two sides x = 0 and x = b seen as simply supported sides, and the other sides y = 0 and y = l seen as generalized simply supported edges.
2.1.2. Deflection Calculation of Part I
2.1.3. Deflection Calculation of Part II
- (1)
- Moment of the two generalized simply supported edges is zero, i.e.,
- (2)
- Deflection of the two generalized simply supported sides is assumed, i.e., , and can be given:
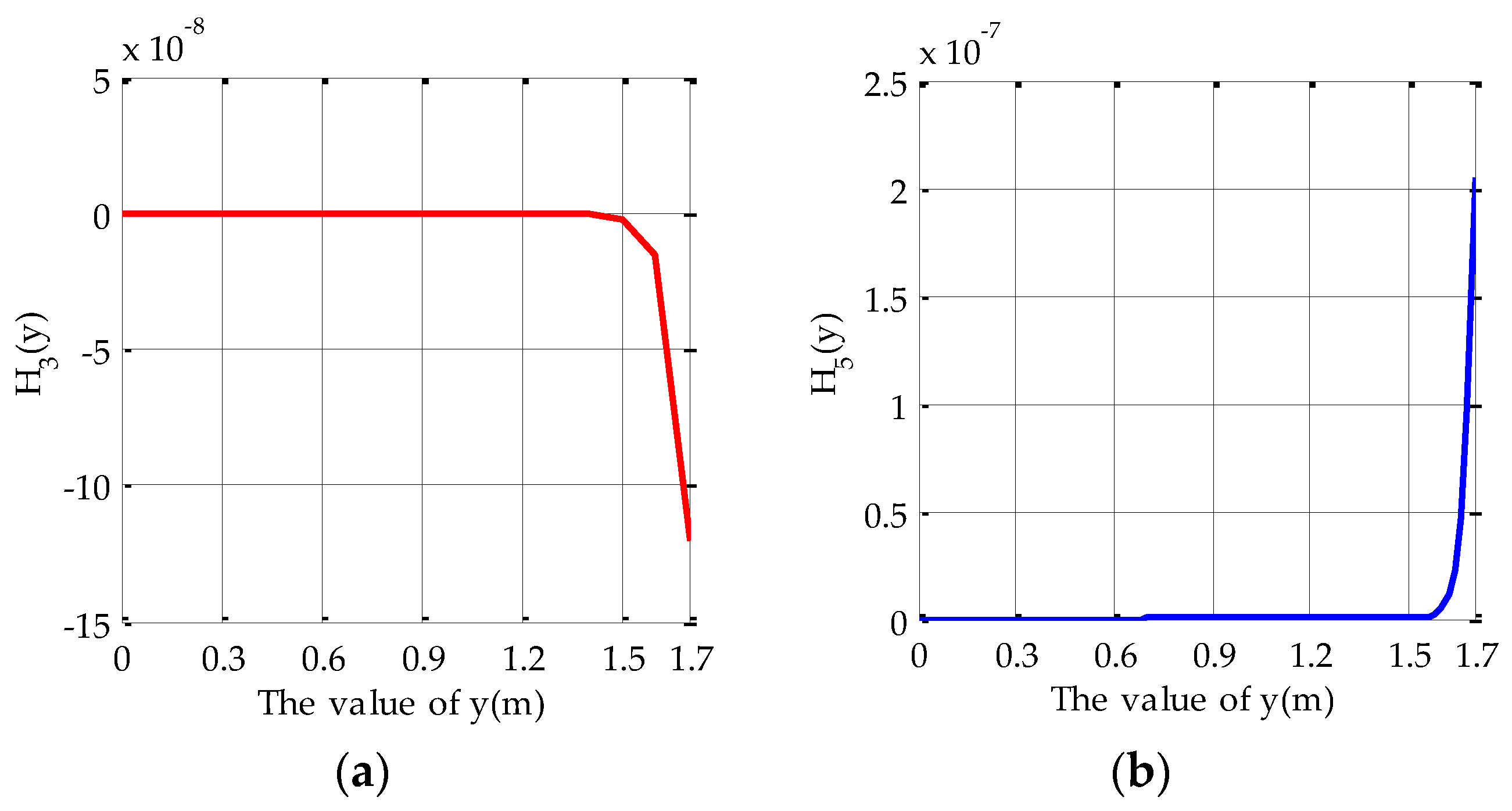
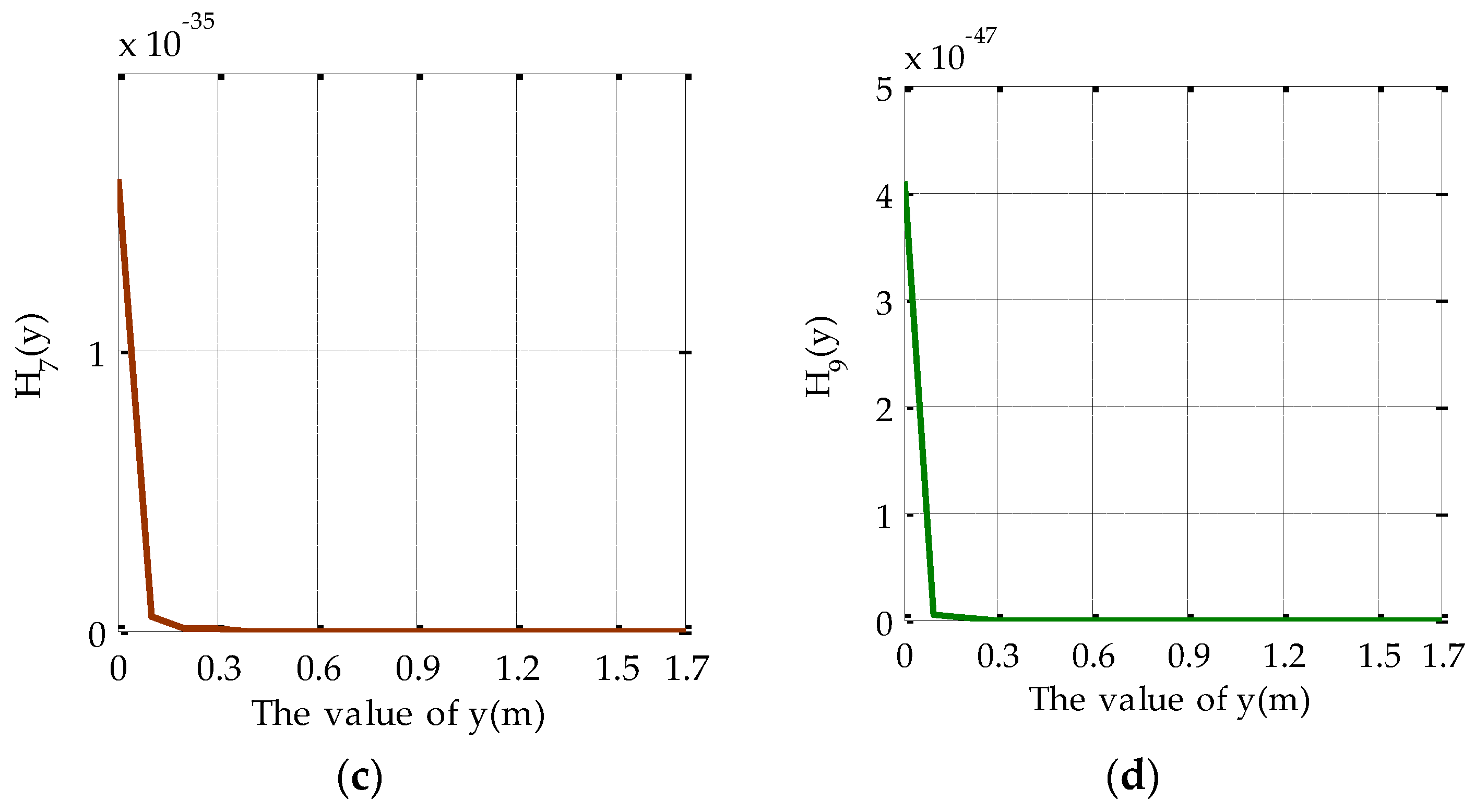
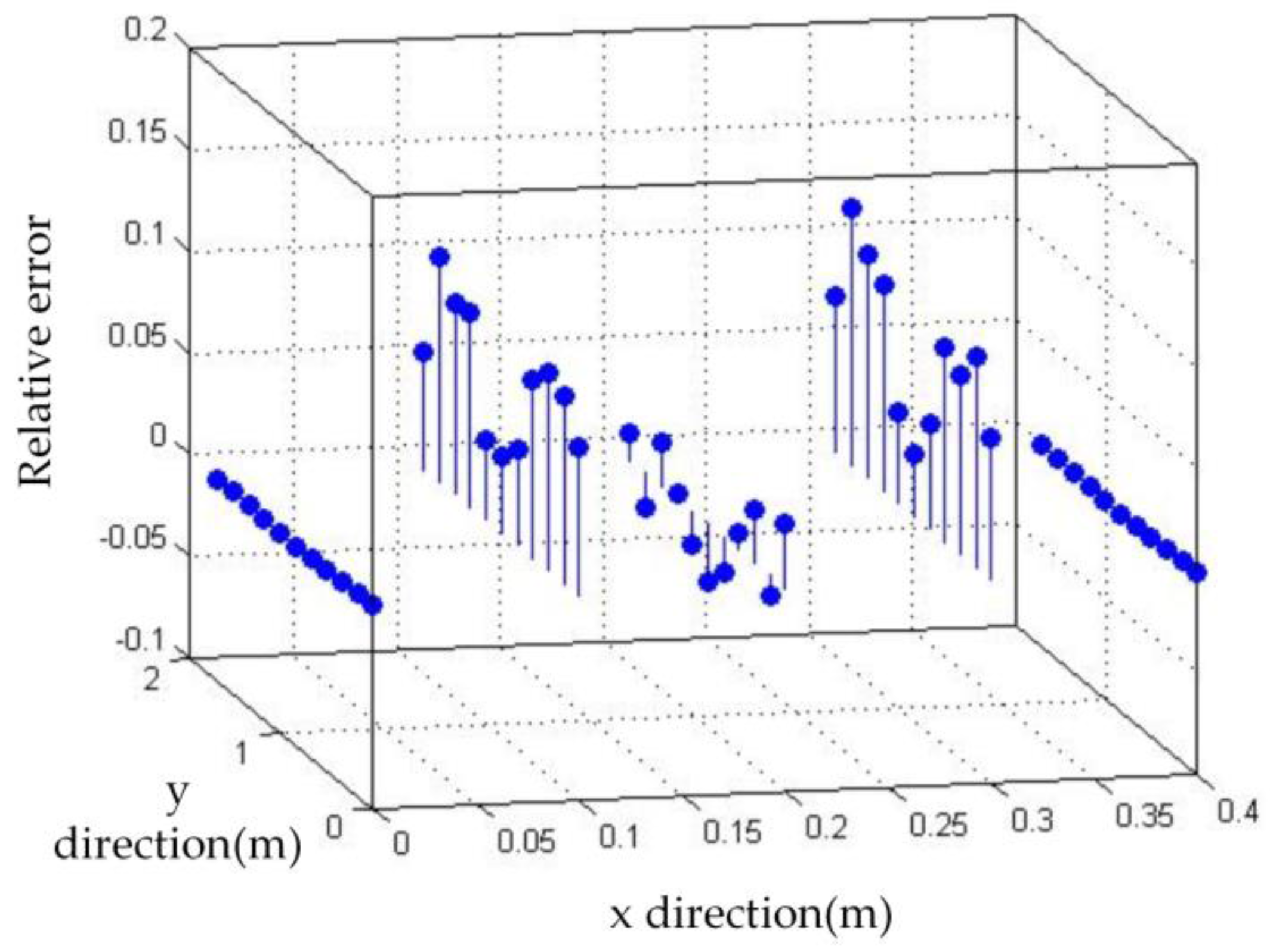
2.2. Analysis of Model Error
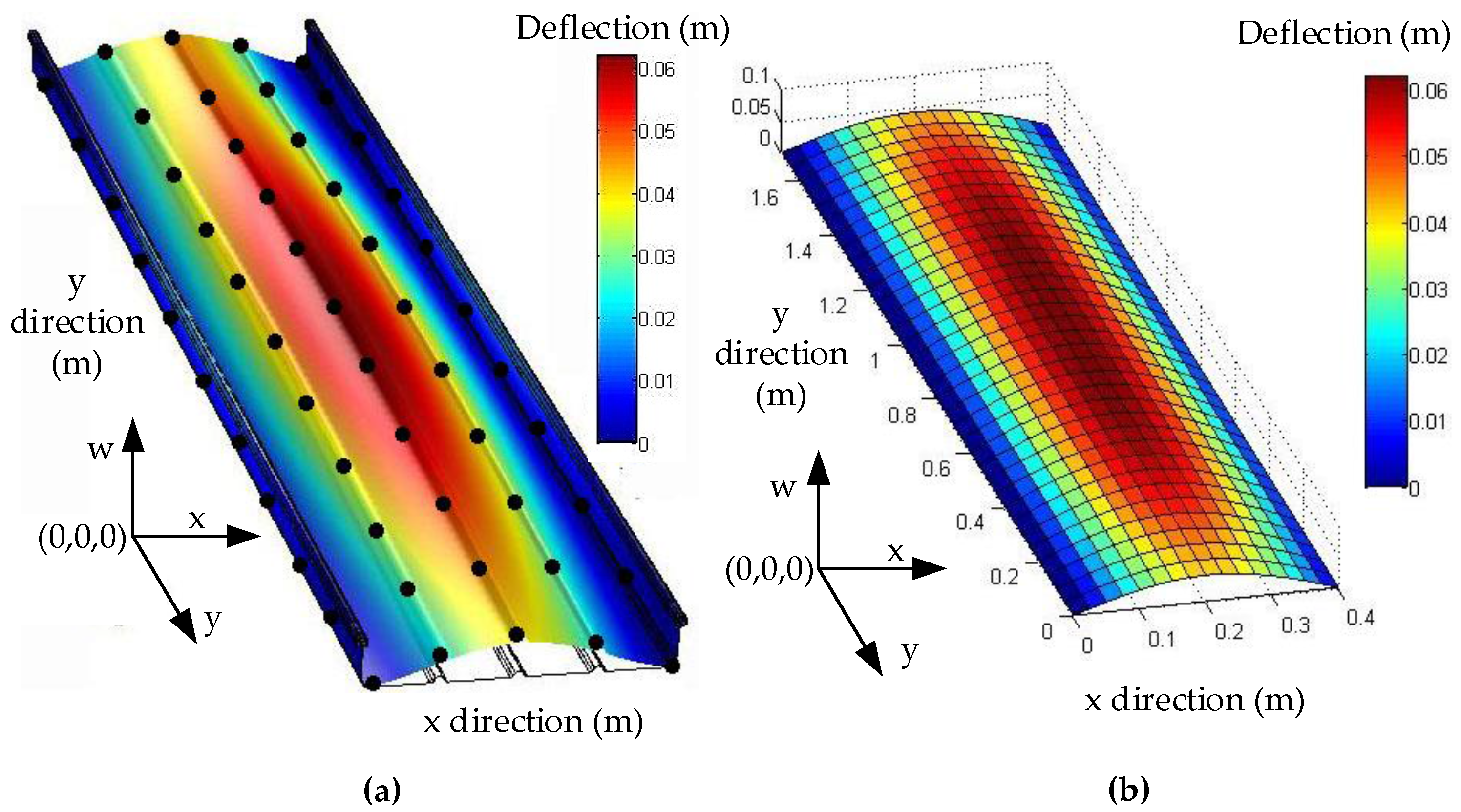
3. Simulations and Experiments
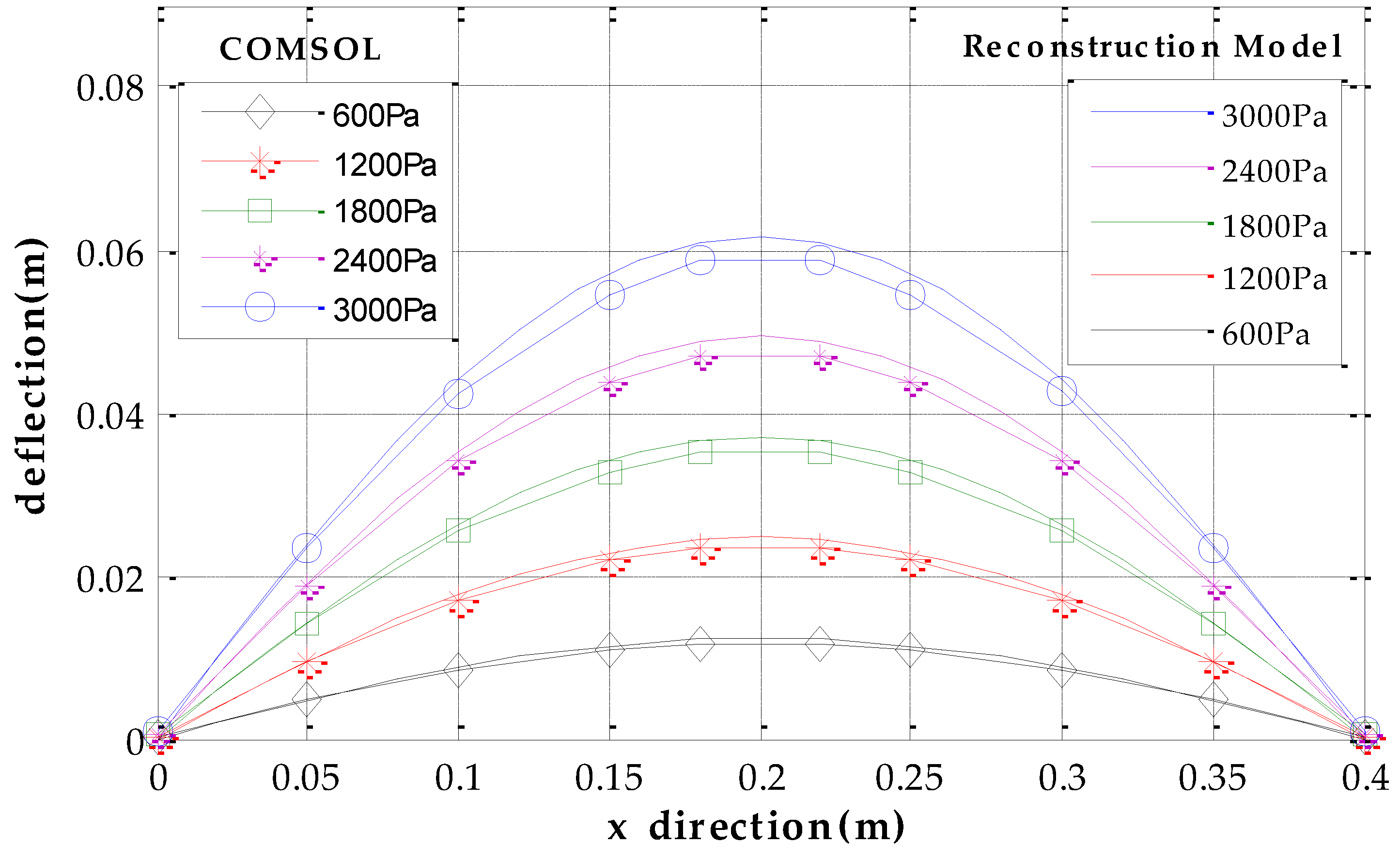
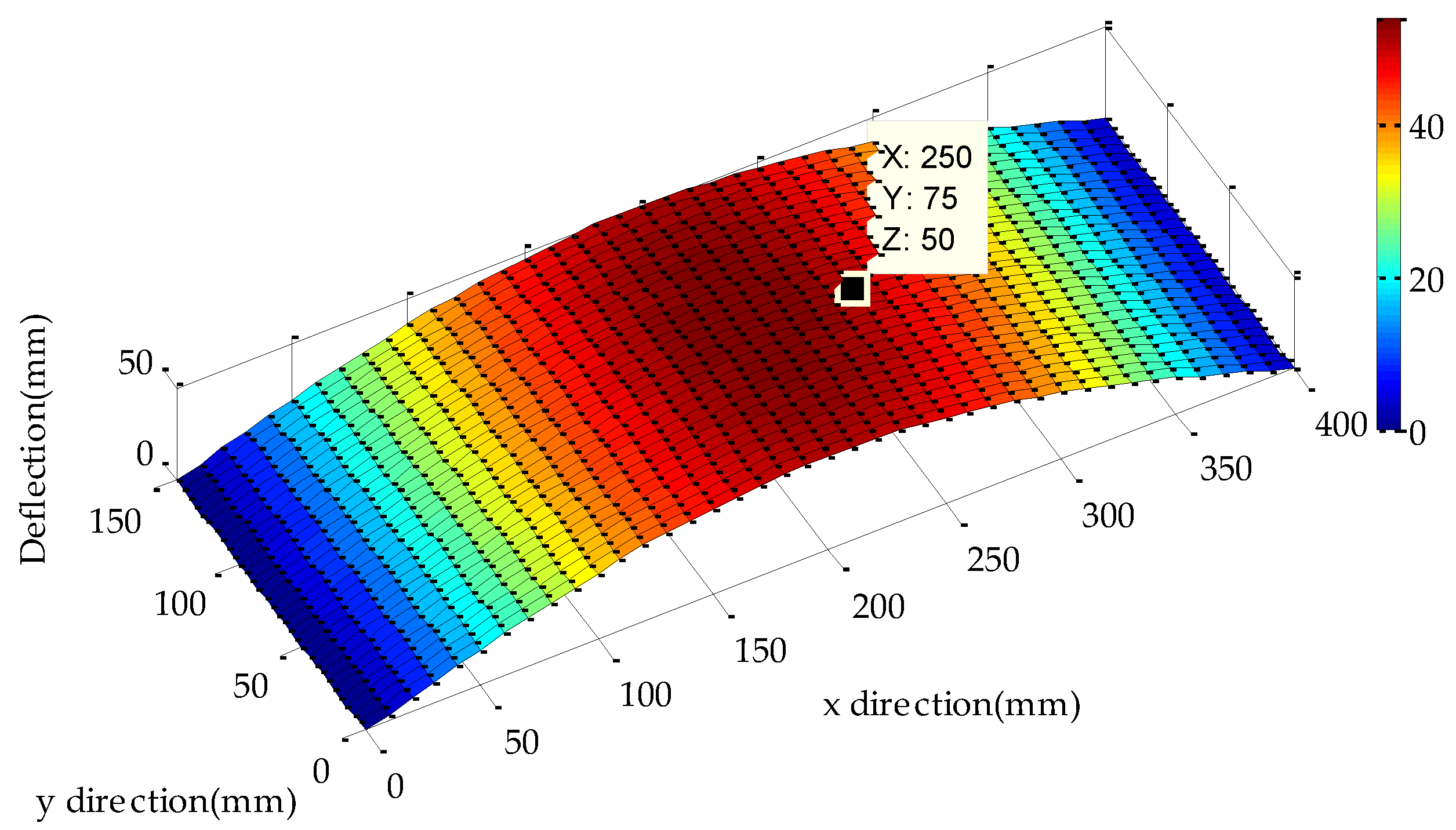
3.1. Simulation and Discussions
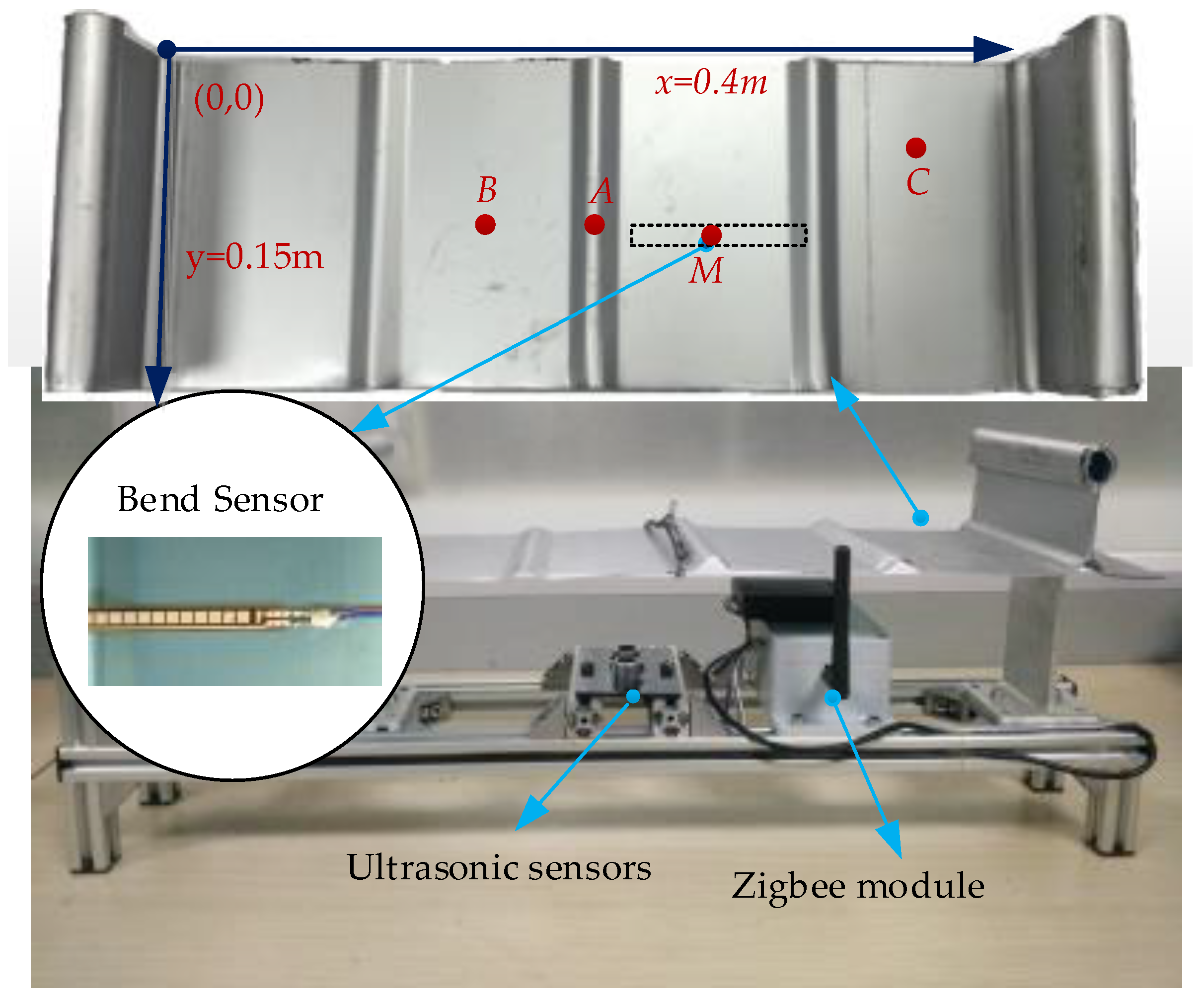
3.2. Experimental Platform
3.3. Experimental Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
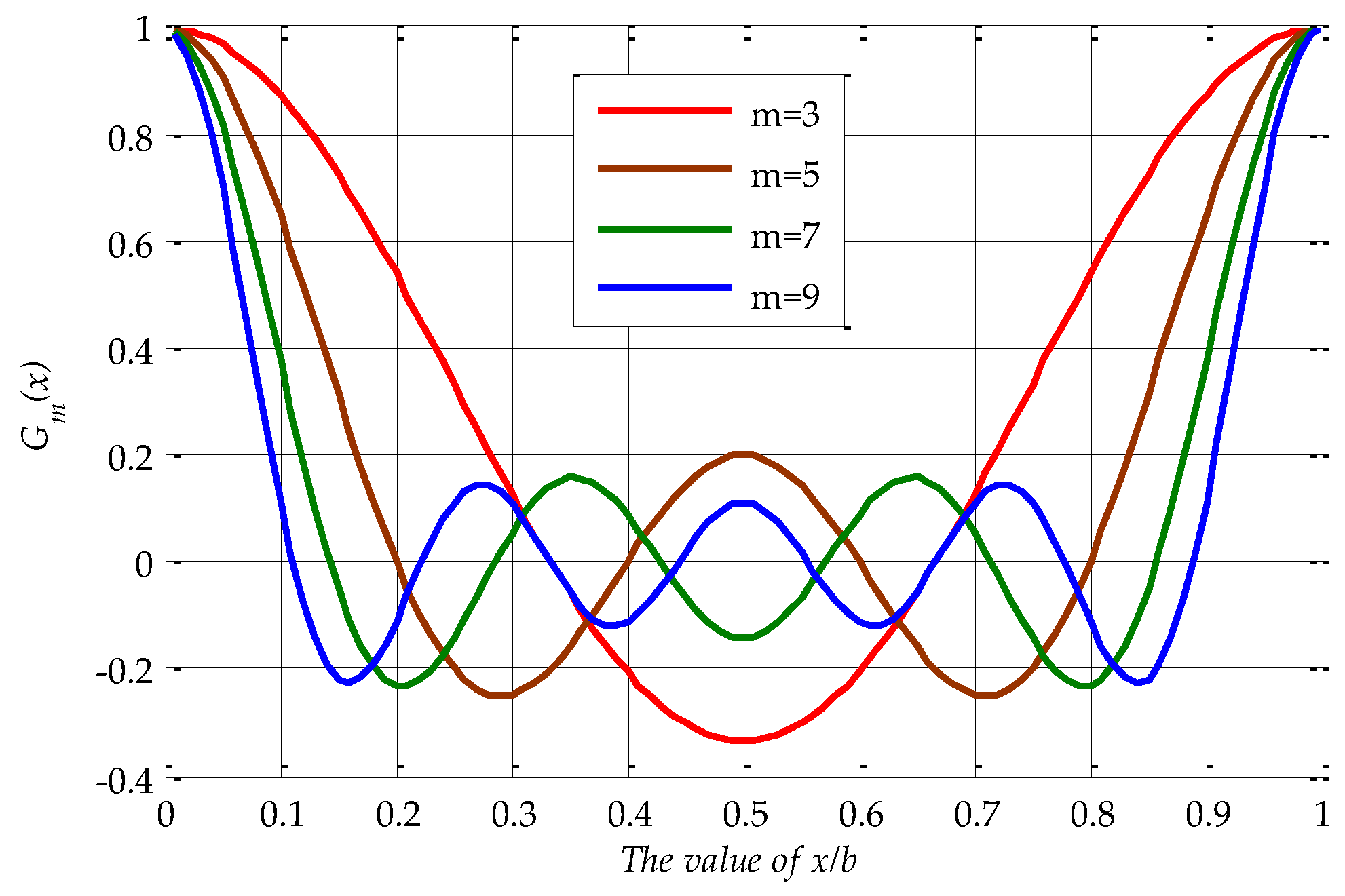
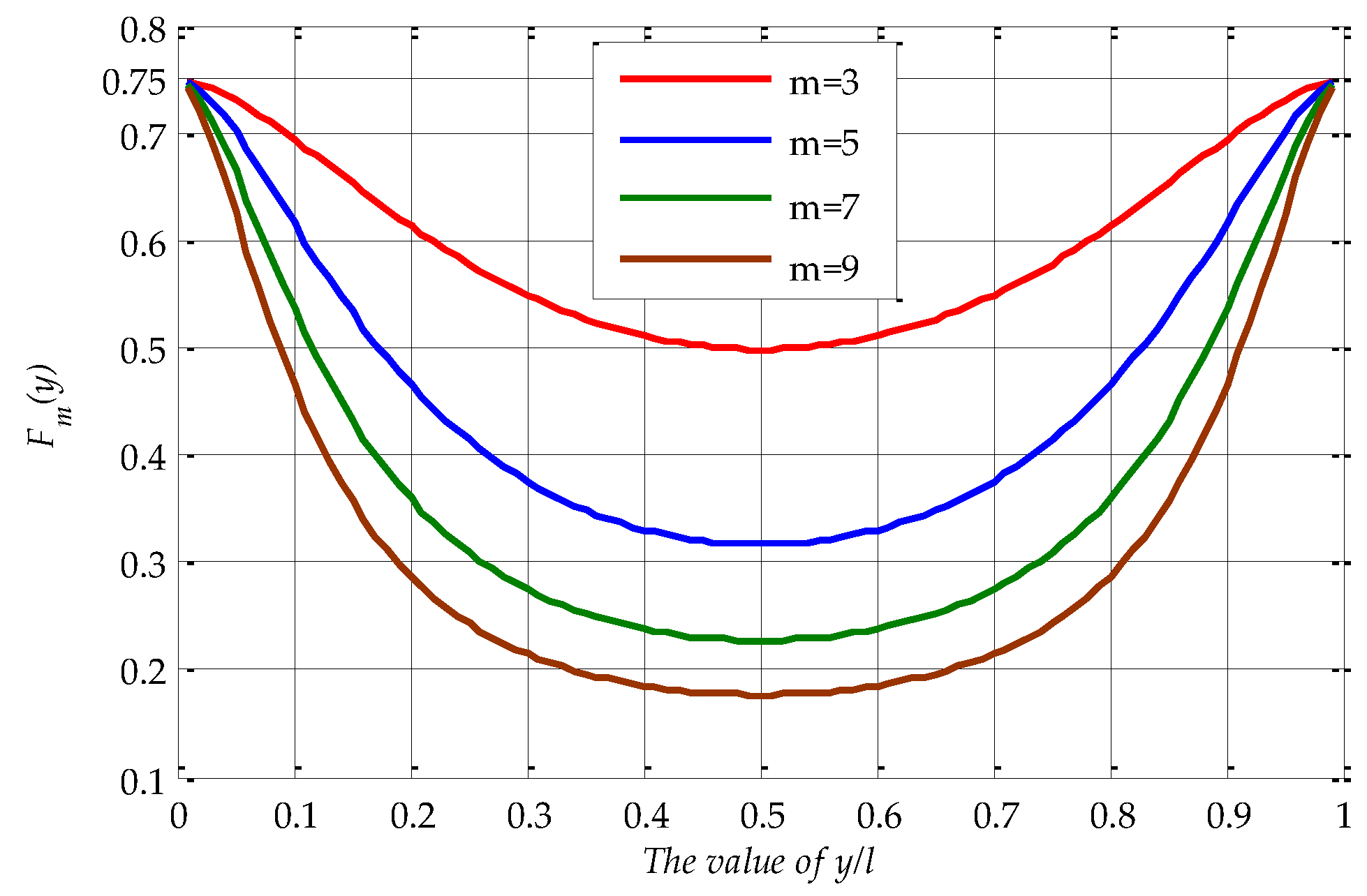
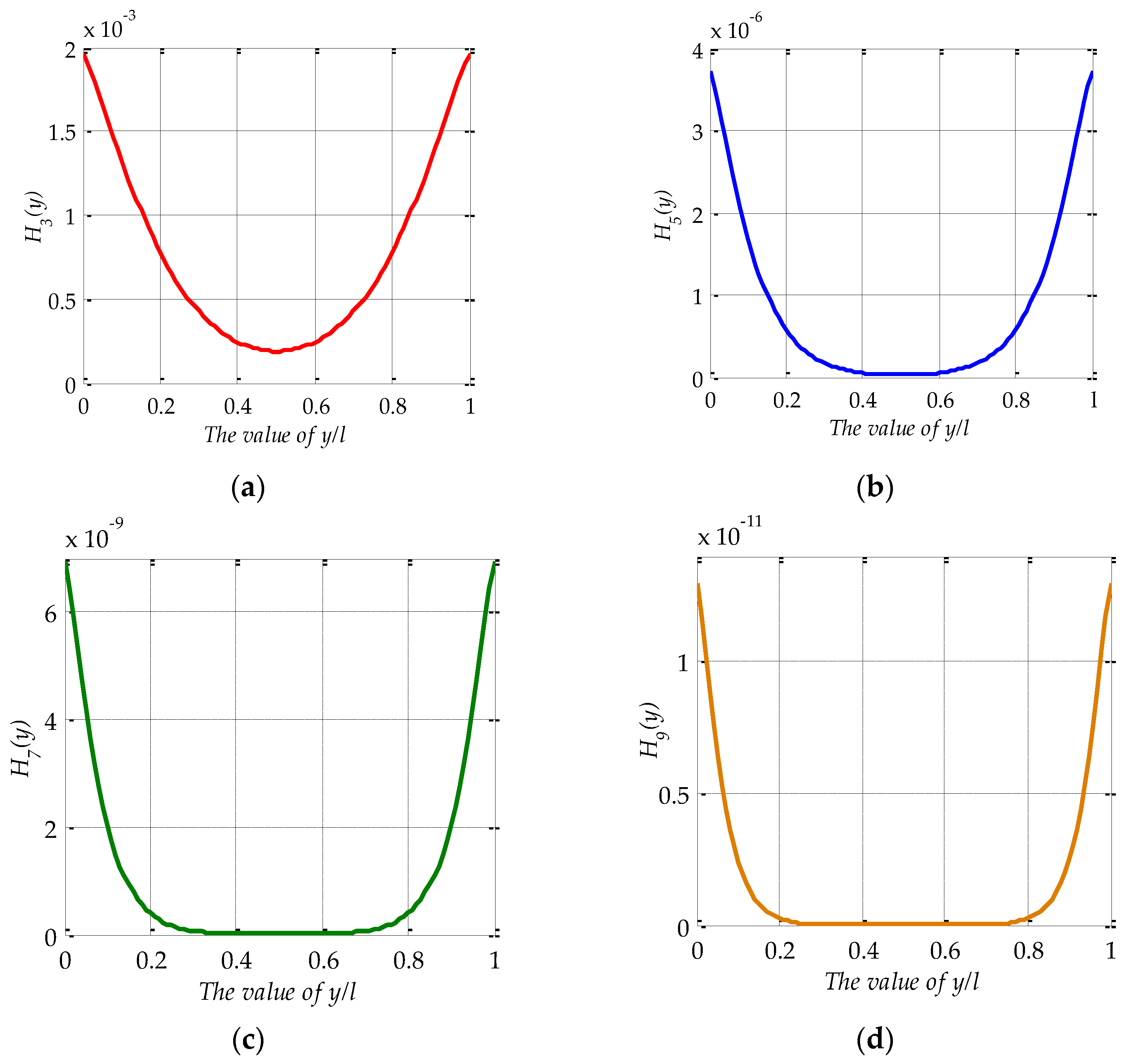
Appendix B
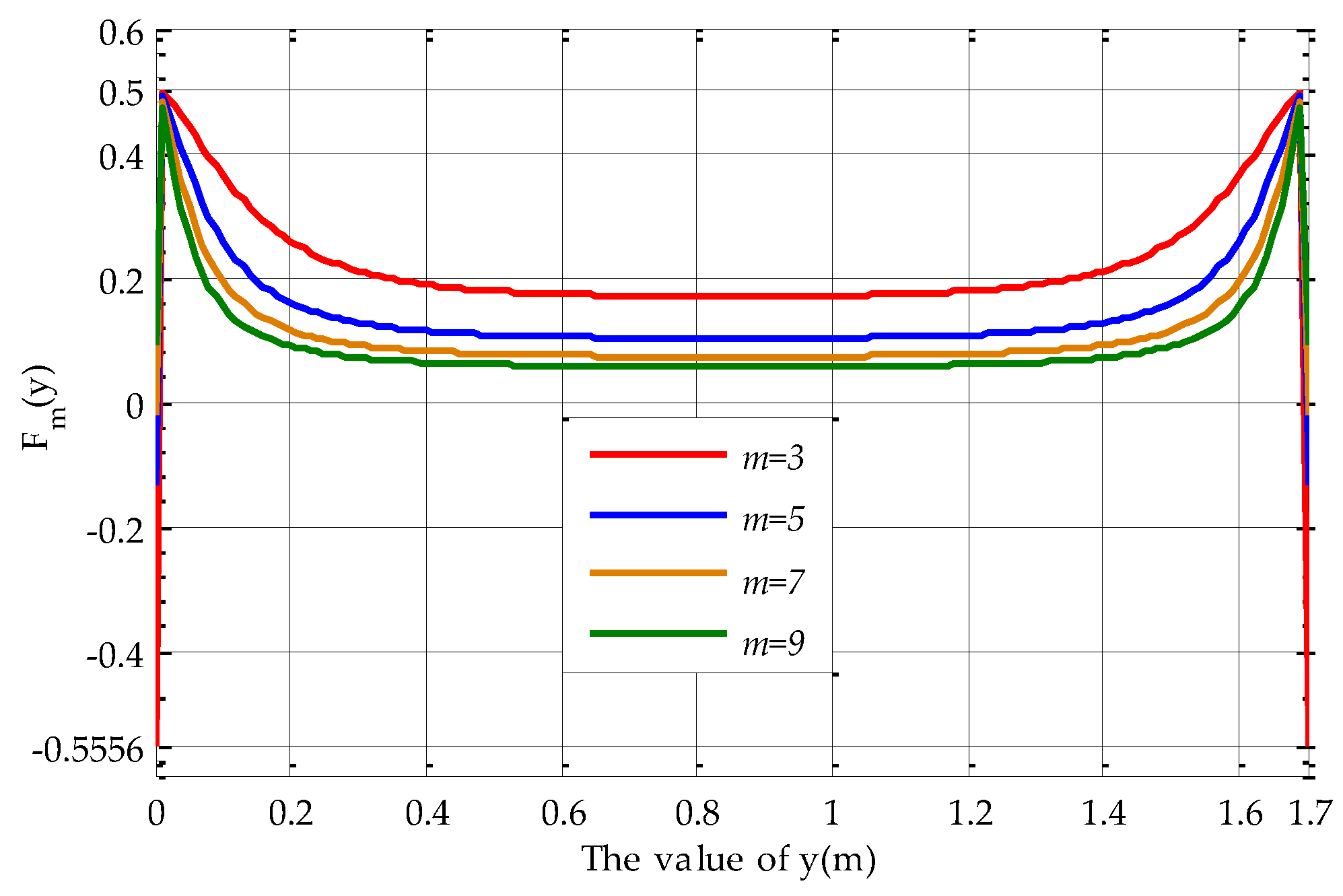
References
- Huang, W.; Dong, W.M. Introduction for metal roofing development and application classification. Archit. Technol. 2015, 12, 1103–1107. [Google Scholar]
- Luo, Y.F.; Zheng, X.J.; Guo, X.N.; Li, D.Z.; Hu, Z. Loading behavior analysis of an aluminum ally roof structure system under wind loads. J. Chongqing Univ. 2013, 36, 94–100. [Google Scholar]
- Baskaran, A.; Molleti, S.; Ko, S.; Shoemaker, L. Wind uplift performance of composite metal roof assemblies. J. Archit. Eng. 2012, 18, 2–15. [Google Scholar] [CrossRef]
- Long, W.Z. Discussion on improving metal roof anti wind technology The roof of Beijing Capital International Airport T3 do not be lifted by the wind fourth times again. China Constr. Metal Struct. 2013, 13, 62–68. [Google Scholar]
- Ying, X.J.; Zhong, J.H. Analysis on damage cause of the metal roof for the stadium of qiongtai normal college & its reinforcement. China Build. Waterproofing 2015, 11, 14–17. [Google Scholar]
- Li, Y.H.; Wang, Y.; Chase, J.G.; Mattila, J.; Myung, H.; Sawodny, O. Survey and introduction to the focused section on mechatronics for sustainable and resilient civil infrastructure. IEEE/ASME Trans. Mechatron. 2013, 18, 1637–1646. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.S.; Basily, B.B.; Gucunski, N.; Yi, J.G.; Maher, A.; Romero, F.A.; Parvardeh, H. Mechatronic systems design for an autonomous robotic system for high-efficiency bridge deck inspection and evaluation. IEEE/ASME Trans. Mechatron. 2013, 18, 1655–1664. [Google Scholar] [CrossRef]
- Graham, R.E.; Kamer, T.; Bob, W. Development of a multi-purpose wireless network for the structural health monitoring of a suspension bridge. In Proceedings of the IET Conference on Wireless Sensor Systems (WSS 2012), London, UK, 18–19 June 2012. [Google Scholar]
- Park, J.W.; Sim, S.H.; Jung, H.J. Displacement estimation using multimetric data fusion. IEEE/ASME Trans. Mechatron. 2013, 18, 1675–1682. [Google Scholar] [CrossRef]
- Lin, C.J.; Yau, H.T.; Lee, C.Y.; Tung, K.H. System identification and semiactive control of a squeeze-mode magnetorheological damper. IEEE/ASME Trans. Mechatron. 2013, 18, 1691–1701. [Google Scholar] [CrossRef]
- Fan, H.C.; Zhang, Z.; Zhu, X.J. Application of FBG in flexible surface test. Mech. Electr. Eng. Mag. 2009, 26, 40–43. [Google Scholar]
- Chan, T.H.T.; Ashebo, D.B.; Tam, H.Y.; Yu, Y.; Chan, T.F.; Lee, P.C.; Gracia, E.P. Vertical displacement measurements for bridges using optical fiber sensors and CCD cameras. Struct. Health Monit. 2009, 8, 243–249. [Google Scholar] [CrossRef]
- Jeong, U.; Cho, K.J. A novel low-cost, large curvature bend sensor based on a Bowden-cable. Sensors 2016, 16, 961. [Google Scholar] [CrossRef] [PubMed]
- Marco, L.; Denis, P.; Alessio, V.; Candido, F.P.; Alessandro, C. Development of a Flexible Lead-Free Piezoelectric Transducer for Health Monitoring in the Space Environment. Micromachines 2015, 6, 1729–1744. [Google Scholar]
- Chiolerio, A.; Roppolo, I.; Sangermano, M. Radical diffusion engineering: Tailored nanocomposite materials for piezoresistive inkjet printed strain measurement. RSC Adv. 2013, 3, 3446–3452. [Google Scholar] [CrossRef]
- Gentner, R.; Classen, J. Development and evaluation of a low-cost sensor glove for assessment of human finger movements in neurophysiological settings. J. Neurosci. Methods 2009, 178, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Tognetti, A.; Lorussi, F.; Carbonaro, N.; de Rossi, D. Wearable Goniometer and Accelerometer Sensory Fusion for Knee Joint Angle Measurement in Daily Life. Sensors 2015, 15, 28435–28455. [Google Scholar] [CrossRef] [PubMed]
- Stoppa, M.; Chiolerio, A. Wearable electronics and smart textiles: A critical review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [PubMed]
- Nakai, H.; Miki, T.; Ohgaki, K. Analytical method for critical strength of thin-walled steel frames. Mem. Fac. Eng. Osaka City Univ. 1985, 26, 233–250. [Google Scholar]
- Zhong, Y.; Chen, J.Y.; Wang, S.Y. Analytical solution for rectangular thin cantilever plate. Chin. J. Comput. Mech. 2006, 23, 368–372. [Google Scholar]
- Batista, M. New analytical solution for bending problem of uniformly loaded rectangular plate supported on corner points. IES J. Part A Civ. Struct. Eng. 2010, 3, 75–84. [Google Scholar] [CrossRef]
- Nishawala, V.V. A Study of Large Deflection of Beams and Plates. Master’s Thesis, Rutgers State University, New Brunswick, NJ, USA, 2011. [Google Scholar]
- Van, G.; Robert, A. Analytical method for the construction of solutions to the Föppl-von Kármán equations governing deflections of a thin flat plate. Int. J. Non-Linear Mech. 2012, 47, 1–6. [Google Scholar]
- Segovia, E.; Ferrer, B.; Ramis, J.; Martinez, J.; Arenas, J.P. Vibration Modal Analysis of a Thin Folded Elastic Structure using a Levy-type Solution. Int. J. Acoust. Vib. 2012, 17, 191–199. [Google Scholar] [CrossRef]
- Song, Y.H.; Yang, L.M.; Wang, Q.S.; Li, Y.X. Deformation characteristic study of metal roof panel under wind uplift loading. Build. Struct. 2015, 45, 87–91. [Google Scholar]
- Wang, X.B.; Chen, J.J.; Liang, Z.T. Randomicity analysis of the piezothermoelasticity intelligent thin plate by appling the numerical method. J. Xidian Univ. 2008, 35, 592–599. [Google Scholar]
- Zhang, Z.R.; Zhang, X.W.; Lü, W.G. Numerical method based on compatible manifold element for thin plate bending. Chin. J. Mech. Eng. 2010, 23, 100–109. [Google Scholar] [CrossRef]
- Turevsky, I.; Sankara, H.G.; Suresh, K. An efficient numerical method for computing the topological sensitivity of arbitrary shaped features in plate bending. Int. J. Numer. Methods Eng. 2009, 79, 1683–1702. [Google Scholar] [CrossRef]
- He, X.M.; Zou, W.M. Infinitely many positive solutions for Kirchhoff-type problems. Nonlinear Anal. 2009, 70, 1407–1414. [Google Scholar] [CrossRef]
- Banerjee, A.; Bhattacherya, B.; Mallika, K. Large deflection of cantilever beams with geometric non-linearity: Analytical and numerical approaches. Int. J. Non-Linear Mech. 2008, 5, 366–376. [Google Scholar] [CrossRef]
- Simmonds, J.G. Exact Levy-type solutions for plate bending exist for transversely isotropic but not for general monoclinic materials. J. Elast. 2004, 75, 49–56. [Google Scholar] [CrossRef]
- GB50896-2013 M.O. Technical Code for Application of Profiled Metal Sheets; Ministry of Housing and Urban-Rural Construction of the People’s Republic of China, and General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2014.
- GB50009 M.O. Load Code for the Design of Building Structures; Ministry of Housing and Urban-Rural Construction of the People’s Republic of China, and General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2012.
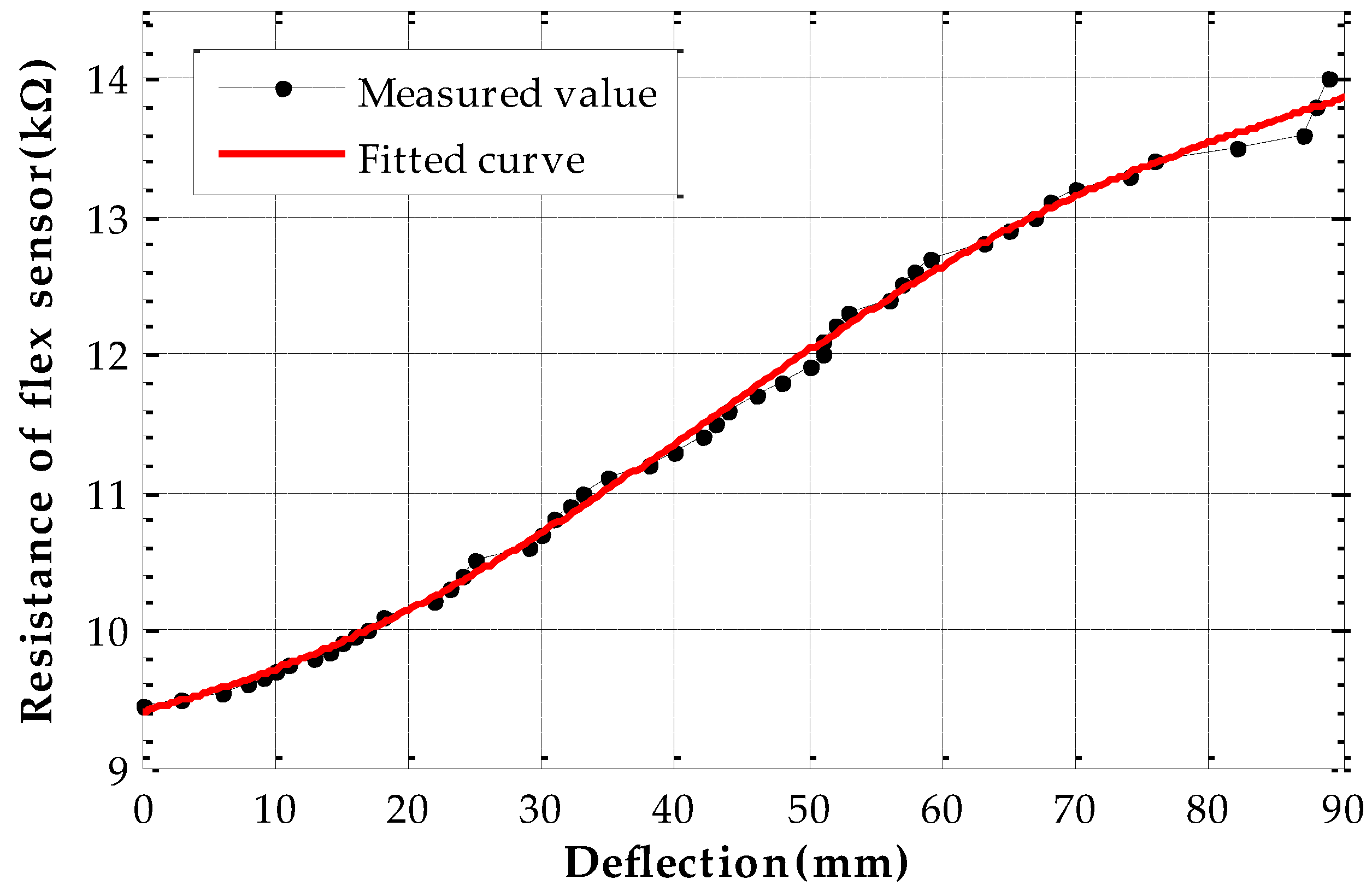
- Flex Sensor Manufacturers Spectra Symbol. Available online: http://www.spectrasymbol.com/flex-sensor (accessed on 12 April 2016).



| Material | Length l (mm) | Width b (mm) | Thickness d (mm) | Poisson Ratio | Young Modulus (Pa) E (N/m2) |
|---|---|---|---|---|---|
| AA3004 Al-Mg-Mn alloy | 1700 | 400 | 1 | 0.3 | 7 × 1010 |
| Roof Material | Lock Edge | Free Edge | Thickness | Poisson Ratio | Young’s Modulus |
|---|---|---|---|---|---|
| l (mm) | b (mm) | d (mm) | μ | E (N/m2) | |
| AA3004 Al-Mg-Mn alloy | 150 | 400 | 1 | 0.3 | 7 × 1010 |
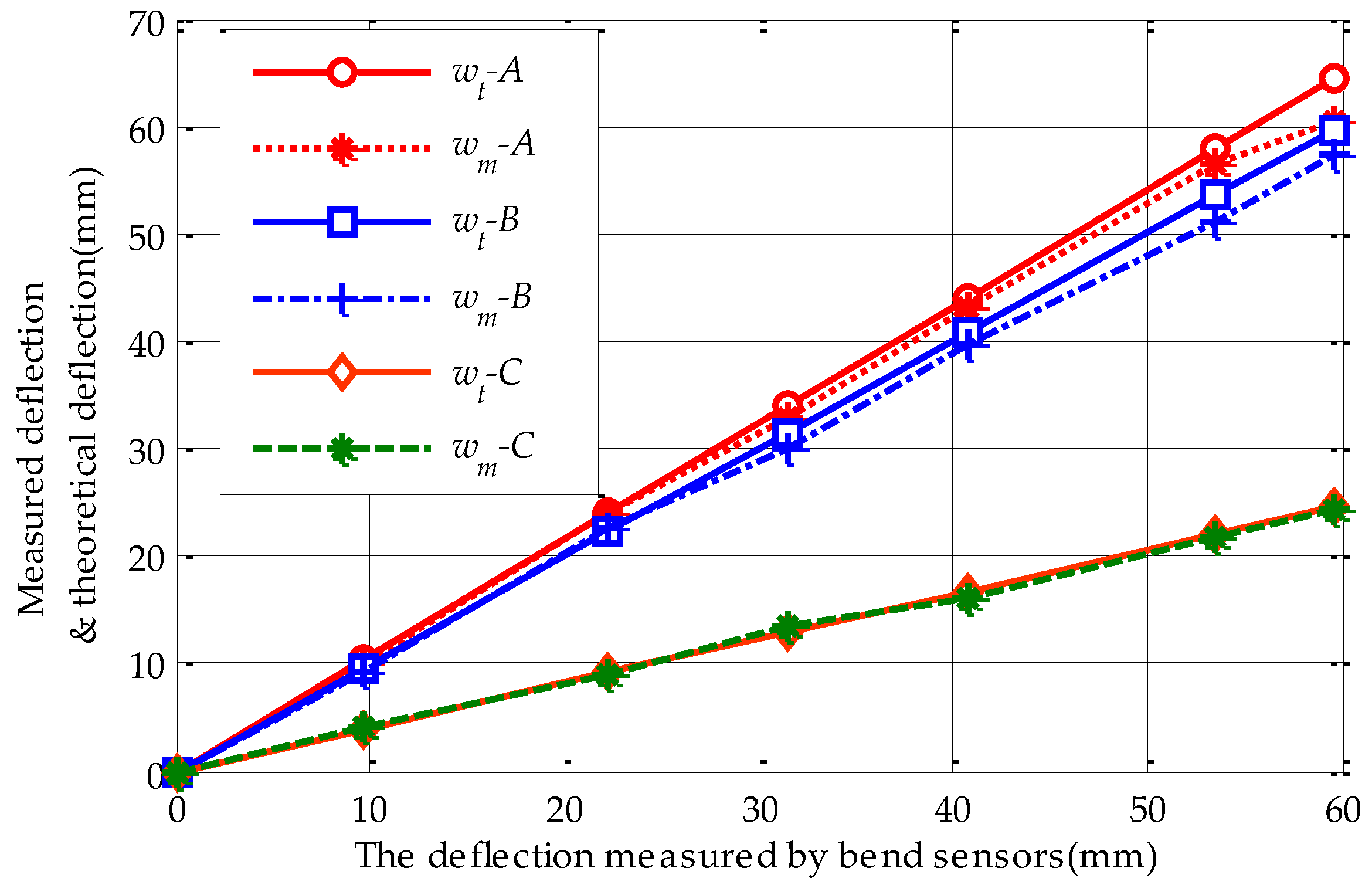
| Measured Points | Deflection (mm) | Max Relative Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| M | 0 | 9.6 | 22.3 | 31.5 | 40.7 | 53.5 | 59.6 | ||
| A | TV | 0 | 10.4 | 24.1 | 34.1 | 42.7 | 57.9 | 64.5 | 7.1% |
| MV | 0 | 10.2 | 22.5 | 33.0 | 42.0 | 54.6 | 62.0 | ||
| B | TV | 0 | 9.6 | 22.3 | 31.5 | 40.7 | 53.5 | 59.6 | 3.6% |
| MV | 0 | 9.3 | 21.5 | 32.7 | 42.1 | 53.8 | 57.5 | ||
| C | TV | 0 | 3.9 | 9.2 | 13.0 | 20.1 | 22.0 | 24.6 | 5.3% |
| TV | 0 | 3.8 | 8.9 | 12.5 | 19.1 | 21.5 | 23.9 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Cui, L.; Li, Y.; An, C. Inspection and Reconstruction of Metal-Roof Deformation under Wind Pressure Based on Bend Sensors. Sensors 2017, 17, 1054. https://doi.org/10.3390/s17051054
Yang L, Cui L, Li Y, An C. Inspection and Reconstruction of Metal-Roof Deformation under Wind Pressure Based on Bend Sensors. Sensors. 2017; 17(5):1054. https://doi.org/10.3390/s17051054
Chicago/Turabian StyleYang, Liman, Langfu Cui, Yunhua Li, and Chao An. 2017. "Inspection and Reconstruction of Metal-Roof Deformation under Wind Pressure Based on Bend Sensors" Sensors 17, no. 5: 1054. https://doi.org/10.3390/s17051054






