A Carrier Estimation Method Based on MLE and KF for Weak GNSS Signals
Abstract
:1. Introduction
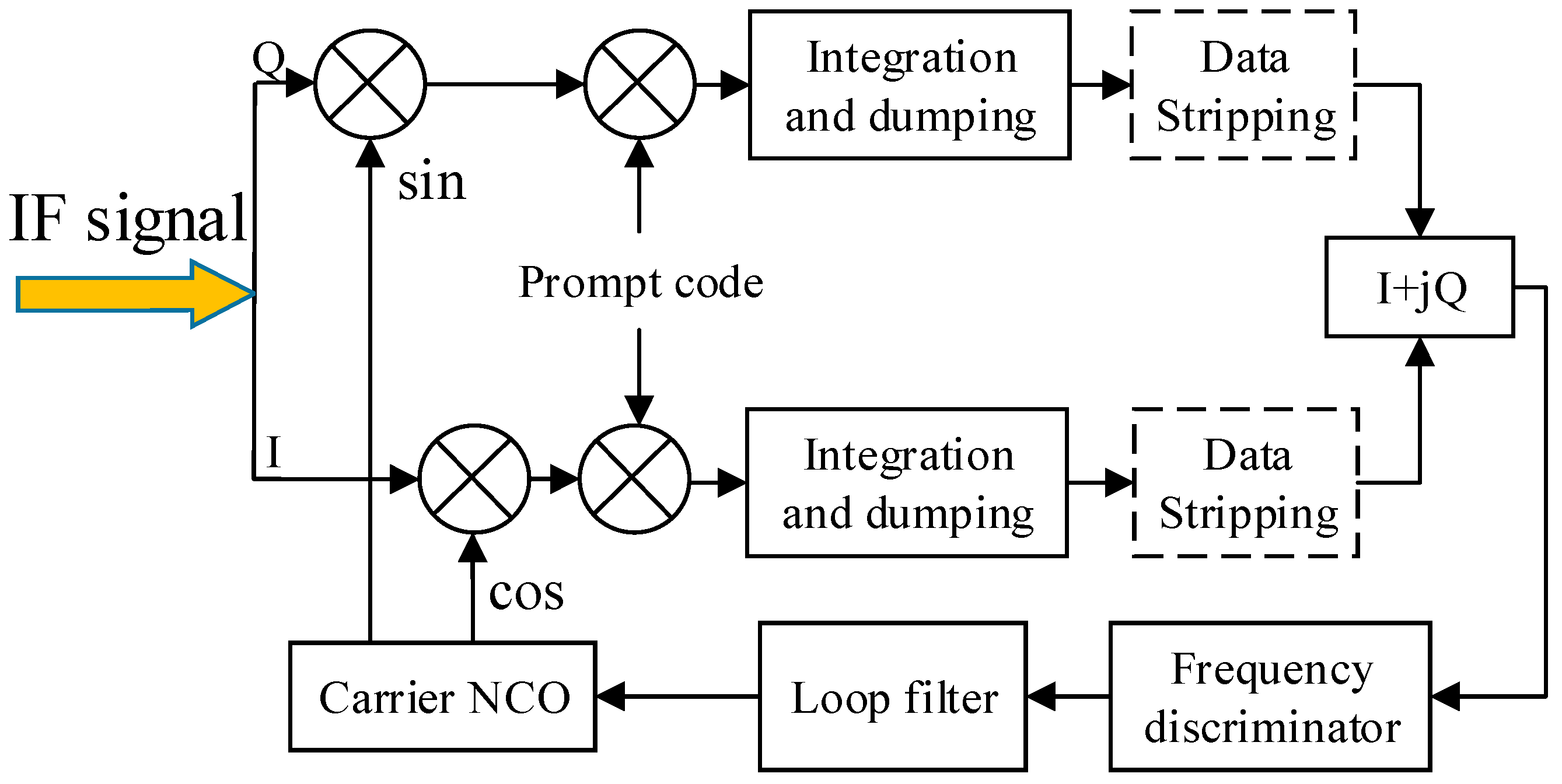
2. Signal Model
3. MLE Discriminator
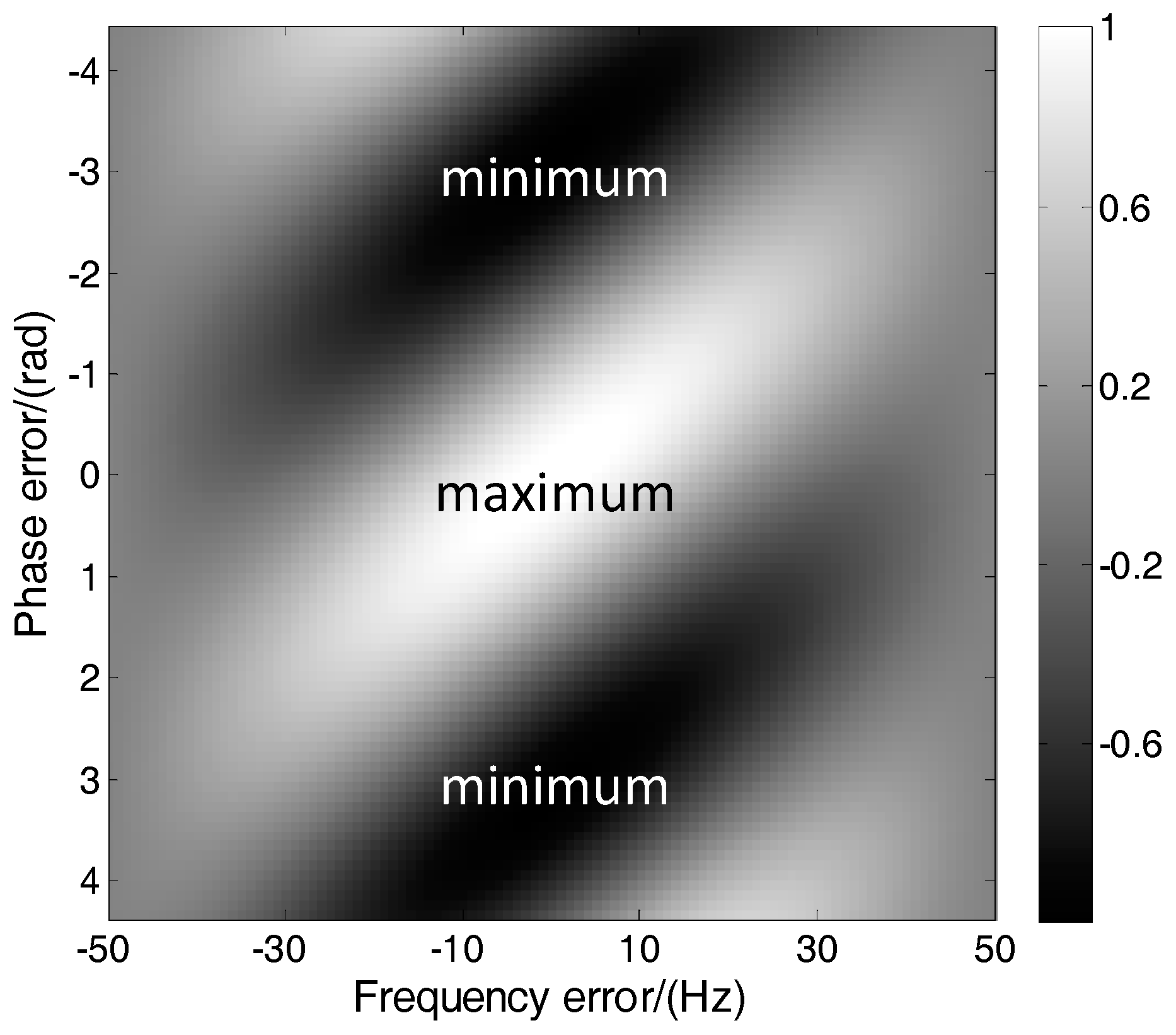
3.1. Cost Function of MLE
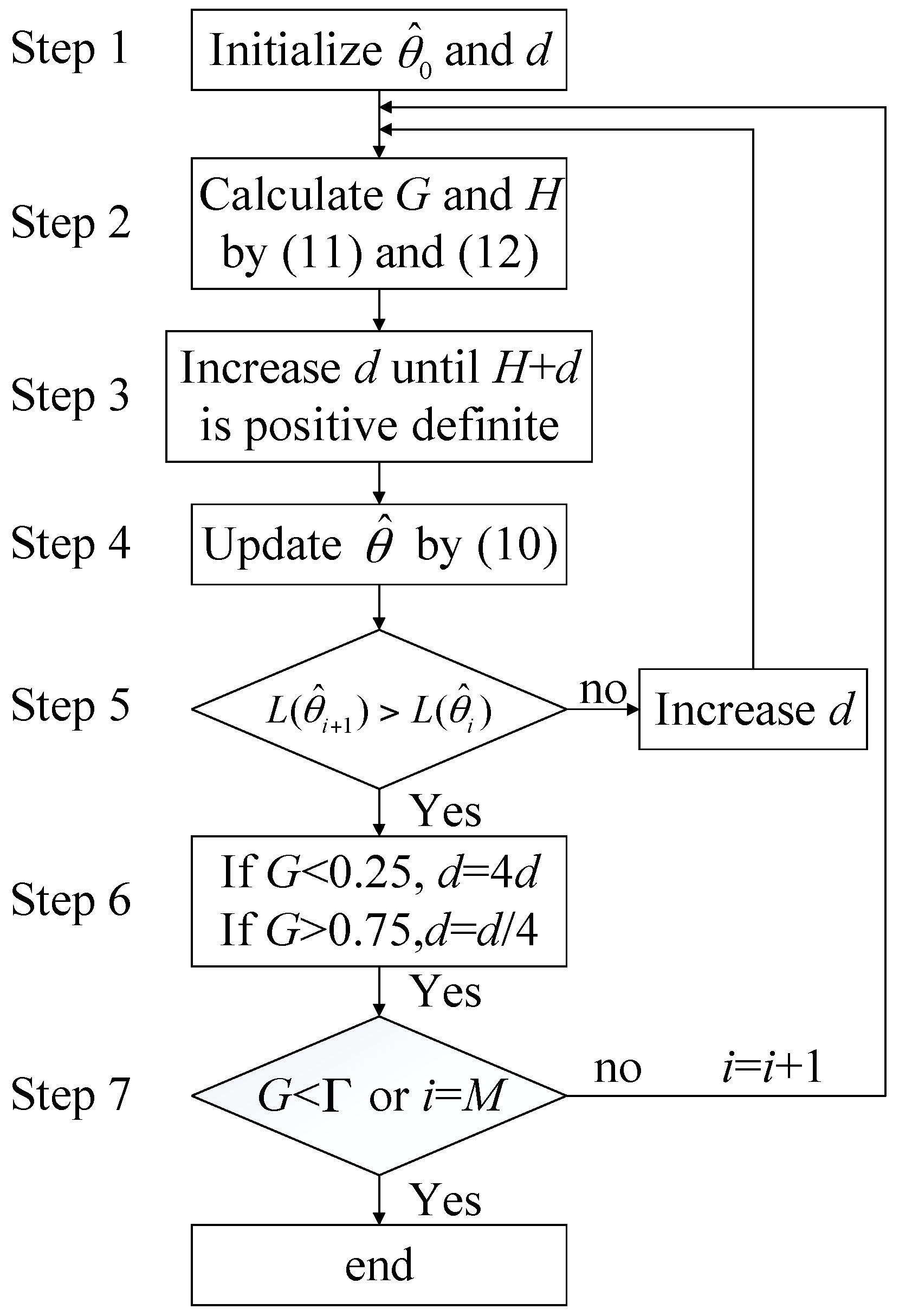
3.2. Parameters Estimation by LM Algorithm
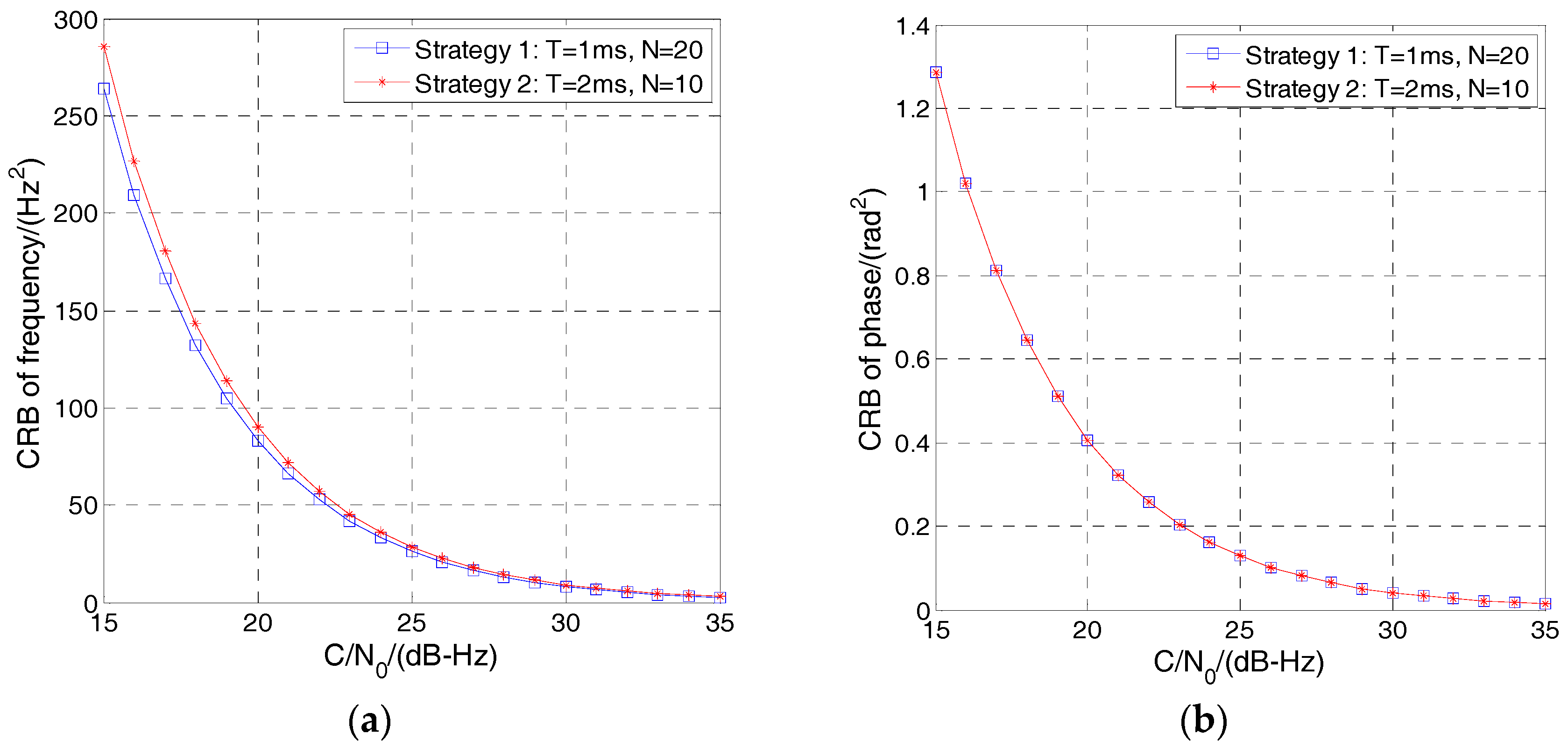
3.3. Cramér–Rao Bound (CRB)
3.4. Dynamic Characteristics
3.5. Computation Cost
4. Adaptive Kalman Filter
4.1. Basic Equations of KF
4.2. ML-KF Loop
5. Simulation Results
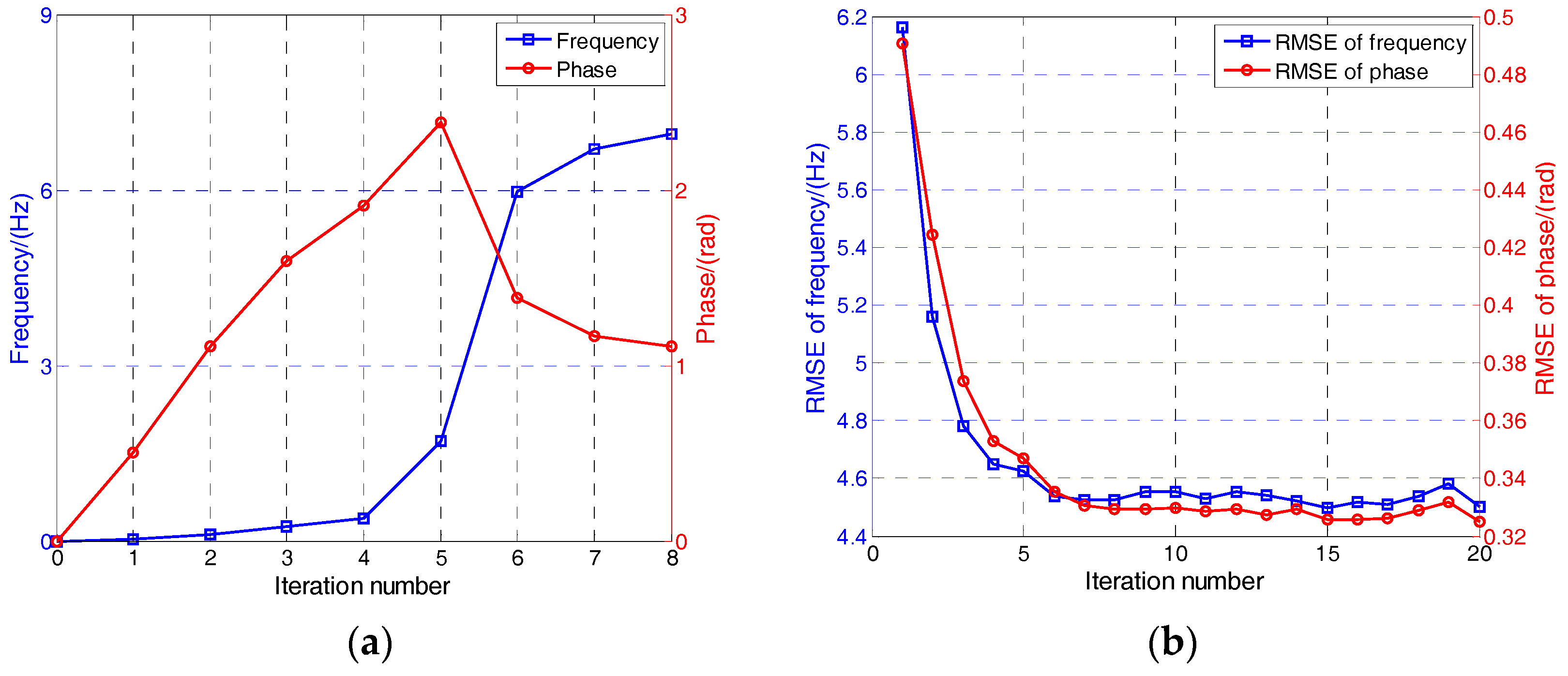
5.1. Simulation Results of MLE Discriminator
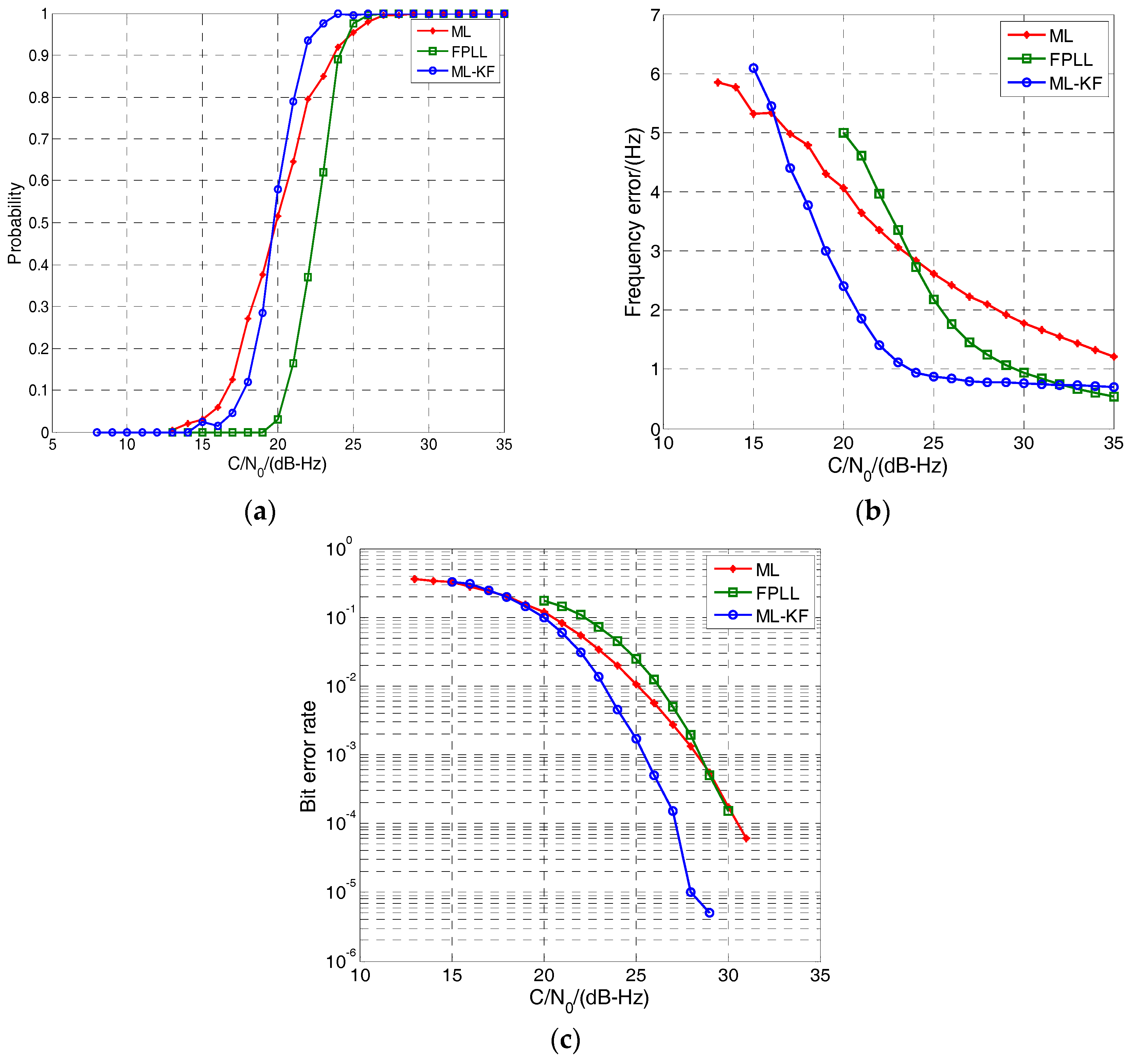
5.2. Simulation Results of ML-KF Loop
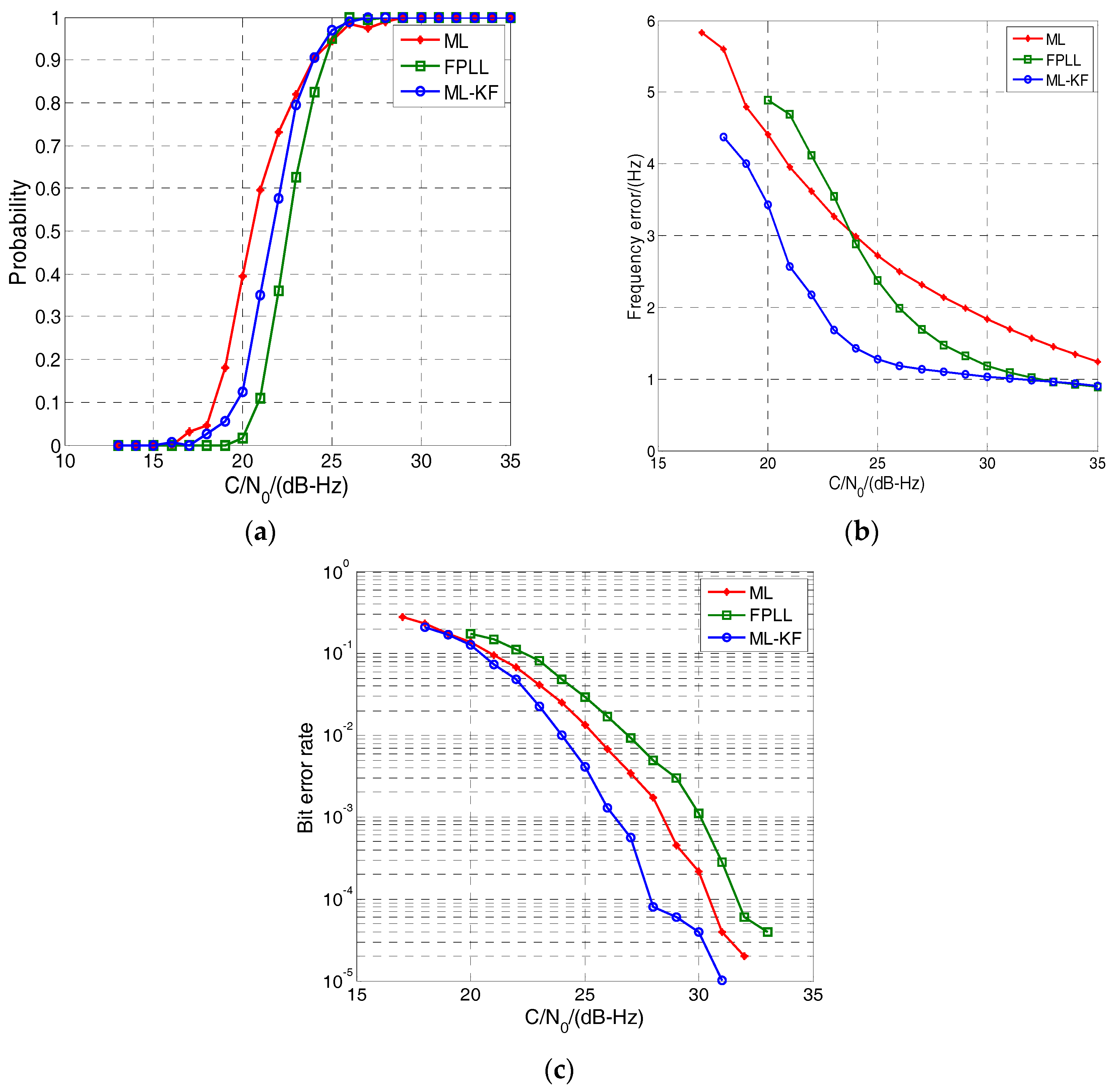
5.3. Monte Carlo Simulations for Sensitivity and Accuracy
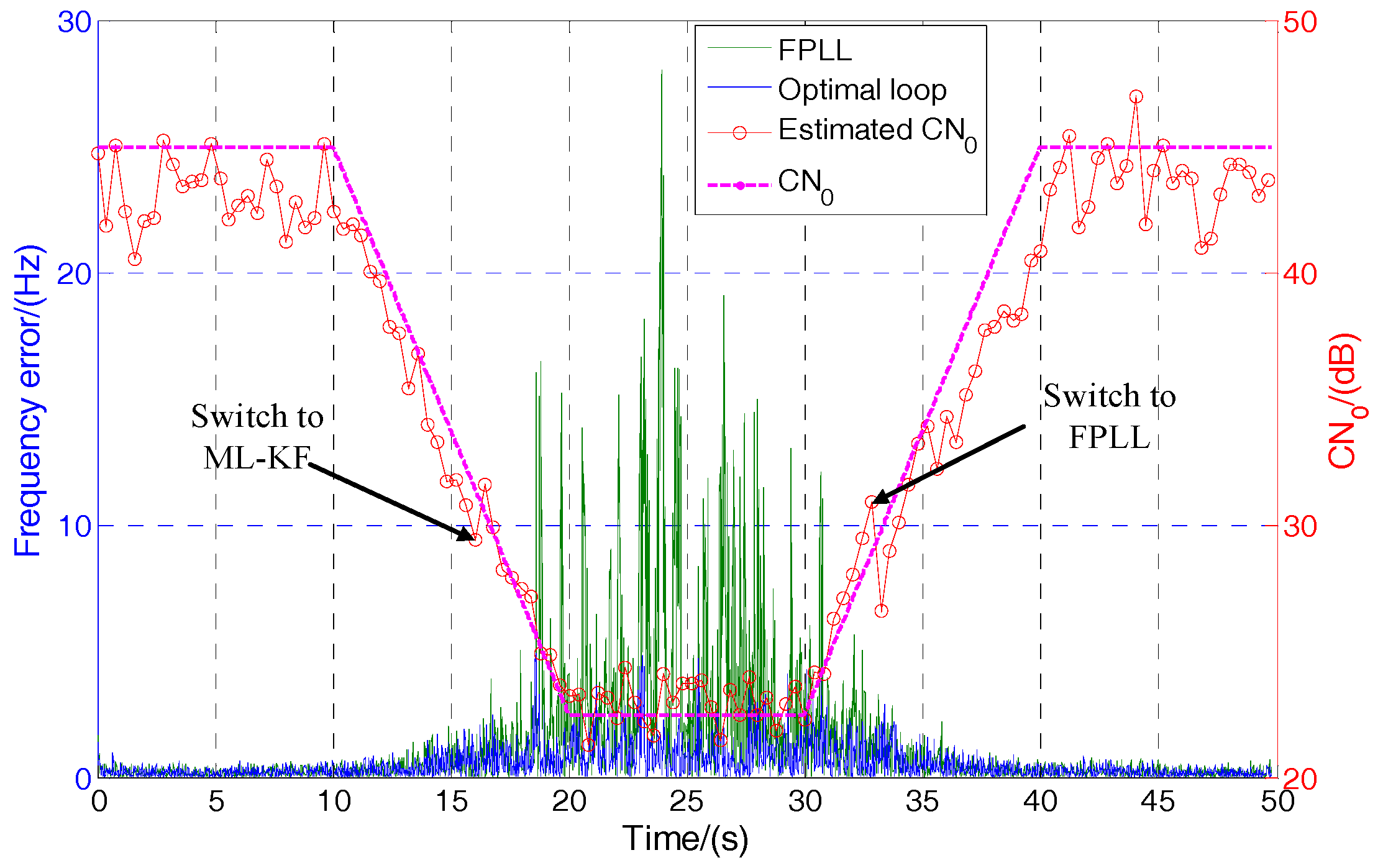
5.4. Optimal Loop Design
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kaplan, E.D.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: London, UK, 2006. [Google Scholar]
- Shanmugam, S.K.; Nielsen, J.; Lachapelle, G.; Shanmugam, S.K. Differential signal processing schemes for enhanced GPS acquisition. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 164–170. [Google Scholar]
- Wu, C.; Xu, L.; Zhang, H.; Zhao, W. A block zero-padding method based on DCFT for L1 parameter estimations in weak signal and high dynamic environments. Front. Inf. Technol. Electron. Eng. 2015, 16, 796–804. [Google Scholar] [CrossRef]
- Gao, G.; Lachapelle, G. INS-assisted high sensitivity GPS receivers for degraded signal navigation. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, Fort Worth, TX, USA, 26–29 September 2007; pp. 2977–2989. [Google Scholar]
- Hurd, W.J.; Statman, J.I.; Vilnrotter, V.A. High Dynamic GPS Receiver Using Maximum Likelihood Estimationand Frequency Tracking. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 425–437. [Google Scholar] [CrossRef]
- Sahmoudi, M.; Amin, M.G. Improved maximum-likelihood time delay estimation for GPS positioning in multipath, interference and low SNR environments. In Proceedings of the 2006 IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; pp. 876–882. [Google Scholar]
- Sokhandan, N.; Curran, J.T.; Broumandan, A.; Lachapelle, G. An advanced GNSS code multipath detection and estimation algorithm. GPS Solut. 2016, 20, 627–640. [Google Scholar] [CrossRef]
- Jong-Hoon, W.; Pany, T.; Eissfeller, B. Iterative Maximum Likelihood Estimators for High-Dynamic GNSS Signal Tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2875–2893. [Google Scholar]
- Won, J.H.; Pany, T.; Eissfeller, B. Noniterative Filter-Based Maximum Likelihood Estimators for GNSS Signal Tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1100–1114. [Google Scholar] [CrossRef]
- Closas, P.; Fernandez-Prades, C.; Fernandez-Rubio, J.A. Maximum likelihood estimation of position in GNSS. IEEE Signal Process. Lett. 2007, 14, 359–362. [Google Scholar] [CrossRef]
- Closas, P.; Fernandez-Prades, C.; Fernandez-Rubio, J.A. Cramer-Rao Bound Analysis of Positioning Approaches in GNSS Receivers. IEEE Trans. Signal Process. 2009, 57, 3775–3786. [Google Scholar] [CrossRef]
- Ziedan, N.I. GNSS Receivers for Weak Signals; Artech House: Norwood, MA, USA, 2006; pp. 116–117. [Google Scholar]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory. Part III. Papoulis Probab. Random Var. Stoch. Process. 1968, 1, 177–183. [Google Scholar]
- Mendel, J.M. Lessons in Estimation Theory for Signal Processing, Communications, and Control; Prentice-Hall International Inc.: Upper Saddle River, NJ, USA, 1995; pp. 384–386. [Google Scholar]
- Lowe, S.T. Voltage Signal-to-Noise Ratio (SNR) Nonlinearity Resulting From Incoherent Summations. Telecommun. Mission Oper. Prog. Rep. 1999, 137–138. [Google Scholar]
- Hongyang, Z.; Luping, X.; Yu, Y.; Shibin, S.; Yanghe, S. A High Sensitivity and Robustness Carrier-tracking Loop for Vehicular Applications. IET Sci. Meas. Technol. 2017. [Google Scholar] [CrossRef]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons: Hoboken, NJ, USA, 1997; pp. 190–241. [Google Scholar]
- O’Driscoll, C.; Petovello, M.G.; Lachapelle, G. Choosing the coherent integration time for Kalman filter-based carrier-phase tracking of GNSS signals. GPS Solut. 2011, 15, 345–356. [Google Scholar] [CrossRef]
- Ward, P.W. Performance comparisons between FLL, PLL and a novel FLL-assisted-PLL carrier tracking loop under RF interference conditions. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; pp. 783–795. [Google Scholar]
- Sharawi, M.S.; Akos, D.M.; Aloi, D.N. GPS C/N0 estimation in the presence of interference and limited quantization levels. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 227–238. [Google Scholar] [CrossRef]



| Discriminator Update Time (ms) | 20 | 40 | 60 | 80 | 100 | 200 |
| Dynamic Tolerance (m/s2) | 357 | 44.6 | 19.8 | 11.1 | 7.1 | 1.8 |
| SNR Gain (dB) | 76.1 | 72.9 | 74.7 | 75.9 | 76.9 | 79.9 |
| Parameter | Value |
|---|---|
| Carrier-to-noise ratio C/N0 | 28 dB-Hz |
| Sampling rate fs | 5.714 MHz |
| Integration time T | 1 ms |
| Observation point number N | 20 |
| Iteration number threshold M | 20 |
| Gradient threshold | 0.01 |
| Discriminator Algorithm | |
|---|---|
| Two-order FLL | where denotes four-quadrant arctangent, , |
| Three-order PLL | where denotes the two-quadrant arctangent. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, L.; Yan, B.; Zhang, H.; Luo, L. A Carrier Estimation Method Based on MLE and KF for Weak GNSS Signals. Sensors 2017, 17, 1468. https://doi.org/10.3390/s17071468
Zhang H, Xu L, Yan B, Zhang H, Luo L. A Carrier Estimation Method Based on MLE and KF for Weak GNSS Signals. Sensors. 2017; 17(7):1468. https://doi.org/10.3390/s17071468
Chicago/Turabian StyleZhang, Hongyang, Luping Xu, Bo Yan, Hua Zhang, and Liyan Luo. 2017. "A Carrier Estimation Method Based on MLE and KF for Weak GNSS Signals" Sensors 17, no. 7: 1468. https://doi.org/10.3390/s17071468





