Sampling and Kriging Spatial Means: Efficiency and Conditions
Abstract
:1. Introduction
2. Spatial Random Field Representation of Attributes and Their Means
3. SSM of OSPM
4. Mean Kriging of OSPM
5. Case Study I
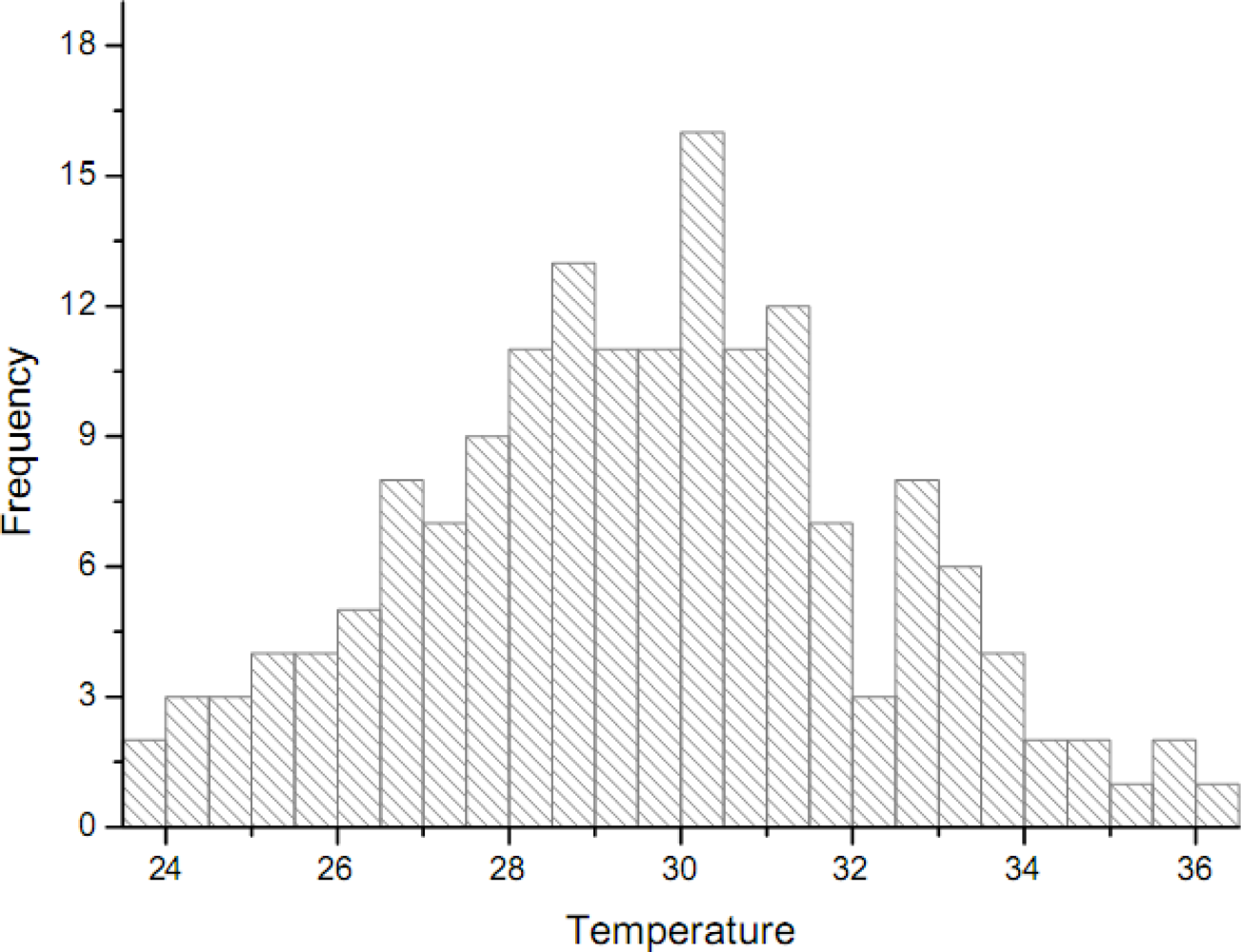
5.1. Study Area
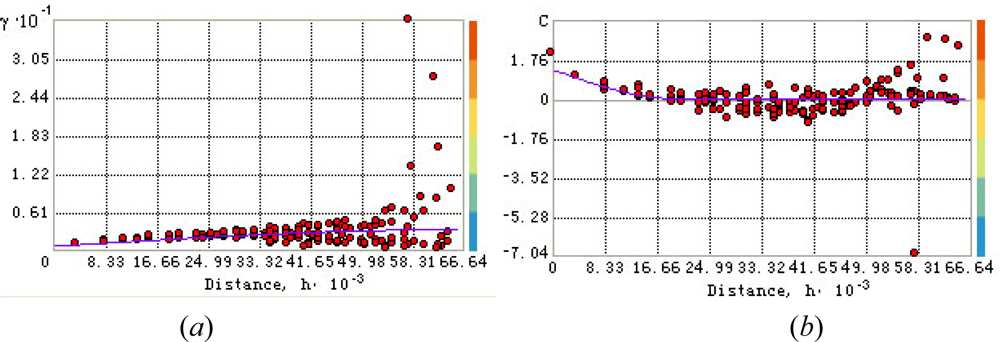
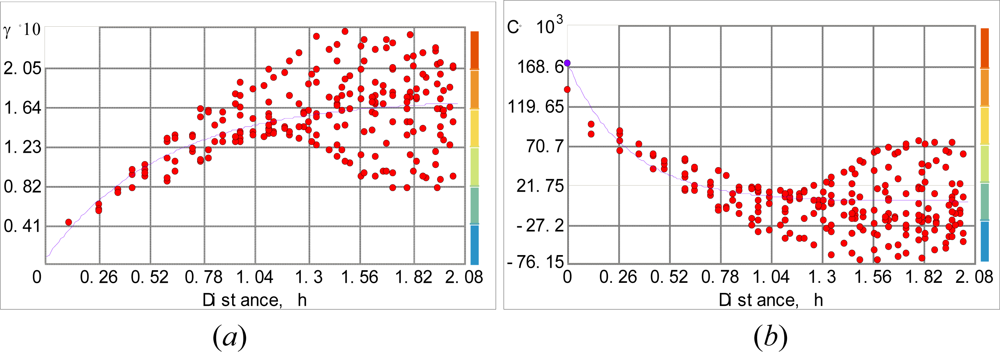
5.2. Variogram and Covariance Modeling
5.3. Spatial Temperature Mmeans Obtained by the Various Techniques
6. Case Study II
6.1. The Study Region
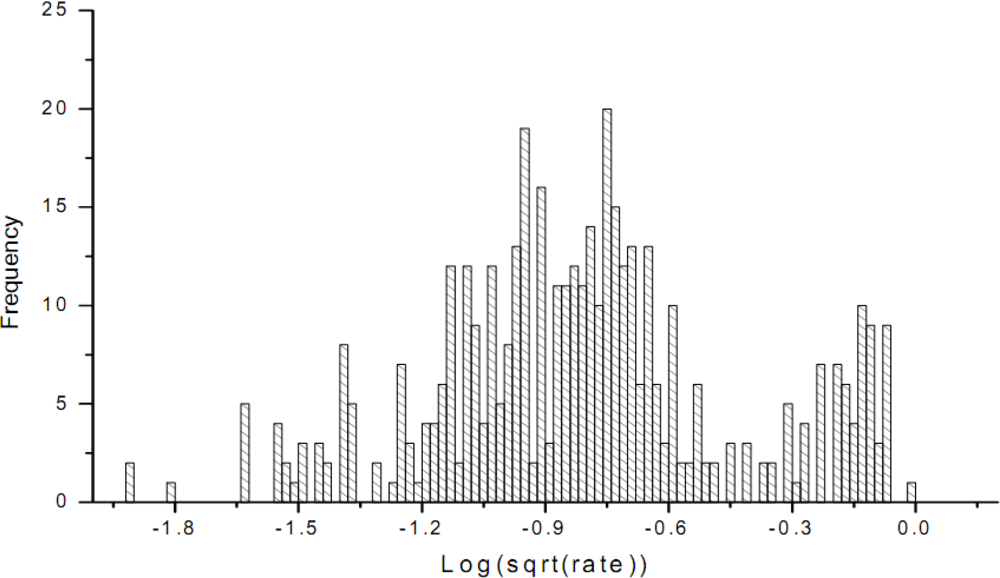
6.2. Transformation of the Target Variable
6.3. Modeling the Variogram
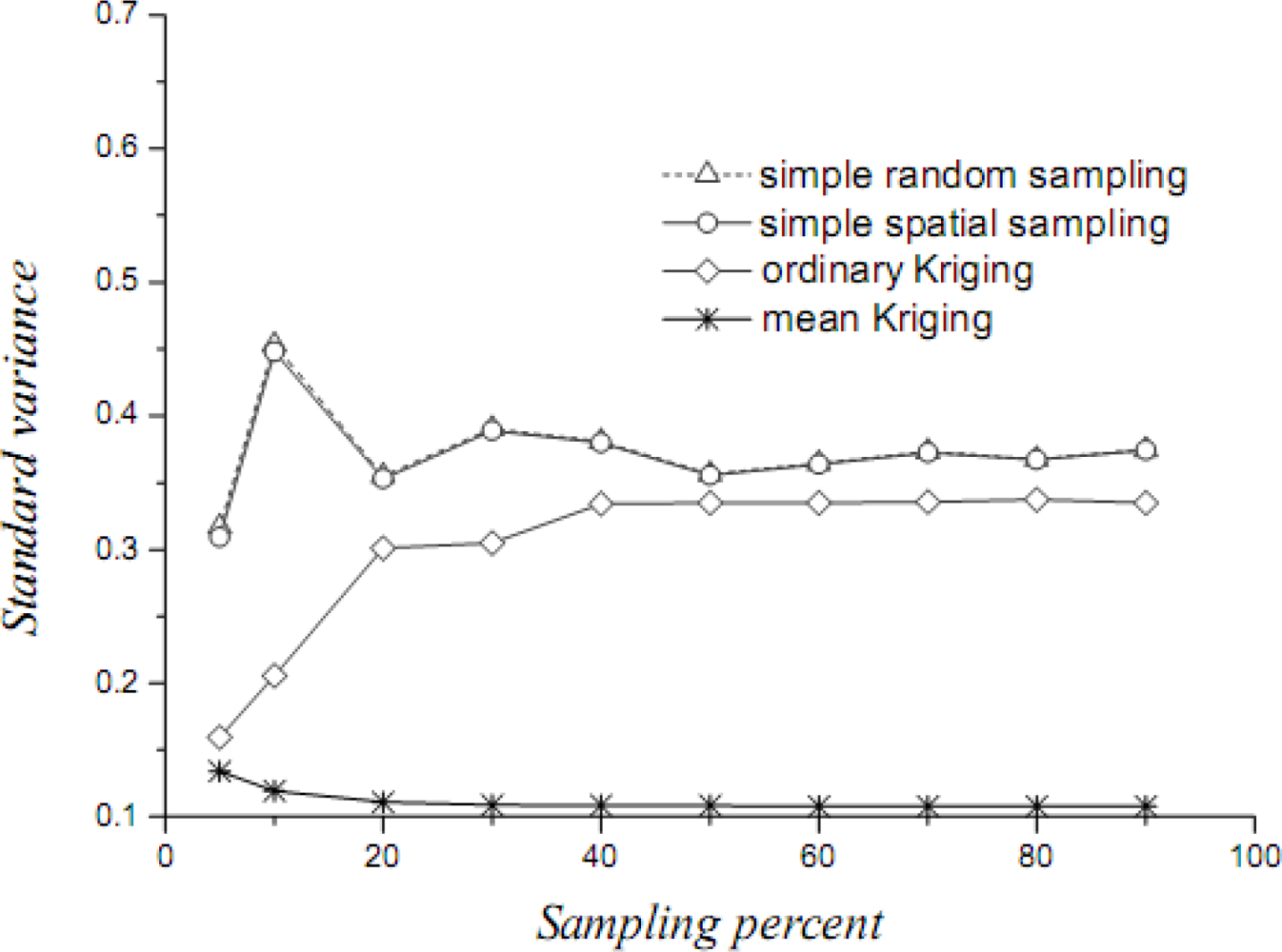
6.4. Sample Estimates of the Rate of Cultivated Land
7. Discussion and Conclusions
Acknowledgments
References
- Christakos, G.; Bogaert, P.; Serre, M.L. Temporal GIS; Springer-Verlag: New York, USA, 2002. [Google Scholar]
- Wu, B.F. China crop watch system with remote sensing. J. Remote Sens (in Chinese) 2004, 8, 481–478. [Google Scholar]
- Yang, X.; Zhu, B.; Wang, X.; Li, C.; Zhou, Z.; Chen, J.; Wang, X.; Yin, J.; Lu, X. Late Quaternary environmental changes and organic carbon density in the Hunshandake Sandy Land, eastern Inner Mongolia, China. Glob. Planet. Change 2008, 61, 70–78. [Google Scholar]
- Arrow, K.; Dasgupta, P.; Maler, K.G. Evaluating projects and assessing sustainable development in imperfect economics. Enviro. Resour. Econ 2003, 26, 647–685. [Google Scholar]
- Christakos, G. Modern statistical analysis and optimal estimation of geotechnical data. Eng. Geol 1985a, 22, 175–200. [Google Scholar]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev 1959, 87, 367–374. [Google Scholar]
- Olea, R.A. Geostatistics for Engineers and Earth Scientists; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Bayraktar, H.; Turalioglu, F.S. A Kriging-based approach for locating a sampling site-in the assessment of air quality. Stoch. Environ. Res. Risk Assess 2005, 19, 301–305. [Google Scholar]
- Brus, D.J.; Gruijter, J.J.D. Random sampling of geostatistical modeling? Choosing between design-based and model-based sampling strategies for soil (with discussion). Geoderma 1997, 80, 1–44. [Google Scholar]
- Gandin, L. Objective Analysis of Meteorological Fields. Gidrometeorologicheskoe Izdatel'stvo 1963, (English translation. Israel Program for Scientific Translation: Jerusalem, Israel, 1965).
- Haining, R. Estimating spatial means with an application to remote sensing data. Commun. Stat. -Theory Methods 1988, 17, 537–597. [Google Scholar]
- Saito, H.; Zimmerman, D.A.; Coburn, T.C. Geostatistical interpolation of object counts collected from multiple strip transects: ordinary Kriging versus finite domain Kriging. Stoch. Environ. Res. Risk Assess 2005, 19, 71–85. [Google Scholar]
- Christakos, G. Recursive parameter estimation with applications in earth sciences. Math. Geol 1985b, 17, 489–515. [Google Scholar]
- Courtier, P.; Talagrand, O. Variational assimilation of meteorological observations with the direct and adjoint shallow-water equations. Tellus 1990, 42A, 531–549. [Google Scholar]
- Daley, R. Atmospheric Data Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Li, X.; Yeh, A.G. Modelling sustainable urban development by the integration of constrained cellular automata and GIS. Int. J. Geogr. Inf. Sci 2000, 14, 131–152. [Google Scholar]
- Serre, M.L.; Christakos, G. BME studies of stochastic differential equations representing physical laws-Part II. 5th Annual Confer, Intern Assoc for Mathematical Geology, Trondheim, Norway, 1999; pp. 93–98.
- Christakos, G.A. Bayesian/maximum-entropy view to the spatial estimation problem. Math. Geol 1990, 22, 763–776. [Google Scholar]
- Christakos, G. Spatiotemporal information systems in soil and environmental sciences. Geoderma 1998, 85, 141–179. [Google Scholar]
- Kolovos, A.; Christakos, G.; Serre, M.L.; Miller, C.T. Computational BME solution of a stochastic advection-reaction equation in the light of site-specific information. Water Resour. Res 2002, 38, 1318–1334. [Google Scholar]
- Papantonopoulos, G.; Modis, K. A BME solution of the stochastic three-dimensional Laplace equation representing a geothermal field subject to site-specific information. Stoch. Environ. Res. Risk Assess 2006, 20, 23–32. [Google Scholar]
- Courtier, P.J.; Derber, R.; Errico, J.; Louis, F.; Vukicevic, T. Important literature on the adjoint, variational methods and the Kalman filter in meteorology. Tellus 1993, 45A, 342–357. [Google Scholar]
- Derber, J.C. A variational continuous assimilation technique. Mon. Wea. Rev 1989, 117, 2437–2446. [Google Scholar]
- Fillion, L.; Errico, R.M. Variational assimilation of precipitation data using moist-convective parameterization schemes: a 1D-VAR study. Mon. Wea. Rev 1997, 125, 2917–2942. [Google Scholar]
- Ott, W.; Hunt, B.R.; Szunyogh., I.; Zimin, A.V.; Kostelich, E.J.; Corazza, M.; Kalnay, E.; Patil, D.J.; Yorke, J.A. A local ensemble Kalman filter for atmospheric data assimilation. Tellus 2004, 56, 415–428. [Google Scholar]
- Zhang, C.S.; Fay, D.; McGrath, D.; Grennan, E.; Carton, O.T. Use of trans-Gaussian kriging for national soil geochemical mapping in Ireland. Geochemistry-Exploration. Environ. Anal 2008, 8, 255–265. [Google Scholar]
- Christakos, G.; Kolovos, A.; Serre, M.L.; Vukovich, F. Total ozone mapping by integrating data bases from remote sensing instruments and empirical models. IEEE Trans. Geosci. Remote Sensing 2004, 42, 991–1008. [Google Scholar]
- Goodman, J.M. Space Weather and Telecommunications; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ripley, B.D. Spatial Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Zhu, A.X.; Hudson, B.; Burt, J.; Lubich, K.; Simonson, D. Soil mapping using GIS, expert knowledge, and fuzzy logic. Soil Sci. Soc. Am. J 2001, 65, 1463–1472. [Google Scholar]
- Cochran, W.G. Sampling Techniques; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Griffith, D.A.; Haining, R.; Arbia, G. Heterogeneity of attribute sampling error in spatial data sets. Geogr. Anal 1994, 26, 300–320. [Google Scholar]
- Haining, R. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Christakos, G. Random Field Models in Earth Sciences; Dover Publications Inc: Mineola, NY, USA, 2005. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Dingman, S.L.; Seely-Reynolds, D.M.; Reynolds, R.C., III. Application of Kriging to estimating mean annual precipitation in a region of orographic influence. J. Am. Water Resour. Assoc 1988, 24, 329–339. [Google Scholar]
- Rodriguez-Iturbe, I.; Mejia, J.M. The design of rainfall networks in time and space. Water Resour. Res 1974, 10, 714–728. [Google Scholar]
- Ghosh, B. Random distances within a rectangle and between two rectangles. Bull. Calcutta Math. Soc 1951, 43, 17–24. [Google Scholar]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr 1970, 46, 234–240. [Google Scholar]
- Grimmett, G.R. Probability and Random Processes; Oxford Science Publications: New York, NY, USA, 1992. [Google Scholar]
- Shi, W.Z.; Tian, T. A hybrid interpolation method for the refinement of regular grid digital elevation model. Int. J. Geogr. Inf. Sci 2006, 20, 53–67. [Google Scholar]
- Christakos, G. Modern Spatiotemporal Geostatistics; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Krejcr, P. Development of the Kriging method with application. Appl. Math 2002, 47, 217–230. [Google Scholar]
- Pardo-Ig´uzquiza, E.; Dowd, P.A. Empirical maximum likelihood Kriging: the general case. Math. Geol 2005, 37, 477–492. [Google Scholar]

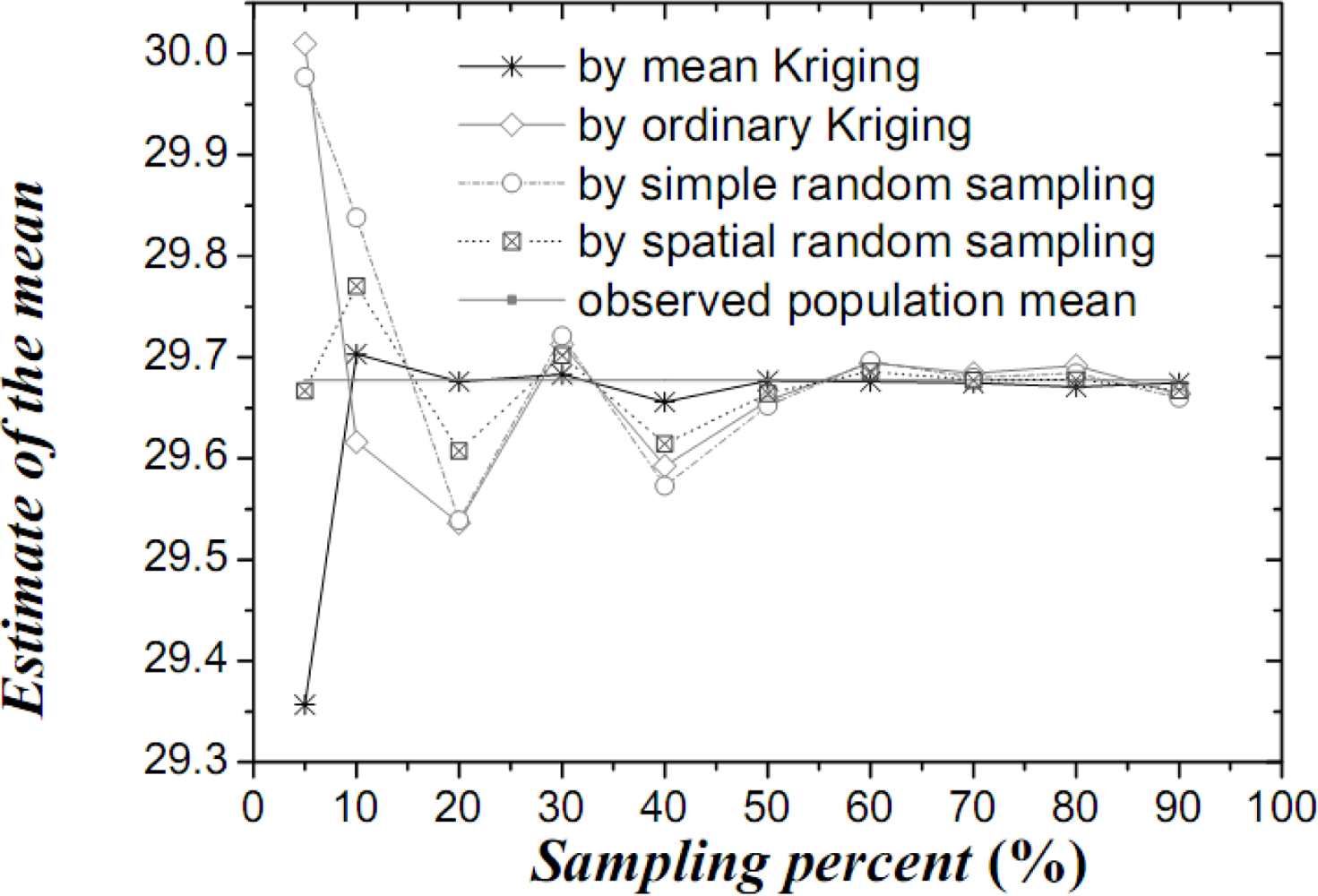
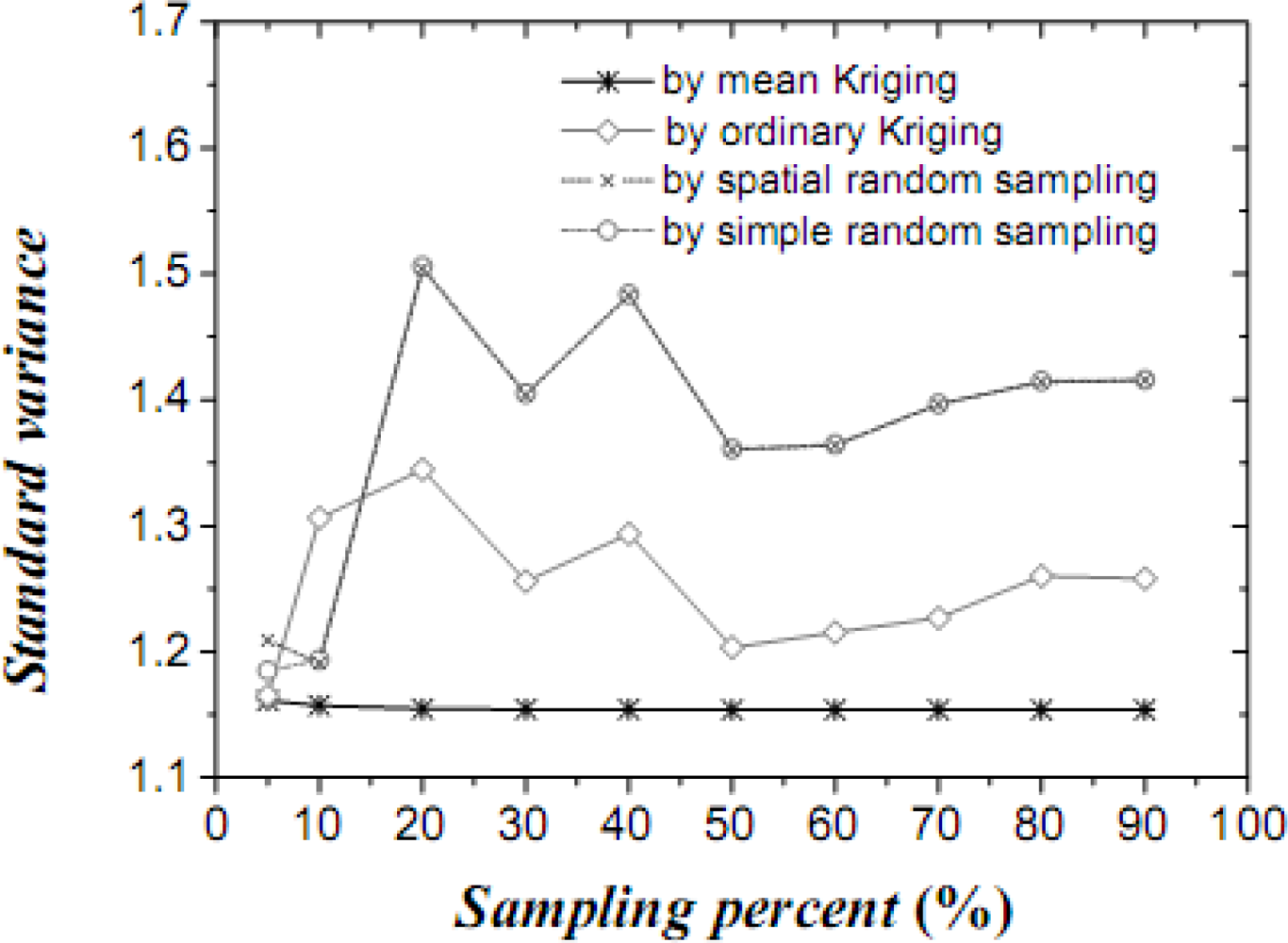
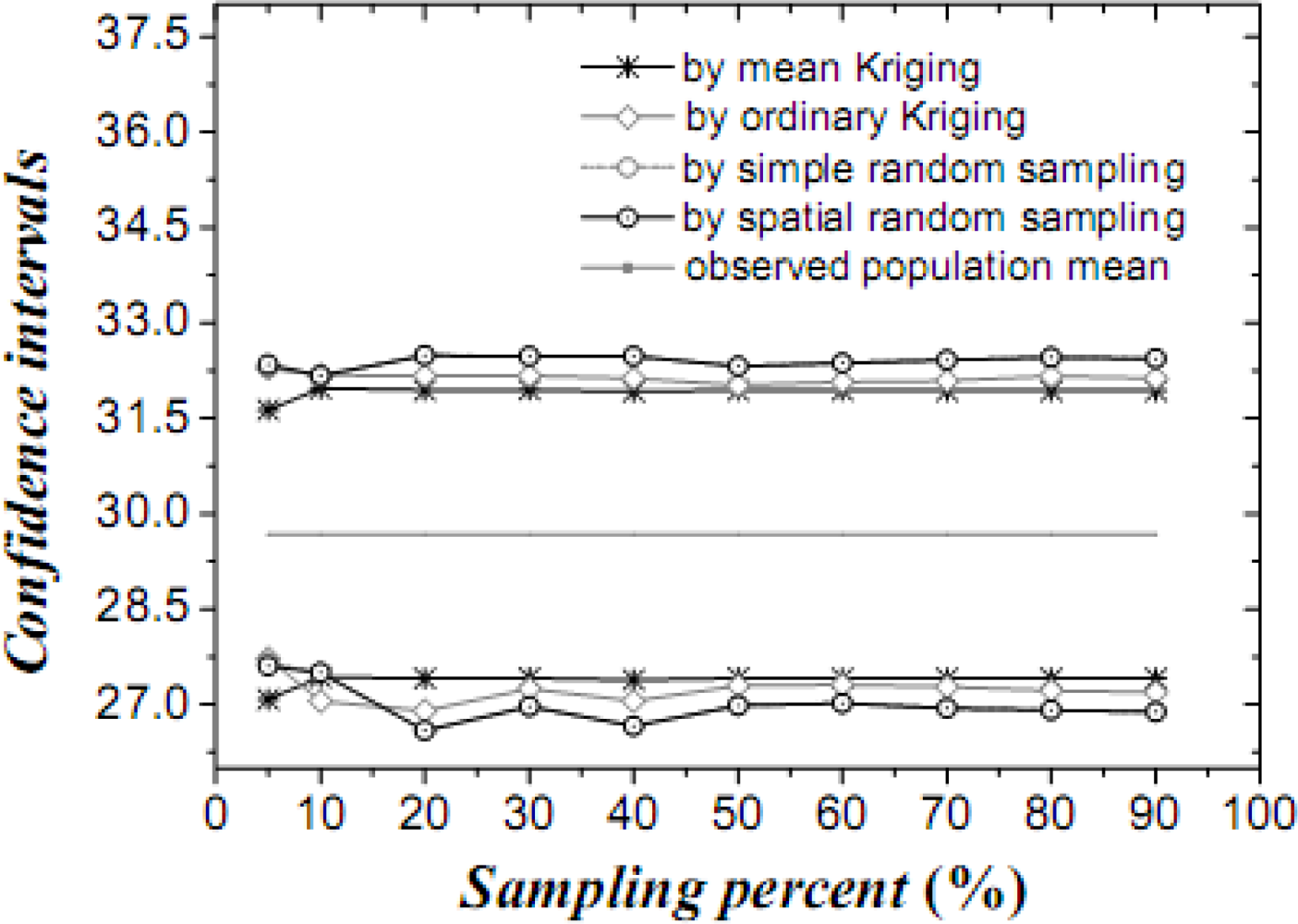



| Technique | Spatial mean (°C) | Standard deviation (°C) | 95% confidence interval |
|---|---|---|---|
| Simple random sampling | 29.70 | 1.194 | [27.43, 31.97] |
| Spatial random sampling | 29.84 | 1.19 | [27.50, 32.17] |
| Ordinary Kriging | 29.62 | 1.31 | [27.06, 32.18] |
| Mean Kriging | 29.84 | 1.16 | [27.49, 32.18] |
| N* | Minimum | Maximum | Mean | Std. Deviation | Skewness | |
|---|---|---|---|---|---|---|
| Statistic | Std. Error | |||||
| 438 | .0218 | .9977 | .2003 | .2171401 | 1.570 | .117 |
| Technique | Spatial mean | Standard variance | 95% confidence interval |
|---|---|---|---|
| Simple random sampling | 0.2040 | 0.20561 | [−0.199, 0.607] |
| Spatial random sampling | 0.2041 | 0.20083 | [−0.199, 0.607] |
| Ordinary Kriging | 0.1984 | 0.04226 | [0.1154, 0.281] |
| Mean Kriging | 0.1966 | 0.014218 | [0.1687, 0.2245] |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, J.-F.; Li, L.-F.; Christakos, G. Sampling and Kriging Spatial Means: Efficiency and Conditions. Sensors 2009, 9, 5224-5240. https://doi.org/10.3390/s90705224
Wang J-F, Li L-F, Christakos G. Sampling and Kriging Spatial Means: Efficiency and Conditions. Sensors. 2009; 9(7):5224-5240. https://doi.org/10.3390/s90705224
Chicago/Turabian StyleWang, Jin-Feng, Lian-Fa Li, and George Christakos. 2009. "Sampling and Kriging Spatial Means: Efficiency and Conditions" Sensors 9, no. 7: 5224-5240. https://doi.org/10.3390/s90705224




