Multiple Attribute Group Decision-Making Methods Based on Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators
Abstract
:1. Introduction
2. Preliminaries
2.1. The Trapezoidal Fuzzy Numbers
2.2. The Linguistic Set
- If i > j, then si > sj (that means is better than );
- there exists negative operator: neg(si) > sl−i−1;
- if si ≥ sj, ( is not worse than ), then max(si,sj) = si;
- if , ( is not better than ), then min(si,sj) = si.
2.3. The Trapezoidal Fuzzy Two-Dimensional Linguistic Variable
2.4. Partitioned Bonferroni Mean
3. The Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators
3.1. The Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators
- When q = 0:
- When p = 1, q = 0:
- When p = 1, q = 1
3.2. The Trapezoidal Fuzzy Two-Dimensional Linguistic Weighted Partitioned Bonferroni Mean Aggregation Operators
- When q = 0
- When p = 1, q = 0
- When p = 1, q = 1
4. A Multiple Attribute Group Decision-Making Method Based on TF2DLWPBM Operator
5. An Illustrated Example
- G1: The unhealthy resources and consumption restrictions
- G2: The sustainable development of the river basin’s economy
- G3: People’s environmental awareness in the river basin
- G4: The species diversity in the river basin
- G5: The resilience of the river basin
5.1. The Evaluation Steps
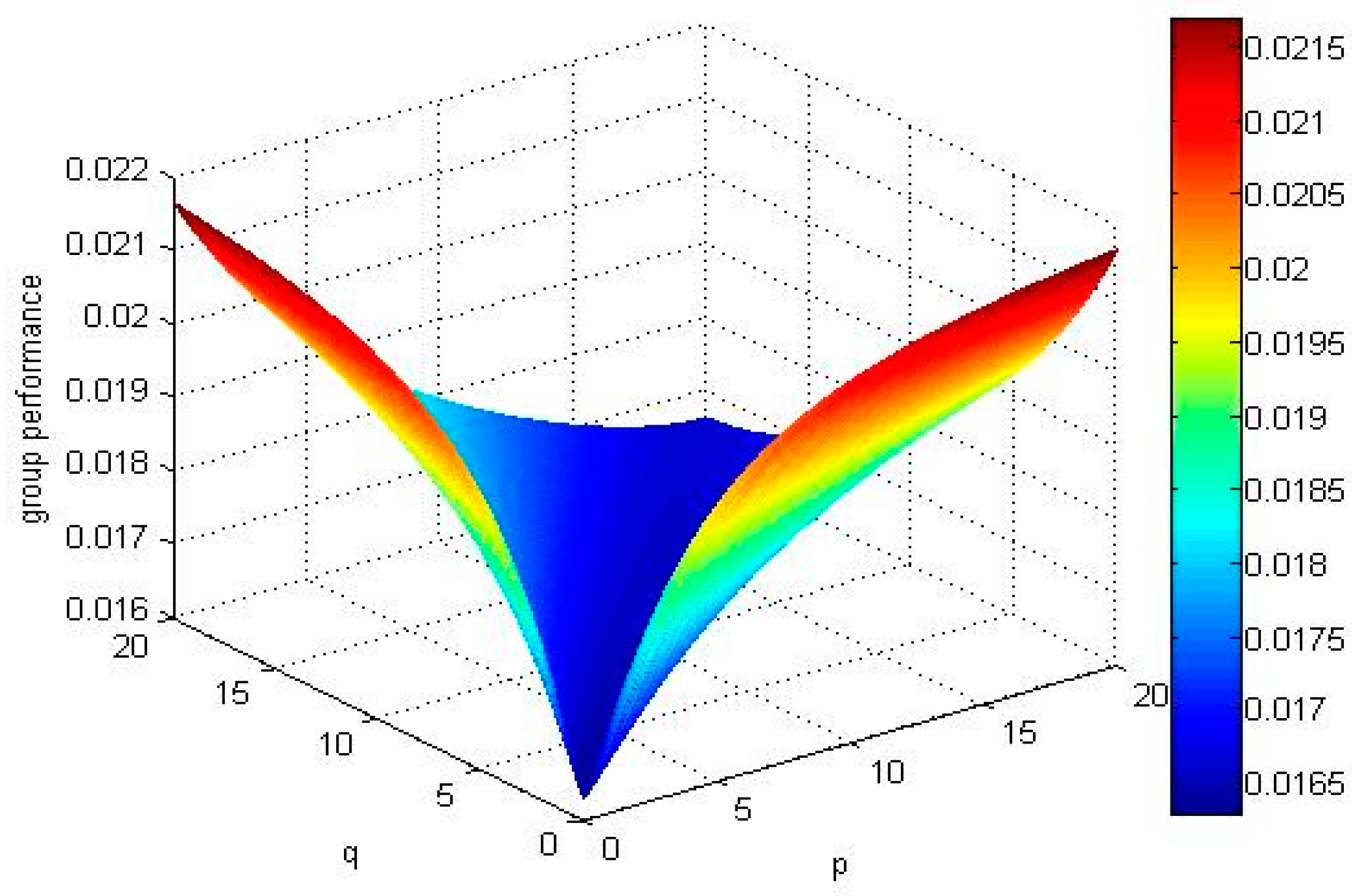
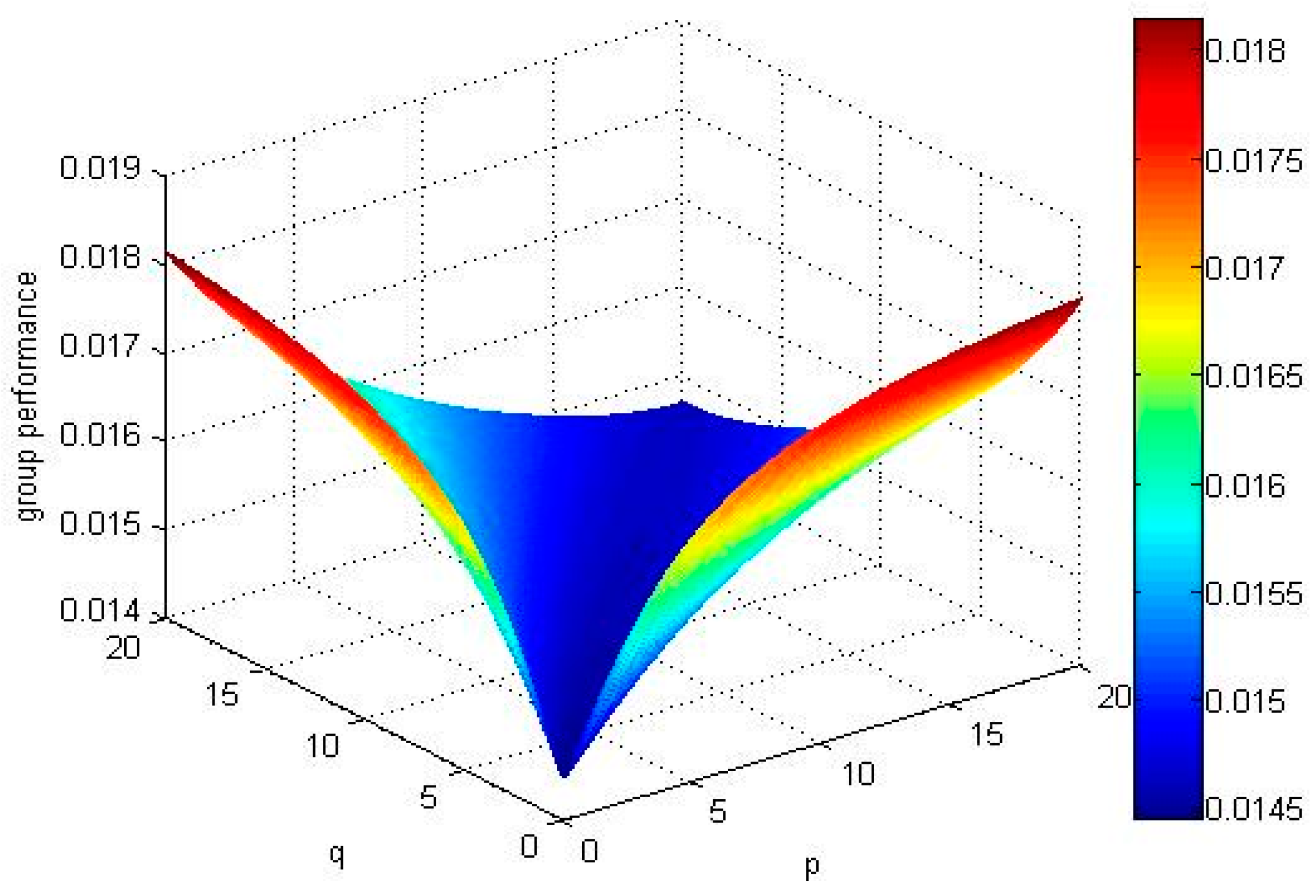
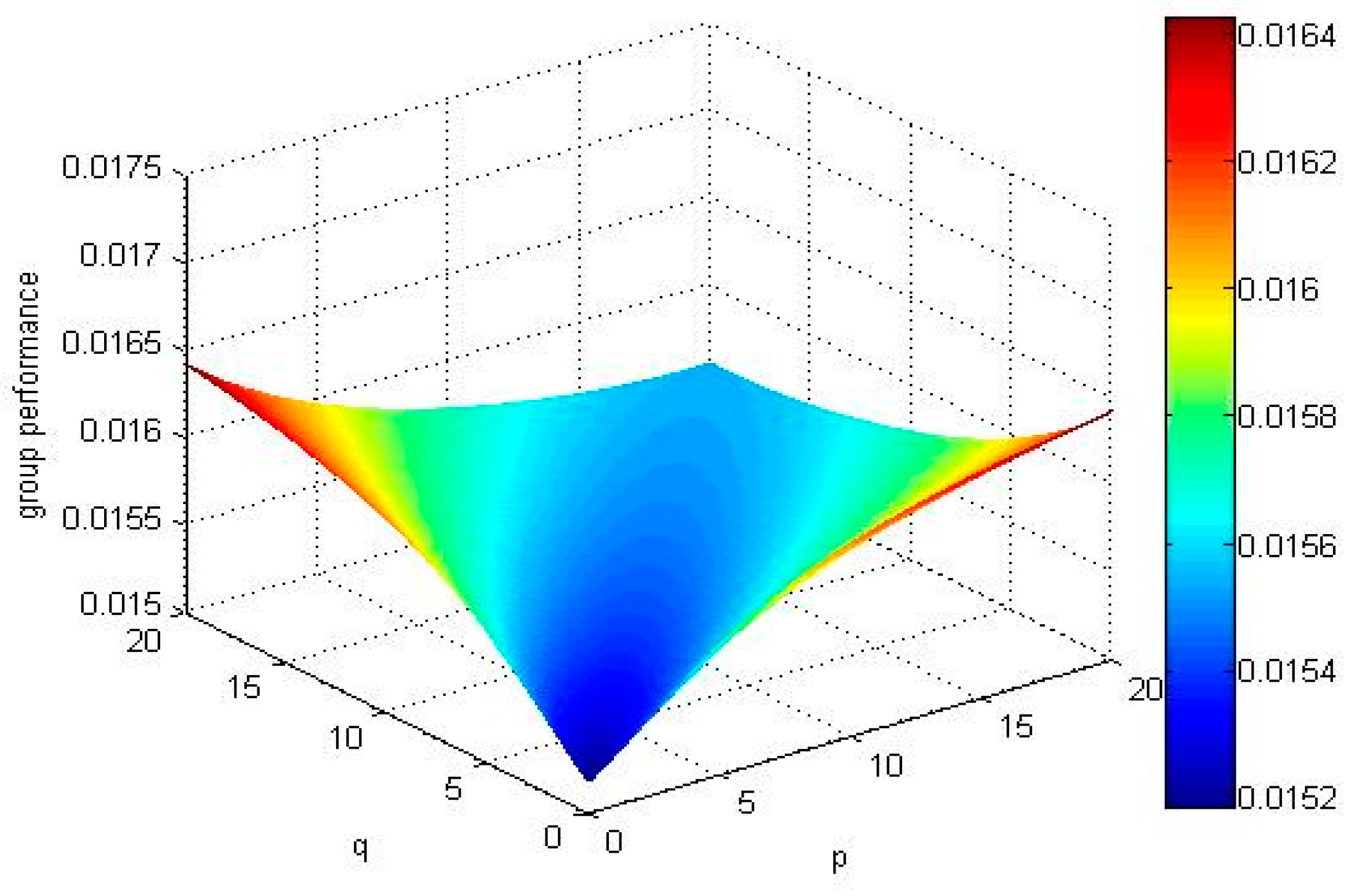
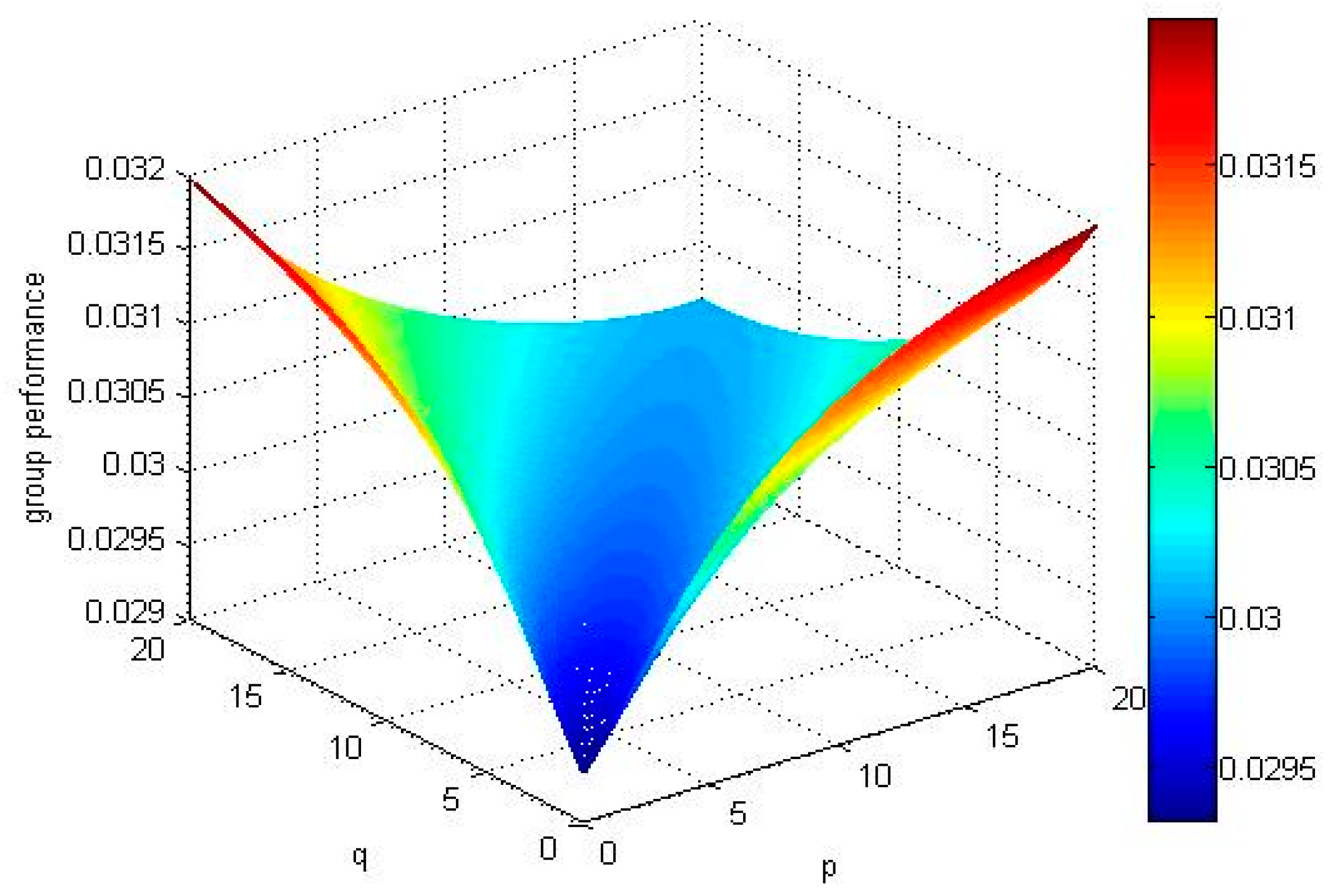
5.2. Discussion
- When p = 1 and q < 4.1 or q = 1, p < 4.1, the ordering of alternatives is , the best alternative is .
- When p = 1 and q = 4.1 or q = 1, p = 4.1, the ordering of alternatives is .
- When p = 1 and q > 4.1 or q = 1, p > 4.1, the ordering of alternatives is , the best alternative is .
5.3. Comparison with the Other Methods
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, Z. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Cheng, P.F.; Zhou, X.H.; Tang, X.P. A decision making method based on the uncertain linguistic. Stat. Decis. 2006, 24, 145–147. [Google Scholar]
- Zhang, N.C.; Li, Z.L.; Liu, C.Y. Choice of landing area based on uncertain linguistic information multiple attribute decision making. Ship Electron. Eng. 2007, 27, 53–56. [Google Scholar]
- Xu, Z.S. Linguistic aggregation operators: An overview. In Fuzzy Sets and Extensions: Representation, Aggregation and Models; Bustince, H., Herrera, F., Montero, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 163–181. [Google Scholar]
- Liu, F.; Zhang, W.G.; Wang, Z.X. A goal programming model for incomplete interval multiplicative preference relations and its application in group decision-making. Eur. J. Oper. Res. 2012, 218, 747–754. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Chang, C.-H.; Lu, J.R. The extended qualiflex method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making. Eur. J. Oper. Res. 2013, 226, 615–625. [Google Scholar] [CrossRef]
- Liu, P.; Jin, F. Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inf. Sci. 2012, 205, 58–71. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Wei, G. Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making. Appl. Soft Comput. 2010, 10, 423–431. [Google Scholar] [CrossRef]
- Li, D.-F. The gowa operator based approach to multiattribute decision making using intuitionistic fuzzy sets. Math. Comput. Model. 2011, 53, 1182–1196. [Google Scholar] [CrossRef]
- Dong, J.; Wan, S. A new method for multi-attribute group decision making with triangular intuitionistic fuzzy numbers. Kybernetes 2016, 45, 158–160. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Topsis method for multi-attribute group decision-making under single-valued neutrosophic environment. Neural Comput. Appl. 2015, 27, 727–737. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.Q.; Zhang, H.Y.; Chen, X.H. Multi-criteria group decision-making approach based on 2-tuple linguistic aggregation operators with multi-hesitant fuzzy linguistic information. Int. J. Fuzzy Syst. 2016, 18, 81–97. [Google Scholar] [CrossRef]
- Zhu, W.D.; Zhou, G.Z.; Yang, S.L. An approach to group decision making based on 2-dimensional linguistic assessment information. Syst. Eng. 2009, 27, 113–118. [Google Scholar]
- Liu, P.D.; Zhang, X. An approach to group decision making based on 2-dimensional uncertain linguistic assessment information. Technol. Econ. Dev. Econ. 2012, 18, 424–437. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, G.Z.; Zhu, W.D. Research on peer review system for the National Science Foundation based on two-dimensionalal semantics evidence reasoning. China Soft Sci. 2012, 2, 176–182. [Google Scholar]
- Yu, X.H.; Xu, Z.S.; Liu, S.S.; Chen, Q. 2012, Multi-criteria decision making with 2-dimensional linguistic aggregation techniques. Int. J. Intell. Syst. 2010, 27, 539–562. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Liu, P. Multiple attribute group decision-making methods based on trapezoidal fuzzy two-dimension linguistic power generalized aggregation operators. Soft Comput. 2015, 20, 2689–2704. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, Y.M. The aggregation operators based on the 2-dimension uncertain linguistic information and their application to decision making. Int. J. Mach. Learn. Cybern. 2015, 7, 1–18. [Google Scholar] [CrossRef]
- Liu, P.; Teng, F. Multiple attribute decision-making method based on 2-dimension uncertain linguistic density generalized hybrid weighted averaging operator. Soft Comput. 2016, 1–14. [Google Scholar] [CrossRef]
- Liu, P.; He, L.; Yu, X. Generalized hybrid aggregation operators based on the 2-dimension uncertain linguistic information for multiple attribute group decision making. Group Decis. Negot. 2015, 25, 103–126. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Yager, R.R. On generalized Bonferroni mean operators for multi-criteria aggregation. Int. J. Approx. Reason. 2009, 50, 1279–1286. [Google Scholar] [CrossRef]
- Yager, R.R.; Beliakov, G.; James, S. On generalized Bonferroni means. In Proceedings of the Eurofuse Workshop Preference Modelling Decision Analysis, Pamplona, Spain, 16–18 September 2009; pp. 16–18. [Google Scholar]
- Beliakov, G.; James, S.; Yager, R.R. Generalized Bonferroni mean operators in multi-criteria aggregation. Fuzzy Sets Syst. 2010, 161, 2227–2242. [Google Scholar] [CrossRef]
- Dutta, B.; Guha, D. Partitioned bonferroni mean based on linguistic 2-tuple for dealing with multi-attribute group decision making. Appl. Soft Comput. 2015, 37, 166–179. [Google Scholar] [CrossRef]
- Wei, G.; Zhao, X.; Lin, R.; Wang, H. Corrigendum to uncertain linguistic bonferroni mean operators and their application to multiple attribute decision making. Appl. Math. Model. 2013, 37, 5277–5285. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.S.; Zhu, B. Generalized intuitionistic fuzzy Bonferroni means. Int. J. Intell. Syst. 2012, 27, 23–47. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man Cybern. B 2011, 41, 568–578. [Google Scholar]
- Jiang, X.P.; Wei, G.W. Some Bonferroni mean operators with 2-tuple linguistic information and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 2153–2162. [Google Scholar]
- Liu, X.; Tao, Z.; Chen, H.; Zhou, L. A new interval-valued 2-tuple linguistic bonferroni mean operator and its application to multiattribute group decision making. Int. J. Fuzzy Syst. 2016, 19, 86–108. [Google Scholar] [CrossRef]
- Liu, P.D.; Chen, S.M.; Liu, J.L. Multiple attribute group decision making based on intuitionistic fuzzy interaction partitioned Bonferroni mean operators. Inf. Sci. 2017, 411, 98–121. [Google Scholar] [CrossRef]
- Liu, Z.M.; Liu, P.D. Intuitionistic uncertain linguistic partitioned Bonferroni means and their application to multiple attribute decision-making. Int. J. Syst. Sci. 2017, 48, 1092–1105. [Google Scholar] [CrossRef]
- Li, R.J. Theory and Application on the Fuzzy Multiple Attribute Decision Making; Science Press: Beijing, China, 2002. [Google Scholar]
- Su, Z.B. Study on Consistency Issues and Sorting Methods Based on Three Kinds of Judgement Matrix in FAHP; Xi’an University of Technology: Xi’an, China, 2006. [Google Scholar]
- Degani, R.; Bortolan, G. The problem of linguistic approximation in clinical decision making. Int. J. Approx. Reason. 1988, 2, 144–162. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E. Linguistic decision analysis: Steps for solving decision problems under linguistic information. Fuzzy Sets Syst. 2000, 115, 67–82. [Google Scholar] [CrossRef]
- Dutta, B.; Guha, D. Trapezoidal intuitionistic fuzzy Bonferroni means and its application in multi-attribute decision making. In Proceedings of the IEEE International Conference on Fuzzy System (FUZZ-IEEE, 2013), Hyderabad, India, 7–10 July 2013. [Google Scholar]
- Copping, A.; Hanna, L.; Van Cleve, B.; Blake, K.; Anderson, R.M. Environmental risk evaluation system—An approach to ranking risk of ocean energy development on coastal and estuarine environments. Estuaries Coasts 2015, 38, 287–302. [Google Scholar] [CrossRef]
- Roussiez, V.; Ludwig, W.; Radakovitch, O.; Probst, J.-L.; Monaco, A.; Charrière, B.; Buscail, R. Fate of metals in coastal sediments of a mediterranean flood-dominated system: An approach based on total and labile fractions. Estuar. Coast. Shelf Sci. 2011, 92, 486–495. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hipel, K.W.; Dang, Y. An improved grey relational analysis approach for panel data clustering. Expert. Syst. Appl. 2015, 42, 9105–9116. [Google Scholar] [CrossRef]
- Yin, K.; Zhang, Y.; Li, X. Research on storm-tide disaster losses in China using a new grey relational analysis model with the dispersion of panel data. Int. J. Environ. Res. Public Health 2017, 14, 1330. [Google Scholar] [CrossRef] [PubMed]
- Polidoro, B.A.; Carpenter, K.E.; Collins, L. The Loss of Species: Mangrove Extinction Risk and Geographic Areas of Global Concern. PLoS ONE 2010, 5, e10095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, P.D. A novel method for hybrid multiple attribute decision making. Knol.-Based Syst. Sci. 2009, 79, 131–143. [Google Scholar]
- Shi, L.L. The Research on Aggregation Operators Based on Trapezoidal Two-Dimension Linguistic Numbers. Master’s Thesis, School of Management Science and Engineering, Shandong University of Finance and Economics, Jinan, China, 2016; pp. 35–50. [Google Scholar]


| p, q | Ranking | ||
|---|---|---|---|
| p = 1 q = 0 | |||
| p = 1 q = 1 | |||
| p = 1 q = 2 | |||
| p = 1 q = 4 | |||
| p = 1 q = 5 | |||
| p = 2 q = 2 | |||
| p = 0 q = 1 | |||
| p = 2 q = 1 | |||
| p = 4 q = 1 | |||
| p = 5 q = 1 | |||
| p = 2 q = 2 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, K.; Yang, B.; Li, X. Multiple Attribute Group Decision-Making Methods Based on Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators. Int. J. Environ. Res. Public Health 2018, 15, 194. https://doi.org/10.3390/ijerph15020194
Yin K, Yang B, Li X. Multiple Attribute Group Decision-Making Methods Based on Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators. International Journal of Environmental Research and Public Health. 2018; 15(2):194. https://doi.org/10.3390/ijerph15020194
Chicago/Turabian StyleYin, Kedong, Benshuo Yang, and Xuemei Li. 2018. "Multiple Attribute Group Decision-Making Methods Based on Trapezoidal Fuzzy Two-Dimensional Linguistic Partitioned Bonferroni Mean Aggregation Operators" International Journal of Environmental Research and Public Health 15, no. 2: 194. https://doi.org/10.3390/ijerph15020194





