The Burr X Pareto Distribution: Properties, Applications and VaR Estimation

Abstract

In this paper, a new three-parameter Pareto distribution is introduced and studied. We discuss various mathematical and statistical properties of the new model. Some estimation methods of the model parameters are performed. Moreover, the peaks-over-threshold method is used to estimate Value-at-Risk (VaR) by means of the proposed distribution. We compare the distribution with a few other models to show its versatility in modelling data with heavy tails. VaR estimation with the Burr X Pareto distribution is presented using time series data, and the new model could be considered as an alternative VaR model against the generalized Pareto model for financial institutions.

1. Introduction

The Pareto (P) distribution is very versatile, and a variety of uncertainties can be usefully modelled by it. It has several applications in actuarial science, economics, finance, life testing, survival analysis and telecommunications because of its heavy tail properties. The probability density function (pdf) and cumulative distribution function (cdf) of the P distribution are given (for $x>\beta$) by:

$$g(x;\alpha ,\beta )=\frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{-\alpha }\mathrm{and}G(x;\alpha ,\beta )=1-{\left(\frac{x}{\beta }\right)}^{-\alpha },$$

where $\beta >0$ is a scale parameter and $\alpha >0$ is a shape parameter. This distribution is a special form of the Pearson Type VI distribution. Since the P distribution has a reversed-J pdf shape and a decreasing hazard rate function (hrf), it may sometimes be insufficient to model data. Generally, practical problems require a wider range of possibilities for the medium risk, for example when the lifetime data present a bathtub-shaped hrf, such as human mortality and machine life cycles. For this reason, researchers developed various extensions and modified forms of the P distribution to obtain a more flexible model with different numbers of parameters. Some of them can be cited as follows: Exponentiated P (EP) (Stoppa 1990; Gupta et al. 1998), Beta P (BP) (Akinsete et al. 2008), Kumaraswamy P (KwP) (Bourguignon et al. 2013), Kumaraswamy generalized P (Nadarajah and Eljabri 2013), P ArcTan (PAT) (Gómez-Déniz and Calderín-Ojeda 2015), exponentiated Weibull P (Afify et al. 2016) and Weibull P (WP) distributions (Tahir et al. 2016). On the other hand, Yousof et al. (2016) defined the cdf of the Burr X-G(BX-G) family (for $x\in \Re$) by:

$$F(x;\delta ,\xi )={\left(1-exp\left\{-{\left[\frac{G(x;\xi )}{\overline{G}(x;\xi )}\right]}^2\right\}\right)}^{\delta },$$

(1)

where $\delta >0$ is the shape parameter and $\xi =$ ${\xi }_k=$ (${\xi }_1,{\xi }_2,\cdots$) is a parameter vector. The BX-G density function becomes:

$$f(x;\delta ,\xi )=\frac{2\delta g(x;\xi )G(x;\xi )}{\overline{G}{(x;\xi )}^3}exp\left\{-{\left[\frac{G(x;\xi )}{\overline{G}(x;\xi )}\right]}^2\right\}{\left(1-exp\left\{-{\left[\frac{G(x;\xi )}{\overline{G}(x;\xi )}\right]}^2\right\}\right)}^{\delta -1}.$$

(2)

This generator can supply the flexibility of pdf and hrf to any baseline distribution model (Yousof et al. 2016).

In this paper, we introduce a new extended P distribution, called the Burr X Pareto (BXP) model, based on the BX-G family. With this idea, we construct the new BXP distribution as more flexible than the P distribution and provide a comprehensive description of some of its mathematical properties. We prove empirically that the BXP model provides better fits than some extensions and generalizations of the P, some of which have one extra model parameter, and the others have the same number of parameters, by means of two applications to real data. We hope that the new distribution will attract wider applications in reliability, engineering and other areas of research.

The rest of the paper is organized as follows. In Section 2, we define the BXP model. In Section 3, we provide a useful mixture representation for its pdf. In Section 4, we derive some of its general mathematical properties. Some estimation methods of the model parameters are performed in Section 5. In Section 6, simulation results to assess the performance of the proposed maximum likelihood estimation procedure are discussed. In Section 7, we provide two applications to real data to illustrate the importance and flexibility of the new family. Value-at-Risk estimation with the BXP distribution is presented in Section 8. Finally, some concluding remarks are presented in Section 9.

2. The New Model

In this section, we define the BXP model and provide some plots for its pdf and hrf. The BXP cdf is given by:

$$F(x;\delta ,\alpha ,\beta )={\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta },x>\beta >0,\alpha ,\delta >0.$$

(3)

The pdf corresponding to (3) is given by:

$$\begin{array}{c}f(x;\delta ,\alpha ,\beta )=2\delta \frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{2\alpha }\left[1-{\left(\frac{x}{\beta }\right)}^{-\alpha }\right]exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\\ \times {\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta -1}.\end{array}$$

(4)

Lemma 1 provides random number generations from the BXP and some relations and of the BXP distribution with the well-known Burr X and uniform distributions.

Lemma 1.

(a) If a random variable Y follows the Burr X distribution with shape parameter δ and scale parameter one, then the random variable $X=\beta {(1+Y)}^{(1/\alpha )}$ follows the BXP $(\delta ,\alpha ,\beta )$ distribution.

(b) If a random variable Y follows the uniform distribution on [0,1], then the random variable:

$$X=\beta {\left(1+\sqrt{-log(1-Y^{1/\delta })}\right)}^{1/\alpha }$$

follows the BXP $(\delta ,\alpha ,\beta )$ distribution.

Proof. 

The proofs of (a) and (b) are obtained by the transformation method. ☐

The hrf, reversed hazard rate function and cumulative hazard rate function of $X$ are given, respectively, by:

$$h(x;\delta ,\alpha ,\beta )=\frac{2\delta \frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{2\alpha }\left[1-{\left(\frac{x}{\beta }\right)}^{-\alpha }\right]exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}{\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta -1}}{1-{\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta }},$$

$$r\left(x;\delta ,\alpha ,\beta \right)=\frac{2\delta \frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{2\alpha }\left[1-{\left(\frac{x}{\beta }\right)}^{-\alpha }\right]exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}}{\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}$$

and:

$$H(x;\delta ,\alpha ,\beta )=-\left[log{\left(1-exp\left\{-{\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta }\right].$$

In Figure 1, we sketched the possible pdf and hrf shapes of the BXP distribution for some selected parameter values. Figure 1 shows that the BXP distribution has various pdf and hrf shapes.

3. Expansions of pdf and cdf

In this section, we provide a very useful linear representation for the BXP density function. If $\left|z\right|<1$ and $b>0$ is a real non-integer, the power series holds:

$${\left(1-z\right)}^{b-1}=\stackrel{\infty }{\sum _{i=0}}\frac{{\left(-1\right)}^i\Gamma \left(b\right)}{i!\Gamma \left(b-i\right)}{z}^i.$$

(5)

For simplicity, ignoring the dependence of $G\left(x\right)$ and $g\left(x\right)$ on $\xi$ and applying (5) to (4), we have:

$$f\left(x\right)=2\delta \frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{2\alpha }\left[1-{\left(\frac{x}{\beta }\right)}^{-\alpha }\right]\stackrel{\infty }{\sum _{i=0}}\frac{{\left(-1\right)}^i\Gamma \left(\delta \right)}{i!\Gamma \left(\delta -i\right)}exp\left\{-\left(i+1\right){\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}.$$

(6)

Applying the power series to the term $exp\left\{-\left(i+1\right){\left[{\left(\frac{x}{\beta }\right)}^{\alpha }-1\right]}^2\right\}$, Equation (6) becomes:

$$f\left(x\right)=2\delta \frac{\alpha }{x}{\left(\frac{x}{\beta }\right)}^{-\alpha }\stackrel{\infty }{\sum _{i,j=0}}\frac{{\left(-1\right)}^{i+j}{\left(i+1\right)}^j\Gamma \left(\delta \right)}{i!j!\Gamma \left(\delta -i\right)}\frac{{\left[1-{\left(\frac{x}{\beta }\right)}^{-\alpha }\right]}^{2j+1}}{{\left(\frac{x}{\beta }\right)}^{-\alpha \left(2j+3\right)}}.$$

(7)

Consider the series expansion:

$${\left(1-z\right)}^{-b}=\stackrel{\infty }{\sum _{k=0}}\frac{\Gamma \left(b+k\right)}{k!\Gamma \left(b\right)}{z}^k,\left|z\right|<1,b>0.$$

(8)

Applying the expansion in (8) to (7) for the term ${\left(\frac{x}{\beta }\right)}^{-\alpha \left(2j+3\right)}$, Equation (7) becomes:

$$f\left(x\right)=\stackrel{\infty }{\sum _{j,k=0}}{\Omega }_{j,k}{\pi }_{2\left(j+1\right)+k}(x;\alpha ,\beta ),$$

(9)

where:

$${\Omega }_{j,k}=\frac{2\delta {\left(-1\right)}^j\Gamma \left(\delta \right)\Gamma \left(2j+k+3\right)}{j!k!\Gamma \left(2j+3\right)\left(2j+k+2\right)}\stackrel{\infty }{\sum _{i=0}}\frac{{\left(-1\right)}^i{\left(i+1\right)}^j}{i!\Gamma \left(\delta -i\right)}$$

and:

$${\pi }_{2\left(j+1\right)+k}(x;\alpha ,\beta )=\left[2\left(j+1\right)+k\right]g(x;\alpha ,\beta )G{(x;\alpha ,\beta )}^{2j+k+1}.$$

Equation (9) reveals that the density of X can be expressed as expansions of the EP densities. Therefore, several mathematical properties of the new family can be obtained by knowing those of the EP distribution. Similarly, the cdf of the BXP family can also be expressed as a mixture of EP cdfs given by:

$$F\left(x\right)=\stackrel{\infty }{\sum _{j,k=0}}{\Omega }_{j,k}{\Pi }_{2\left(j+1\right)+k}\left(x;\alpha ,\beta \right)$$

(10)

where:

$${\Pi }_{2\left(j+1\right)+k}\left(x\right)=G{(x;\alpha ,\beta )}^{2\left(j+1\right)+k}$$

is the cdf of the EP family with power parameter $2\left(j+1\right)+k$.

4. Properties

In this section, we will provide some mathematical properties of the BXP distribution.

4.1. Moments

The r-th ordinary moment of X is given by ${\mu }_r^{\prime }=E\left(X^r\right)={\int }_{-\infty }^{\infty }{x}^{r}f\left(x\right)dx.$ By using Equation (9), we obtain:

$${\displaystyle {\mu }_r^{\prime }=\sum _{j,k=0}^{\infty }{\Omega }_{j,k}E(Y_{2(j+1)+k}^r),}$$

$E(Y_{2(j+1)+k}^r)$ is the r-th ordinary moment of EP distribution with power parameter $2(j+1)+k$.

The j-th order central moment can be obtained by the following relationship:

$$\begin{array}{c}\hfill {\mu }_j=E[{(X-\mu )}^j]=\sum _{r=0}^j\left(\genfrac{}{}{0pt}{}{j}{r}\right){\mu }_r{}^{\prime }{(-\mu )}^{j-r}\mathrm{for}j=2,3,\dots ,\end{array}$$

where $\mu =E\left(X\right)$.

For the skewness and kurtosis coefficients, we have:

$$\sqrt{{\beta }_1}=\sqrt{\frac{{\mu }_3^2}{{\mu }_2^3}}\mathrm{and}{\beta }_2=\frac{{\mu }_4}{{\mu }_2^2}.$$

The values for mean, variance, $\sqrt{{\beta }_1}$ and ${\beta }_2$ for selected values of $\delta ,\alpha$ and $\beta$ are shown in

Table 1. Mean, variance, coefficients of skewness and kurtosis for different values of parameters.

$(\mathit{\delta },\mathit{\alpha },\mathit{\beta })$	$\mathit{\mu }$	$\mathit{V}\mathit{a}\mathit{r}\left(\mathit{X}\right)$	$\sqrt{{\mathit{\beta }}_1}$	${\mathit{\beta }}_2$
(0.5, 0.5, 0.5)	1.2801	1.1395	0.7311	4.4238
(1, 1, 1)	1.6330	0.9671	−1.2539	3.2132
(2, 2, 2)	2.5365	1.7311	−1.9644	4.3986
(1, 2, 3)	2.9606	5.9323	−0.8355	1.3785
(4, 2, 0.5)	0.7411	0.0415	−4.1218	17.7934
(10, 2, 0.25)	0.4074	0.0011	−6.3710	97.4674
(0.25, 5, 2)	0.4962	1.2671	1.4287	2.6058
(0.9, 5, 1.8)	1.0633	1.5440	0.0255	0.7191

. We can say that the BXP model can be useful for various data modelling in terms of skewness and kurtosis.

4.2. Residual and Reversed Residual Life

The n-th moment of the residual life, say $m_n\left(t\right)=E[{(X-t)}^n\mid X>t]$, $n=1,2$, …, uniquely determines $F\left(x\right)$. The n-th moment of the residual life of X is given by:

$$m_n\left(t\right)=\frac{1}{1-F\left(t\right)}{\int }_t^{\infty }{(x-t)}^{n}dF\left(x\right).$$

Therefore,

$$m_n\left(t\right)=\frac{1}{1-F\left(t\right)}\stackrel{\infty }{\sum _{j,k=0}}\stackrel{n}{\sum _{r=0}}{\Omega }_{j,k}\left(\genfrac{}{}{0pt}{}{n}{r}\right){\left(-t\right)}^{n-r}{\beta }^n\left[2\left(j+1\right)+k\right]{\mathbf{B}}_t\left(1-\frac{n}{\alpha },2\left(j+1\right)+k\right),\forall n\le \alpha .$$

where:

$${\mathbf{B}}_z\left(a,b\right)={\int }_0^z{w}^{a-1}{\left(1-w\right)}^{b-1}dw$$

is the incomplete beta function.

The Mean Residual Life (MRL) function or the life expectation at age t defined by $m_1\left(t\right)=E\left[(X-t)\mid X>t\right]$ follows by setting $n=1$ in the last equation.

The n-th moment of the reversed residual life, say $M_n\left(t\right)=E\left[{(t-X)}^n\mid X\le t\right]$ for $t>0$ and $n=1,2$, … uniquely determines $F\left(x\right)$. We obtain:

$$M_n\left(t\right)=\frac{1}{F\left(t\right)}{\int }_0^t{(t-x)}^{n}dF\left(x\right).$$

Then, the n-th moment of the reversed residual life of X becomes:

$$M_n\left(t\right)=\frac{1}{F\left(t\right)}\stackrel{\infty }{\sum _{j,k=0}}\stackrel{n}{\sum _{r=0}}{\Omega }_{j,k}{\left(-1\right)}^r\left(\genfrac{}{}{0pt}{}{n}{r}\right)t^{n-r}{\beta }^n\left[2\left(j+1\right)+k\right]{\mathbf{B}}_t\left(1-\frac{n}{\alpha },2\left(j+1\right)+k\right),\forall n\le \alpha .$$

The mean inactivity time (MIT) or mean waiting time is given by $M_1\left(t\right)=E[(t-X)\mid X\le t]$, and it can be obtained easily by setting $n=1$ in the above equation.

4.3. Order Statistics

Order statistics make their appearance in many areas of statistical theory and practice. Let $X_1,\dots ,X_n$ be a random sample from the BXP of distributions, and let $X_{\left(1\right)},\dots ,X_{\left(n\right)}$ be the corresponding order statistics. The pdf of the i-th order statistic, say $X_{i:n}$, can be written as:

$$f_{i:n}\left(x\right)=\frac{f\left(x;\delta ,\alpha ,\beta \right)}{\mathrm{B}\left(i,n-i+1\right)}\sum _{j=0}^{n-i}{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n-i}{j}\right)F^{j+i-1}\left(x\right).$$

(11)

Using (3), (4) and (10), we get:

$$f\left(x\right)F{\left(x\right)}^{j+i-1}=\sum _{w,k=0}^{\infty }{t}_{w,k}{\pi }_{2\left(w+1\right)+k}\left(x\right),$$

where:

$$t_{w,k}=\frac{2\delta {\left(-1\right)}^w\Gamma \left(2w+k+3\right)}{w!k!\Gamma \left(2w+3\right)\left(2w+k+2\right)}\sum _{m=0}^{\infty }{\left(-1\right)}^m{\left(m+1\right)}^w\left(\genfrac{}{}{0pt}{}{\delta \left(j+i\right)-1}{m}\right).$$

The pdf of $X_{i:n}$ can be expressed as:

$$f_{i:n}\left(x\right)=\sum _{w,k=0}^{\infty }\sum _{j=0}^{n-i}\frac{{\left(-1\right)}^j(\genfrac{}{}{0pt}{}{n-i}{j})b_{w,k}}{\mathrm{B}\left(i,n-i+1\right)}{\pi }_{2\left(w+1\right)+k}\left(x\right).$$

Then, the density function of the BXP order statistics is a mixture of EP densities. Based on the last equation, we note that the properties of $X_{i:n}$ follow from those properties of $Y_{2w+k+2}$. For example, the moments of $X_{i:n}$ can be expressed as:

$$E\left(X_{i:n}^q\right)=\sum _{w,k=0}^{\infty }\sum _{j=0}^{n-i}\frac{{\left(-1\right)}^j(\genfrac{}{}{0pt}{}{n-i}{j})t_{w,k}}{\mathrm{B}\left(i,n-i+1\right)}{\beta }^q\left[2\left(w+1\right)+k\right]\mathbf{B}\left(1-\frac{q}{\alpha },2\left(w+1\right)+k\right),\forall q\le \alpha .$$

(12)

5. Estimation Methods

In this section, we consider the maximum likelihood, least square and weighted least square estimation of the parameters of the BXP distribution.

5.1. Maximum Likelihood Estimation

We consider the estimation of the unknown parameters of the BXP model from complete samples by the maximum likelihood method. The maximum likelihood estimators (MLEs) of the parameters of the BXP $(\delta ,\alpha ,\beta )$ model are now discussed. Let $x_1,\dots ,x_n$ be a random sample of this distribution with parameter vector $\Theta ={(\delta ,\alpha ,\beta )}^{⊺}$. The log-likelihood function for $\delta$ is given by:

$$\begin{array}{ccc}\hfill \ell & =& nlog2+nlog\delta +nlog\alpha -2\alpha log\beta +\sum _{i=1}^{n}log\left(1-{\beta }^{\alpha }{x}_i^{-\alpha }\right)\hfill \\ & & +\left(2\alpha -1\right)\sum _{i=1}^{n}log{x}_i+\sum _{i=1}^{n}log{s}_i+\left(\delta -1\right)\sum _{i=1}^{n}log\left(1-s_i\right),\hfill \end{array}$$

where $s_i=exp\left\{-{\left[{\left(\frac{x_i}{\beta }\right)}^{\alpha }-1\right]}^2\right\}$.

The last equation can be also maximized either by using the different programs such as R (optim function), SAS (PROC NLMIXED) or by solving the nonlinear likelihood equations obtained by differentiating ℓ. We note that since $x\in \left(\beta ,\infty \right),$ the MLE of the $\beta$ parameter cannot be obtained in the usual way. Hence, the MLE of $\beta$ is the first order statistic $X_{\left(1\right)}$ (Johnson et al. 1994).

The components of the score vector, $\mathbf{U}\left(\Theta \right)=\frac{\partial \ell }{\partial \Theta }={\left(\frac{\partial \ell }{\partial \delta },\frac{\partial \ell }{\partial \alpha }\right)}^{⊺}$, are:

$$U_{\delta }=\frac{n}{\delta }+\sum _{i=1}^{n}log\left(1-exp\left\{-{\left[{\left(\frac{x_i}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right),$$

and:

$$U_{\alpha }=\frac{n}{\alpha }-2log\beta -\sum _{i=1}^n\frac{{\left(\frac{x}{\beta }\right)}^{-\alpha }log\left(\frac{x}{\beta }\right)}{1-{\beta }^{\alpha }{x}_i^{-\alpha }}+2\sum _{i=1}^{n}log{x}_i+\sum _{i=1}^n\frac{m_i}{s_i}-\left(\delta -1\right)\sum _{i=1}^n\frac{m_i}{1-s_i}$$

where:

$$m_i=-2s_i\left[{\left(\frac{x_i}{\beta }\right)}^{\alpha }-1\right]{\left(\frac{x_i}{\beta }\right)}^{\alpha }log\left(\frac{x_i}{\beta }\right).$$

For fixed $\beta$, the interval estimation of the model parameters requires the $2\times 2$ observed information matrix $J(\Theta )=\left\{J_{ij}\right\}$ for $i,j=\delta ,\alpha$. The multivariate normal $N_2(0,J{(\widehat{\Theta })}^{-1})$ distribution, under standard regularity conditions, can be used to provide approximate confidence intervals for the unknown parameters, where $J(\widehat{\Theta })$ is the total observed information matrix evaluated at $\widehat{\Theta }$. Then, approximate $100(1-\delta )\%$ confidence intervals for $\delta$ and $\alpha$ can be determined by:

$\widehat{\delta }\pm z_{\zeta /2}\sqrt{{\widehat{J}}_{\delta \delta }}$ and $\widehat{\alpha }\pm z_{\zeta /2}\sqrt{{\widehat{J}}_{\alpha \alpha }}$ , where $z_{\zeta /2}$ is the upper $\zeta$-th percentile of the standard normal model.

5.2. Ordinary and Weighted Least Squares

In this section, we use the least square (LS) and weighted least square (WLS) estimators (Swain et al. 1988) to estimate the parameters of the BXP distribution. Let $X_{\left(1\right)},\dots ,X_{\left(n\right)}$ be the order statistics of a random sample of size n from the BXP defined in (4), then the least square estimators (LSEs) of the unknown parameters $\delta$, $\alpha$ and $\beta$ of the BXP distribution can be obtained by minimizing:

$$\sum _{i=1}^n{\left[{\left(1-exp\left\{-{\left[{\left(\frac{x_{\left(i\right)}}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta }-\frac{i}{n+1}\right]}^2,$$

with respect to unknown parameters $\delta$, $\alpha$ and $\beta$.

The weighted least square estimators (WLSEs) of the unknown parameters $\delta$, $\alpha$ and $\beta$ follow by minimizing:

$$\sum _{i=1}^n\frac{{\left(n+1\right)}^2\left(n+2\right)}{n-i+1}{\left[{\left(1-exp\left\{-{\left[{\left(\frac{x_{\left(i\right)}}{\beta }\right)}^{\alpha }-1\right]}^2\right\}\right)}^{\delta }-\frac{i}{n+1}\right]}^2,$$

with respect to unknown parameters $\delta$, $\alpha$ and $\beta$.

6. Simulation Study

Here, we perform the simulation study for MLEs of the BXP distribution. We generate $N=1000$ samples of sizes $n=50$, 100, 200 from selected BXP distributions. The random numbers generation is simulated by:

$$x=\beta {\left(1+\sqrt{-log(1-u^{1/\delta })}\right)}^{1/\alpha },$$

where u is a uniform random number on [0,1]. We also calculate the empirical mean, standard deviations (sd), bias and mean square error (MSE) of the MLEs. The empirical bias and MSE are calculated by:

$$Bia{s}_{\widehat{h}}=\frac{1}{N}{\sum }_{i=1}^N\left(h-{\widehat{h}}_i\right)$$

and:

$$MS{E}_{\widehat{h}}=\frac{1}{N}{\sum }_{i=1}^N{\left(h-{\widehat{h}}_i\right)}^2$$

respectively, where $h=(\delta ,\alpha ,\beta )$. All results of MLEs were obtained using the optim-CG routine in the R programme. The empirical results of this simulation study are reported in

Table 2. The empirical means, sds (given in $\left(·\right)$), biases (given in $[·]$) and MSEs (given in $\{·\}$) for the special BXP distributions.

Parameters	$\mathit{n}=50$			$\mathit{n}=100$			$\mathit{n}=200$
$\mathit{\delta },\mathit{\alpha },\mathit{\beta }$	$\widehat{\mathit{\delta }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{\delta }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	$\widehat{\mathit{\delta }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$
3, 1.5, 2	3.0144	1.5495	2.0286	2.9995	1.5247	2.0159	3.0001	1.5125	2.0060
	(0.1831)	(0.1585)	(0.1155)	(0.0399)	(0.1059)	(0.0757)	(0.0400)	(0.0648)	(0.0485)
	[0.0144]	[0.0494]	[0.0286]	[−0.0005]	[0.0247]	[0.0160]	[0.0001]	[0.0125]	[0.0059]
	{0.0330}	{0.0270}	{0.0140}	{0.0016}	{0.0117}	{0.0060}	{0.0016}	{0.0043}	{0.0023}
3, 2, 1	3.0772	2.0550	1.0040	3.0019	2.0093	1.0021	3.0016	2.0073	1.0013
	(0.2928)	(0.2053)	(0.0443)	(0.0212)	(0.0976)	(0.0211)	(0.0203)	(0.0851)	(0.0182)
	[0.0772]	[0.0550]	[0.0040]	[0.0019]	[0.0093]	[0.0021]	[0.0016]	[0.0073]	[0.0013]
	{0.0900}	{0.0443}	{0.0020}	{0.0004}	{0.0095}	{0.0004}	{0.0004}	{0.0072}	{0.0003}
5, 0.5, 5	5.0863	0.5111	5.1216	5.0044	0.5012	5.0065	4.9954	0.4996	4.9970
	(0.2792)	(0.0290)	(0.3641)	(0.0404)	(0.0095)	(0.0490)	(0.0400)	(0.0084)	(0.0439)
	[0.0863]	[0.0111]	[0.1216]	[0.0044]	[0.0012]	[0.0065]	[−0.0046]	[−0.0004]	[−0.0030]
	{0.0838}	{0.0010}	{0.1447}	{0.0072}	{0.00008}	{0.0071}	{0.0054}	{0.00007}	{0.0070}
10, 30, 20	10.0407	30.0438	20.0024	10.0009	30.0013	19.9998	9.9984	29.9980	20.0001
	(0.2318)	(0.2809)	(0.0101)	(0.0110)	(0.0130)	(0.0086)	(0.0101)	(0.0120)	(0.0059)
	[0.0406]	[0.0438]	[0.0024]	[0.0009]	[0.0013]	[−0.0002]	[−0.0016]	[−0.0020]	[0.0001]
	{0.0543}	{0.0793}	{0.0001}	{0.0001}	{0.0001}	{0.00007}	{0.0001}	{0.0001}	{0.00004}
4, 0.5, 0.5	3.9077	0.5147	0.5265	4.0179	0.5121	0.5203	4.0012	0.5052	0.5079
	(0.1261)	(0.0532)	(0.0926)	(0.1010)	(0.0411)	(0.0711)	(0.0878)	(0.0246)	(0.0440)
	[−0.0923]	[0.0147]	[0.0265]	[0.0179]	[0.0121]	[0.0203]	[0.0012]	[0.0052]	[0.0079]
	{0.0356}	{0.0030}	{0.0100}	{0.0164}	{0.0018}	{0.0054}	{0.0076}	{0.0006}	{0.0019}

. Table 2 shows that when the sample size increases, the empirical means approach the true parameter value. For the same case, the standard deviations, biases and MSEs decrease in all the cases as expected. Therefore, the MLE method works very well to estimate the model parameters of the BXP distribution.

7. Real Data Modelling

In this section, we present two applications based on the real datasets to show the flexibility of the BXP distribution. The BXP model is compared with the WP, BP, KwP, PAT and P distributions. The cdfs of the above distributions are given (for $x>\beta$ and $a,\alpha ,\delta >0$) by:

$$F_{WP}\left(x\right)=1-exp\left\{-{\left[{\left(x/\beta \right)}^{\alpha }-1\right]}^{\delta }\right\},$$

$$F_{KwP}\left(x\right)=1-{\left\{1-{\left[1-{\left(x/\beta \right)}^{-\alpha }\right]}^a\right\}}^{\delta },$$

$$F_{EP}\left(x\right)={\left[1-{\left(x/\beta \right)}^{-\alpha }\right]}^{\delta },$$

$$F_{PAT}\left(x\right)=1-{tan}^{-1}\left[\alpha {\left(\beta /x\right)}^{\delta }\right]{\left[{tan}^{-1}\alpha \right]}^{-1}$$

and:

$$F_{BP}\left(x\right)=\frac{1}{\mathrm{B}\left(a,\delta \right)}{\int }_0^{1-{\left(\beta x^{-1}\right)}^{\alpha }}{w}^{a-1}{\left(1-w\right)}^{\delta -1}dw.$$

In order to see the best model, we obtain the Akaike Information Criteria (AIC), Corrected Akaike Information Criterion (CAIC), Bayesian Information Criterion (BIC), Hannan–Quinn Information Criterion (HQIC) and Kolmogorov–Smirnov (KS) goodness of-fit statistic to see the fitting of the models to dataset. In general, the best model can be chose as the one that has the smallest values of the AIC, CAIC, BIC, HQIC and KS statistics. All computations of the MLEs are performed by the maxLik routine in the R program.

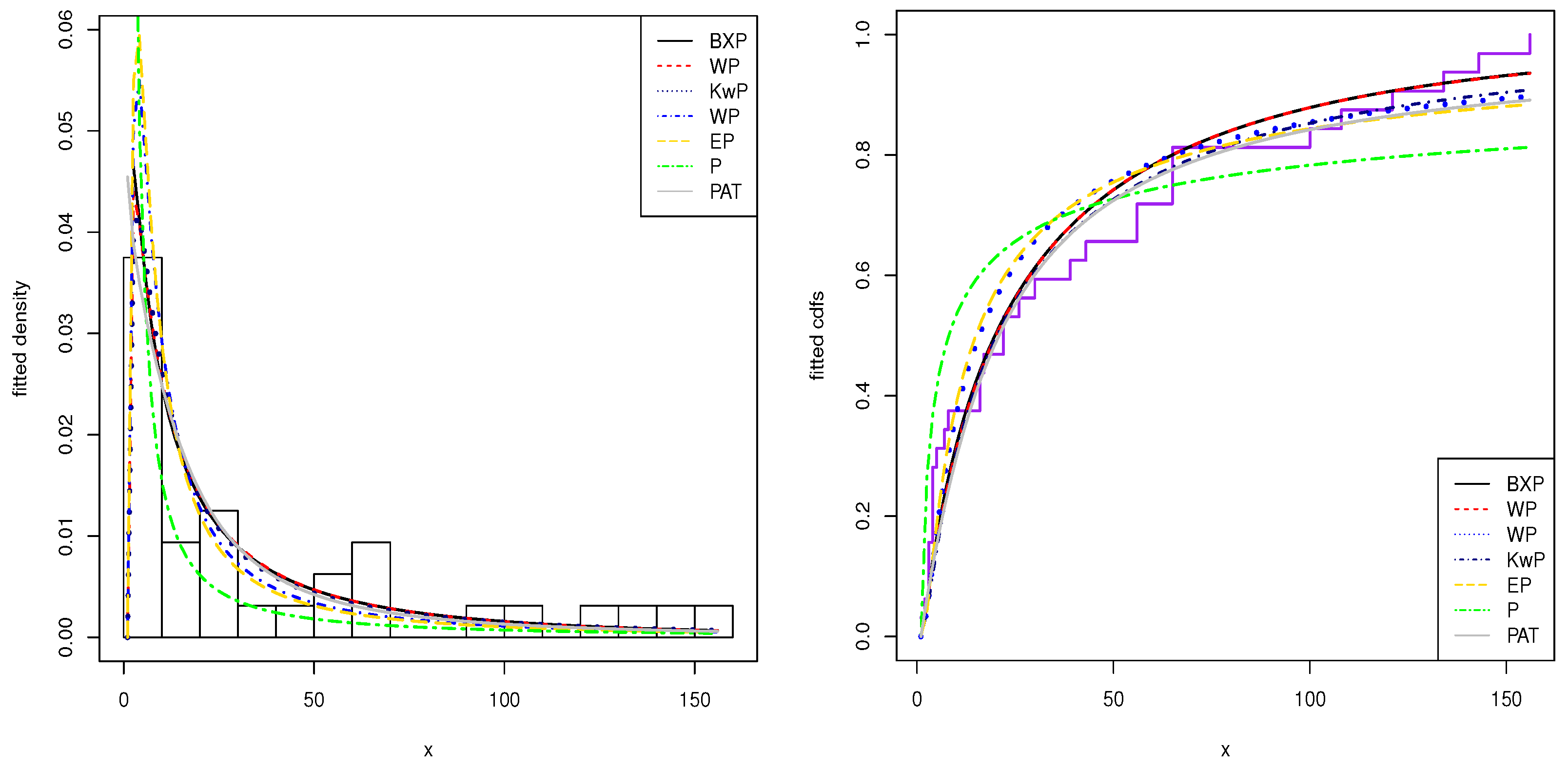
The first dataset gives the survival times, in weeks, of 33 patients suffering from acute myelogenous leukaemia. These data have been introduced by Feigl and Zelen (1965) and analysed by Mead et al. (2017). The data are: 65, 156, 100, 134, 16, 108, 121, 4, 39, 143, 56, 26, 22, 1, 1, 5, 65, 56, 65, 17, 7, 16, 22, 3, 4, 2, 3, 8, 4, 3, 30, 4, 43. This dataset is well known as being bathtub hrf-shaped.

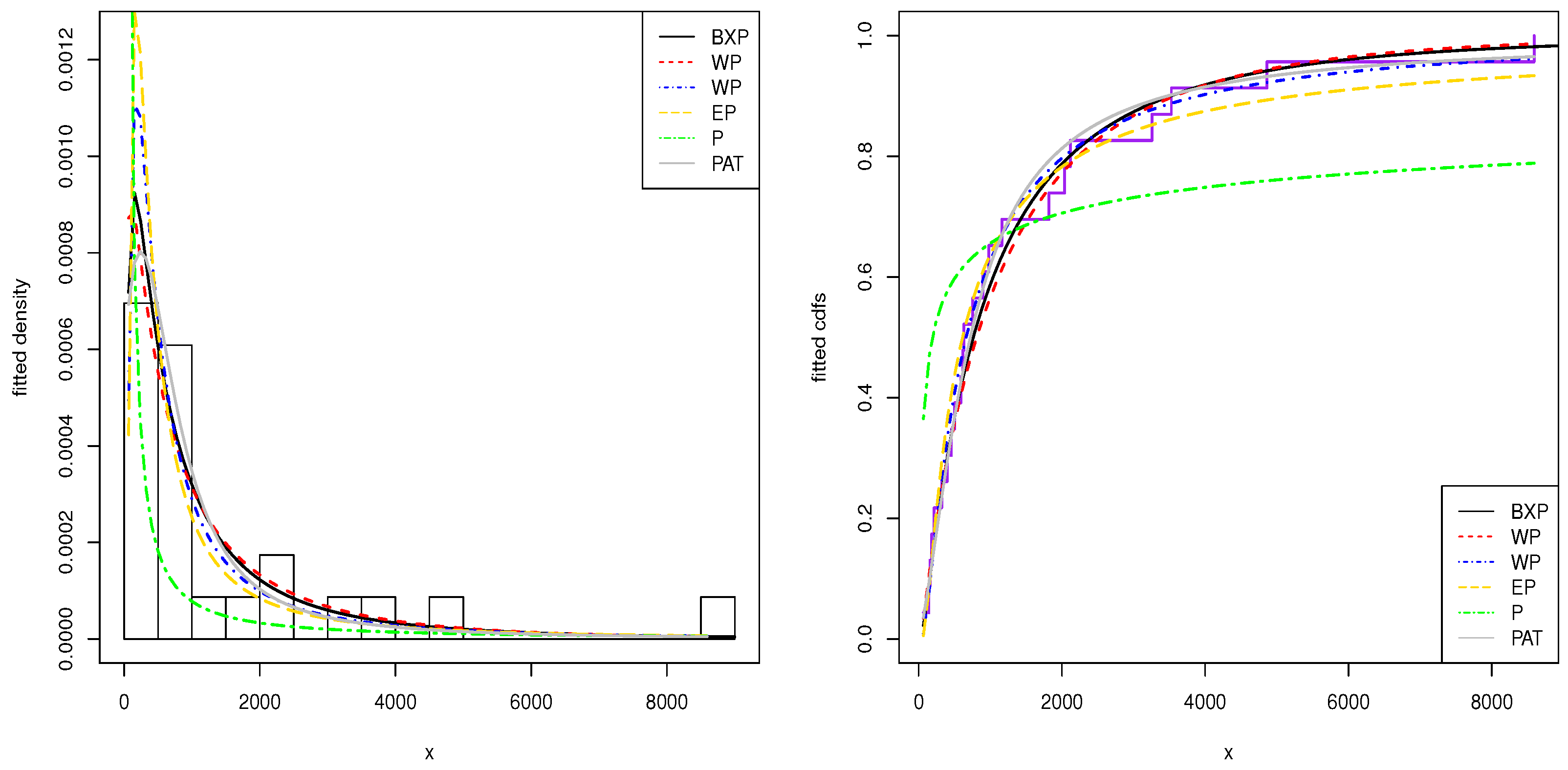
The second data-set shows the time intervals of the successive earthquakes in the last century in the North Anatolia fault zone between $39.{00}^{\circ }$ to $42.{00}^{\circ }$ north latitude and $39.{00}^{\circ }$ to $40.{00}^{\circ }$ east longitude. This dataset was introduced and analysed by Kuş (2007). This dataset is well known as being decreasing hrf-shaped.

For both datasets, the estimated parameters based on the MLE method are given in

Table 3. MLEs and their standard errors (in parentheses) for both datasets. P, Pareto; PAT, P ArcTan; KwP, Kumaraswamy P; WP, Weibull P; BP, Beta P; EP, Exponentiated P.

Leukaemia Data
Model	$\widehat{\mathit{\delta }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{a}}$	$\widehat{\mathit{\beta }}$
BXP	0.8505	0.1900		1
	(0.1785)	(0.0146)
PAT	0.8603	12.6124		1
	(0.1428)	(6.6619)
KwP	2.3992	0.0007	1,828,015	1
	(0.0291)	(0.0001)	(5.9317)
WP	1.8274	0.1994		1
	(0.2846)	(0.0145)
BP	51.9800	0.0239	3.8540	1
	(0.1240)	(0.0048)	(0.6551)
EP	4.3606	0.7089		1
	(1.3221)	(0.1192)
P		0.3319		1
		(0.0596)
Earthquake Data
BXP	1.9916	0.1678		9
	(0.5622)	(0.0117)
PAT	1.1704	168.1574		9
	(0.0667)	(5.9619)
WP	2.9843	0.1408		9
	(0.4949)	(0.0074)
BP	60.8341	0.0428	12.5592	9
	(1.0981)	(0.0053)	(0.9570)
EP	26.9837	0.8707		9
	(5.7196)	(0.0770)
P		0.2264		9
	(0.0472)

, whereas the values of the information criteria and goodness-of-fit statistics are given in

Table 4. Goodness-of-fit statistics for both datasets. CAIC, Corrected Akaike Information Criterion; HQIC, Hannan–Quinn Information Criterion.

Leukaemia Data
Model	AIC	CAIC	BIC	HQIC	KS
BXP	295.0115	295.4401	297.8795	295.9464	0.1328
PAT	301.1477	301.5763	304.0157	302.0826	0.1398
KwP	298.9148	299.8037	303.2167	300.3171	0.1486
WP	295.2830	295.7116	298.1510	296.2179	0.1418
BP	301.5970	302.4859	305.8990	302.9994	0.1494
EP	300.9643	301.3929	303.8323	301.8992	0.1630
P	319.1294	319.2673	320.5634	319.5968	0.2733
Earthquake Data
BXP	381.9004	382.5004	384.1714	382.4715	0.0817
PAT	383.7187	384.3187	385.9897	384.2899	0.0971
WP	382.3901	382.9901	384.6610	382.9612	0.0962
BP	384.5029	385.7661	387.9094	385.3597	0.0819
EP	384.3233	384.9233	386.5943	384.8944	0.1038
P	420.6338	420.8243	421.7693	420.9194	0.4218

. Since MLE of the $\beta$ equals the minimum order statistics, we suppose it as known to be the minimum value the dataset. Table 4 shows that the BXP distribution has the lowest values of these statistics among all the fitted models. Hence, it could be chosen as the best model under these criteria for both datasets.

The histogram of these datasets and the estimated pdfs and cdfs of the application models are displayed in Figure 2 and Figure 3. From the this figure, we show that the BXP model provides the best fit to these datasets as compared to other models.

8. Value-at-Risk Estimation with the BXP Distribution

In this section, the performance of BXP distribution in estimating Value-at-Risk (VaR) is discussed and compared with the Generalized P (GP) distribution. GP is a widely-used distribution in actuarial sciences, economics and statistics to model the tail of the distribution that contains extreme events. VaR is one of the most popular approaches to measure market risk. From a statistical point of view, the VaR entails the estimation of the quantile of the distribution of returns. The VaR for a long position (left tail of the distribution function) over a given time horizon tis defined as:

$$Va{R}_p=F^{-1}\left(p\right),$$

where F is the distribution function of financial losses, $F^{-1}$ denotes the inverse of F and p is the quantile at which VaR is calculated.

The Peaks-Over-Threshold (POT) method is used to model the tail of the distribution. POT is based on the distribution of exceedances over a given threshold. The conditional excess distribution, $F_u$, can be defined as follows:

$$F_u\left(y\right)=P(X-u\le y/X>u),0\le y\le x_F-u,$$

(13)

where random variable X represents the financial losses, u is the threshold, $y=X-u$ are the excesses and $x_F\le \infty$ is the right endpoint of F. $F_u\left(y\right)$ can be re-defined as follows:

$$\begin{array}{c}{F}_u\left(y\right)=\frac{Pr\{X-u\le y,X>u\}}{Pr(X>u)}=\frac{F(y+u)-F\left(u\right)}{1-F\left(u\right)}\hfill \\ =\frac{F\left(x\right)-F\left(u\right)}{1-F\left(u\right)}.\hfill \end{array}$$

(14)

The Balkema and De Haan (1974) and Pickands (1975) theorem shows that for a sufficiently high threshold u, the excess distribution function $F_u$ can be approximated by the GP distribution:

$$\begin{array}{c}{F}_u\left(y\right)\approx G_{\xi ,\sigma }\left(y\right),\mathrm{u}\to \infty \hfill \\ G_{\xi ,\sigma }\left(y\right)=\left\{\begin{array}{c}1-{(1+\xi \frac{y}{\sigma })}^{-1/\xi },\xi \ne 0\hfill \\ 1-e^{-y/\sigma },\xi =0\hfill \end{array}\right.\hfill \end{array},$$

(15)

where $y\ge 0$ for $\xi \ge 0$ and $0\le y\le \frac{\sigma }{\xi }$ for $\xi <0$ and $\xi$ and $\sigma$ are shape and scale parameters of the GP distribution, respectively. Isolating $F\left(x\right)$ from (14), we get:

$$F\left(x\right)=(1-F\left(u\right))F_u\left(y\right)+F\left(u\right),$$

(16)

where $F_u\left(y\right)$ is the GP distribution and $F\left(u\right)=(n-N_u)/\phantom{(n-N_u)n}n$. Then, substituting (14) in (16), the following estimate for $F\left(x\right)$ is obtained:

$$\widehat{F}\left(x\right)=1-\frac{N_u}{n}{(1+\frac{\widehat{\xi }}{\widehat{\sigma }}(x-\widehat{u}))}^{-1/\widehat{\xi }},$$

(17)

where $\widehat{\xi }$ and $\widehat{\sigma }$ are maximum likelihood estimates of $\xi$ and $\sigma$, respectively. Inverting (17) for a given probability p, $Va{R}_p$ can be obtained as:

$$Va{R}_p=\widehat{u}+\frac{\widehat{\sigma }}{\widehat{\xi }}\left[{\left(\frac{n}{N_u}\left(1-p\right)\right)}^{-\widehat{\xi }}-1\right].$$

(18)

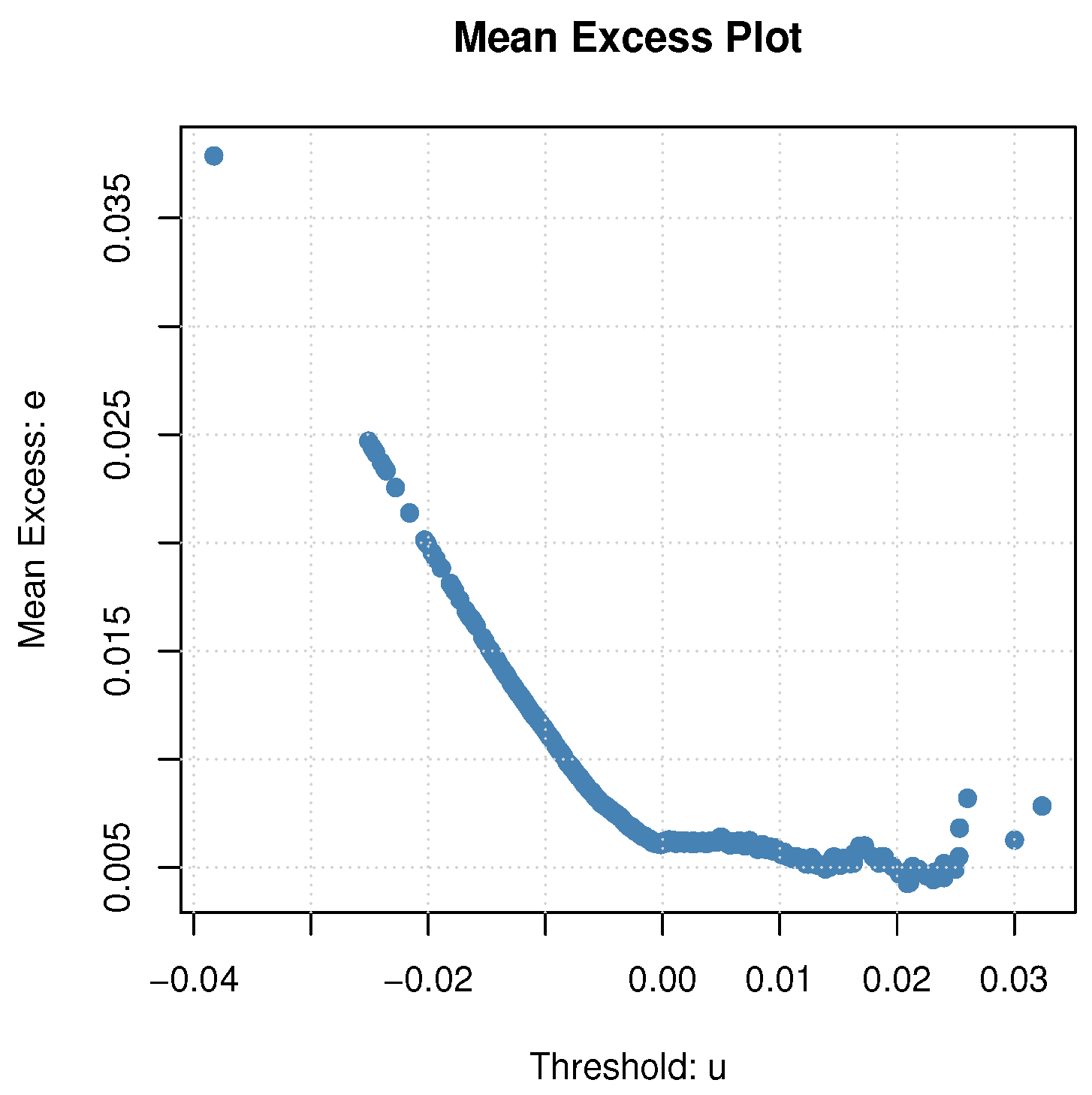
Threshold selection is a difficult task and an essential part for tail modelling with the GP distribution. The most used method is the Mean Excess (ME) plot for the determination of the threshold. The ME function can be defined as follows:

$$e_n\left(u\right)=\frac{{\displaystyle \sum _{i=1}^n}(X_i-u)}{{\displaystyle \sum _{i=1}^n}{I}_{\left\{X_i>u\right\}}},$$

(19)

where I is the indicator function. When the empirical ME function is a positively sloped straight line above a certain threshold u, it is evidence that the used dataset follows the GP distribution with a positive $\xi$ parameter.

Here, the BXP distribution is adopted in the POT method. It is assumed that BXP provides a good approximation to $F_u\left(y\right)$ for a sufficiently high threshold u. Then, substituting the cdf of BXP in (16), the new estimate for $F\left(x\right)$ can be obtained as:

$$\widehat{F}\left(x\right)=\left(1-\frac{n-N_u}{n}\right){\left(1-exp\left(-{\left[{\left(\frac{x}{\widehat{\beta }}\right)}^{\widehat{\alpha }}-1\right]}^2\right)\right)}^{\widehat{\delta }}+\frac{n-N_u}{n}.$$

(20)

The $Va{R}_p$ can be obtained by inverting (20) for a given probability p, as follows:

$$Va{R}_p=\widehat{u}+\widehat{\beta }{\left\{1+{\left[-log\left(1-{\left(\frac{n\left(p-1\right)}{N_u}\right)}^{\frac{1}{\widehat{\delta }}}\right)\right]}^{\frac{1}{2}}\right\}}^{\frac{1}{\widehat{\alpha }}},$$

(21)

where $\widehat{\beta },\widehat{\delta }$ and $\widehat{\alpha }$ are the maximum likelihood estimates of $\beta ,\delta$ and $\alpha$, respectively.

8.1. S&P-500

To evaluate and compare the performance of the BXP with GP distribution in terms of VaR accuracy, the S&P-500 index is used. The used time series data contain 1465 daily log returns from 4 January 2012 to 27 October 2017. The descriptive statistics of S&P-500 are given in Table 4.

Table 5. Summary statistics for the S&P-500 index.

Descriptive Statistics	S&P-500
Number of observations	1465
Minimum	−0.0402
Maximum	0.0383
Mean	0.0004
Median	0.0004
Std.Deviation	0.007
Skewness	−0.322
Kurtosis	5.403
Jarque–Bera	377.839 (<0.001)
Ljung–Box	28.516 (0.098)

shows that the mean returns are closed to zero. The Jarque–Bera statistics in Table 5 also show that the null hypothesis of normality is rejected at any level of significance, as evidenced by the high excess kurtosis and negative skewness. Thus, it is clear that log returns of S&P-500 indexes have non-normal characteristics, excess kurtosis and fat tails. The result of the Ljung–Box test indicates that the raw returns are free from autocorrelation. Therefore, BXP and GP distributions could be applied to the independent and identically distributed observations.

The ME plot is used to determine the optimal threshold value for the POT method. Figure 4 displays the ME plot of the S&P-500 dataset. The optimal threshold could be chosen as 0.02 for the used dataset. It is near the 90% quantile value of the S&P-500.

Table 6. MLEs, corresponding standard errors (in second line) and goodness-of-fit statistics for the S&P-500.

Models	Parameters					Goodness-of-Fit
	$\mathit{\xi }$	$\mathit{\delta }$	$\mathit{\sigma }$	$\mathit{\alpha }$	$\mathit{\beta }$	$-\mathit{\ell }$	KS	${\mathit{A}}^{*}$	${\mathit{W}}^{*}$
BXP		3.2480		0.1893	4.89818 × 10${}^{-5}$	−93.4016	0.1427	0.3809	0.0556
		1.0266		0.0120	-
GP	0.0847		0.0057			−88.7171	0.1498	0.4039	0.0661
	0.1996		0.0015

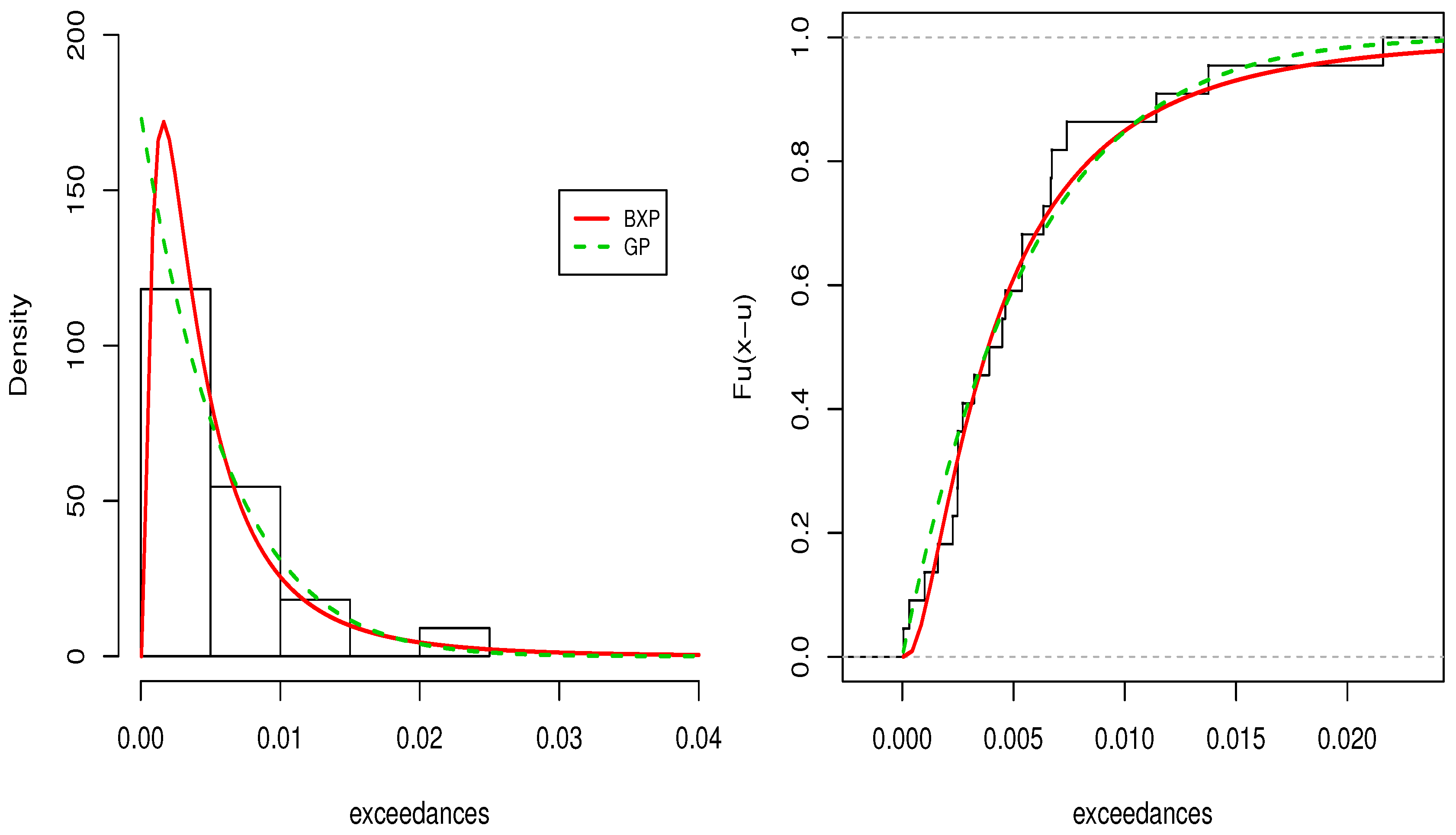
shows the estimated parameters of BXP distribution and GP distribution using the POT method for the S&P-500 dataset. Based on the figures in Table 6, we conclude that since the BXP distribution has the lowest values of these statistics, BXP provides better fits than the GP distribution for tail modelling of S&P-500 indexes. Figure 5 displays the fitted pdf and cdfs of the BXP and GP distributions. Figure 5 reveals that the BXP distribution provides superior fits to the used dataset.

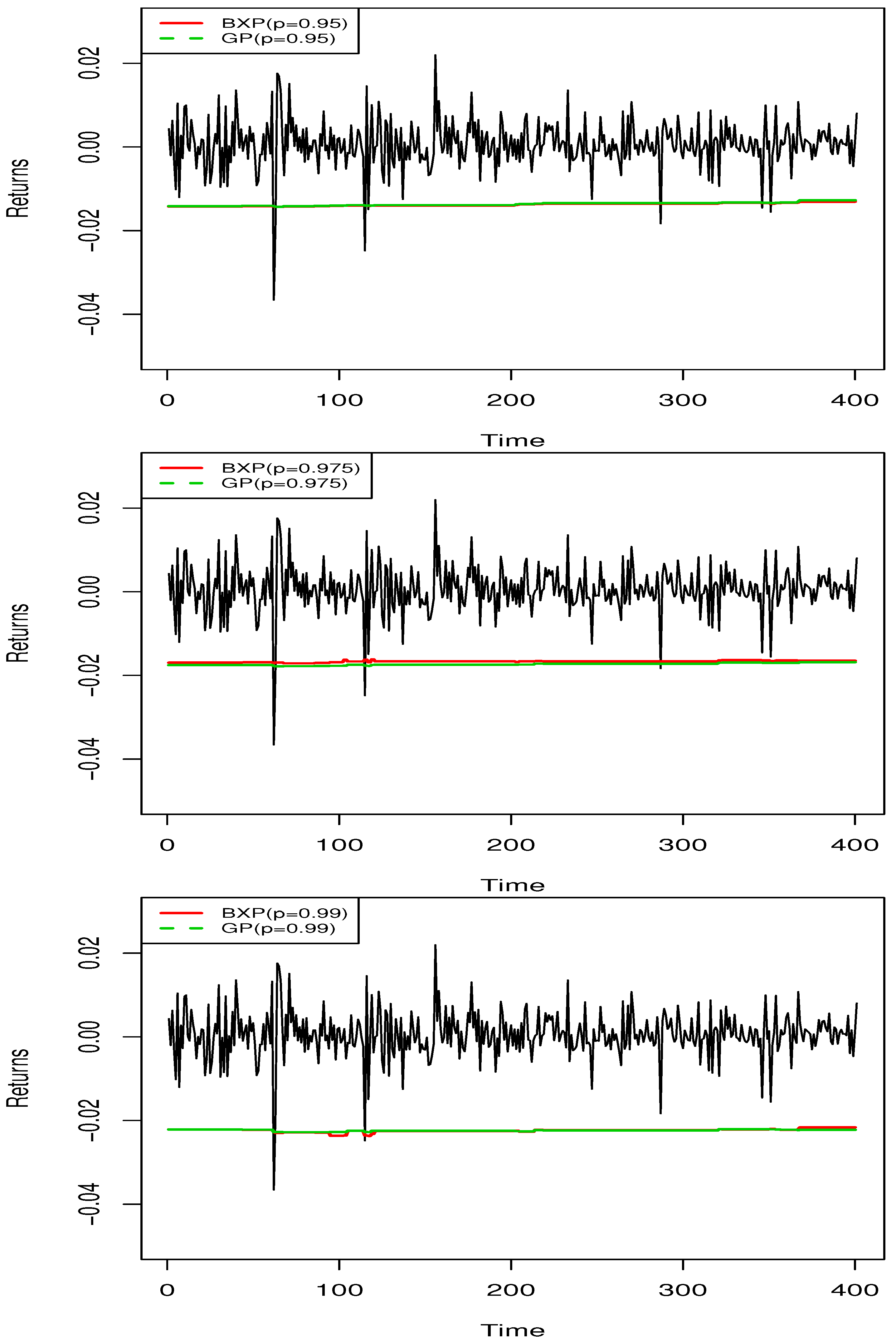
Here, VaR is estimated with the GP and BXP distribution using the POT method for values of $p=0.95,0.975$ and $0.99$. The rolling window estimation method is used to evaluate the out-of-sample performance of the GP and BXP models. The first 1064 daily returns are used as the window length, and the next 400 data points are considered as out-of-sample period. Figure 6 displays daily VaR estimates of the BXP and GP models. Based on Figure 6, it is clear that the BXP and GP models produce similar VaR estimates. Therefore, the BXP model could be considered as an alternative VaR model against to GP model for financial institutions.

In VaR estimation, using the POT method is applied to raw return data assuming the distribution to be stationary or unconditional without considering the time-varying volatility. The POT method can also be considered as a dynamic model, where the conditional distribution of F is taken into account and the volatility of returns is captured. The dynamic POT method based on the BXP distribution, combined with the generalized autoregressive conditional heteroscedasticity type process, introduced by Bollerslev (1986), could be considered as future work of this study.

9. Conclusions

In this study, we proposed a new distribution that was referred to as the Burr X Pareto (BXP) using the Burr X generator. Some mathematical properties were obtained. The estimation of the model parameters is performed by the MLE, LS and WLS methods. We compare the distribution with a few other models using two real datasets. It is expected that the BXP distribution will serve as a better alternative in modelling real-life datasets. Value-at-Risk estimation with the BXP distribution is presented using time series data, we showed that the new model could be considered as an alternative VaR model against the generalized Pareto model for financial institutions.