Battery State-Of-Charge Estimation Based on a Dual Unscented Kalman Filter and Fractional Variable-Order Model
Abstract
:1. Introduction
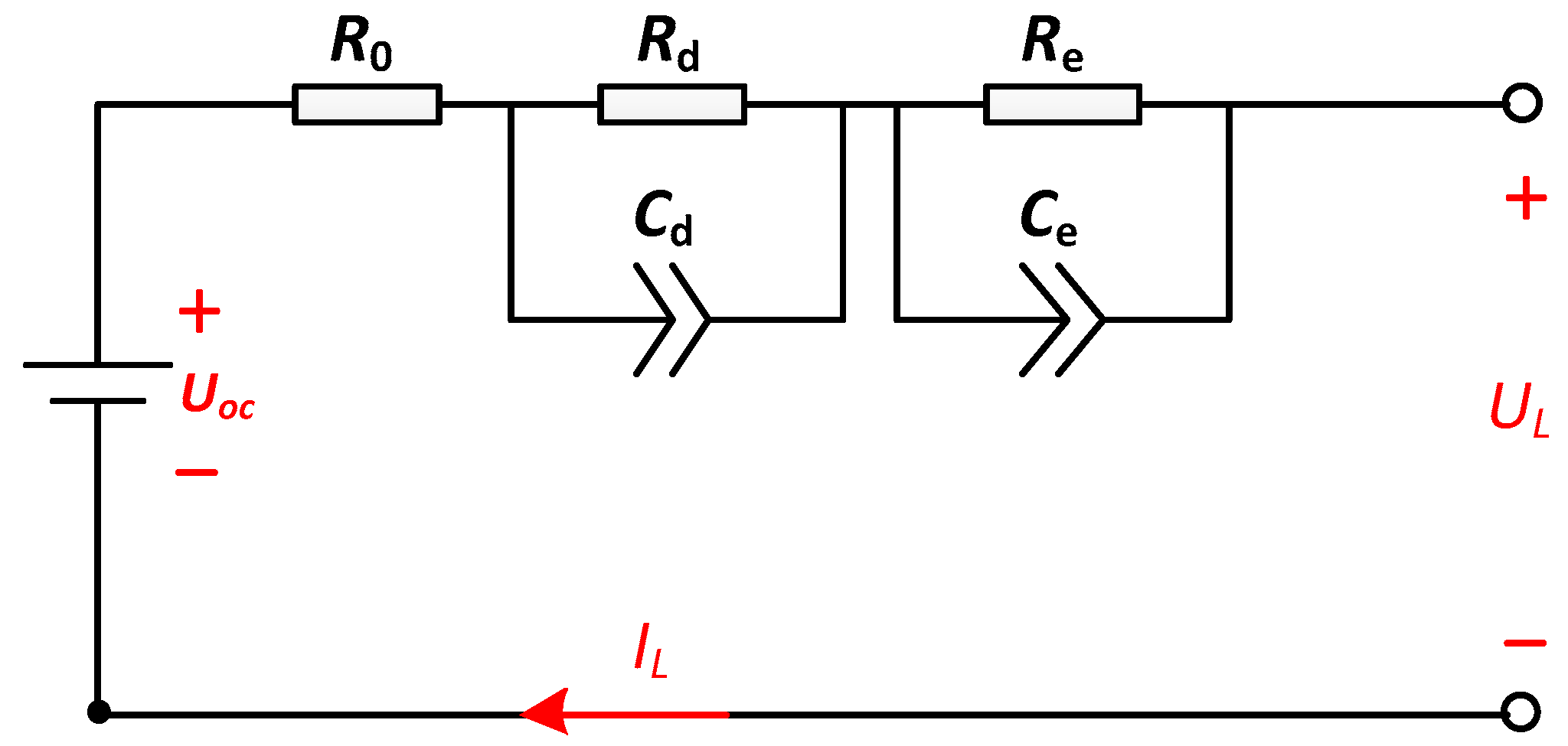
2. Fractional Order Calculus and Fractional Battery Model
3. State Estimation Using an Unscented Fractional Kalman Filter
- (a)
- Sigma points generation
- (b)
- State estimation time update
- (c)
- State error covariance time update
- (d)
- Output update
- (e)
- State estimate measurement update
- (f)
- State error covariance measurement update
4. Fractional Order Estimation Using a Dual Filter
- (a)
- Sigma points generationwhere denotes the covariance of the order noise.
- (b)
- Order estimation time and measurement updatewhere denotes the covariance of the measurement noise caused by the uncertain order variation.
- (c)
- Order error covariance measurement updatewhere is the forgetting factor.
5. Experiments and Validations
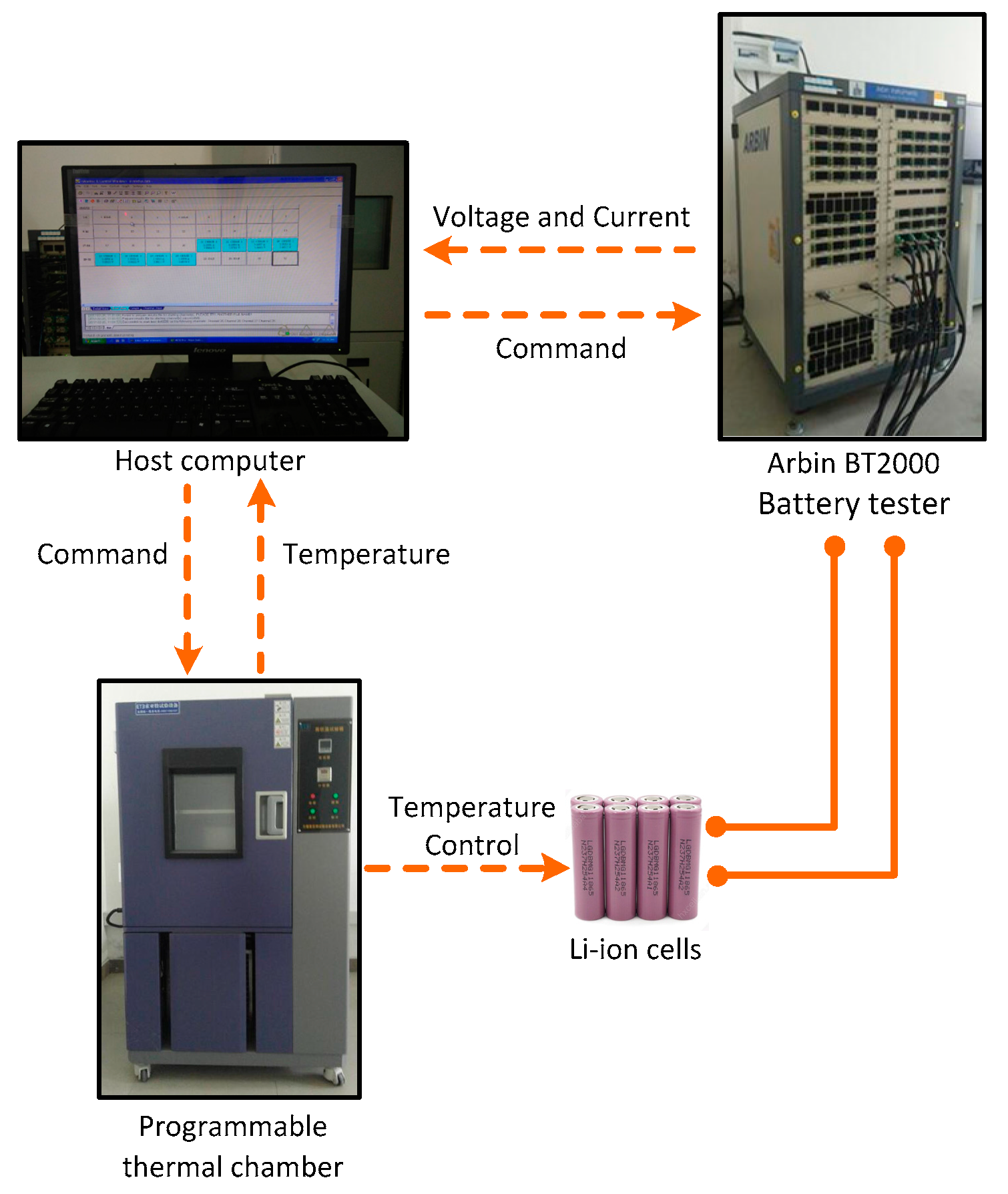
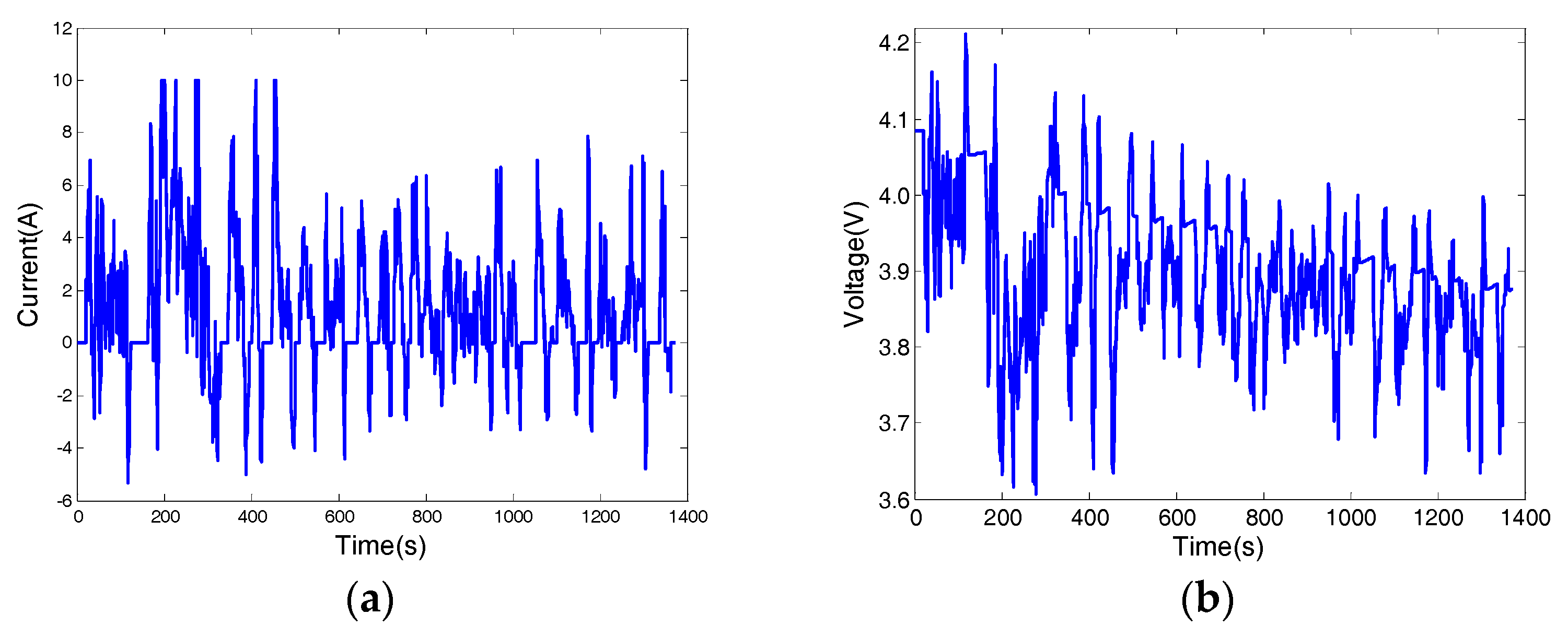
5.1. Experimental Setup
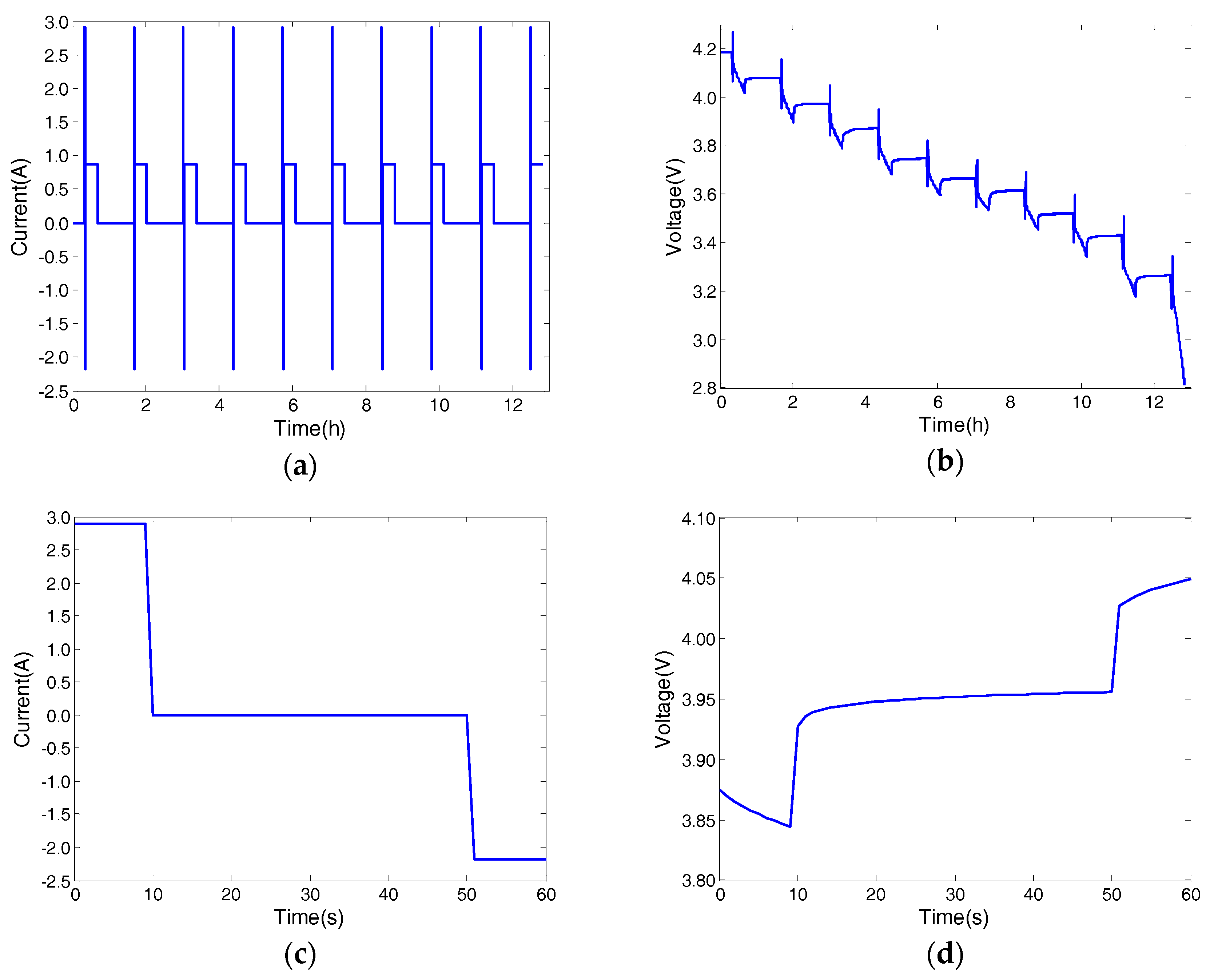
5.2. Static Capacity and HPPC Test
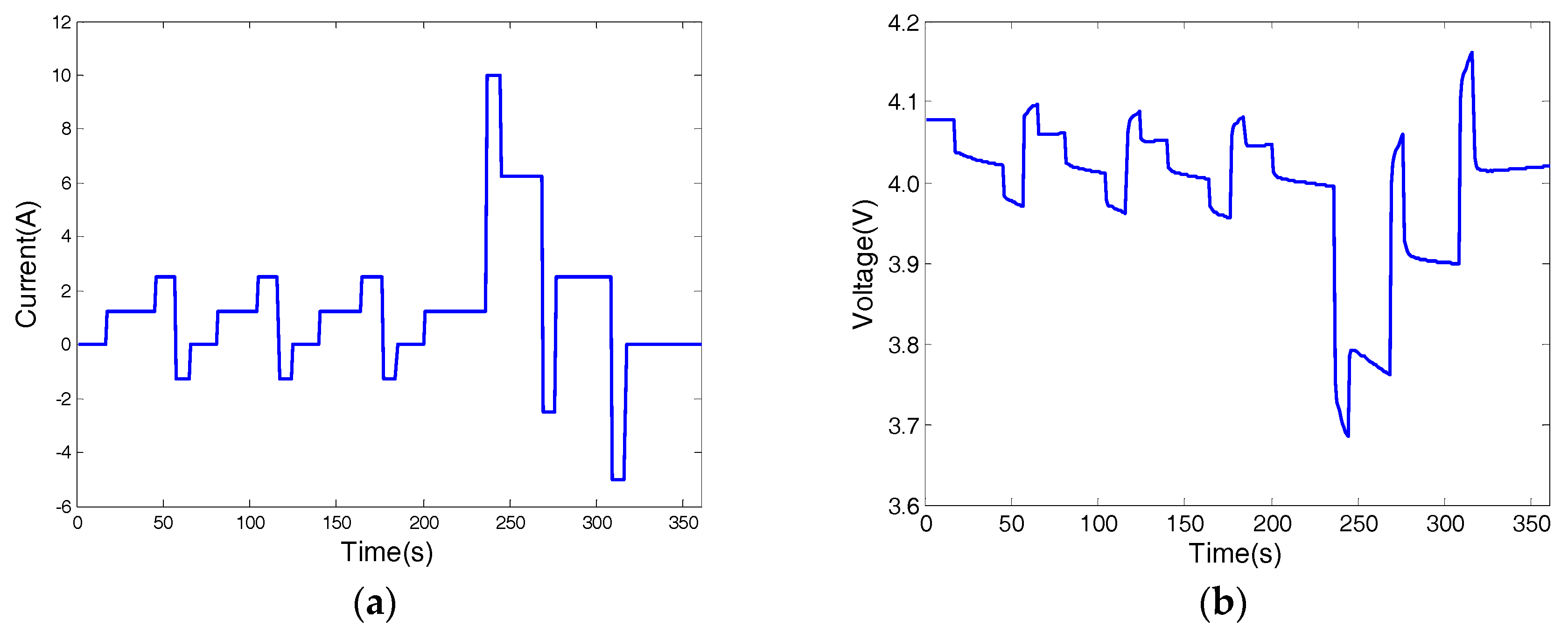
5.3. The Dynamic Stress Test
5.4. The Federal Urban Dynamic Schedule Test
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Kalawoun, J.; Biletska, K.; Suard, F.; Montaru, M. From a novel classification of the battery state of charge estimators toward a conception of an ideal one. J. Power Sources 2015, 279, 694–706. [Google Scholar] [CrossRef]
- Cuma, M.U.; Koroglu, T. A comprehensive review on estimation strategies used in hybrid and battery electric vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Li, J.; Klee Barillas, J.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for lifepo4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisner, D.E. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Design and implementation of a fuzzy logic-based state-of-charge meter for li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836. [Google Scholar] [CrossRef]
- Grewal, S.; Grant, D. A novel technique for modelling the state of charge of lithium ion batteries using artificial neural networks. In Proceedings of the Twenty-Third International Telecommunications Energy Conference, Edinburgh, UK, 14–18 October 2001. [Google Scholar]
- Shen, Y. Adaptive online state-of-charge determination based on neuro-controller and neural network. Energy Convers. Manag. 2010, 51, 1093–1098. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilán, J.A.V. Support vector machines used to estimate the battery state of charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Álvarez Antón, J.C.; García Nieto, P.J.; de Cos Juez, F.J.; Sánchez Lasheras, F.; González Vega, M.; Roqueñí Gutiérrez, M.N. Battery state-of-charge estimator using the svm technique. Appl. Math. Model. 2013, 37, 6244–6253. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Smith, K.A.; Rahn, C.D.; Wang, C.-Y. Model-based electrochemical estimation and constraint management for pulse operation of lithium ion batteries. IEEE Trans. Control Syst. Technol. 2010, 18, 654–663. [Google Scholar] [CrossRef]
- Ashwin, T.R.; McGordon, A.; Widanage, W.D.; Jennings, P.A. Modified electrochemical parameter estimation of ncr18650bd battery using implicit finite volume method. J. Power Sources 2017, 341, 387–395. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar]
- Plett, G.L. Extended kalman filtering for battery management systems of lipb-based hev battery packs. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Sierociuk, D.; Dzielinski, A.; Sarwas, G.; Petras, I.; Podlubny, I.; Skovranek, T. Modelling heat transfer in heterogeneous media using fractional calculus. Philos. Trans. R. Soc. A 2013, 371, 20120146. [Google Scholar] [CrossRef] [PubMed]
- Freeborn, T.J. A survey of fractional-order circuit models for biology and biomedicine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Wu, H.; Yuan, S.; Yin, C. A lithium-ion battery fractional order state space model and its time domain system identification. In Proceedings of the FISITA 2012 World Automotive Congress; Springer: Berlin, Germany, 2013; pp. 795–805. [Google Scholar]
- Wang, B.; Li, S.E.; Peng, H.; Liu, Z. Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 2015, 293, 151–161. [Google Scholar] [CrossRef]
- Zou, Y.; Li, S.E.; Shao, B.; Wang, B. State-space model with non-integer order derivatives for lithium-ion battery. Appl. Energy 2016, 161, 330–336. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, S.E.; Moura, S.J.; Peng, H. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional model. IEEE Trans. Control Syst. Technol. 2017, 25, 3–11. [Google Scholar] [CrossRef]
- Zhong, F.; Li, H.; Zhong, S.; Zhong, Q.; Yin, C. An soc estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 127–144. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Xiao, R.; Shen, J.; Li, X.; Yan, W.; Pan, E.; Chen, Z. Comparisons of modeling and state of charge estimation for lithium-ion battery based on fractional order and integral order methods. Energies 2016, 9, 184. [Google Scholar] [CrossRef]
- Yu, W.; Luo, Y.; Pi, Y. Fractional order modeling and control for permanent magnet synchronous motor velocity servo system. Mechatronics 2013, 23, 813–820. [Google Scholar] [CrossRef]
- Hajiloo, A.; Nariman-zadeh, N.; Moeini, A. Pareto optimal robust design of fractional-order pid controllers for systems with probabilistic uncertainties. Mechatronics 2012, 22, 788–801. [Google Scholar] [CrossRef]
- Gabano, J.-D.; Poinot, T. Fractional identification algorithms applied to thermal parameter estimation. IFAC Proc. Vol. 2009, 42, 1316–1321. [Google Scholar] [CrossRef]
- Narang, A.; Chen, T.; Shah, S.L. Continuous-time model identification of fractional-order models with time delays. IET Control Theory Appl. 2011, 5, 900–912. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998; Volume 198. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: London, UK, 2010. [Google Scholar]
- Sierociuk, D.; Macias, M.; Malesza, W.; Sarwas, G. Dual estimation of fractional variable order based on the unscented fractional order kalman filter for direct and networked measurements. Circuits Syst. Signal Process. 2016, 35, 2055–2082. [Google Scholar] [CrossRef]
- Hasan, R.; Scott, J.B. Fractional behaviour of rechargeable batteries. In Proceedings of the 2016 Electronics New Zealand Conference (ENZCon 2016), Wellington, New Zealand, 17–18 November 2016; Electronics New Zealand Inc.: Hamilton, New Zealand, 2016; pp. 111–114. [Google Scholar]
- Sadli, I.; Urbain, M.; Hinaje, M.; Martin, J.-P.; Raël, S.; Davat, B. Contributions of fractional differentiation to the modelling of electric double layer capacitance. Energy Convers. Manag. 2010, 51, 2993–2999. [Google Scholar] [CrossRef]
- Samadani, E.; Farhad, S.; Scott, W.; Mastali, M.; Gimenez, L.E.; Fowler, M.; Fraser, R.A. Empirical modeling of lithium-ion batteries based on electrochemical impedance spectroscopy tests. Electrochim. Acta 2015, 160, 169–177. [Google Scholar] [CrossRef]
- Swamy, T.; Chiang, Y.-M. Electrochemical charge transfer reaction kinetics at the silicon-liquid electrolyte interface. J. Electrochem. Soc. 2015, 162, A7129–A7134. [Google Scholar] [CrossRef]
- Caballero-Aguila, R.; Hermoso-Carazo, A.; Linares-Pérez, J. Extended and unscented filtering algorithms in nonlinear fractional order systems with uncertain observations. Appl. Math. Sci. 2012, 6, 1471–1486. [Google Scholar]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of lifepo4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Sun, F.; Dorrell, D. Online parameter identification of ultracapacitor models using the extended kalman filter. Energies 2014, 7, 3204–3217. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, K.; Ravey, A.; Gao, F.; Miraoui, A. Parameter sensitivity analysis for fractional-order modeling of lithium-ion batteries. Energies 2016, 9, 123. [Google Scholar] [CrossRef]
- Belt, J.R. Battery Test Manual for Plug-In Hybrid Electric Vehicles; Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2010.
- USCAR. Manuals: Electric Vehicle Battery Test Procedures Manual. Available online: http://www.uscar.org/guest/publications (accessed on 30 August 2017).
- Robertson, D.C.; Christophersen, J.P.; Bennett, T.; Walker, L.K.; Wang, F.; Liu, S.; Fan, B.; Bloom, I. A comparison of battery testing protocols: Those used by the us advanced battery consortium and those used in china. J. Power Sources 2016, 306, 268–273. [Google Scholar] [CrossRef]
- EPA Urban Dynamometer Driving Schedule (UDDS). Available online: https://www.epa.gov/emission-standards-reference-guide/epa-urban-dynamometer-driving-schedule-udds (accessed on 30 August 2017).
- Xiong, R.; Sun, F.; Gong, X.; He, H. Adaptive state of charge estimator for lithium-ion cells series battery pack in electric vehicles. J. Power Sources 2013, 242, 699–713. [Google Scholar] [CrossRef]

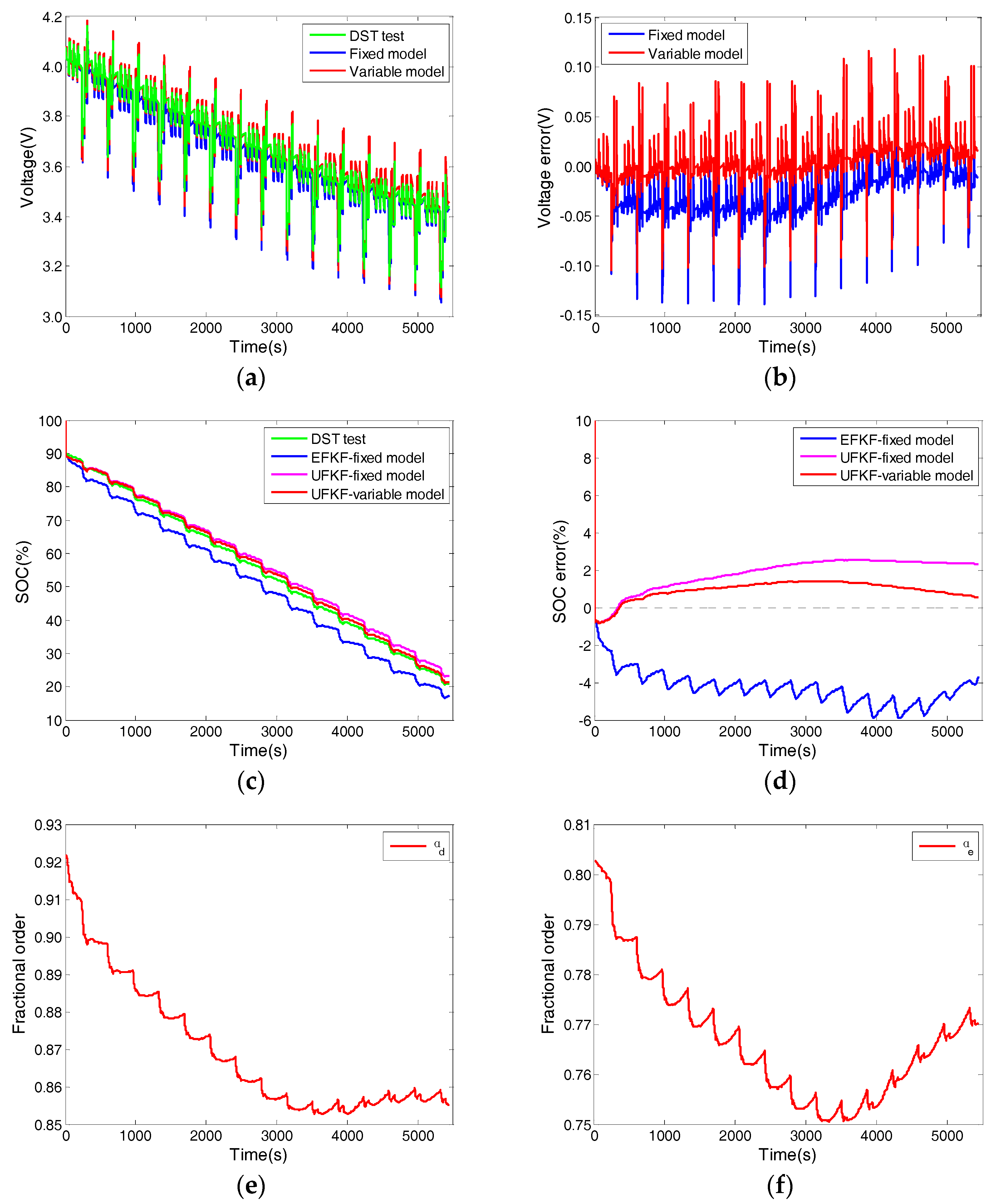
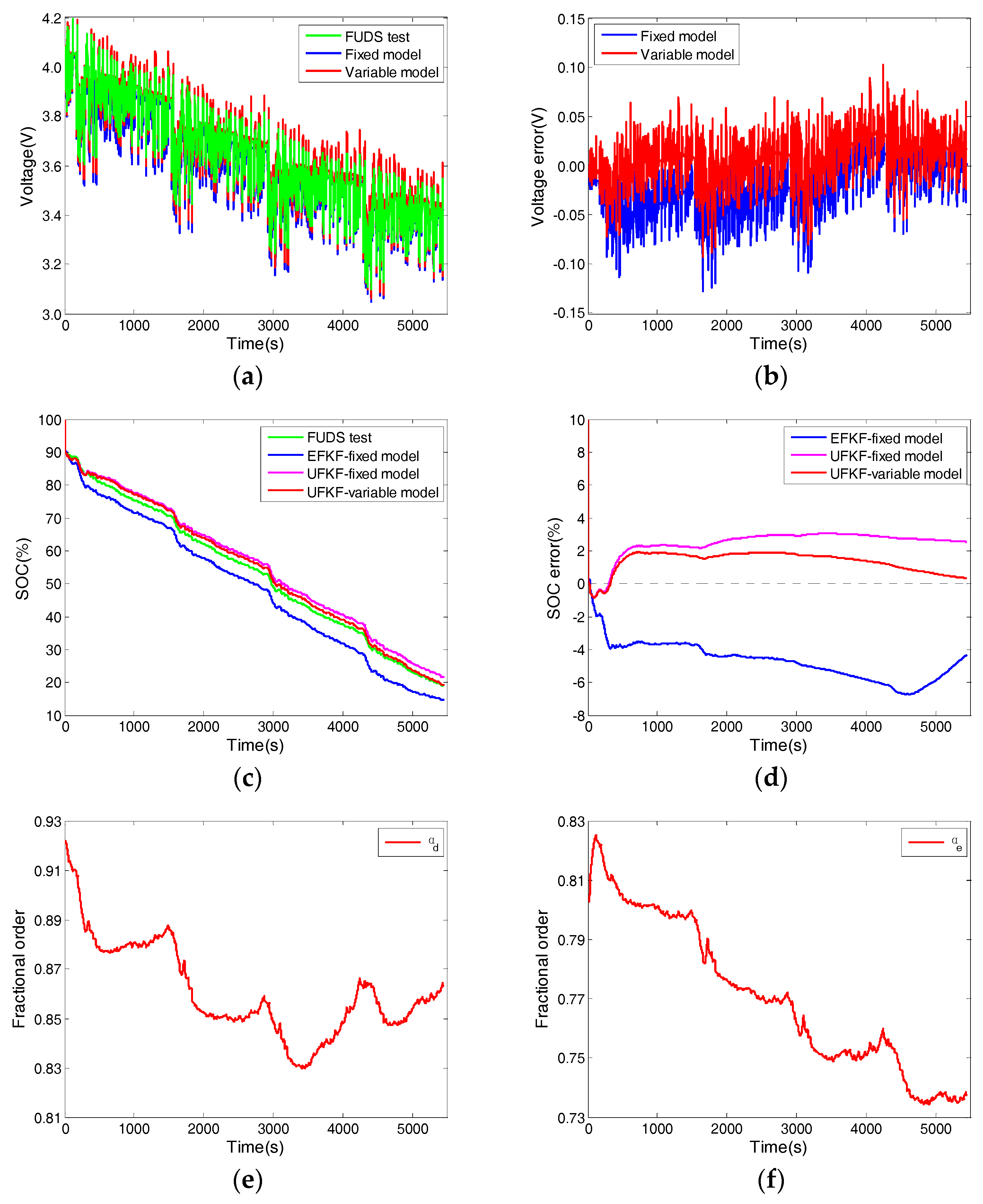
| Parameter | Value |
|---|---|
| 0.0384 | |
| 0.0531 | |
| 0.0474 | |
| 2958.6246 | |
| 29,992.5891 | |
| 0.9219 | |
| 0.8028 |
| Test Profile | Fixed-Order Model | Variable-Order Model |
|---|---|---|
| DST | 35.970 | 19.658 |
| FUDS | 38.024 | 21.734 |
| Test Profile | EFKF with Fixed-Order Model | UFKF with Fixed-Order Model | UFKF with Variable-Order Model |
|---|---|---|---|
| DST | 4.379 | 2.018 | 1.071 |
| FUDS | 4.827 | 2.590 | 1.503 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Chen, W.; Tan, X. Battery State-Of-Charge Estimation Based on a Dual Unscented Kalman Filter and Fractional Variable-Order Model. Energies 2017, 10, 1577. https://doi.org/10.3390/en10101577
Cai M, Chen W, Tan X. Battery State-Of-Charge Estimation Based on a Dual Unscented Kalman Filter and Fractional Variable-Order Model. Energies. 2017; 10(10):1577. https://doi.org/10.3390/en10101577
Chicago/Turabian StyleCai, Ming, Weijie Chen, and Xiaojun Tan. 2017. "Battery State-Of-Charge Estimation Based on a Dual Unscented Kalman Filter and Fractional Variable-Order Model" Energies 10, no. 10: 1577. https://doi.org/10.3390/en10101577




