Sensitivity Analysis to Control the Far-Wake Unsteadiness Behind Turbines
Abstract
:1. Introduction
2. Methodology
2.1. Turbine Modelling
2.2. Discrete Linear Instability Analysis
2.3. Discrete Adjoints
2.4. Discrete Sensitivities
2.5. Numerical Flow Solutions Using a High Order Method
2.6. Summary of the Methodology for Stability and Sensitivity Analysis
- Compute a steady base flow using a numerical solver. High order h/p methods are preferred to obtain find solutions with low numerical errors. We time march the compressible Navier–Stokes Equations (1), until the residual falls below . If we do not obtain convergence, the case is considered unstable and we do not perform the stability analysis.
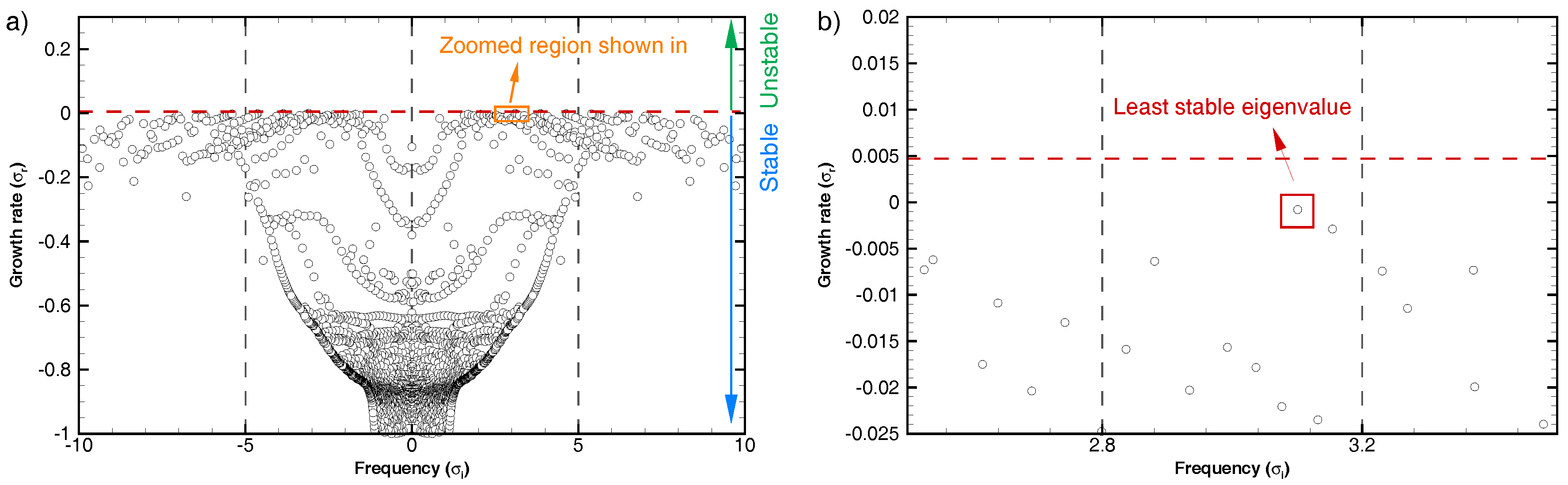
- Having computed all direct eigenvalues/eigenvectors, we select the least stable and compute its adjoint, see Section 2.3.
- With the direct and adjoint modes, it is possible to compute the Hessian matrix associated to the sensitivities detailed in Section 2.4. Subsequently, the sensitivities to base flow modifications and to localised forcing can be calculated using Equations (5).
3. Results
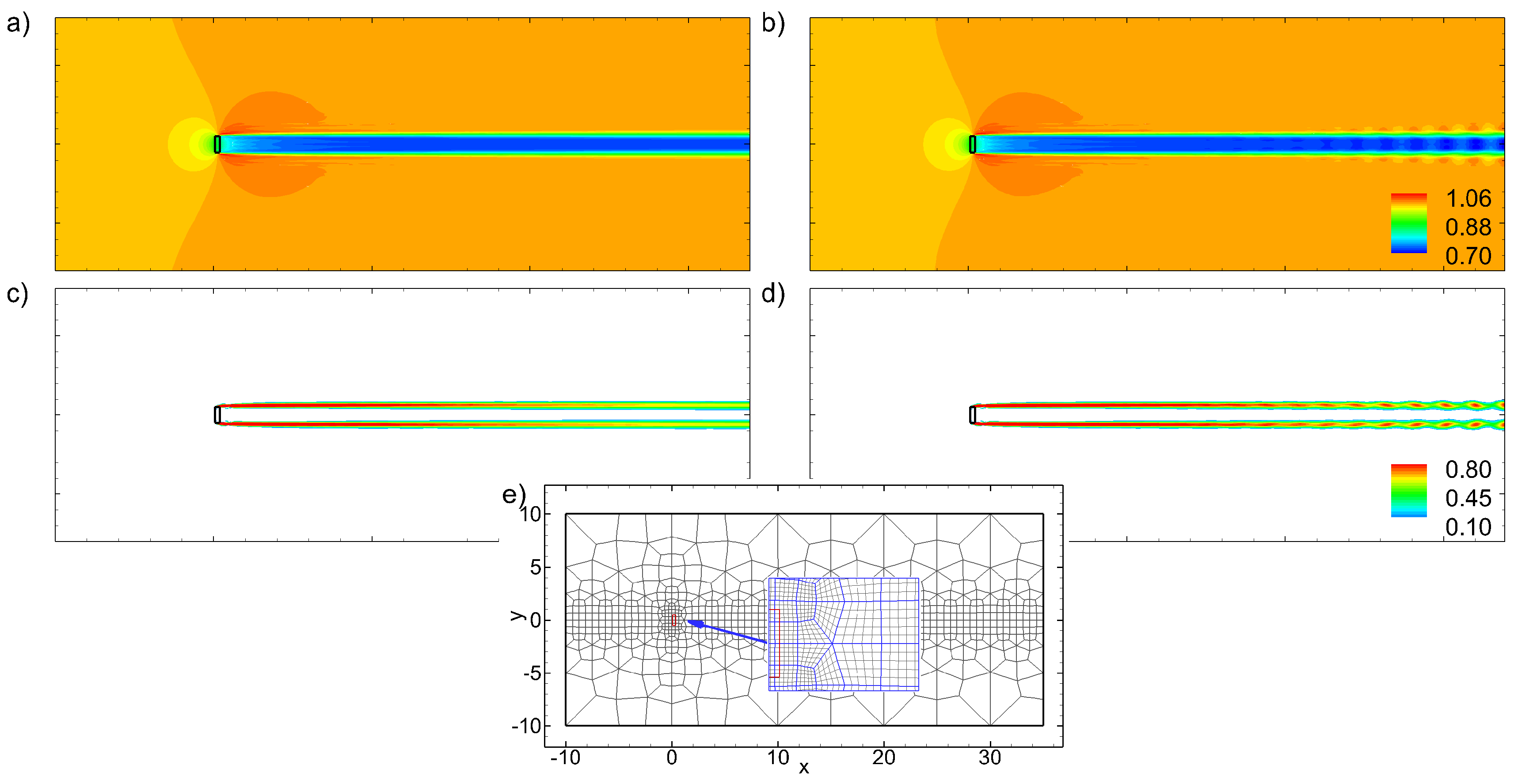
3.1. Preliminaries
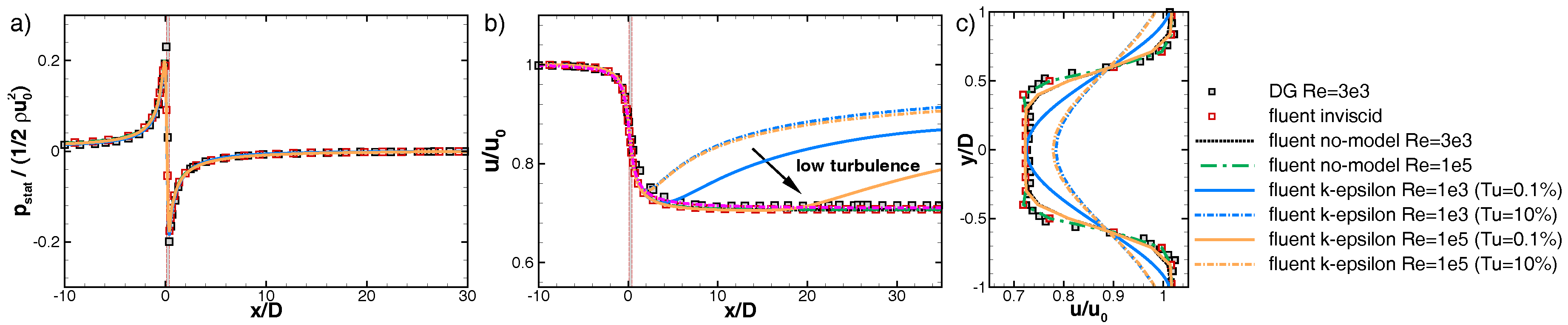
3.2. Mesh Convergence
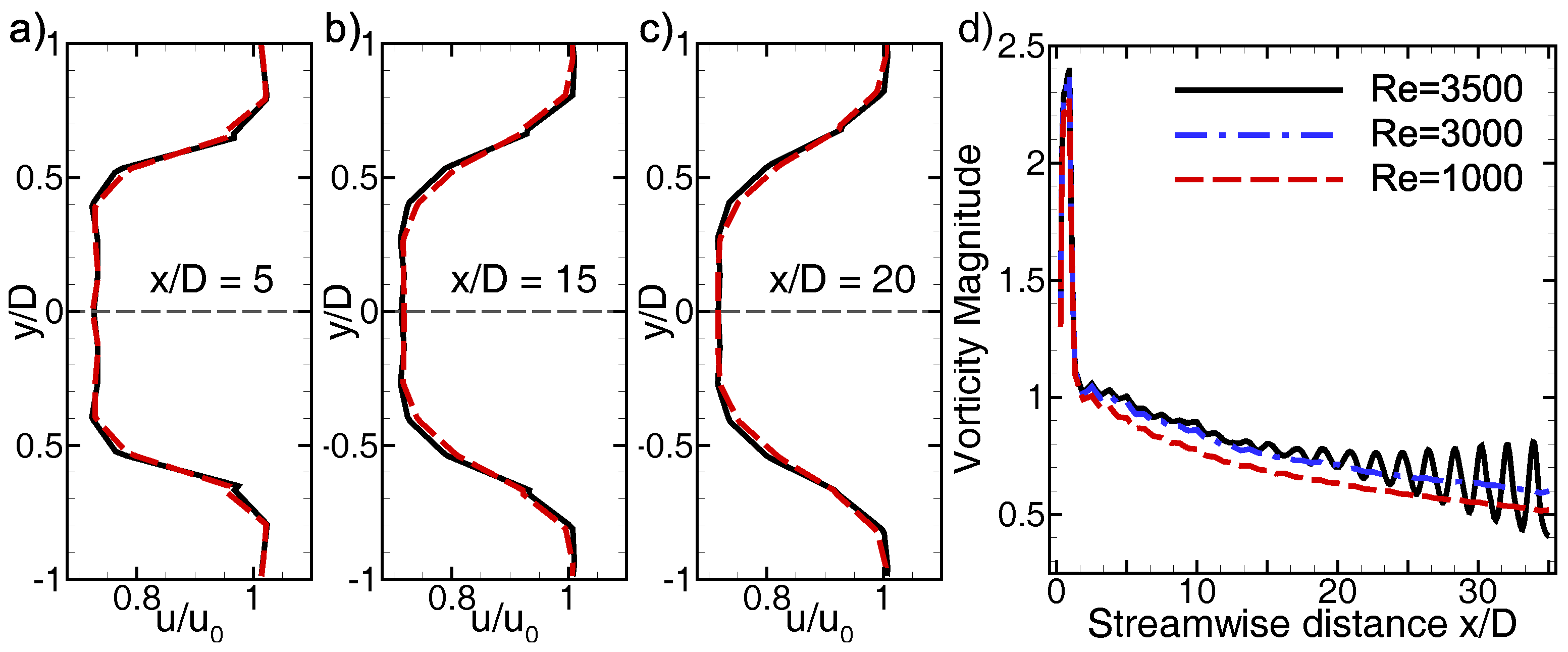
3.3. The Onset of Wake Unsteadiness
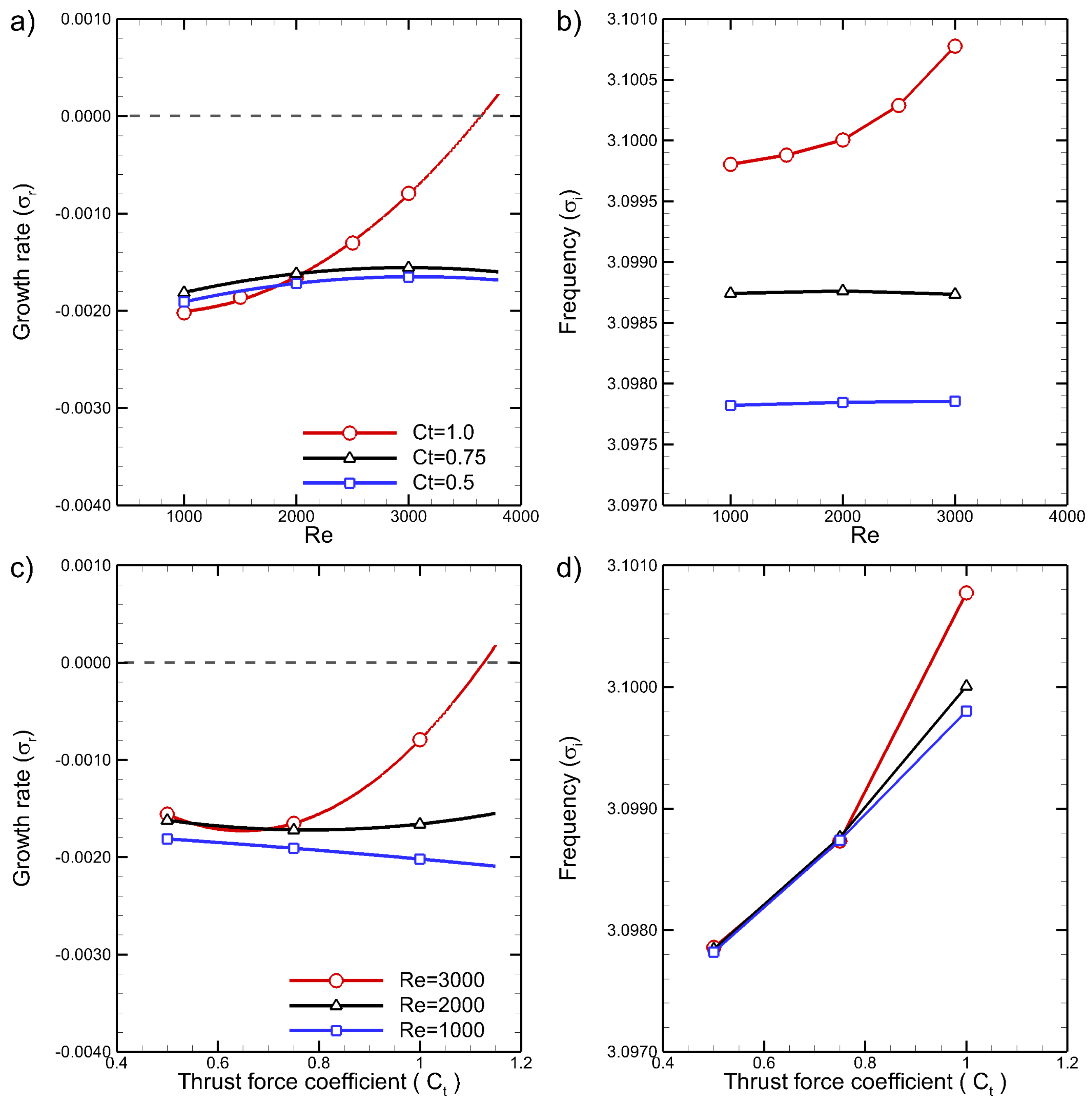
3.4. Stability Analysis
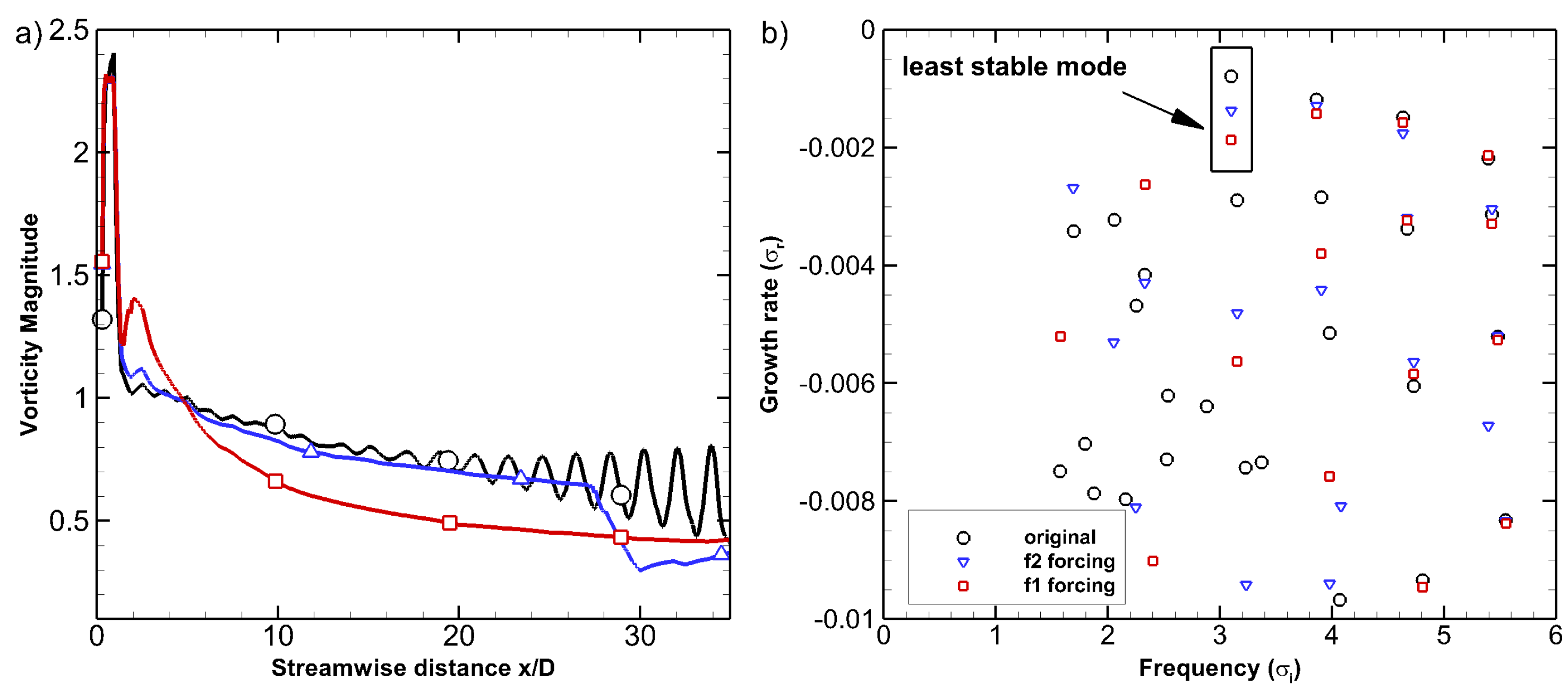
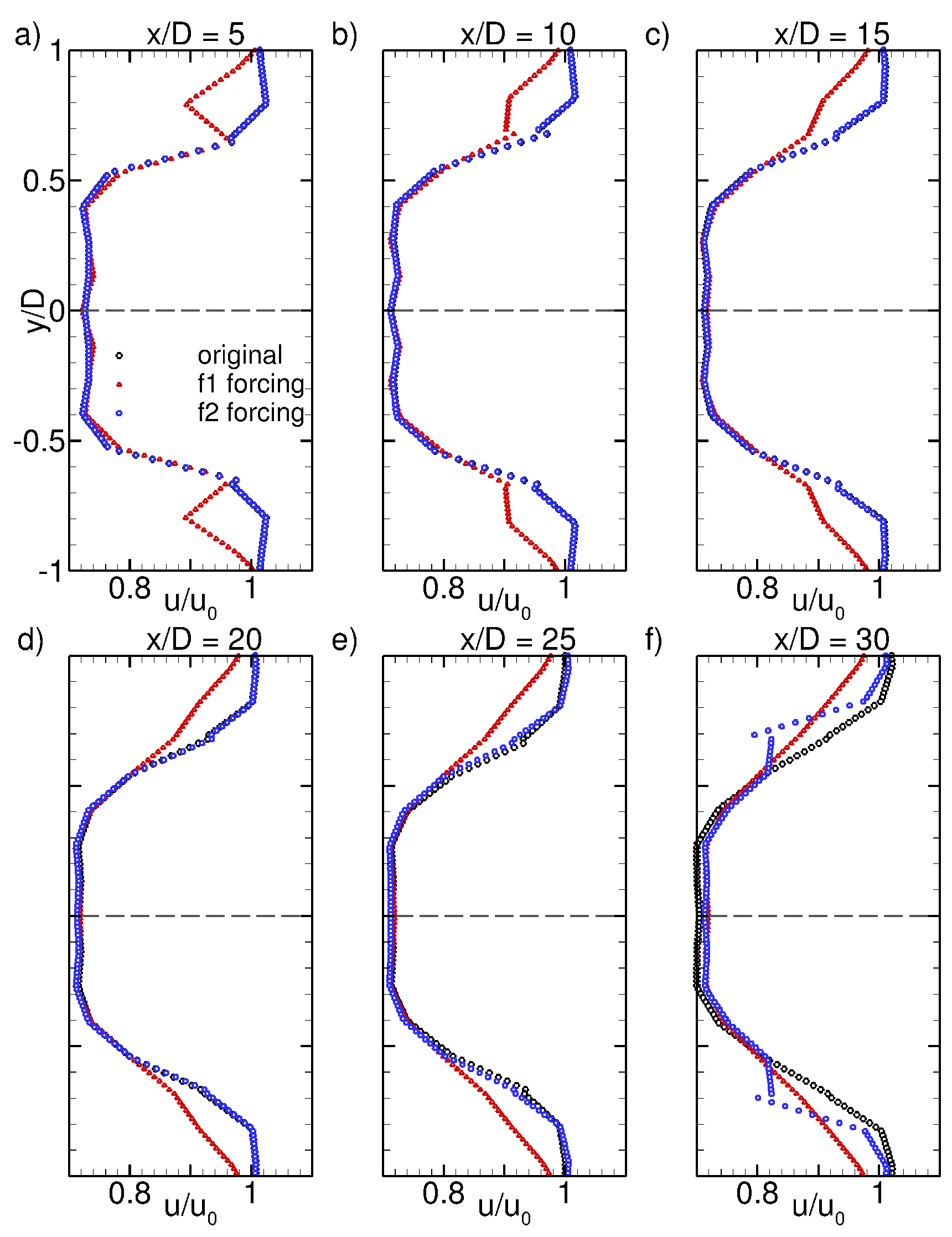
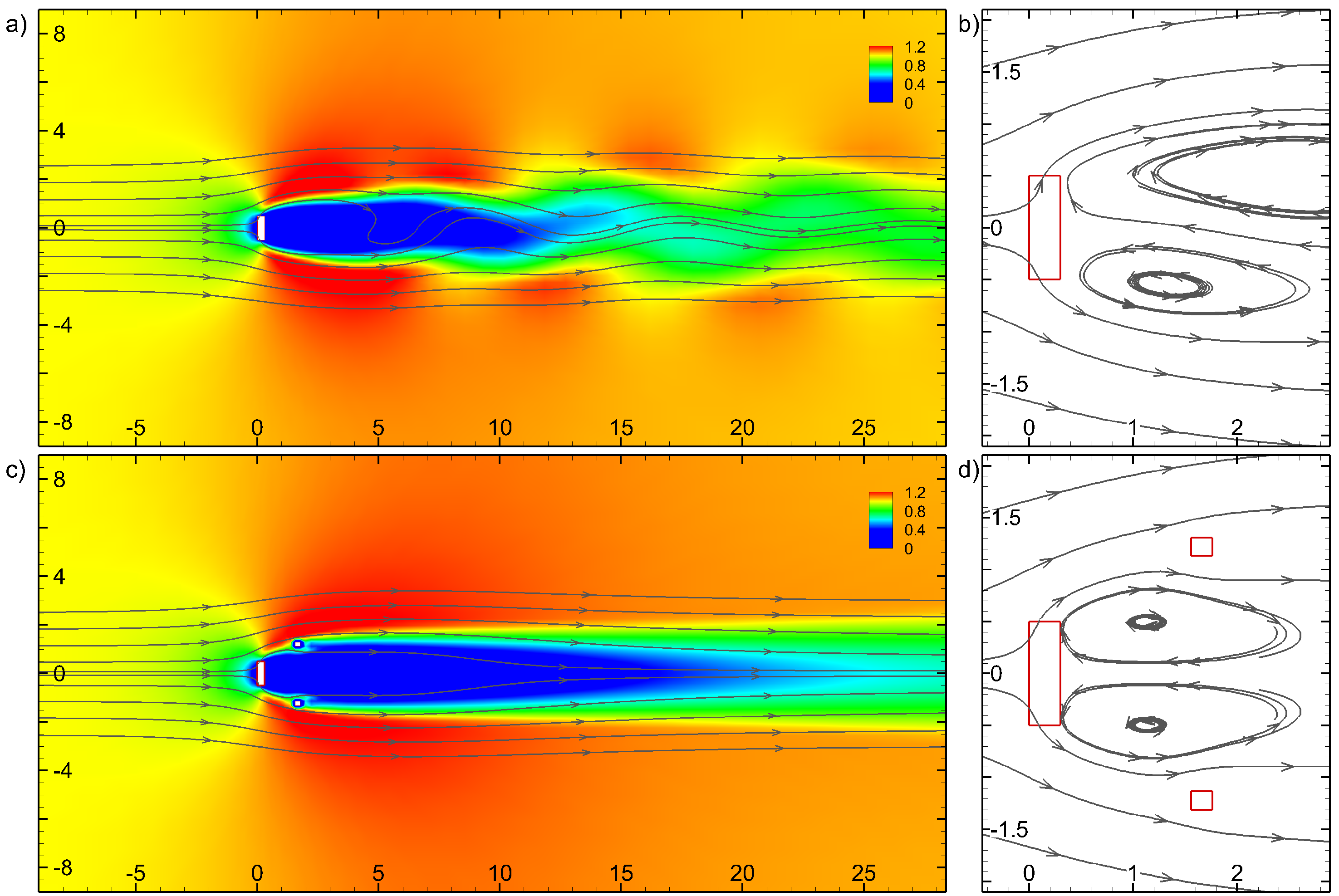
3.5. Wake Control Using Sensitivity Analysis
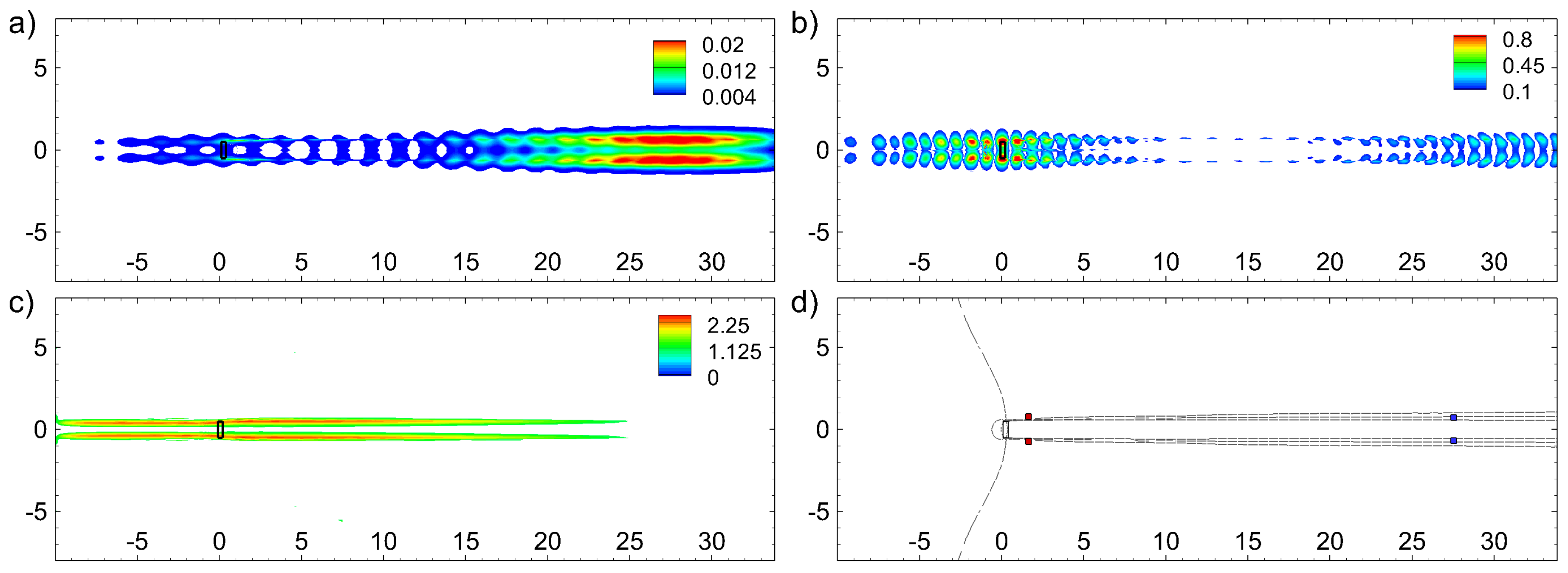
3.5.1. Sensitivity Analysis
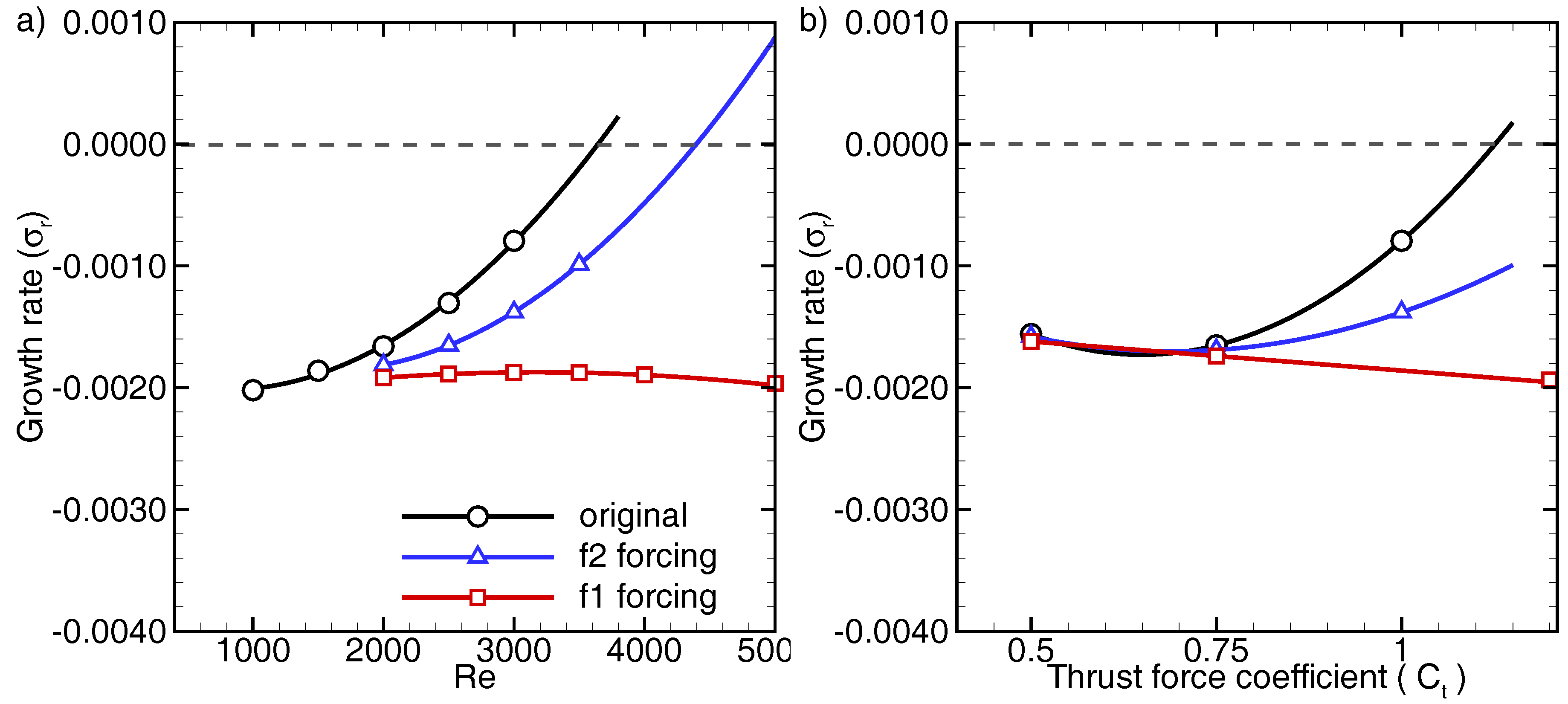
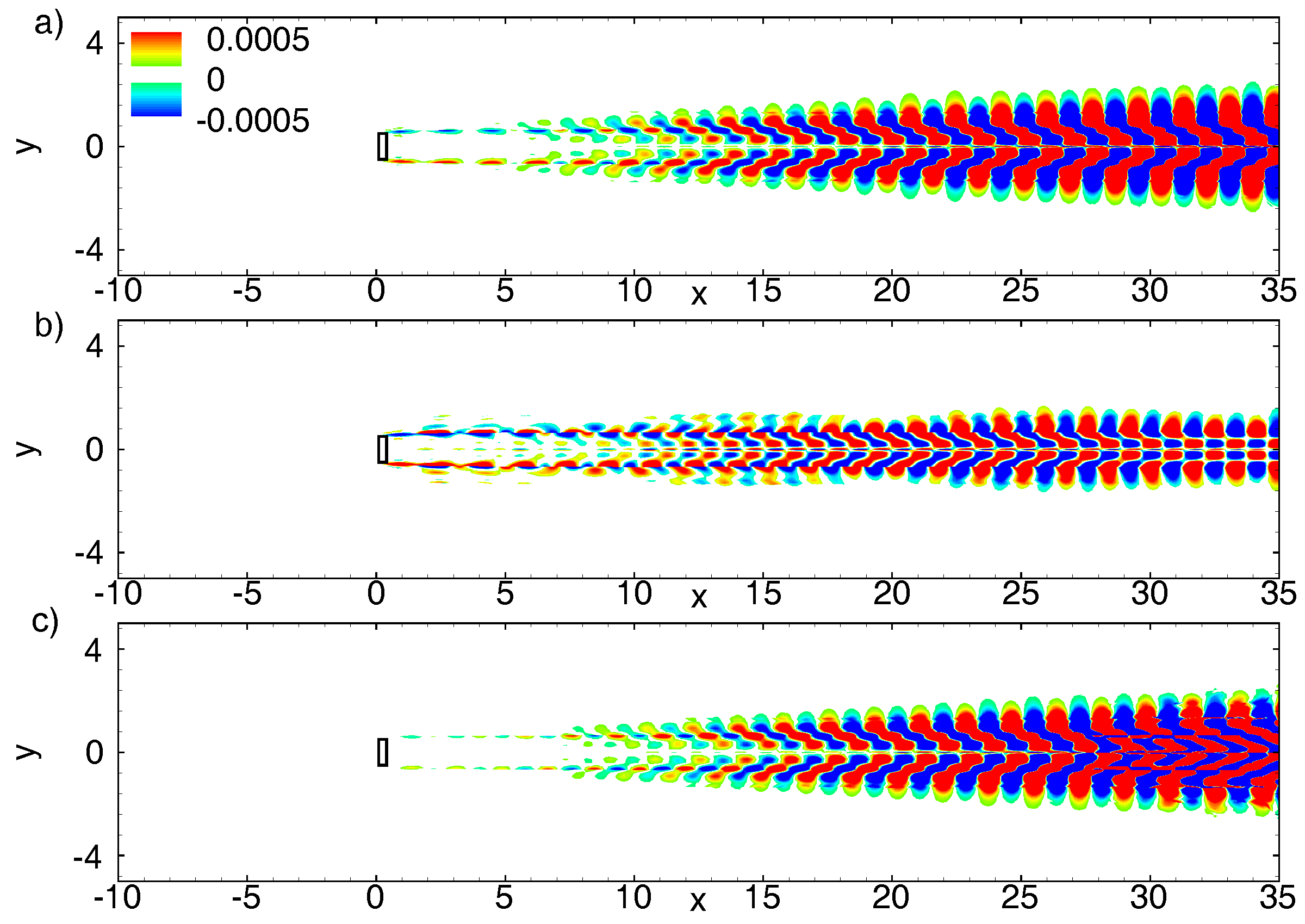
3.5.2. Wake Stabilisation
4. Wake Control at Higher Reynolds Numbers
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Stevens, R.J.A.M.; Meneveau, C. Flow Structure and Turbulence in Wind Farms. Annu. Rev. Fluid Mech. 2017, 49, 311–339. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sorensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Schmid, P.; Henningson, D. Stability and Transition in Shear Flows; Springer: New York, NY, USA, 2001. [Google Scholar]
- Giannetti, F.; Luchini, P. Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 2007, 581, 167–197. [Google Scholar] [CrossRef]
- Marquet, O.; Sipp, D.; Jacquin, L. Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 2008, 615, 221–252. [Google Scholar] [CrossRef]
- Luchini, P.; Bottaro, A. Adjoint Equations in Stability Analysis. Annu. Rev. Fluid Mech. 2014, 46, 493–517. [Google Scholar] [CrossRef]
- Browne, O.; Rubio, G.; Ferrer, E.; Valero, E. Sensitivity analysis to unsteady perturbations of complex flows: A discrete approach. Int. J. Numer. Methods Fluids 2014, 76, 1088–1110. [Google Scholar] [CrossRef]
- Ferrer, E.; de Vicente, J.; Valero, E. Low cost 3D global instability analysis and flow sensitivity based on dynamic mode decomposition and high-order numerical tools. Int. J. Numer. Methods Fluids 2014, 76, 169–184. [Google Scholar] [CrossRef]
- Iorio, M.C.; Gonzalez, L.M.; Ferrer, E. Direct and adjoint global stability analysis of turbulent transonic flows over a NACA0012 profile. Int. J. Numer. Methods Fluids 2014, 76, 147–168. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, L.M.; Ferrer, E.; Diaz-Ojeda, H.R. Onset of three dimensional flow instabilities in lid-driven circular cavities. Phys. Fluids 2017, 29, 064102. [Google Scholar] [CrossRef]
- Strykowski, P.; Sreenivasan, K. On the formation and suppression of vortex at low Reynolds numbers. J. Fluid Mech. 1990, 218, 71–107. [Google Scholar] [CrossRef]
- Meliga, P.; Sipp, D.; Chomaz, M. Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluids Mech. 2010, 660, 499–526. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; Blackburn, H.; Sherwin, S. Nonlinear optimal suppression of vortex shedding from a circular cylinder. J. Fluids Mech. 2015, 775, 241–265. [Google Scholar] [CrossRef] [Green Version]
- Rankine, W. On the mechnical principles of the action of propellers. Trans. Inst. Nav. Archit. 1865, 6, 13–39. [Google Scholar]
- Froude, R. On the part played in propulsion by differences of fluid pressure. Trans. Inst. Nav. Archit. 1889, 30, 390–423. [Google Scholar]
- Sorensen, J.; Shen, W. Numerical Modeling of Wind Turbine Wakes. ASME J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2003. [Google Scholar]
- Porte-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Ivanell, S.; Mikkelsen, R.; Sørensen, J.N.; Henningson, D. Stability analysis of the tip vortices of a wind turbine. Wind Energy 2010, 13, 705–715. [Google Scholar] [CrossRef]
- Iungo, G.V.; Viola, F.; Camarri, S.; Porté-Agel, F.; Gallaire, F. Linear stability analysis of wind turbine wakes performed on wind tunnel measurements. J. Fluids Mech. 2013, 737, 499–526. [Google Scholar] [CrossRef]
- Viola, F.; Iungo, G.; Camarri, S.; Porté-Agel, F.; Gallaire, F. Prediction of the hub vortex instability in a wind turbine wake: Stability analysis with eddy-viscosity models calibrated on wind tunnel data. J. Fluids Mech. 2014, 750. [Google Scholar] [CrossRef]
- Ashton, R.; Viola, F.; Camarri, S.; Gallaire, F.; Iungo, G.V. Hub vortex instability within wind turbine wakes: Effects of wind turbulence, loading conditions, and blade aerodynamics. Phys. Rev. Fluids 2016, 1, 073603. [Google Scholar] [CrossRef]
- McAdam, R.A.; Houlsby, G.T.; Oldfield, M.L.G. Experimental measurements of the hydrodynamic performance and structural loading of the Transverse Horizontal Axis Water Turbine: Part 1. Renew. Energy 2013, 59, 105–114. [Google Scholar] [CrossRef]
- Draper, S.; Houlsby, G.T.; Oldfield, M.L.G.; Borthwick, A.G.L. Modelling tidal energy extraction in a depth-averaged coastal domain. IET Renew. Power Gener. 2010, 4, 545–554. [Google Scholar] [CrossRef] [Green Version]
- Draper, S.; Nishino, T.; Adcock, T.; Taylor, P. Performance of an ideal turbine in an inviscid shear flow. J. Fluids Mech. 2012, 796, 86–112. [Google Scholar] [CrossRef] [Green Version]
- Myers, L.E.; Bahaj, A.S. An experimental investigation simulating flow effects in first generation marine current energy converter arrays. Renew. Energy 2012, 37, 28–36. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porte-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound. Layer Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Aubrun, S.; Espana, G.; Loyer, S.; Hayden, P.; Hancock, P. Is the actuator disc concept sufficient to model the far-wake of a wind turbine? In Progress in Turbulence and Wind Energy IV; Springer: Berlin, Germany, 2012; pp. 227–230. [Google Scholar]
- Kang, S.; Yang, X.; Sotiropoulos, F. On the onset of wake meandering for an axial flow turbine in a turbulent open channel flow. J. Fluids Mech. 2014, 744, 376–403. [Google Scholar] [CrossRef]
- Espana, G.; Aubrun, S.; Loyer, S.; Devinant, P. Spatial study of the wake meandering using modelled wind turbines in a wind tunnel. Wind Energy 2011, 14, 923–937. [Google Scholar] [CrossRef]
- Medici, D.; Alfredsson, P.H. Measurements behind model wind turbines: Further evidence of wake meandering. Wind Energy 2008, 11, 211–217. [Google Scholar] [CrossRef]
- Larsen, G.C.; Madsen, H.A.; Thomsen, K.; Larsen, T.J. Wake meandering: A pragmatic approach. Wind Energy 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Lanchester, F. A contribution to the theory of propulsion and the screw propeller. J. Am. Soc. Nav. Eng. 1915, 27, 509–510. [Google Scholar] [CrossRef]
- Betz, A. Das Maximum der theoretisch möglichen Ausnutzung des Windes durch Windmotoren. Z. Gesamte Turbinenwes. 1920, 26, 307–309. [Google Scholar]
- Leishman, G. Principles of Helicopter Aerodynamics (Cambridge Aerospace Series), 2nd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Burton, T.D.; Sharpe, N.J.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons Ltd.: West Sussex, UK, 2011. [Google Scholar]
- Whelan, J.; Graham, J.; Peiro, J. A free-surface and blockage correction for tidal turbines. J. Fluids Mech. 2009, 624, 281–291. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluids Mech. 2012, 708, 596–606. [Google Scholar] [CrossRef]
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Le, K.H. Improving Transient Stability in a Grid-Connected Squirrel-Cage Induction Generator Wind Turbine System Using a Fuzzy Logic Controller. Energies 2015, 8, 6328–6349. [Google Scholar] [CrossRef] [Green Version]
- Munters, W.; Meyers, J. An optimal control framework for dynamic induction control of wind farms and their interaction with the atmospheric boundary layer. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Blackburn, H.; Sheridan, J. Two and Three Dimensional Stability Analysis of an Optimum Glauert Rotor at Low Reynolds Number. In Proceedings of the 19th Australasian Fluid Mechanics Conference, RMIT University, Melbourne, Australia, 8–11 December 2014; pp. 1–4. [Google Scholar]
- Mettot, C.; Renac, F.; Sipp, D. Computation of eigenvalue sensitivity to base flow modifications in a discrete framework: Application to open-loop control. J. Comput. Phys. 2014, 269, 234–258. [Google Scholar] [CrossRef]
- Chandler, G.; Juniper, M.; Nichols, J.; Schmid, P. Adjoint algorithms for the Navier-Stokes equations in the low Mach number limit. J. Comput. Phys. 2012, 231, 1900–1916. [Google Scholar] [CrossRef]
- Barkley, D.; Blackburn, H.M.; Sherwin, S.J. Direct optimal growth analysis for timesteppers. Int. J. Numer. Methods Fluids 2008, 57, 1435–1458. [Google Scholar] [CrossRef]
- Lyness, J.; Moler, C. Numerical Differentiation of Analytic Functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Kompenhans, M.; Rubio, G.; Ferrer, E.; Valero, E. Adaptation strategies for high order discontinuous Galerkin methods based on Tau-estimation. J. Comput. Phys. 2016, 306, 216–236. [Google Scholar] [CrossRef]
- Kompenhans, M.; Rubio, G.; Ferrer, E.; Valero, E. Comparisons of p-adaptation strategies based on truncation- and discretisation-errors for high order discontinuous Galerkin methods. Comput. Fluids 2016, 139, 36–46. [Google Scholar] [CrossRef]
- Kopriva, D. Implementing Spectral Methods for Partial Differential Equations: Algorithms for Scientists and Engineers, 1st ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- ANSYS Academic Research. Fluent Manual 16.2; ANSYS, Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Tammisola, O.; Lundell, F.; Schlatter, P.; Wehrfritz, A.; Söderberg, L. Global linear and nonlinear stability of viscous confined plane wakes with co-flow. J. Fluids Mech. 2011, 675, 397–434. [Google Scholar] [CrossRef]
- Tammisola, O. Oscillatory sensitivity patterns for global modes in wakes. J. Fluids Mech. 2012, 701, 251–277. [Google Scholar] [CrossRef]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluids Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Perez, J.M.; Le Clainche, S.; Vega, J.M. Alternative 3D instability analysis of the wake of a circular cylinder. In Proceedings of the 8th AIAA Theoretical Flow Mechanics Conference, Denver, CO, USA, 5–9 June 2017. AIAA-2017-4021. [Google Scholar]



| P-Order | % Error () | % Error () | ||
|---|---|---|---|---|
| 3 | −0.002287 | 13.611 | 3.0998769 | 0.002 |
| 4 | −0.002019 | 0.298 | 3.099801 | 9.678 × |
| 5 | −0.002013 | - | 3.099798 | - |
| Turbine Thrust | Reynolds Number Re | |||||
|---|---|---|---|---|---|---|
| 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | |
| 0.50 | S | S | S | S | S | S |
| 0.75 | S | S | S | S | S | S |
| 1.00 | S | S | S | S | S | U |
| 1.20 | S | S | U | U | U | U |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrer, E.; Browne, O.M.F.; Valero, E. Sensitivity Analysis to Control the Far-Wake Unsteadiness Behind Turbines. Energies 2017, 10, 1599. https://doi.org/10.3390/en10101599
Ferrer E, Browne OMF, Valero E. Sensitivity Analysis to Control the Far-Wake Unsteadiness Behind Turbines. Energies. 2017; 10(10):1599. https://doi.org/10.3390/en10101599
Chicago/Turabian StyleFerrer, Esteban, Oliver M.F. Browne, and Eusebio Valero. 2017. "Sensitivity Analysis to Control the Far-Wake Unsteadiness Behind Turbines" Energies 10, no. 10: 1599. https://doi.org/10.3390/en10101599





