1. Introduction
A wireless sensor network (WSN) is an intelligent system with data collection, data fusion and independent transmission, which involves in many applications such as military surveillance, embedded systems, computer networks and communications. It consists of several sensors and each node is generally small in size and has a battery of limited capacity and energy. The lifetimes of WSNs thus are extremely limited by the total energy available in the batteries. Thus, using optimal techniques for energy management such as energy harvesting (EH), we can prolong the lifetime and duration of maintenance-free operation of WSNs. For instance, the energy existing in our environment from solar, wind, and thermal sources is converted into that can be used electrically. The advantages of EH-WSN solutions include high reliability, low energy needs, time savings, ecological compatibility and cost benefits [
1,
2,
3]. In EH-WSN, each sensor node provides two functionalities: sensing, transmitting data to the fusion center (FC), and harvesting energy from ambient energy sources. The FC collects and reconstructs the observed signal by querying only a subset of sensors [
4,
5]. In order to reduce the energy consumption while forwarding observations to FC, we consider an innovative data gathering and reconstruction process based on three key subproblems: (i) compressive sensing (CS) based data acquisition; (ii) transmission of sparse random projection under fading for adapting random energy availability in EH systems; and (iii) CS based data reconstruction.
Data collected from wireless sensors are typically correlated, and are thus compressible in some appropriate domains. According to the CS theory, if a signal
is compressible, it can be well approximated using a small number
of orthogonal transform coefficients [
6,
7,
8]. Based on the CS model, the FC receives a compressed approximation of the original signal at multiple nodes by exploiting dense random matrix, i.e., all of the EH sensors in the networks participate in forwarding observations, and the FC randomly chooses them. However, in order to avoid this situation, which consumes a large amount of energy, we first have to build a sparse random projection such that the information can be extracted from any
k-sparse signal. Second, we need to design a suitable recovery algorithm to reconstruct the original signal with good accuracy for given energy neutral conditions. Therefore, it would be good for EH sensors to prolong their lifetime and for FC to query an appropriate number of random projections and to still reconstruct a good approximation. Regarding sparse random projections, a good random projection will preserve all pairwise distances with a high probability. Thus, it can be used as a reliable estimator of distances in the original space. In [
9], the authors proposed a distributed compressive sensing scheme for WSNs, where the sparsity of the random projections is used consistently to reduce the computational complexity and the communication cost. They also proved that the sparse random projections are sufficient to recover a data approximation that is comparable to the optimal
k-term approximation with a high probability. With the fading channel and energy-harvesting constraints, the problems regarding sparsity of random projections are studied in [
10,
11]. In [
10], the authors only considered additive white Gaussian noise (AWGN) channels, while, in [
11], the authors focused on Rayleigh fading channels and investigated sufficient conditions for guaranteeing a reliable and computationally-efficient data approximation for the sparse random projections. Due to the harvesting conditions, the sensors typically have different energy harvesting rates that lead to different available energy constraints. However, the sparsity factors in the aforementioned works have been assumed to be homogeneous for all sensors and were kept fixed for entire transmission states. Thus, they cannot be responsive to battery dynamics and channel conditions. To overcome those issues, we consider a dynamic sparsity factor that relates to the available energy constraints of wireless sensors and transmission between them, and then build a sparse random projection matrix that is stable and robust under channel fading effects and CS recovery.
The main purpose of this paper is to study sparse representation and sparse random projection for EH WSNs under fading channels. We consider a problem of data transmission in EH WSNs where multiple sensors send spatially-correlated data to a fusion center using amplify-and-forward (AF) protocol over independent Rayleigh fading channels with additive noise. Supposing that the measured data are compressible under an approximate orthogonal transform, our task is first choosing a certain number of sensors to query according to the desired approximation error by designing a sparse random projection matrix, and then exploiting the CS recovery algorithm to obtain an optimal approximation. Inspired by the work in [
12] on sparse random projections for heavy-tailed data, we propose a random projection-based CS scheme where the sparsity factor is dynamic due to energy constraints. We also prove that, under the fading channel condition, our projection matrix still satisfies the restricted isometry property (RIP) for successful recovery in CS.
The organization of this paper is as follows. In
Section 2, we introduce the problem of recovering a signal observed by an EH WSN under channel fading, and briefly introduce the compressive sensing. In
Section 3, we present our construction on basis representations for compressible data and sparse random projection design.
Section 4 proves that our sparse random matrices preserve the pairwise distance under the fading and guarantee the reconstruction accuracy subject to the energy constraints. The simulation results and conclusion are presented in
Section 5 and
Section 6, respectively.
Notations: We denote as a matrix whose entries are , as the matrix inverse operation, as the conjugate transpose, as the floor operation, as the number of elements in a given set T, and as the expectation and the variance operators, respectively. The norm of a vector is defined as for a positive integer p. We call a signal is a k-sparse vector if . The notation denotes the complexity operation, denotes the circularly symmetric complex Gaussian distribution with mean and covariance , and means that is distributed according to , alternatively, .
4. Proposed Distributed Algorithm and Analysis
4.1. Sparse Random Projection with Fading Channels
Suppose that we have two input vectors
(alternatively,
) and the random matrix
given in Equation (
3). The corresponding projections of
and
are defined by
We also assume that under fading the channel matrix is independent of the random matrix . Thus, we have
The sparse random projection is desired to have the properties of length, distance, and inner product preservation. We need to check that those properties are still preserved under fading channel conditions. In order to check the length preservation of the sparse random matrix , we first express , where
Thus, .
For the distance preservation, we have
Similarly, we can compute the inner product as , where
Thus, the inner product is still preserved by applying since we have .
4.2. Stability and Robustness of Sparse Random Projections
By partitioning the sparse random matrix into , where each has size and ( and will be determined later), the corresponding measurement can be split into vectors . Each is defined as
We let
, where
and
. Thus, we can perform
where
and
. The corresponding means, variances of
,
, and their covariances can be calculated as
The detailed derivations of Equations (
21)–(25) are given in the
Appendix A. Thus, we obtain
For any , using the Chebychev’s inequality and the fact that , we have
We have also used the fact that for any data vector
, it satisfies the peak-to-total energy condition, i.e.,
[
10]. Following the approach given in [
9], the probability that an estimate lies outside the tolerable approximation interval cannot exceed
, where
. Setting
yields
, and setting
gives
for some constant
. Finally, for
, the sparse random matrix
can preserve all the pairwise inner products within an approximation error
with the probability of at least
.
Remark 1 (Complexity Analysis). According to CS model with a dense random matrix [6,8], it requires at least measurements for obtaining an approximation via -minimization problem in Equation (4) with probability exceeding , and the CS decoding has computational complexity . On the other hand, the sparse random projection scheme requires at least random projections and the corresponding decoding process takes , where M is the number of measurements. Since , using sparse random projection attains low decoding complexity, which makes it applicable for EH sensors, while the FC can request a little more measurements from sensors and recover the signal with a better approximation. Our proposed scheme has inherited this advantage and optimized the sparsity level, which adapts to channel conditions and energy constraints. 4.3. Sparsity Level and RIP Verification
Following the signal model in Equation (
1), i.e.,
, the decoding process is to recover the sparse signal
instead of recovering the sensor data
by using Equation (
4). However, we must verify that
satisfies the sparse basis representation in
and the matrix
obeys the RIP condition to guarantee successful recovery via
-minimization.
To analyze the feasibility of the measurement matrix and the sparse basis design, we have to answer the following two questions:
- (1)
Is it reasonable to select
obtained from
Section 3.2 as an orthogonal basis for
?
- (2)
For the matrix
obtained from
Section 3.3, does
obey the RIP condition?
First, as we demonstrated in
Section 3.2, the matrix
is obviously an orthogonal basis in
from an appropriate transformation. Otherwise, it can be an overcomplete dictionary from data learning approach, which promised to represent a wider range of signal phenomena [
16].
Second, in order to show that the random variable is highly concentrated about , we can assume that the row of is independent of . Fixing , and with each row of satisfying the sub-Gaussian distribution, we prove that will satisfy the RIP with high probability, i.e.,
To do that, we prove that each part of the matrix satisfies the RIP for complex data , i.e.,
First, in order to to prove Equation (
30), by letting
, we have
Then, following Theorem 4.2 of [
18], we obtain
and
. Thus,
Fixing an index set with , there are possible k-dimensional subspaces of and the probability of a k-sparse vector satisfying is given by . Here, we use the Sterling’s approximation, which states that . Thus, it leads to . Finally, we conclude that the probability of satisfying the RIP for all k-sparse vector approaches . Similarly, we obtain the same result for .
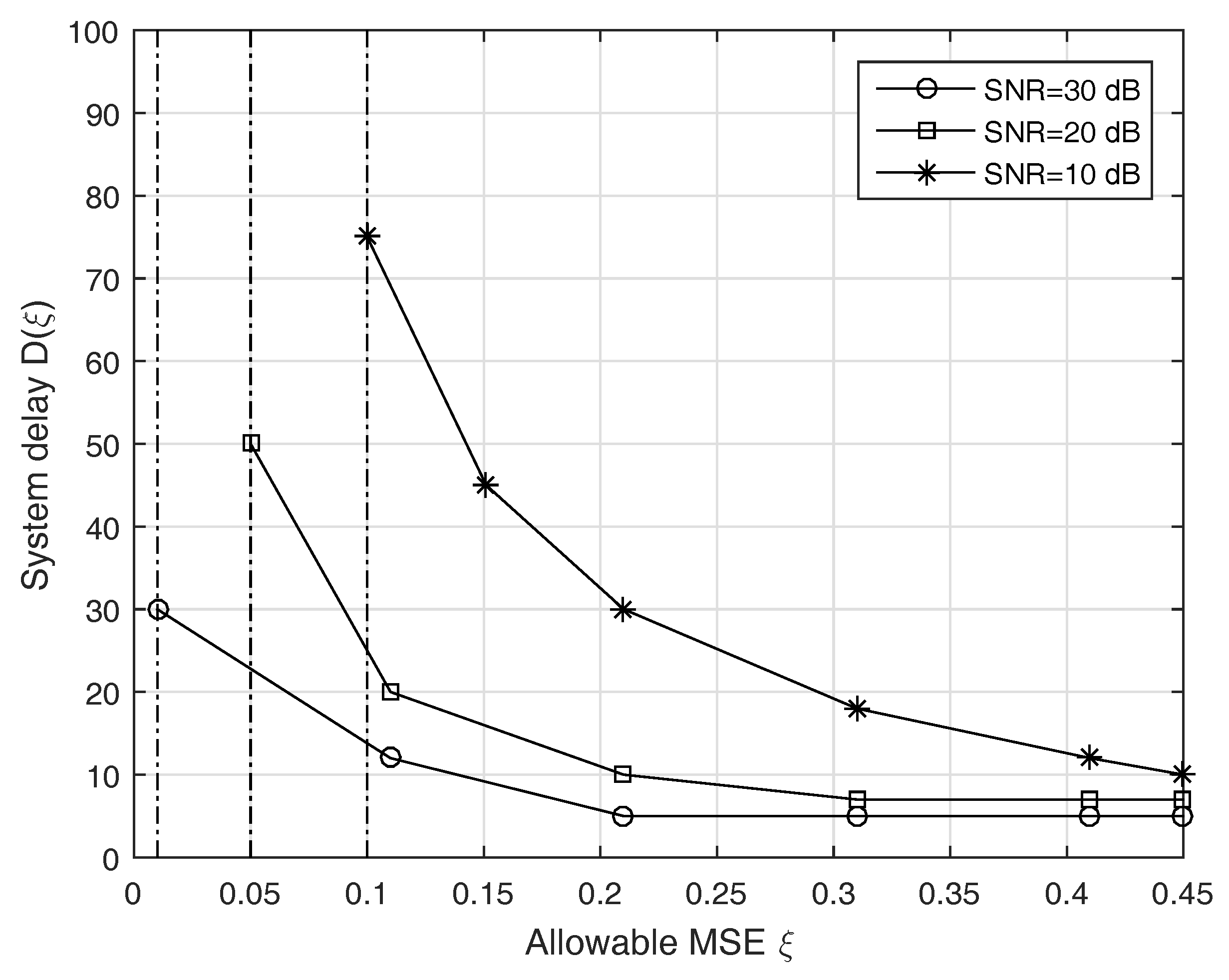
Remark 2 (trade-off between the MSE and the system delay). There exists a trade-off between the system delay and the approximation error, which is described as follows. For an allowable mean-square error (MSE) , the achievable system delay is defined aswhere ξ relates to the bounded error in Equation (6). Thus, the total energy consumption for all sensors is
. In order to minimize the total network energy consumption,
should be chosen to be as large as possible, or maximizing
as shown in Equation (
15), which leads to the following problem.
Remark 3 (throughput maximum problem). The optimal power allocation in Equation (15) can be obtained by solving the maximum output problem [19], which is given by Here, and the value is a constant that depends on the hardware limitations. The above problem can be efficiently solved by using the iterative resource allocation algorithm method [19]. 5. Simulation Results
We now present the results of a number of numerical simulations that illustrate the effectiveness of our approach. All simulations are performed in MATLAB R2015a (version 8.5.0.197613 (R2015a), The MathWorks Inc., Seoul, Korea) on a 3.60 GHz Intel Core i7 machine with 8 GB of RAM. We use MATLAB codes of the competing algorithms for our numerical studies. The vector
was assumed to be uniformly distributed in the interval
. In our work, we used the basis pursuit de-noising algorithm [
20] to compute the sparse solution in Equation (
4). We evaluate the performance based on the MSE, which is given by
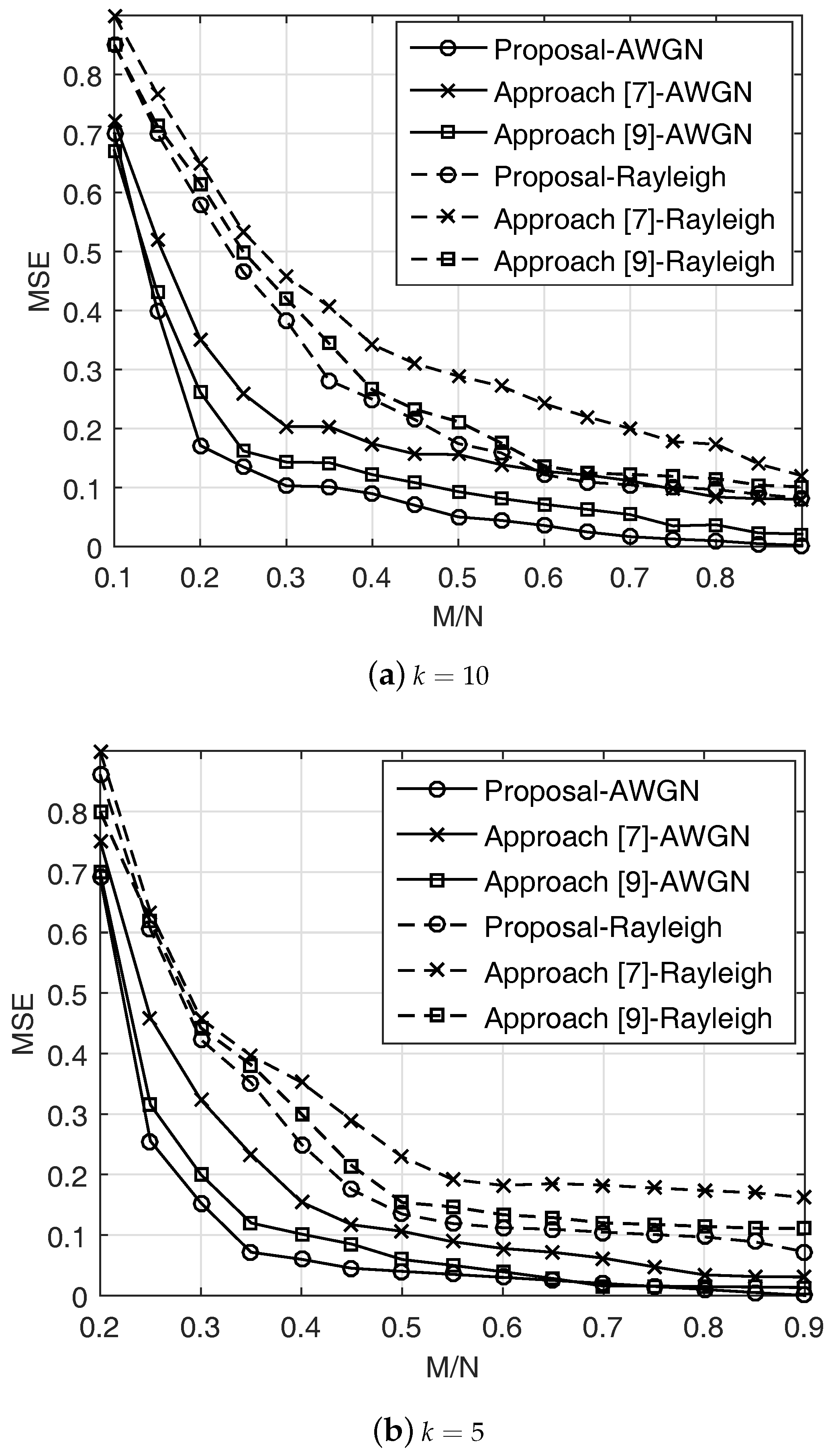
Figure 1 plots the MSE versus the compression ratio
for support cardinality
k and fading channels plotted for
, and
is uniformly distributed in the interval
dB,
, where
dB and
to guarantee a stable recovery [
6]. When
dB,
was set at 0.25 as the conventional baseline. In order to minimize the total energy consumption, we can perform the power allocation among different transmission time slots subject to the causality of the harvested energy, which refers to the resource allocation problem with energy constraint. Note that the sparsity level in Equation (
15) is still adaptive since the optimal power allocations
obtained by solving the maximum output problem [
1] are dynamic. The MSE values decrease as
k decreases, as expected. We observed that the proposed scheme performs well compared to the conventional ones with AWGN and Rayleigh fading channels. The performance gap between those schemes is getting smaller when the ratio
increases. This is because when
M is large enough, the MSE may not achieve any improvements. We notice that the sparsity level of the random projection determines the amount of communication. Increasing the sparsity level yields to decrease the preprocessing cost but unfortunately increase the latency to recover a CS approximation. We will show this trade-off in the simulation results.
Figure 2 shows the outage probability with several
intervals when
and
. The outage probability is defined as the probability that the matrix
does not satisfy the RIP, which scales as
as shown in Equation (
32). For sufficiently large number
M, we observe that the optimal compressed rate
decreases as the sparsity level
increases. This means the number of measurements
M must approximately obey
for effective CS recovery, while it is large enough for minimizing the outage probability. Moreover, from the result in
Section 4.2, since
M is proportional to
, the larger value of
leads to a smaller compressed ratio
for a fixed
N.
Figure 3 illustrates a trade-off between the system delay and the MSE threshold
for the proposed approach as we have discussed in Remark 2 when
and
. We observed that the proposed scheme achieves a better trade-off when either SNR or
increases as expected. This is because higher SNR means the signal is more clearly readable, the CS recovery procedure will be much easier. Moreover, for a tight MSE threshold, the procedure of choosing the estimate to minimize the expected MSE will take longer, since the best MSE scaling depends on the value of
M.
Remark 4 (sparsity level option). This scheme is developed for transformative sensing mechanisms, which can be used in conjunction with current or upcoming EH capabilities in order to enable the deployment of energy neutral EH WSNs with practical network lifetime and improve data gathering rates. However, the sparsity level in Equation (15) should be carefully chosen to maintain a good trade-off between the MSE and the system complexity. For example, when the channel condition is not good, we should select large enough (e.g., to guarantee an acceptable MSE. 6. Conclusions
In this paper, we have aimed to address the problem of recovering a sparse signal observed by a resource constrained in EH-WSNs for optimal data transmission strategy. By exploiting sparse random projections, there are significant reductions of the data measurements to be made. First, we studied a basis representation that can make the measurement matrix sufficiently sparse. The EH sensors store the sparse random projections of data, and thus the FC can estimate using compressive sensing with a sufficient number of measurements of sensors. Due to fading channels, the sparsity level can be adaptively chosen according to the available harvested energy at each EH sensor. This approach provides a better trade-off of the query latency and the desired approximation error, and also speeds up the processing time. We plan to generalize this concept in future work to incorporate sparsity of user activity and imperfect channel information as well. In addition, we would to like to emphasize that there are many ideas in the literature that would certainly enhanced our proposed scheme. We mentioned a few such possibilities as the following. First, we limited our analysis on AF protocol while different approach such as applying channel coding, and then using a modulation scheme for data transmission can be a huge open field. Second, approximation recovery for imperfect data via different norm, e.g., -norm , can be promising due to its high quality of solutions and various types of sensing matrices that can be used in the CS reconstruction algorithms. Third, it needs to further discuss how to design the sparsity parameter of the random projection matrix based on different channel fading statistics so that the number of measurements required for signal recovery at the FC is minimized. Finally, for many application of interests, we often have prior information on addition constraints, e.g., rate-energy trade-off for simultaneous information and power transfer in EH-WSNs. Thus, other sparse random projections can be provided according to those constraints.