H-Shaped Multiple Linear Motor Drive Platform Control System Design Based on an Inverse System Method
Abstract
:1. Introduction
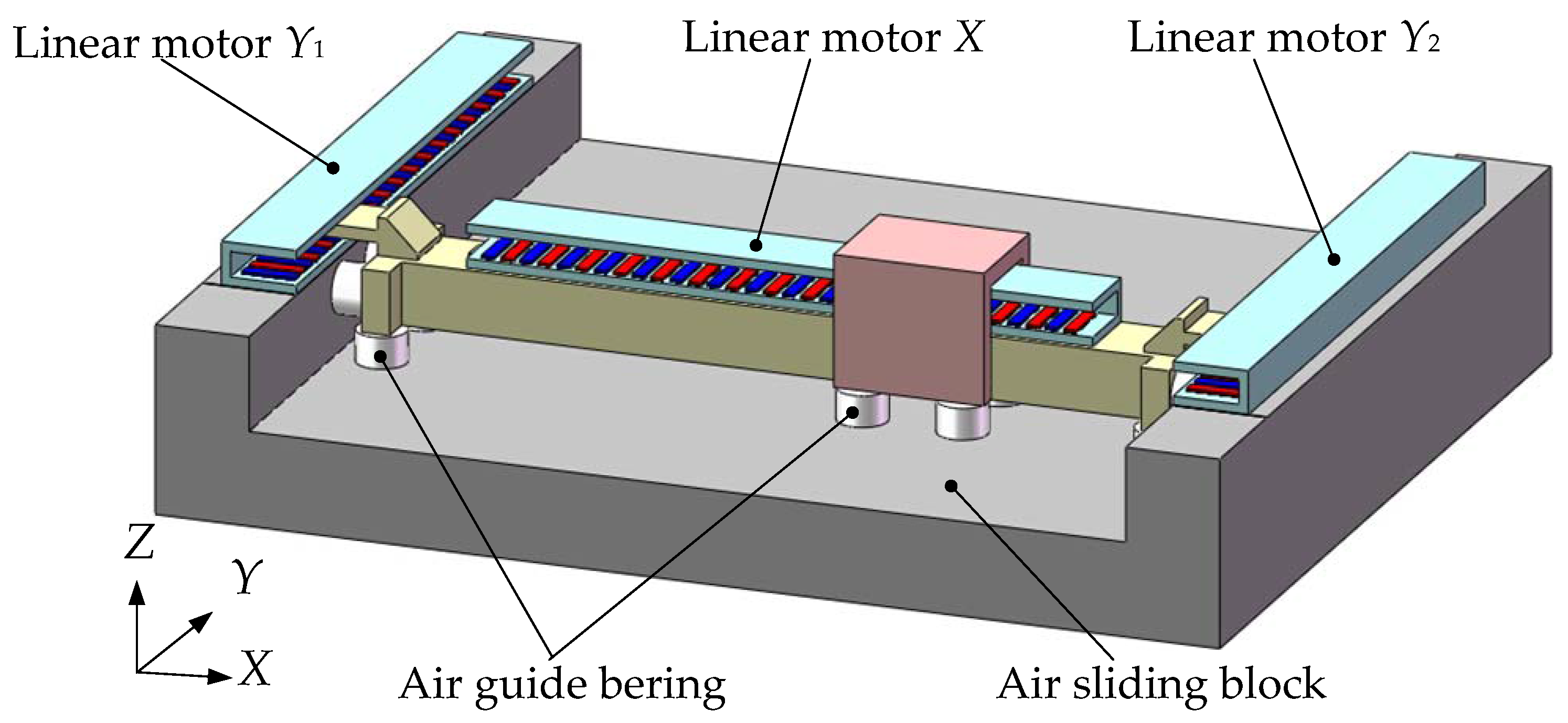
2. An H-Type Platform Driven by Multiple Permanent Magnet Synchronous Linear Motors
2.1. Platform Structure
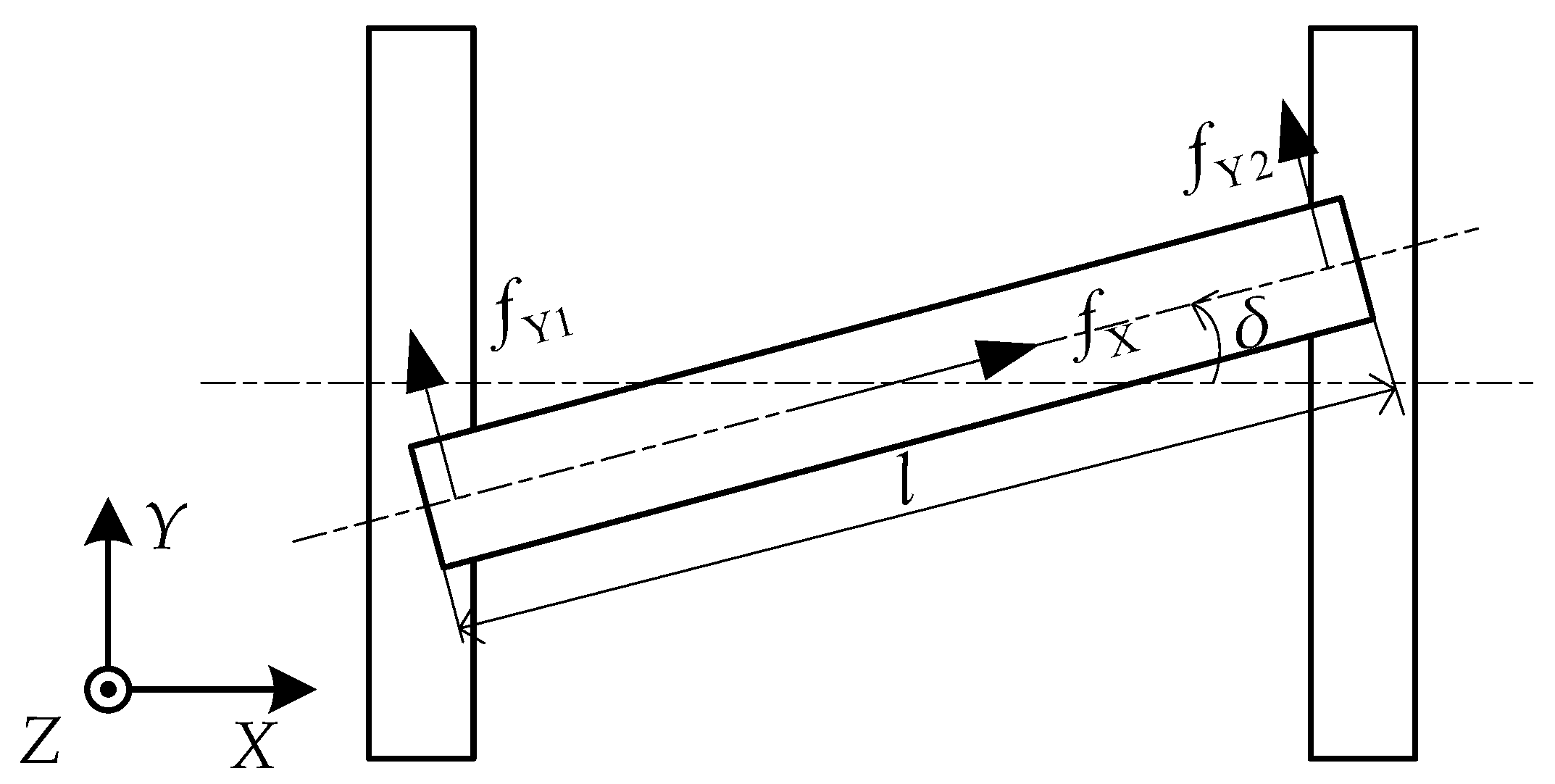
2.2. Mechanical Analysis
3. Pre-Analysis for Permanent Magnet Synchronous Linear Motor Control System
3.1. ABC Coordinate System to d-q Coordinate System
3.2. Mathematical Model
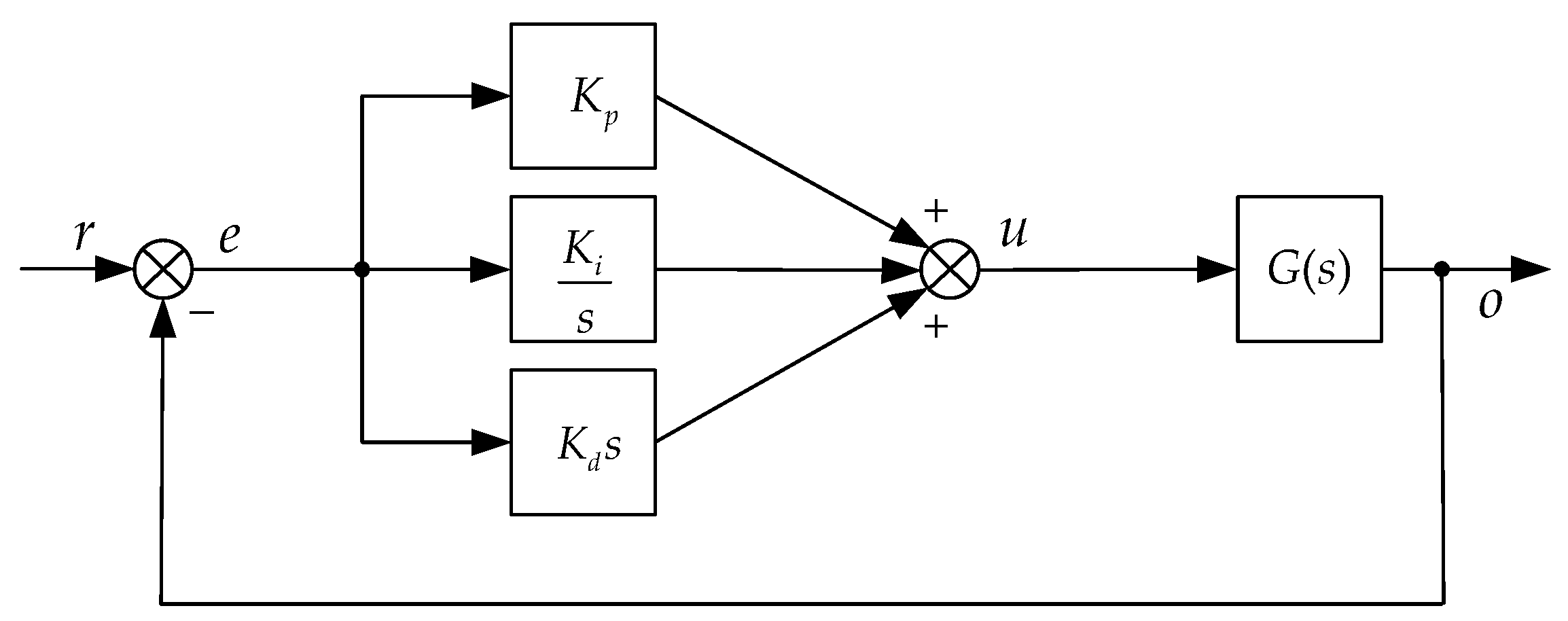
3.3. PID Controller
4. Inverse System Model and Control System Design
4.1. Inverse System Decoupling
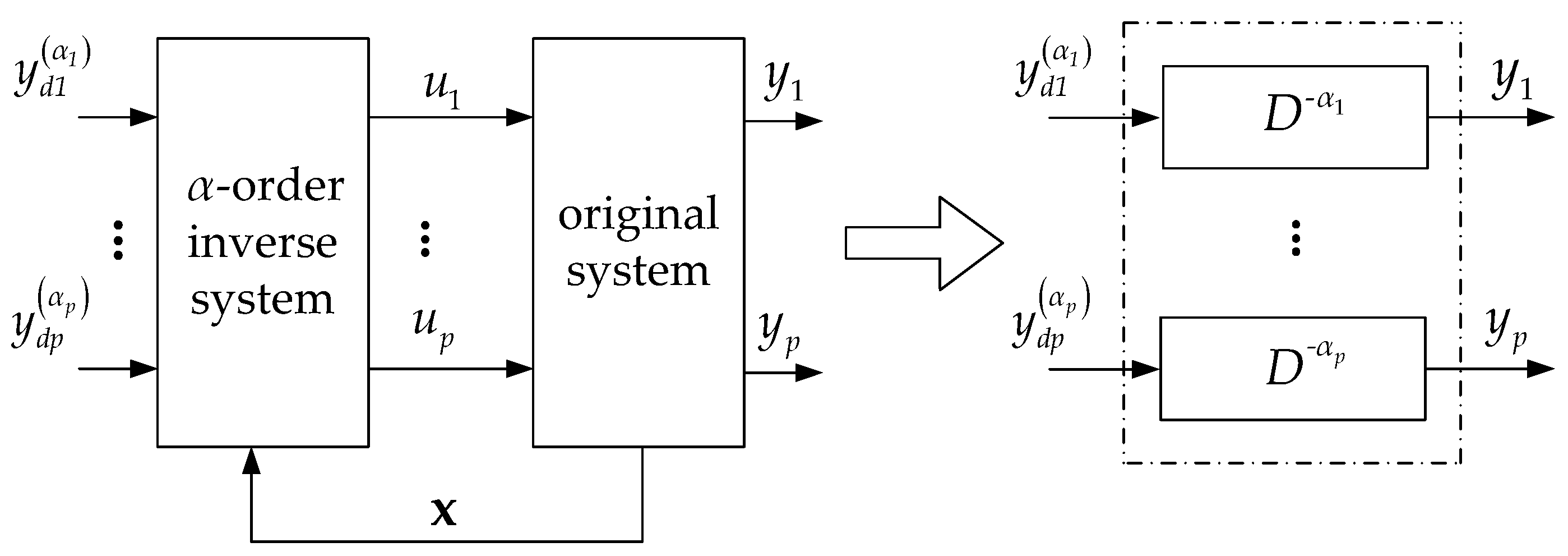
4.1.1. Inverse System Theory
4.1.2. Inverse System Condition
- At (x0, u0), the following equation is satisfied:where is the k-th order Lie derivative.
- The r × m order matrix shown as follows is nonsingular, which indicates the rank of the matrix .
4.2. H-Shaped Platform State Equation
4.3. Decoupling Design
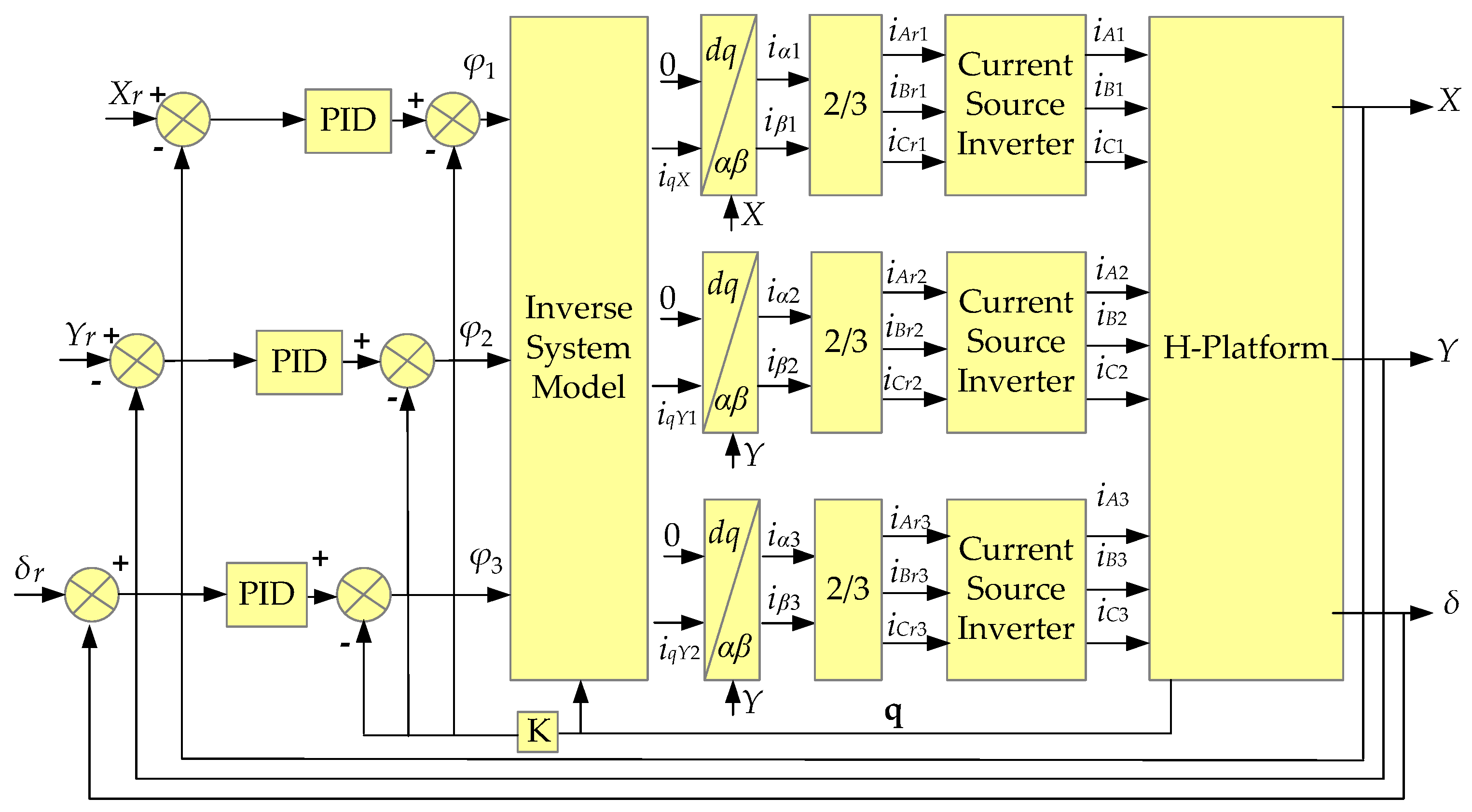
4.4. Control System Structure
5. Simulation and Analysis
5.1. Synchronous Deviation Analysis
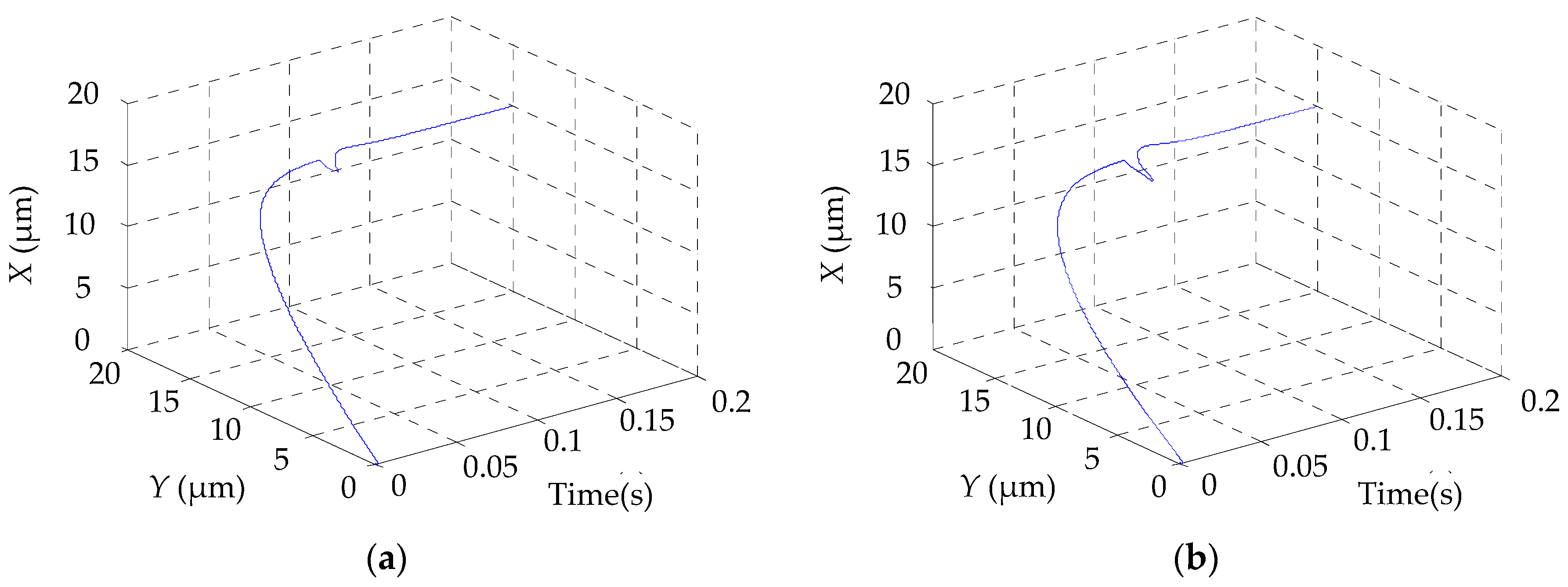
5.2. H-Platform Trajectory Analysis
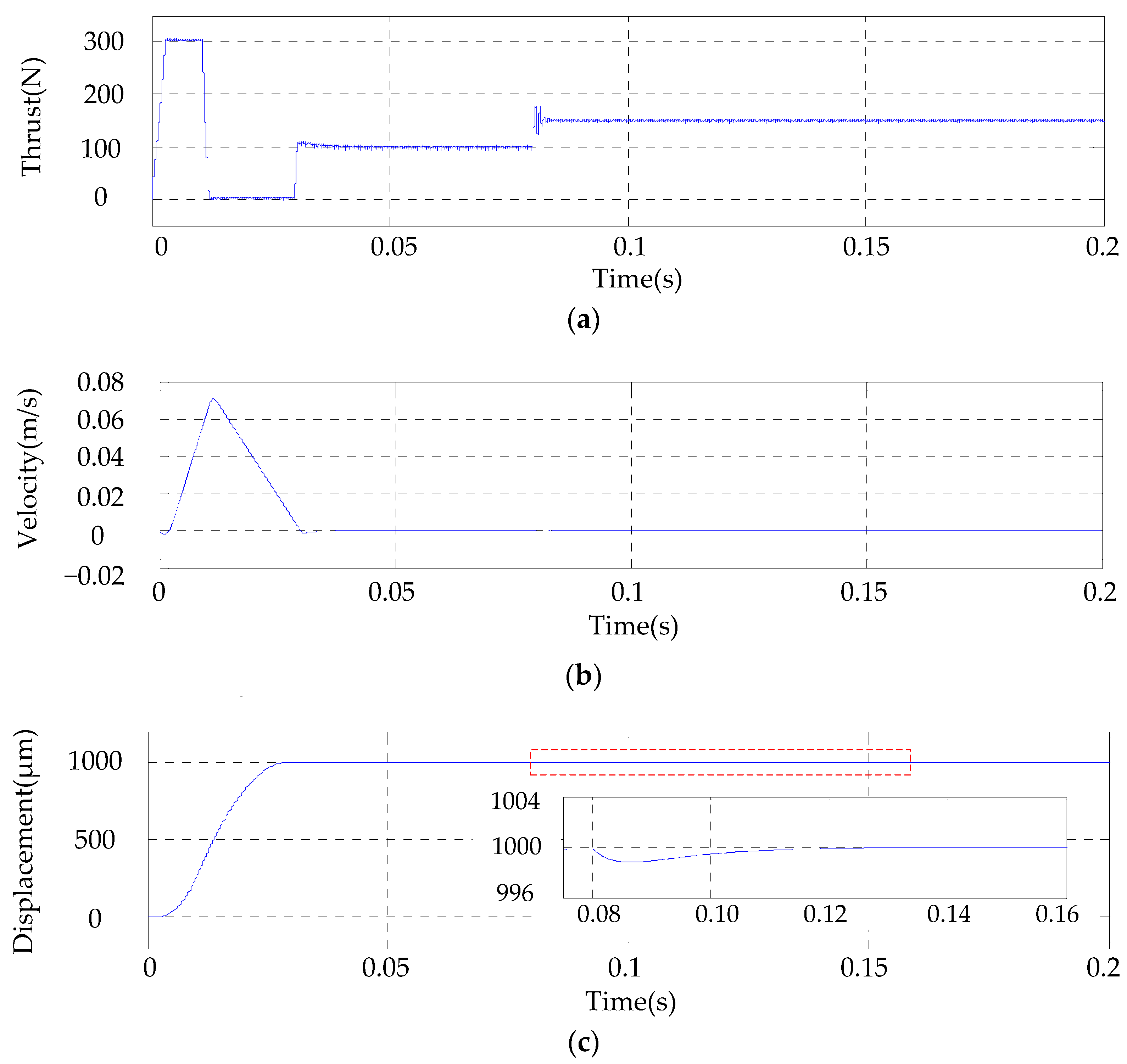
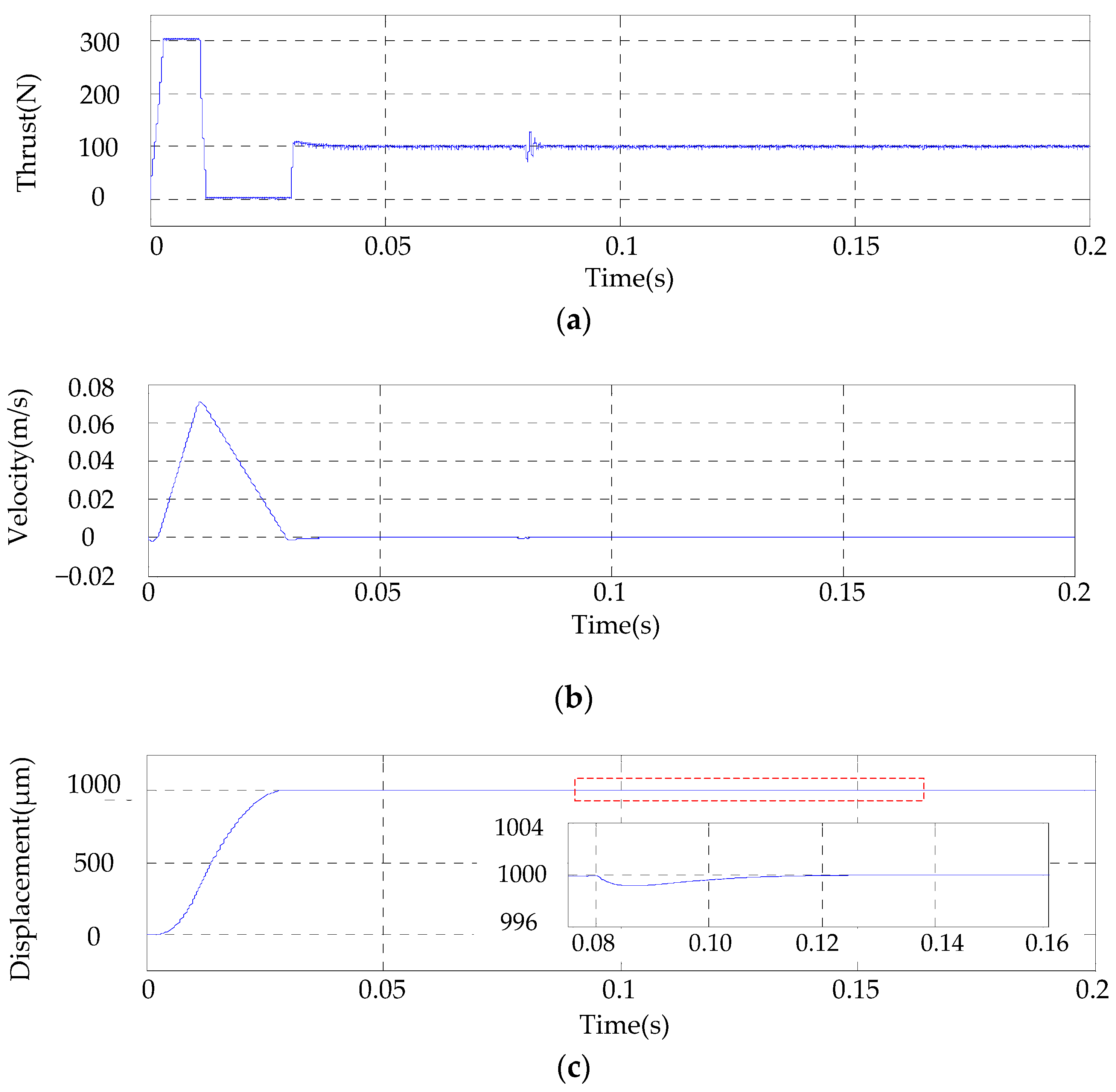
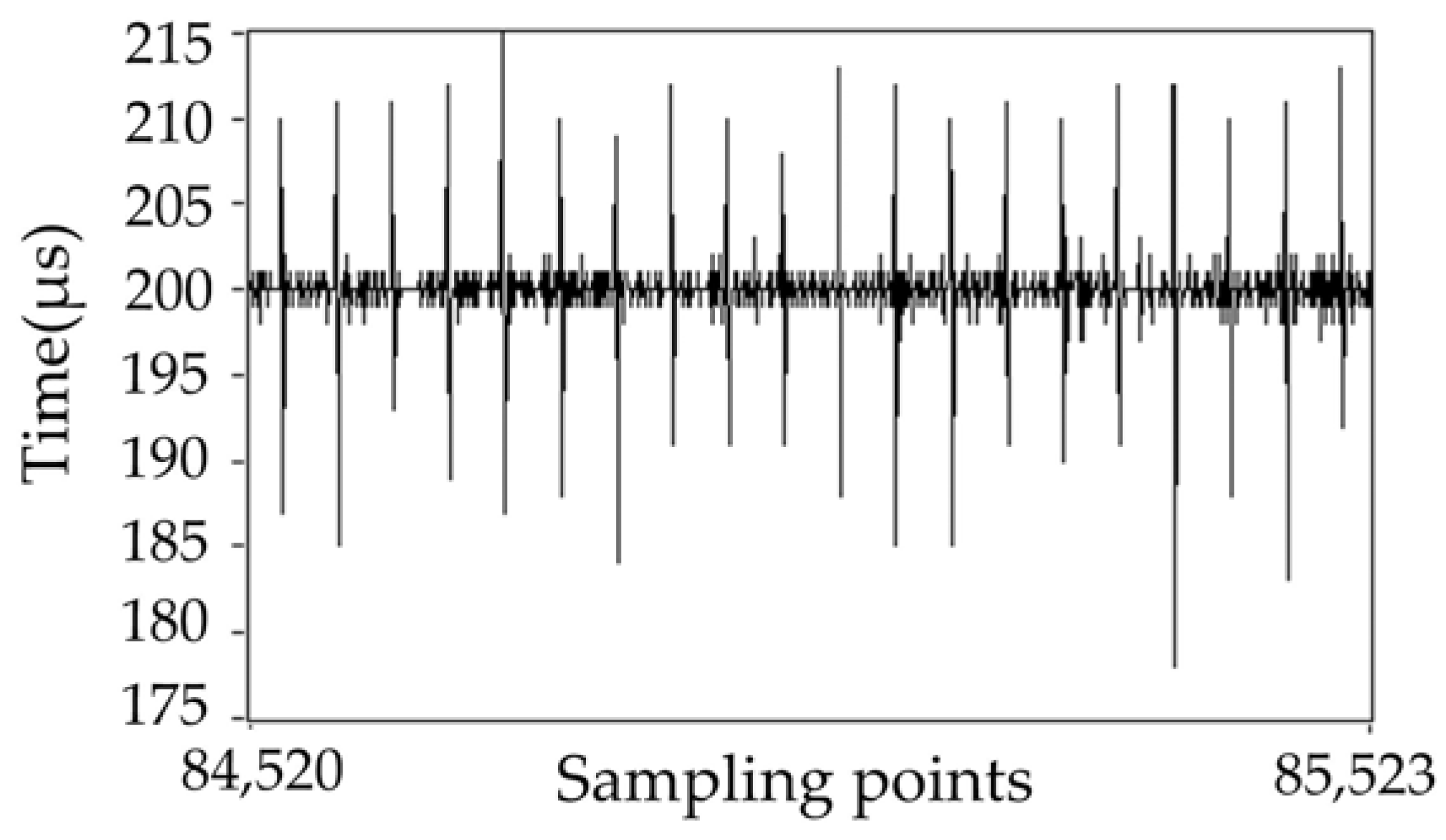
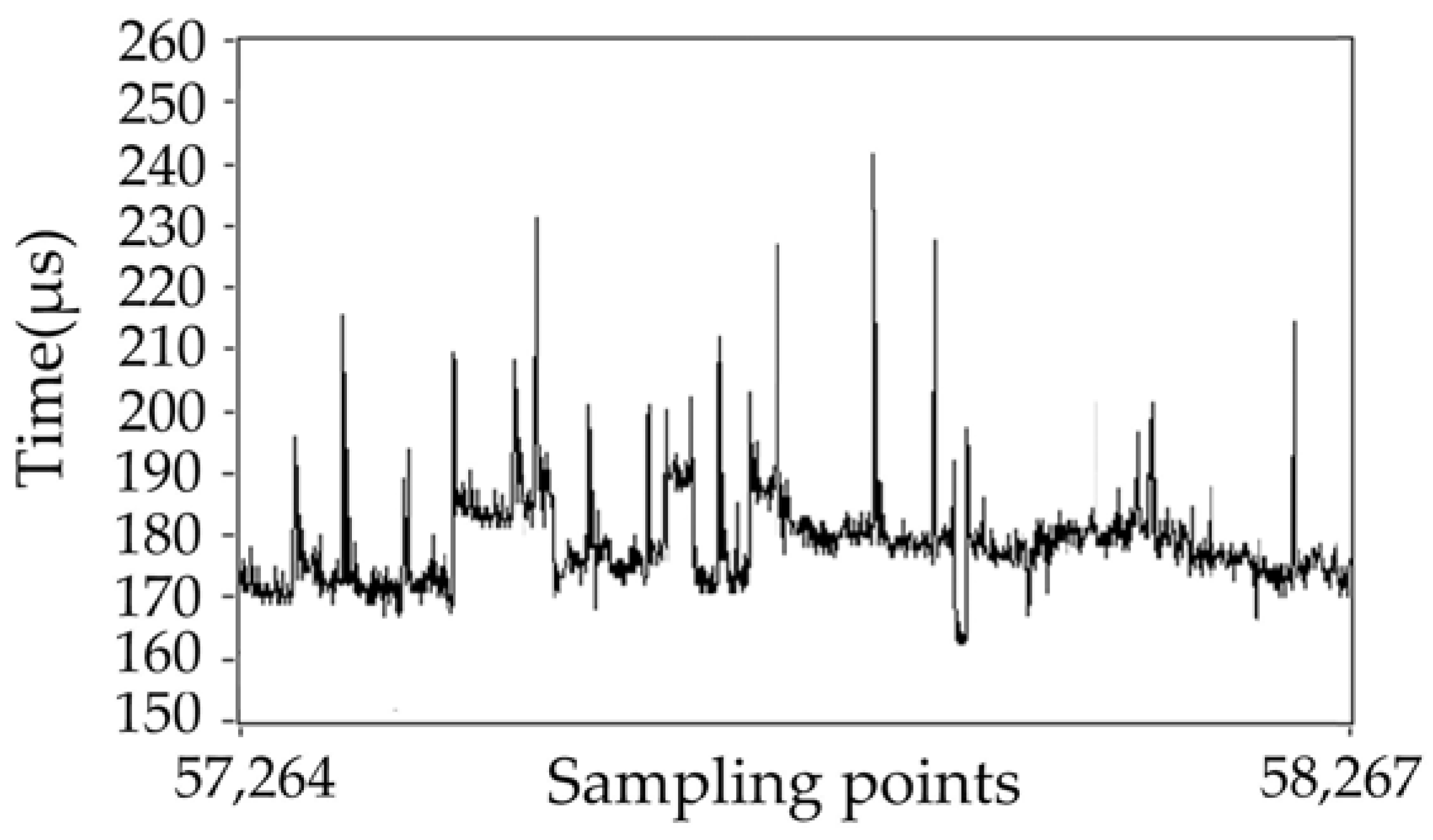
5.3. System Real-Time Performance Validation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rovers, J.M.M.; Jansen, J.W.; Compter, J.C.; Lomonova, E.A. Analysis Method of the Dynamic Force and Torque Distribution in the Magnet Array of a Commutated Magnetically Levitated Planar Actuator. IEEE Trans. Ind. Electron. 2012, 59, 2157–2166. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Kim, J.W. Design and Control of a Compact Lightweight Planar Position Moving over a Concentrated-Field Magnet Matrix. IEEE/ASME Trans. Mechatron. 2013, 18, 1090–1099. [Google Scholar] [CrossRef]
- Wang, L.M.; Tang, Y.P. Fuzzy Cross-coupling Control for Dual Linear Motors based on Preview Feedforward Compensation. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 2138–2142. [Google Scholar]
- Koren, Y. Cross-coupled Biaxial Computer Control for Manufacture Systems. ASME J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Yan, M.T.; Lee, M.H.; Yen, P.L. Theory and Application of a Combined Self-tuning Adaptive Control and Cross Coupling Control in a Retrofit Milling Machine. Mechatronics 2005, 15, 193–211. [Google Scholar] [CrossRef]
- Lin, F.J.; Hsieh, H.J.; Chou, P.H.; Lin, Y.S. Digital Signal Processor-Based Cross-Coupled Synchronous Control of Dual Linear Motors via Functional Link Radial Basis Function Network. IET Control Theory Appl. 2011, 5, 552–564. [Google Scholar] [CrossRef]
- Shi, R.; Lou, Y.J.; Shao, Y.Q.; Li, J.G.; Chen, H.Y. A Novel Contouring Error Estimation for Position-loop Cross-Coupled Control of Biaxial Servo Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea, 28–30 May 2016; pp. 2197–2202. [Google Scholar]
- Barton, K.L.; Alleyne, A.G. A Cross-Coupled Iterative Learning Control Design for Precision Motion Control. IEEE Trans. Control Syst. Technol. 2008, 16, 1218–1231. [Google Scholar] [CrossRef]
- Sun, D.; Shao, X.; Feng, G. A Model-Free Cross-Coupled Control for Position Synchronization of Multi-Axis Motions: Theory and Experiments. IFAC Proc. Vol. 2005, 38, 1–6. [Google Scholar] [CrossRef]
- Sun, D. Position Synchronization of Multiple Motion Axes with Adaptive Coupling Control. Automatica 2003, 39, 997–1005. [Google Scholar] [CrossRef]
- Sun, D.; Feng, G.; Lam, C.M.; Dong, H. Orientation Control of a Differential Mobile Robot through Wheel Synchronization. IEEE/ASME Trans. Mechatron. 2005, 10, 345–351. [Google Scholar] [CrossRef]
- Zhao, D.; Li, S.; Gao, F.; Zhu, Q. Robust Adaptive Terminal Sliding Mode-Based Synchronized Position Control for Multiple Motion Axed Systems. IET Control Theory Appl. 2009, 3, 136–150. [Google Scholar] [CrossRef]
- Wang, L.M.; Zhang, Z.X.; Li, X.Y. The IT2FNN Synchronous Control for H-type Gantry Stage Driven by Dual Linear Motors. In Proceedings of the 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; pp. 4716–4721. [Google Scholar]
- Lin, F.J.; Chou, P.H.; Lin, Y.S. DSP-Based Cross-Coupled Synchronous Control for Dual Linear Motors via Intelligent Complementary Sliding Mode Control. IEEE Trans. Ind. Electron. 2012, 59, 1061–1073. [Google Scholar] [CrossRef]
- Yu, D.M.; Liu, D.; Hu, Q. Synchronous Control for a Dual Linear Motor of Moving Gantry Machining Centers Based on Improved Sliding Mode Variable Structure and Decoupling Control. In Proceedings of the IEEE Control and Decision Conference, Taiyuan, China, 23–25 May 2012; pp. 2525–2528. [Google Scholar]
- Sun, X.D.; Shi, Z.; Chen, L.; Yang, Z.B. Internal Model Control for a Bearingless Permanent Magnet Synchronous Motor Based on Inverse System Method. IEEE Trans. Energy Convers. 2016, 31, 1539–1548. [Google Scholar] [CrossRef]
- Fang, J.C.; Ren, Y. Decoupling Control of Magnetically Suspended Rotor System in Control Moment Gyros Based on an Inverse System Method. IEEE/ASME Trans. Mechatron. 2012, 17, 1133–1144. [Google Scholar] [CrossRef]
- Wang, X.R.; Ma, H. Research on Feedback Linearization Control of Three-Phase Inverter Based on Inverse System. In Proceedings of the IEEE Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 1353–1357. [Google Scholar]
- Wang, T.S.; Liu, C.C.; Lei, G.; Guo, Y.G.; Zhu, J.G. Model Predictive Direct Torque Control of Permanent Magnet Synchronous Motors with Extended Set of Voltage Space Vectors. IET Electr. Power Appl. 2017, 11, 1376–1382. [Google Scholar] [CrossRef]
- Wang, X.D.; Xia, T.; Xu, X.Z.; Feng, H.C. Design of the Particle Swarm Optimized PID for Permanent Magnet Synchronous Linear Motor. In Proceedings of the IEEE International Conference on Electrical Machines and Systems, Hangzhou, China, 22–25 October 2014; pp. 2289–2293. [Google Scholar]
- Cheema, M.A.M.; Fletcher, J.E.; Rahman, M.F.; Xiao, D. Optimal, Combined Speed, and Direct Thrust Control of Linear Permanent Magnet Synchronous Motors. IEEE Trans. Energy Convers. 2016, 31, 947–958. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| Pole pitch τ | 16 | Mm |
| Flux of permanent magnet ψf | 0.211 | Wb |
| Winding resistance of each phase R | 2.1 | Ω |
| Air gap h | 1 | Mm |
| q-axis inductance Lq | 0.0163 | H |
| d-axis inductance Lq | 0.0163 | H |
| Mass of mover | 0.6 | Kg |
| Rotational inertia J | 0.382 | kg·m2 |
| force arm in Y direction l | 0.42 | M |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, C.; Zhang, C.; Lu, H. H-Shaped Multiple Linear Motor Drive Platform Control System Design Based on an Inverse System Method. Energies 2017, 10, 1990. https://doi.org/10.3390/en10121990
Qin C, Zhang C, Lu H. H-Shaped Multiple Linear Motor Drive Platform Control System Design Based on an Inverse System Method. Energies. 2017; 10(12):1990. https://doi.org/10.3390/en10121990
Chicago/Turabian StyleQin, Caiyan, Chaoning Zhang, and Haiyan Lu. 2017. "H-Shaped Multiple Linear Motor Drive Platform Control System Design Based on an Inverse System Method" Energies 10, no. 12: 1990. https://doi.org/10.3390/en10121990





