High-Gain Disturbance Observer-Based Robust Load Frequency Control of Power Systems with Multiple Areas

Abstract

This paper proposes a high-gain disturbance observer (HDOB)-based controller for load frequency control (LFC) of power systems with multiple areas. The main goal of LFC problem is to maintain the frequency to its nominal value. The objective of this paper is to reject frequency variations due to abrupt load changes and diverse uncertainties (e.g., inertia and damping parameters, and interconnection topology, etc.) by employing the HDOB for the LFC. The simulation results demonstrate the effectiveness of the proposed HDOB-based LFC by showing that it successfully rejects frequency variations owing to load changes and frequency variations occurring in various locations in interconnected power systems. Besides, it is shown that the proposed LFC can eliminate frequency deviations although there are delays in transmission among the power systems with multiple areas.

1. Introduction

Frequency is an important quality index in power systems since it indicates if the balance between the electrical load and the power supplied by generators is maintained. A large frequency deviation can harm equipment, decay load performance, cause the transmission lines to be overloaded, damage protection schemes, and ultimately lead to the frequency instability. Frequency instability is the condition where the system fails to maintain its frequency within a certain operating point. Since frequency is proportional to the rotational speed of the generator, the problem of frequency control may be directly translated into a speed control problem of turbine-generator unit.

Frequency control is constructed by three levels: primary, secondary, and tertiary control. Primary control is provided in all generating units and responds within few seconds. As soon as the imbalance occurs, the governor changes its speed with a certain proportional action. Under normal operation, the primary control can attenuate small frequency deviation, but for larger deviation, secondary control is needed. Since the primary control is nothing but the proportional control from control theoretic point of view, it cannot guarantee the zero-steady state error. Secondary control is provided to steer frequency deviation to zero. Secondary control is commonly referred as load frequency control (LFC). Following a serious situation, if the frequency is quickly dropped to a critical value, tertiary control may be required to restore the nominal frequency.

In this paper, interconnected power systems are considered. Interconnected electric power systems allow utilizing tie-lines to transmit power from one area to another area. Hence any load disruption can cause frequency fluctuation due to change of tie line power deviation. LFC aims to drive frequency deviation and tie line power deviation to zero under unknown load in power systems. The effect of the system frequency due to load power change is described by a swing equation [1]. However, the component of power systems such as generators and loads are dynamic, thus result in uncertain parameters in the swing equation. Hence the LFC has to be able to handle the frequency under this circumstance. The LFC needs to get the frequency from all interconnected areas and its own frequency to determine the proper control effort. Because of transmission distance and filters in measurement devices, the frequency measurements are delayed which may harm the response of the LFC. Therefore, considering the measurement delay is important in designing a proper LFC.

Classical control strategies for the LFC use integral of tracking error as a control signal [1]. However, those methods are incapable of dealing with parameter variations and nonlinearities effectively. Studies on the LFC has been reported using a suboptimal LFC regulator to handle the limitation of power systems observability [2,3]. Various adaptive control techniques are proposed for plant parameter changes in [4,5]. Despite the promising concept of adaptive controllers, the control algorithm is too complicated to implement in large scale systems and can show poor transient performance which can be critical in power systems. Several papers propose an observer for dealing with uncertain load changing in power systems with multiple areas [6,7,8,9,10,11,12,13,14,15,16]. In [6,7,8], a disturbance observer is considered to handle large-scale wind power in power systems. In these applications, the uncertainty and external disturbance are viewed as a total disturbance and rejected by an active disturbance observer proposed by [9,10,11,12,13]. The disturbance is estimated using an extended state observer (ESO) in [15]. However, from [16], higher order ESO is needed to get the perfect estimation. In principle, an exact system model has to be known to design such disturbance observers, which hardly holds in practice due to uncertain parameters (e.g., inertia and damping parameters) in the system.

In this paper, a high-gain disturbance observer (HDOB)-based robust LFC [17] is designed and applied to power systems with multiple areas in order to reject frequency deviations. The HDOB- based LFC consists of two parts: controller for the nominal model and HDOB. The control for the nominal model is designed first under the assumption that there are no uncertainties in the system under consideration. Then, a HDOB is designed to estimate all uncertainties including model uncertainties and external disturbances, and the estimated disturbance is added to the nominal control to reject uncertainties.

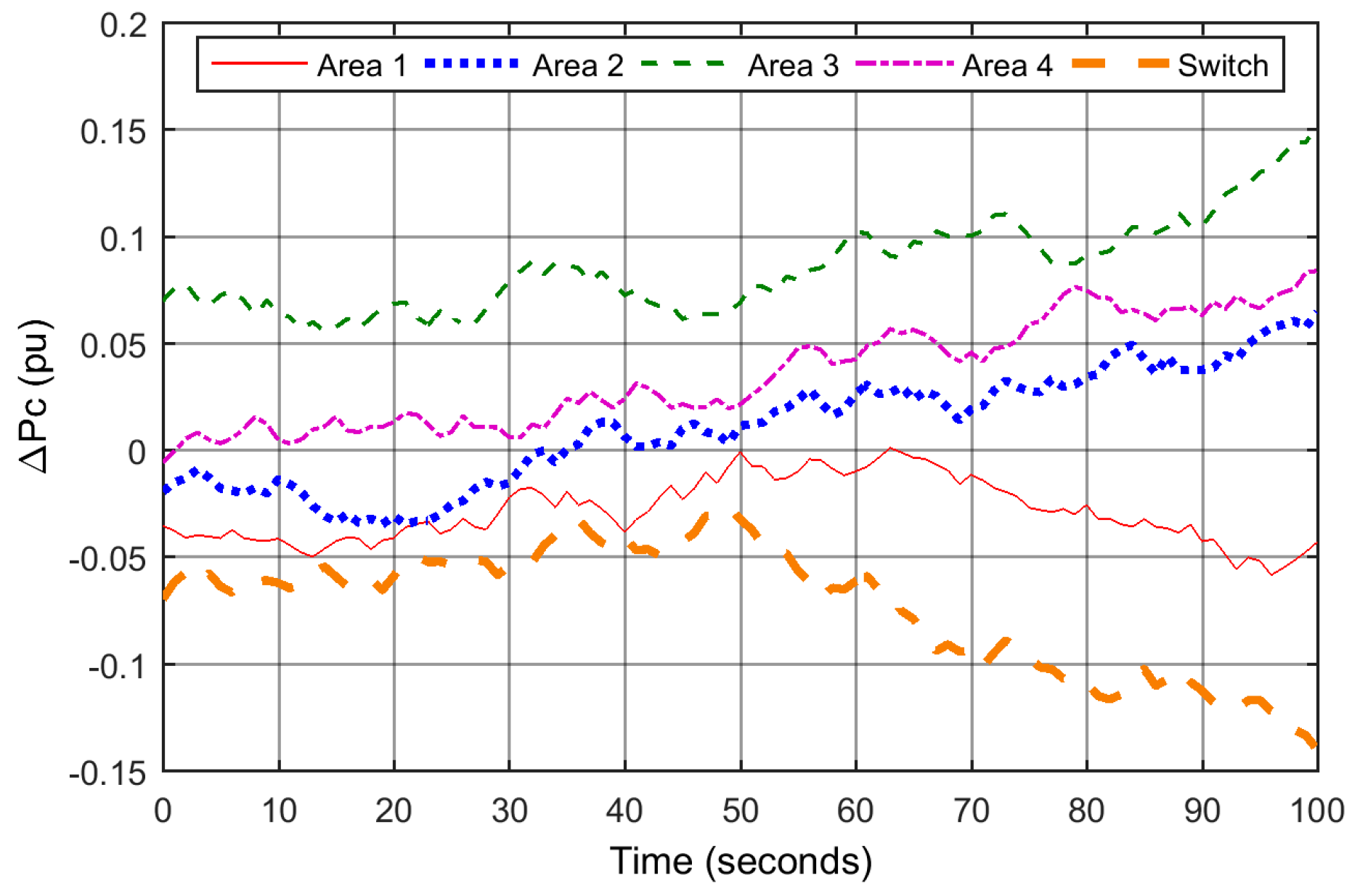
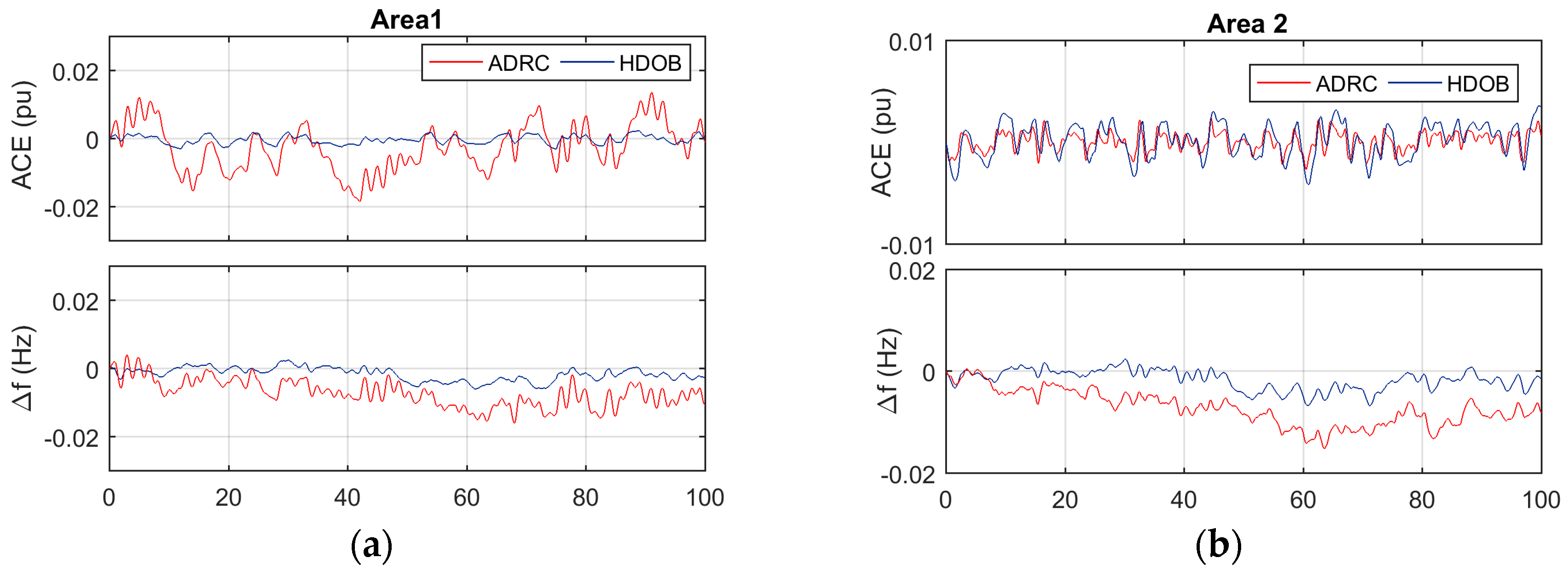
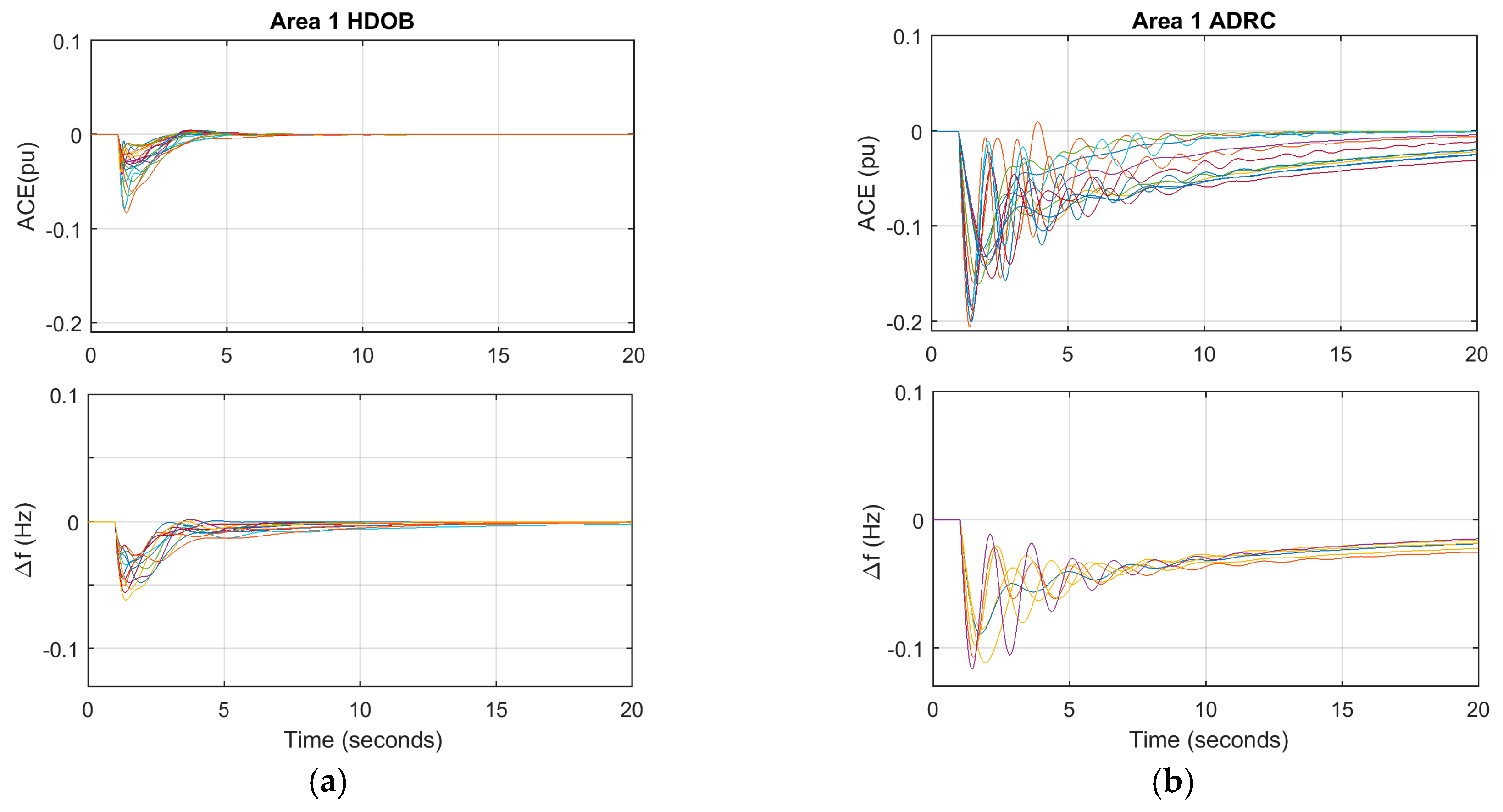
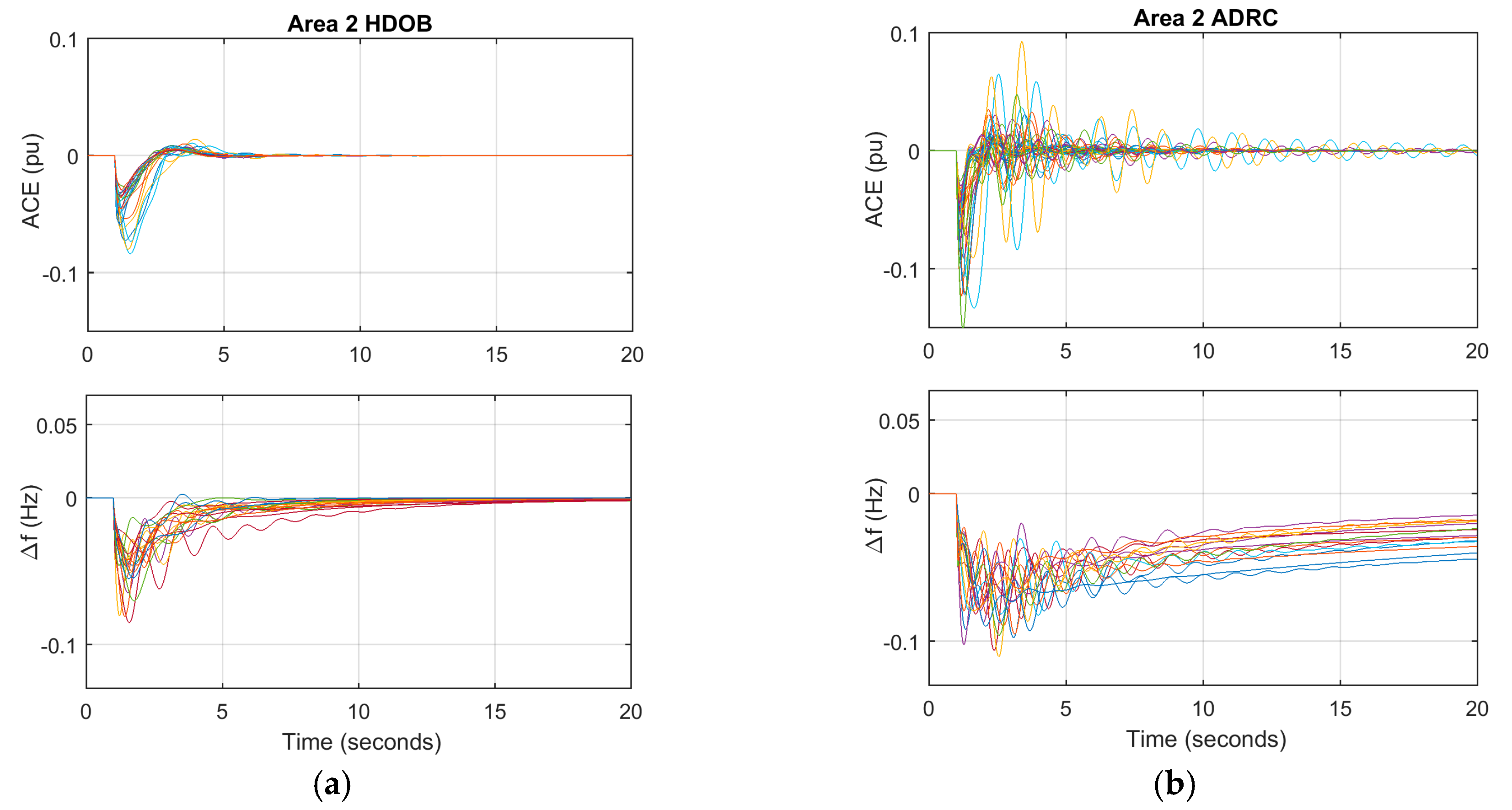
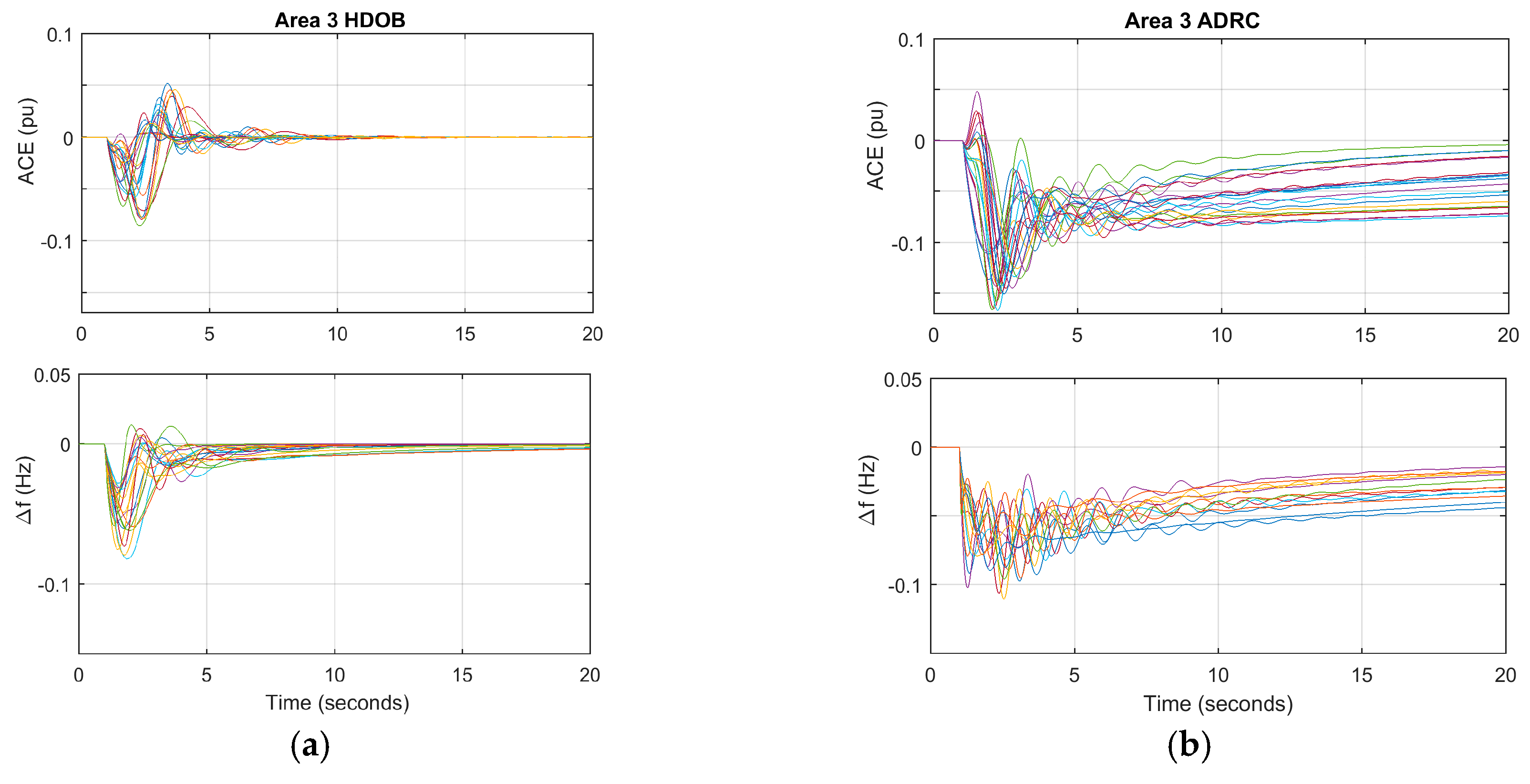
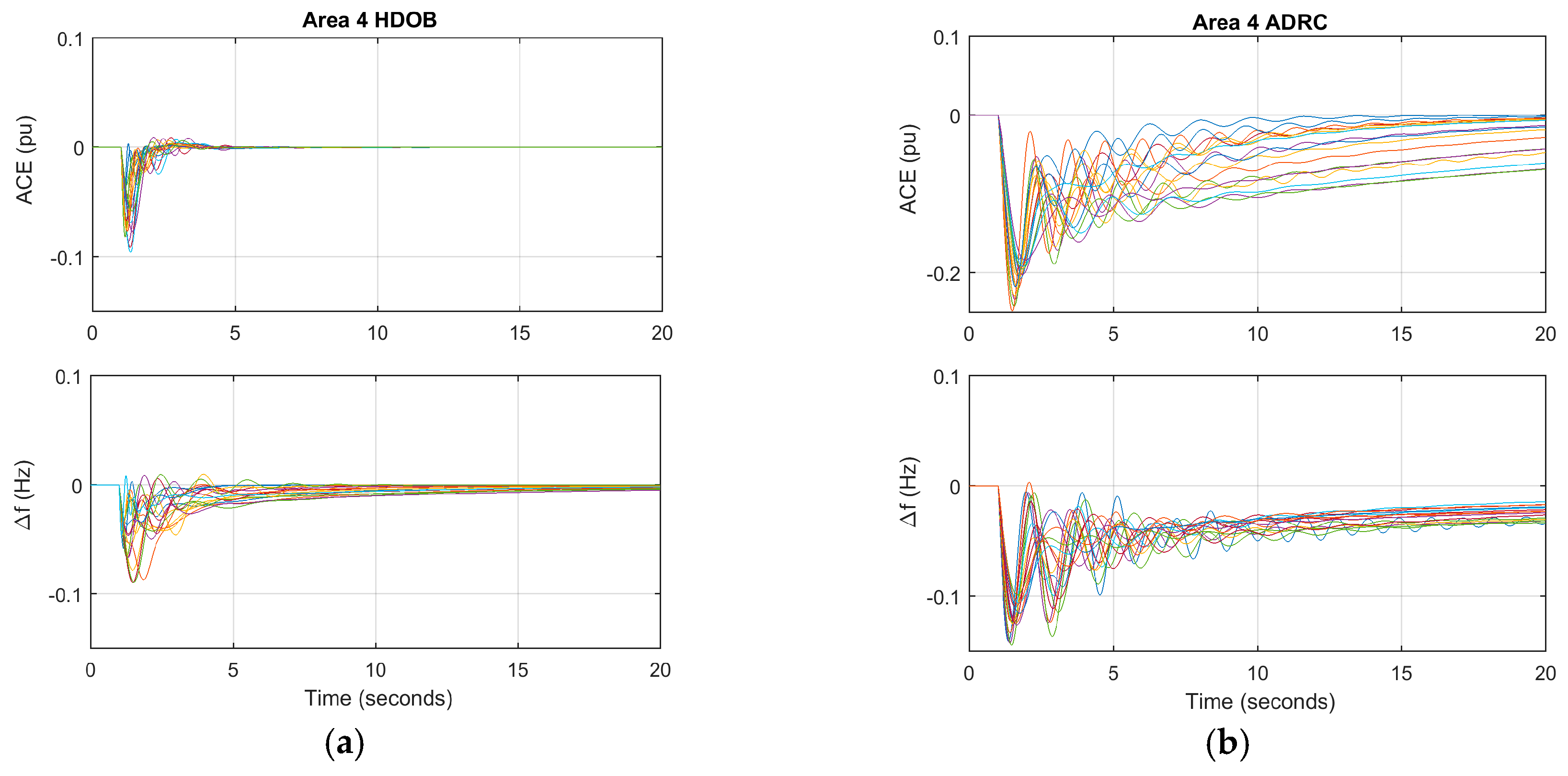
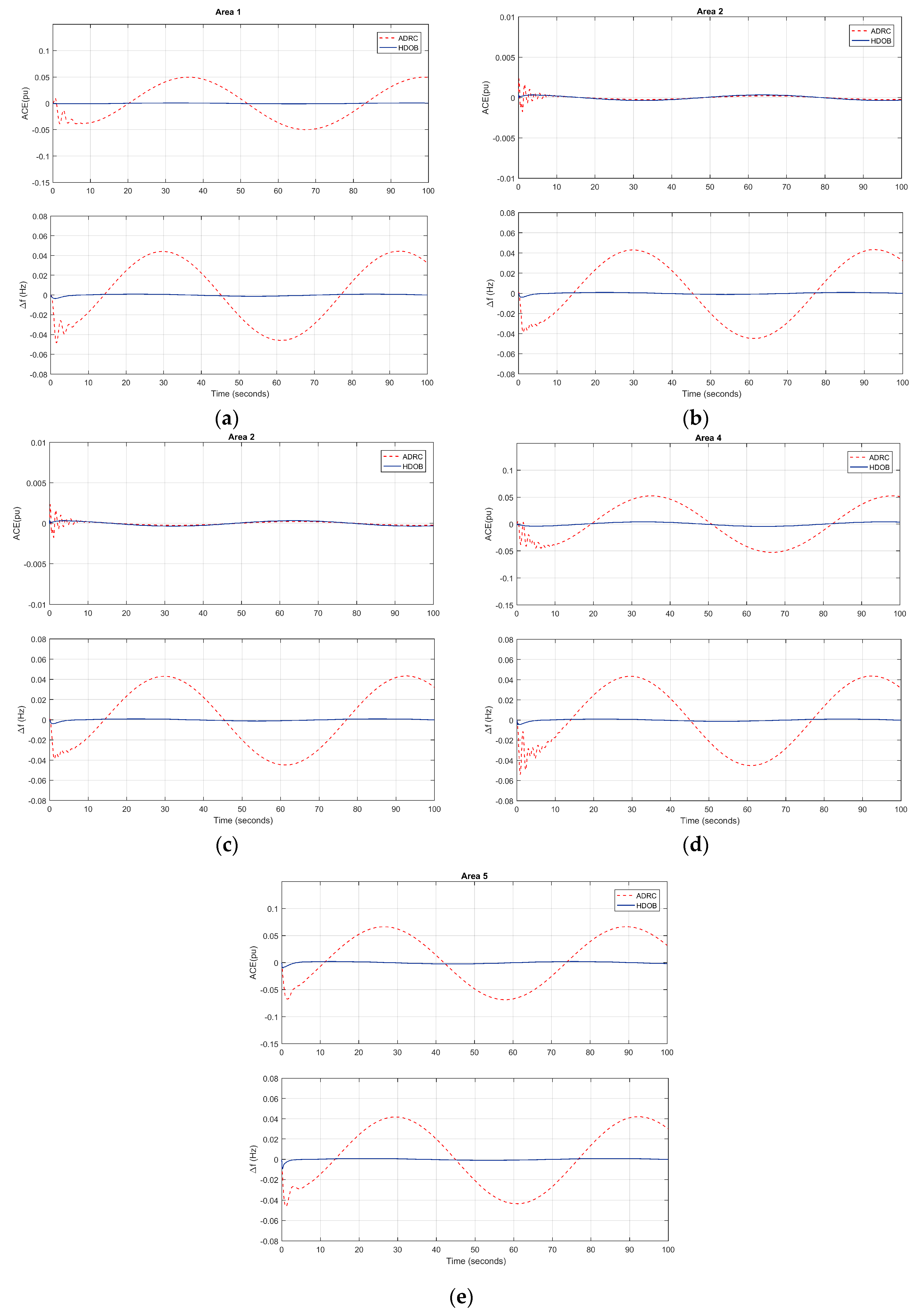
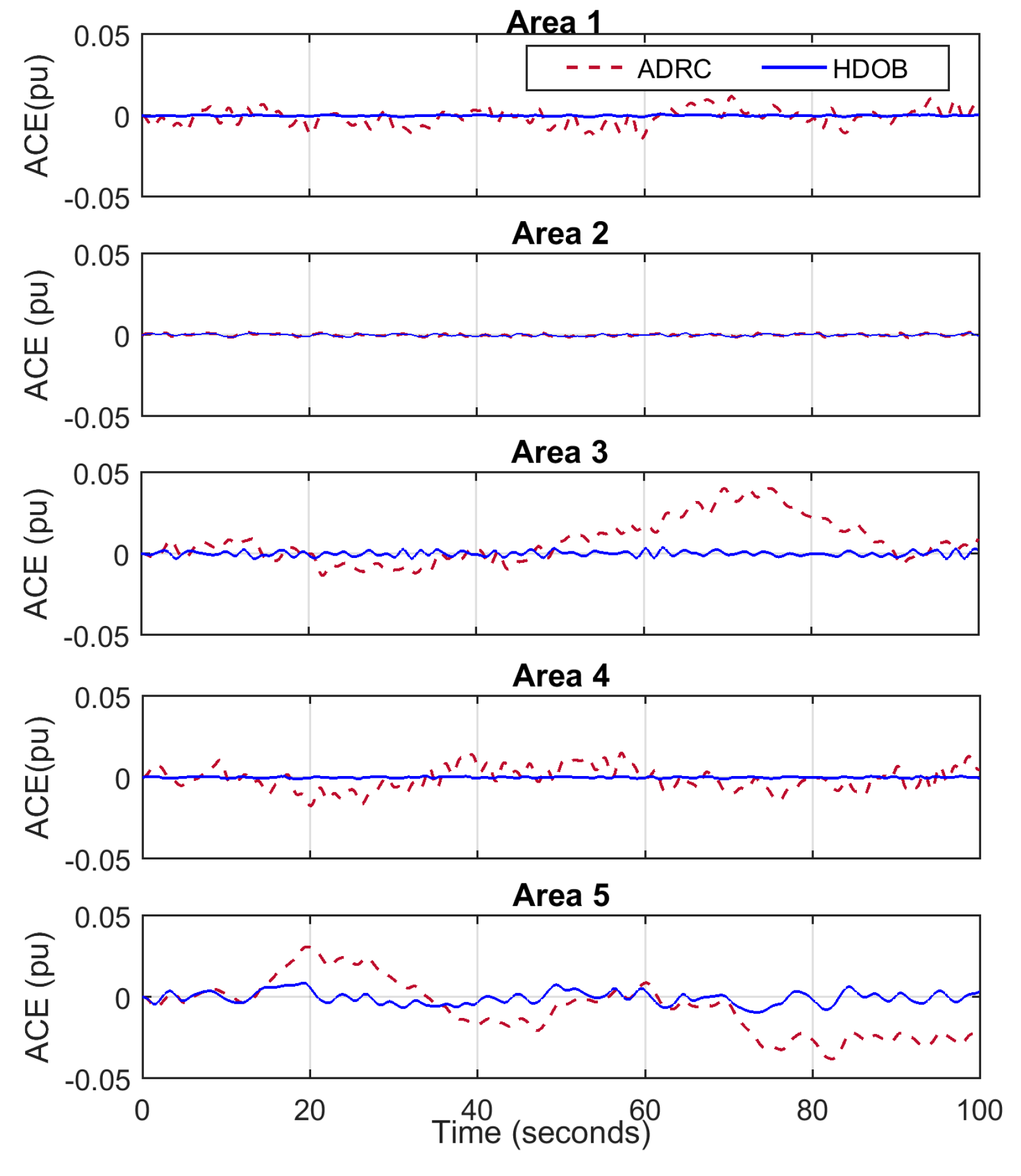
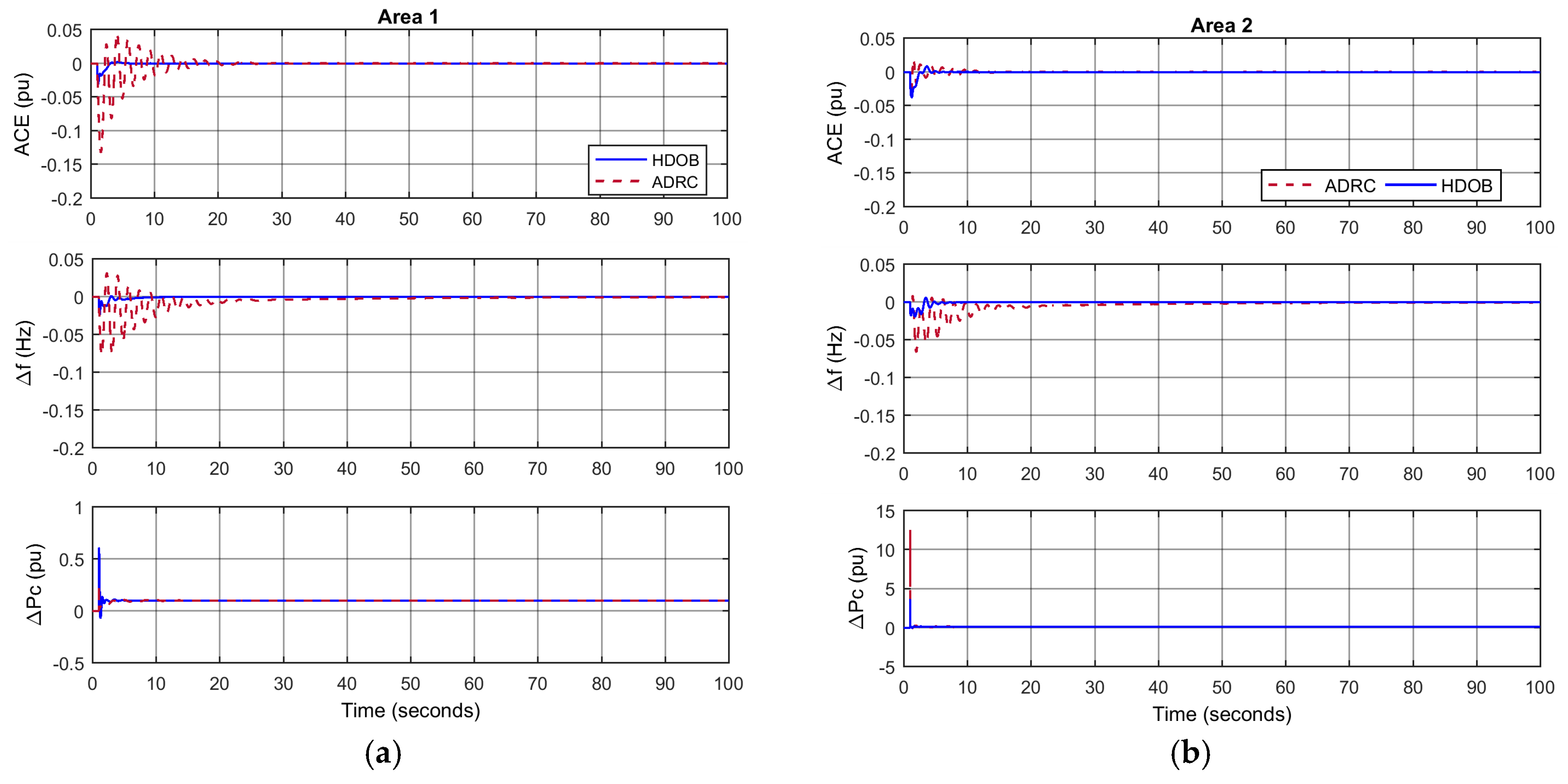
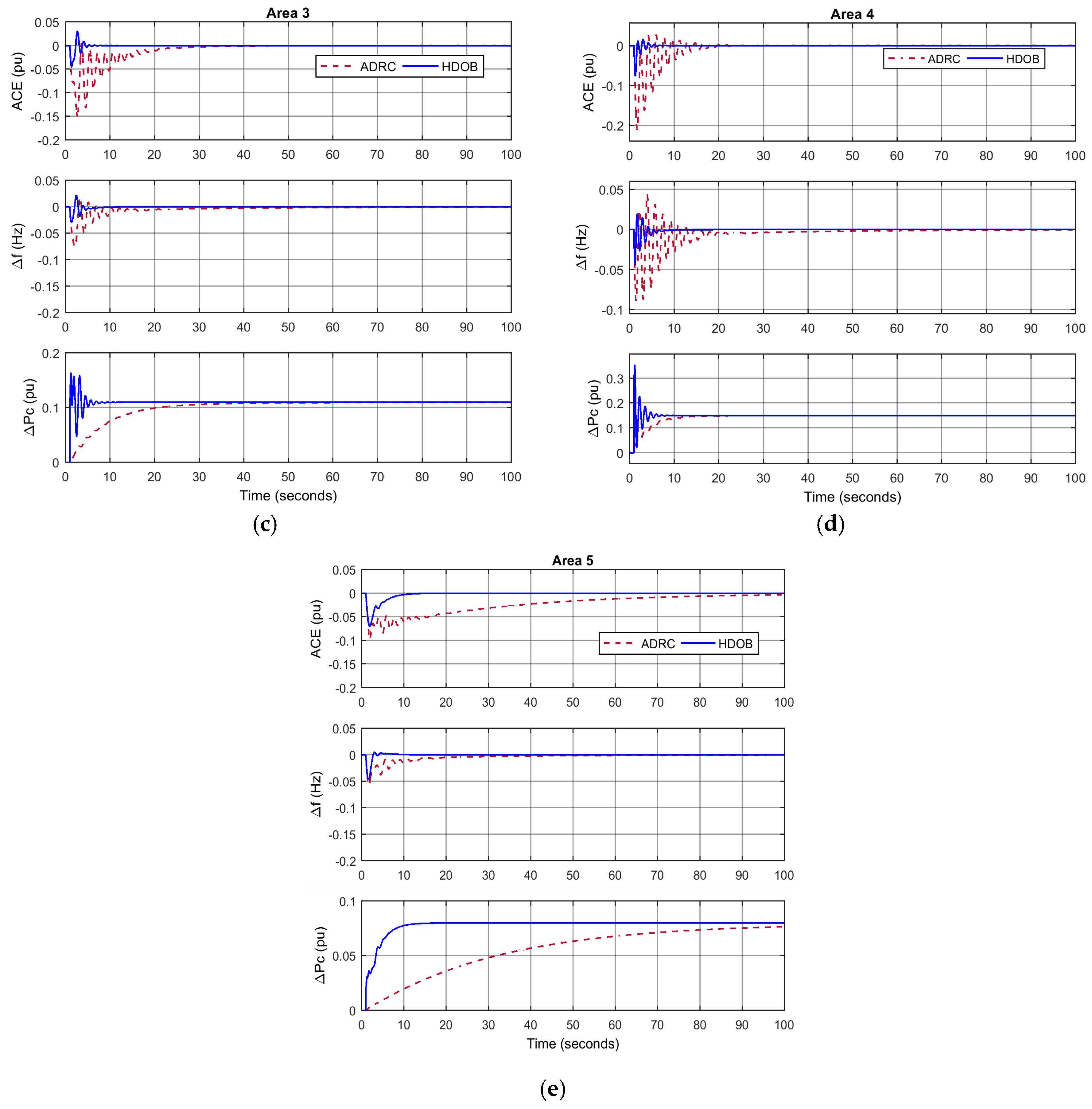
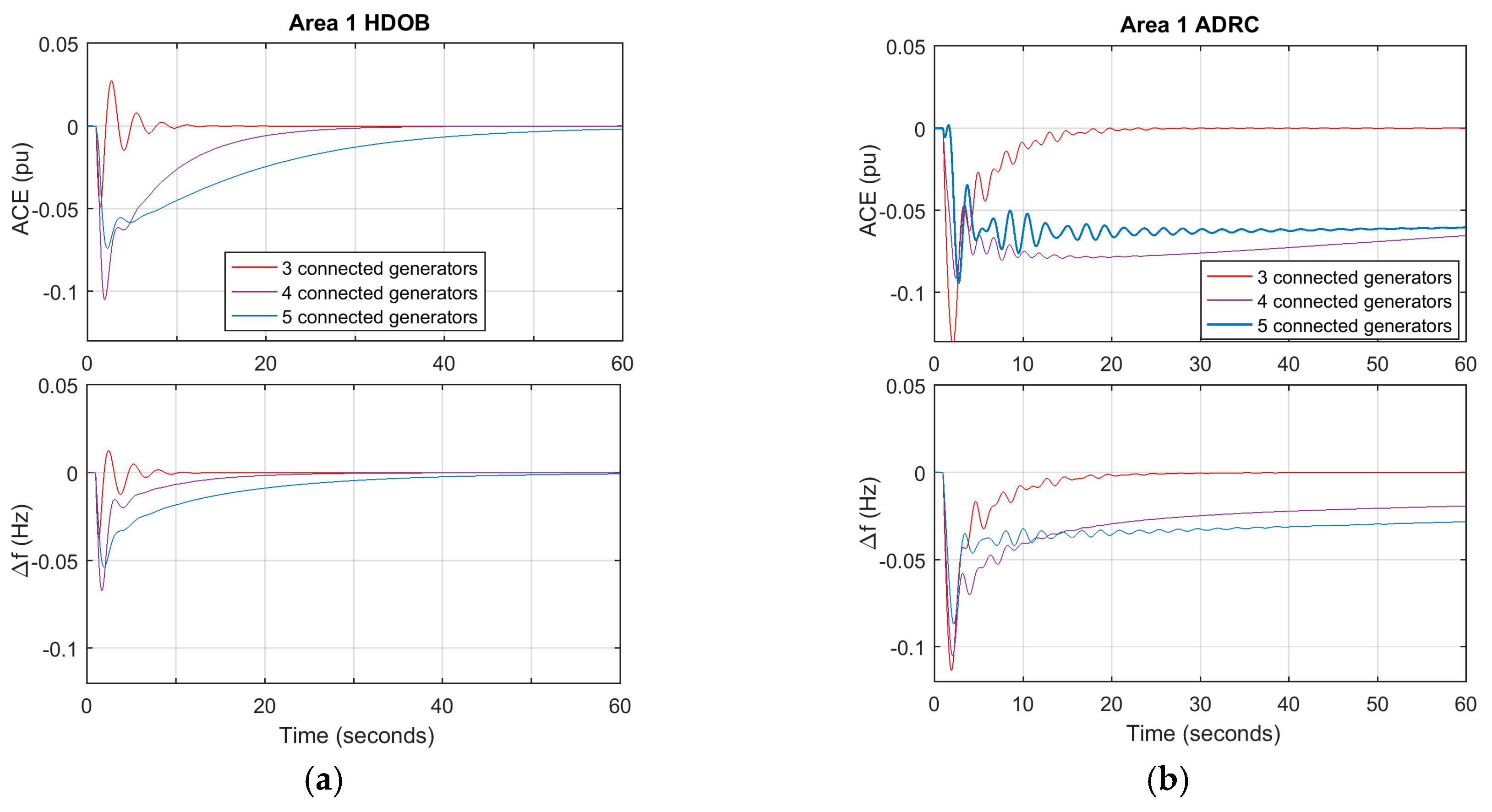
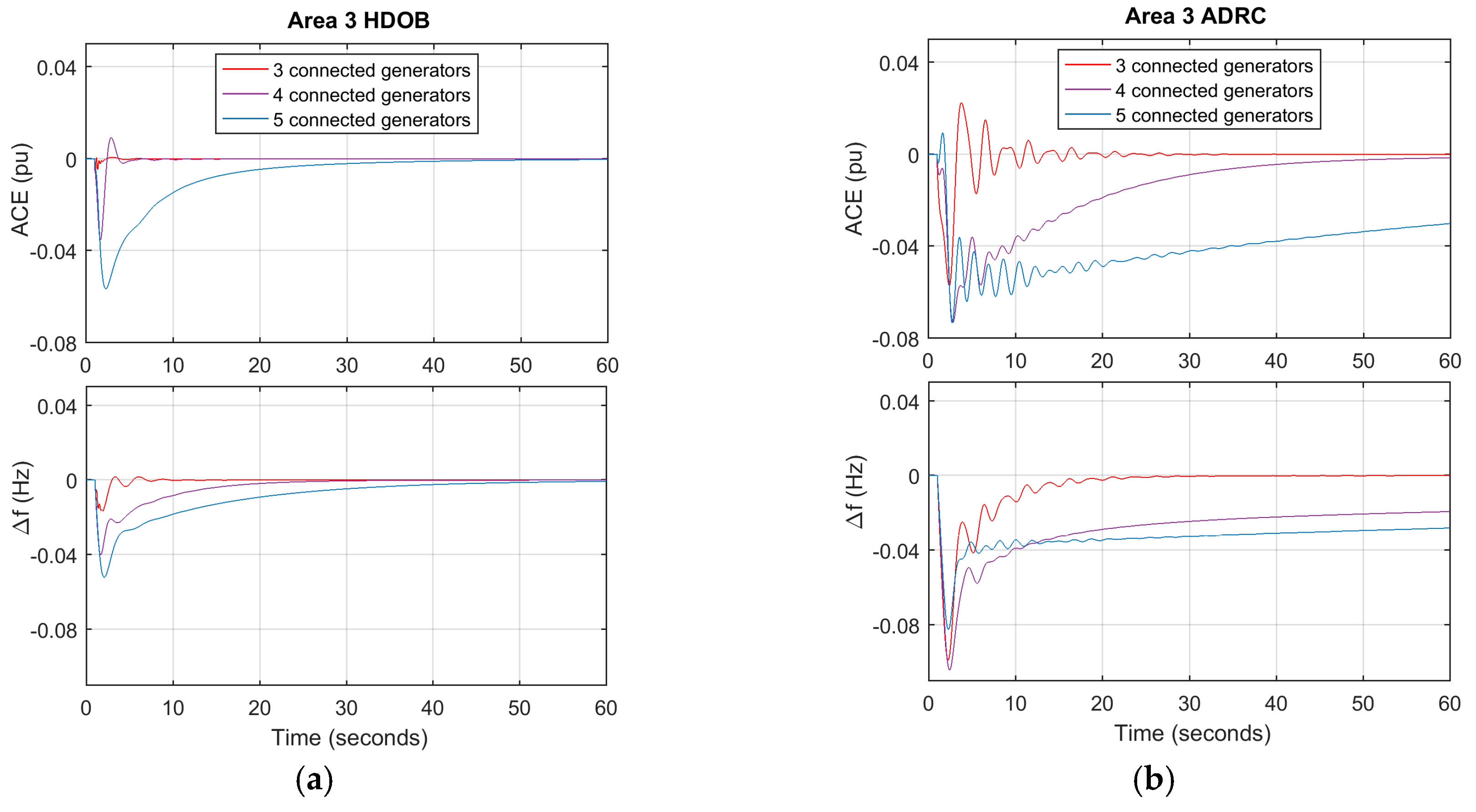
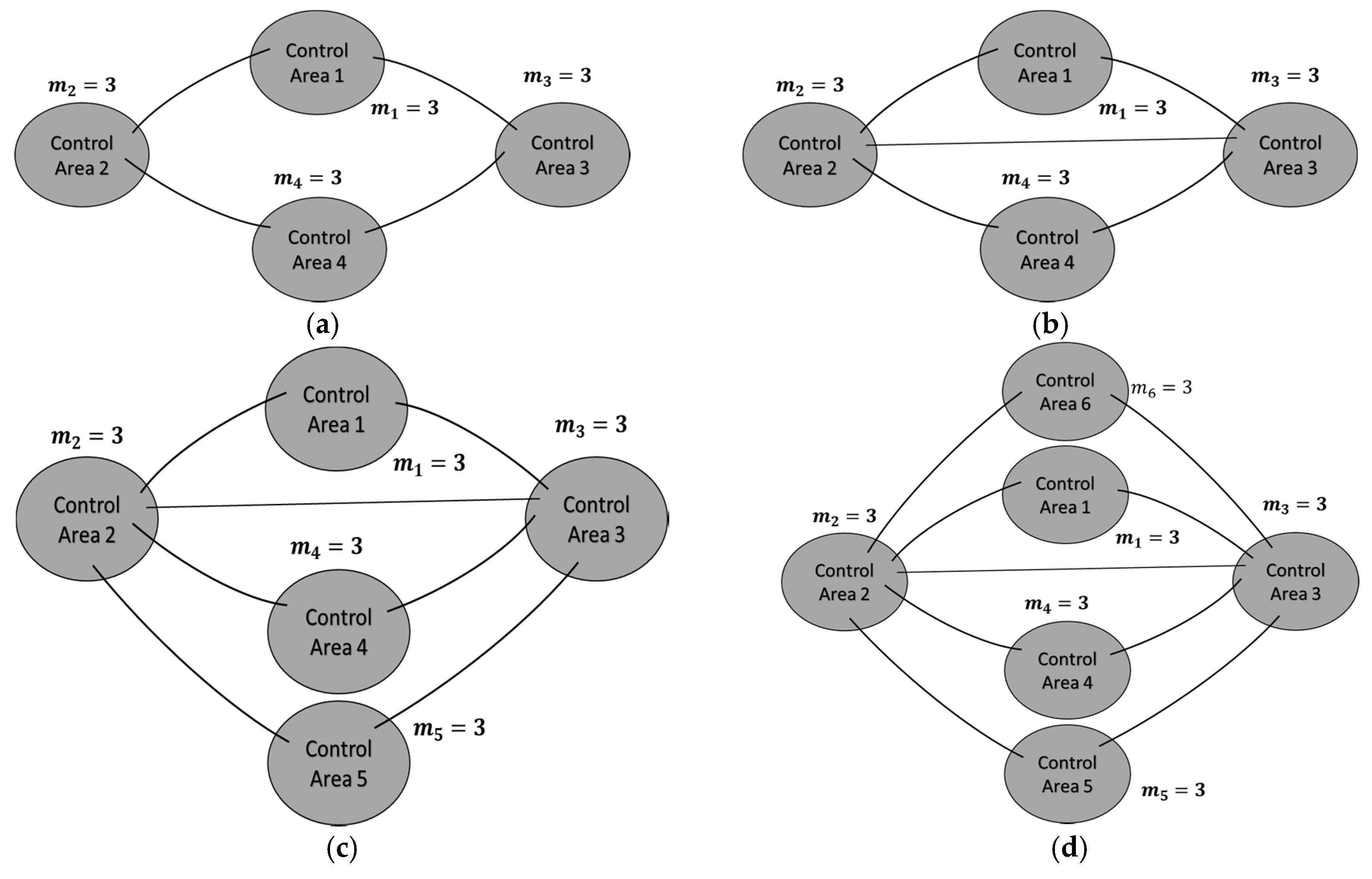
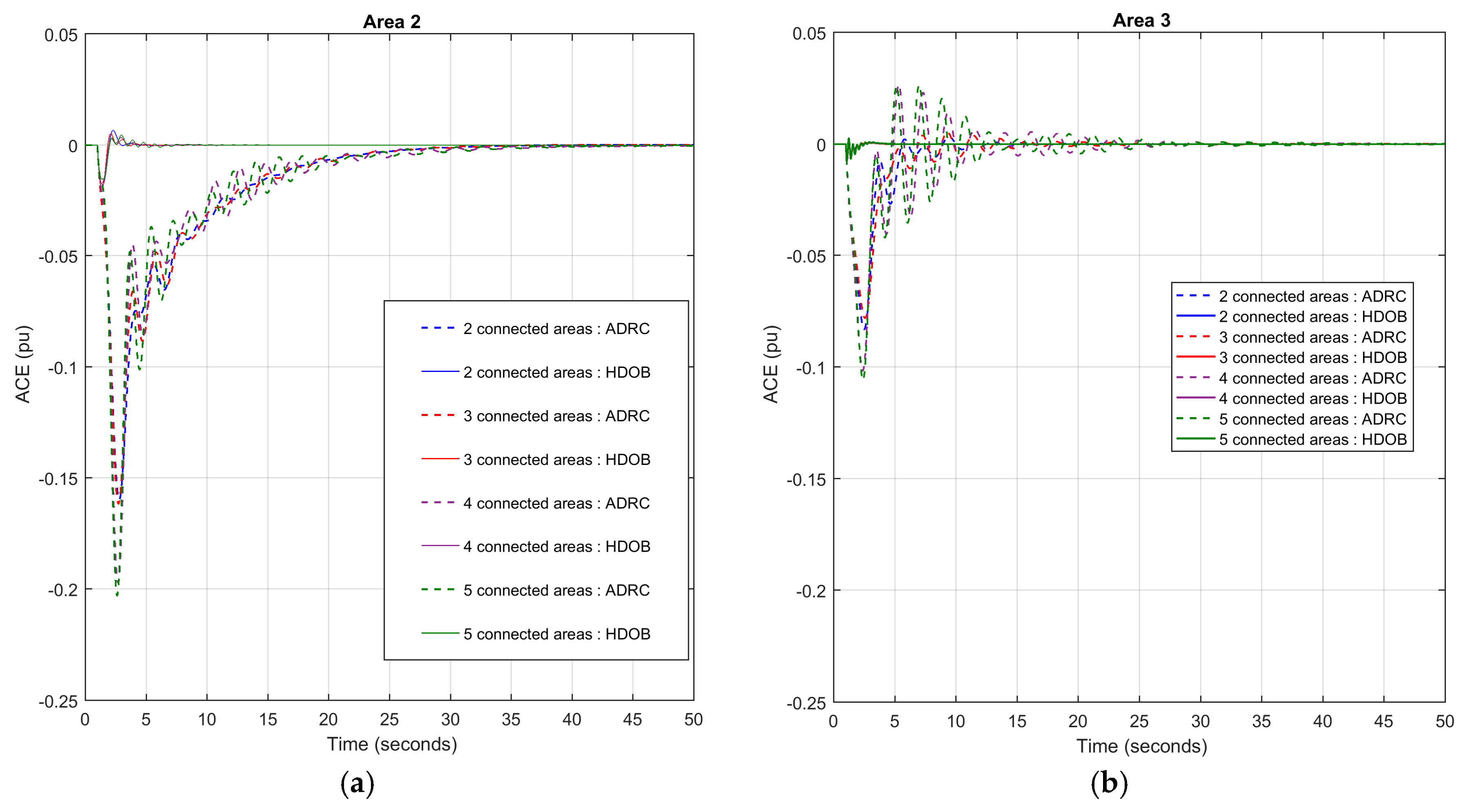
For the purpose of showing the effectiveness of the proposed scheme, three simulation results are given. One shows that the proposed HDOB-based LFC can eliminate the frequency deviation induced by load changes taking place at various locations in power systems under uncertainties in the inertia and damping parameters in the swing equation. The second simulation result demonstrates that the proposed LFC can get rid of the frequency deviation despite the measurement delay which can lead to harmful effect in existing approaches. In addition, a severe uncertainty in power systems is that a generator can trip or even one area can be disconnected from the other power systems areas due to severe fault or operational reason. So, it is necessary to investigate robustness of the proposed LFC against such topology changes. Simulation results demonstrate that the HDOB-based LFC indeed shows robustness against topologies in one area power system and between areas.

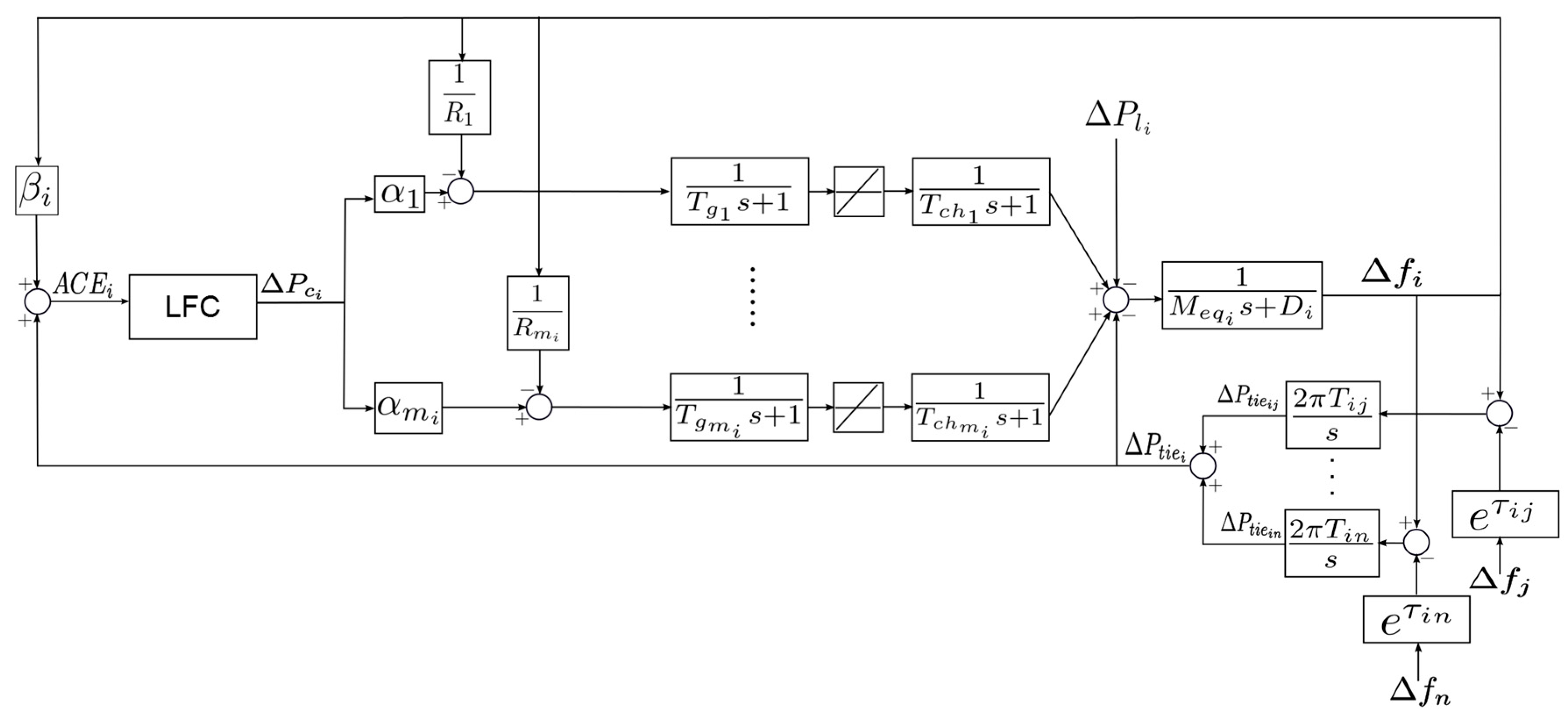
2. Dynamic Model of Power Systems with Multiple Areas

In this section, a mathematical model of power systems with multiple areas for LFC design is introduced [1,11]. A typical power systems with multiple areas is considered in this paper (Figure 1). As shown in Figure 1, each control area has its own load power change $\Delta P_{l_i}.$ Unpredicted fluctuations of load power $\Delta P_{l_i}$ is treated as a disturbance for the system. Under this circumstance, both primary and secondary controls attempt to remove the frequency deviation in each area. The droop coefficient $R_j$ represents the proportional gain used in the primary control. Furthermore, the objective is to design a secondary control (LFC) to improve the result of the primary control.

From Figure 1, the system is comprised of the generators, as an electrical power generation, and a load. The number of the generators in the $i$th area is denoted as $m_i.$The generator model consists of two major generation units: a governor and a turbine. Both are represented in a first order linearized model. The dynamics of the governor can be expressed as:

$$G_{gov}=\frac{1}{T_{g_j}s+1},$$

(1)

and the dynamics of non-reheating turbine unit can be expressed as:

$$G_{tur}=\frac{1}{T_{c{h}_j}s+1},$$

(2)

where $T_{g_j}$ and $T_{c{h}_j}$ are the time constants of the governor and the turbine model in the $j$th generator.

The basis for attaining the regulation function is the tie line bias control concept that is introduced over 50 years ago [18] and widely used to model the power flow between two or more buses [2,3,4,5,6,9,10,11,19,20]. Tie line power deviation $\Delta P_{ti{e}_i}$ is defined as the deviation power exported to the $i$th area and is equal to the sum of all outflowing line power changes in the line that connects to the $i$th area with its neighboring areas:

$$\Delta P_{ti{e}_i}={\displaystyle \sum }_j\Delta P_{ti{e}_{ij}}.$$

(3)

Tie line power change in the $i$th area corresponding to the $j$th area, $\Delta P_{ti{e}_{ij}}$ is defined as:

$$\Delta P_{ti{e}_{ij}}=\frac{2\pi T_{ij}}{s}\left(\Delta f_i-\Delta f_j\right),$$

(4)

where $T_{ij}$ is synchronizing torque coefficient and $\Delta f_i$ and $\Delta f_j$ are frequency deviation of the $i$th area and the $j$th area. For the purpose of taking the measurement delay from the $i$th area to the $j$th area into account, delay ${\tau }_{ij}$ is applied. See $e^{{\tau }_{ij}}$ in Figure 1.

In this LFC model, strongly connected and synchronized generators are in one area power system. Assuming that all generators have coherent response of load changing, yields an equivalent equation as follows:

$$G_{e{q}_i}=\frac{1}{M_{e{q}_i}s+D_i},$$

(5)

where the effects of system loads are lumped into a single damping constant $D_i$ with the summation of inertia constants of all generating units denoted as $M_{e{q}_i}$. Area control error (ACE) is used to obtain power deviation reference. $AC{E}_i$ represents the surplus or deficiency of the $i$th area generation and is the summation of tie line power deviation $\Delta P_{ti{e}_i}$ and frequency deviation $\Delta f_i$ multiplied by bias factor ${\beta }_i$:

$$AC{E}_i=\Delta P_{ti{e}_i}+{\beta }_i\Delta f_i.$$

(6)

Along with the primary control, the secondary control converts ACE to a command and drives the speed changer of the governing system. Then the speed governing characteristic is shifted to a new set point and results in the matching load demand. Each corresponding generator produces energy based on its constant share control effort α_k.

Let generating energy $\Delta P_{c_i}\left(t\right)$ as control input $u\left(t\right)$. For $m_i$connected generators in the $i$th area, frequency deviation $\Delta f_{i }$ can be represented in a function of $u\left(t\right)$, load change $\Delta P_{l_i}\left(t\right)$, and the summation of all frequency deviation from other areas $\Delta f_d\left(t\right)$. The function can be written in frequency domain as follows:

$$\begin{array}{c}\Delta f_{i }\left(s\right)=\frac{1}{M_{e{q}_i}.s+D_i}[\left(\frac{{\alpha }_1}{{\rho }_1\left(s\right)}+\frac{{\alpha }_2}{{\rho }_2\left(s\right)}+\dots +\frac{{\alpha }_k}{{\rho }_{m_i}\left(s\right)}\right)U\left(s\right)\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\left(\frac{1}{R_1{\rho }_1\left(s\right)}+\frac{1}{R_2{\rho }_2\left(s\right)}+\dots +\frac{1}{R_k{\rho }_{m_i}\left(s\right)}\right)\Delta f_{i }\left(s\right)- \Delta P_{l_i}\left(s\right)+\frac{T}{s}{e}^{-\tau }\Delta f_d\left(s\right)]\hfill \end{array}$$

(7)

where ${\alpha }_k$ is the constant share effort for the $k$th generator, $T$ and ${\rho }_k\left(s\right)$ are defined as

$$T=2\pi {{\displaystyle \sum }}_j{T}_{ij},$$

(8)

$${\rho }_k\left(s\right)=\left(T_{g_k}s+1\right)\left(T_{c{h}_k}s+1\right).$$

(9)

Hence, the general function of frequency deviation $\Delta f_{i }$ is written as follows:

$$\Delta f_i\left(s\right)=\frac{1}{\gamma \left(s\right)}\left(\sigma \left(s\right)u\left(s\right)-\Delta P_{l_i}\left(s\right)+\frac{T}{s}{e}^{-\tau }\Delta f_d\left(s\right)\right)$$

(10)

where:

$$\begin{array}{c}\gamma \left(s\right)=M_{e{q}_i}s+D_i+{{\displaystyle \sum }}_{k=1}^{m_i}\frac{1}{R_k{\rho }_k\left(s\right)},\\ \sigma \left(s\right)={{\displaystyle \sum }}_{k=1}^{m_i}\frac{{\alpha }_k}{{\rho }_k\left(s\right)}.\end{array}$$

(11)

In this LFC problem, the ACE is considered as the system output $y\left(t\right)$. With $\Delta f_{i }$ defined in (10), the output $y\left(t\right)$ can be expressed as:

$$\begin{array}{cc}Y\left(s\right)\hfill & =\frac{1}{\gamma \left(s\right)}\left[\left({\beta }_i+\frac{T}{s}\right)\sigma \left(s\right)U\left(s\right)-\left({\beta }_i+\frac{T}{s}\right)\Delta P_{l_i}\left(s\right)+\frac{T}{s}\left({\beta }_i+\frac{T}{s}-\gamma \left(s\right)\right)e^{-\tau }\Delta f_d\left(s\right)\right]\hfill \\ & =G_u\left(s\right)U\left(s\right)+G_l\left(s\right)\Delta P_{l_i}\left(s\right)+G_f\left(s\right)e^{-\tau }\Delta f_d\left(s\right),\hfill \end{array}$$

(12)

where $Y\left(s\right)$ is the Laplace transform of $y\left(t\right)$. In (12), $G_l\left(s\right)\Delta P_{l_i}\left(s\right)$ and $G_f\left(s\right)e^{-\tau }\Delta f_d\left(s\right)$ can be treated as one external disturbance $D_{ex}\left(s\right)$. In other words, the $i$th area considers neighboring frequency deviation and power load change as its external disturbance. In view of (12), the input-output relation of the system in the $i$th area can be written as:

$$Y\left(s\right)=G_u\left(s\right)U\left(s\right)+D_{ex}\left(s\right)$$

(13)

where $G_u\left(s\right)$ is defined as:

$$G_u\left(s\right)=\frac{1}{\gamma \left(s\right)}\left({\beta }_i+\frac{T}{s}\right)\sigma \left(s\right)=\frac{a_{\left(2m_i-1\right)}{s}^{\left(2m_i-1\right)}+a_{\left(2m_i-2\right)}{s}^{\left(2m_i-2\right)}+\dots +a_{1}s+a_0}{b_{\left(2m_i+2\right)}{s}^{\left(2m_i+2\right)}+b_{\left(2m_i+1\right)}{s}^{\left(2m_i+1\right)}+\dots +b_{1}s+b_0}.$$

(14)

Multiplying right and left side in (13) with $1/G_u\left(s\right)$ yields:

$$\left(c_3{s}^3+c_2{s}^2+c_{1}s+c_0+c_{left}\left(s\right)\right)Y\left(s\right)=U\left(s\right)+\frac{D_{ex}\left(s\right)}{G_u\left(s\right)},$$

(15)

where $c_{left}\left(s\right)$ is a proper transfer function. For the purpose of the controller design, it is desirable to obtain a simplest possible model. To this end, the previous equation can be written as:

$$\begin{array}{cc}\left(s^3\right)Y\left(s\right)\hfill & =\frac{1}{c_3}U\left(s\right)+\frac{1}{c_3}\frac{D_{ex}\left(s\right)}{G_u\left(s\right)}-\left(\frac{c_2{s}^2+c_{1}s+c_0+c_{left}\left(s\right)}{c_3}\right)Y\left(s\right)\hfill \\ & =:gU\left(s\right)+D\left(s\right)\hfill \end{array}$$

(16)

where $D\left(s\right)$ denotes a lumped disturbance and $g$ is a parameter. Hence, in the time domain, the model can be expressed as:

$$\stackrel{⃛}{y}\left(t\right)=gu\left(t\right)+d\left(t\right)$$

(17)

where $d\left(t\right)$ is the inverse Laplace transform of $D\left(s\right)$. The corresponding state space model is given by:

$$\begin{gathered} \dot{\mathbf{x}}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\mathbf{x}+\left[\begin{array}{c}0\\ 0\\ g\end{array}\right]u+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]d, \\ y=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\mathbf{x} \end{gathered}$$

(18)

where $x={\left[\begin{array}{ccc}y& \dot{y}& \ddot{y}\end{array}\right]}^T.$ Note that $g$ is determined by other parameters, for example, $T_{g_i}$, $T_{c{h}_i}$, and $M_{e{q}_i}$ and so on. In general, inertia parameter $M_{e{q}_i}$ and damping constant $D_i$ are uncertain. Hence, $g$ is uncertain as well but its upper and lower bounds can be known since those of $M_{e{q}_i}$ and $D_i$ can be known. This paper pays particular attention to the uncertainties in $M_{e{q}_i}$ and $D_i$. Consequently, the resulting model (18) is a third order uncertain model with unknown bounded external disturbances. As a matter of fact, it is not easy to design an observer due to the uncertain parameter $g$ since it is not clear which value is used for $g$ in the observer model. Note that $y\left(t\right)$ representing ACE is the only measurable signal in general.

With the uncertain model in mind, the LFC problem is to design $u$ using the measurement $y\left(t\right)$ such that $\mathbf{x}$ converges to zero despite uncertain $g$ and external disturbance $d$. Note that convergence of $\mathbf{x}$ to zero implies that the frequency is regulated to its nominal value.

The nominal model of the uncertain model can be assumed as:

$$\begin{gathered} \dot{\mathbf{x}}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\mathbf{x}+\left[\begin{array}{c}0\\ 0\\ \overline{g}\end{array}\right]u_r, \\ y=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\mathbf{x} \end{gathered}$$

(19)

where $u_r$ is the controller for the nominal model and $\overline{g}$ denotes the nominal parameter of $g$.

For this nominal model, there are many standard control design methods to regulate the state. For example, pole placement and linear quadratic regulator (LQR) are the representatives of such methods. However, difficulty here is that the original model is uncertain and, in general, the state $x$ is not measurable. Hence, the objective of the LFC is to design a robust output feedback stabilizing control for (18). For control design, it is assumed that the lumped disturbance $d\left(t\right)$ is unknown and bounded. In the next section, a HDOB based robust output feedback control design is presented.

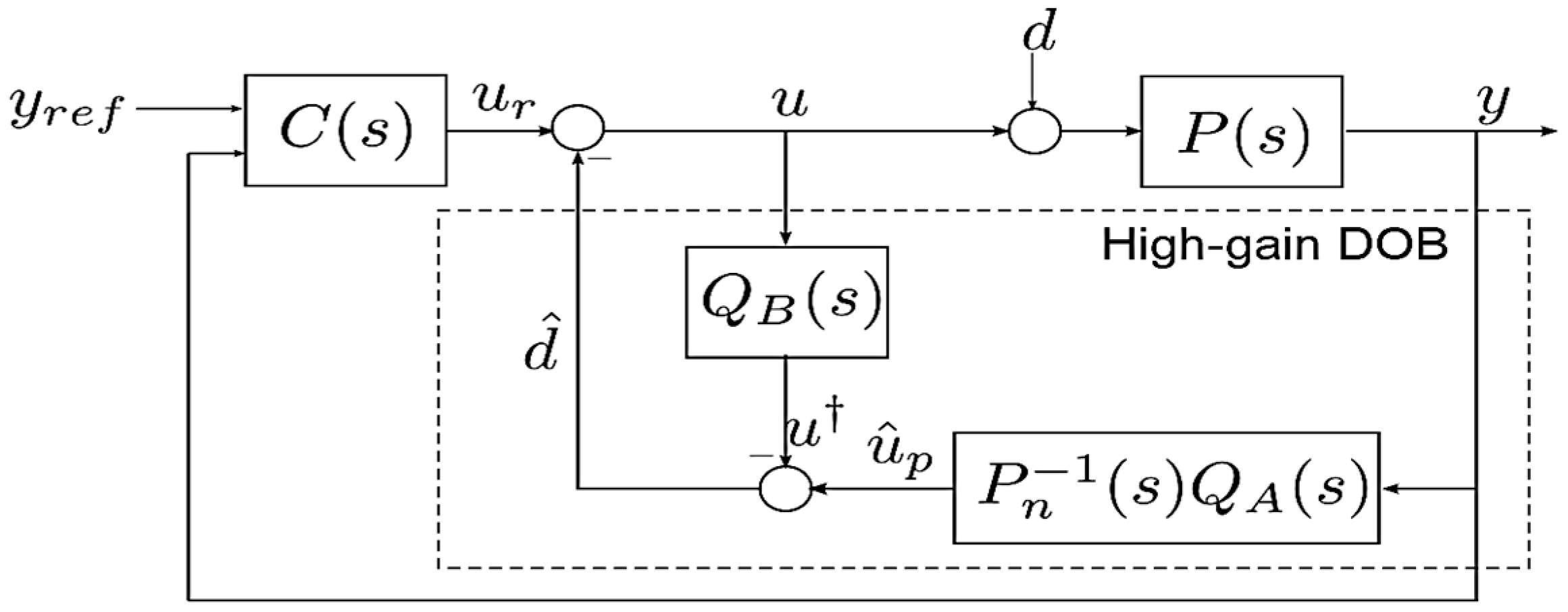
3. Review of HDOB Based Controller

This section briefly reviews the basic concept of the HDOB in [17]. The dynamic system in Figure 1 shows that each control area has different physical parameters and coefficients for the droop control. This makes the problem even more challenging, that the controller should be able to handle the presence of disturbances as well as the parameter uncertainties. Regarding this issues, a HDOB based controller is employed as it is known to be robust against large parameter uncertainties and external disturbances.

The structure of HDOB based controller is described by Figure 2 where $y$ is the plant output, and u is the control signal [17]. $Q_A$ and $Q_B$ are stable low pass filters, $C\left(s\right)$ is the controller for the nominal model, $P\left(s\right)$ uncertain dynamic system and $P_n\left(s\right)$ is the nominal model given by:

$$P\left(s\right):\{\begin{array}{l}{\dot{x}}_i= x_{i+1 , }i=1,\dots ,n-1\hfill \\ {\dot{x}}_n= {\varphi }_1{x}_1+\dots +{\varphi }_n{x}_n+g\left(u+d\right)\hfill \\ y=x_1\hfill \end{array},$$

(20)

$$P_n\left(s\right):\{\begin{array}{l}{\dot{\overline{x}}}_i= {\overline{x}}_{i+1 ,} i=1,\dots ,n-1\hfill \\ {\dot{\overline{x}}}_n= {\overline{\varphi }}_1{x}_1+\dots +{\overline{\varphi }}_n{x}_n+\hfill \\ y={\overline{x}}_1\hfill \end{array}\overline{g}{u}_r,$$

(21)

where ${\varphi }_i$ and $g$ denote the uncertain parameters of $P\left(s\right)$, $x_i$ the state of the plant $P\left(s\right)$, ${\overline{\varphi }}_i$ and $\overline{g}$ are known nominal parameters of $P_n\left(s\right)$, ${\overline{x}}_i$ the state of the nominal $P_n\left(s\right)$.

Suppose that $P_n\left(s\right)$ is the same as $P\left(s\right)$. By multiplying plant output y with the inverse of nominal model $P_n^{-1}$, we could obtain ${\widehat{u}}_p$ which is roughly the same as the actual input to the uncertain system, i.e., $u+d$. The estimated disturbance $\widehat{d}$ is obtained by subtracting ${\widehat{u}}_p$with filtered control input $u^{†}.$ Low pass filter $Q_{A }$ and $Q_{B }$ are formulated as:

$$Q_A\left(s\right)=Q_B\left(s\right)=\frac{{\alpha }_0}{{\left(\tau s\right)}^n+{\alpha }_{n-1}{\left(\tau s\right)}^{n-1}+\dots +{\alpha }_1\tau s+{\alpha }_0}.$$

(22)

Thus, filtered nominal model $P_n^{-1}{Q}_A$ can be written in state space as:

$$P_n^{-1}\left(s\right)Q_A\left(s\right):\dot{\mathbf{q}}={\mathbf{A}}_{\alpha \tau }\mathbf{q}+{\mathbf{B}}_{\alpha \tau }\mathrm{y}$$

(23)

where:

$${\mathbf{A}}_{\alpha \tau }=\left[\begin{array}{ccc}-B_{\alpha \tau }& |& \begin{array}{c}{\mathbf{I}}_{n-1}\\ {\mathbf{0}}_{n-1}^T\end{array}\end{array}\right], {\mathbf{B}}_{\alpha \tau }=\left[\begin{array}{c}\frac{1}{\tau }{\alpha }_{n-1}\\ ⋮\\ \frac{1}{{\tau }^n}{\alpha }_0\end{array}\right]$$

(24)

with ${\alpha }_i^{\text{'}}s$ and $\tau >0$ design parameters, and $q$ is the state vector of $P_n^{-1}{Q}_A$. With the parameters given earlier, ${\widehat{u}}_p$ can be expressed as:

$${\widehat{u}}_p=\frac{1}{\overline{\mathcal{g}}}({\dot{\mathbf{q}}}_n-{\overline{\mathsf{\varphi }}}^T\mathbf{q})=-\frac{{\alpha }_0}{{\tau }_n}\frac{1}{\overline{\mathcal{g}}}(q_1-\mathrm{y})-\frac{1}{\overline{\mathcal{g}}}{\overline{\mathsf{\varphi }}}^T\mathbf{q},$$

(25)

where ${\overline{\mathsf{\varphi }}=[{\overline{\varphi }}_1...{\overline{\varphi }}_n]}^T$. While the filtered control signal u is defined as $u^{†}=p_1$ that can be written in a state space as:

$$Q_B(S):\dot{\mathbf{p}}={\mathbf{A}}_{\alpha \tau }\mathbf{p}+\frac{{\alpha }_0}{{\tau }^n}\mathbf{B}u$$

(26)

where $p$ is the state vector of $Q_B$ with $\mathbf{B}={\left[\begin{array}{cc}{\mathbf{0}}_{n-1}& 1\end{array}\right]}^T$. Consequently, the HDOB estimates the disturbance $\widehat{d}$ with:

$$\widehat{d}={\widehat{u}}_p-u^{†}.$$

(27)

As shown in Figure 2, the closed-loop system consists of the uncertain system $P\left(s\right)$, the nominal controller $C\left(s\right)$, and (22)–(27). The proposed HDOB based robust control is given by:

$$u=u_r-d.$$

(28)

Assumption 1.

All the uncertain parameters in $P\left(s\right)$ and the unknown external disturbance $d$ in (20) are bounded.

Assumption 2.

The stabilizing control $u_r$ for nominal model $P_n\left(s\right)$ is given.

Theorem 1.

[17] Suppose that Assumptions 1 and 2 are satisfied. Then, there exists ${\tau }^{*}$ for a given $ϵ>0$ such that the HDOB based control (19) with any $0<\tau <{\tau }^{*}$ results in:

$$\underset{t\to \infty }{lim}||\mathbf{x}(t)-\overline{\mathbf{x}}(t)||<\mathsf{\epsilon }.$$

(29)

The idea behind the HDOB based control is that the HDOB makes the input-output relation of the combined system of $P\left(s\right)$ and HDOB almost the same as that of $P_n\left(s\right)$ by canceling the estimated disturbance. Hence, the nominal control $u_r$ can stabilize the whole system. Another important feature of the employed HDOB is that the state the $P_n^{-1}\left(s\right)Q_A\left(s\right)$, i.e., $q$, is, in fact, the state estimate of the uncertain plant $P\left(s\right)$ [17,21]. This feature is importantly used in the proposed LFC design.

4. HDOB Based LFC for the $i$th Area

In this section, the proposed HDOB based LFC is presented. In accordance with the design procedure in the previous section, the nominal control is designed first. In order to design the nominal control $u_r$ for the nominal model (18), any state feedback control law can be employed. For example, using pole placement or LQR, we can design $u_r$ as follows:

$$u_r=\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]\mathbf{x}=\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]\left[\begin{array}{c}\mathrm{y}\\ \dot{\mathrm{y}}\\ \ddot{\mathrm{y}}\end{array}\right],$$

(30)

where $k_1,k_2,k_3$ are feedback gains and they are determined such that:

(31)

becomes asymptotically stable. In this paper, the state feedback gain $k_1, k_2$ and $k_3$ are determined using LQR method. The performance index is:

$$J={{\displaystyle \int }}_0^{\infty }[{\mathbf{q}}^T(t)\mathbf{Qq}(t)+u^T(t)\mathbf{R}u(t)]\mathrm{d}t,$$

(32)

where $\mathbf{Q}$ and $\mathbf{R}$ are weighting matrices. The optimal state feedback control gains are computed by minimizing $J$ and given by:

$$\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]=-{\mathbf{R}}^{-1}{\overline{\mathbf{B}}}^T\mathbf{P}$$

(33)

where $\overline{\mathbf{B}}={\left[\begin{array}{ccc}0& 0& \overline{g}\end{array}\right]}^T$, and $\mathbf{P}$ is the solution of the Riccati equation. Since $\mathbf{x}$ is not measurable, we can use its estimate $\mathbf{q}$ in the nominal control $u_r$. Hence, the nominal control is:

$$u_r=-\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]\mathbf{q}.$$

(34)

The HDOB can be designed according to the design method explained in the previous section with $n=3$. Based on these, the proposed HDOB based LFC is given by:

$$\mathrm{u}={\mathrm{u}}_r-\mathrm{sat}\left(\widehat{d}\right)=\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]\mathbf{q}-\mathrm{sat}\left(\widehat{d}\right),$$

(35)

where $\widehat{d}$ is the output of the HDOB given in (27) and function $\mathrm{sat}()$ designates the saturation function. The saturation function is employed at the output of the HDOB to avoid the peaking phenomenon which means that a very large control value due to a small $\tau$ can make the state of the system very large as well. Since the HDOB designated in this paper is a high-gain observer type, employing such a saturation function is necessary [22,23]. The HDOB consists of two design parameters: ${\alpha }_i^{\text{'}}s$ and $\tau$. Since the nominal model is a third order model, the parameter ${\alpha }_i^{\text{'}}s$ are chosen such that $s^3+{\alpha }_2{s}^2+{\alpha }_{1}s+{\alpha }_0$ becomes stable. In addition, $\tau$ is determined sufficiently small.

5. Case Study

In this section, the proposed method is tested to validate its performance against the parameter uncertainties and abrupt load changes in three different cases. Since the moment inertia of generators $M_{eq}$ may varies within a certain bounded interval, first the simulations are carried out to confirm the robustness of the proposed controller to handle this uncertainty. Second, measurement delay between interconnected areas are considered with two different load changes: random and large amplitude step load. Third, simulations with different number of interconnected areas and generators are carried out to look into robustness of the proposed LFC against different network topologies of power systems.

5.1. Frequency Control without LFC

To understand the incompleteness of primary control in handling the frequency problem in interconnected power systems, a simulation without LFC is done. The dynamic model of each area is shown in Figure 1 with its parameters taken from [24] in

Table A1. Parameters of power systems with multiple areas. (In the case of ${M_{eq}}_i$ and $D_i$, their upper and lower bounds are written).

Generating Unit Parameters	Area 1	Area 2	Area 3	Area 4	Area 5
$m_i$	3	2	4	3	3
$T_{g_{1,\dots ,{\mathrm{m}}_{\mathrm{i}}}}$	0.08; 0.06; 0.07	0.06; 0.06	0.075; 0.08; 0.06; 0.08	0.08; 0.06; 0.07	0.082; 0.065; 0.063
$T_{c{h}_{1,\dots ,{\mathrm{m}}_{\mathrm{i}}}}$	0.4; 0.36; 0.42	0.44; 0.32	0.44; 0.45; 0.32; 0.40	0.43; 0.36; 0.41	0.45; 0.33; 0.42
$R_{1,\dots ,{\mathrm{m}}_{\mathrm{i}}}$	3; 3; 3.3	3.2273; 2.6667	3.54; 3.7; 3.6667; 3	3.1; 2.8; 3.01	2.9; 2.4; 3.22
$Ramp rat{e}_{1,\dots ,{\mathrm{m}}_{\mathrm{i}}}$	8; 8; 4	12;8	8; 8; 8; 8	8; 8; 9	8; 8; 9
${\alpha }_{1,\dots ,{\mathrm{m}}_{\mathrm{i}}}$	0.4; 0.3; 0.3	0.4; 0.6	0.2; 0.2; 0.3; 0.3	0.3; 0.5; 0.2	0.3; 0.3; 0.4
β	1.0753	1.4902	0.922	1.0321	0.9718
$D_i$	0.0150 × [0.7 1.3]	0.0140 × [0.7 1.3]	0.0150 × [0.7 1.3]	0.0160 × [0.7 1.3]	0.0130 × [0.7 1.3]
$M_{e{q}_i}$	0.4867 × [0.7 1.3]	0.3517 × [0.7 1.3]	1.006 × [0.7 1.3]	0.557 × [0.7 1.3]	0.45 × [0.7 1.3]

. The primary control is employed with two different types of loads. Firstly, random load changes are applied in five-area power systems. The load change variation is chosen between −0.15 p.u. and 0.15 p.u. After that, a large amplitude of step load is added in each area. When small random load variations occur in the system, the primary control can manage the ACE with error 0–0.14 p.u. (Figure 3a). However, from Figure 3b, when a large amplitude of step load is applied, the primary control fails to drive the ACE to zero. Therefore, a LFC is required to achieve the frequency regulation after employing the primary control.

5.2. Robustness against Uncertain Moment of Inertia $M_{e{q}_i}$ and Damping Coeficient $D_i$

The proposed control is tested in the interconnected power system as illustrated in Figure 4. In this network, each area is assumed to have its own LFC. In addition, unlike existing results, the simulation study is conducted under the assumption that each area has different number of generators $m_i$ as follows: $m_1=3, m_2=2, m_3=4,m_4=3, m_5=4$, and that $M_{e{q}_i}$ and $D_i$ are uncertain but their upper and lower bounds are known which results in uncertain $g$. For simulation, arbitrary values for uncertain ${M_{eq}}_i$ and $D_i$ are selected from the intervals in Table A1 and the corresponding $g$ is as follows:

$$g_1\in {10}^4[0.76 20.4], g_2\in {10}^4[0.02 52.7], g_3\in {10}^4[1.72 139], g_4\in {10}^4[1.10 29.7], g_5\in {10}^4[6.02 488].$$

The system is tested with three different load changes: small random, large-amplitude load changes and oscillating load changes. At first, the random loads in Figure 5 are applied and compared with the active disturbance rejection control (ADRC) from [11]. As can be seen in Figure 6, both controllers successfully manage the ACE with the presence of random loads and uncertain parameters in the swing equation. However, in Area 1, 3 and 4, the HDOB has less ACE and $\Delta f$ compared to the ADRC. Even though in Area 2 and Area 5 the HDOB generates the same ACE as the ADRC, but the HDOB produces smaller $\Delta f$ than the ADRC in these areas.

In the second case, a large amplitude of step load change is applied to each area at $t=1$ s. For this purpose, the following load changes are used with nominal power $P_{nominal}=1000 \mathrm{MW}$.

$$\Delta {P_l}_1=100 \mathrm{MW}, \Delta {P_l}_2=120 \mathrm{MW}, \Delta {P_l}_3=110 \mathrm{MW}, \Delta {P_l}_4=150 \mathrm{MW}, \Delta {P_l}_5=80 \mathrm{MW},$$

In order to investigate the robustness, the simulations are run 200 times and different ${M_{eq}}_i$ and $D_i$ are chosen randomly from the intervals in each simulation. The responses due to different parameters are shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 for Area 1–5.

The results are also compared with responses by ADRC and shows the HDOB yields less error in ACE and $\Delta f$ in transient time and faster responses. In the third case, oscillating disturbances are added to each control area to ensure the stability under the presence of oscillating disturbances from electromagnetic power converters. The disturbances are presented in Figure 12, and the simulation results are presented in Figure 13. As shown in the results, the HDOB successfully eliminates the oscillating disturbances and performs better than the ADRC.

5.3. Robustness against the Delay

In this scenario, the measurement delays between interconnected areas are taken into account. The delay is chosen as 0.5 s with the random and step load changes as the previous simulation are used. Again, uncertain parameters for $M_{eq}$ and $D_i$ used in the previous simulation are also applied in this simulation. One simulation result is presented in Figure 14 for random load changes, and Figure 15 for step load changes. As a matter of fact, over 200 simulations, quite similar results are obtained. Figure 14 and Figure 15 indicate that both controllers drive the ACE to zero in despite of the delay. However, the proposed HDOB based LFC produces less frequency deviation and faster response than the ADRC. Hence, the HDOB has better performance in dealing with measurement delay under both load variations. See

Table A3. $\frac{1}{100}{{\displaystyle \int }}_0^{100}\Delta f\left(t\right)\mathrm{d}t$.

Figure Number	Area 1		Area 2		Area 3		Area 4		Area 5
	ADRC	HDOB	ADRC	HDOB	ADRC	HDOB	ADRC	HDOB	ADRC	HDOB
6	−0.007	−0.001	−0.007	−0.001	−0.007	−0.001	−0.007	−0.001	−0.007	−0.002
7–11	−0.009	−7 × 10−4	−0.011	−0.001	−0.013	−0.001	−0.014	−0.003	−0.014	−0.002
13	0.004	1.0 × 10−4	0.004	1.0 × 10−4	0.004	1.0 × 10−4	0.004	1.1 × 10−4	0.004	9.2 × 10−5
14	−0.001	−2.9 × 10−5	2.9 × 10−5	3.2 × 10−5	0.0078	7.5 × 10−5	−9.5 × 10−4	−4.9 × 10−6	−0.007	−4.8 × 10−4
15	−0.004	−3.3 × 10−4	−0.004	−3.3 × 10−4	−0.004	−3.3 × 10−4	−0.003	−3.3 × 10−4	−0.004	−3.3 × 10−4

in Appendix A for quantitative values of frequency deviation.

5.4. Robustness against Power Systems Topology

This section covers about the performance of LFC in various power system topology. As can be seen in the dynamic system illustrated in Figure 1, the topology can be varying in the number of generators $m_i$ and number of interconnected areas. Hence the interest is to know the effect of LFC responses in terms of different number of generators $m_i$ and number of interconnected areas. Furthermore, it is also important to confirm the capability of the proposed method in different power system topology. The effect of $m_i$ and number of interconnected areas are studied separately and compare with the response of ADRC. The $\pm 20\%$ of $M_{eq}$ and $D_i$ are chosen as parameters simulations.

5.4.1. Robustness against Different Number of Generators $m_i$

At first the simulation is conducted to know the effect of the controller with changing $m_i$. The different topologies as shown in Figure 16 are used. The responses after applying 105 MW step load changes in $t=1$ s are compared with ADRC and presented in Figure 17 and Figure 18. Clearly the performances of both controllers are getting degraded as $m_i$ increases. However, the HDOB has better performance regardless of the value of $m_i$.

5.4.2. Robustness against Different Number of Connected Areas

In this scenario, the network topologies as shown in Figure 19 are considered. First, the study starts with two connected areas in Area 2 and Area 3 (Figure 19a), then the number of connected areas is increased by one and it is continued until Area 2 and 3 are connected to five areas (Figure 19d). For the sake of convenience, the number of connected areas in Area 2 is denoted by $n_2$, and $n_3$ for Area 3, respectively. The simulations are carried out to study the effect of LFC with increasing $n_i$. In addition, it is also important to confirm the robustness of the designed LFC in different topology. The responses after applying 105 MW step load changes at $t=1$s are depicted in Figure 20. As can be seen, the proposed HDOB based LFC shows consistent performance in regulating ACE (the solid lines) with the changing $n_i$. On the contrary, in ADRC results, increasing $n_i$ by two or three decreases the ACE by 0.05 p.u. and makes the overshoot larger (see the dashed lines).

6. Conclusions

In this paper, LFC for power systems with multiple areas using the HDOB is designed. With the load changing tested in the system, the HDOB-based LFC suppresses maximum deviation in frequency and maintains the tie line power interchanges. The advantage of the HDOB-based LFC over existing results is that it reduces frequency deviations robustly in the presence of parameter uncertainties and transmission delay. In addition, it successfully eliminates the frequency deviation under topology variations of multiple areas.