A Real-Time SOSM Super-Twisting Technique for a Compound DC Motor Velocity Controller
Abstract
:1. Introduction
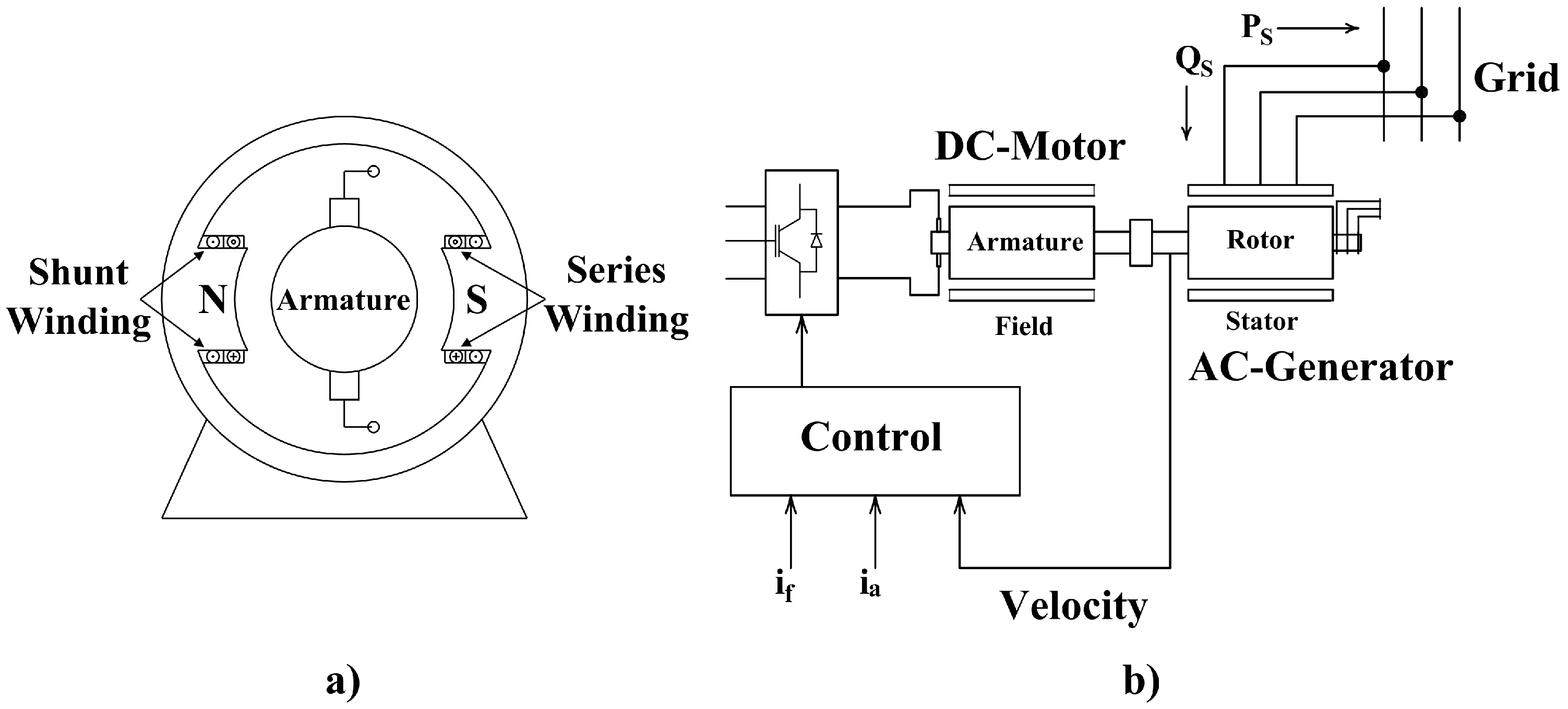
2. Direct Current Motor Mathematical Model
3. State Feedback Linearization
4. Classical PI Controller
5. Second-Order Sliding Mode Super-Twisting Controller
6. Robust Differentiator
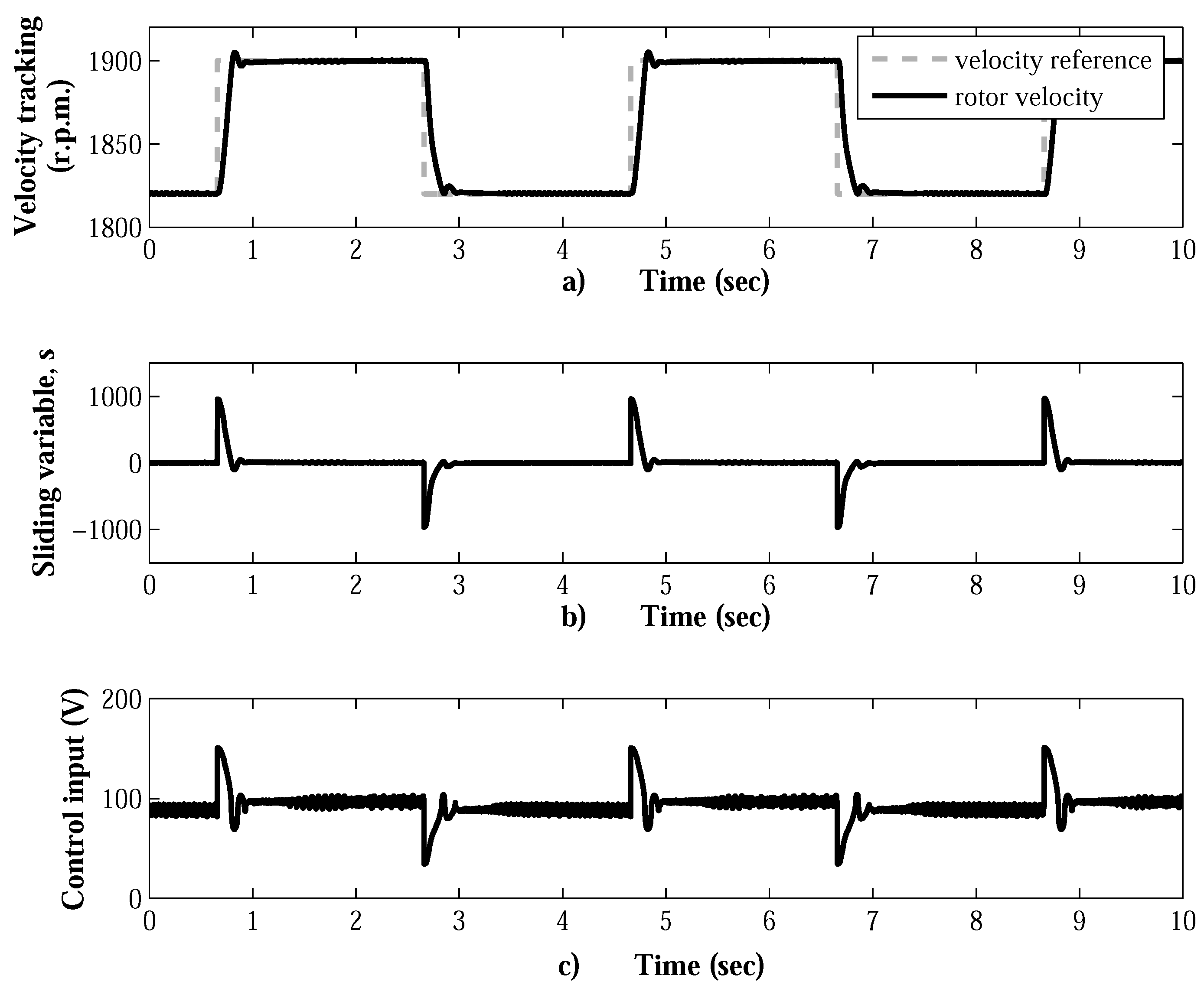
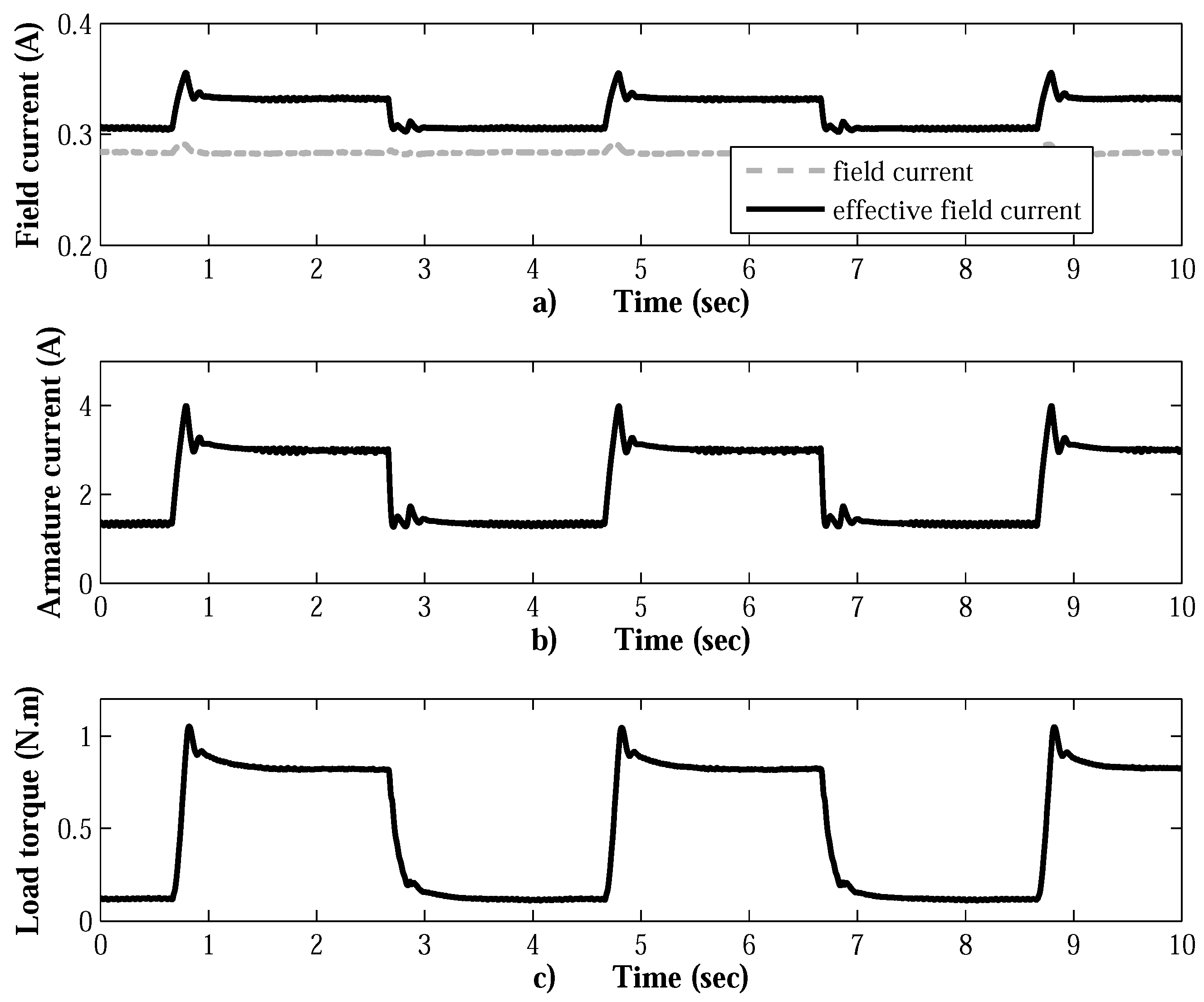
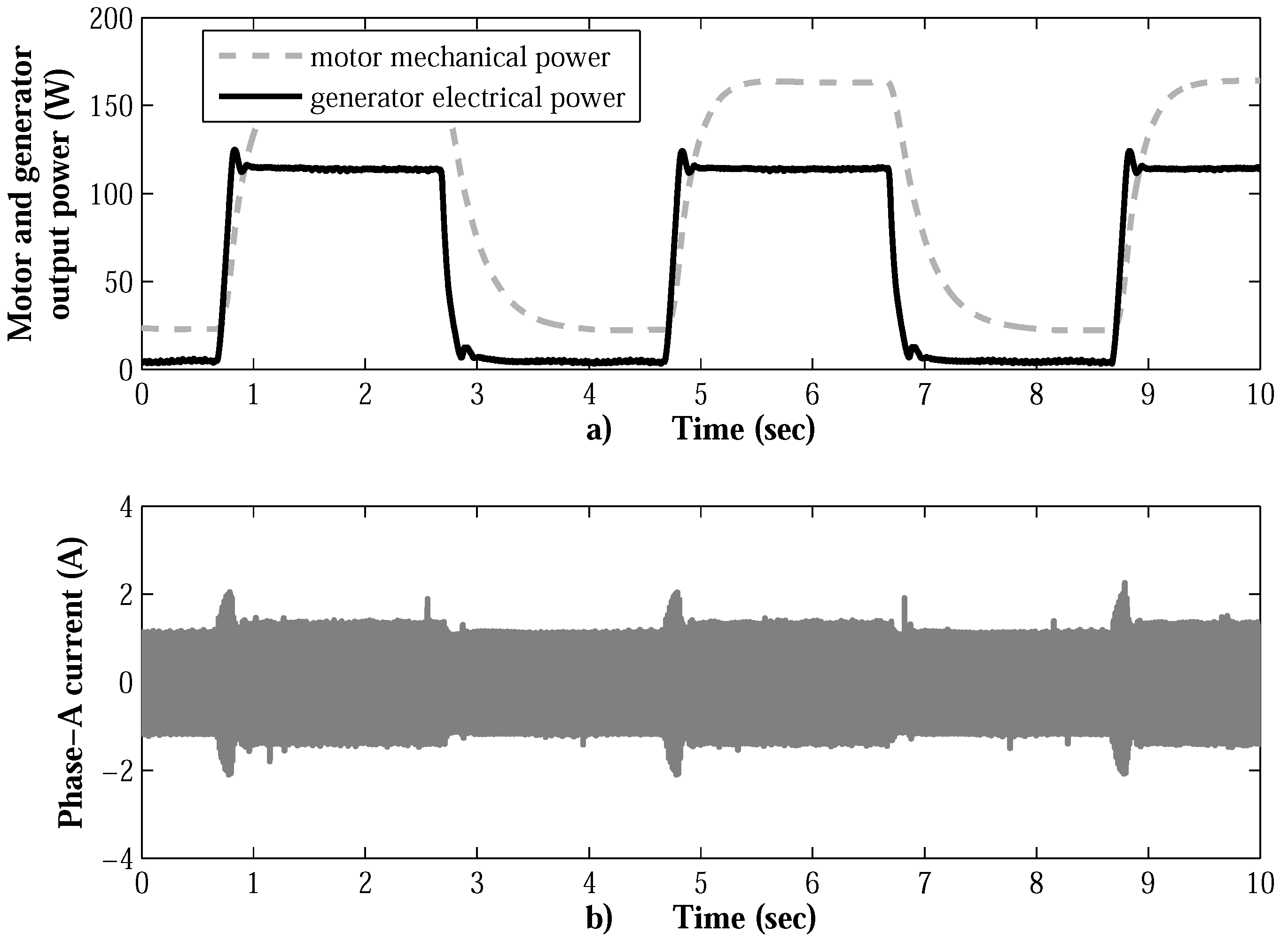
7. Experimental Results
- A D1154 Baldor compound DC motor mechanically coupled to an 8231-02 Lab-Volt squirrel-cage induction generator.
- A BEI HS35 incremental optical encoder with 2048 pulses mounted on the shaft train.
- A measurement interface with HX 05-NP current sensors to measure the field and armature currents.
- A dSPACE DS1103 data acquisition board which is linked with the real-time interface (RTI) as the display device.
- A SEMITEACH IGBT module converter by Semikron.
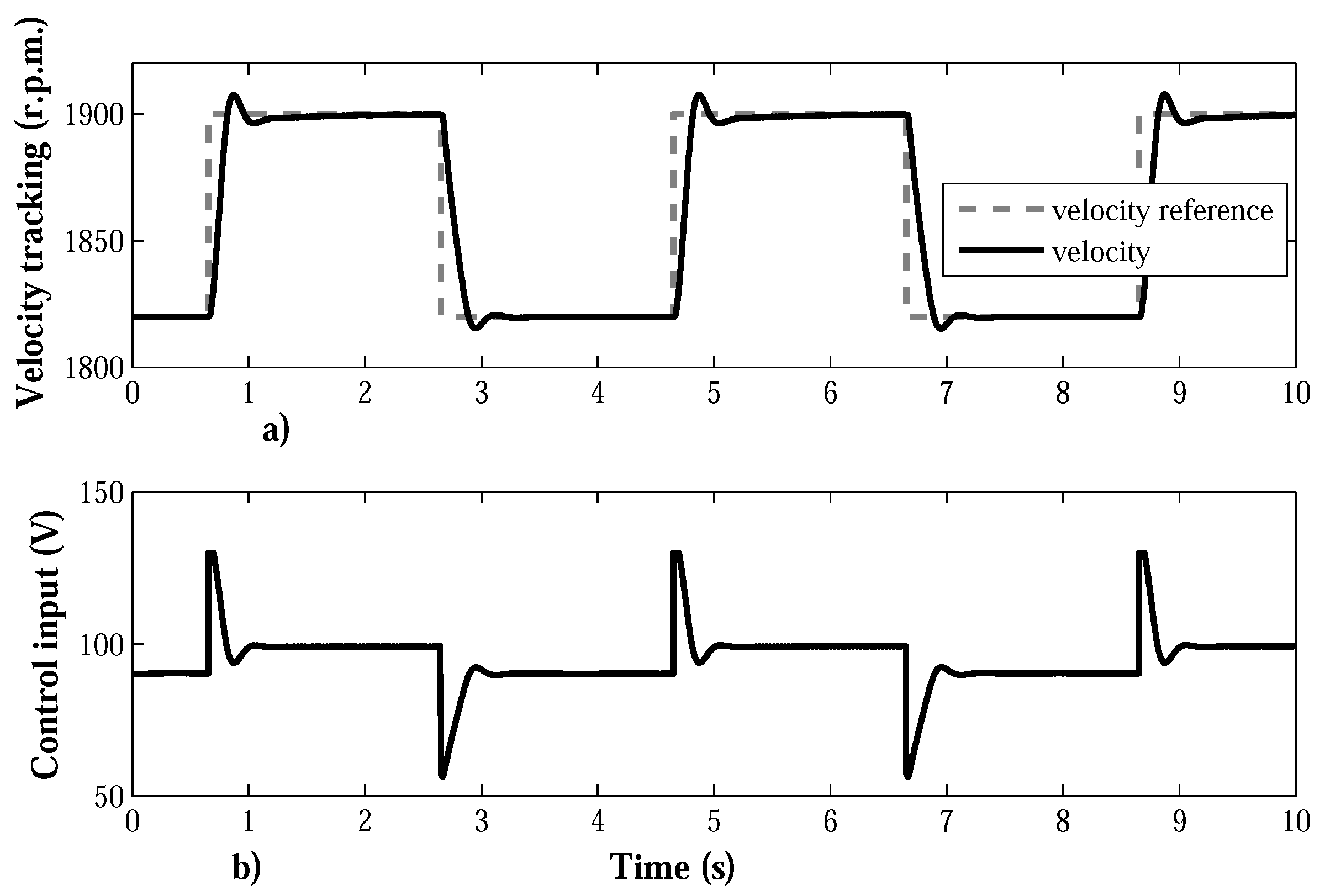
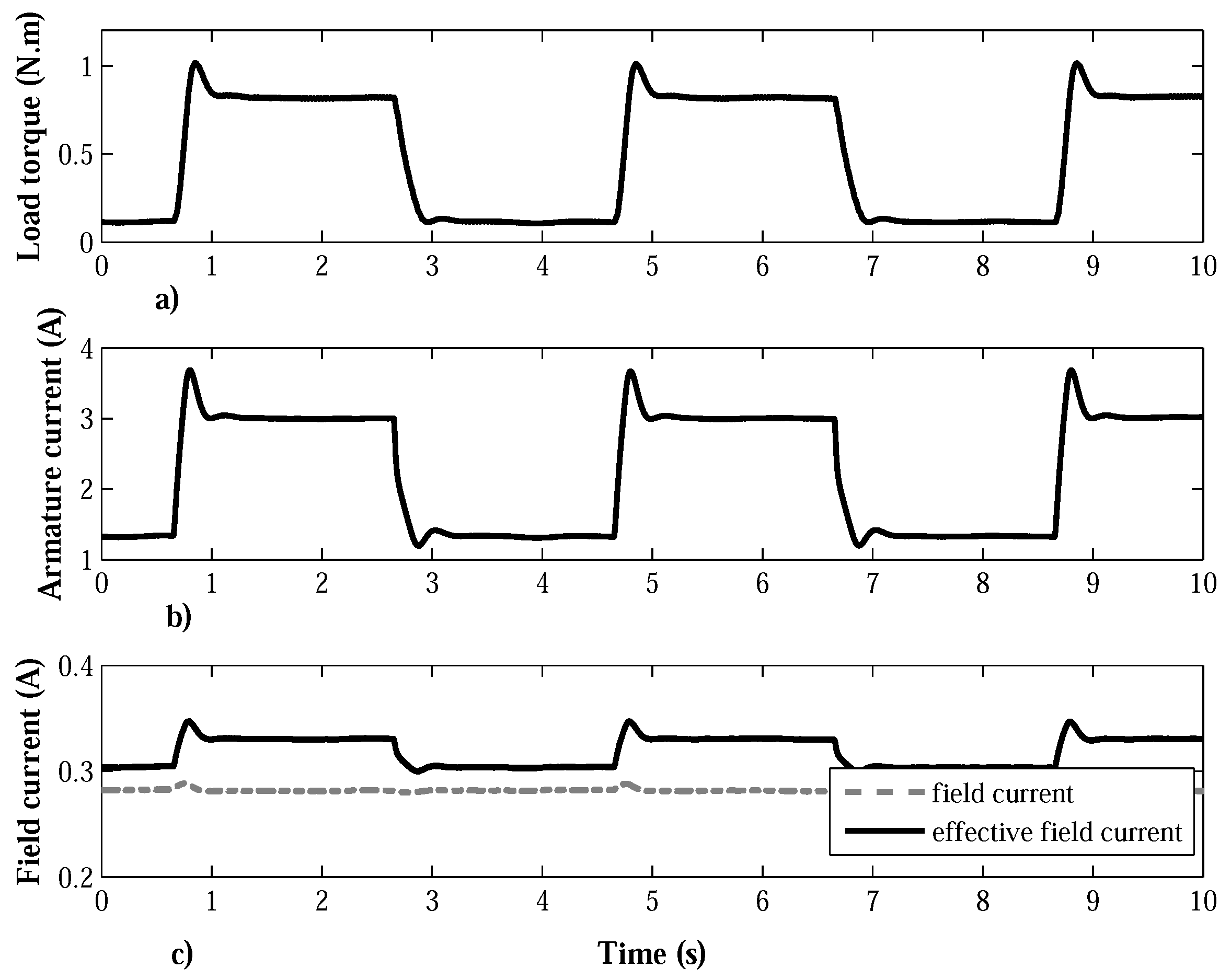
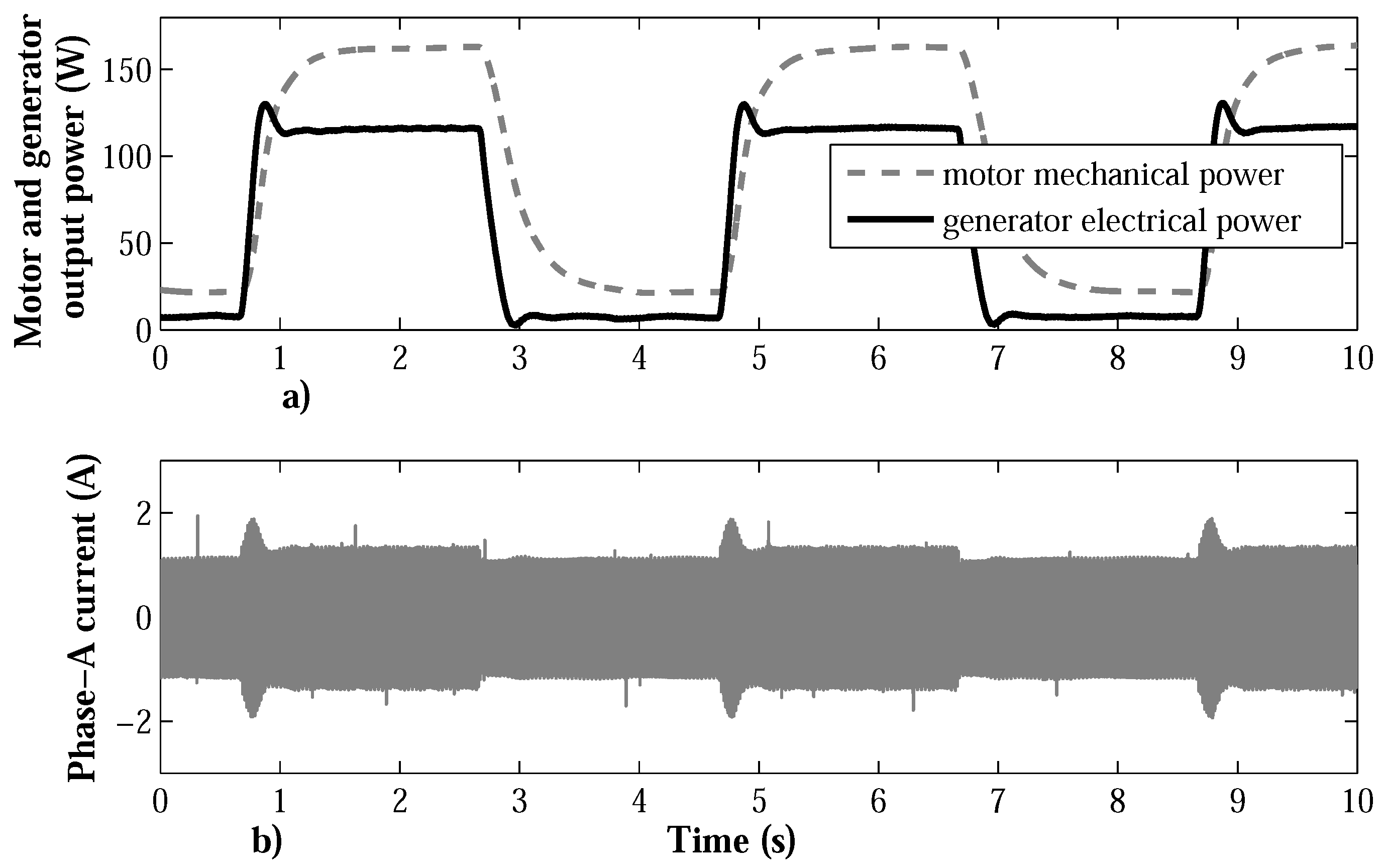
7.1. Proportional Integral Velocity Controller
7.2. SOSM Super-Twisting Velocity Controller
8. Conclusions
Author Contributions
Conflicts of Interest
References
- Vieira, F.E.; Sales, L.; Bezerra, F. Wind Turbine Torque-Speed Feature Emulator Using a dc Motor. In Proceedings of the IEEE Power Electronics Conference, Gramado, Brazil, 27–31 October 2013. [Google Scholar]
- Kouadria, S.; Belfedhal, S.; Meslem, Y.; Berkouk, M. Development of Real Time Wind Turbine Emulator Based on DC Motor Controlled by Hysteresis Regulator. In Proceedings of the International Renewable and Sustainable Energy Conference, Ouarzazate, Morocco, 7–9 March 2013. [Google Scholar]
- Rhif, A. Stabilizing sliding mode control design and application for a DC motor speed control. Int. J. Inf. Technol. Control Autom. 2012, 2, 39–48. [Google Scholar] [CrossRef]
- Castañeda, C.E.; Loukianov, A.G.; Sanchez, E.N.; Castillo-Toledo, B. Discrete-time neural sliding-mode block control for a dc motor with controlled flux. IEEE Trans. Ind. Electron. 2012, 59, 1194–1207. [Google Scholar] [CrossRef]
- Ahmed, M.; Mazin, Z. Combined armature and field fuzzy speed control of a DC motor for efficiency enhancement. Al-Rafidain Eng. 2012, 20, 117–129. [Google Scholar]
- Moleykutty, G.; Kartik, B.; Alan, C. Model reference controlled separately excited DC motor. Neural Comput. Appl. 2010, 19, 343–351. [Google Scholar]
- Morfin, O.A.; Ruiz-Cruz, R.; Loukianov, A.G.; Sanchez, E.N.; Castellanos, M.I. Torque controller of a doubly-fed induction generator impelled by a DC motor for wind system applications. IET Renew. Power Gener. 2013, 8, 484–497. [Google Scholar] [CrossRef]
- Utkin, V. On convergence time and disturbance rejection of supert-twisting control. IEEE Trans. Autom. Control 2013, 58, 2013–2017. [Google Scholar] [CrossRef]
- Salas, O.; Castañeda, H.; DeLeon-Morales, J. Observed-based adaptive supertwisting control strategy for a 2-DOF helicopter. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013. [Google Scholar]
- Gonzalez, T.; Moreno, J.A.; Fridman, L. Variable gain super-twisting sliding mode control. IEEE Trans. Autom. Control 2012, 57, 2100–2105. [Google Scholar] [CrossRef]
- Evangelista, C.l.; Puleston, P.; Valenciaga, F.; Fridman, L. Lyapunov-designed super-twisting sliding mode control for wind energy conversion optimization. IEEE Trans. Ind. Electron. 2013, 60, 538–545. [Google Scholar] [CrossRef]
- Franklin, G.; Powell, D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J. Sliding Mode Control in Electromechanical Systems; Taylor & Francis: London, UK, 1999. [Google Scholar]
- Fridman, L.; Levant, A. Higher Order Sliding Modes as a Natural Phenomenon in Control Theory; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 1995; Volume 217, pp. 107–133. [Google Scholar]
- Chalanga, A.; Kamal, S.; Fridman, L.; Bandyopadhyay, B.; Moreno, J.A. Implementation of super-twisting control: Super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancún, Mexico, 9–11 December 2008. [Google Scholar]
- Moreno, J.A.; Osorio, M. Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst. 2012, 349, 685–699. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]


| DC Motor Nameplate Data | DC Motor Model Parameters | ||
|---|---|---|---|
| Power | 746 W | Armature resistance | 2.18 |
| Field Voltage | 115 V | Armature inductance | 13.5 mH |
| Armature current | 8.0 A | Series resistance | 0.28 |
| Field current | 0.5 A | Series inductance | 2.7 mH |
| Rotor velocity | 1750 r.p.m. | Shunt field resistance | 240 |
| Shunt field inductance, | 0.642 H | ||
| Constant motor | 1.227 | ||
| Inertia moment | 0.0026 N·m· | ||
| Friction coefficient | 0.0016 N·m·s | ||
| Generator inertia moment | 0.0022 N·m· | ||
| Generator friction coefficient | 0.0012 N·m·s | ||
| Turn-ratio | 0.0163 | ||
| Time-Domain Specification | PI Controller | SOSM Controller Estimated | SOSM Controller Calculated |
|---|---|---|---|
| Rise time (s) | 0.11 | 0.085 | 0.094 |
| Rise settling time (s) | 0.49 | 0.26 | 0.214 |
| Rise overshoot (%) | 10 | 6.2 | 3.7 |
| Peak time (s) | 0.22 | 0.17 | 0.17 |
| Falling time (s) | 0.17 | 0.12 | 0.14 |
| Falling settling time (s) | 0.35 | 0.29 | 0.29 |
| Falling overshoot (%) | 6.3 | 0 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morfin, O.A.; Castañeda, C.E.; Valderrabano-Gonzalez, A.; Hernandez-Gonzalez, M.; Valenzuela, F.A. A Real-Time SOSM Super-Twisting Technique for a Compound DC Motor Velocity Controller. Energies 2017, 10, 1286. https://doi.org/10.3390/en10091286
Morfin OA, Castañeda CE, Valderrabano-Gonzalez A, Hernandez-Gonzalez M, Valenzuela FA. A Real-Time SOSM Super-Twisting Technique for a Compound DC Motor Velocity Controller. Energies. 2017; 10(9):1286. https://doi.org/10.3390/en10091286
Chicago/Turabian StyleMorfin, Onofre A., Carlos E. Castañeda, Antonio Valderrabano-Gonzalez, Miguel Hernandez-Gonzalez, and Fredy A. Valenzuela. 2017. "A Real-Time SOSM Super-Twisting Technique for a Compound DC Motor Velocity Controller" Energies 10, no. 9: 1286. https://doi.org/10.3390/en10091286










