A Fuzzy Gravitational Search Algorithm to Design Optimal IIR Filters
Abstract
:1. Introduction
2. IIR Filter Design
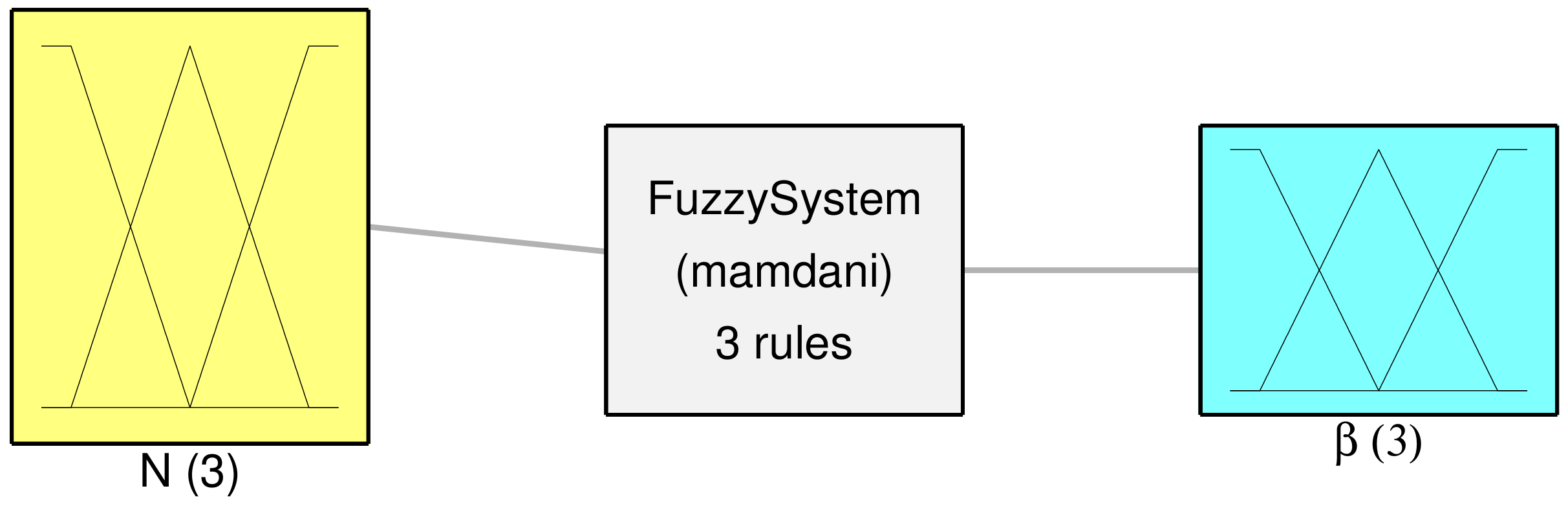
3. The Fuzzy Gravitational Search Algorithm
| Algorithm 1 Fuzzy Gravitational Search Algorithm |
| 1: Random initialization of the coefficients (see S1). 2: Settings of the fuzzy output extrema values and initialization of the first two values of (see S2). 3: For each iteration from 1 to (see S3): 4: Search space boundaries control (see S3.1) 5: Agents evaluation (see S3.2) 6: Agents masses calculation (see S3.3). 7: Gravitational constant calculation (see S3.4). 8: computation (see S3.5) 9: Agents acceleration computation (see S3.6). 10: Population progress calculation (see S3.7). 11: Computation of fuzzy- (see S3.8). 12: Agents velocity and position computation (see S3.9). 13: Final computation of the best coefficients (see S4). |
- ,
- ,
- ...,
- ,
- ,
- ,
- ...,
- .
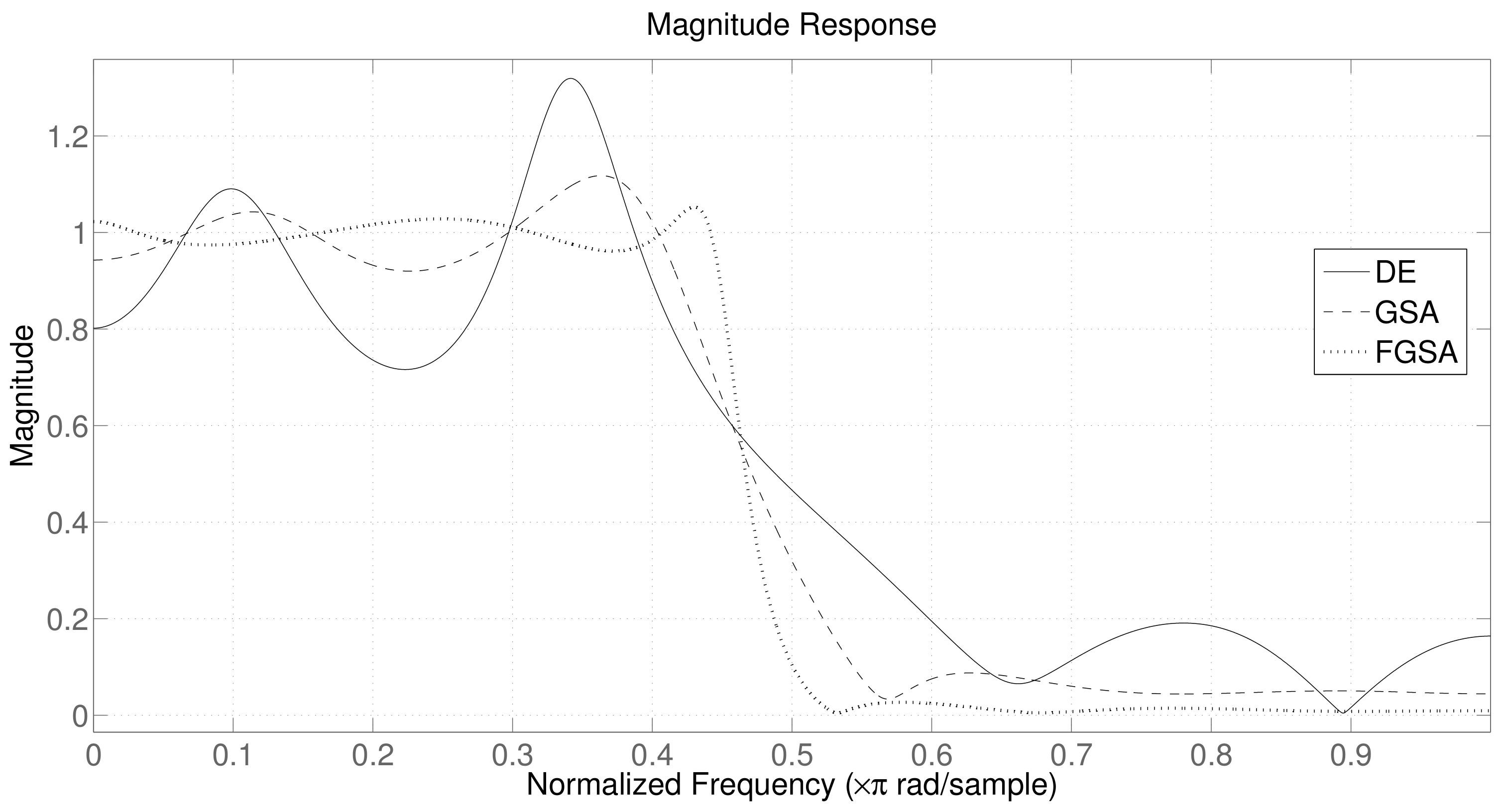
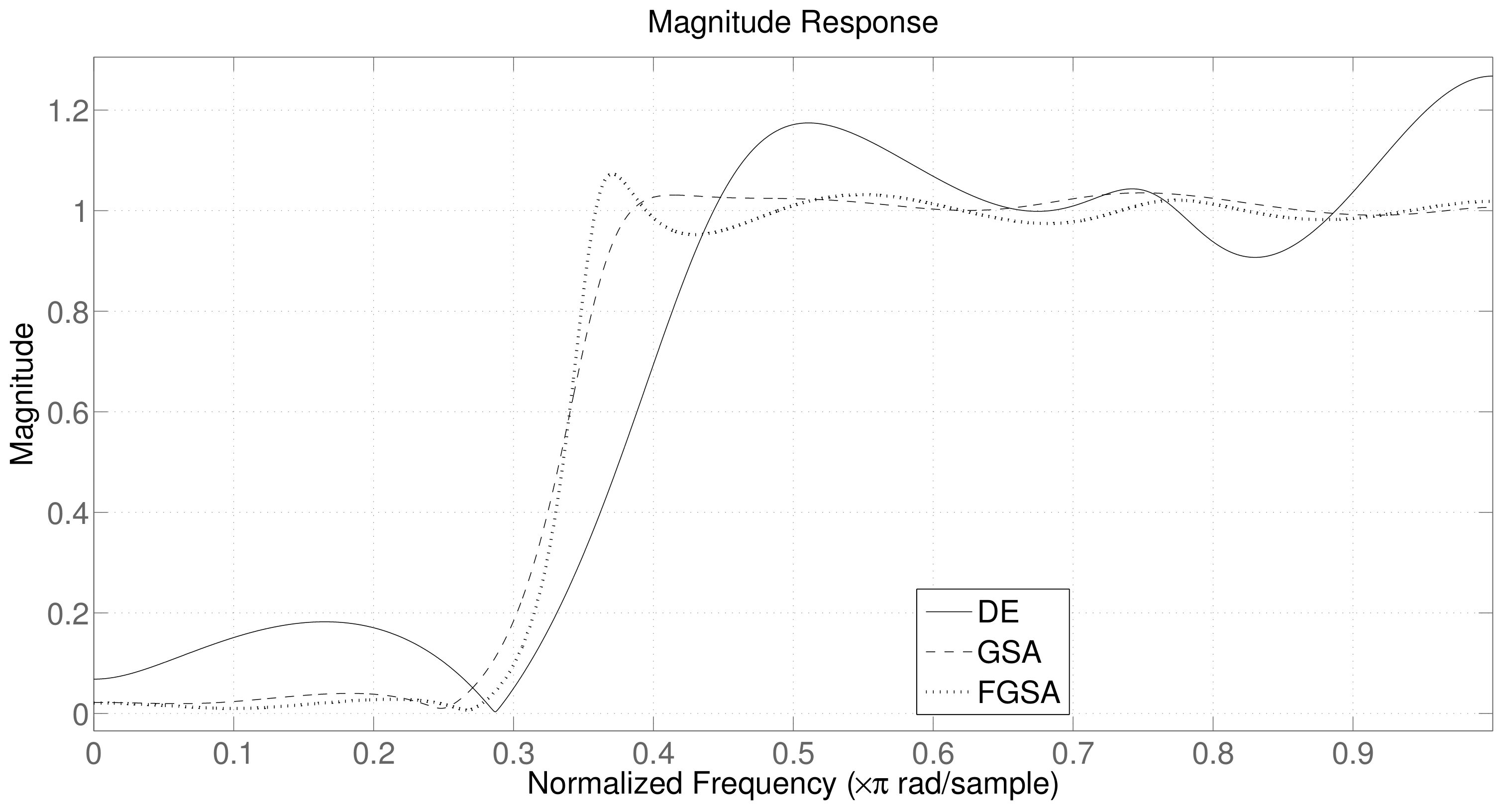
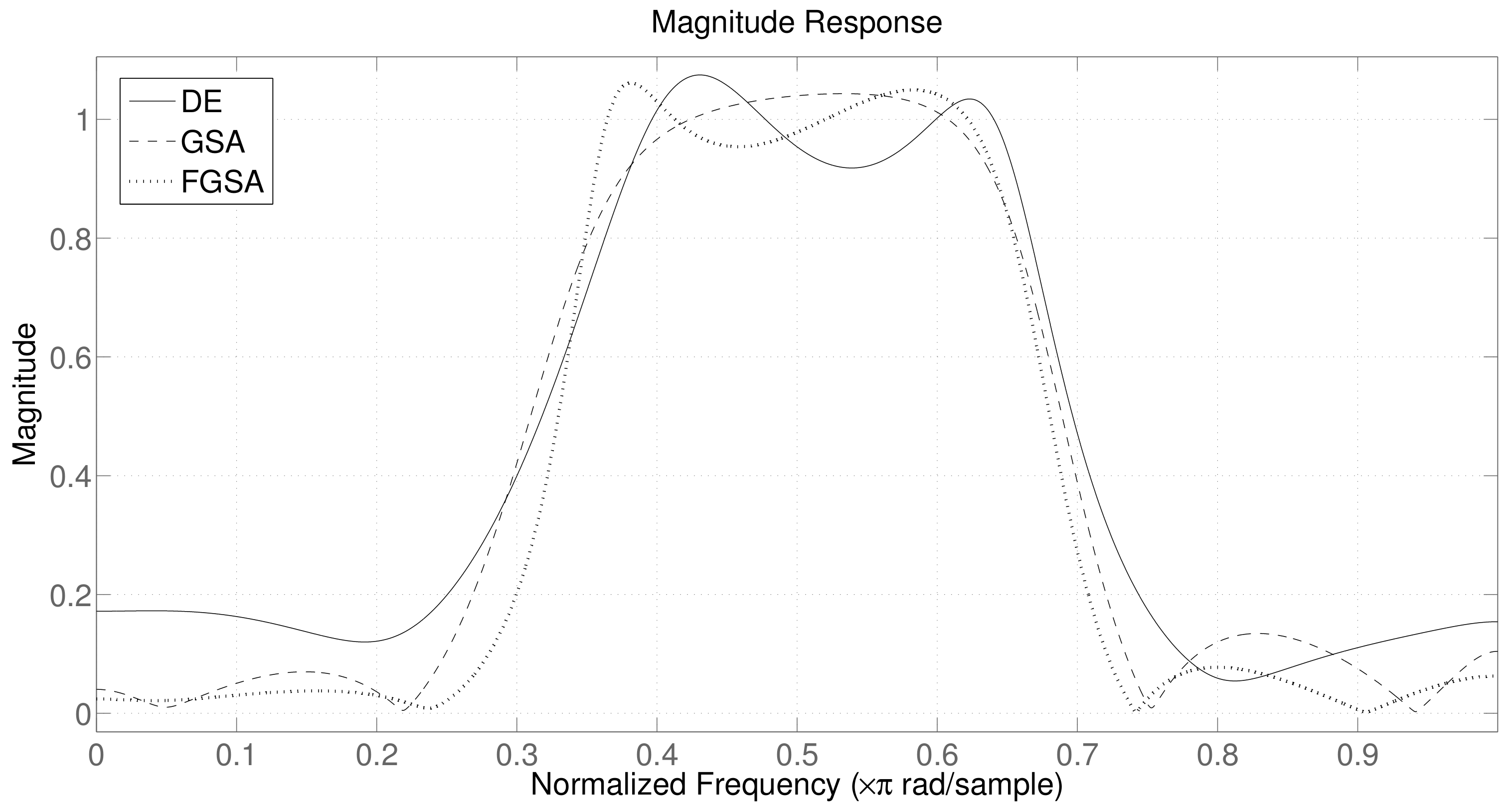
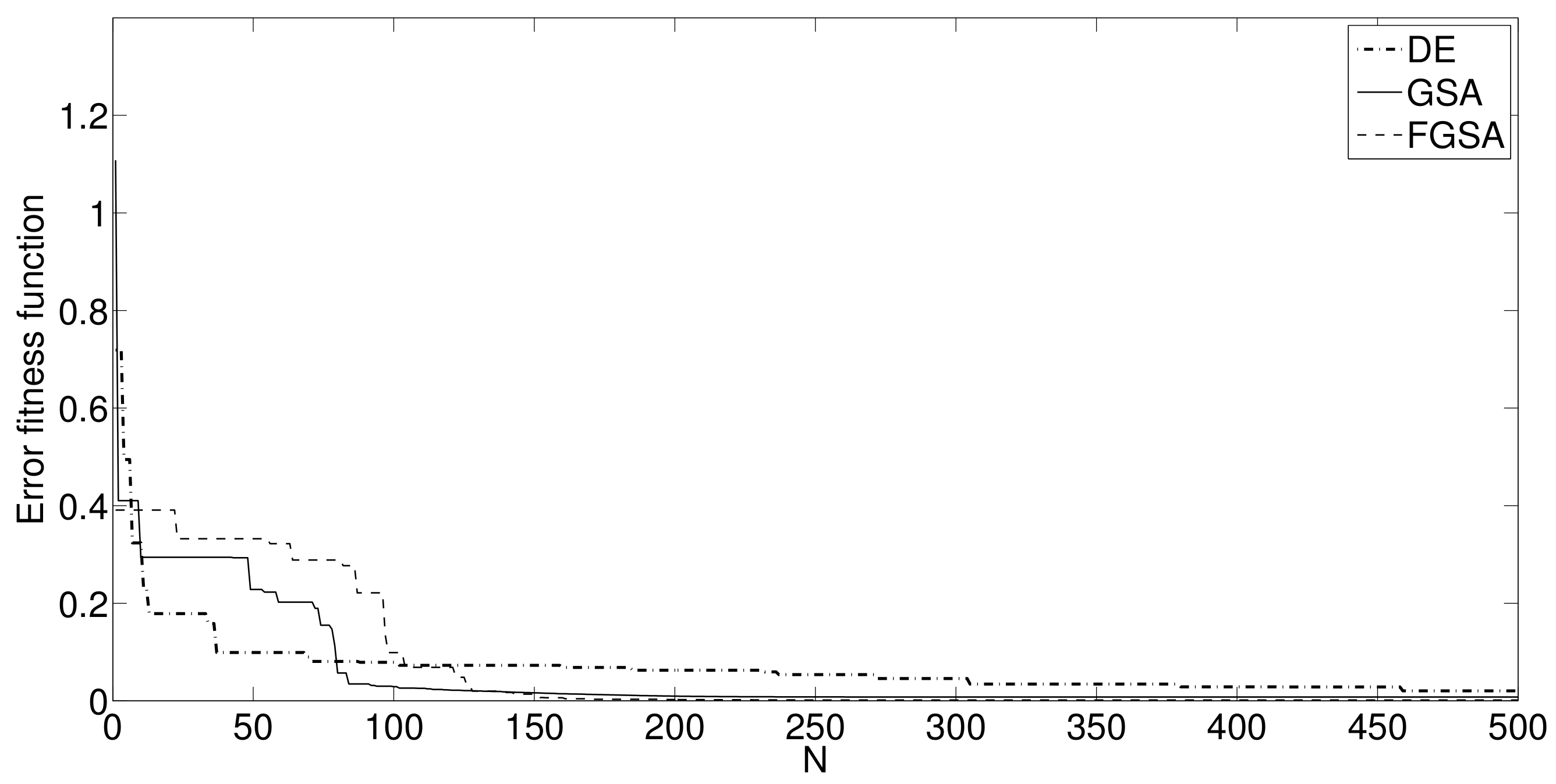
4. Experimental Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Antoniou, A. Digital Signal Processing: Signals, Systems, and Filters; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Lu, W.S.; Antoniou, A. Design of digital filters and filter banks by optimization: A state of the art review. In Proceedings of the 2000 10th European Signal Processing Conference, Tampere, Finland, 4–8 September 2000; Volume 1, pp. 351–354. [Google Scholar]
- Mikhael, R.; Agathoklis, P.; Xiao, C. Design of linear-phase recursive filters by optimization of model reduced non-recursive filters. In Proceedings of the 2003 PACRIM IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Ictoria, BC, Canada, 28–30 August 2003. [Google Scholar]
- Chen, B.S.; Peng, S.C.; Chiou, B.-W. IIR filter design via optimal Hankel–norm approximation. IEE Proc. G Circuits Devices Syst. 1992, 139, 586–590. [Google Scholar] [CrossRef]
- Lu, W.S.; Hinamoto, T. Optimal Design of IIR Frequency-Response-Masking Filters Using Second-Order Cone Programming. IEEE Trans. Circuits Syst. 2003, 50, 1401–1412. [Google Scholar]
- Lu, W.S.; Hinamoto, T. Optimal design of IIR digital filters with robust stability using conic-quadratic-programming. IEEE Trans. Signal Process. 2003, 51, 1581–1592. [Google Scholar]
- Lai, X.; Lin, Z. Minimax Phase Error Design of IIR Digital Filters With Prescribed Magnitude and Phase Responses. IEEE Trans. Signal Process. 2012, 60, 980–986. [Google Scholar] [CrossRef]
- Nongpiur, R.C.; Shpak, D.J.; Antoniou, A. Design of IIR Digital Differentiators Using Constrained Optimization. IEEE Trans. Signal Process. 2014, 62, 1729–1739. [Google Scholar] [CrossRef]
- Lai, X.; Lin, Z. Iterative Reweighted Minimax Phase Error Designs of IIR Digital Filters With Nearly Linear Phases. IEEE Trans. Signal Process. 2016, 64, 2416–2428. [Google Scholar] [CrossRef]
- Lang, M.C. Least-squares design of IIR filters with prescribed magnitude and phase responses and a pole radius constraint. IEEE Trans. Signal Process. 2000, 48, 3109–3121. [Google Scholar] [CrossRef]
- Duarte, C.; Barner, K.E.; Goossen, K. Design of IIR Multi-Notch Filters Based on Polynomially-Represented Squared Frequency Response. IEEE Trans. Signal Process. 2016, 64, 2613–2623. [Google Scholar] [CrossRef]
- Pei, S.C.; Shyu, J.J.; Huang, Y.D.; Chan, C.H. Improved Methods for the Design of Variable Fractional-Delay IIR Digital Filters. IEEE Trans. Circuits Syst. 2012, 59, 989–1000. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Storn, R. Differential evolution design of an IIR-filter with requirements for magnitude and group delay. In Proceedings of the IEEE International Conference on Evolutionary Computation (ICEC), Nagoya, Japan, 20–22 May 1996; pp. 268–273. [Google Scholar]
- Storn, R. Designing nonstandard filters with differential evolution. IEEE Signal Process. Mag. 2005, 22, 103–106. [Google Scholar] [CrossRef]
- Pan, S.T. Evolutionary Computation on Programmable Robust IIR Filter Pole-Placement Design. IEEE Trans. Instrum. Meas. 2011, 60, 1469–1479. [Google Scholar] [CrossRef]
- Karaboga, N. Digital IIR Filter Design Using Differential Evolution Algorithm. EURASIP J. Appl. Signal Process. 2005, 8, 1269–1276. [Google Scholar] [CrossRef]
- Dai, C.; Chen, W.; Zhu, Y. Seeker Optimization Algorithm for Digital IIR Filter Design. IEEE Trans. Ind. Electron. 2010, 57, 1710–1718. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Hartmann, A.; Lemos, J.M.; Costa, R.S.; Vinga, S. Identifying IIR filter coefficients using particle swarm optimization with application to reconstruction of missing cardiovascular signals. Eng. Appl. Artif. Intell. 2014, 34, 193–198. [Google Scholar] [CrossRef]
- Aimi, H.; Suyama, K. Multi-Constrained IIR Filter Design Using PSO. In Proceedings of the International Symposium on Electronics and Smart Devices, Bandung, Indonesia, 29–30 November 2016; pp. 258–263. [Google Scholar]
- Wang, Y.; Li, B.; Chen, Y. Digital IIR filter design using multi-objective optimization evolutionary algorithm. Appl. Soft Comput. 2011, 12, 1851–1857. [Google Scholar] [CrossRef]
- Tsai, J.T.; Chou, J.H. Design of Optimal Digital IIR Filters by Using an Improved Immune Algorithm. IEEE Trans. Signal Process. 2006, 54, 4582–4596. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; Bradford Books; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Zhang, G.X.; Jin, W.D.; Jin, F. Multi-criterion satisfactory optimization method for designing IIR digital filters. In Proceedings of the ICCT 2003 International Conference on Communication Technology, Beijing, China, 9–11 April 2003; pp. 1484–1490. [Google Scholar]
- Liu, Y.; Shao, S.Q.; Zhao, H.; Liao, X.F.; Yu, J.B. An application of genetic algorithms with guiding strategy in the design of digital filters. In Proceedings of the Communications, Circuits and Systems, Chengdu, China, 27–29 June 2004; pp. 1141–1145. [Google Scholar]
- Chang, W.-D. Coefficient estimation of IIR filter by a multiple crossover genetic algorithm. Comput. Math. Appl. 2006, 51, 1437–1444. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, X. Cooperative Coevolutionary Genetic Algorithm for Digital IIR Filter Design. IEEE Trans. Ind. Electron. 2007, 54, 1311–1318. [Google Scholar] [CrossRef]
- Pan, S.T. Design of Robust D-Stable IIR Filters Using Genetic Algorithms With Embedded Stability Criterion. IEEE Trans. Signal Process. 2009, 57, 3008–3016. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Saha, S.K.; Kar, R.; Mandal, D.; Ghoshal, S.P. Gravitation search algorithm: Application to the optimal IIR filter design. J. King Saud Univ. Eng. Sci. 2014, 26, 69–81. [Google Scholar] [CrossRef]
- Saha, S.K.; Kar, R.; Mandal, D.; Ghoshal, S.P. Optimal IIR filter design using Gravitational Search Algorithm with Wavelet Mutation. J. King Saud Univ. Comput. Inf. Sci. 2015, 27, 25–39. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Petriu, E.M.; Preitl, S.; Radac, M.B. Fuzzy logic-based adaptive gravitational search algorithm for optimal tuning of fuzzy controlled servo systems. IET Control Theory Appl. 2013, 7, 99–107. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Petriu, E.M.; Preitl, S.; Radac, M.B. Adaptive GSA-based optimal tuning of PI controlled servo systems with reduced process parametric sensitivity, robust stability and controller robustness. IEEE Trans. Cybern. 2014, 44, 1997–2009. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, B.; Valdez, F.; Melin, P.; Prado-Arechiga, G. Fuzzy logic in the gravitational search algorithm enhanced using fuzzy logic with dynamic alpha parameter value adaptation for the optimization of modular neural networks in echocardiogram recognition. Appl. Soft Comput. 2015, 37, 245–254. [Google Scholar] [CrossRef]
- Gonzalez, B.; Valdez, F.; Melin, P.; Prado-Arechiga, G. Fuzzy logic in the gravitational search algorithm for the optimization of modular neural networks in pattern recognition. Exp. Syst. Appl. 2015, 42, 5839–5847. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L. Revised gravitational search algorithms based on evolutionary-fuzzy systems. Algorithms 2017, 10, 44. [Google Scholar] [CrossRef]
- Olivas, F.; Valdez, F.; Ostillo, O. Gravitational Search Algorithm with parameter adaptation through a fuzzy logic system. In Nature-Inspired Design of Hybrid Intelligent Systems; Studies in Computational Intelligence; Springer: New York, NY, USA, 2016; Volume 667, pp. 391–405. [Google Scholar]
- Gonzalez, B.; Valdez, F.; Melin, P. A Gravitational Search Algorithm Using Type-2 Fuzzy Logic for Parameter Adaptation. In Nature-Inspired Design of Hybrid Intelligent Systems; Studies in Computational Intelligence; Springer: New York, NY, USA, 2016; Volume 667, pp. 127–138. [Google Scholar]
- Askari, H.; Zahiri, S.H. Data Classification Using Fuzzy-GSA. In Proceedings of the International Conference on Computer and Knowledge Engineering, Mashhad, Iran, 13–14 October 2011; pp. 6–11. [Google Scholar]
- Zahiri, S.H. Fuzzy gravitational search algorithm an approach for data mining. Iran. J. Fuzzy Syst. 2012, 9, 21–37. [Google Scholar]
- Sombra, A.; Valdez, F.; Melin, P.; Castillo, O. A new gravitational search algorithm using fuzzy logic to parameter adaptation. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1068–1074. [Google Scholar]
- Khabisi, F.S.; Rashedi, E. Fuzzy gravitational search algorithm. In Proceedings of the International E-Conference on Computer and Knowledge Engineering, Mashhad, Iran, 18–19 October 2012; pp. 156–160. [Google Scholar]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Karaboga, N.; Cetinkaya, B. Design of minimum phase digital IIR filters by using genetic algorithm. In Proceedings of the 2004 NORSIG 6th Nordic IEEE 6th Nordic Signal Processing Symposium, Espoo, Finland, 9–11 June 2004; pp. 29–32. [Google Scholar]
- Luitel, B.; Venayagamoorthy, G.K. Particle swarm optimization with quantum infusion for the design of digital filters. In Proceedings of the IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008; pp. 1–8. [Google Scholar]
- Luitel, B.; Venayagamoorthy, G.K. Differential evolution particle swarm optimization for digital filter design. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 3954–3961. [Google Scholar]
- Dumitrescu, B.; Niemisto, R. Multistage IIR filter design using convex stability domains defined by positive realness. IEEE Trans. Signal Process. 2004, 52, 962–974. [Google Scholar] [CrossRef]
- Tseng, C.; Lee, S. Minimax design of stable IIR digital filter with prescribed magnitude and phase responses. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 547–551. [Google Scholar] [CrossRef]
- Jiang, A.; Kwan, H.K. IIR digital filter design with new stability constraint based on argument principle. IEEE Trans. Circuits Syst. 2009, 56, 583–593. [Google Scholar] [CrossRef]
- Azizipanah-Abarghooee, R.; Terzija, V.; Golestaneh, F. Multiobjective Dynamic Optimal Power Flow Considering Fuzzy-Based Smart Utilization of Mobile Electric Vehicles. IEEE Trans. Ind. Inform. 2016, 12, 503–514. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy logic to approximate reasoning using linguistic synthesis. IEEE Trans. Comput. 1977, 26, 1182–1191. [Google Scholar] [CrossRef]
- Precup, R.-E.; David, R.-C.; Petriu, E.M.; Radac, M.-B.; Preitl, S.; Fodor, J. Evolutionary optimization-based tuning of low-cost fuzzy controllers for servo systems. Knowl. Based Syst. 2013, 38, 74–84. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Abraham, A. Neural Network and Fuzzy System for the tuning of Gravitational Search Algorithm parameters. Exp. Syst. Appl. 2018. [Google Scholar] [CrossRef]
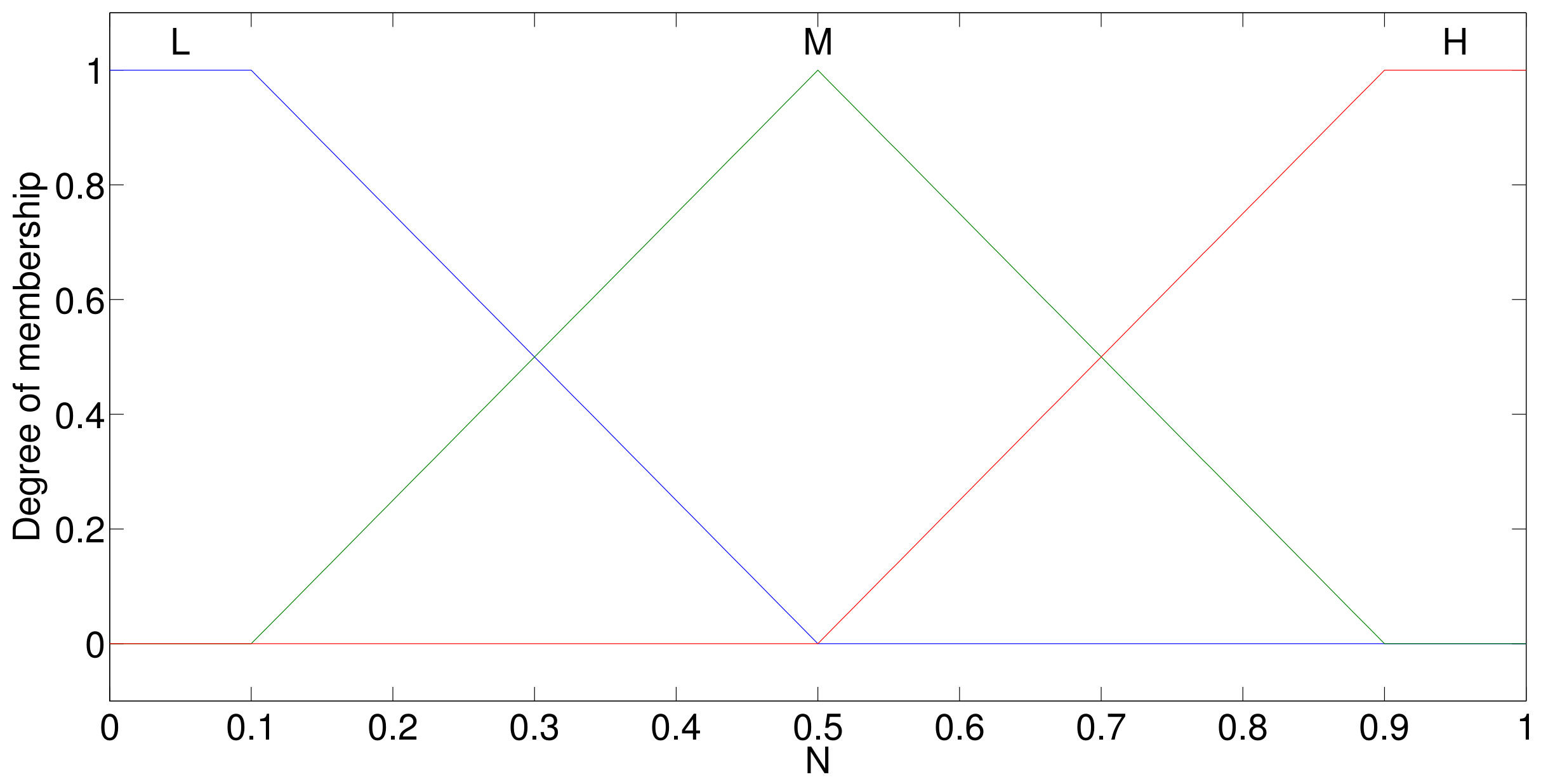

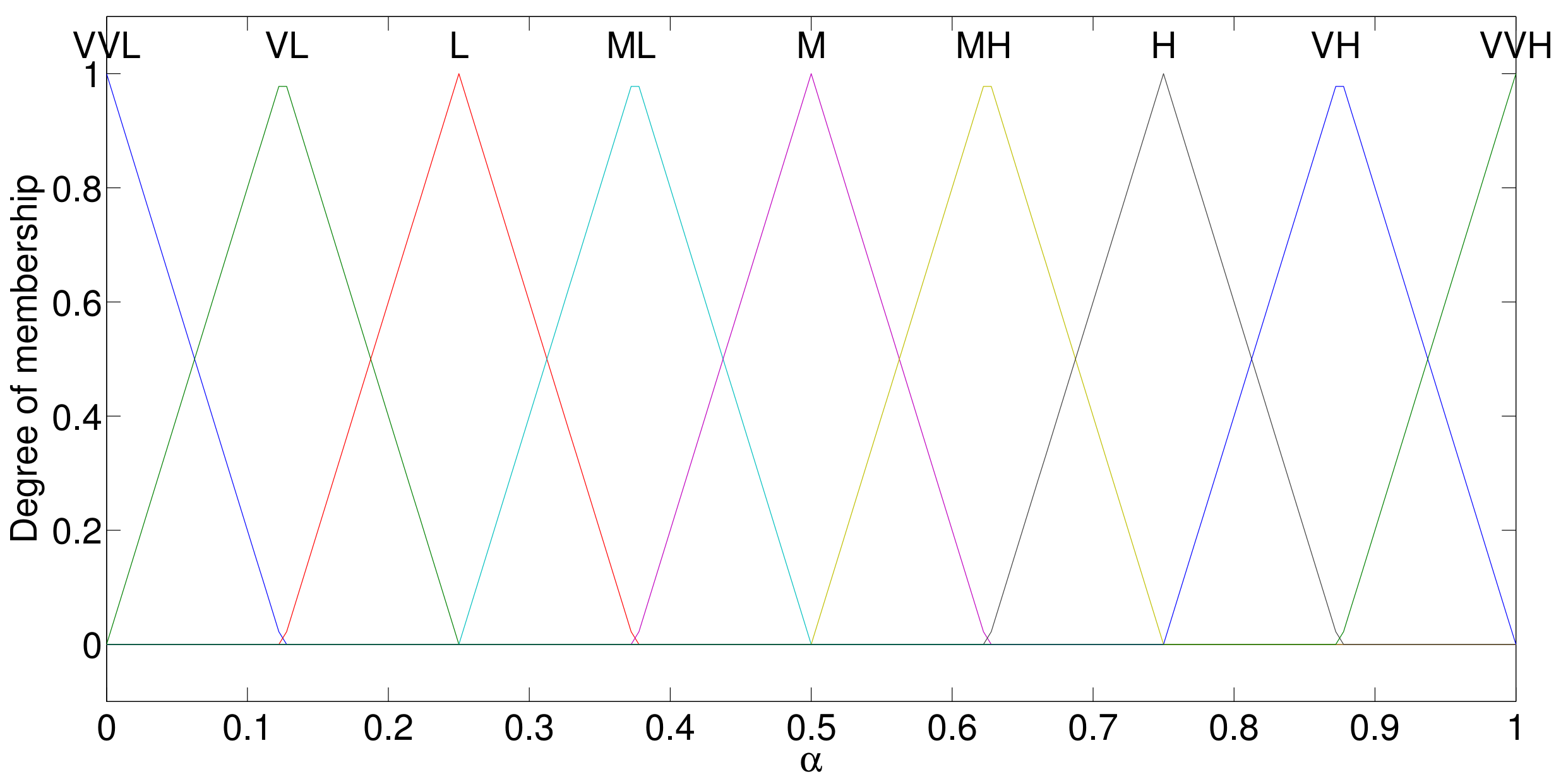


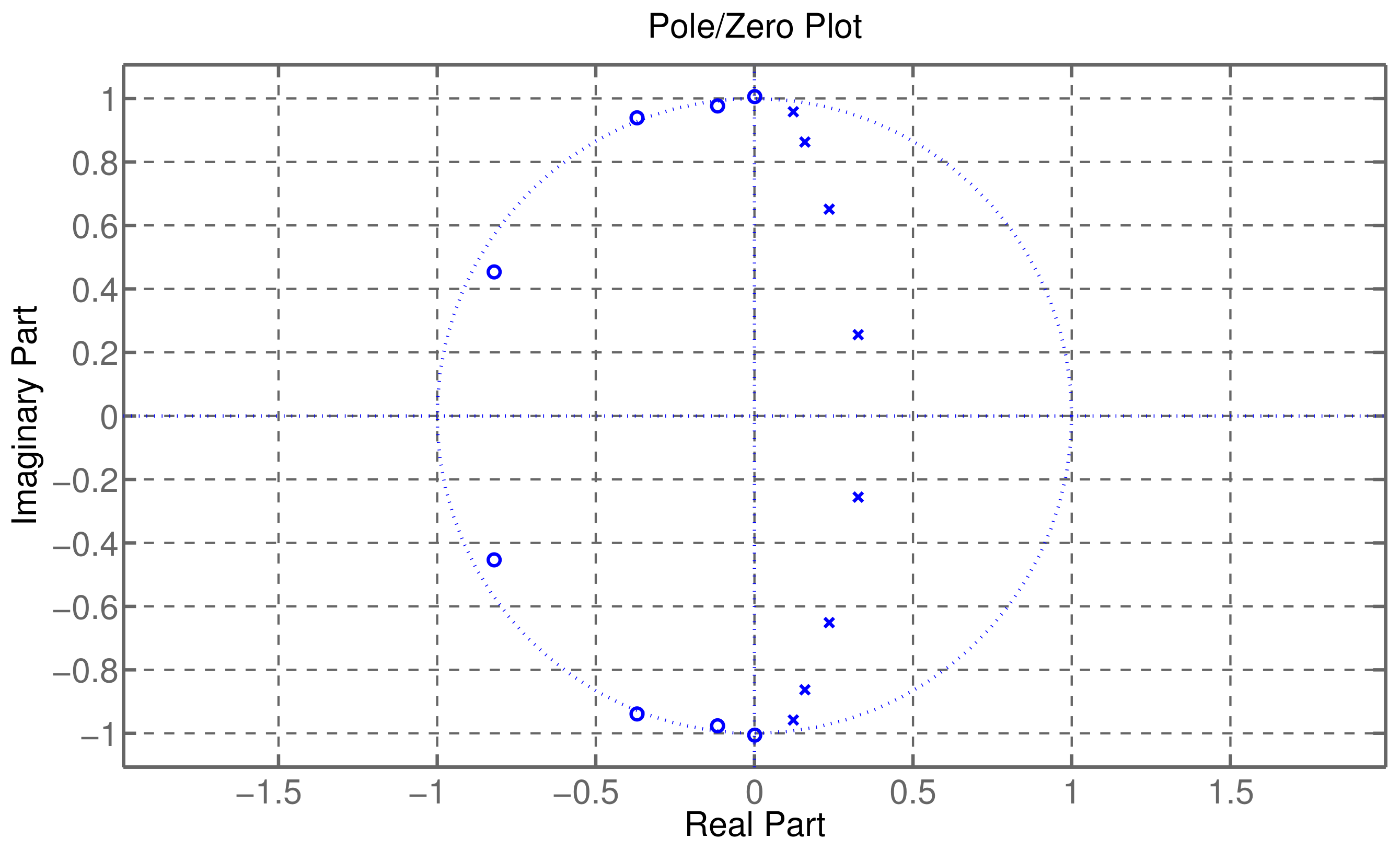
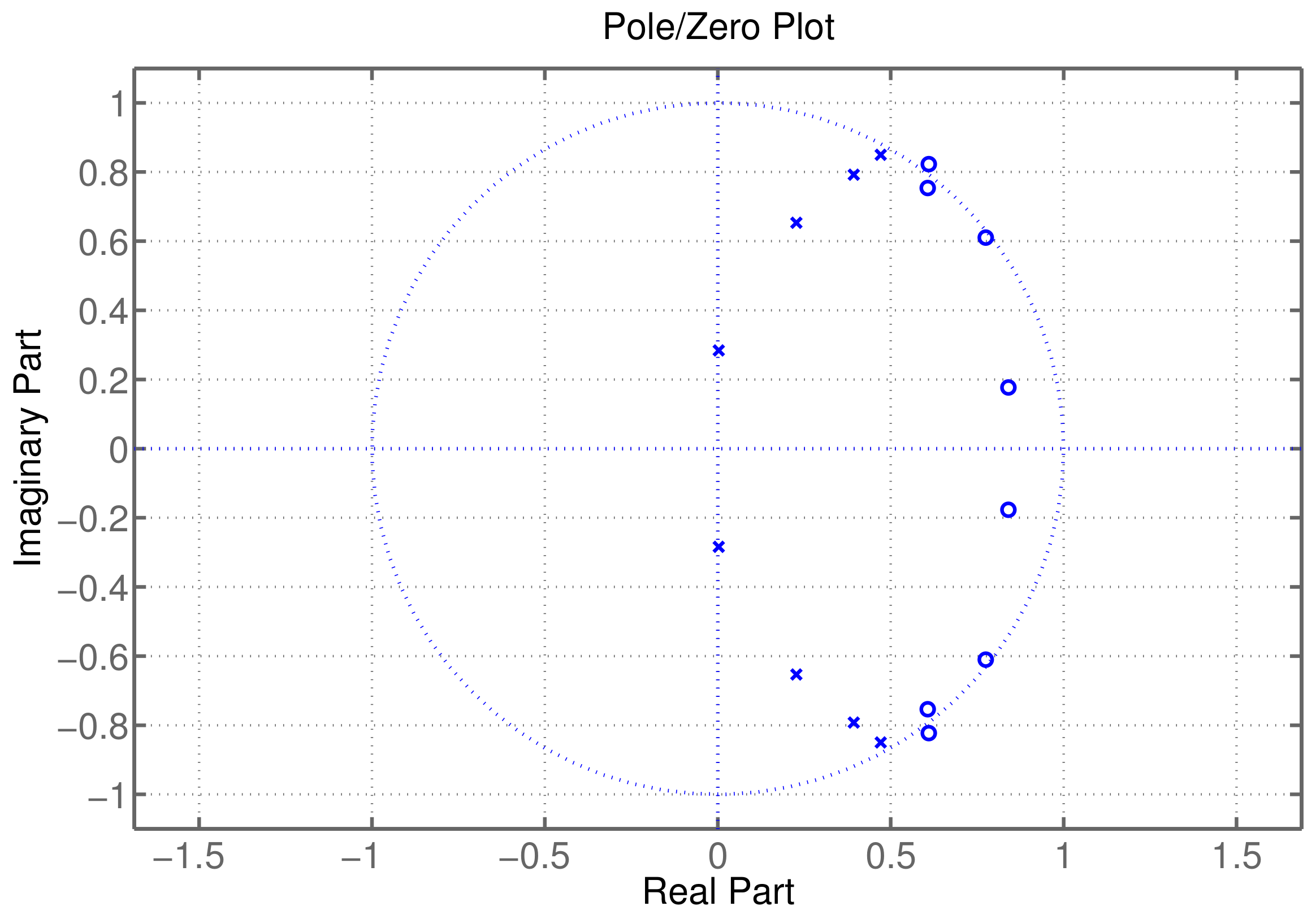
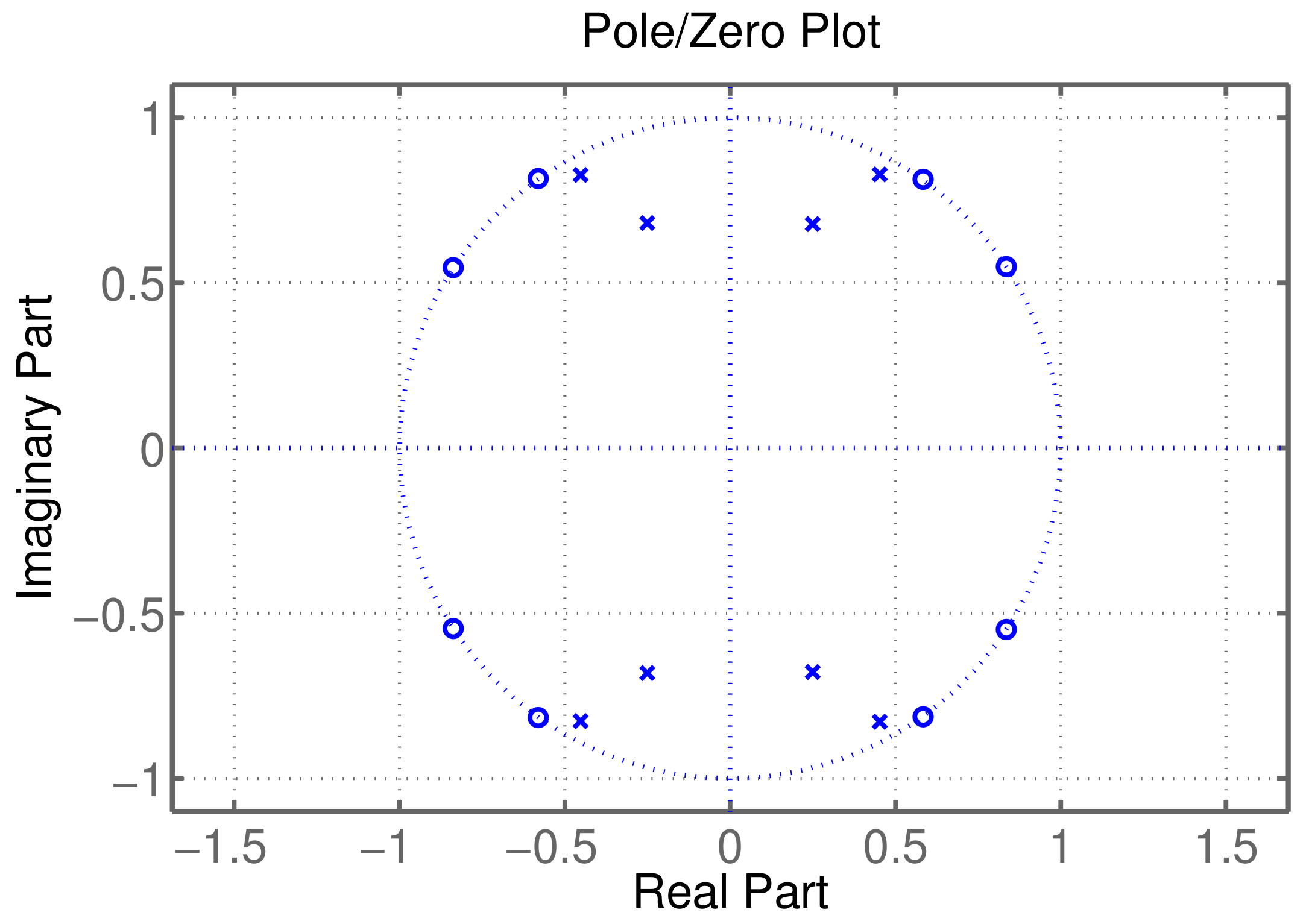
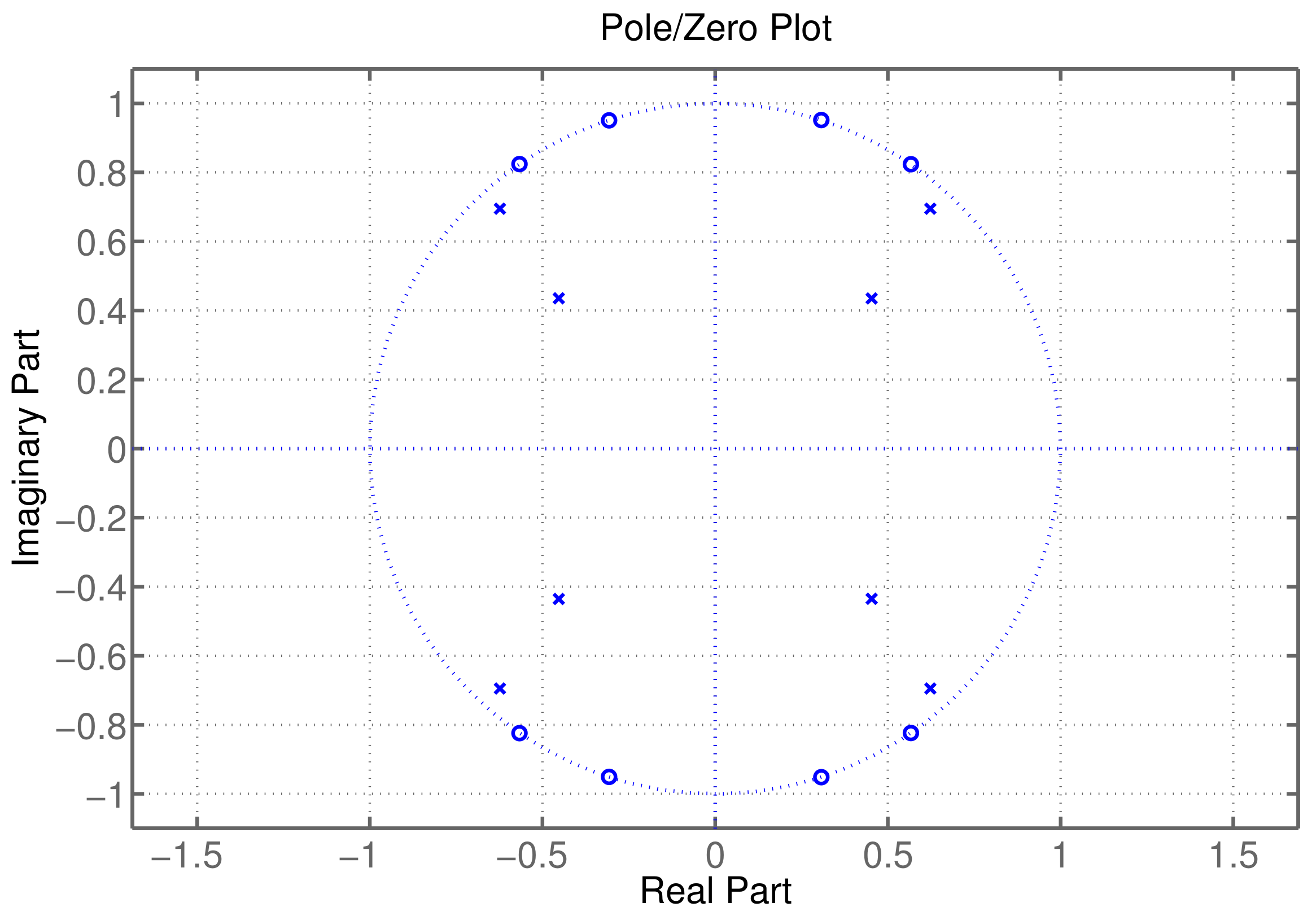
| N | ||
|---|---|---|
| L | L | L |
| L | M | VL |
| L | H | VVL |
| M | L | MH |
| M | M | M |
| M | H | ML |
| H | L | VVH |
| H | M | VH |
| H | H | H |
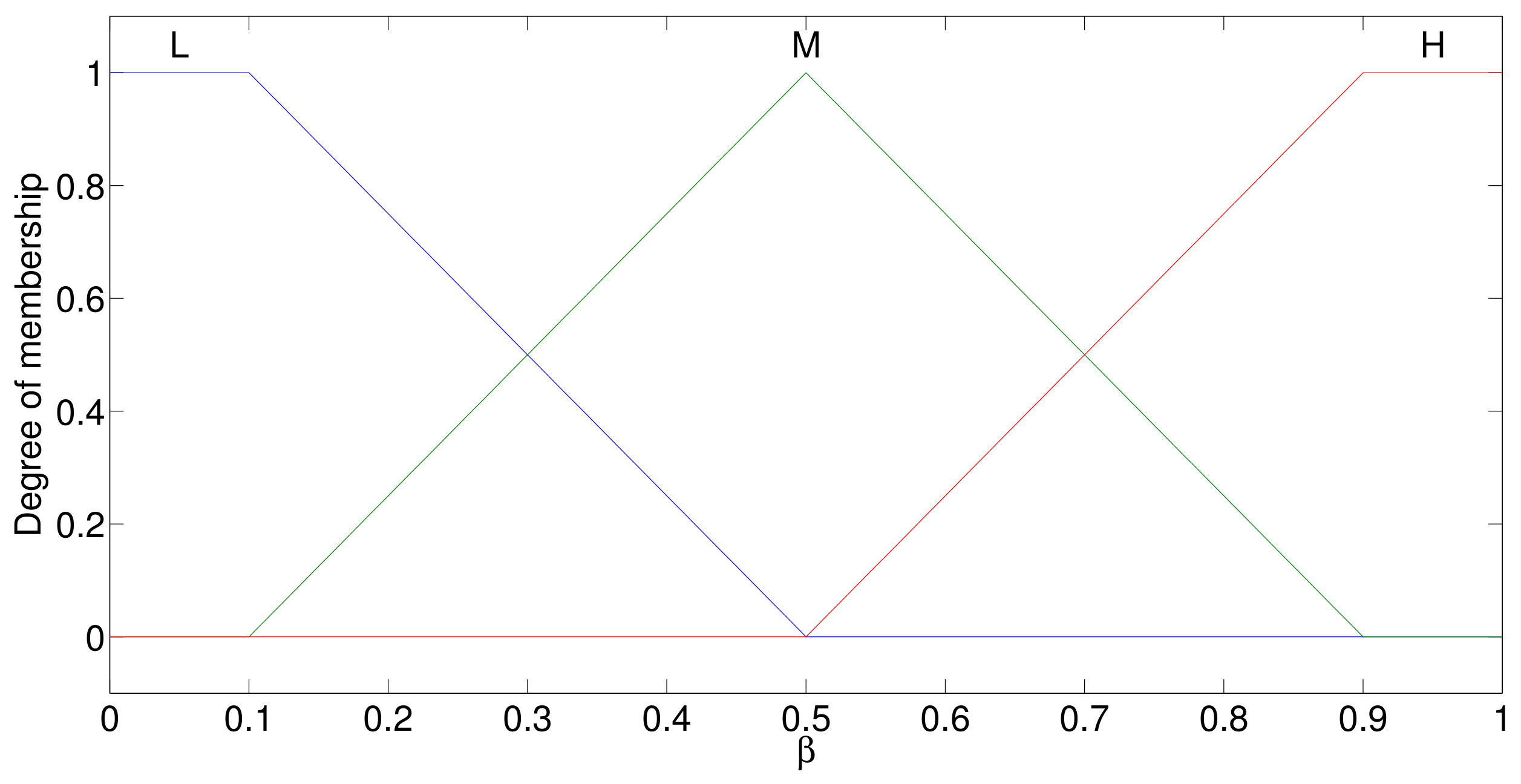
| N | |
|---|---|
| L | H |
| M | M |
| H | L |
| Filter | w | ||||
|---|---|---|---|---|---|
| LP | 0.01 | 0.001 | 0.45 | 0.50 | - |
| HP | 0.01 | 0.001 | 0.35 | 0.30 | - |
| BP | 0.01 | 0.001 | 0.35 and 0.65 | 0.3 and 0.7 | 0.3 |
| SB | 0.01 | 0.001 | 0.25 and 0.55 | 0.3 and 0.7 | 0.4 |
| Algorithm | PB-Ripple | SB-Ripple | tb |
|---|---|---|---|
| Differential Evolution (DE) | 0.209371 | 0.174627 | 0.430534 |
| 0.092159 | 0.100366 | 0.188224 | |
| Gravitational Search Algorithm (GSA) | 0.067816 | 0.066199 | 0.120964 |
| 0.016867 | 0.016857 | 0.029634 | |
| Fuzzy Gravitational Search Algorithm (FGSA) | 0.065990 | 0.061591 | 0.101172 |
| 0.022298 | 0.017547 | 0.027451 |
| Algorithm | PB-Ripple | SB-Ripple | tb |
|---|---|---|---|
| Differential Evolution | 0.301758 | 0.136288 | 0.401888 |
| 0.154653 | 0.087169 | 0.155471 | |
| Gravitational Search Algorithm | 0.047248 | 0.057344 | 0.195117 |
| 0.016758 | 0.010286 | 0.098803 | |
| Fuzzy Gravitational Search Algorithm | 0.067245 | 0.058384 | 0.217318 |
| 0.030699 | 0.011865 | 0.073569 |
| Algorithm | PB-Ripple | SB-Ripple | tb |
|---|---|---|---|
| Differential Evolution | 0.158257 | 0.463677 | 0.014583 |
| 0.096243 | 0.489097 | 0.413012 | |
| Gravitational Search Algorithm | 0.067377 | 0.080152 | 0.127604 |
| 0.024833 | 0.015516 | 0.041768 | |
| Fuzzy Gravitational Search Algorithm | 0.070821 | 0.076286 | 0.131966 |
| 0.017908 | 0.017812 | 0.061376 |
| Algorithm | PB-Ripple | SB-Ripple | tb |
|---|---|---|---|
| Differential Evolution | 0.254731 | 0.077870 | 0.248177 |
| 0.127932 | 0.041679 | 0.136460 | |
| Gravitational Search Algorithm | 0.078905 | 0.074704 | 0.117773 |
| 0.022983 | 0.014319 | 0.028508 | |
| Fuzzy Gravitational Search Algorithm | 0.066908 | 0.083628 | 0.111458 |
| 0.023753 | 0.026077 | 0.034889 |
| Algorithm | ||||
|---|---|---|---|---|
| Differential Evolution | 0.016140 | 0.017622 | 0.021384 | 0.029527 |
| 0.004195 | 0.005027 | 0.003965 | 0.004395 | |
| Gravitational Search Algorithm | 0.006185 | 0.004209 | 0.011853 | 0.010370 |
| 0.004130 | 0.003159 | 0.006739 | 0.004559 | |
| Fuzzy Gravitational Search Algorithm | 0.004364 | 0.006941 | 0.010368 | 0.011207 |
| 0.004154 | 0.005924 | 0.006368 | 0.008748 |
| Algorithm | ||||
|---|---|---|---|---|
| Differential Evolution | 0.6900 | 0.6460 | 0.9900 | 0.8660 |
| Gravitational Search Algorithm | 0.4840 | 0.5640 | 0.5200 | 0.6360 |
| Fuzzy Gravitational Search Algorithm | 0.4560 | 0.5080 | 0.5580 | 0.6440 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelusi, D.; Mascella, R.; Tallini, L. A Fuzzy Gravitational Search Algorithm to Design Optimal IIR Filters. Energies 2018, 11, 736. https://doi.org/10.3390/en11040736
Pelusi D, Mascella R, Tallini L. A Fuzzy Gravitational Search Algorithm to Design Optimal IIR Filters. Energies. 2018; 11(4):736. https://doi.org/10.3390/en11040736
Chicago/Turabian StylePelusi, Danilo, Raffaele Mascella, and Luca Tallini. 2018. "A Fuzzy Gravitational Search Algorithm to Design Optimal IIR Filters" Energies 11, no. 4: 736. https://doi.org/10.3390/en11040736




